Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting
Abstract
1. Introduction
2. Methodology
2.1. Framework for NCPI Inversion Model
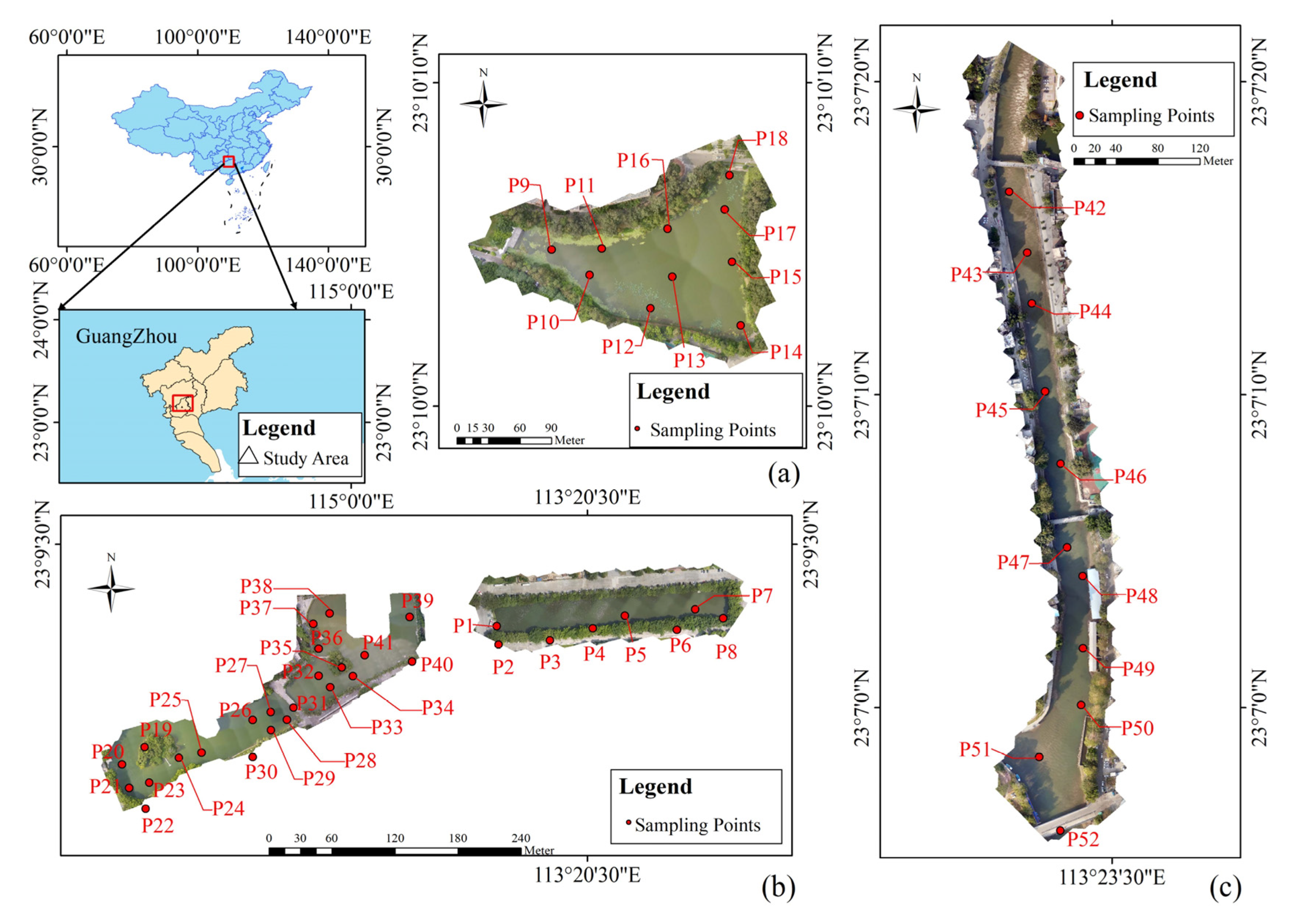
2.2. Study Area
2.3. In Situ Data Collection
2.4. Airborn Multispectral Imagery Preprocessing
2.5. Spectral Data Preprocessing
2.6. Modeling Approaches
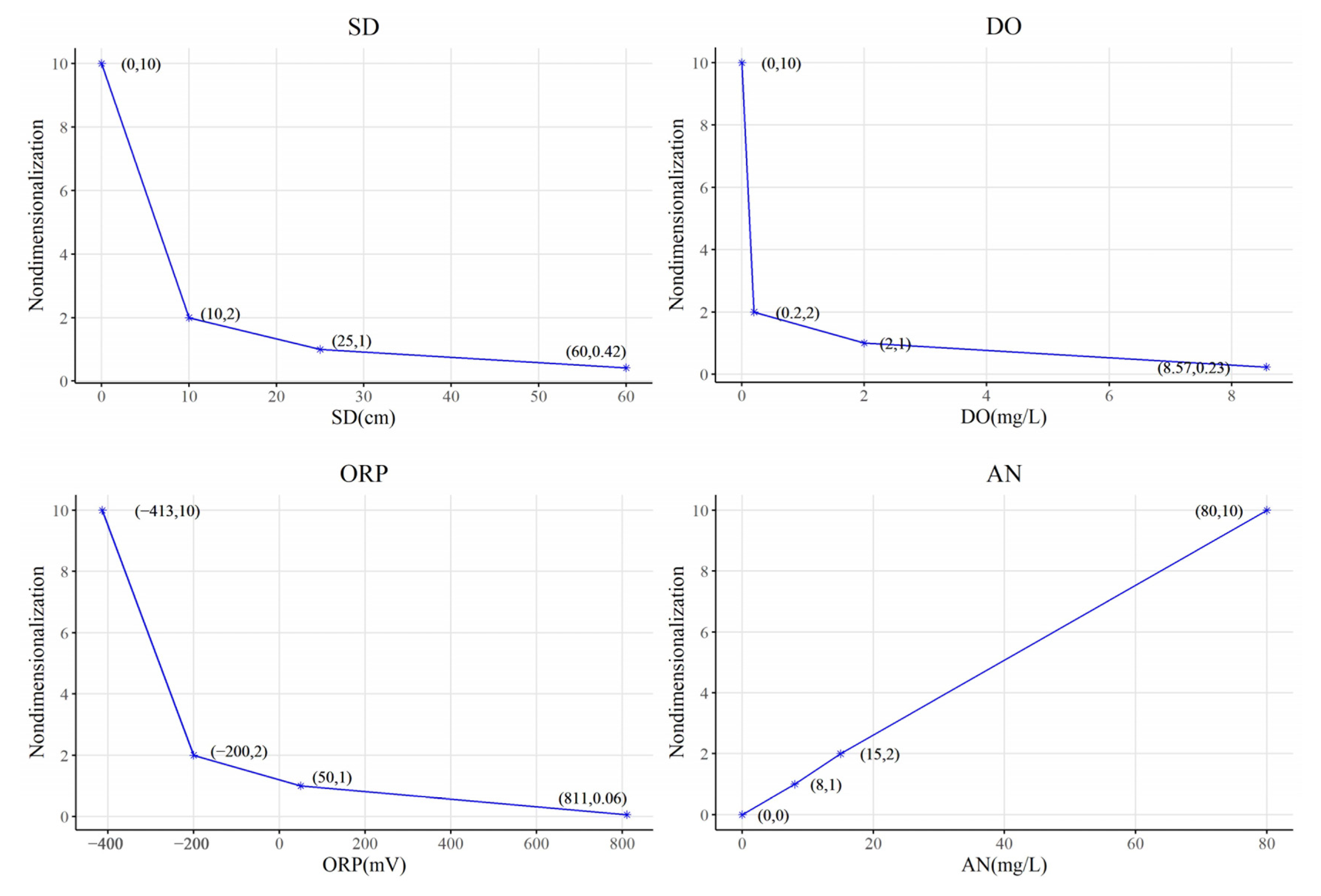
2.6.1. Nemerow Comprehensive Pollution Index
2.6.2. Extreme Gradient Boosting Regression and Other Models
2.6.3. Model Evaluation
3. Results
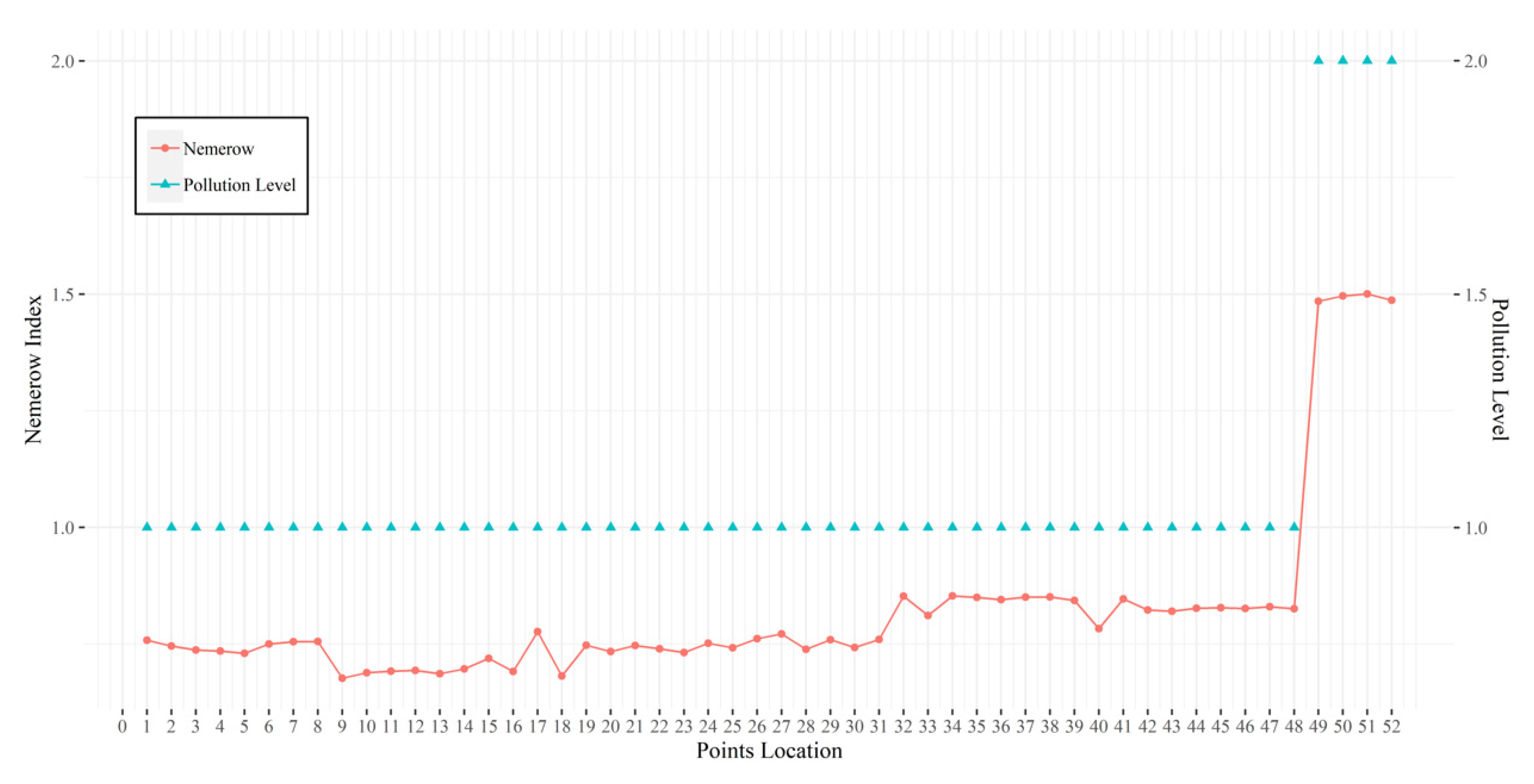
3.1. In Situ Data Analysis
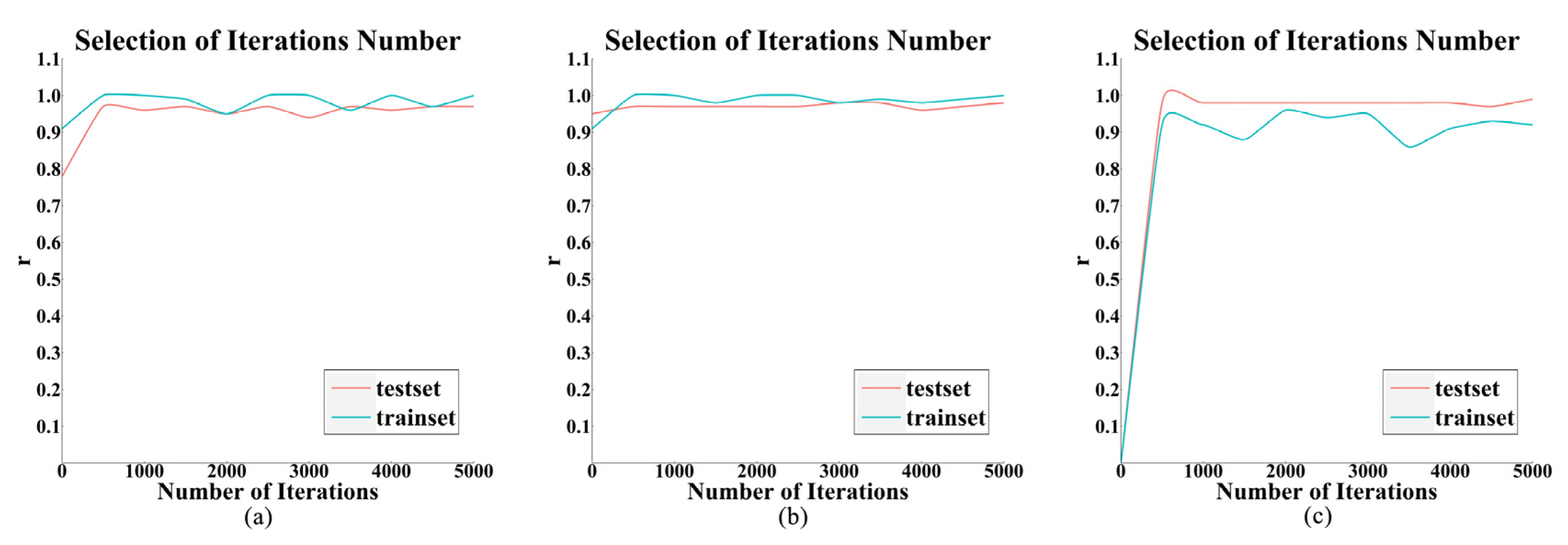
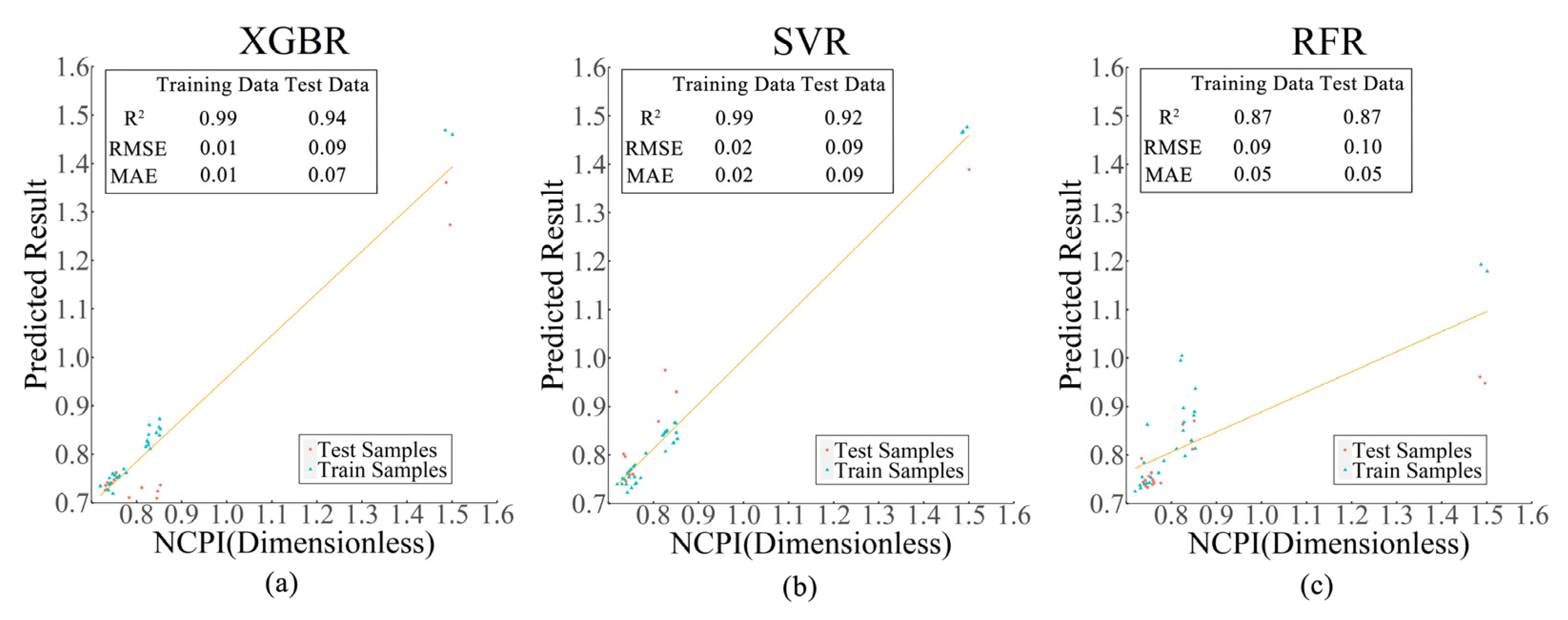
3.2. Model Optimization and Accuracy Evaluation
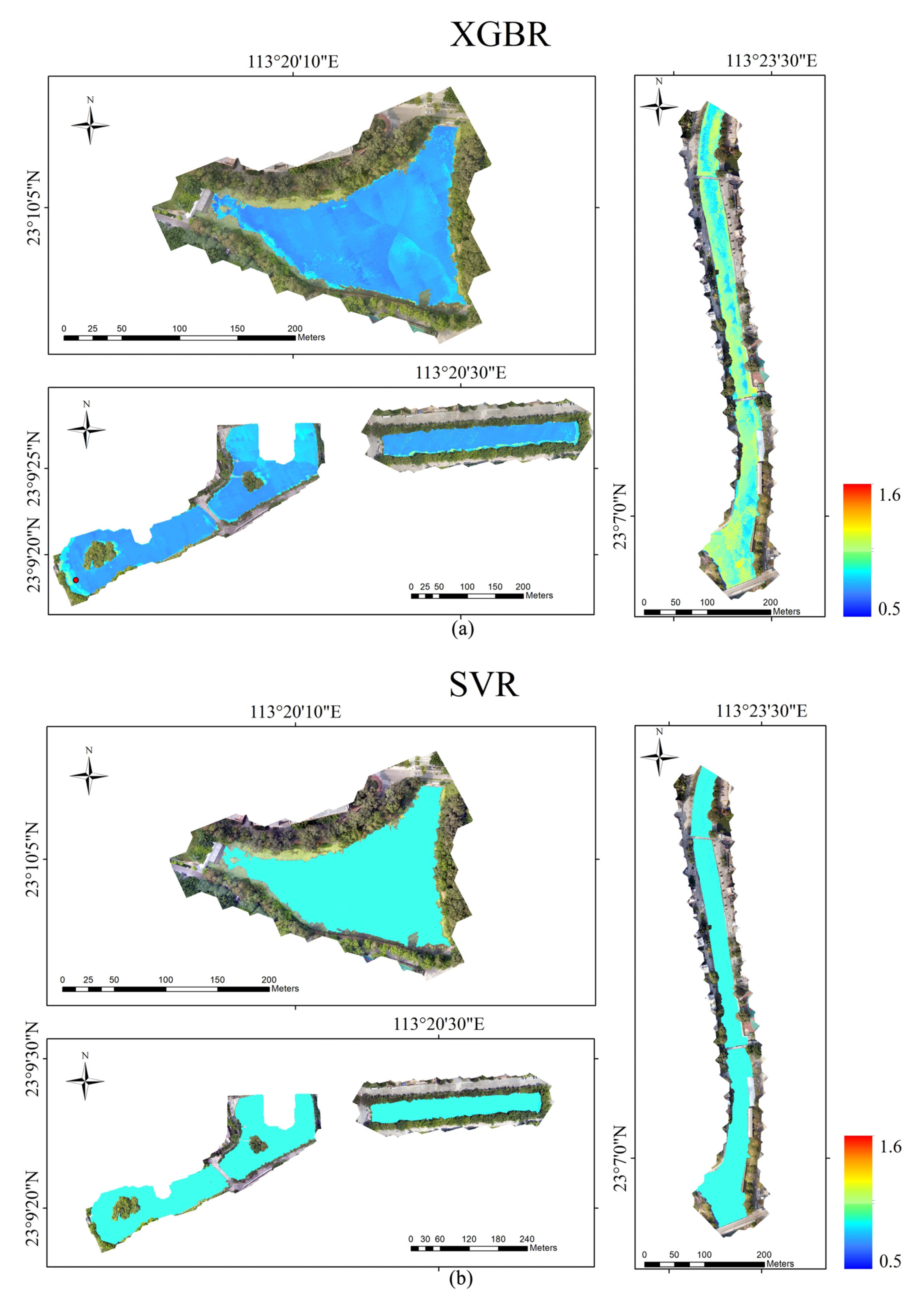
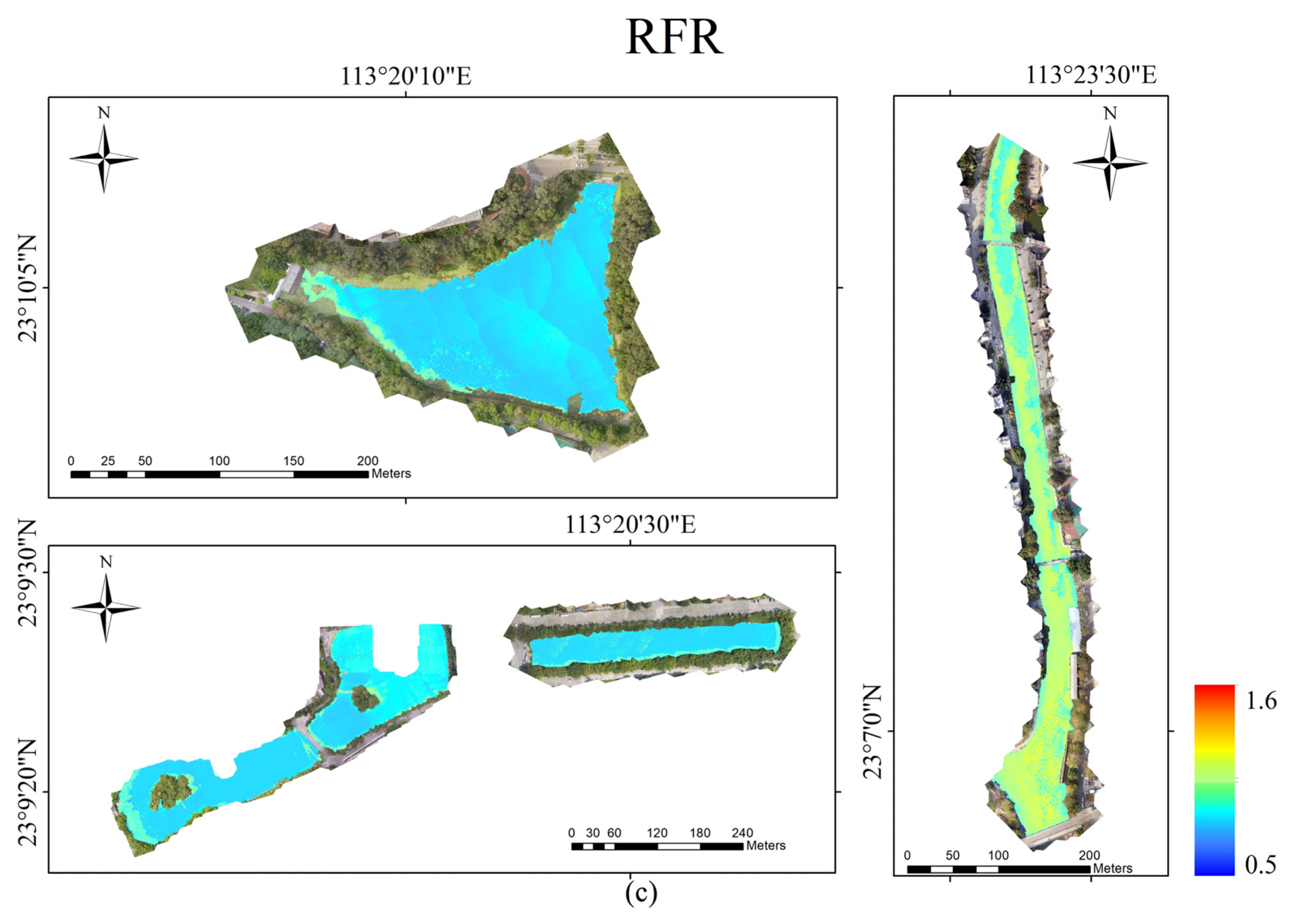
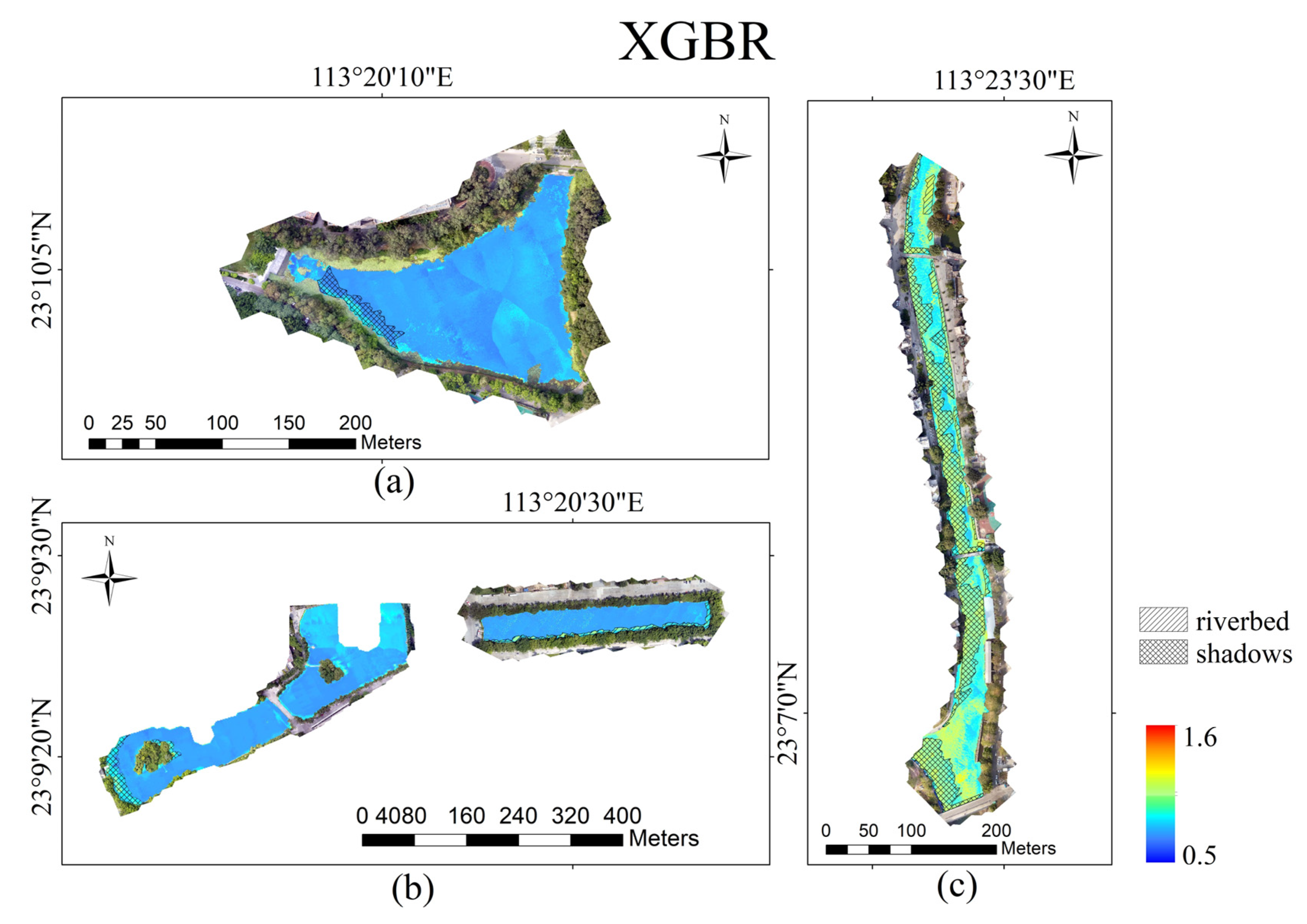
3.3. UAV-Borne Image Inversion Based on Three Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Liu, X.D.; Lu, J. Urban River Pollution Control and Remediation. Procedia Environ. Sci. 2012, 13, 1856–1862. [Google Scholar] [CrossRef]
- Fan, K.; Jia, J.; Sun, P.; Liang, H. Pollution control of urban black-odor water bodies. Ecol. Econ. 2017, 13, 344–350. [Google Scholar]
- Hashim, S.; Xie, Y.B.; Hashim, I.; Ahmad, I. Urban River Pollution Control Based on Bacterial Technology. Appl. Mech. Mater. 2014, 692, 127–132. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H. Water pollution during China’s industrial transition. Environ. Dev. 2013, 8, 57–73. [Google Scholar] [CrossRef]
- Defu, H.; Ruirui, C.; Enhui, Z.; Na, C.; Bo, Y.; Huahong, S.; Minsheng, H. Toxicity bioassays for water from black-odor rivers in Wenzhou, China. Environ. Sci. Pollut. Res. 2015, 22, 1731–1741. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Shen, Q.; Zhou, Q.; Fan, C.; Shao, S. Precontrol of algae-induced black blooms through sediment dredging at appropriate depth in a typical eutrophic shallow lake. Ecol. Eng. 2015, 77, 139–145. [Google Scholar] [CrossRef]
- Song, C.; Liu, X.; Song, Y.; Liu, R.; Gao, H.; Han, L.; Peng, J. Key blackening and stinking pollutants in Dongsha River of Beijing: Spatial distribution and source identification. J. Environ. Manag. 2017, 200, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Pan, M.; Zhao, J.; Zhen, S.; Heng, S.; Wu, J. Effects of the combination of aeration and biofilm technology on transformation of nitrogen in black-odor river. Water Sci. Technol. 2016, 74, 655–662. [Google Scholar] [CrossRef]
- Peter, A.; Köster, O.; Schildknecht, A.; von Gunten, U. Occurrence of dissolved and particle-bound taste and odor compounds in Swiss lake waters. Water Res. 2009, 43, 2191–2200. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Cheng, K.; Lei, T. Reservoir trophic state evaluation using Landsat TM images. J. Am. Water Resour. Assoc. 2001, 37, 1321–1334. [Google Scholar] [CrossRef]
- Watanabe, F.; Alcântara, E.; Rodrigues, T.; Imai, N.; Barbosa, C.; Rotta, L. Estimation of Chlorophyll-a Concentration and the Trophic State of the Barra Bonita Hydroelectric Reservoir Using OLI/Landsat-8 Images. Int. J. Environ. Res. Public Heal. 2015, 12, 10391–10417. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Ma, R.; Loiselle, S.A.; Shen, Q.; Yin, H.; Zhang, Y. Optical characterization of black water blooms in eutrophic waters. Sci. Total Environ. 2014, 482–483, 174–183. [Google Scholar] [CrossRef]
- Thiemann, S.; Kaufmann, H. Determination of Chlorophyll Content and Trophic State of Lakes Using Field Spectrometer and IRS-1C Satellite Data in the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2000, 73, 227–235. [Google Scholar] [CrossRef]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Han, W.; Zhao, Q.; Jin, Y.; Yuan, L.; Luo, W. Black and Odorous Water Body Recognition Based on GF-2 Image. Spacecr. Recovery Remote Sens. 2022, 43, 120–128. [Google Scholar]
- Yao, J.; Zeng, X.; Yi, J. Using Remote Sensing Technology to Monitoring Water Pollution of Shanghai Suzhou River. Image Technol. 2003, 2, 3–7. [Google Scholar]
- Zhou, X.; Liu, C.; Akbar, A.; Xue, Y.; Zhou, Y. Spectral and Spatial Feature Integrated Ensemble Learning Method for Grading Urban River Network Water Quality. Remote Sens. 2021, 13, 4591. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Zang, W.; Lin, J.; Wang, Y.; Tao, H. Investigating small-scale water pollution with UAV Remote Sensing Technology. In Proceedings of the 2012 World Automation Congress (WAC) Puerto, Vallarta, Mexico, 24–28 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-Borne Hyperspectral Remote Sensing: From Observation and Processing to Applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Su, T.; Chou, H. Application of Multispectral Sensors Carried on Unmanned Aerial Vehicle (UAV) to Trophic State Mapping of Small Reservoirs: A Case Study of Tain-Pu Reservoir in Kinmen, Taiwan. Remote Sens. 2015, 7, 10078–10097. [Google Scholar] [CrossRef]
- Olivetti, D.; Roig, H.; Martinez, J.; Borges, H.; Ferreira, A.; Casari, R.; Salles, L.; Malta, E. Low-Cost Unmanned Aerial Multispectral Imagery for Siltation Monitoring in Reservoirs. Remote Sens. 2020, 12, 1855. [Google Scholar] [CrossRef]
- Kageyama, Y.; Takahashi, J.; Nishida, M.; Kobori, B.; Nagamoto, D. Analysis of water quality in Miharu dam reservoir, Japan, using UAV data. IEEJ Trans. Electr. Electron. Eng. 2016, 11, S183–S185. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Liu, Y.; Sun, M.; Chen, H.; Wang, X. Inversion of River and Lake Water Quality Parameters by UAV Hyperspectral Imaging Technology. Yangtze River 2020, 51, 205–212. [Google Scholar]
- Zang, C.; Shen, F.; Yang, Z. Aquatic Environmental Monitoring of Inland Waters Based on Hyperspectral Remote Sensing. Remote Sens. Nat. Resour. 2021, 33, 45–53. [Google Scholar]
- Morel, A.Y.; Gordon, H.R. Report of the working group on water color. Bound.-Layer Meteorol. 1980, 18, 343–355. [Google Scholar] [CrossRef]
- Gege, P. WASI-2D: A software tool for regionally optimized analysis of imaging spectrometer data from deep and shallow waters. Comput. Geosci. 2014, 62, 208–215. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Huang, C.; Zou, J.; Li, Y.; Yang, H.; Shi, K.; Li, J.; Wang, Y.; Xia, C.; Zheng, F. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China. Isprs J. Photogramm. Remote Sens. 2014, 93, 29–39. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Yu, G.; Oyama, Y.; Yoshimura, K.; Fukushima, T. A hybrid algorithm for estimating the chlorophyll-a concentration across different trophic states in Asian inland waters. ISPRS J. Photogramm. 2015, 102, 28–37. [Google Scholar] [CrossRef]
- Tavares, M.H.; Lins, R.C.; Harmel, T.; Fragoso, C.R., Jr.; Martínez, J.; Motta-Marques, D. Atmospheric and sunglint correction for retrieving chlorophyll- a in a productive tropical estuarine-lagoon system using Sentinel-2 MSI imagery. ISPRS J. Photogramm. 2021, 174, 215–236. [Google Scholar] [CrossRef]
- Neil, C.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Sheela, A.M.; Letha, J.; Joseph, S.; Ramachandran, K.K.; Sanalkumar, S.P. Trophic state index of a lake system using IRS (P6-LISS III) satellite imagery. Environ. Monit. Assess. 2011, 177, 575. [Google Scholar] [CrossRef] [PubMed]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring C Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Wang, H.; Hladik, C.M.; Huang, W.; Milla, K.; Edmiston, L.; Harwell, M.A.; Schalles, J.F. Detecting the spatial and temporal variability of chlorophyll-a concentration and total suspended solids in Apalachicola Bay, Florida using MODIS imagery. Int. J. Remote Sens. 2010, 31, 439–453. [Google Scholar] [CrossRef]
- Ekstrand, S. Landsat TM based quantification of chlorophyll-a during algae blooms in coastal waters. Int. J. Remote Sens. 1992, 13, 1913–1926. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Lavery, P.; Pattiaratchi, C.; Wyllie, A.; Hick, P. Water quality monitoring in estuarine waters using the landsat thematic mapper. Remote Sens. Environ. 1993, 46, 268–280. [Google Scholar] [CrossRef]
- Huang, W.; Chen, S.; Yang, X.; Johnson, E. Assessment of chlorophyll-a variations in high- and low-flow seasons in Apalachicola Bay by MODIS 250-m remote sensing. Environ. Monit. Assess. 2014, 186, 8329–8342. [Google Scholar] [CrossRef] [PubMed]
- Xian, C.; Zhang, Y.; Zhang, M.; Jiang, T.; Lin, P.; Shang, X. Research on Inversion Model of Water Quality of Wenruitang River Using High Resolution IKONOs Imagery. China Rural. Water Hydropower 2017, 3, 90–95. [Google Scholar]
- Gross, L.; Thiria, S.; Frouin, R. Applying artificial neural network methodology to ocean color remote sensing. Ecol. Model. 1999, 120, 237–246. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of Leaf Nitrogen Content in Wheat Using New Hyperspectral Indices and a Random Forest Regression Algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef]
- Lin, X. Using Random Forest for Classification and Regression. Chin. J. Appl. Entomol. 2013, 50, 1190–1197. [Google Scholar]
- Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, Z.; Li, J.; Wang, R.; Shi, L.; Miao, S.; Lv, H.; Li, Y. Estimation of CDOM concentration in inland lake based on random forest using Sentinel- 3A OLCI. J. Lake Sci. 2018, 30, 979–991. [Google Scholar]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ghani, A.A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2015, 22, 6208–6219. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2022, 34, 8501–8510. [Google Scholar] [CrossRef]
- Leong, W.C.; Bahadori, A.; Zhang, J.; Ahmad, Z. Prediction of water quality index (WQI) using support vector machine (SVM) and least square-support vector machine (LS-SVM). Int. J. River Basin Manag. 2019, 19, 149–156. [Google Scholar] [CrossRef]
- Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- Wei, L.F.; Huang, C.; Wang, Z.X.; Wang, Z.; Zhou, X.C.; Cao, L.Q. Monitoring of Urban Black-Odor Water Based on Nemerow Index and Gradient Boosting Decision Tree Regression Using UAV-Borne Hyperspectral Imagery. Remote Sens. 2019, 11, 2402. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of China. The Guideline for Urban Black and Odorous Water Treatment; Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2015. (In Chinese)
- Brady, J.P.; Ayoko, G.A.; Martens, W.N.; Goonetilleke, A. Development of a hybrid pollution index for heavy metals in marine and estuarine sediments. Environ. Monit. Assess. 2015, 187, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Ren, H.; Liu, Y.; Zheng, Y.; Liu, Y.; Dong, J. Mapping Water Quality Parameters in Urban Rivers from Hyperspectral Images Using a New Self-Adapting Selection of Multiple Artificial Neural Networks. Remote Sens. 2020, 12, 336. [Google Scholar] [CrossRef]
- Huang, M.; Kim, M.S.; Delwiche, S.R.; Chao, K.; Qin, J.; Mo, C.; Esquerre, C.; Zhu, Q. Quantitative analysis of melamine in milk powders using near-infrared hyperspectral imaging and band ratio. J. Food Eng. 2016, 181, 10–19. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.; Rundquist, D. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters-art. no. 1938. Geophys. Res. Lett. 2003, 30, 1938. [Google Scholar]
- Carmen, C.C.; Jose, A.D.G.; Jordi, D.M.; Boris, A.H.S.; Jose, L.C.A.; Federico, A.C.T.; Ramon, D. An UAV and Satellite Multispectral Data Approach to Monitor Water Quality in Small Reservoirs. Remote Sens. 2020, 12, 1514. [Google Scholar]
- Sachidananda, M.; Deepak, R.M. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll- a concentration in turbid productive waters. Remote Sens. Environ. 2011, 117, 394–406. [Google Scholar]
- Alawadi, F.; Bostater, C.R.; Mertikas, S.P.; Neyt, X.; Velez-Reyes, M. Detection of surface algal blooms using the newly developed algorithm surface algal bloom index SABI). In Proceedings of the Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2010, Toulouse, France, 18 October 2010; pp. 782506–7825014. [Google Scholar]
- Brivio, P.A.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Nijad, K.; Jean, B.; Mohamed, A.; Vittorio, B. Monitoring water quality in the coastal area of Tripoli (Lebanon) using high-resolution satellite data. ISPRS J. Photogramm. 2008, 63, 488–495. [Google Scholar]
- Li, Y.; Zhang, Z.; Fei, Y.; Wang, Z. Improvement of Nemerow index method and its application. Water Resour. Prot. 2009, 25, 48–50. [Google Scholar] [CrossRef][Green Version]
- Yuan, X.; Abouelenien, M. A multi-class boosting method for learning from imbalanced data. Int. J. Granul. Comput. Rough Sets Intell. Syst. 2015, 4, 13. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, M.; Pei, Y.; Jin, H. A Model-Driven Method for Quality Reviews Detection: An Ensemble Model of Feature Selection; 2016. In Proceeding of the Fifteenth Wuhan International Conference on E-Business (WHICEB2016), Wuhan China, 27–29 May 2016. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. CoRR 2016, abs/1603.02754. [Google Scholar]
- Wen, K.; Li, Y.; Wang, H.; Yang, J.; Jing, W.; Yang, C. Estimating Inland Water Depth Based on Remote Sensing and Machine Learning Technique. Trop. Geogr. 2020, 40, 314–322. [Google Scholar]
- Liu, F.; Dong, F.Y. Research on diagnosis and test for multicollinearity in econometrics. J. Zhongyuan Univ. Technol. 2020, 31, 44–48. [Google Scholar]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Juan, G.A.; Robert, W.N. Prediction of Optical and Non-Optical Water Quality Parameters in Oligotrophic and Eutrophic Aquatic Systems Using a Small Unmanned Aerial System. Drones 2019, 4, 1. [Google Scholar]

| Band Combination (BC) | Band Math | Reference | Band Combination (BC) | Band Math | Reference |
|---|---|---|---|---|---|
| BC1 | B1/B2 | Simple ratio | BC15 | B4/B3 | Simple ratio |
| BC2 | B1/B3 | Simple ratio | BC16 | B4/B5 | Simple ratio |
| BC3 | B1/B4 | Simple ratio | BC17 | B5/B1 | Simple ratio |
| BC4 | B1/B5 | Simple ratio | BC18 | B5/B2 | Simple ratio |
| BC5 | B2/B1 | Simple ratio | BC19 | B5/B3 | Simple ratio |
| BC6 | B2/B3 | Simple ratio | BC20 | B5/B4 | Simple ratio |
| BC7 | B2/B4 | Simple ratio | BCB1 | (B2 − B1)/(B2 + B1) | Normalized indices |
| BC8 | B2/B5 | Simple ratio | 3BDA | (B3−1 − B4−1) ×B5 | [59] |
| BC9 | B3/B1 | Simple ratio | 3BDA_MOD | (B3−1 − B4−1) | [60] |
| BC10 | B3/B2 | Simple ratio | NDCI | (B4 − B3)/(B4 + B3) | [61] |
| BC11 | B3/B4 | Simple ratio | NDVI | (B5 − B3)/(B5 + B3) | [61] |
| BC12 | B3/B5 | Simple ratio | SABI | (B5 − B3)/(B1 + B2) | [62] |
| BC13 | B4/B1 | Simple ratio | KIVU | (B1 − B3)/B2 | [63] |
| BC14 | B4/B2 | Simple ratio | Kab1 | 1.67 − 3.94 × ln(B1) + 3.78 × ln(B2) | [64] |
| Characteristic Index | Mild | Severe |
|---|---|---|
| SD(cm) | 25—10 | <10 |
| DO(mg/L) | 0.2—2.0 | <0.2 |
| ORP(mV) | −200—50 | <−200 |
| AN(mg/L) | 8.0—15 | >15 |
| Modeling Method | Training Data | Test Data | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| RFR | 0.87 | 0.09 | 0.05 | 0.87 | 0.10 | 0.05 |
| SVR | 0.99 | 0.02 | 0.02 | 0.92 | 0.09 | 0.09 |
| XGBR | 0.99 | 0.01 | 0.01 | 0.94 | 0.09 | 0.07 |
| Modeling Method | Computing Time (s) | Max Value | Min Value |
|---|---|---|---|
| In-situ Measurement | — | 1.50 | 0.76 |
| RFR | 130.7 | 1.31 | 0.74 |
| SVR | 109.4 | 0.92 | 0.82 |
| XGBR | 88.1 | 1.51 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Hu, H.; Luo, Y.; Lei, X.; Wu, D.; Jiang, J. Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting. Water 2022, 14, 3354. https://doi.org/10.3390/w14213354
Wang F, Hu H, Luo Y, Lei X, Wu D, Jiang J. Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting. Water. 2022; 14(21):3354. https://doi.org/10.3390/w14213354
Chicago/Turabian StyleWang, Fangyi, Haiying Hu, Yunru Luo, Xiangdong Lei, Di Wu, and Jie Jiang. 2022. "Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting" Water 14, no. 21: 3354. https://doi.org/10.3390/w14213354
APA StyleWang, F., Hu, H., Luo, Y., Lei, X., Wu, D., & Jiang, J. (2022). Monitoring of Urban Black-Odor Water Using UAV Multispectral Data Based on Extreme Gradient Boosting. Water, 14(21), 3354. https://doi.org/10.3390/w14213354






