Abstract
Supply-demand-based optimization (SDO) is a swarm-based optimizer. However, it suffers from several drawbacks, such as lack of solution diversity and low convergence accuracy and search efficiency. To overcome them, an effective supply-demand-based optimization (ESDO) is proposed in this study. First, an enhanced fitness-distance balance (EFDB) and the Levy flight are introduced into the original version to avoid premature convergence and improve solution diversity; second, a mutation mechanism is integrated into the algorithm to improve search efficiency; finally, an adaptive local search strategy (ALS) is incorporated into the algorithm to enhance the convergence accuracy. The effect of the proposed method is verified based on the comparison of ESDO with several well-regarded algorithms using 23 benchmark functions. In addition, the ESDO algorithm is applied to tune the parameters of the fractional-order proportional integral derivative (FOPID) controller of the water turbine governor system. The comparative results reveal that ESDO is competitive and superior for solving real-world problems.
1. Introduction
With the development of social economy and technology, many complex optimization problems have appeared in the fields of communication, transportation, machinery, e-commerce, automation, materials and economics [1,2,3,4,5,6,7,8,9,10]. Meta-heuristic algorithms, an effective tool, simulate one or some natural processes in nature and have unique advantages in solving complex optimization problems. The No-Free−Lunch (NFL) theorem [11] proves that any optimizers cannot provide the best solutions for all different optimization problems. Therefore, plenty of meta-heuristics have sprung up in recent years according to different inspirations. Meta-heuristic algorithms can be divided into three categories: evolutionary-based (EB), physis-based (PB), and swarm-based (SB).
The most representative EB is the genetic algorithm (GA) [12], which simulates the evolution process of biological groups in nature. With the development of GA, many improved versions and variants have emerged, but most of them obtain high-quality solutions through mutation, crossover and selection steps. Other EBs are genetic programming (GP) [13], evolution strategies (ES) [14] and evolutionary programming (EP) [15].
PBs simulate the physical laws in nature. The annealing algorithm (SA) is a classical PB. The theoretical idea behind SA is the motion of molecules in a solid material as it cools gradually from high temperature. In recent years, numerous new physics-inspired algorithms have been proposed, including gravitational search algorithm (GSA) [16], atom search algorithm (ASO) [17], electromagnetic mechanism-like algorithm (EM) [18], central force optimization (CFO) [19], hysteretic optimization (HO) [20], charged system search (CSA) [21], Lichtenberg algorithm (LA) [22], henry gas solubility optimizer (HGSO) [23], optics inspired optimization (OIO) [24], and so on.
SBs simulate the collective behaviors of natural or artificially formed organizations. Particle swarm algorithm (PSO) [25], a well-known optimizer, has received a high degree of attention and widespread concern from scholars of many various fields. Since its emergence, other new SBs have been developed, including bacteria foraging optimization (BFO) [26], manta ray foraging optimization (MRFO) [27], virus colony search (VCS) [28], cuckoo search algorithm (CS) [29], artificial ecosystem-based optimization (AEO) [30], trees social relations optimization (TSR) [31], tuna swarm optimization (TSO) [32], black widow optimization algorithm (BWOA) [33], etc. Among three types of meta-heuristic algorithms, since SBs have an inherent advantage in exploration and exploitation, they have a larger family and are more competitive in solving complex optimization problems.
Inspired by supply-demand relation of commodities in economics, a swarm-based optimizer called supply-demand-based optimization (SDO) is proposed [34]. It simulates the cobweb model in market economy mathematically. Due to its simplicity and feasibility, it can achieve a balance between exploration and exploitation. Therefore, since the emergence of SDO, it has attracted a wide attention and has been applied in different fields. Ali et al. [35] used SDO for dielectric strength test and obtained the optimal value of SIR/TiO2 filler parameter percentage under different conditions. Ginidi et al. [36] extracted the electrical parameters of different photovoltaic models through SDO, and the comparisons with other algorithms showing that SDO is highly competitive. Alturki et al. [37] applied SDO to the selection problem of hybrid energy system, it can obtain lower loss of power supply probability (LPSP) and lower annualized system cost (ASC). Jing et al. [38] proposed an improved SDO algorithm for the prediction of foundation pit deformation, and the results demonstrated its feasibility and effectiveness. Ibrahim et al. [39] used SDO to estimate the parameters of induction motor and obtained a small deviation.
The operating state of the water turbine governor system is closely related to the stability of hydropower station operation and the safety of power consumption. Therefore, the parameter selection of the water turbine governor system becomes an important subject worthy of long-term study. At the beginning of the study, the parameters are obtained mainly through a large number of empirical formulas derived from field tests. However, the application value obtained by this method is not proportional to the time and financial consumption. The emergence of PID regulation law improves this situation, and is widely used because of its simple operation and good robustness. With the in-depth study of computer technology, it is found that traditional integer-order PID control law cannot be well modeled and analyzed for some complex non-linear engineering problems. The water turbine governor system has strong memory dependence, and its dynamic process can be better described by fractional-order calculus. The most intuitive difference between fractional-order PID (FOPID) controller and traditional integer-order PID controller is that there are two more adjustable parameters in FOPID, which can achieve better control effect. Therefore, the FOPID controller has strong application value.
The rise of intelligent optimization techniques provides a more effective method for parameter adjustment of FOPID controller. Vanchinathan et al. [40] applied the artificial bee colony algorithm to tuning for brushless DC motor. Oguzhan Karahan [41] used FOPID controller in core power control in molten salt reactors and adjusted the parameters by using the cuckoo algorithm. Munagala [42] performed robustness analysis on FOPID controller in an AVR system by using chaotic black widow algorithm. These studies demonstrated the superiority of FOPID in effectiveness of different control systems.
Although SDO as a swarm-based optimizer has better optimization ability than some other optimizers when handling optimization problems, it still has some big promotion space. SDO has the limitations of solution diversity, search efficiency and solution accuracy when tracking complex problems. Therefore, to overcome the drawbacks, this study designs an effective SDO termed ESDO; it incorporates the EFDB and Levy flight, mutation mechanism and adaptive local search strategy into SDO to perform global search. The effect of ESDO is verified based on the comparative results of ESDO with several well-regarded algorithms on a set of benchmark functions and tuning FOPID controller of water turbine governor. The results verify the efficiency and superiority of ESDO. The major difference of our study and its competitors is that ESDO makes three different strategies to improve its overall optimization performance in terms of solution diversity, convergence accuracy and search efficiency.
The rest of this study is as follows. Section 2 gives the main structure of SDO and provides the proposed ESDO by combining several strategies. In Section 3, the experimental results on some functions are investigated to assess the effectivity of the proposed ESDO. Section 4 provides an application of ESDO in tuning the FOPID controller of a water turbine governor. Section 5 gives some conclusions of the study.
2. Effective Supply-Demand-Based Optimization (ESDO)
2.1. Supply-Demand-Based Optimization (SDO)
In SDO [34], there are d commodity prices and quantities as candidate solutions and possible candidate solutions, respectively. After evaluation, the one with better fitness is selected as the current candidate solution. The mathematical expressions for commodity price and quantity are:
where and represent the price vectors and quantity vectors in each market, and and represent the price and quantity of the th commodity in the th market, respectively. There are n markets in total.
Then, the fitness values of all prices and quantities are evaluated by the following functions:
where represents transposition of the matrix.
The vector of the equilibrium price and quantity are represented by:
where and are the random numbers in , and are the Roulette Wheel Selection.
The expressions of demand function and supply function are given by, respectively:
where and respectively represent the th price and quantity of commodity at time , and and are respectively the demand weight and supply weight.
Substituting (7) into (8), the demand equation can be rewritten into the following form:
Therefore, the commodity price is updated by adjusting the values of and , and it is updated according to the equilibrium price relative to the current price. and can be expressed as:
where, is equivalent to the stability mode in the supply and demand mechanism, emphasizing the exploitation ability, is equivalent to the instability mode and emphasizing the overall exploration ability. Figure 1 shows the two modes of SDO.
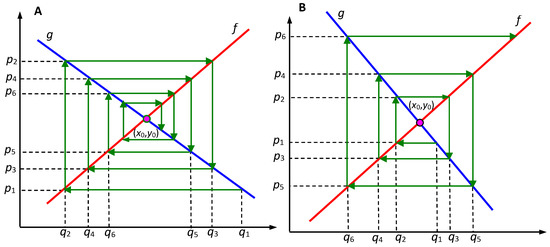
Figure 1.
(A) stability mode, (B) instability mode [34].
2.2. Proposed Method
Since SDO easily suffers from low search efficiency and misses some better solutions, ESDO is an enhanced version of SDO in order to overcome them. For SDO, the fitness value of each solution and the distance between each solution and the best solution are very two important factors affecting the search efficiency of the algorithm for the optimal solution. In this study, inspired by a fitness-distance balance (FDB) [43], an enhanced fitness-distance balance (EFDB) is developed to replace the selection for the equilibrium quantity and price of commodities. Meanwhile, to strengthen exploration ability of the algorithm in the search space, a Levy flight strategy is introduced to the weight to improve the convergence ability. A mutation mechanism is employed to enhance the search efficiency of SDO. Meanwhile, an adaptive local search strategy is used to improve the convergence accuracy of the algorithm. ESDO is a newly presented optimizer and not yet applied in any real-world application.
2.2.1. Combining Enhanced Fitness-Distance Balance (EFDB) and Levy Flight
In [44], Kati et al. proposed an improved version of SDO, in which the equilibrium quantity is replaced with the commodity quantity selected by the FDB method to provide diversity. In this study, according to [44], we propose the EFDB method, in which the equilibrium quantity and price of commodities are replaced with the commodity quantity and price by using the FDB method, respectively. This method can further strengthen the solution diversity. The following is a specific description to the EFDB method. The fitness value of commodity price is calculated by [43]:
The equilibrium price vector x0 is redefined by:
As an analogy, the equilibrium quantity vector y0 is redefined by:
where
where normFyi is the normalized fitness value of Fyi, normDyi is the normalized distance value of the ith commodity, It is the current iteration and MaxIt is the maximum number of iterations. This selection method combines the fitness and the distance to calculate the score for each individual in the population. Therefore, this strategy can effectively improve solution diversity and avoid local solutions. In addition, inspecting Equation (16), in the early iterations, the selection for the equilibrium quantity and price of commodities takes into account the largest fitness value and the furthest distance from the current optimal individual so far, it will contribute to exploration; in the later iterations, the selection focuses more on the fitness value rather than the distance, it will be dedicated to exploitation.
The Levy flight [45,46] whose step-width obeys non-uniform Levy distribution, is a random walk; thus, it has the superior ability to enhance exploring space search [47]. The step-width of the Levy flight is produced by [48,49]:
where λ is a stability/tail index, s is the step-width and u and v obey the normal distribution, respectively:
where Γ denotes the standard Gamma function and b = 1.5.
L(s) ~ t−λ (1≤ λ ≤ 3)
u ~ N(0,1), v ~ N(0,1),
The weight in Equation (10) is reformulated by:
2.2.2. The Mutation Mechanism
To improve the search efficiency of the algorithm, the mutation mechanism is employed in this study. Although some different mutation strategies are introduced in the literature [50,51,52], the Gaussian mutation is one of the most frequently used mutation methods since it is more effective and simpler to implement [53]. So, in ESDO, the supply function and demand function are modified by, respectively:
where
rn ~ N(0,1)
2.2.3. Adaptive Local Search (ALS) Strategy
Local search strategy is an important way to improve the current best solution. The chaotic local search is a classic local search (CLS) method [54], which used the chaotic map to improve the solution quality by searching the neighborhood around the best solution so far. However, the step-size for this local search cannot decrease as iterations go on, which will affect the solution accuracy and search efficiency. So, to dynamically adjust the step-size of the local search, an adaptive local search (ALS) strategy is given by:
is a new current solution generated at time t.
The update of the current best solution is given by:
If the fitness value of is better than that of , the current best solution is replaced with the new one, or it remains unchanged. It can be observed from Equation (28) that a bigger step-size contributes to exploration in the early iterations, with the increase of iterations and, a small step-size is greatly dedicated to exploitation. In addition to improving the convergence accuracy, this adaptive search strategy also strengthens the balance between exploration and exploitation to some extent.
2.2.4. The Proposed ESDO Algorithm
By introducing the EFDB method and Levy flight, the mutation mechanism, and the ALS strategy to strengthen the optimization performance, the ESDO algorithm is proposed. The pseudocode of ESDO algorithm is given in Figure 2.

Figure 2.
Pseudocode of ESDO algorithm.
3. Experimental Results and Analysis
3.1. Test Functions and Parameter Setting
To assess the performance of the ESDO algorithm, a classical suit of benchmark set, containing 23 test functions (see Table A1 in Appendix A for details), are employed. The 23 benchmark functions include 7 unimodal functions (UFs) (F1–F7), 6 multimodal functions (MFs) (F8–F13) and 10 low-dimensional multimodal functions (LMFs) (F14–F23). Meanwhile, several competitive optimizers, including whale optimization algorithm (WOA) [55], gray wolf optimizer (GWO) [56], and GSA, are used and their results are provided for a comparison. For all the considered optimizers, the population size and the maximum number of iterations are set to 50 and 500, respectively. The ESDO algorithm is firstly analyzed qualitatively based on exploration and exploitation. Then, the Wilcoxon signed-rank test and Friedman test are statistically analyzed, respectively. The experimental results are based on 30 independent runs. The other parameter settings of all the considered optimizers are described in Table 1.

Table 1.
Parameter setting of each algorithm.
3.2. Exploitation Analysis
The functions F1–F7 having only one extremum are used to assess exploitation of algorithms. The comparison results of the algorithms on these UNs are listed in Table 2, in which the underline indicates the best value among all the algorithms. From this table, ESDO provides better solutions on functions F1–F5 and F7 in terms of mean and Std. ESDO performs as well as SDO and GWO on function F6. Therefore, ESDO obtains better results on most of UNs. Figure 3 shows the convergence curves of the algorithms on F1–F7. ESDO exhibits superior convergence rate over other optimizers in exploiting the optimal solution.

Table 2.
Comparison results of UNs (F1–F7).
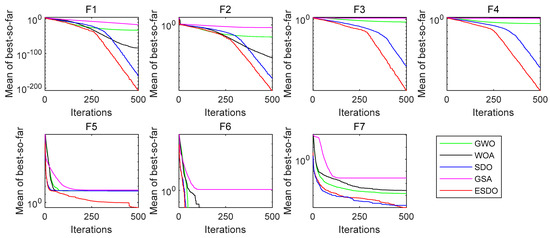
Figure 3.
Convergence comparisons of UNs.
3.3. Exploration Analysis
The functions F8–F23 having multiple extrema are used to evaluate exploration of algorithms. The comparison results of the algorithms on these functions are shown in Table 3 and Table 4. Inspecting Table 3, ESDO obviously outperforms other optimizers on function F12 and F13. ESDO, SDO and WOA provide the same results in terms of mean on functions F9 and F10. In addition, ESDO is third best algorithm on function F7. The performance of ESDO ranks only second to WOA on function F8. Observing Table 4, for F15 and F20, ESDO obtains the second-best results, which are only inferior to those of SDO. For functions F16–F19 and F22–F23, ESDO, SDO and one of other algorithms offer the same best results. For F21, ESDO provides the best results. The convergence curves of the algorithms on F8–F23 are depicted in Figure 4 and Figure 5, which manifests that ESDO has better convergence performance with comparison to other algorithms when tackling these test functions.

Table 3.
Comparison results of MNs (F8–F13).

Table 4.
Comparison results of LMNs (F14–F23).
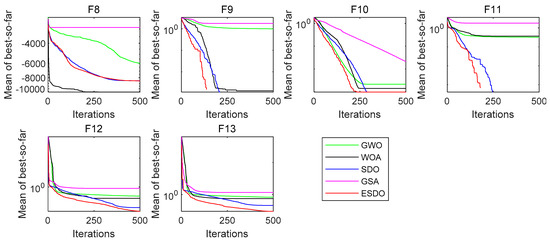
Figure 4.
Convergence comparisons of MNs (F8–F13).
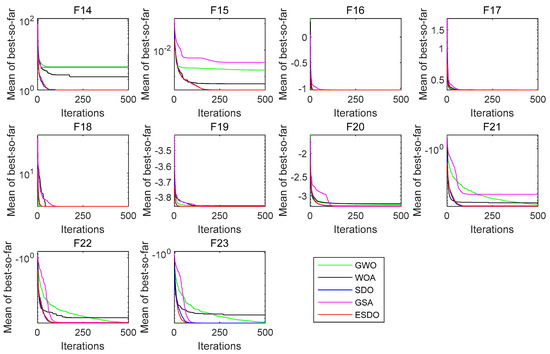
Figure 5.
Convergence comparisons of LMNs (F14–F23).
3.4. Statistical Analysis
To evaluate the overall performance of ESDO and rank it statistically, the Wilcoxon signed-rank test (WSRT) [57] and Friedman test (FT) [58] are employed, respectively. Table 5 and Table 6 provide the results of WSRT. In the table, “=” indicates there is no significant difference between ESDO and its competitor for a considered problem, “+” indicates that the performance of ESDO is better than that of a competitor for a considered problem and “−” is the opposite. Table 7 summarizes the results of WSRT in Table 5 and Table 6. In Table 7, The WSRT results reveal that ESDO is superior to SDO, GWO, WOA and GSA on functions 7, 18, 22 and 17 out of 23, respectively, indicating the superior performance of ESDO to its competitors statistically. Figure 6 depicts the rank of each function for the comparative optimizers, Figure 7 gives the mean of these ranks. From Figure 7, ESDO ranks the first among the considered optimizers, demonstrating that it exhibits the best optimization ability compared to its counterparts.

Table 5.
WSRT results of ESDO for SDO and WOA.

Table 6.
WSRT results of ESDO for GWO and GSA.

Table 7.
Statistics results of WSRT for ESDO.
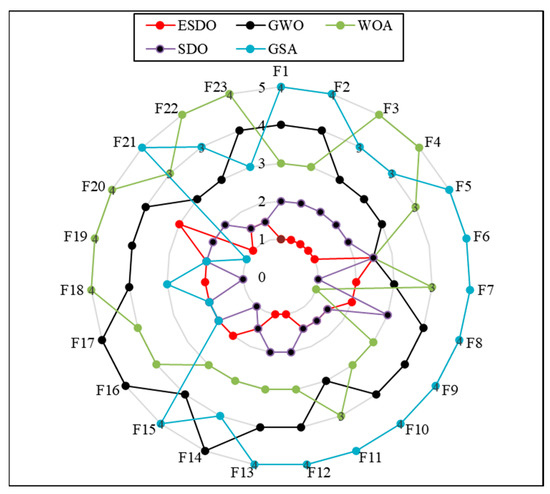
Figure 6.
Ranks of different algorithms for each function.
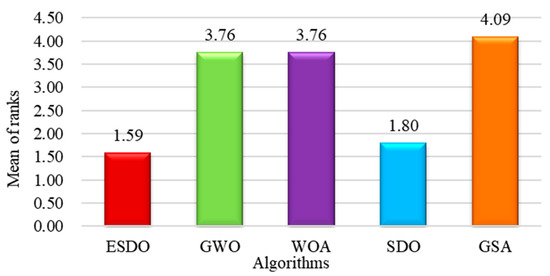
Figure 7.
Mean of ranks of different algorithms.
4. ESDO for FOPID Controller of Water Turbine Governor System
4.1. System Description
The traditional integer-order PID controller has only three parameters (,,) [59], while the FOPID controller used in this experiment has five parameters (,,,,), so as to achieve more accurate control. Theoretically, and can take any number. In the case of , FOPID is converted to integer-order PID.
The transfer function of FOPID is described by:
where , and represent the proportional coefficient, integral coefficient and differential coefficient, respectively, represents the Laplace operator, and and represent the exponents of the integral operator and the differential operator, respectively. represents the differential time constant.
The variation of the unit load produces a deviation e. The FOPID controller will convert this difference into an adjustment signal. After receiving the signal, the mechanical hydraulic system will operate to adjust the opening of the guide vane, and then adjust the flow and restore the speed. Figure 8 is the FOPID model of the water turbine governor system.
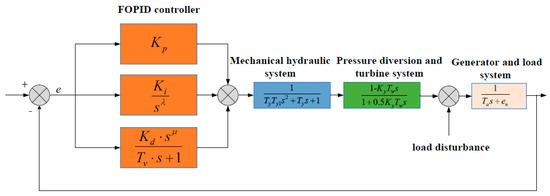
Figure 8.
FOPID block diagram of the water turbine governor system.
4.2. Experimental Results and Analysis
This study is simulated by MATLAB/Simulink. The fitness function uses the time multiplication error integration criterion and is defined by:
where is the deviation of the actual output from the expected output.
The specific experimental settings and parameter values are shown in Table 8.

Table 8.
The specific experimental settings and parameter values.
In this experiment, in order to be more practical, four different working conditions under 0–20% load are adopted, and the controller performance from ESDO is compared with that from SDO, WOA and GSA under each working condition. Each algorithm runs 20 times, and the average optimal fitness value, overshoot and adjustment time based on 20 experiments are compared to verify the parameter setting effect of ESDO on the FOPID controller. Under different load conditions, the overshoot is represented by the maximum value. The simulation results are shown in Table 9. The convergence curve of average fitness, convergence curves of average FOPID parameters and the speed response curves obtained of the average FOPID parameters under different load conditions are shown in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20, respectively.

Table 9.
Experimental results at 4%, 8%, 12%, and 16% loads.
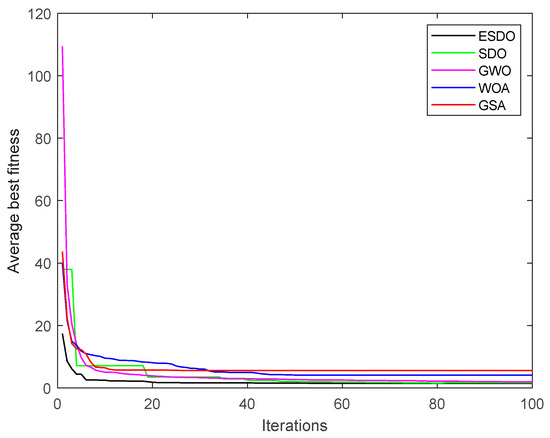
Figure 9.
Convergence curves of average fitness with 4% load.
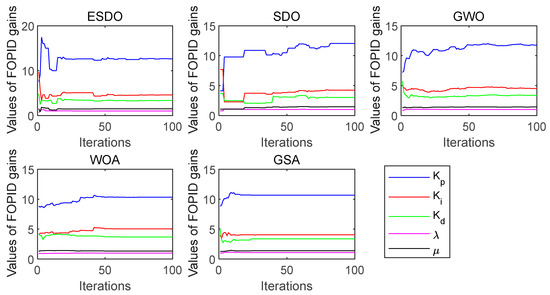
Figure 10.
Convergence curves of FOPID parameters with 4% load.
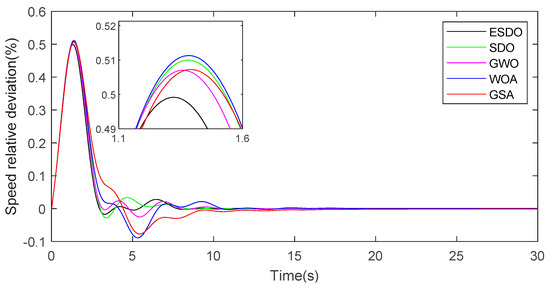
Figure 11.
Speed response curves with 4% load.
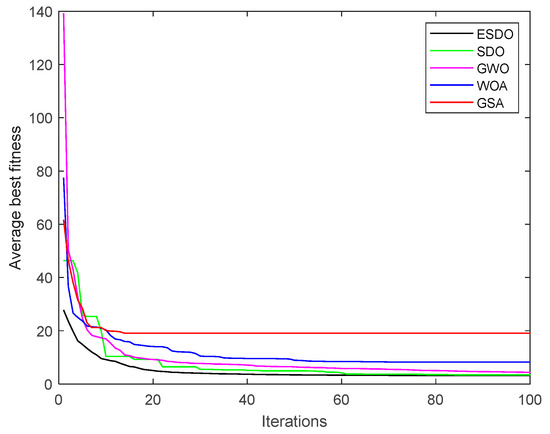
Figure 12.
Convergence curves of average fitness with 8% load.
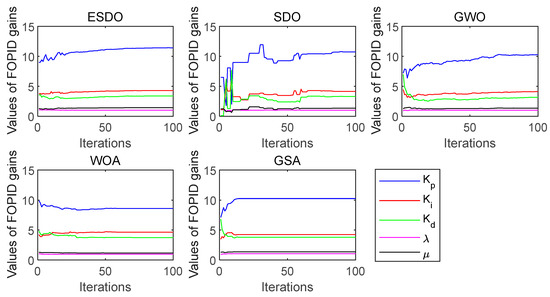
Figure 13.
Convergence curves of FOPID parameters with 8% load.
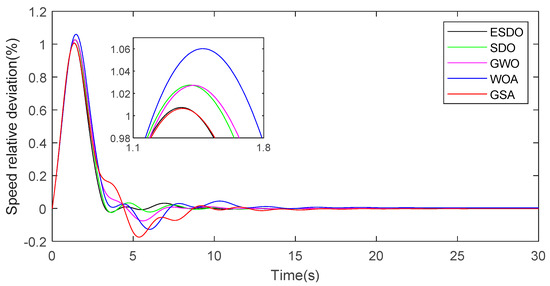
Figure 14.
Speed response curves with 8% load.
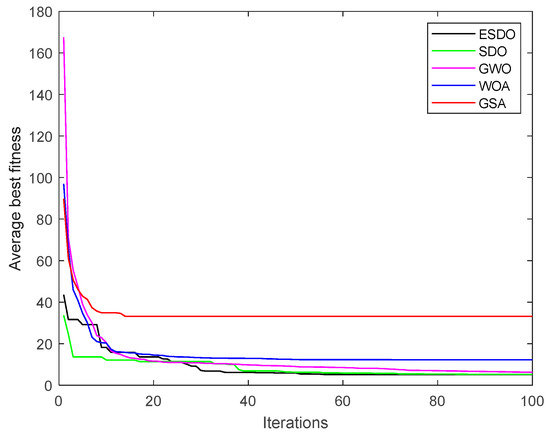
Figure 15.
Convergence curves of average fitness with 12% load.
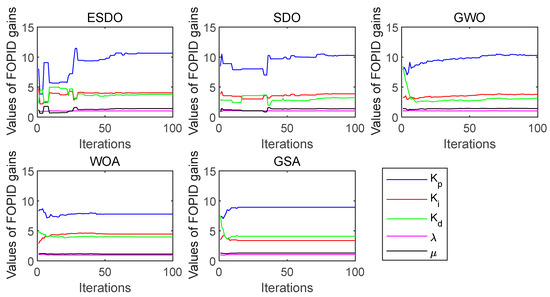
Figure 16.
Convergence curves of FOPID parameters with 12% load.
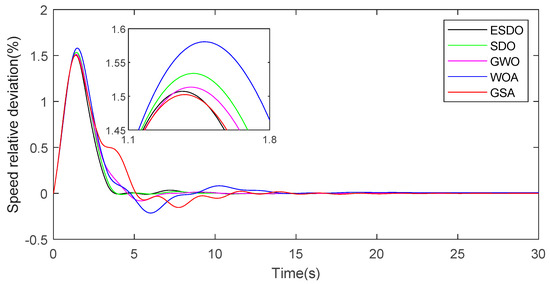
Figure 17.
Speed response curves with 12% load.
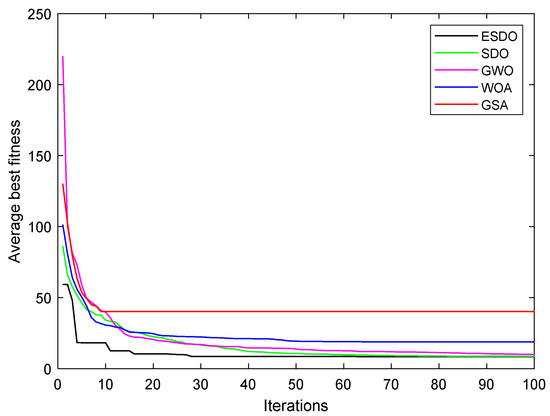
Figure 18.
Convergence curves of average fitness with 16% load.
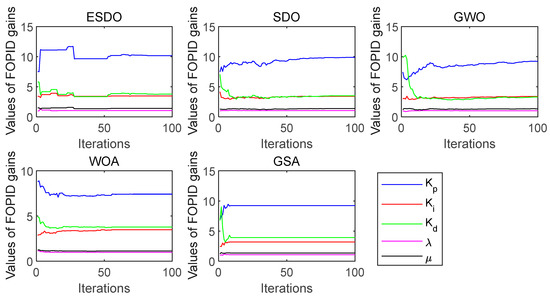
Figure 19.
Convergence curves of FOPID parameters with 16% load.
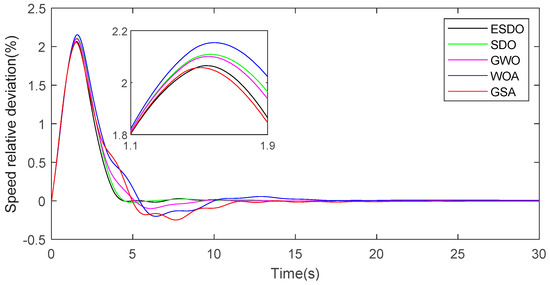
Figure 20.
Speed response curves with 16% load.
Under 4% load, the fitness value of the FOPID controller offered by ESDO is the smallest among the five algorithms, which shows that ESDO can jump out of local optimum well and find the global optimum; meanwhile, it effectively improves the optimization accuracy. From the convergence curves under 4% load in Figure 9, the convergence rate of ESDO is also faster than other algorithms, which indicates that ESDO has the strongest ability to find the best solution among these algorithms. The overshoot and adjustment time are two important indicators to measure whether a control system is stable. It can be seen from Table 9 that under the condition of 4% load, the overshoot and adjustment time obtained are the minimum after the governor of the water turbine is tuned by ESDO. The trend of the response curves in Figure 11 shows that after the peak value, the oscillation amplitude of the curve obtained by ESDO is the smallest, and it can reach a stable value quickly. On the contrary, the oscillation amplitude of the response curves obtained by SDO, GWO, WOA and GSA are very large, and the state is very unstable. It proves that the dynamic regulation ability of the FOPID controller offered by ESDO is stronger than those offered by the other four algorithms, and the turning parameters of the turbine governor with ESDO can make the control system more stable and efficient.
Under 8% load, the fitness value of the FOPID controller offered by ESDO is also the smallest, showing that the global exploration ability and local exploitation ability of ESDO are significantly enhanced. The convergence curves of average fitness in Figure 12 demonstrate that, under the 8% load condition, ESDO can quickly find the optimal value in the optimization process, greatly improving the efficiency of the algorithm. After the governor of the water turbine is tuned by different algorithms, the overshoot of the FOPID controller offered by ESDO is only second to that offered by GSA and very close to that offered by GSA, but the adjustment time of the FOPID controller offered by ESDO is far better than that offered by GSA. It can be found from Figure 14 that the FOPID controller from ESDO also has the smallest oscillation amplitude and the smallest duration, the FOPID controller from GSA has the largest oscillation amplitude and the longest duration, and the FOPID controllers from SDO, GWO and WOA are in between. Considering comprehensively, under 8% load condition, ESDO also has the strongest optimization ability for the FOPID controller among the five algorithms.
When the load is 12%, the FOPID controller offered by ESDO also gets the minimum fitness value. From Figure 15, although the convergence speed of ESDO is slower than that of SDO at the beginning of the iteration, in the middle of the iteration, ESDO outperforms SDO. At this time, the convergence speed of ESDO is the fastest, and it tends to jump out of the local extreme value to find a smaller value. Moreover, in the regulation system, the overshoot of the FOPID controller offered by ESDO is relatively good, and the adjustment time is also the smallest. From the speed response curves in Figure 17, after the first peak, the ESDO curve is very stable with little fluctuation, while the response curves of the FOPID controller offered by other algorithms fluctuate greatly and last a long time.
When the load is 16%, the fitness value of the FOPID controller offered by ESDO is still the smallest. From Figure 18, there is a fast convergence speed at the beginning of iteration, and its ability to jump out of local extreme value is also the strongest among all algorithms. According to the speed response curves in Figure 20, the overshoot of of the FOPID controller offered by ESDO is very close to that offered by GSA, which is better than those offered by other algorithms. The adjustment time of the FOPID controller offered by ESDO is the shortest among all algorithms, after falling from the peak, the fluctuation weakens rapidly and finally tends to be stable.
Therefore, through tuning the FOPID parameters of the water turbine governor under different load conditions, these convincing results reveal that ESDO is excellent in tackling real-world engineering applications.
5. Conclusions
To better handle optimization problems, an effective supply-demand-based optimization (ESDO) is proposed, it combines three strategies, including the enhanced fitness-distance balance (EFDB) with Levy flight, mutation mechanism and adaptive local search, to improve solution diversity, and convergence accuracy and search efficiency. The experimental results of ESDO with several well-regarded algorithms on 23 benchmark functions discover that ESDO has superior optimization ability. In addition, the practicability of ESDO is also verified by tuning the parameters of the FOPID controller of the water turbine governor system. The experimental results show that the turbine governor system tuned by ESDO is better than those tuned by other algorithms in terms of response time and overshoot.
In this study, some secondary and high-level terms are ignored when establishing the hydraulic turbine simulation model, and higher-order models can be established in the future. The implementation method of FOPID can also be improved.
In future studies, ESDO could be specifically intended to handle a variety of problems in hydraulic engineering, such as optimal allocation of power station [60], intelligent fault diagnosis of turbine [61] and optimal design of gate [62,63,64].
Author Contributions
Conceptualization, W.Z. and L.W.; methodology, H.Z. and W.Z.; software, Z.Z.; validation, Z.Z., K.Z. and H.Z.; formal analysis, H.Z.; investigation, writing—original draft preparation, W.Z and H.Z.; writing—review and editing, H.Z.; visualization, L.W.; supervision, L.W.; project administration L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Unimodal test functions.
Table A1.
Unimodal test functions.
| Name | Function | D | Range | |
| Sphere | ||||
| Schwefel2.22 | ||||
| Schwefel1.2 | ||||
| Schwefel2.21 | ||||
| Rosenbrock | ||||
| Step | ||||
| Quartic |

Table A2.
Multimodal test functions.
Table A2.
Multimodal test functions.
| Name | Function | D | Range | |
| Schwefel | ||||
| Rastrigin | ||||
| Ackley | ||||
| Griewank | ||||
| Penalized | ||||
| Penalized2 |

Table A3.
Low-dimension Multimodal test functions.
Table A3.
Low-dimension Multimodal test functions.
| Name | Function | D | Range | |
| Foxholes | ||||
| Kowalik | ||||
| Six Hump Camel | ||||
| Branin | ||||
| GoldStein-Price | ||||
| Hartman 3 | ||||
| Hartman 6 | ||||
| Shekel 5 | ||||
| Shekel 7 | ||||
| Shekel 10 |
References
- Lu, R.R.; Wang, J.Y.; Fu, X.T.; Lin, S.H.; Wang, Q.; Zhang, B. Performance analysis and optimization for UAV-based FSO communication systems. Phys. Commun. 2022, 51, 101594. [Google Scholar] [CrossRef]
- Beus, M.; Krpan, M.; Kuzle, I.; Pandžić, H.; Parisio, A. A model predictive control approach to operation optimization of an ultracapacitor bank for frequency control. IEEE Trans. Energy Convers. 2021, 36, 1743–1755. [Google Scholar] [CrossRef]
- Chang, C.; Han, M. Production scheduling optimization of prefabricated building components based on dde algorithm. Math. Probl. Eng. 2021, 2021, 6672753. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.; Wei, G. An enhanced black widow optimization algorithm for feature selection. Knowl.-Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Yoo, S.; Oh, S. Flow analysis and optimization of a vertical axis wind turbine blade with a dimple. Eng. Appl. Comp. Fluid Mech. 2021, 15, 1666–1681. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Yildiz, A.R.; Mehta, P. Manta ray foraging optimization algorithm and hybrid Taguchi salp swarm-Nelder–Mead algorithm for the structural design of engineering components. Mater. Test. 2020, 64, 706–713. [Google Scholar] [CrossRef]
- Zeinalzadeh, A.; Pakatchian, M.R. Evaluation of novel-objective functions in the design optimization of a transonic rotor by using deep learning. Eng. Appl. Comp. Fluid Mech. 2021, 15, 561–583. [Google Scholar] [CrossRef]
- Pei, H.; Cui, Y.; Kong, B.; Jiang, Y.; Shi, H. Structural parameters optimization of submerged inlet using least squares support vector machines and improved genetic algorithm-particle swarm optimization approach. Eng. Appl. Comp. Fluid Mech. 2021, 15, 503–511. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An enhanced hybrid arithmetic optimization algorithm for engineering applications. Comput. Meth. Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Huning, A. Evolutionsstrategie. optimierung technischer systeme nach prinzipien der biologischen evolution. Arch. Philos. Law Soc. Philos. 1976, 62, 298–300. [Google Scholar]
- David, B.F. Artificial Intelligence through Simulated Evolution. In Evolutionary Computation: The Fossil Record; Wiley-IEEE Press: Hoboken, NJ, USA, 1998; pp. 227–296. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl.-Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.J. Electromagnetism-like Mechanism Algorithm. In Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Intelligent Systems Reference Library; Springer: Cham, Switzerland, 2014; Volume 62, pp. 347–354. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new metaheuristic with applications in applied electromagnetics. Prog. Electromagn. Res. 2007, 77, 425–491. [Google Scholar] [CrossRef]
- Pál, K.F. Hysteretic optimization for the Sherrington-Kirkpatrick spin glass. Phys. A Stat. Mech. Its Appl. 2006, 367, 261–268. [Google Scholar] [CrossRef][Green Version]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Oliver, G.A.; Cunha, S.S., Jr.; Gomes, G.F. Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Syst. Appl. 2021, 170, 114522. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comp. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Kashan, A.H. A new metaheuristic for optimization: Optics inspired optimization (OIO). Comput. Oper. Res. 2015, 55, 99–125. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, IEEE, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Levy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; IEEE Publications: Piscataway, NJ, USA; pp. 210–214. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Artificial ecosystem-based optimization: A novel nature-inspired meta-heuristic algorithm. Neural Comput. Appl. 2020, 32, 9383–9425. [Google Scholar] [CrossRef]
- Alimoradi, M.; Azgomi, H.; Asghari, A. Trees social relations optimization algorithm: A new Swarm-Based metaheuristic technique to solve continuous and discrete optimization problems. Math. Comput. Simul. 2022, 194, 629–664. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.R.; Han, B.; Tang, A. Tuna swarm optimization: A novel swarm-based metaheuristic algorithm for global optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef]
- Peña-Delgado, A.F.; Peraza-Vázquez, H.; Almazán-Covarrubias, J.H.; Torres Cruz, N.; García-Vite, P.M.; Morales-Cepeda, A.B.; Ramirez-Arredondo, J.M. A novel bio-inspired algorithm applied to selective harmonic elimination in a three-phase eleven-level inverter. Math. Probl. Eng. 2020, 2020, 8856040. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Supply-Demand-Based Optimization: A Novel Economics-Inspired Algorithm for Global Optimization. IEEE Access 2019, 7, 73182–73206. [Google Scholar] [CrossRef]
- Ali, A.M.; Nasrat, L.; Hassan, M.H.; Elsayed, S.K.; Kamel, S. Supply Demand-Based Optimization Algorithm for Estimating Break Down Voltage of Silicon Rubber Insulators. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaíso, Chile, 6–9 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Ginidi, A.R.; Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E. Supply demand optimization algorithm for parameter extraction of various solar cell models. Energy Rep. 2021, 7, 5772–5794. [Google Scholar] [CrossRef]
- Alturki, F.A.; Al-Shamma’a, A.A.; Farh, H.M.; AlSharabi, K. Optimal sizing of autonomous hybrid energy system using supply-demand-based optimization algorithm. Int. J. Energy Res. 2021, 45, 605–625. [Google Scholar] [CrossRef]
- Jing, C.; Wang, H.; Li, H. Deformation Prediction of Foundation Pit Based on Exponential Power Product Model of Improved Algorithm. Geofluids 2021, 2021, 7055693. [Google Scholar] [CrossRef]
- Ibrahim, S.A.; Kamel, S.; Hassan, M.H.; Elsayed, S.K.; Nasrat, L. Developed Algorithm Based on Supply-Demand-Based Optimizer for Parameters Estimation of Induction Motor. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22–26 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Vanchinathan, K.; Selvaganesan, N. Adaptive fractional order PID controller tuning for brushless DC motor using artificial bee colony algorithm. Results Control Optim. 2021, 4, 100032. [Google Scholar] [CrossRef]
- Karahan, O. Design of optimal fractional order fuzzy PID controller based on cuckoo search algorithm for core power control in molten salt reactors. Prog. Nucl. Energy 2021, 139, 103868. [Google Scholar] [CrossRef]
- Munagala, V.K.; Jatoth, R.K. Improved fractional PIλDμ controller for AVR system using Chaotic Black Widow algorithm. Comput. Electr. Eng. 2022, 97, 107600. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Kati, M.; Kahraman, H.T. Improving supply-demand-based optimization algorithm with fdb method: A comprehensive research on engineering design problems. Mühendislik Bilimleri Ve Tasarım Derg. 2020, 8, 156–172. [Google Scholar] [CrossRef]
- Hu, G.; Chen, L.; Wang, X.; Wei, G. Differential Evolution-Boosted Sine Cosine Golden Eagle Optimizer with Lévy Flight. J. Bionic Eng. 2022, 2022, 1–36. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. Optimization of reservoir operation at Klang Gate Dam utilizing a whale optimization algorithm and a Lévy flight and distribution enhancement technique. Eng. Appl. Comp. Fluid Mech. 2021, 15, 1682–1702. [Google Scholar] [CrossRef]
- Liu, J.; Shi, J.; Hao, F.; Dai, M. A novel enhanced global exploration whale optimization algorithm based on Lévy flights and judgment mechanism for global continuous optimization problems. Eng. Comput. 2022, 2022, 1–29. [Google Scholar] [CrossRef]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes. Phys. Rev. E 1994, 49, 4677–4683. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Higashi, N.; Iba, H. Particle swarm optimization with Gaussian mutation. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003; pp. 72–79. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S. An Improved Tunicate Swarm Algorithm with Best-random Mutation Strategy for Global Optimization Problems. J. Bionic Eng. 2022, 19, 1177–1202. [Google Scholar] [CrossRef]
- Alireza, A.L.F.I. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems. Acta Autom. Sin. 2011, 37, 541–549. [Google Scholar] [CrossRef]
- Lu, H.; Sriyanyong, P.; Song, Y.H.; Dillon, T. Experimental study of a new hybrid PSO with mutation for economic dispatch with non-smooth cost function. Int. J. Electr. Power Energy Syst. 2010, 32, 921–935. [Google Scholar] [CrossRef]
- Tang, Z.; Tao, S.; Wang, K.; Lu, B.; Todo, Y.; Gao, S. Chaotic Wind Driven Optimization with Fitness Distance Balance Strategy. Int. J. Comput. Intell. Syst. 2022, 15, 46. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 2012, 32, 674–701. [Google Scholar] [CrossRef]
- Zhao, W.; Shi, T.; Wang, L.; Cao, Q.; Zhang, H. An adaptive hybrid atom search optimization with particle swarm optimization and its application to optimal no-load PID design of hydro-turbine governor. J. Comput. Des. Eng. 2021, 8, 1204–1233. [Google Scholar] [CrossRef]
- Hemeida, M.G.; Ibrahim, A.A.; Mohamed, A.A.A.; Alkhalaf, S.; El-Dine, A.M.B. Optimal allocation of distributed generators DG based Manta Ray Foraging Optimization algorithm (MRFO). Ain Shams Eng. J. 2021, 12, 609–619. [Google Scholar] [CrossRef]
- Chen, C.; Mo, C. A method for intelligent fault diagnosis of rotating machinery. Digit. Signal Prog. 2004, 14, 203–217. [Google Scholar] [CrossRef]
- Liu, J.; Li, D.; Wu, Y.; Liu, D. Lion swarm optimization algorithm for comparative study with application to optimal dispatch of cascade hydropower stations. Appl. Soft. Comput. 2020, 87, 105974. [Google Scholar] [CrossRef]
- Lu, P.; Zhou, J.; Wang, C.; Qiao, Q.; Mo, L. Short-term hydro generation scheduling of Xiluodu and Xiangjiaba cascade hydropower stations using improved binary-real coded bee colony optimization algorithm. Energy Conv. Manag. 2015, 91, 19–31. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Wu, Y.; Yang, Z.; Xu, J. Dynamic multi-swarm differential learning Harris Hawks Optimizer and its application to optimal dispatch problem of cascade hydropower stations. Knowl.-Based Syst. 2022, 242, 108281. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).