Numerical Simulation of Axial-Flow Pump Cavitation Based on Variable Frequency Speed Regulation
Abstract
:1. Introduction
2. Pump Model, Griding and Boundary Conditions
2.1. Computational Model
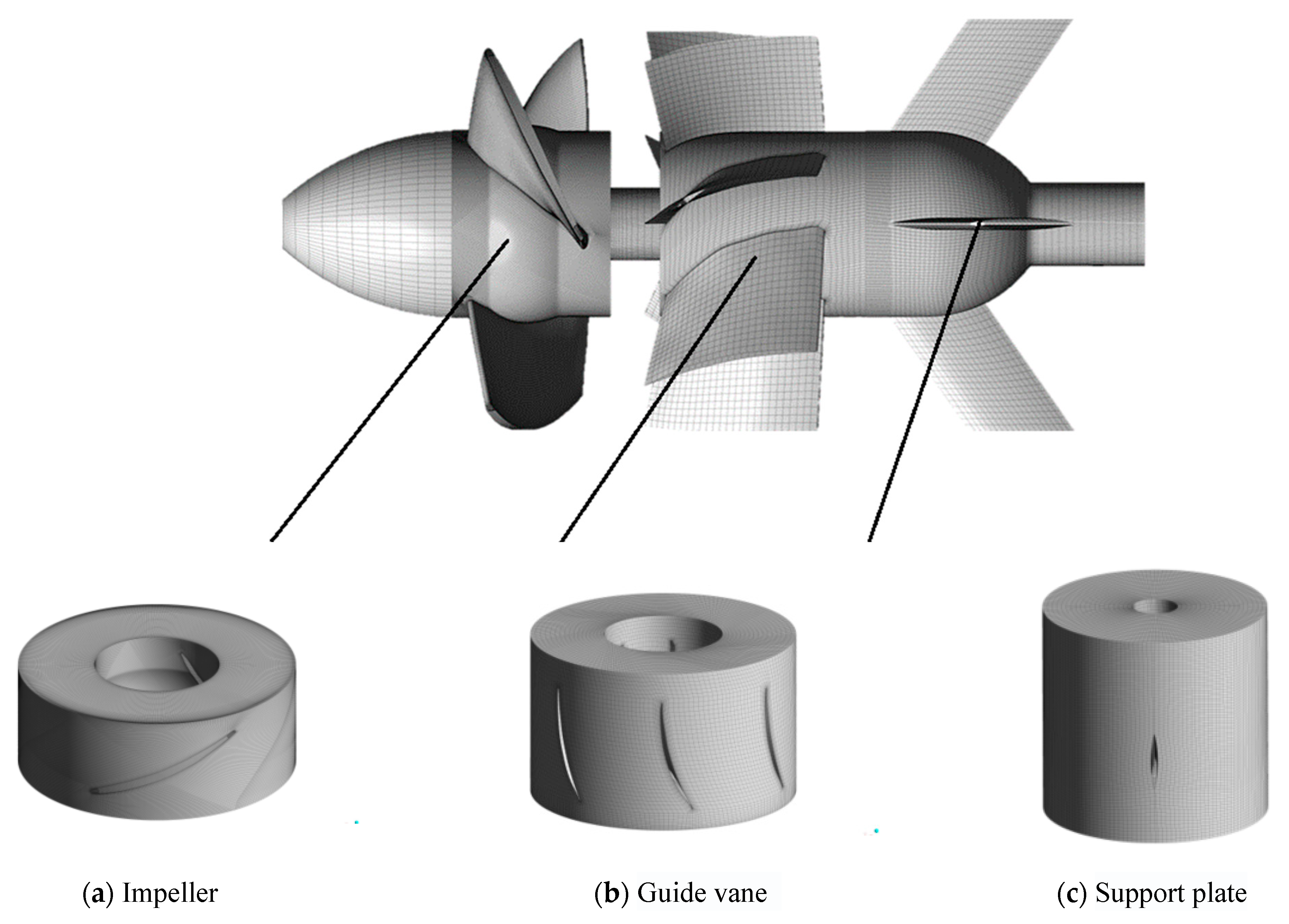
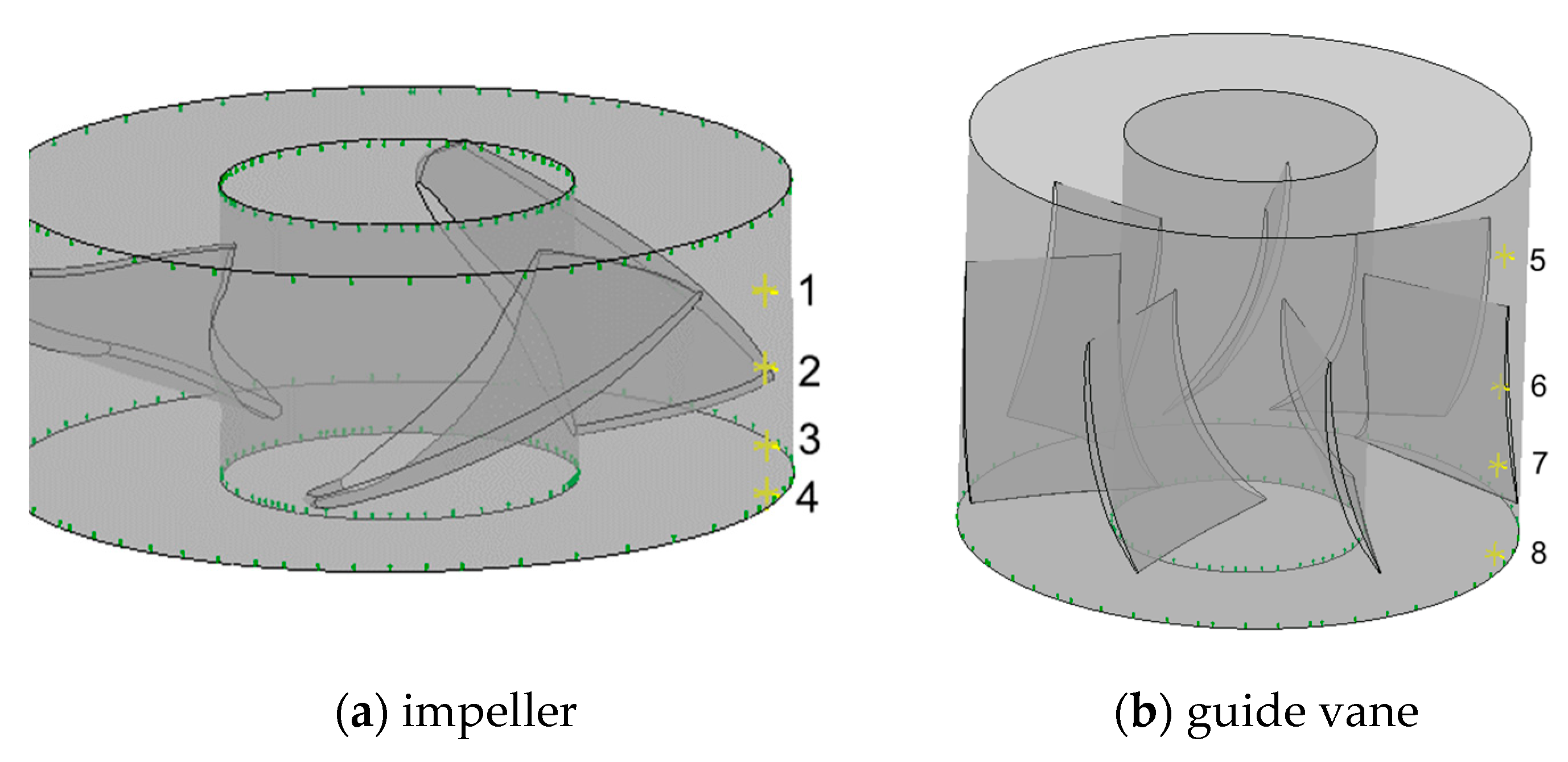
2.2. Grid Segmentation
2.3. Numerical Methods
2.4. Frontier Conditions
2.5. Cavitation Model
- ——Vacuum radius;
- ——Vacuum surface pressure;
- ——Infinity field pressure;
- ——Liquid density;
- ——Motion viscosity of liquids;
- ——Liquid surface tension factor.
- ——Vacuum volume fraction;
- ——Vacuum density;
- ——The speed of the bubble;
- , ——Sources of mass transfer during vacuole growth and collapse.
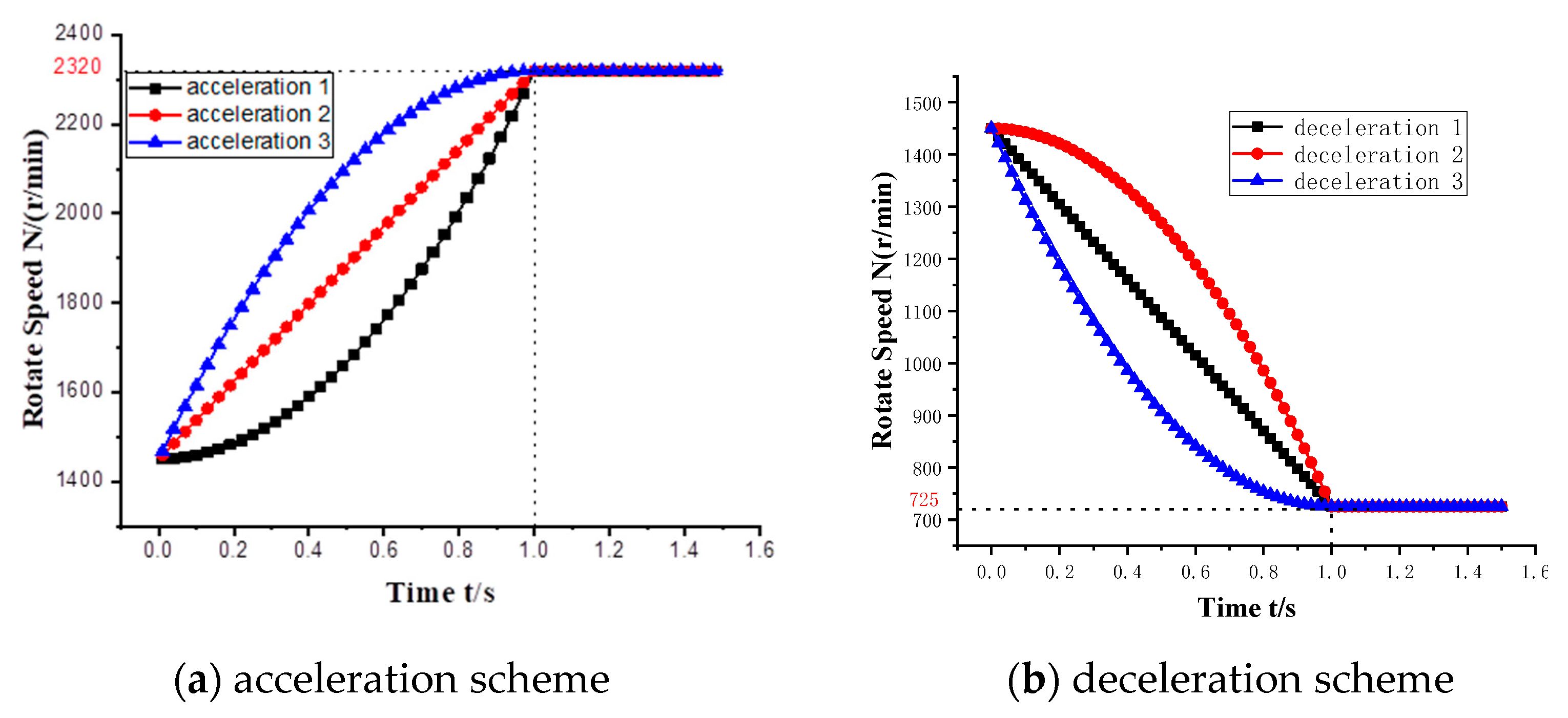
2.6. VVVF Scheme
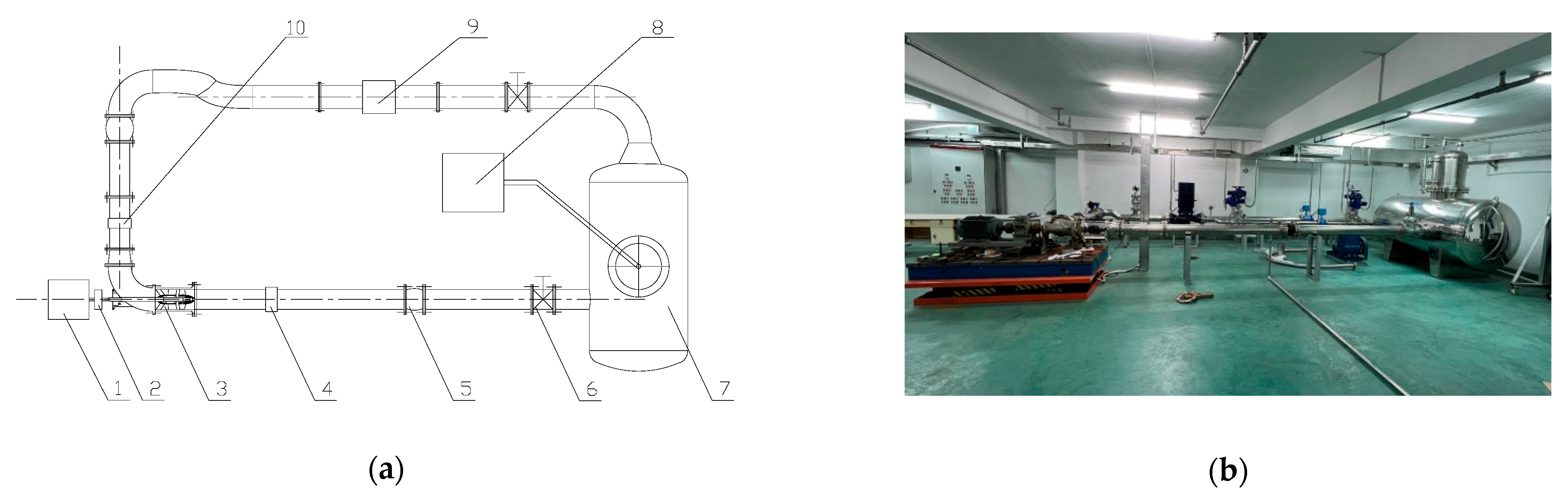
3. Experimental Model and Device
3.1. Experiment Apparatus
3.2. Experiment Method
4. Result and Discussion
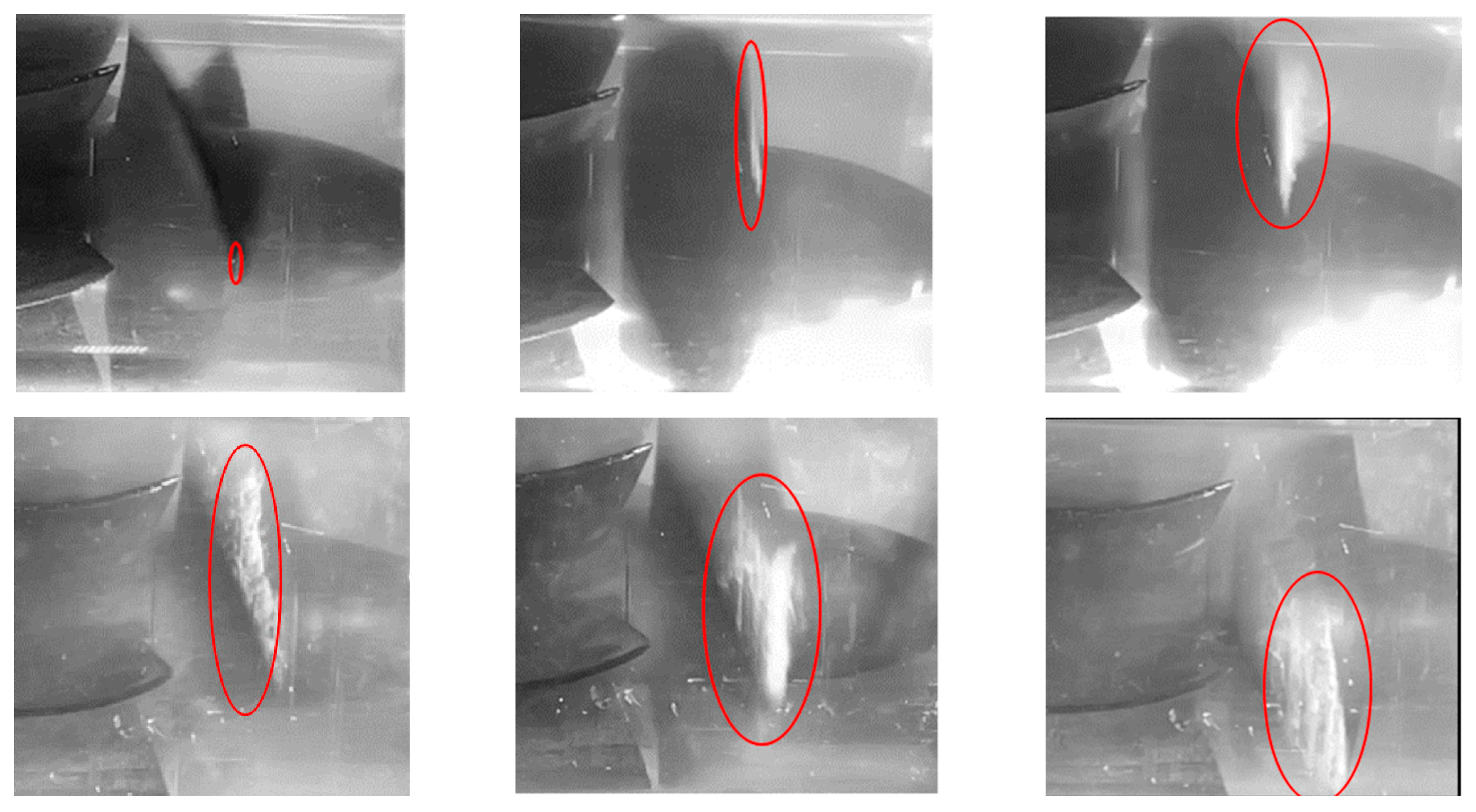
4.1. Production of Cavitation in Axial Flow Pump
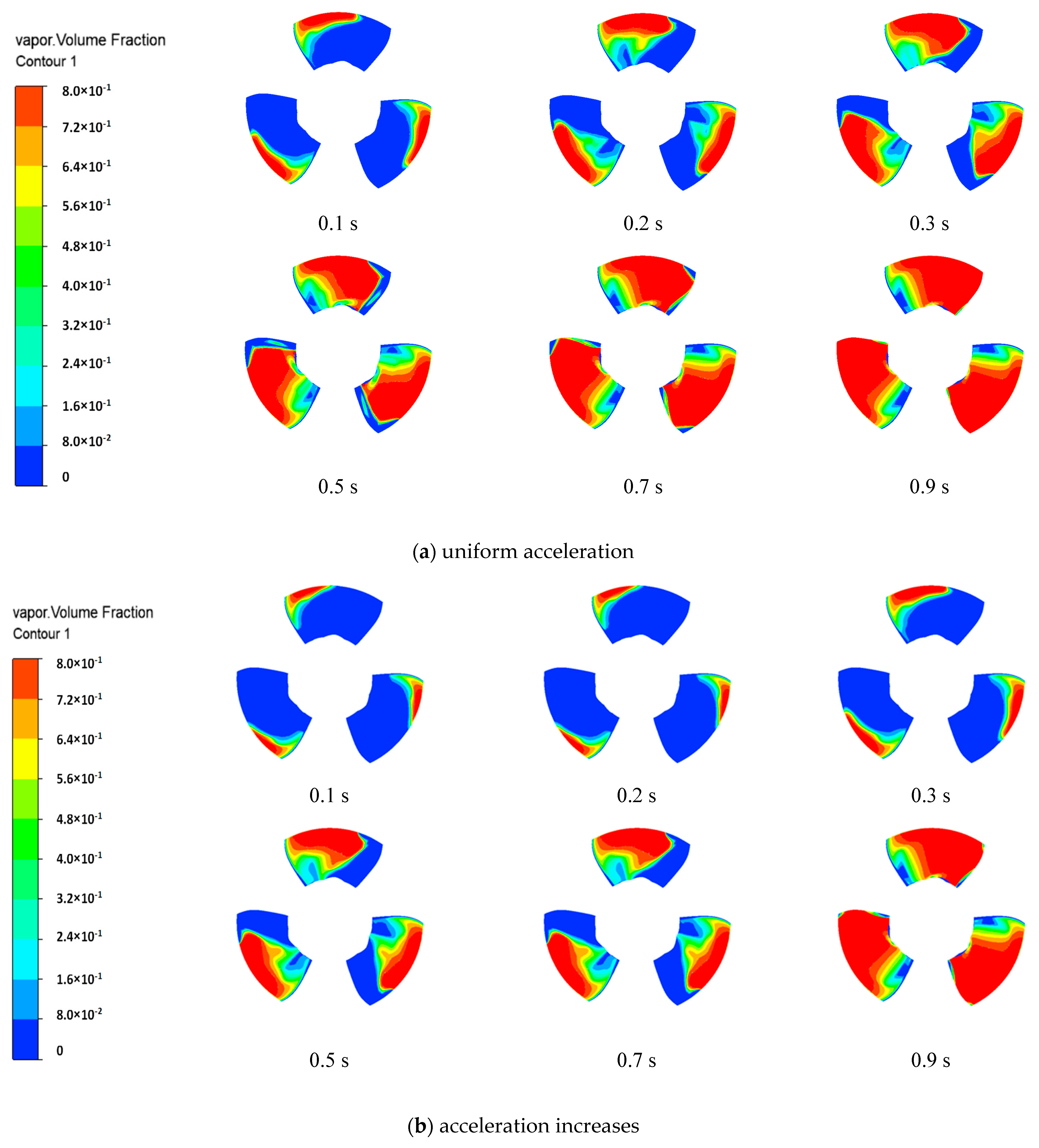
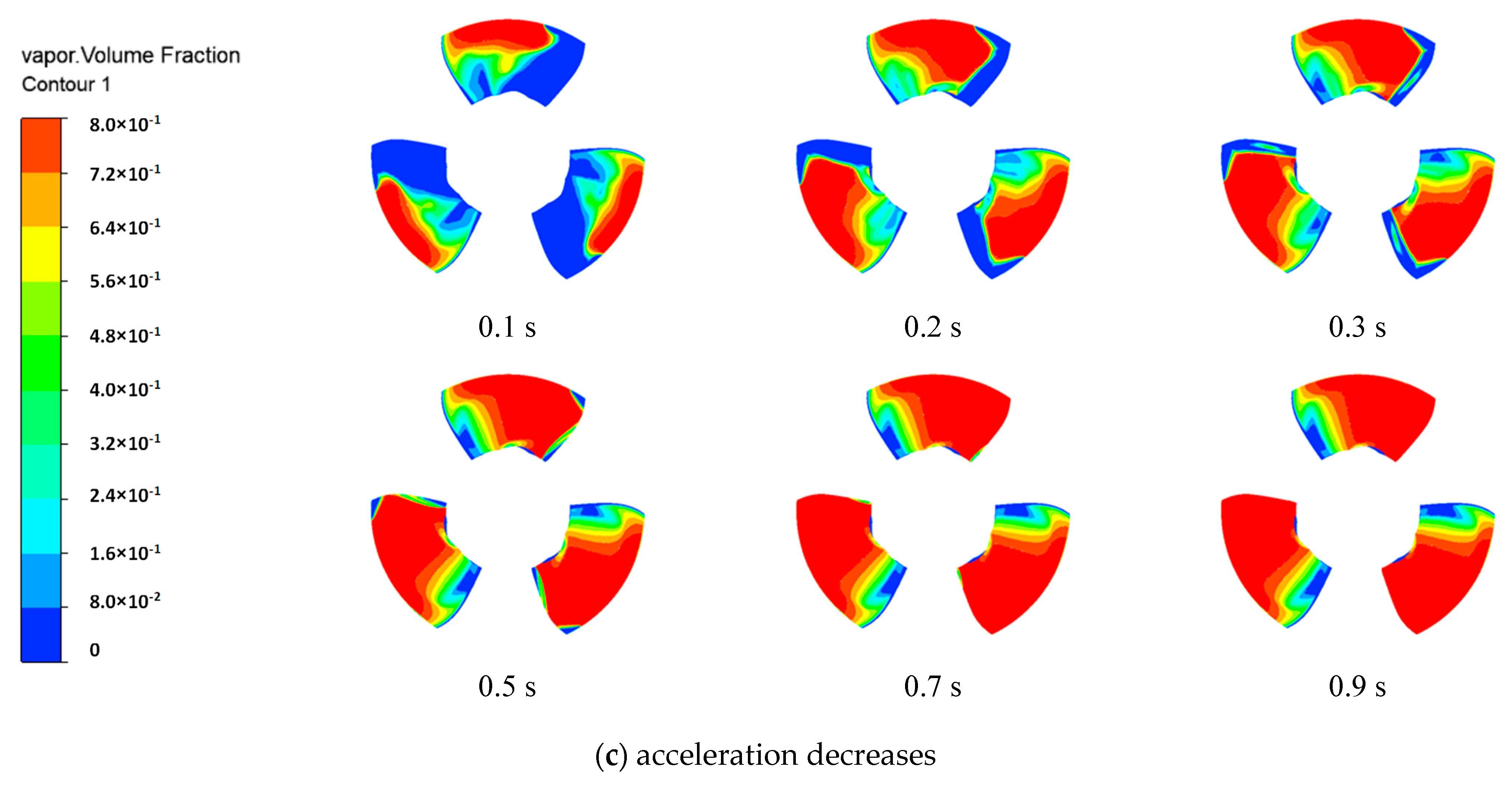
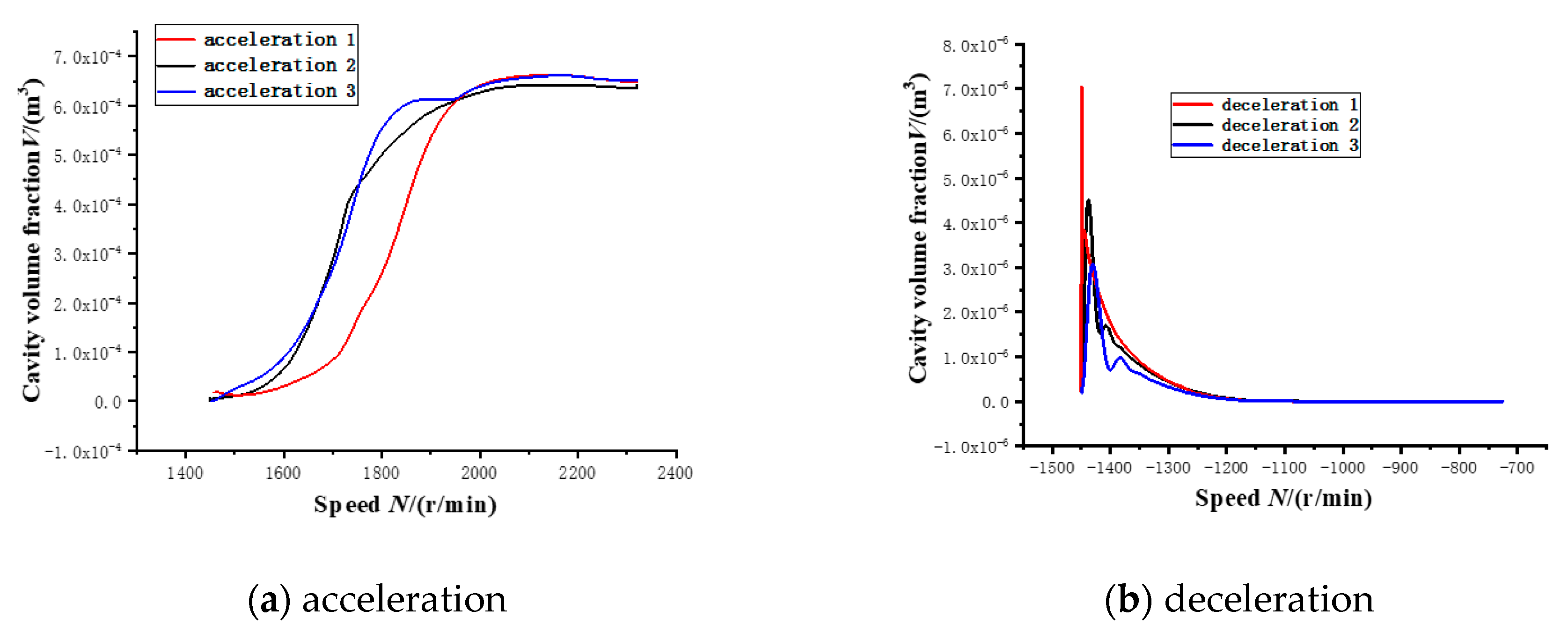
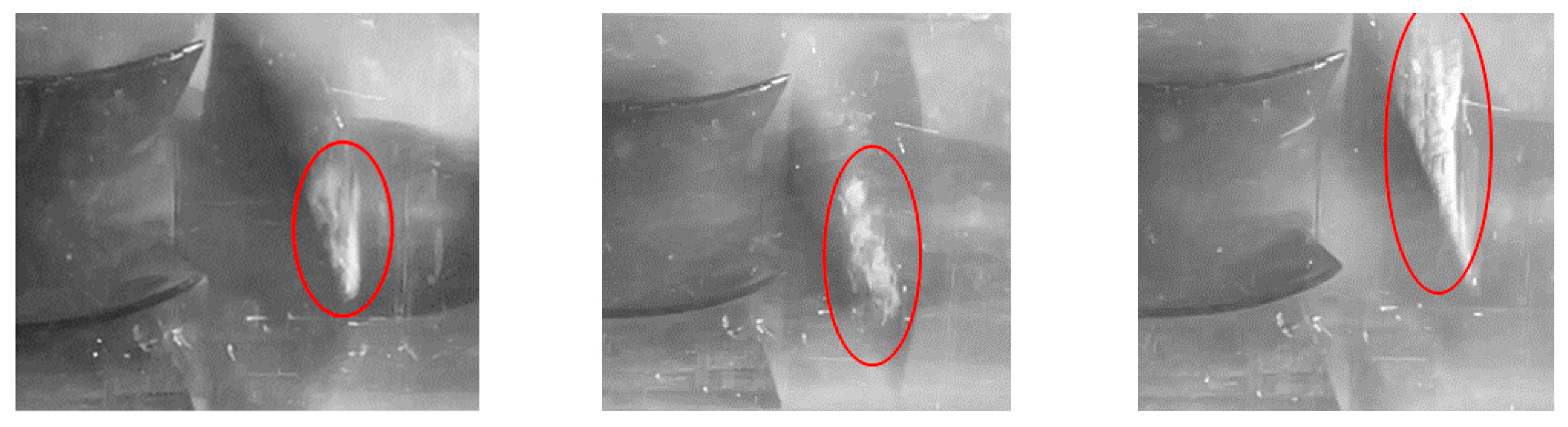
4.2. The Evolution of Cavitation in the Process of VVVF
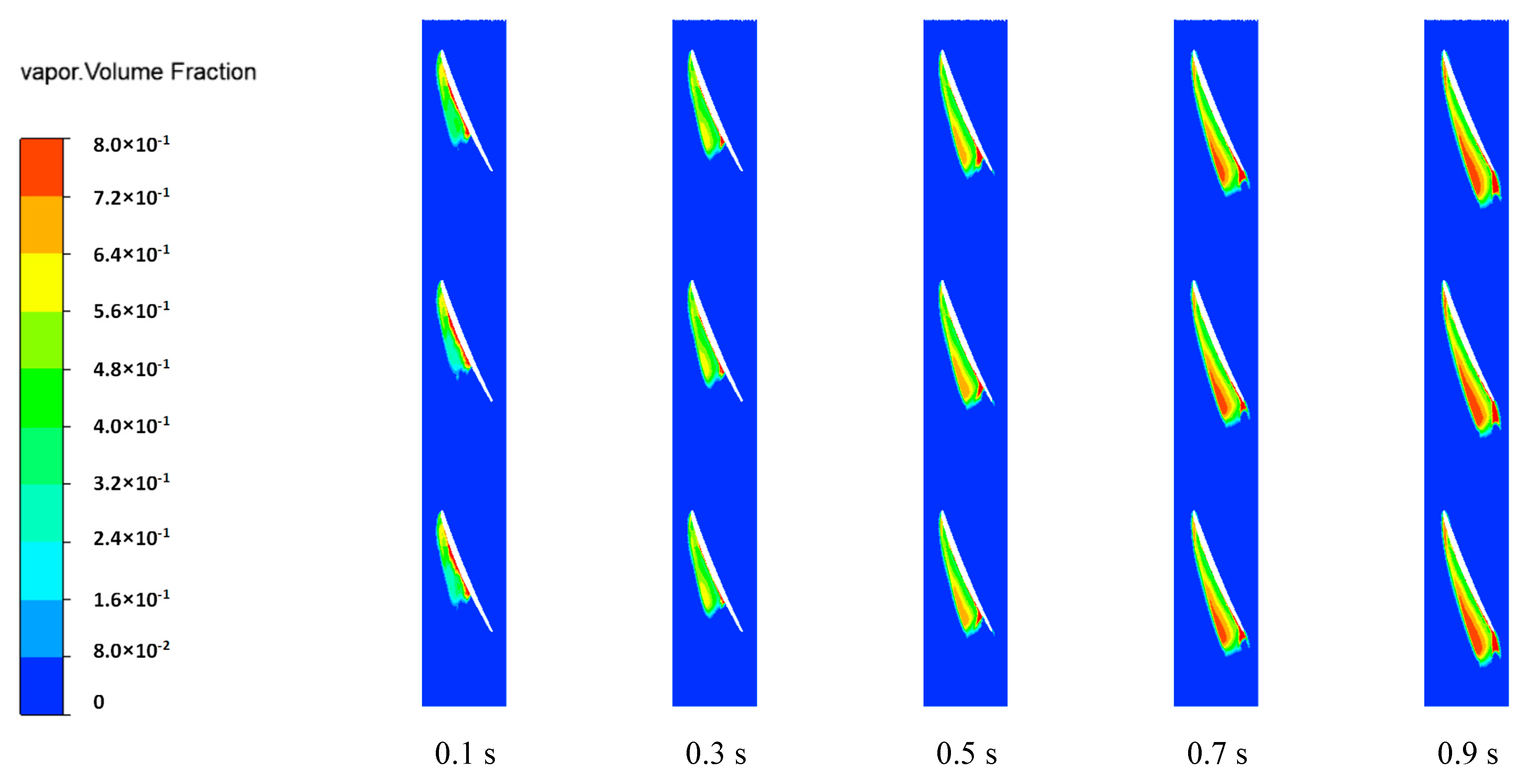
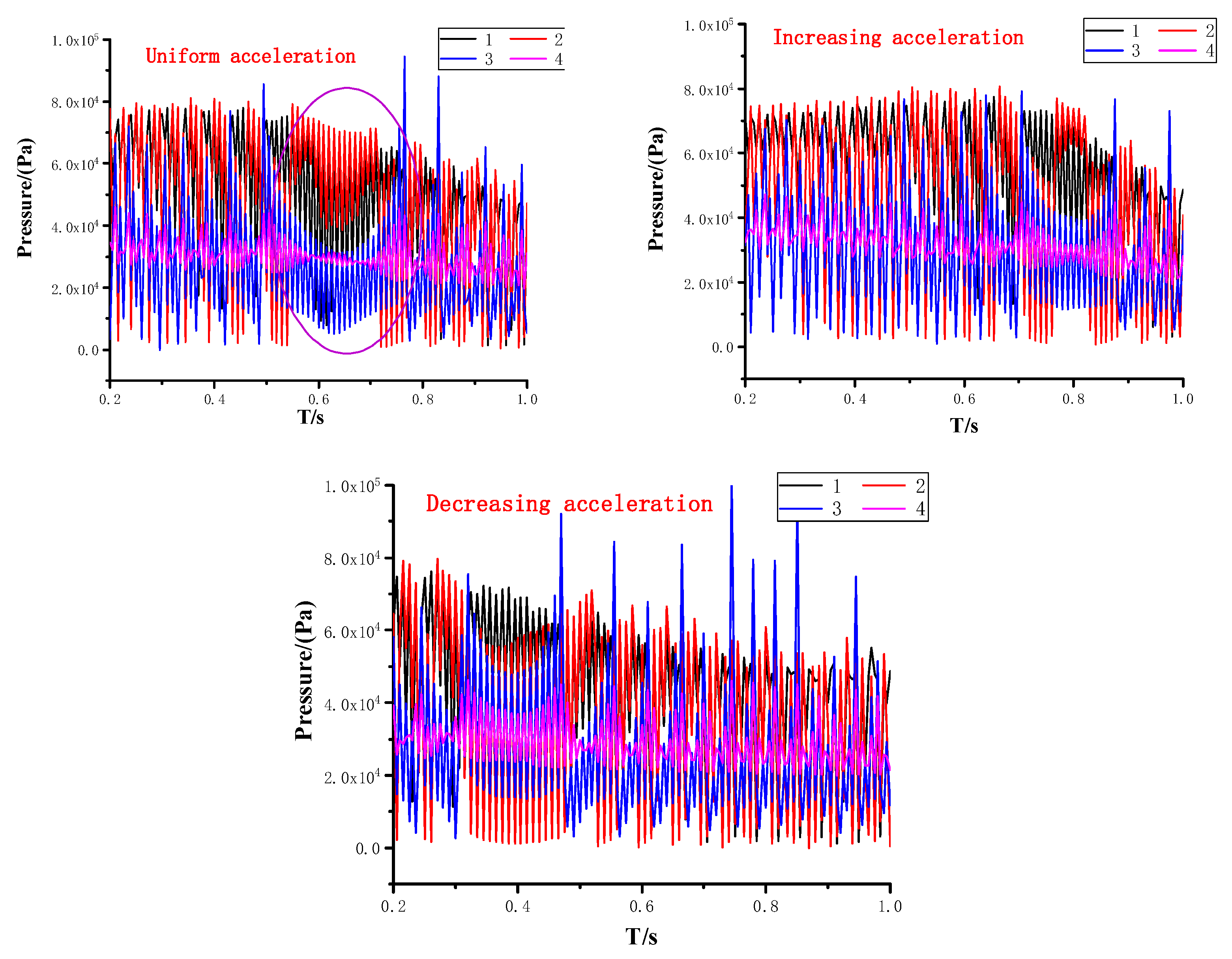
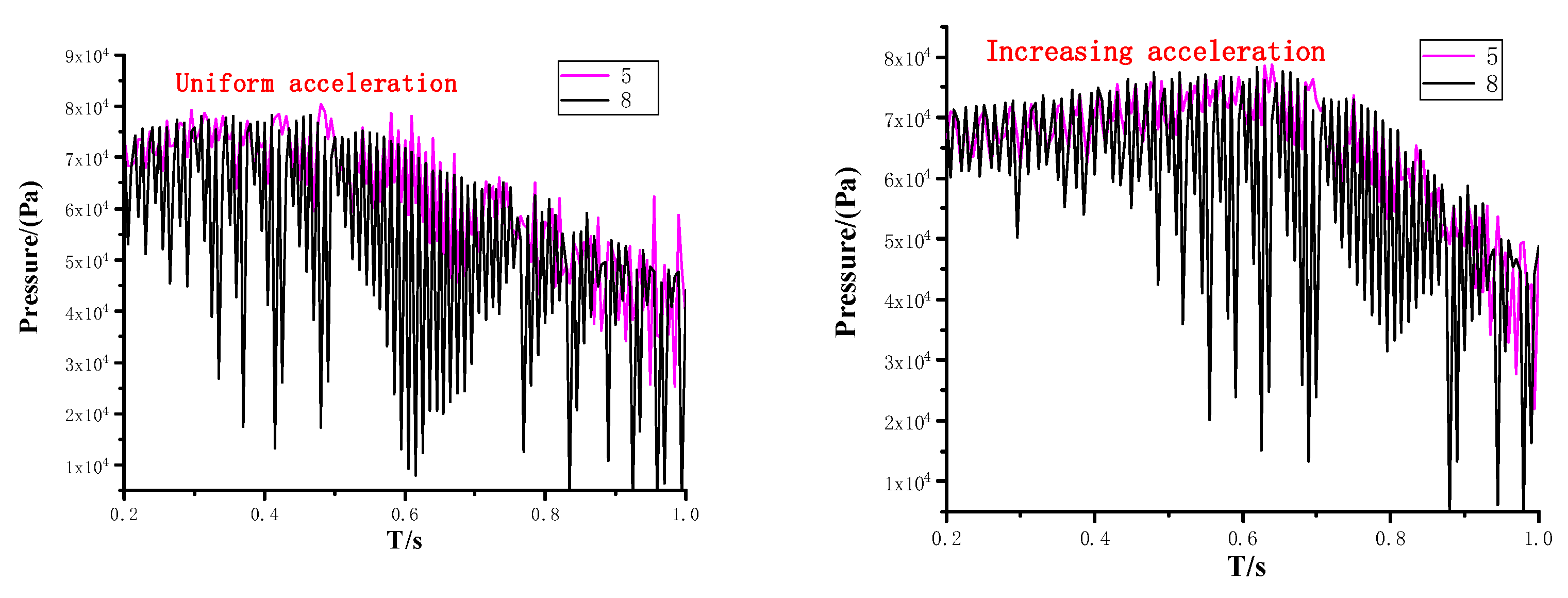
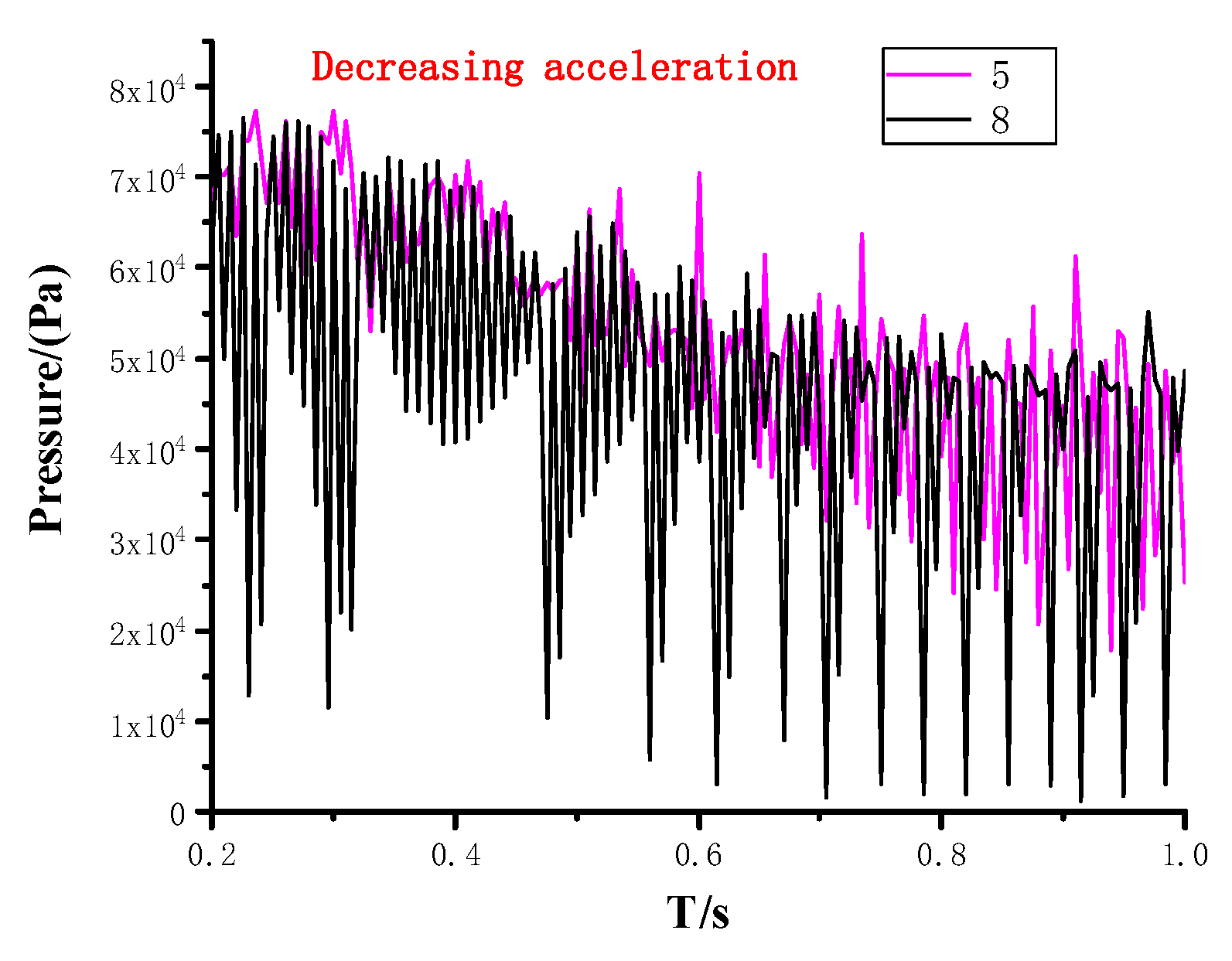
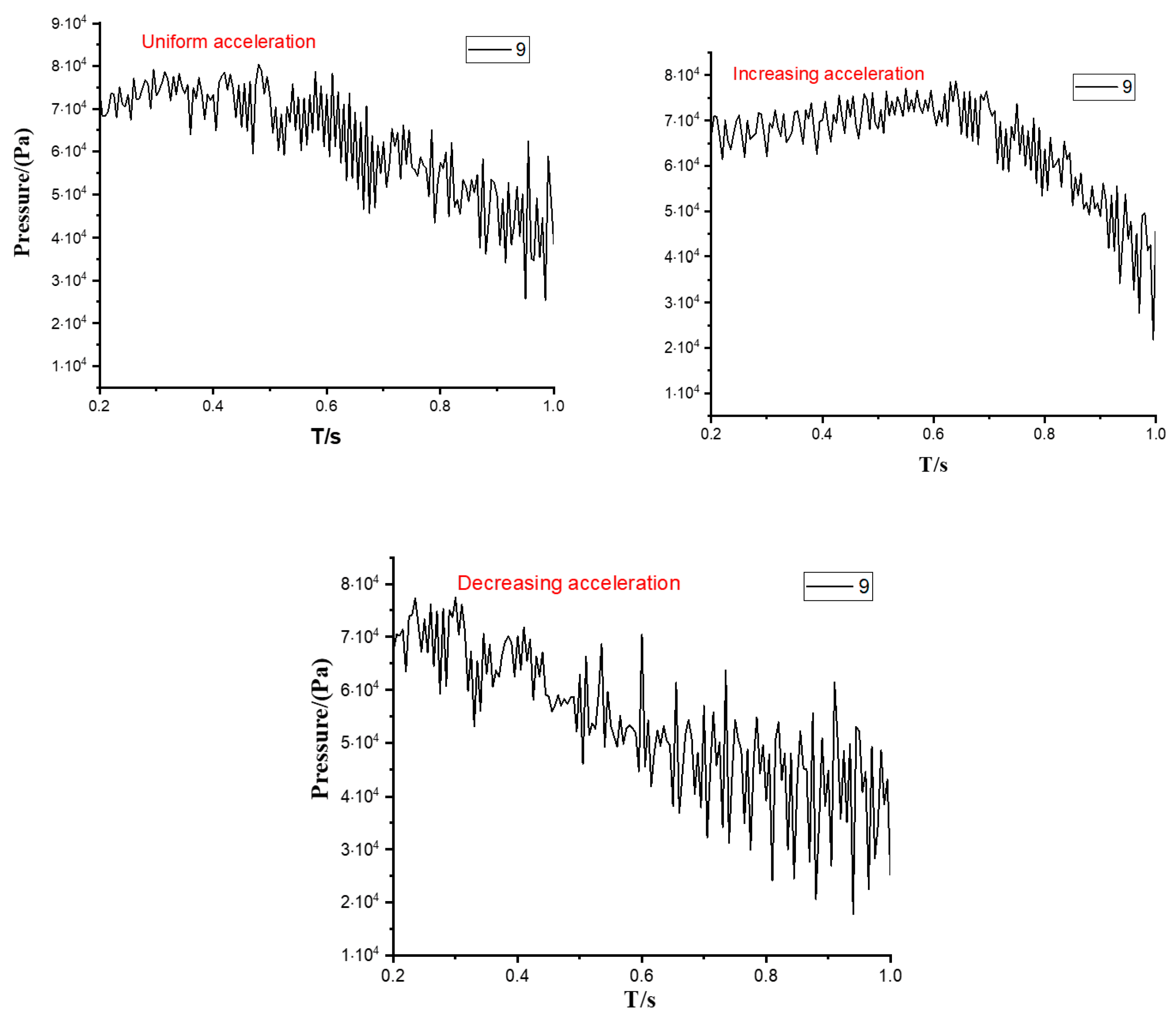
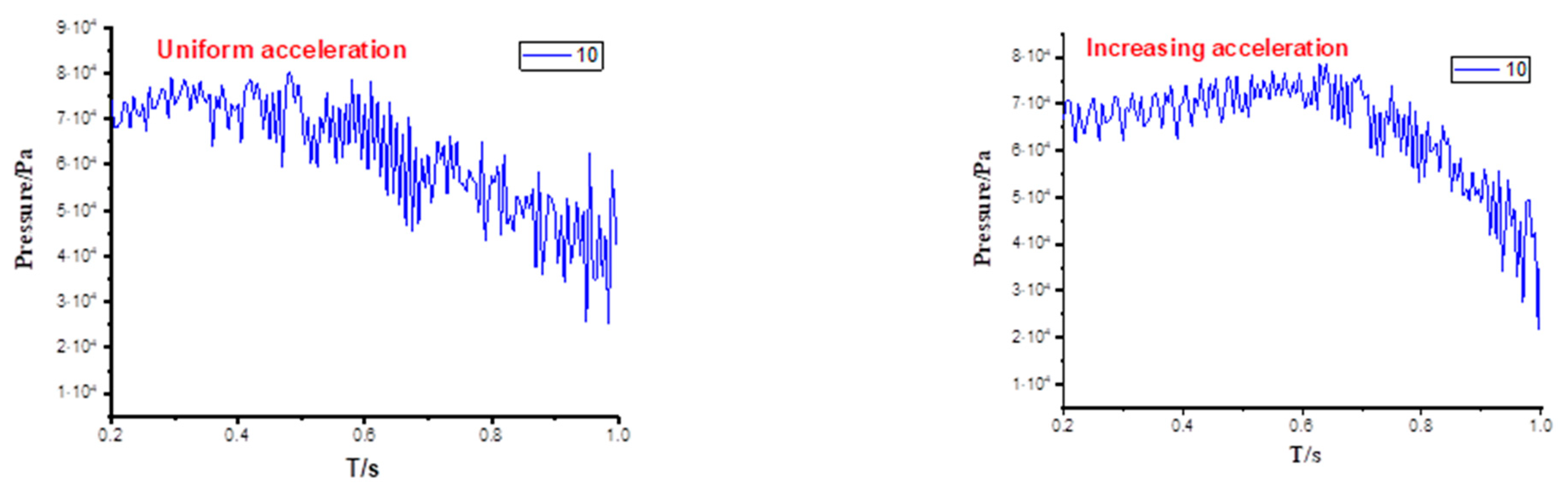
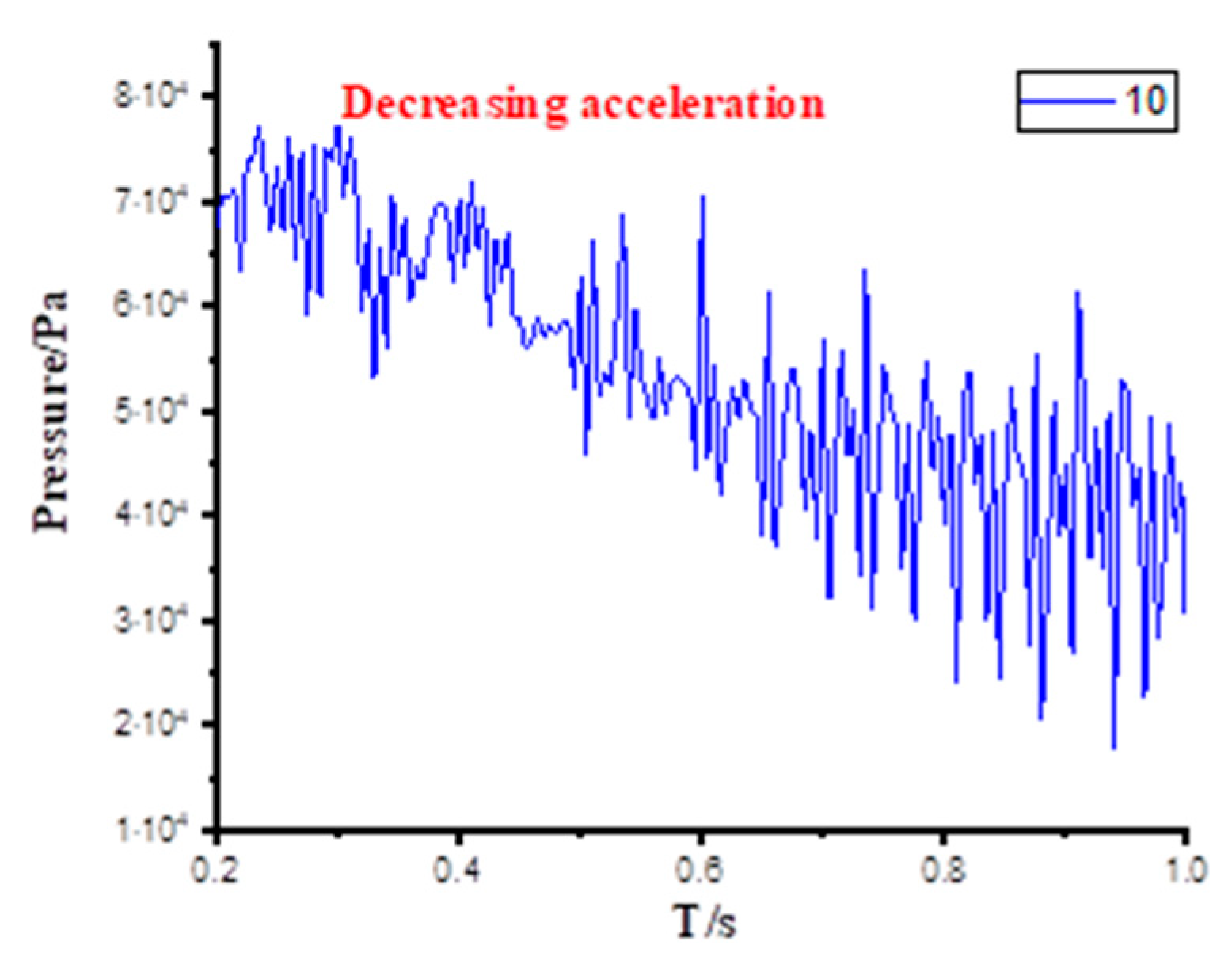
4.3. Influence of Cavitation on Pressure Distribution
4.4. Experiment Results
5. Conclusions
- (1)
- The main area of cavitation is in the impeller region. The impeller rotation speed has a significant effect on cavitation. Excessive rotation speed will make cavitation extend rapidly. Under the frequency conversion scheme with reduced acceleration, it takes only 0.2 s for the impeller surface to completely cavitate.
- (2)
- The growth rate of cavitation mainly depends upon the stability of velocity. In the case of constant acceleration, the growth rate of cavitation is the slowest. However, in the two-variable acceleration schemes, the growth rate of cavitation accelerates, and the change trend is the same.
- (3)
- The pressure distribution in the pump will be seriously affected by cavitation. All three acceleration schemes generate large pressure fluctuation. Under the uniform acceleration scheme with constant acceleration, the fluctuation range of the pressure is more balanced, and the pressure drop is slow. Under the acceleration scheme with increasing acceleration, the pressure fluctuation amplitude increases, and the pressure decline velocity accelerates. Under the acceleration scheme with decreasing acceleration, the pressure in the early stage shows a downward trend with violent fluctuations and gradually tends to be flat in the later stage.
- (4)
- Compared with the three VVVF schemes, the variable acceleration scheme with decreasing acceleration should be avoided as far as possible in order to reduce the influence of cavitation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.; Ye, Y.; Wang, H. Smart watershed and its application prospect. Syst. Eng. Theory Pract. 2011, 06, 1174–1181. [Google Scholar]
- Wang, C.; An, G.; Yuan, C. Smart water development and key technology research. Henan Water Conserv. S.—N. Water Transf. 2015, 14, 98–100. [Google Scholar]
- Ding, C. Centrifugal Pump and Axial Flow Pump; Machine Press: Beijing, China, 1981. [Google Scholar]
- He, J.; Zhang, Y. Current situation and development of axial flow pump. Water Pump Technol. 1998, 06, 29–33. [Google Scholar]
- Liu, X.; Su, Q.; Wu, L.; Yang, X. The small pump station is reformed to save electricity and increase income. Nantong Daily 2009, 6, A01. [Google Scholar]
- Liang, W.; Ai, G.; Dong, W.; Wu, Z.; Zhu, J.; Liu, Y. Effect of cavitation on rotating solid coupling characteristics of axial flow pump blade. Large Mot. Technol. 2021, 5, 92–98. [Google Scholar]
- Liang, W.; Hou, C.; Dong, W.; Wei, Q.; Wu, Z. Numerical analysis of cavitation characteristics of horizontal axial flow pump. J. Drain. Irrig. Mach. Eng. 2020, 38, 764–769. [Google Scholar]
- Wang, J.; Pan, X.; Li, L. Cavitation of axial flow pump. J. Drain. Irrig. Mach. Eng. 2020, 38, 764–769. [Google Scholar]
- Gao, Y.; Hou, Y.; Yang, Z.; Zhang, T. Static stress characteristics of axial-flow pump impeller under cavitation condition. Agric. Eng. 2018, 8, 84–90. [Google Scholar]
- Wu, C.; Tang, F.; Yang, F.; Xie, C.; Sun, D. Effect of cavitation on energy conversion characteristics of impeller of axial flow pump. Adv. Water Resour. Hydropower Sci. Technol. 2019, 39, 49–74. [Google Scholar]
- Fu, S.; Yuan, Z.; Kan, K.; Chen, H.; Han, X.; Liang, X.; Liu, H.; Tian, X. Numerical simulation and experimental study of transient characteristics in an axial flow pump during start-up. Renew. Energy 2020, 119, 1879–1887. [Google Scholar]
- Zhao, Y.; Chen, Q. Application of PLC and frequency control technology in the constant pressure water supply of pump station. Ind. Instrum. Autom. Equip. 2004, 15, 56–65. [Google Scholar]
- Hu, C.; Sang, R. PLC is used to realize variable frequency constant pressure water supply control system of pump station. Drain. Irrig. Mach. 2005, 13, 42–45. [Google Scholar]
- Feng, Z.M.; Guo, C.; Zhang, D.; Cui, W.; Tan, C.; Xu, X.; Zhang, Y. Variable speed drive optimization model and analysis of the comprehensive performance of beam pumping unit. J. Pet. Sci. Eng. 2020, 191, 107155. [Google Scholar] [CrossRef]
- Dmitriev, A.; Gerasimov, V. To the issue of energy efficiency of using frequency-controlled centrifugal pump units. Matec Web Conf. 2018, 170, 03017. [Google Scholar] [CrossRef]
- Cimorelli, L.; Covelli, C.; Molino, B.; Pianese, D. Optimal Regulation of Pumping Station in Water Distribution Networks Using Constant and Variable Speed Pumps: A Technical and Economical Comparison. Energies 2020, 13, 2530. [Google Scholar] [CrossRef]
- Li, L.-M.; Wang, Z.-D.; Li, X.-J.; Wang, Y.-P.; Zhu, Z.-C. Very Large Eddy Simulation of Cavitation from Inception to Sheet/Cloud Regimes by A Multiscale Model. China Ocean. Eng. 2021, 35, 361–371. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Zhu, Z.; Lin, P.; Li, L. Boundary vorticity analysis and shedding dynamics of transient cavitation flow around a twisted hydrofoil. J. Fluids Eng. 2020, 143, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Wang, W.; Li, L.; Huo, Y. Numerical investigation on the evolution of forces and energy features in thermo-sensitive cavitating flow. Eur. J. Mech.—B/Fluids 2020, 84, 233–249. [Google Scholar] [CrossRef]
- Li, Z. Study on Cavitation Flow in Axial Flow Pump; Jiangsu University: Zhenjiang, China, 2011. [Google Scholar]
- Lv, X.; Zhen, Y.; Zhang, D.; Yu, A. CFD analysis of cavitation flow characteristics of axial-flow pump based on FBM model. S.—N. Water Divers. Water Sci. Technol. 2020, 18, 150–165. [Google Scholar]
- Fu, Y.; Yuan, J.; Yuan, S.; Pace, G.; D’Agostino, L.; Huang, P.; Li, X. Numerical and experimental analysis of flow phenomena in a centrifugal pump operating under low flow rates. J. Fluids Eng. 2015, 137, 011102. [Google Scholar] [CrossRef]
- Wu, Y. Method for measuring cavitation performance of axial-flow pump by frequency conversion. Chem. Manag. 2021, 17, 139–141. [Google Scholar]
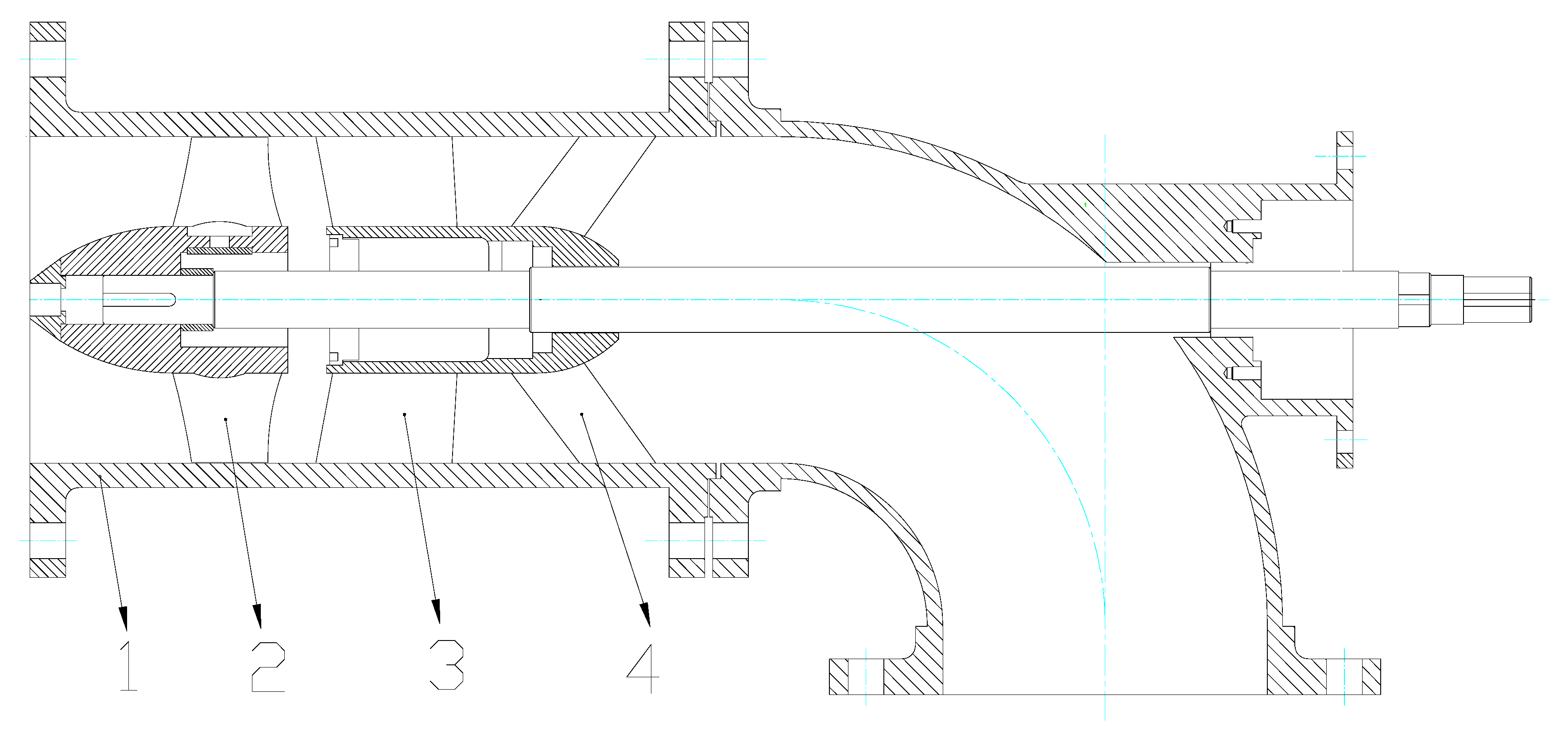
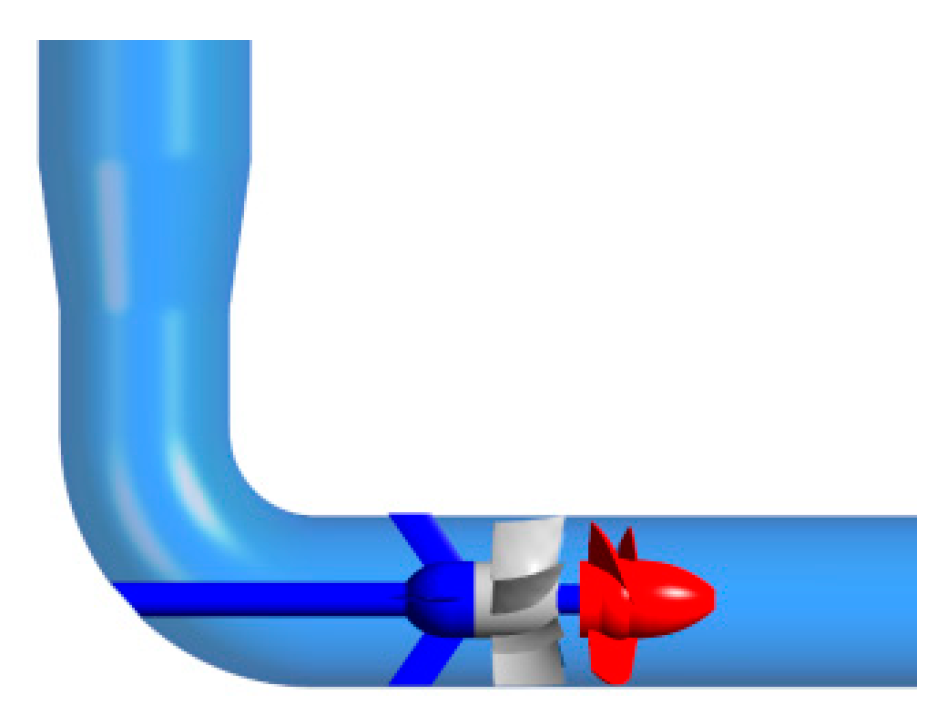





| Main Parameters | Value |
|---|---|
| Flow (m3/h) | 365 |
| Head (m) | 3.02 |
| Number of blades-Zi | 3 |
| Number of guide blades-Zs | 7 |
| Rated speed-n (r/min) | 1450 |
| Impeller inlet diameter-D0 (mm) | 200 |
| Impeller outlet diameter-D2 (mm) | 250 |
| Area | Part | Grid Form | Number of Grid | Number of Nodes |
|---|---|---|---|---|
| Inlet | Stationary domain | Structured grid | 825,000 | 846,651 |
| Impeller | Rotating domain | Structured grid | 6,877,440 | 7,034,616 |
| Guide vane | Stationary domain | Structured grid | 1,355,585 | 1,415,904 |
| Support plate | Stationary domain | Structured grid | 179,520 | 190,400 |
| Bend | Stationary domain | Structured grid | 370,064 | 385,900 |
| Outlet | Stationary domain | Structured grid | 491,040 | 504,100 |
| Name of Hydraulic Component | Settings |
|---|---|
| Inlet | Total pressure: 50 kPa |
| Inlet pipe | Smooth wall surface |
| Impeller | Rotation speed: 1450 r/min Frozen rotor model |
| Guide vane | Smooth wall surface |
| Support plate | Smooth wall surface |
| Bend | Smooth wall surface |
| Outlet | Outlet flow: 365 m3/h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Tan, L.; Shi, W.; Chen, C.; Francis, E.M. Numerical Simulation of Axial-Flow Pump Cavitation Based on Variable Frequency Speed Regulation. Water 2022, 14, 2757. https://doi.org/10.3390/w14172757
Ye J, Tan L, Shi W, Chen C, Francis EM. Numerical Simulation of Axial-Flow Pump Cavitation Based on Variable Frequency Speed Regulation. Water. 2022; 14(17):2757. https://doi.org/10.3390/w14172757
Chicago/Turabian StyleYe, Jincheng, Linwei Tan, Weidong Shi, Cheng Chen, and Egbo Munachi Francis. 2022. "Numerical Simulation of Axial-Flow Pump Cavitation Based on Variable Frequency Speed Regulation" Water 14, no. 17: 2757. https://doi.org/10.3390/w14172757






