A Comparison of Different Water Indices and Band Downscaling Methods for Water Bodies Mapping from Sentinel-2 Imagery at 10-M Resolution

Abstract

Satellite-based remote sensing is important for monitoring the spatial distribution of water resources. The water index is currently one of the most widely used water body extraction methods. Based on Sentinel-2 remote sensing image, this study combines area-to-point regression kriging interpolation, bilinear interpolation, and the Gram–Schmidt (GS) pan-sharpening method with the water indices MNDWI, AWEI_sh and WI₂₀₁₅ to compare different water body extraction methods. The experimental results showed that all water indices have satisfactory extraction ability, with the kappa coefficient as an accuracy threshold above 0.8. Moreover, the GS downscaling method combined with the WI₂₀₁₅ yielded the best performance. This research demonstrates the efficacy of the WI₂₀₁₅ method to extract water bodies in urban areas and its ability to comprehensively describe river water bodies. The findings indicate that high-resolution band information is particularly important for improving low-resolution band downscaling results and can significantly minimize erroneous water body extraction.

1. Introduction

Urban surface water bodies are important factors influencing the urban ecological environment and exert a certain impact on urban public health and people′s quality of life [1,2]. At the same time, urban water bodies play a key role in urban planning, regional climate change, the heat island effect, and water resource utilization [3,4]. In recent years, with adverse factors such as rapid urbanization, environmental degradation, and extreme climate, the water body area in urban cities has been decreasing significantly [5]. Therefore, the accurate and dynamic monitoring of urban surface water bodies has become essential for water resource management and decision-making. As a large-scale and real-time Earth observation technology, remote sensing has been widely used in surface feature recognition and extraction. Accordingly, remote sensing provides feasible technical means for the automatic and precise extraction of urban surface water bodies [6,7]. The growing role of satellite remote sensing technology in water extraction applications is becoming increasingly remarkable. To identify water body features, remote sensing images mainly use spectral differences between water bodies and other ground objects in different wavelength bands. The development of water body remote sensing methods has progressed through several stages, from the initial manual visual interpretation technique to semi-automatic extraction and classification techniques based on spectral features, and then further to extraction methods which couple spectral features and spatial information [8,9,10,11]. Currently, automatic high-precision water body extraction methods based on deep learning represent the gold standard [12,13,14,15].

Water index-based algorithms have become important for implementing rapid water body mapping in large-scale regions. Water index- and threshold-based approaches have been widely used to identify water bodies due to their unique spectral characteristics in the visible and infrared regions. Both approaches have undergone significant evolution. In 1996, McFeeters [16] proposed the normalized difference water index (NDWI) using the value of the green band minus the near-infrared (NIR) band, divided by the sum of the two bands. Under this, water bodies have positive values, while non-water bodies have negative values. Although NDWI can suppress and remove non-water features to a large degree, it fails to efficiently suppress built-up land signals. Consequently, certain features may actually comprise a mixture of water and built-up land noise. In 2006, based on the NDWI, in 2006, Xu proposed a modified normalized difference water index (MNDWI), replacing the NIR band with the shortwave-infrared (SWIR) band, which helped to remove disturbances caused by built-up lands [17]. However, the optimal thresholds varied based on location and time, and the method could not effectively remove shadow noise in some areas. In 2014, Feyisa et al. proposed an automated water extraction index (AWEI) and used different AWEI formats for scenes with shadows (AWEI_sh) and without shadows (AWEI_nsh) [18]. This technique was sufficiently separated and systematic so as to improve the accuracy of water body mapping. Related scholars have used the natural logarithm of each band of the Landsat 7 ETM + image as a proxy of the reflection coefficient and interaction conditions, creating the water index WI₂₀₀₆. Subsequently, the water index WI₂₀₁₅ is based on WI₂₀₀₆, using linear discriminant analysis classification (LDAC) to determine the coefficient of the best segmentation training area category, further improving water extraction accuracy [19].

Many researchers have used moderate resolution imaging spectroradiometer (MODIS) [20], Landsat [21,22], and Sentinel [23,24] multispectral remote sensing images to achieve large-scale water body extraction research based on various water indices, such as MNDWI. In recent years, high-resolution remote sensing technology has achieved significant development. However, these fine spatial solution images, such as Gaofen-2 Satellite (GF-2) and Satellite Pour l′Observation de la Terre (SPOT), have no SWIR band, making it impossible to use the water index method [25]. In contrast, Sentinel-2 provides publicly available images. The Sentinel-2 mission has been organized by the Global Monitoring for Environment and Security. Using a bi-satellite system, it acquires multispectral, high-resolution optical observations over global terrestrial surfaces with a high revisitation frequency, approximately five days. Such a system is important for dynamic land cover mapping and updating. Sentinel-2 carries a multispectral instrument with 13 spectral bands spanning the visible spectrum (VIS) and NIR to SWIR. These spatial resolutions range from 10 to 60 m with a 290 km field of view on the ground [26]. With high-frequency and high-spectral resolution imaging, Sentinel-2 allows intensively and continuously monitoring of the Earth’s surface. Sentinel-2 multispectral instrument imagery includes 20 m resolution SWIR bands and 10 m resolution green and NIR bands, rendering water mapping based on water indices at 10 m resolution possible.

A useful way to improve the performance of water body mapping using Sentinel-2 imagery is to produce water indices results by downscaling the SWIR bands from 20 to 10 m. Trivially, the key challenge lies in accurately increasing the spatial resolution of the SWIR band. Spatial interpolation (such as bilinear interpolation) and image fusion (such as pan-sharpening) are the two most widely used methods to increase the spatial resolution of remote sensing imagery [27]. The spatial interpolation method is directly applied to coarse spatial resolution images without requiring additional datasets. In contrast, image fusion, such as pan-sharpening, is premised on the availability of the fine spatial resolution panchromatic (PAN) band of the same scene, aiming to downscale coarse multispectral imagery to the spatial resolution of the PAN band. Pan-sharpening is widely applied to remote sensing images with coarse multispectral bands and a fine spatial resolution PAN band [28].

Nevertheless, most previous studies primarily evaluated the effect of band downscaling methods or water indices on remote sensing water body extraction. However, combinations of typical band downscaling methods and frequently-used water indices have not been synthetically compared and analyzed. From this perspective, this study aims to compare the results of remote sensing water body extraction based on combinations of different band downscaling methods and water indices. Specifically, the effects of three types of factors on water body extraction were evaluated: (1) the extraction capability of the water indices MNDWI, AWEI_sh, and WI₂₀₁₅; (2) the effect of the SWIR band downscaling results based on area-to-point regression kriging interpolation (ATPRK), bilinear interpolation (BIL), and the Gram–Schmidt (GS) pan-sharpening method; and (3) the segment precision between water/non-water bodies based on the marker-controlled watershed (MCW) algorithm.

2. Materials and Methods

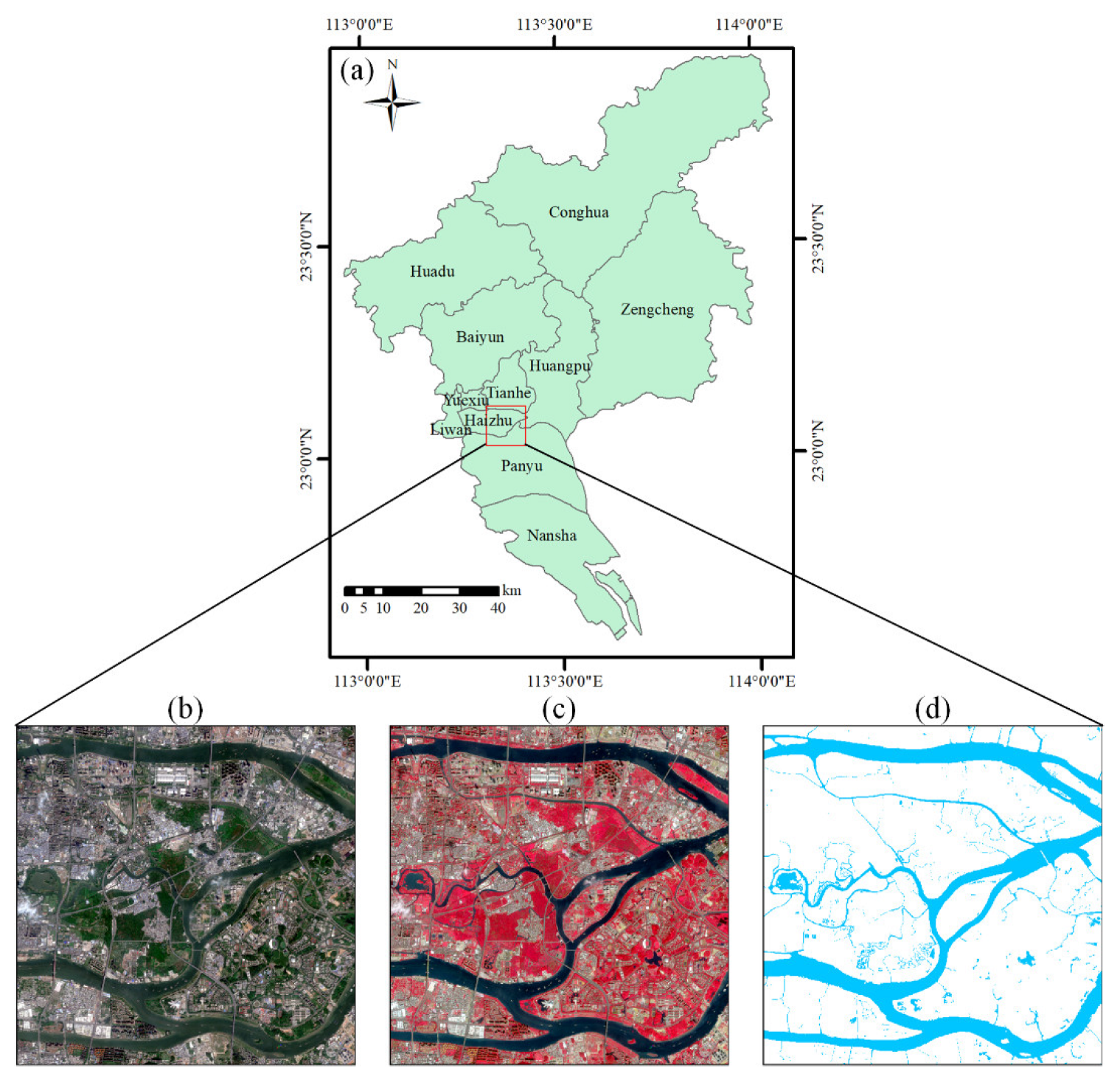
2.1. Study Area

This study is a preliminary exploration to evaluate combinations of several kinds of downscaling methods and water indices in urban cities. Therefore, a typical urban area in Guangzhou city has been chosen for this comparative experiment. The study area covers the northeastern part of Haizhu District and the northernmost area of Panyu District, Guangzhou, covering a total area of more than 100 km² (Figure 1). This urban area mainly includes large water bodies, such as the Haizhu Wetland National Park, Huangpuyong, and Guanzhou waterways, as well as many small water bodies. The densely distributed buildings and their shadows in urban areas tend to significantly interfere with the remote sensing extraction of water bodies, causing poor accuracy.

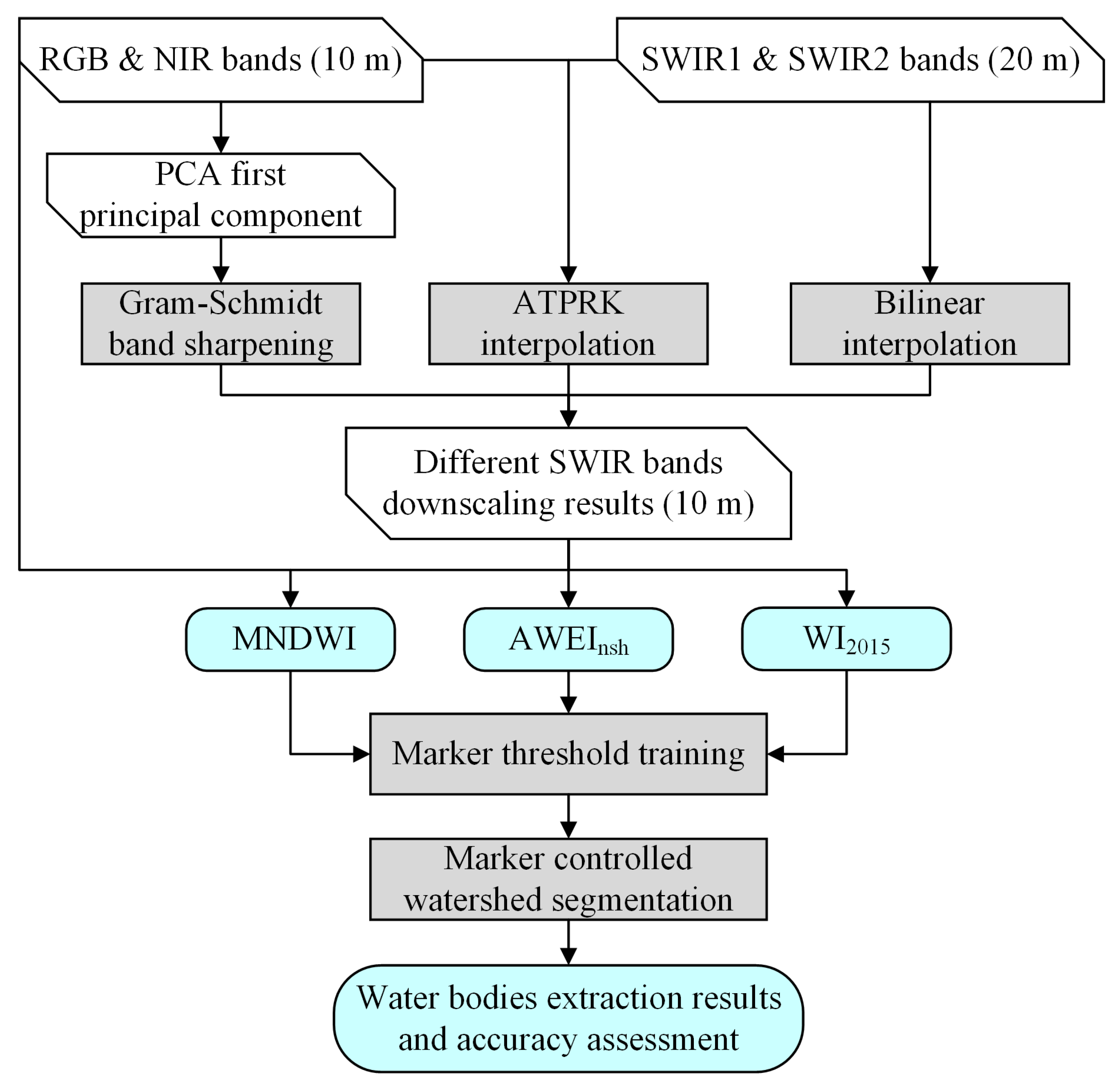
2.2. Methods

Figure 2 shows the workflow for the remote sensing extraction of water bodies. First, the spatial resolutions of the Sentinel-2 SWIR bands were improved to 10 m through BIL, ATPRK interpolation [29], and GS pan-sharpening. Then, the MNDWI, AWEI_sh, and WI₂₀₁₅ water indices were calculated using the 10 m VIS, NIR, and SWIR bands. Next, masker threshold training was performed for each water index image, and the marker-controlled watershed algorithm was used to realize the segmentation and extraction of water bodies. Finally, waterbody reference data were used to evaluate and compare different combinations of band downscaling methods and water indices in terms of extraction accuracy.

2.2.1. Water Indices

NDWI is the first water index proposed for water body remote sensing extraction, based on the combination of the green band ${\mathsf{\rho }}_{\mathrm{green}}$ and the NIR band ${\mathsf{\rho }}_{\mathrm{NIR}}$ of remote sensing images, and is calculated as follows:

$$\mathrm{NDWI}=\frac{{\mathsf{\rho }}_{\mathrm{green}}-{\mathsf{\rho }}_{\mathrm{NIR}}}{{\mathsf{\rho }}_{\mathrm{green}}+{\mathsf{\rho }}_{\mathrm{NIR}}}$$

(1)

NDWI mainly takes advantage of the strong absorption of water in the NIR band and the absence of strong reflectivity from vegetation [16]. It is used to mine water information from an image by suppressing vegetation and highlighting the water body, enhancing the clarity of the resulting images. However, NDWI considers only vegetation factors, ignoring the two key features of buildings and soil. When extracting water information through NDWI, the reflectivity of the green band is much higher than that of the NIR band. As such, the extraction results are often confused with soil and building information. When NDWI was used to extract urban water bodies, there were water bodies with more shadows of buildings, and the effect was poor.

Based on NDWI, the MNDWI modified the band combination of the water index and replaced the NIR band in NDWI with the SWIR band ${\mathsf{\rho }}_{\mathrm{SWIR}}$. The calculation formula is as follows:

$$\mathrm{MNDWI}=\frac{{\mathsf{\rho }}_{\mathrm{Green}}-{\mathsf{\rho }}_{\mathrm{SWIR}}}{{\mathsf{\rho }}_{\mathrm{Green}}+{\mathsf{\rho }}_{\mathrm{SWIR}}}$$

(2)

The spectral characteristics of the building shadows in the green and NIR bands were similar to those of water. Using the SWIR band to replace the NIR band, the contrast between water bodies and building shadows was significantly enhanced, which greatly improved the contrast between these two ground features, ultimately promoting accurate extraction of water body information in cities and towns. Xu [17] conducted experiments using remote sensing images containing different types of water bodies. The analysis revealed that, relative to NDWI, MNDWI could better extract fine features of water bodies, including the distribution of suspended sediments and water quality. Feyisa et al. [18] conducted experiments on Landsat TM images and proposed AWEI for factors such as low classification accuracy and relatively unfixed threshold selection in previous water body information extraction. AWEI_nsh is suitable for settings without shadows, whereas AWEI_sh is designed to eliminate shadows and other ground objects easily confused with water information in the AWEI_nsh extraction results. Therefore, AWEI_sh is suitable for scenes with more shadows; its formula is as follows:

$${\mathrm{AWEI}}_{\mathrm{sh}}={\mathsf{\rho }}_{\mathrm{blue}}+2.5{\mathsf{\rho }}_{\mathrm{Green}}-1.5\left({\mathsf{\rho }}_{\mathrm{NIR}}+{\mathsf{\rho }}_{\mathrm{SWIR}1}\right)-0.25{\mathsf{\rho }}_{\mathrm{SWIR}2}$$

(3)

WI₂₀₀₆ is a water index created using standard variables to analyze the emissivity of the atmospheric surface. The natural logarithm of each band of the Landsat 7 ETM+ images was used to determine the reflection coefficient and interaction conditions. It has been applied to the extraction research of eastern Australian wetlands. In 2015, based on WI₂₀₀₆, Fisher et al. [19] created a new water index, WI₂₀₁₅, which uses LDAC as a coefficient to determine the best segmentation training area category. The calculation formula is as follows:

$${\mathrm{WI}}_{2015}=1.7204+171{\mathsf{\rho }}_{\mathrm{Green}}+3{\mathsf{\rho }}_{\mathrm{Red}}-70{\mathsf{\rho }}_{\mathrm{NIR}}-45{\mathsf{\rho }}_{\mathrm{SWIR}1}-71{\mathsf{\rho }}_{\mathrm{SWIR}2}$$

(4)

2.2.2. Gram–Schmidt Pan-Sharpening

Spatial interpolation and pan-sharpening algorithms are typically used to achieve spatial downscaling of low-resolution bands. The most widely used pan-sharpening algorithms include the principal component analysis (PCA) [29], hue–saturation–value (HSV) [30], high pass filter (HPF) [31], and GS techniques [32]. Specifically, GS exhibits the highest spectral fidelity and can maintain the consistency of the band spectral characteristics before and after pan-sharpening; that is, the high-resolution band data obtained by downscaling retains the spectral characteristics of the original low-resolution band. Therefore, this study uses the GS pan-sharpening algorithm to preserve the original Sentinel-2 SWIR spectral information as much as possible.

There is a lack of panchromatic band information in Sentinel-2 images, whereas GS pan-sharpening requires the incorporation of high-resolution band information, similar to the PAN band. The resolutions of all four VIS/NIR multispectral bands of the Sentinel-2 image have been determined to be 10 m. However, the correlation between the bands tends to lead to data redundancy. The classical PCA method is widely used for the dimensionality reduction of multispectral remote sensing image band information since PCA can compress VIS/NIR multispectral bands into a panchromatic-like band. By linearly transforming the four VIS/NIR bands, mutually orthogonal spectral spaces are generated, in which the first principal component (FPC) contains the most abundant information. Therefore, the FPC can be regarded as a 10 m panchromatic-like band. Through fusion with the FPC using the GS method, the spatial resolution of the SWIR band can be increased to 10 m.

2.2.3. Area-to-Point Regression Kriging (ATPRK)

ATPRK was used to perform remote sensing image band fusion. ATPRK combines the traditional regression kriging interpolation and quantitative remote sensing scale conversion theory. First, one must assume that the band reflectivity $Z^l\left(x_i\right)$ is a random variable of the grid points $x_i\left(\mathrm{i}=1,\dots ,\mathrm{M}\right)$ in the low-resolution band $\mathrm{l}\left(\mathrm{l}=1,\dots ,\mathrm{L}\right)$, M is the number of grid points. $Z^k\left(v_{\mathrm{j}}\right)$ is the random variable of the grid points $v_{\mathrm{j}}\left(\mathrm{j}=1,\dots ,{\mathrm{MF}}^2\right)$ in the high-resolution band $\mathbf{k}\left(\mathbf{k}=1,\dots ,\mathrm{K}\right)$, and $\mathrm{F}$ is the ratio of the high- and low-resolution values. According to the regression kriging theory, the spatial downscaling results of the band $\mathrm{l}$ achieved by ATPRK in the high-resolution grid $v$ are realized by the estimation and addition of the trend term and residual term ${\widehat{m}}^{\mathrm{l}}\left(v\right)$ and ${\widehat{r}}^{\mathrm{l}}\left(v\right)$, respectively), as shown in the following formula:

$${\widehat{Z}}^{\mathrm{l}}\left(v\right)={\widehat{m}}^{\mathrm{l}}\left(v\right)+{\widehat{r}}^{\mathrm{l}}\left(v\right)$$

(5)

At a specific high-resolution grid point $v_0$, the estimated value ${\widehat{m}}^{\mathrm{l}}\left(v_0\right)$ of the trend item was obtained by linear regression of the value $Z^k\left(v_0\right)$ at the high-resolution band $\mathbf{k}$:

$${\widehat{m}}^{\mathrm{l}}\left(v_0\right)={\displaystyle \sum }_{\mathrm{k}=0}^{\mathrm{K}}{\mathrm{a}}_{\mathrm{k}}^{\mathrm{l}}{\mathbf{Z}}^{\mathbf{k}}\left(v_0\right),{\mathbf{Z}}^0\left(v_0\right)=1$$

(6)

According to the assumption of scale invariance, the regression model above is consistent with the regression model established by the value $Z^l\left(x\right)$ at the low-resolution band $\mathrm{l}$ and the value $Z^k\left(x\right)$ at the upscaling band $k$:

$${\mathbf{Z}}^{\mathrm{l}}\left(x\right)={\displaystyle \sum }_{\mathrm{k}=0}^{\mathrm{K}}{\mathrm{a}}_{\mathrm{k}}^{\mathrm{l}}{\mathbf{Z}}^{\mathbf{k}}\left(x\right)+{\mathbf{r}}^{\mathrm{l}}\left(x\right),{\mathbf{Z}}^0\left(x\right)=1,\forall x$$

(7)

where ${\mathbf{r}}^{\mathrm{l}}\left(x\right)$ is the regression residual term at the corresponding band $\mathrm{l}$, and the regression coefficient ${\mathrm{a}}_{\mathrm{k}}^{\mathrm{l}}$ is estimated using least squares.

After performing regression analysis on the trend item, ATPRK interpolation can be used to implement spatial downscaling of the residual item. The ATPRK interpolation downscaling results maintain the original spectral band information. The estimated value ${\widehat{r}}^{\mathrm{l}}\left(v_0\right)$ of the residual term at the corresponding high-resolution band $\mathrm{l},$ is the linear weighted average of the residual term ${\mathbf{r}}^{\mathrm{l}}\left(x_i\right)$ of the low-resolution adjacent grid point:

$${\widehat{r}}^{\mathrm{l}}\left(v_0\right)={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathsf{\lambda }}_{\mathrm{i}}{\mathrm{r}}^{\mathrm{l}}\left(x_i\right),\mathrm{s}.\mathrm{t}.{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathsf{\lambda }}_{\mathrm{i}}=1$$

(8)

where $\mathrm{N}$ is the number of adjacent grid points, and ${\mathsf{\lambda }}_{\mathrm{i}}$ is the corresponding weight value calculated by the following Kriging equations:

$$\left[\begin{array}{cc}\begin{array}{cc}{\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(x_1,x_1\right)& \cdots \\ ⋮& \ddots \end{array}& \begin{array}{cc}{\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(x_1,x_{\mathbf{N}}\right)& 1\\ ⋮& ⋮\end{array}\\ \begin{array}{cc}{\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(x_{\mathbf{N}},x_1\right)& \cdots \\ 1& \cdots \end{array}& \begin{array}{cc}{\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(x_{\mathbf{N}},x_{\mathbf{N}}\right)& 1\\ 1& 0\end{array}\end{array}\right]\left[\begin{array}{c}{\mathsf{\lambda }}_1\\ ⋮\\ {\mathsf{\lambda }}_{\mathbf{N}}\\ \mathsf{\mu }\end{array}\right]=\left[\begin{array}{c}{\mathsf{\gamma }}_{\mathrm{fc}}^{\mathrm{l}}\left(v_0,x_1\right)\\ ⋮\\ {\mathsf{\gamma }}_{\mathrm{fc}}^{\mathrm{l}}\left(v_0,x_{\mathbf{N}}\right)\\ 1\end{array}\right]$$

(9)

where ${\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(x_{\mathbf{i}},x_{\mathbf{j}}\right)$ is the area-to-area variogram between the low-resolution grid points on the band, ${\mathsf{\gamma }}_{\mathrm{fc}}^{\mathrm{l}}\left(v_0,x_{\mathbf{j}}\right)$ is the area-to-point variogram between the high-resolution grid points to be estimated and the low-resolution neighboring grid points, and $\mathsf{\mu }$ is the Lagrangian operator. $s$ is assumed to be the distance between the centers of any two grid points. The variograms ${\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(s\right)$ and ${\mathsf{\gamma }}_{\mathrm{fc}}^{\mathrm{l}}\left(s\right)$ can be calculated by a convolution between the point-to-point variogram ${\mathsf{\gamma }}_{\mathrm{ff}}^{\mathrm{l}}\left(s\right)$ and the point spread function ${\mathrm{h}}^{\mathrm{l}}\left(s\right)$ (* is the convolution operator) [33]:

$$\begin{gathered} {\mathsf{\gamma }}_{\mathrm{fc}}^{\mathrm{l}}\left(s\right)={\mathsf{\gamma }}_{\mathrm{ff}}^{\mathrm{l}}\left(s\right){\ast \mathrm{h}}^{\mathrm{l}}\left(s\right) \\ {\mathsf{\gamma }}_{\mathrm{cc}}^{\mathrm{l}}\left(s\right)={\mathsf{\gamma }}_{\mathrm{ff}}^{\mathrm{l}}\left(s\right){\ast \mathrm{h}}^{\mathrm{l}}\left(s\right){\ast \mathrm{h}}^{\mathrm{l}}\left(-s\right) \end{gathered}$$

(10)

It is essential to determine the point-to-point variogram, calculate the low-resolution residual variogram by fitting, and then perform deconvolution inference. Notably, the point spread function selected in this project is a simple arithmetic average operation. Thus, the area-to-area and area-to-point variograms are converted into the mean values of multiple point-to-point variograms for calculation.

The estimated values of the trend item and residual item of the band at the high-resolution grid point were calculated, and the sum of these two was the final spatial downscaling result. The above calculation process was carried out for the low-resolution bands individually. Finally, the resolution of all bands was unified through the fusion of high-resolution and low-resolution bands.

2.2.4. Marker-Controlled Watershed Segmentation

Previous studies have shown that the MCW algorithm is particularly suitable for waterbody segmentation [34]. Compared with algorithms that use a single threshold to segment water/non-water bodies, such as maximum between-class variance, it performs better at the edges of water bodies. The typical process of using the MCW algorithm to conduct water body extraction includes three steps: (1) marking the water body/non-water body area for each water index image (including MNDWI, AWEI_sh, and WI₂₀₁₅), marking the water body/non-water body area with high reliability; (2) gradient image generation: by applying the Sobel operator to each water index image, calculate and generate the corresponding gradient images, which are then used to determine the boundary and markers between water and non-water bodies; (3) performing water body segmentation based on water body/non-water area markers and gradient images. Here, the watershed algorithm iteratively expands each marker until all unmarked pixels are marked as water or non-water.

The last two steps of the MCW algorithm are relatively fixed, with no parameter involved. However, the water body segmentation result is more sensitive to the water/non-water area marking in the first step. Therefore, it was necessary to calibrate the marking selection parameters. In this study, the threshold method was used to automatically generate water/non-water markings, by combining the real distribution data of the water bodies and a pair of mask thresholds determined for each water index. The left range of the smaller threshold and the right range of the larger oner corresponds to the non-water and water areas, respectively. Notably, the transition range between thresholds is divided into water and non-water bodies by the watershed algorithm.

2.2.5. Accuracy Evaluation Indicators

Taking the waterbody reference data of high-resolution remote sensing images of the study area as the standard, the accuracy of the water body results extracted from Sentinel-2 remote sensing images were evaluated. The following four accuracy evaluation indicators were selected: the producer accuracy (PA), user accuracy (UA), overall accuracy (OA), and kappa coefficient. The calculation methods were as follows:

$$\begin{gathered} \mathrm{PA}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} \\ \mathrm{UA}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} \\ \mathrm{OA}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{T}} \\ \mathrm{Kappa}=\frac{\mathrm{T}\times \left(\mathrm{TP}+\mathrm{TN}\right)-\mathsf{\sum }}{\mathrm{T}\times \mathrm{T}-\mathsf{\sum }} \end{gathered}$$

(11)

where TP is the number of water pixels that are correctly extracted, FN is the number of water pixels that have not been extracted, FP is the number of water pixels that are incorrectly extracted, TN is the number of non-water pixels that are correctly extracted, T is the total number of image pixels, and $\mathsf{\sum }=\left(\mathrm{TP}+\mathrm{FP}\right)\times \left(\mathrm{TP}+\mathrm{FN}\right)+\left(\mathrm{FN}+\mathrm{TN}\right)\times \left(\mathrm{FP}+\mathrm{TN}\right)$.

3. Results

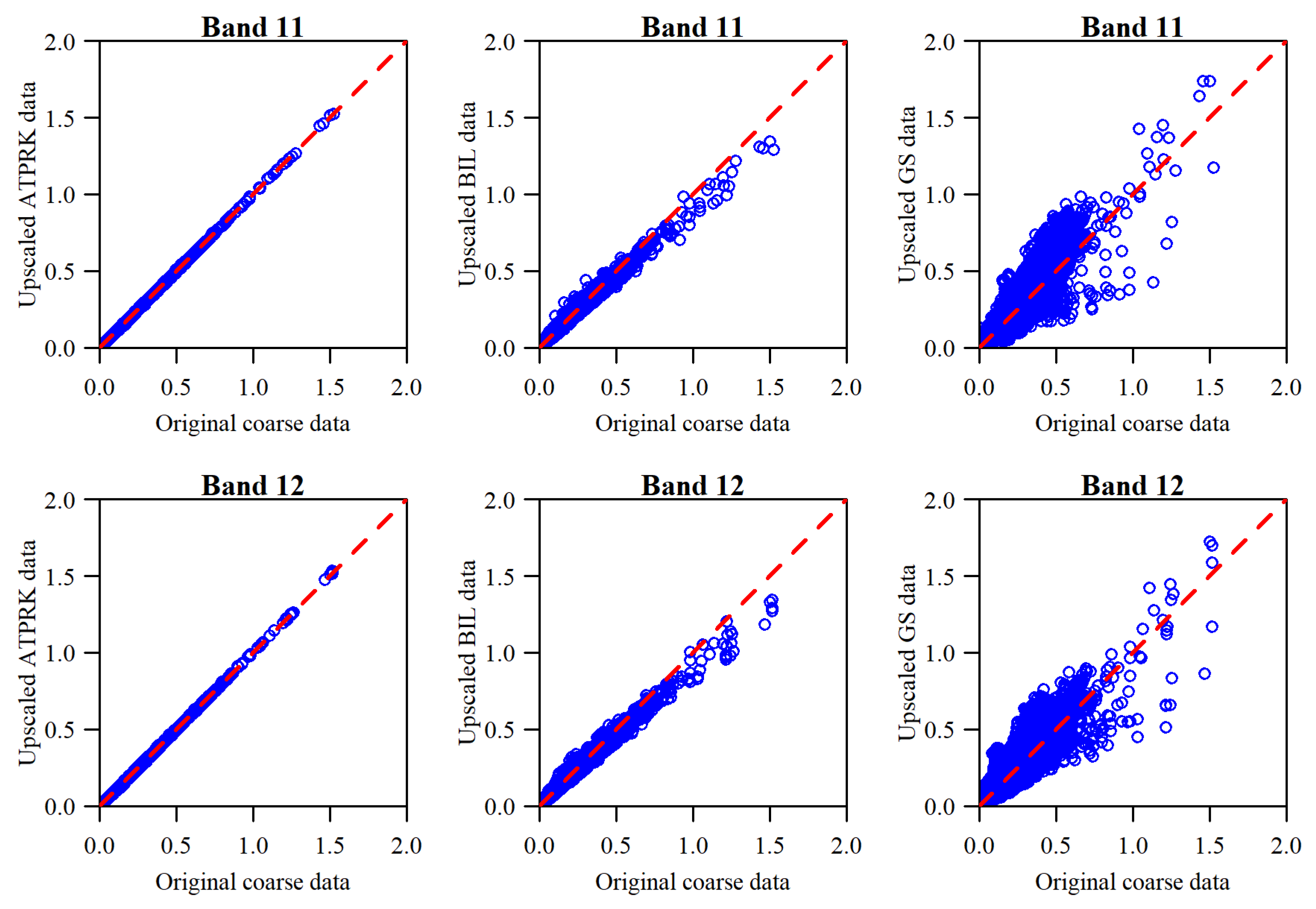
3.1. Band Downscaling Quality

An important criterion for evaluating the quality of a fusion image is its ability to maintain spectral characteristics (i.e., quality preservation). The 10 m band downscaling results generated by the three methods were upscaled to 20 m and then compared with the original 20 m band. Figure 3 shows the scatter plots comparing the upscaled results and the original coarse SWIR bands for the ATPRK, BIL, and GS methods. Notably, the spectral characteristics of each method remain unchanged over different coarse bands. Comparing the quality assurance of different methods, the GS band obtained by upscaling showed the least correlation with the original band. Compared with the GS method, the results of the BIL method had a stronger correlation with the original data but evidently underestimated the high-value area. A significant advantage of the ATPRK method for band fusion was its quality preservation. The comparison results show that ATPRK achieves non-destructive preservation of the original band spectrum information.

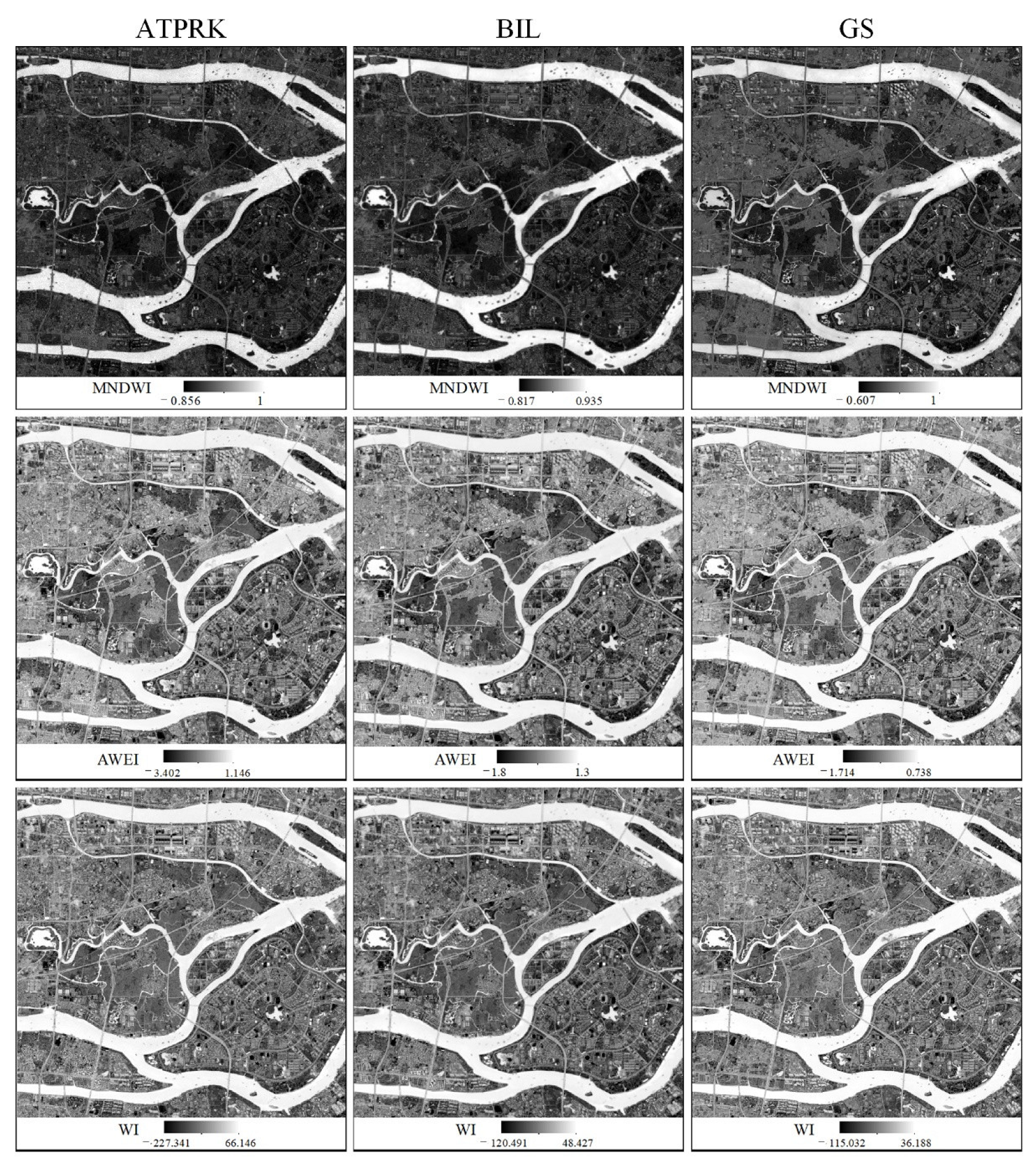
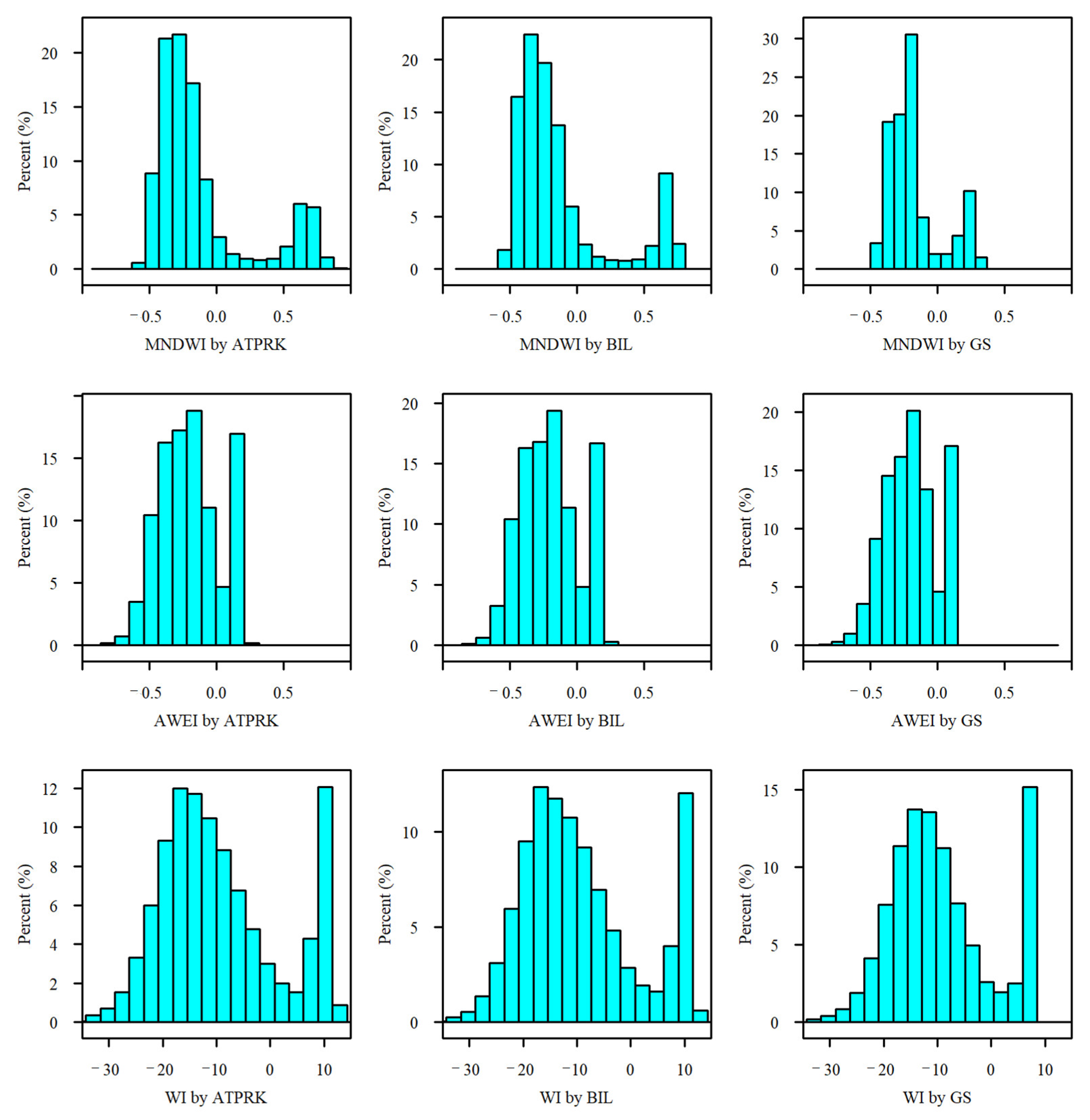
3.2. Water Indices Results

Figure 4 shows the three types of water index results obtained using the BIL, ATPRK, and GS downscaling methods. It is observed that by using the three water indices, the contrast between water bodies and land areas are better highlighted, and the boundaries of the water bodies are sufficiently clear. In the MNDWI image, the contrast between water and land is particularly strong. Conversely, the range of water index values calculated using the SWIR band by downscaling using the ATPRK method was wider than that of the GS and BIL methods. A characteristic of kriging interpolation compared with other interpolation methods was that its interpolation result might exceed the original data range.

Figure 5 shows the histograms of MNDWI, AWEI_sh, and WI₂₀₁₅ water indices using ATPRK, BIL, and GS downscaling methods. All histograms have bimodal shapes, with threshold ranges between water and non-water bodies located at the bottom. The histogram results reveal that the technique of using single threshold values to exactly segment water/non-water bodies belongs to the category of theoretical cases for water index-based extraction methods. Comparatively, the AWEI_sh results derived from the ATPRK, BIL, and GS band downscaling methods all had narrow threshold ranges. Furthermore, for all three water indices, the results derived from the ATPRK and BIL interpolation methods yielded similar numerical ranges, which were wider than those from the GS method.

3.3. Analysis of Water Body Commissions and Omissions

The MCW segmentation algorithm was used to segment each water index image to accurately extract the water body area. By superimposing and comparing the water extraction results with the reference data, misclassified and unidentified water body areas were obtained, as shown in Figure 6 and Figure 7, respectively.

In urban areas, the features most easily misclassified as water bodies are building shadows. Here, we focus on two high building density regions within the study area, which showed obvious shadows on the original image, characterized by similarly low-reflectivity features as water bodies. It can be observed that the water bodies extracted from the water index images were affected by the misclassification of building shadows to a significant extent (e.g., the misclassification in the yellow box). The MNDWI, AWEI_sh, and WI₂₀₁₅ indices corresponding to the BIL method easily misclassified building shadows as water bodies. This was due to the fact that although the BIL interpolation method maintains the original spectral information of the low-resolution NIR band to a certain extent, it does not introduce other high-resolution band information. Therefore, the effect of improving the spatial details is limited. In comparison, the water body extraction results of the MNDWI_ATPRK and WI₂₀₁₅_GS combinations performed better; only a few building shadows were mistakenly identified as water bodies. The results show that the integration of high-resolution band information was particularly important for improving downscaling results of low-resolution bands, which significantly reduced the probability of water body identification. On the other hand, it is difficult to achieve the same effect by relying only on simple spatial interpolation methods (such as the BIL interpolation).

Many small water bodies in the study area were missed or poorly estimated by the three water indices since the ATPRK interpolation, BIL interpolation, and GS pan-sharpening methods unify the spatial resolution of all bands involved in the calculation of the water index to 10 m. Therefore, it is naturally impossible to extract sub-pixel-level small water bodies with a width of less than 10 m. Specifically, the MNDWI_GS and AWEI_sh_GS combinations yielded significant omission errors of a small stream shown in the red box of Figure 7, indicating that the GS pan-sharpening method may be unsuitable for the extraction of small water bodies.

3.4. Quantitative Evaluation of Water Body Extraction Accuracy

In addition to the qualitative and intuitive expression of the results of inaccurate extractions and omissions of water bodies, a variety of precision indicators such as UA were used to quantitatively evaluate the water body extraction results of different downscaling methods and water index combinations.

Table 1. Quantitative evaluation of water body extraction results in different downscaling methods and water indices combinations.

Water Indices	Downscaling Methods	UA	PA	OA	Kappa
MNDWI	ATPRK	95.02%	86.79%	96.45%	0.885
	BIL	94.12%	84.84%	95.92%	0.867
	GS	93.55%	87.56%	96.31%	0.882
AWEIsh	ATPRK	92.32%	87.81%	96.11%	0.876
	BIL	91.51%	87.40%	95.87%	0.868
	GS	93.80%	88.70%	96.57%	0.891
WI2015	ATPRK	93.65%	87.99%	96.41%	0.885
	BIL	92.45%	88.54%	96.27%	0.881
	GS	94.48%	89.10%	96.79%	0.897

shows the accuracy verification indices of water body extraction using the three water indices generated by different downscaling methods. Overall, each combination achieved good water extraction results; several accuracy evaluation indicators, such as UA, were above 80%. The MNDWI against ATPRK had the best UA accuracy (95.02%). The WI₂₀₁₅ for GS provided the best PA accuracy (89.10%), OA accuracy (96.79%), and kappa coefficient (0.897). Overall, the WI₂₀₁₅ calculated using GS downscaling band information yielded the best water extraction effect.

The ATPRK method is designed to preserve the spectral information of observed images. However, the water mapping results of AWEI_sh and WI₂₀₁₅ from ATPRK were poorer than those from GS. The water mapping results are related to the ability of downscaling methods to maintain spectral information. Still, they are also affected by other properties, such as the preservation of spatial details. Similar results were found in a previous study [5]. Although the HPF downscaling method can better preserve the spectral information of the original image, it cannot produce water body maps with higher accuracy than the other methods.

The extraction effects of the three water indices in the study area were reflected by the average accuracy indices of the water body extraction results corresponding to different downscaling methods. MNDWI displayed the highest average UA accuracy (94.23%), implying the least commission errors. WI₂₀₁₅ has the highest average PA value (88.54%), meaning the lowest omission errors. Likewise, the OA and kappa coefficients returned the best results for water bodies extracted by WI₂₀₁₅. Therefore, in this study, it can be concluded that WI₂₀₁₅ performed best on the urban water bodies mapping, while MNDWI and AWEI_sh provided similar performances.

4. Conclusions

Based on Sentinel-2 remote sensing images, this study used BIL interpolation, ATPRK interpolation, and panchromatic sharpening GS spatial downscaling methods to increase the spatial resolution of the SWIR bands to 10 m and calculate the corresponding water indices MNDWI, AWEI_sh, and WI₂₀₁₅. The MCW water segmentation algorithm was used to segment the water/non-water body area on each water index image and qualitatively analyze the water body extraction, inaccurate extractions, and omission results. Finally, combined with UA, PA, OA, and the kappa coefficient, a quantitative evaluation of the water body extraction results by combining the different spatial downscaling methods with water indices was conducted.

Our results indicate that the water index based on Sentinel-2 remote sensing images can effectively extract water body information in urban areas, especially river water bodies. The water body extraction accuracy of different water indices remained above 0.8. The combination of the GS spatial downscaling method and the WI₂₀₁₅ water index yielded the best water body extraction efficiency, with a kappa coefficient of 0.897. The effectiveness and feasibility of using satellite remote sensing technology to monitor the distribution of water bodies were verified.

Limited by the spatial resolution of Sentinel-2 images, the extraction results of each water index did not have enough resolution to provide information on sub-pixel-level, small water bodies with a width less than 10 m. Extracting small water bodies has long been a challenge in remote sensing water body extraction research. In follow-up research, we will implement high-resolution remote sensing images (such as GF-2 images) to comparatively assess the extraction capabilities of various water indices for small water bodies in urban areas.