Effects of Microtopography on Runoff Generation in Plain Farmland: New Insights from an Event-Based Rainfall–Runoff Model
Abstract
:1. Introduction
2. Materials and Methods
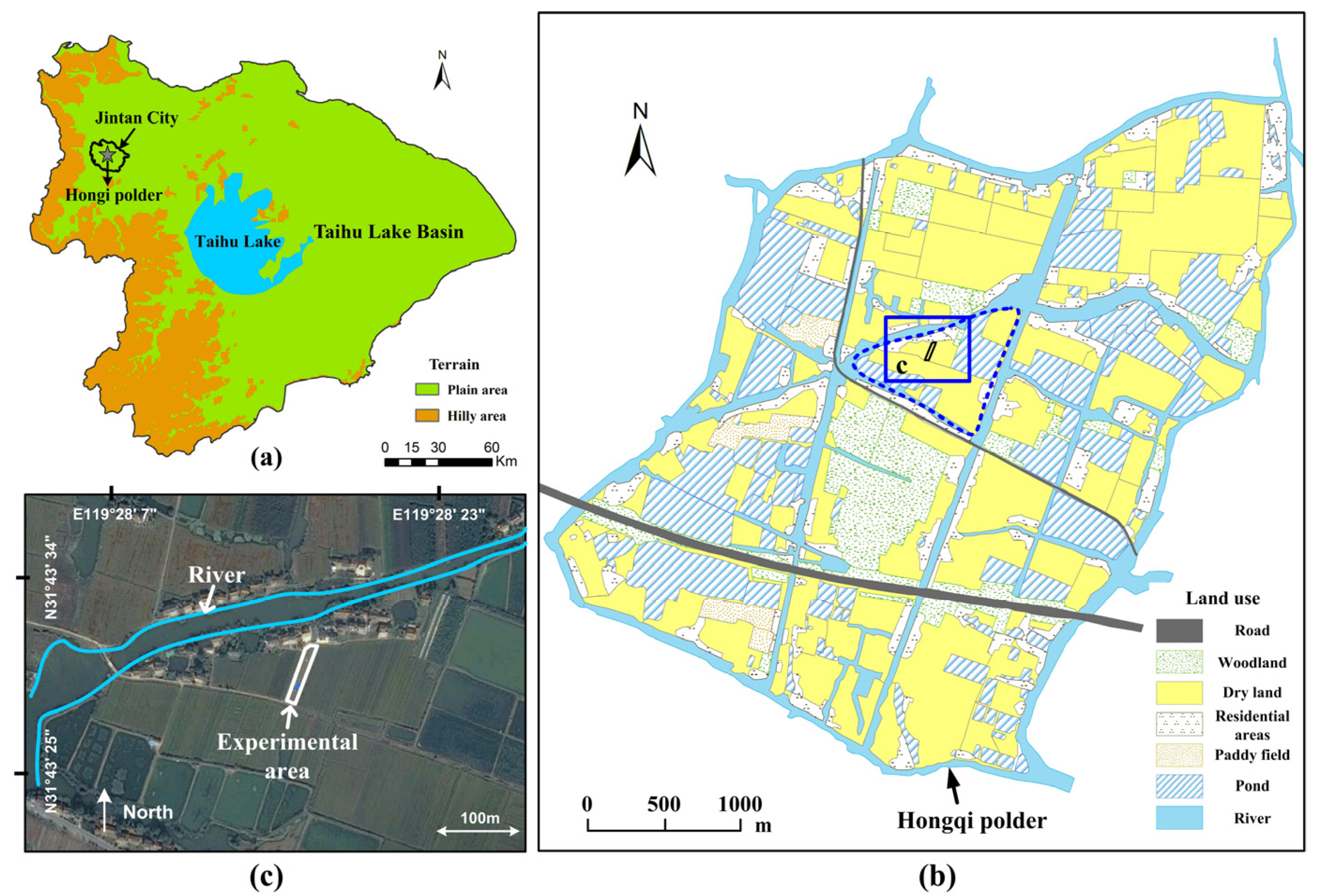
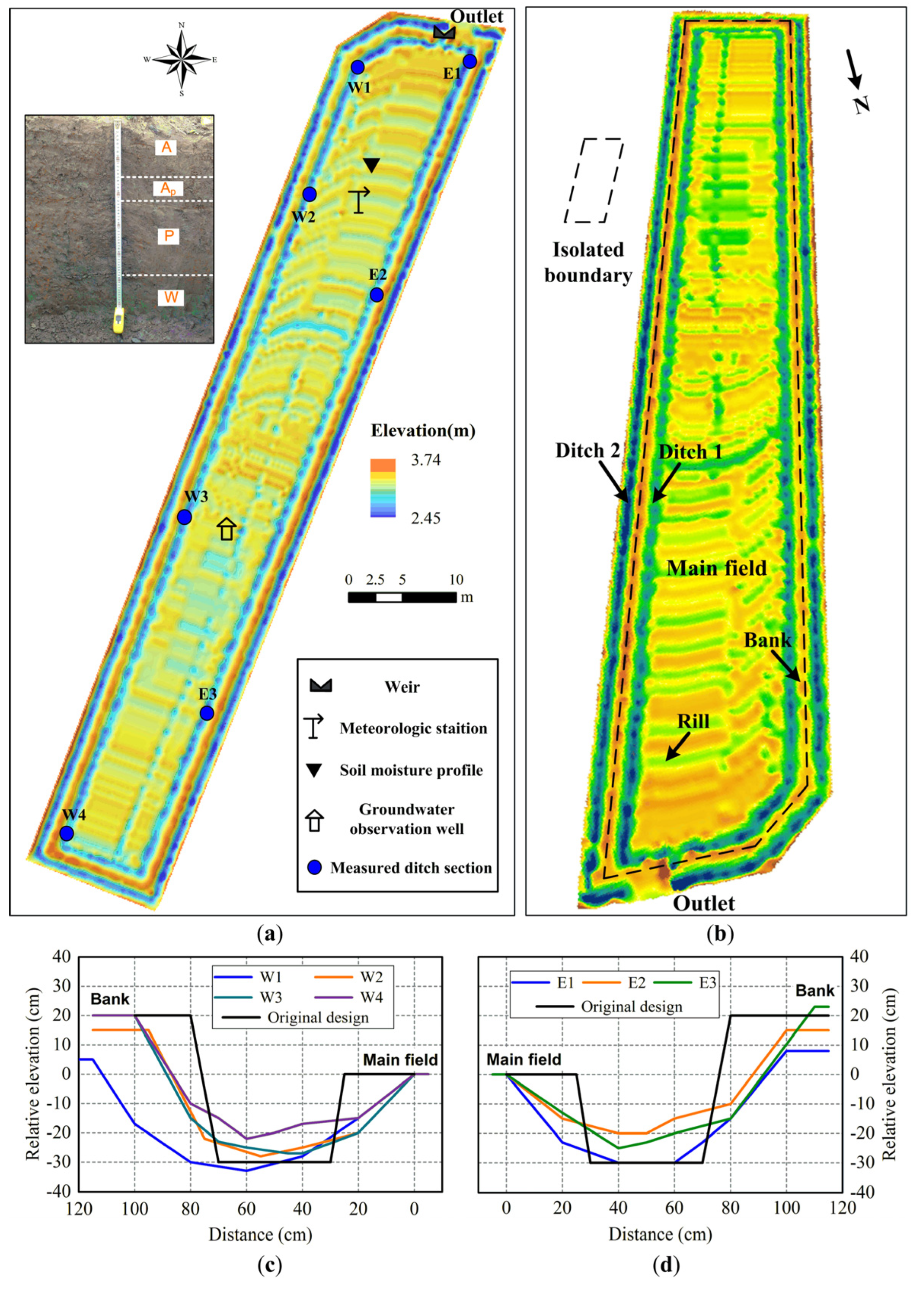
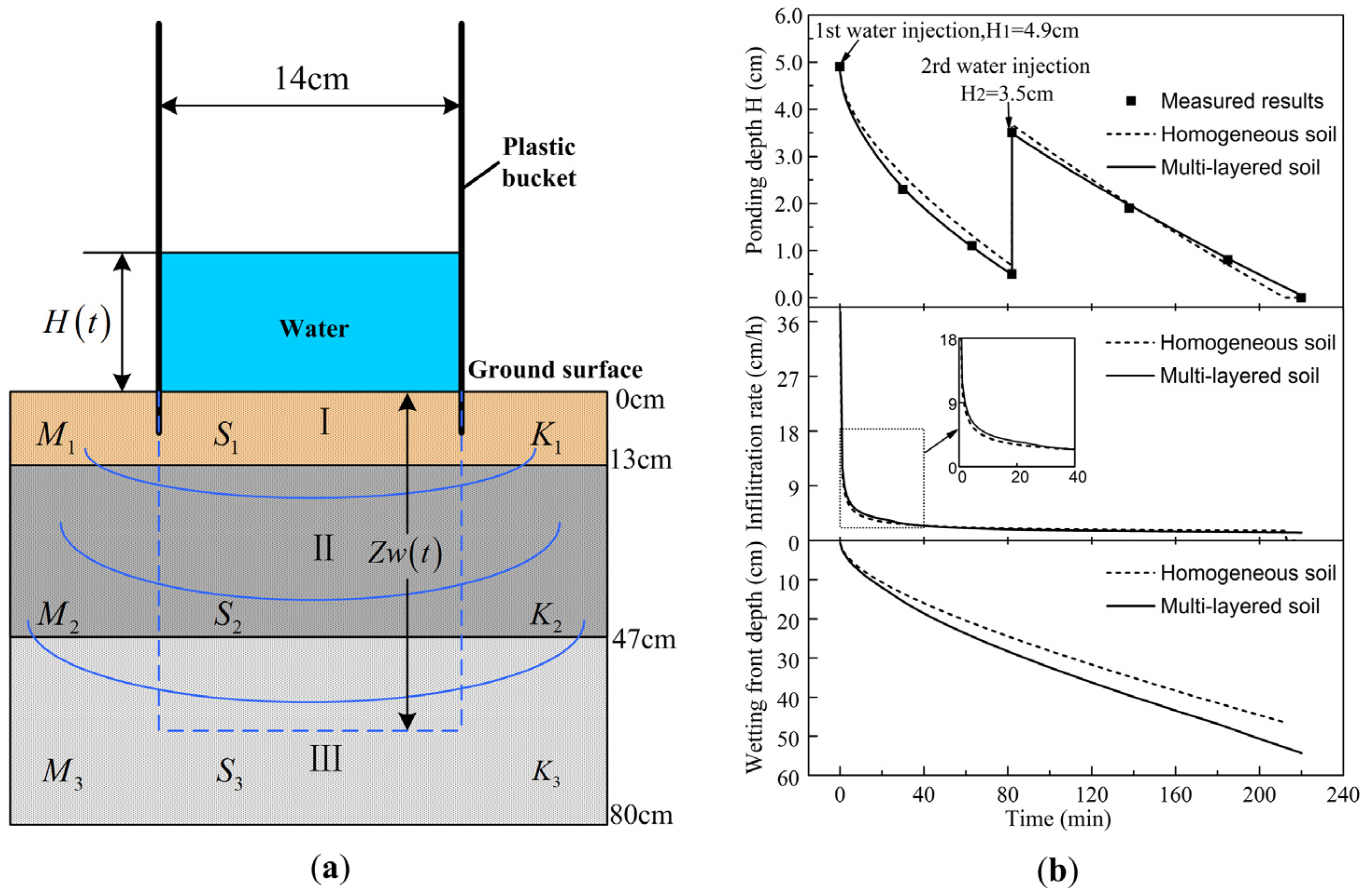
2.1. Site, Instrument, and Soil Sampling
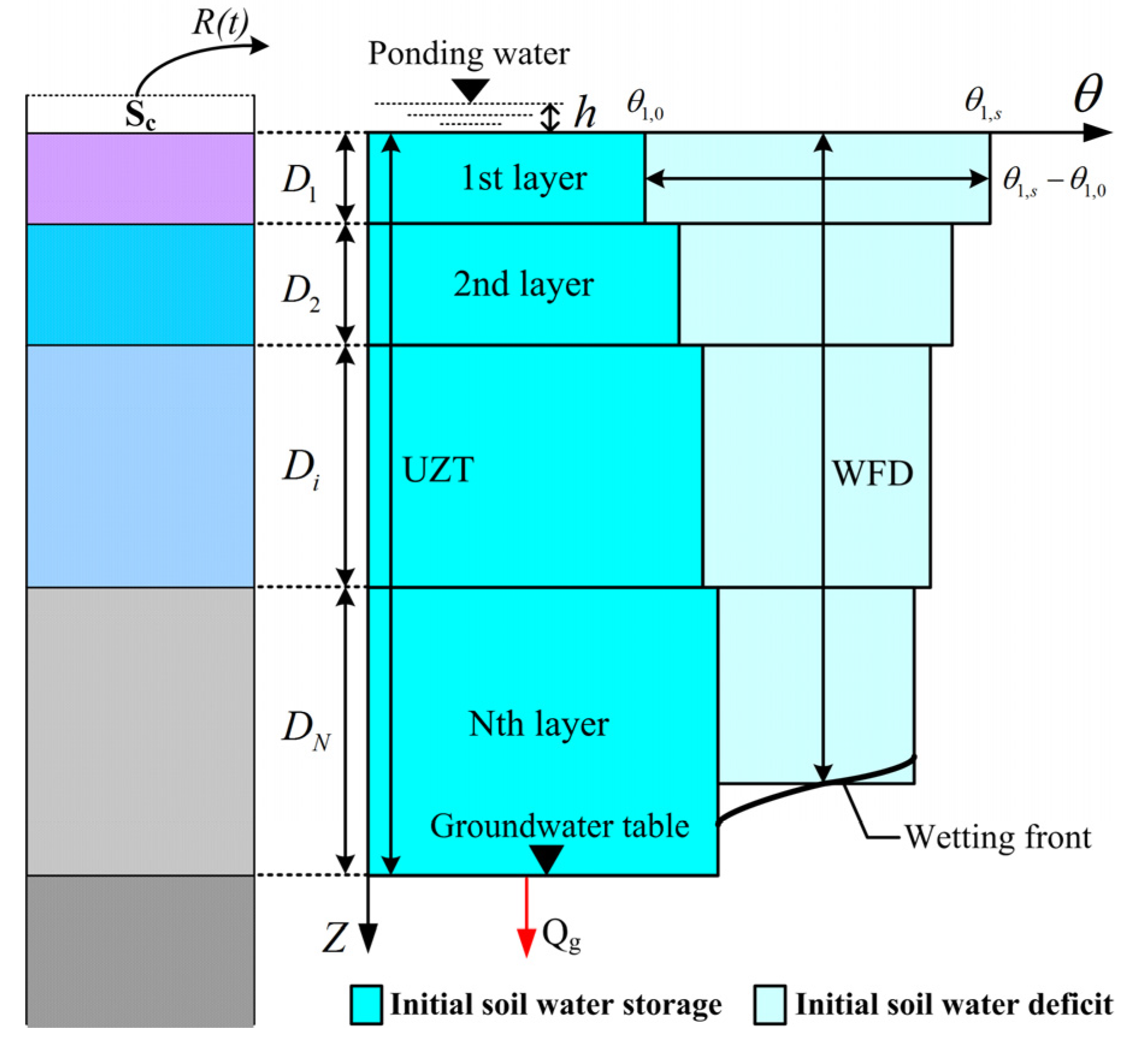
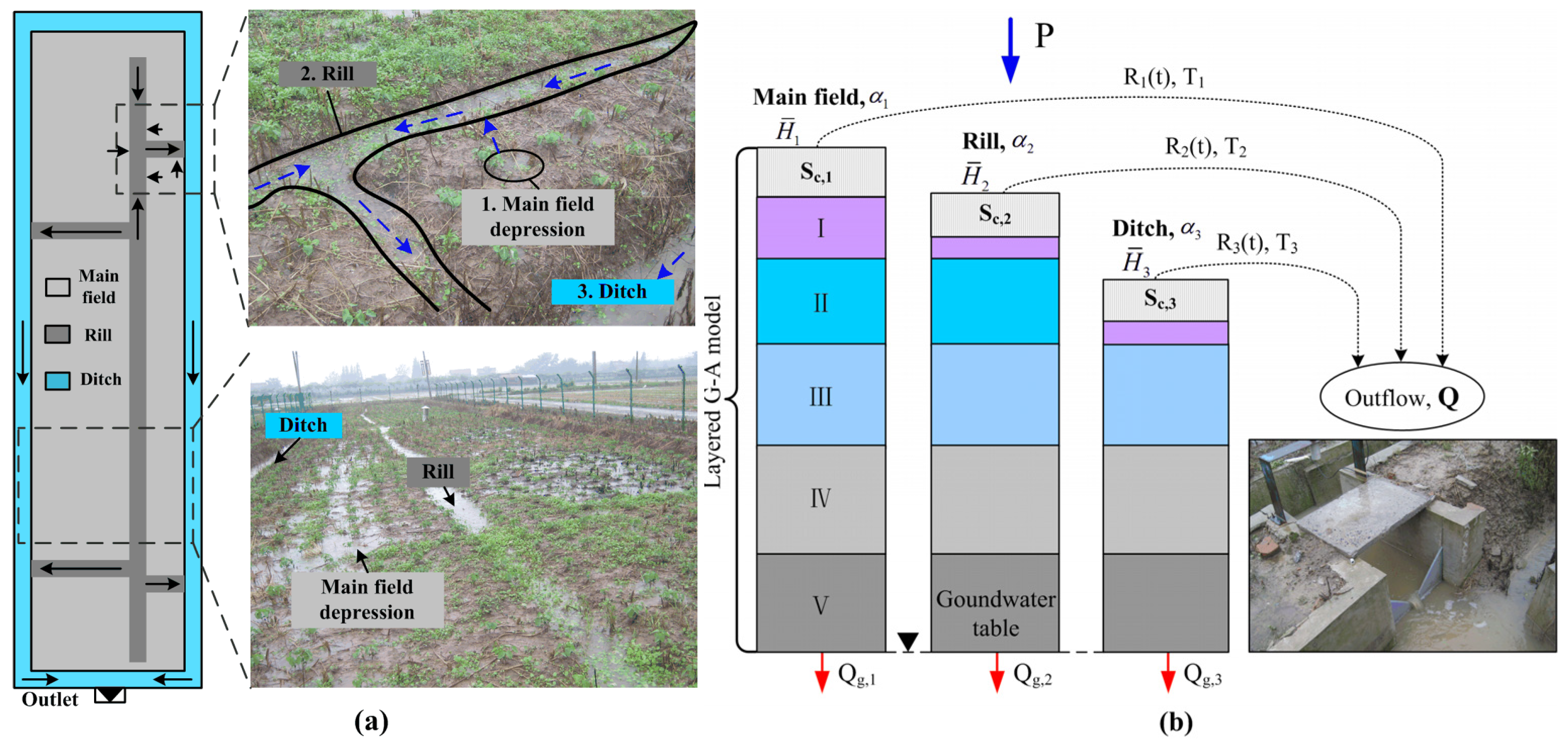
2.2. Model Structure
2.3. Model Performance
2.4. Modeling Cases
3. Results
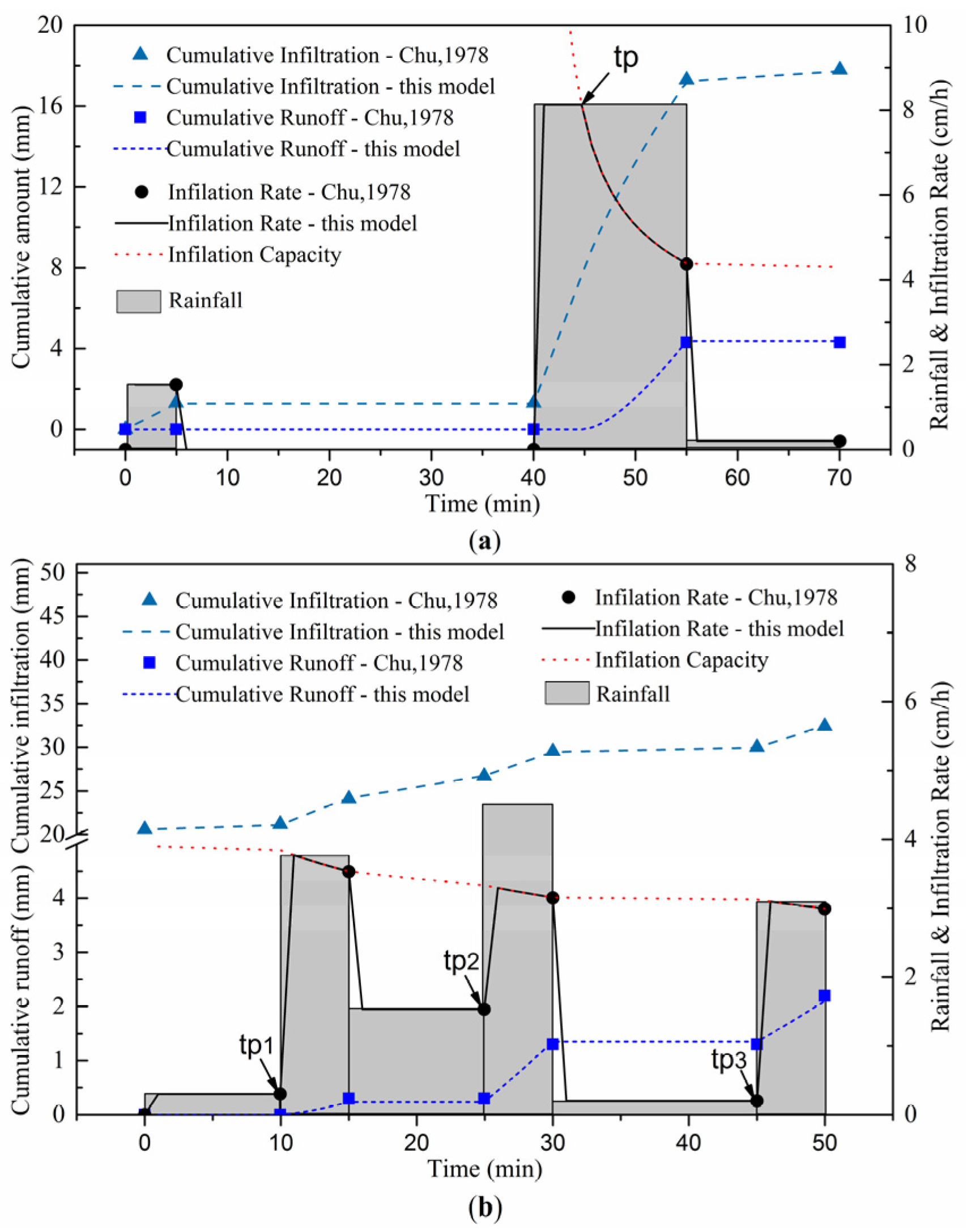
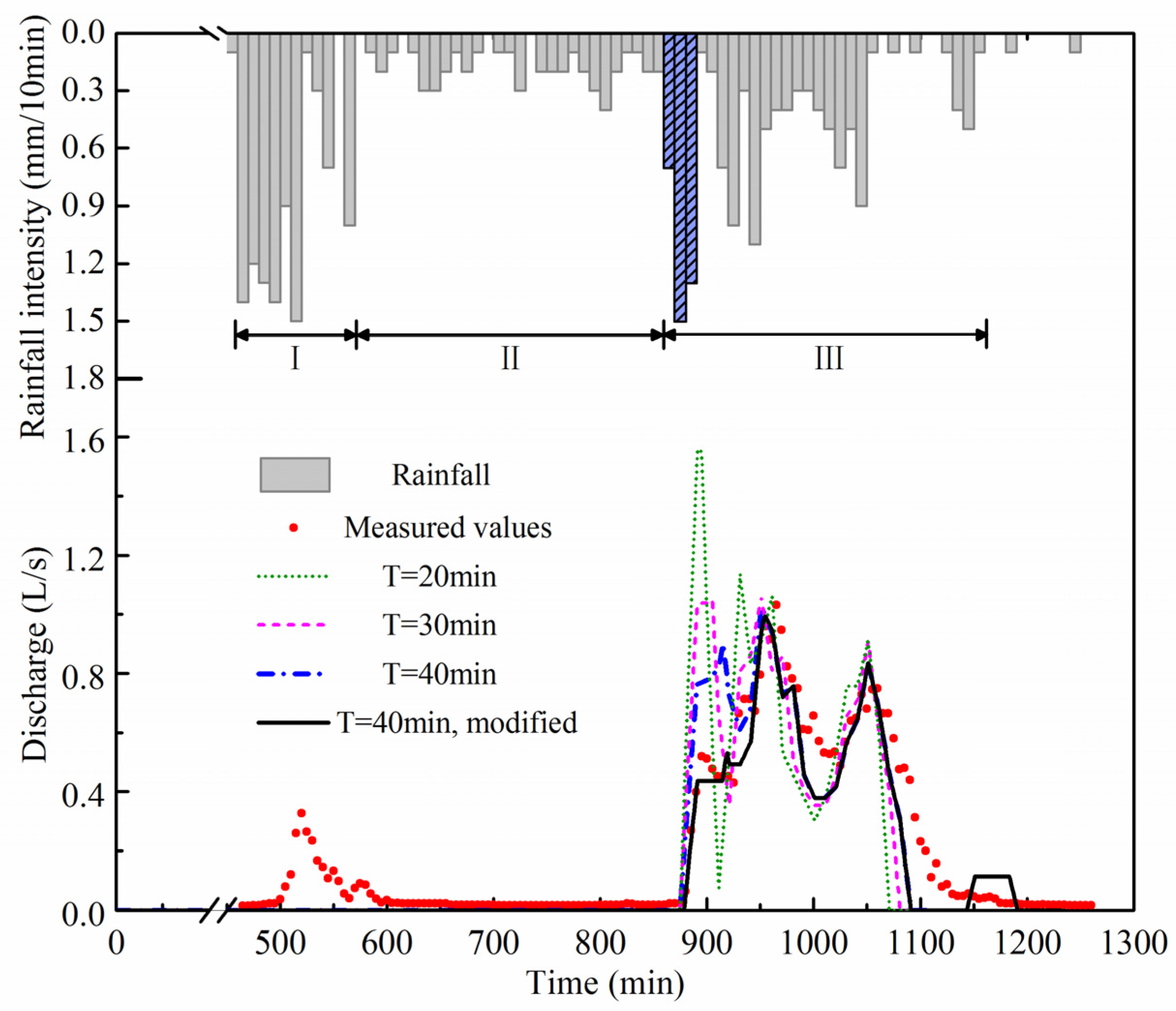
3.1. Homogeneous Soil during Unsteady Rainfall
3.2. Ponding Infiltration Experiment on the Field
3.3. Rainfall–Runoff Events Simulation
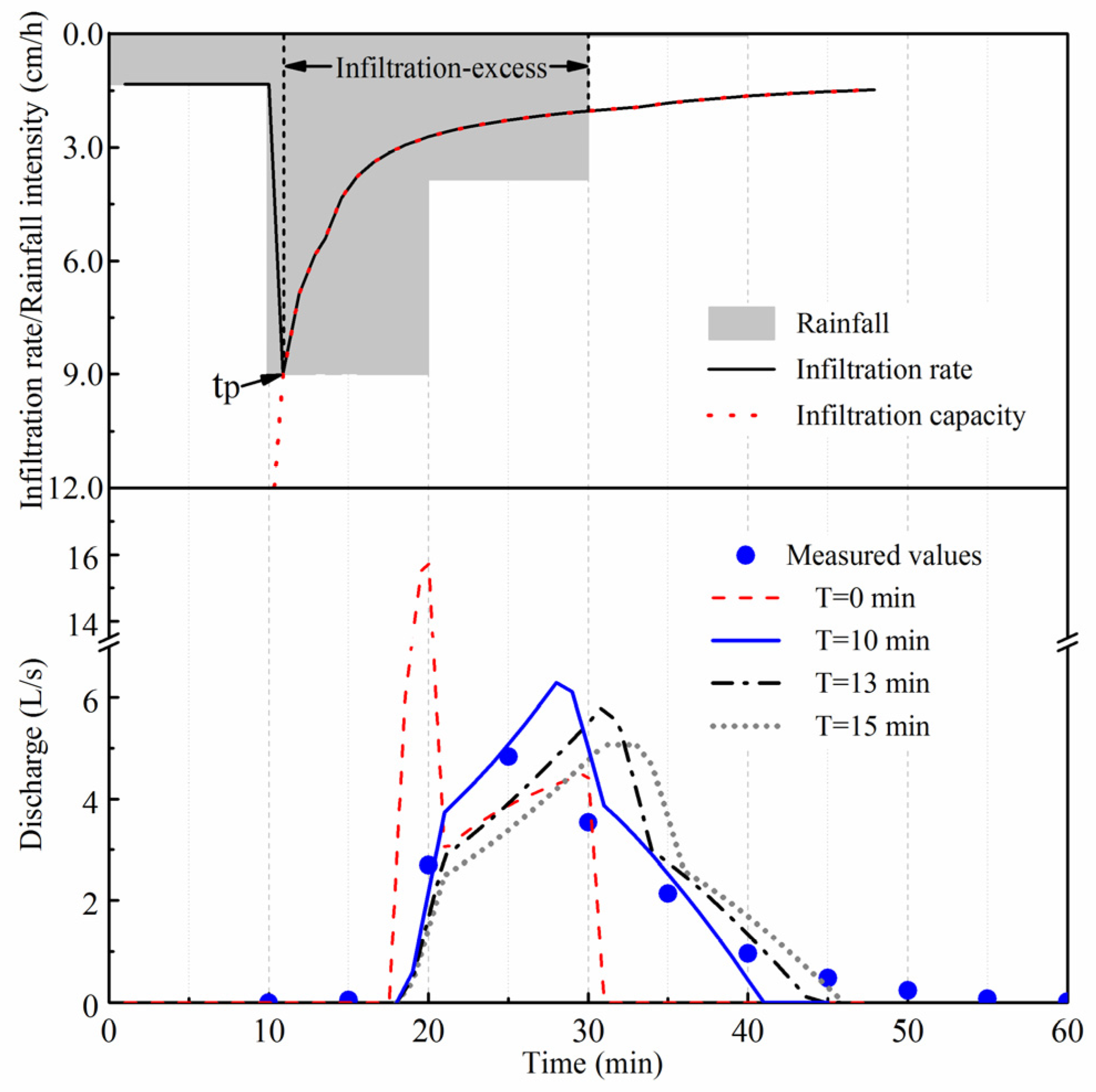
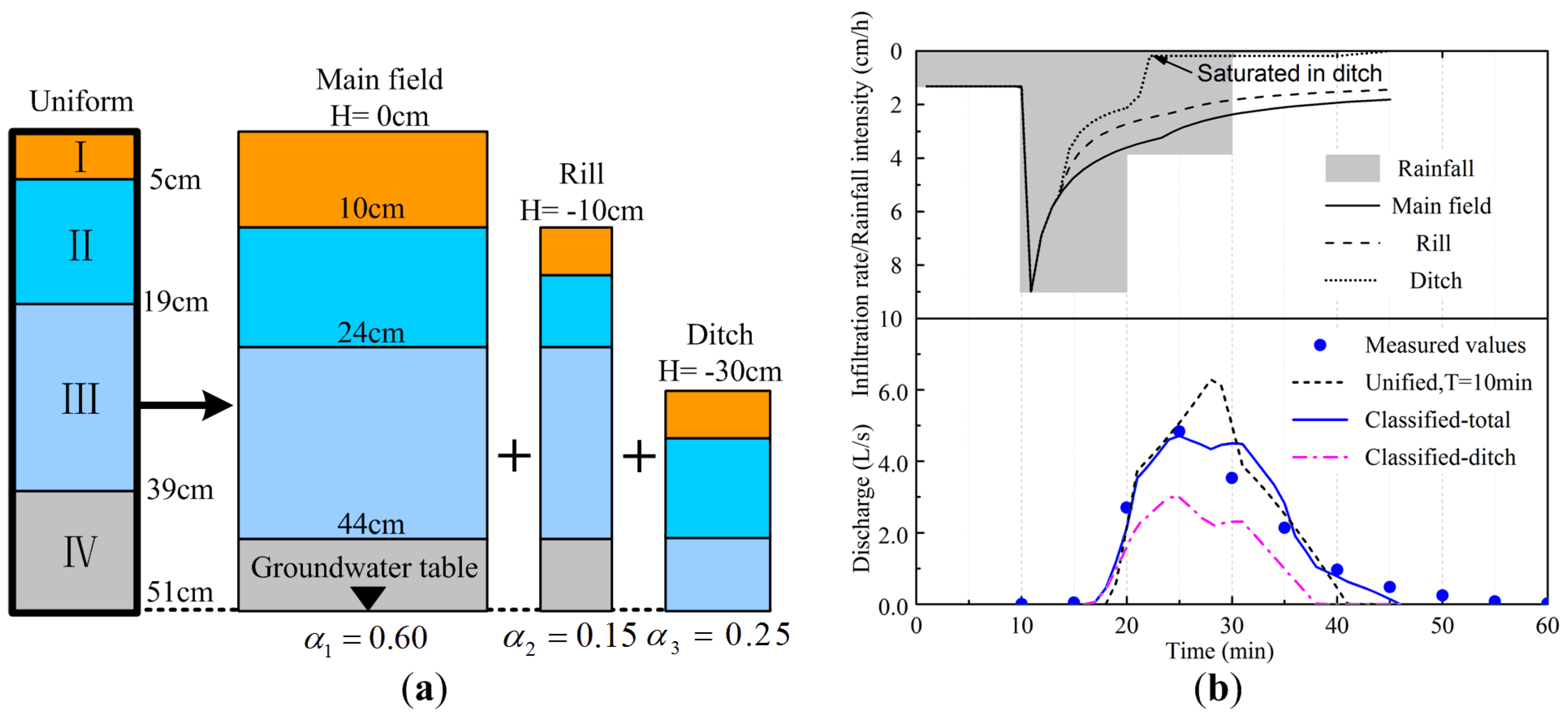
3.3.1. Typical Short-Duration Rainstorm Event
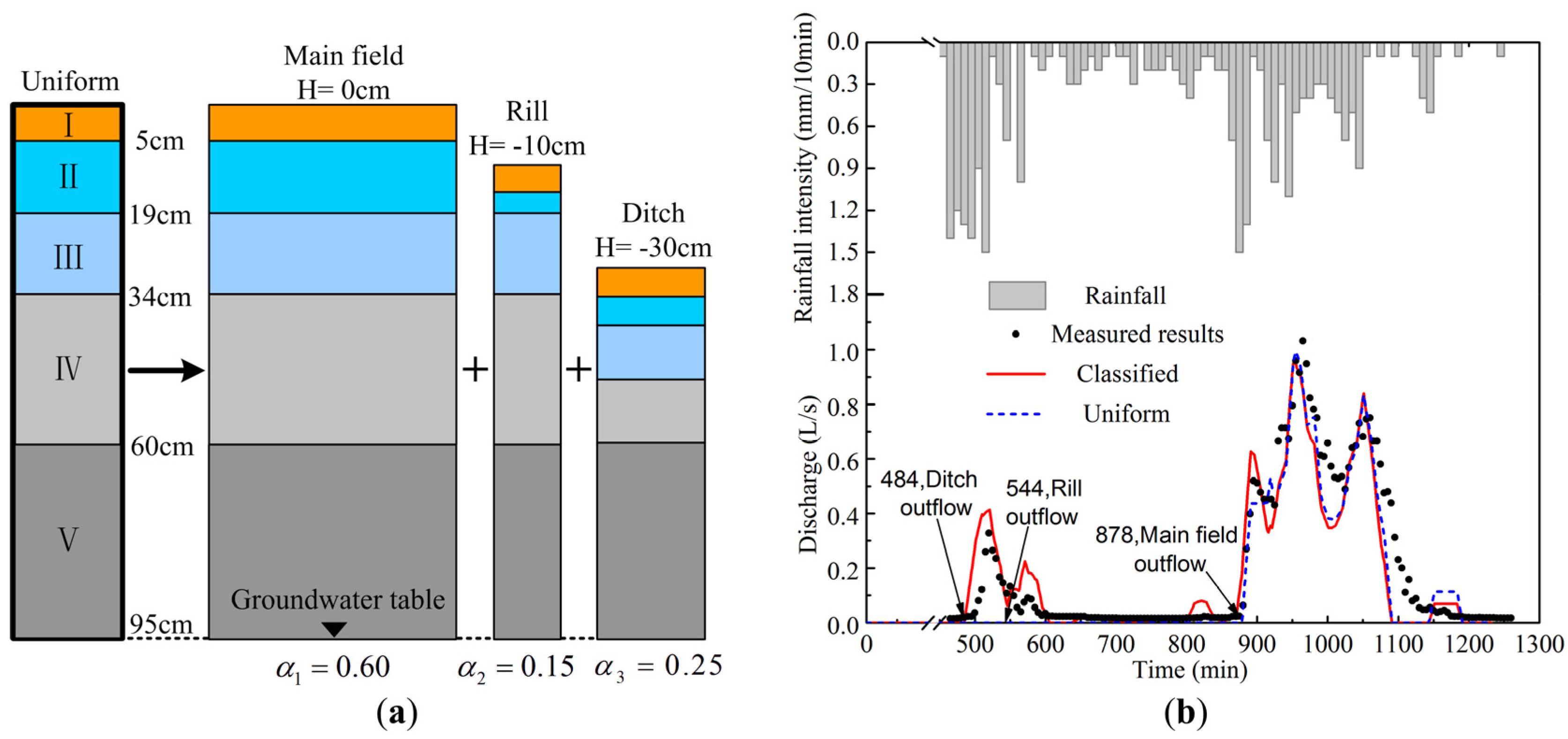
3.3.2. Typical Long-Duration Light Rainfall Event
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, R.; Li, L.; Gao, J. Framework for quantifying rural NPS pollution of a humid lowland catchment in Taihu Basin, Eastern China. Sci. Total Environ. 2019, 688, 983–993. [Google Scholar] [CrossRef] [PubMed]
- Appels, W.M.; Bogaart, P.W.; van der Zee, S.E.A.T.M. Feedbacks Between Shallow Groundwater Dynamics and Surface Topography on Runoff Generation in Flat Fields. Water Resour. Res. 2017, 53, 10336–10353. [Google Scholar] [CrossRef]
- Van der Ploeg, M.J.; Appels, W.M.; Cirkel, D.G.; Oosterwoud, M.R.; Witte, J.-P.M.; van der Zee, S.E.A.T.M. Microtopography as a Driving Mechanism for Ecohydrological Processes in Shallow Groundwater Systems. Vadose Zone J. 2012, 11, 811–822. [Google Scholar] [CrossRef]
- Thompson, S.E.; Katul, G.G.; Porporato, A. Role of microtopography in rainfall-runoff partitioning: An analysis using idealized geometry. Water Resour. Res. 2010, 46, 58–72. [Google Scholar] [CrossRef]
- Frei, S.; Fleckenstein, J.H. Representing effects of micro-topography on runoff generation and sub-surface flow patterns by using superficial rill/depression storage height variations. Environ.Model. Softw. 2014, 52, 5–18. [Google Scholar] [CrossRef]
- Chu, X.; Nelis, J.; Rediske, R. Preliminary Study on the Effects of Surface Microtopography on Tracer Transport in a Coupled Overland and Unsaturated Flow System. J. Hydrol. Eng. 2013, 18, 1241–1249. [Google Scholar] [CrossRef]
- Appels, W.M.; Bogaart, P.W.; van der Zee, S.E.A.T.M. Influence of spatial variations of microtopography and infiltration on surface runoff and field scale hydrological connectivity. Adv. Water Resour. 2011, 34, 303–313. [Google Scholar] [CrossRef]
- Chu, X.; Yang, J.; Chi, Y.; Zhang, J. Dynamic puddle delineation and modeling of puddle-to-puddle filling-spilling-merging-splitting overland flow processes. Water Resour. Res. 2013, 49, 3825–3829. [Google Scholar] [CrossRef]
- Tayfur, G.; Kavvas, M. Spatially Averaged Conservation Equations for Interacting Rill-Interrill Area Overland Flows. J. Hydraul. Eng. 1994, 120, 1426–1448. [Google Scholar] [CrossRef]
- Tayfur, G.; Kavvas, M.L. Areally-averagei overland flow equations at hillslope scale. Hydrol. Sci. J. 1998, 43, 361–378. [Google Scholar] [CrossRef] [Green Version]
- Herzon, I.; Helenius, J. Agricultural drainage ditches, their biological importance and functioning. Biol. Conserv. 2008, 141, 1171–1183. [Google Scholar] [CrossRef]
- Buchanan, B.; Easton, Z.M.; Schneider, R.L.; Walter, M.T. Modeling the hydrologic effects of roadside ditch networks on receiving waters. J. Hydrol. 2013, 486, 293–305. [Google Scholar] [CrossRef]
- Planchon, O.; Esteves, M.; Silvera, N.; Lapetite, J.-M. Microrelief induced by tillage: Measurement and modelling of Surface Storage Capacity. Catena 2001, 46, 141–157. [Google Scholar] [CrossRef]
- Khosh Bin Ghomash, S.; Caviedes-Voullieme, D.; Hinz, C. Effects of erosion-induced changes to topography on runoff dynamics. J. Hydrol. 2019, 573, 811–828. [Google Scholar] [CrossRef]
- Habtezion, N.; Nasab, M.T.; Chu, X. How Does DEM Resolution Affect Microtopographic Characteristics, Hydrologic Connectivity, and Modeling of Hydrologic Processes? Hydrol. Processes 2016, 30, 4870–4892. [Google Scholar] [CrossRef]
- Carvajal, F.; Aguilar, M.A.; Agüera, F.; Aguilar, F.J.; Giráldez, J.V. Maximum Depression Storage and Surface Drainage Network in Uneven Agricultural Landforms. Biosyst. Eng. 2006, 95, 281–293. [Google Scholar] [CrossRef]
- Hansen, B. Estimation of surface runoff and water-covered area during filling of surface microrelief depressions. Hydrol. Processes 2000, 14, 1235–1243. [Google Scholar] [CrossRef]
- Frei, S.; Lischeid, G.; Fleckenstein, J.H. Effects of micro-topography on surface–subsurface exchange and runoff generation in a virtual riparian wetland—A modeling study. Adv. Water Resour. 2010, 33, 1388–1401. [Google Scholar] [CrossRef]
- Dunne, T.; Zhang, W.; Aubry, B.F. Effects of Rainfall, Vegetation, and Microtopography on Infiltration and Runoff. Water Resour. Res. 1991, 27, 2271–2285. [Google Scholar] [CrossRef]
- Chu, X.; Padmanabhan, G.; Bogart, D. Microrelief-Controlled Overland Flow Generation: Laboratory and Field Experiments. Appl. Environ. Soil Sci. 2015, 2015, 642952. [Google Scholar] [CrossRef] [Green Version]
- Appels, W.M.; Bogaart, P.W.; van der Zee, S.E.A.T.M. Surface runoff in flat terrain: How field topography and runoff generating processes control hydrological connectivity. J. Hydrol. 2016, 534, 493–504. [Google Scholar] [CrossRef]
- Chen, L.; Sela, S.; Svoray, T.; Assouline, S. The role of soil-surface sealing, microtopography, and vegetation patches in rainfall-runoff processes in semiarid areas. Water Resour. Res. 2013, 49, 5585–5599. [Google Scholar] [CrossRef]
- Frei, S.; Knorr, K.H.; Peiffer, S.; Fleckenstein, J.H. Surface micro-topography causes hot spots of biogeochemical activity in wetland systems: A virtual modeling experiment. J. Geophys. Res. Biogeosci. 2012, 117, G4. [Google Scholar] [CrossRef]
- Antoine, M.; Javaux, M.; Bielders, C. What indicators can capture runoff-relevant connectivity properties of the micro-topography at the plot scale? Adv. Water Resour. 2009, 32, 1297–1310. [Google Scholar] [CrossRef]
- Yang, J.; Chu, X. Quantification of the spatio-temporal variations in hydrologic connectivity of small-scale topographic surfaces under various rainfall conditions. J. Hydrol. 2013, 505, 65–77. [Google Scholar] [CrossRef]
- Aksoy, H.; Gedikli, A.; Unal, N.E.; Yilmaz, M.; Eris, E.; Yoon, J.; Tayfur, G. Rainfall-Runoff Model Considering Microtopography Simulated in a Laboratory Erosion Flume. Water Resour. Manag. 2016, 30, 5609–5624. [Google Scholar] [CrossRef]
- Mallari, K.J.B.; Arguelles, A.C.C.; Kim, H.; Aksoy, H.; Kavvas, M.L.; Yoon, J. Comparative analysis of two infiltration models for application in a physically based overland flow model. Environ. Earth Sci. 2015, 74, 1579–1587. [Google Scholar] [CrossRef]
- Moussa, R.; Voltz, M.; Andrieux, P. Effects of the spatial organization of agricultural management on the hydrological behaviour of a farmed catchment during flood events. Hydrol. Processes 2002, 16, 393–412. [Google Scholar] [CrossRef]
- Carluer, N.; Marsily, G.D. Assessment and modelling of the influence of man-made networks on the hydrology of a small watershed: Implications for fast flow components, water quality and landscape management. J. Hydrol. 2004, 285, 76–95. [Google Scholar] [CrossRef]
- Tiemeyer, B.; Moussa, R.; Lennartz, B.; Voltz, M. MHYDAS-DRAIN: A spatially distributed model for small, artificially drained lowland catchments. Ecol. Model. 2007, 209, 2–20. [Google Scholar] [CrossRef]
- Haahti, K.; Warsta, L.; Kokkonen, T.; Younis, B.A.; Koivusalo, H. Distributed hydrological modeling with channel network flow of a forestry drained peatland site. Water Resour. Res. 2016, 52, 246–263. [Google Scholar] [CrossRef]
- VanderKwaak, J.E.; Loague, K. Hydrologic-Response simulations for the R-5 catchment with a comprehensive physics-based model. Water Resour. Res. 2001, 37, 999–1013. [Google Scholar] [CrossRef]
- Jain, A.; Indurthy, S.K.V.P. Comparative Analysis of Event-based Rainfall-runoff Modeling Techniques—Deterministic, Statistical, and Artificial Neural Networks. J. Hydrol. Eng. 2003, 8, 93–98. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouvier, C.; Martin, C.; Didon-Lescot, J.-F.; Todorovik, D.; Domergue, J.-M. Assessment of initial soil moisture conditions for event-based rainfall–runoff modelling. J. Hydrol. 2010, 387, 176–187. [Google Scholar] [CrossRef]
- Escobar-Ruiz, V.; Smith, H.G.; Macdonald, N.; Peñuela, A. Simulated event-scale flow and sediment generation responses to agricultural land cover change in lowland UK catchments. Hydrol. Processes 2022, 36, e14474. [Google Scholar] [CrossRef]
- Tian, P.; Feng, J.; Zhao, G.; Gao, P.; Sun, W.; Hörmann, G.; Mu, X. Rainfall, runoff, and suspended sediment dynamics at the flood event scale in a Loess Plateau watershed, China. Hydrol. Processes 2022, 36, e14486. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Li, H.; Faisal, M.; Zhang, Y. Analysis of drainage efficiency under extreme precipitation events based on numerical simulation. Hydrol. Processes 2022, 36, e14624. [Google Scholar] [CrossRef]
- Cerdan, O.; Le Bissonnais, Y.; Govers, G.; Lecomte, V.; van Oost, K.; Couturier, A.; King, C.; Dubreuil, N. Scale effect on runoff from experimental plots to catchments in agricultural areas in Normandy. J. Hydrol. 2004, 299, 4–14. [Google Scholar] [CrossRef]
- Hua, W.; Wang, C.; Chen, G.; Yang, H.; Zhai, Y. Measurement and Simulation of Soil Water Contents in an Experimental Field in Delta Plain. Water 2017, 9, 947. [Google Scholar] [CrossRef]
- Zhai, Y.; Wang, C.; Chen, G.; Wang, C.; Li, X.; Liu, Y. Field-Based Analysis of Runoff Generation Processes in Humid Lowlands of the Taihu Basin, China. Water 2020, 12, 1216. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Kale, R.V.; Sahoo, B. Green-Ampt Infiltration Models for Varied Field Conditions: A Revisit. Water Resour. Manag. 2011, 25, 3505–3536. [Google Scholar] [CrossRef]
- Sander, T.; Gerke, H.H. Preferential Flow Patterns in Paddy Fields Using a Dye Tracer. Vadose Zone J. 2007, 6, 105–115. [Google Scholar] [CrossRef]
- Mishra, S.K.; Sarkar, R.; Dutta, S.; Panigrahy, S. A physically based hydrological model for paddy agriculture dominated hilly watersheds in tropical region. J. Hydrol. 2008, 357, 389–404. [Google Scholar] [CrossRef]
- Tan, X.; Shao, D.; Gu, W.; Liu, H. Field analysis of water and nitrogen fate in lowland paddy fields under different water managements using HYDRUS-1D. Agric. Water Manag. 2015, 150, 67–80. [Google Scholar] [CrossRef]
- Tan, X.; Shao, D.; Liu, H. Simulating soil water regime in lowland paddy fields under different water managements using HYDRUS-1D. Agric. Water Manag. 2014, 132, 69–789. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Feng, J. Green–Ampt Model for Layered Soils with Nonuniform Initial Water Content Under Unsteady Infiltration. Soil Sci. Soc. Am. J. 2008, 72, 1041–1047. [Google Scholar] [CrossRef]
- Kroes, J.G.; Dam, J.C.v.; Bartholomeus, R.P.; Groenendijk, P.; Heinen, M.; Hendriks, R.F.A.; Mulder, H.M.; Supit, I.; van Walsum, P.E.V. SWAP Version 4, Theory Description and User Manual; 1566-7197; Wageningen Environmental Research: Wageningen, The Netherlands, 2017; p. 244. [Google Scholar]
- Beven, K.J. A history of the concept of time of concentration. Hydrol. Earth Syst. Sci. 2020, 24, 2655–2670. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, F. Simulation of Runoff Hydrograph on Soil Surfaces with Different Microtopography Using a Travel Time Method at the Plot Scale. PLoS ONE 2015, 10, e0130794. [Google Scholar]
- Du, J.; Xie, H.; Hu, Y.; Xu, Y.; Xu, C.-Y. Development and testing of a new storm runoff routing approach based on time variant spatially distributed travel time method. J. Hydrol. 2009, 369, 44–54. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. RiverRiver flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chu, S.T. Infiltration during an unsteady rain. Water Resour. Res. 1978, 14, 461–466. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L. Estimating Soil Water Retention from Soil Properties. J. Irrig. Drain. Div. 1982, 108, 166–171. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Barber, M.E.; King, S.G.; Yonge, D.R.; Hathhorn, W.E. Ecology Ditch: A Best Management Practice for Storm Water Runoff Mitigation. J. Hydrol. Eng. 2003, 8, 111–122. [Google Scholar] [CrossRef]
- Li, S.; Wang, X.; Qiao, B.; Li, J.; Tu, J. First flush characteristics of rainfall runoff from a paddy field in the Taihu Lake watershed, China. Environ. Sci. Pollut. Res. 2017, 24, 8336–8351. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Lauvernet, C.; Carluer, N. Shallow water table effects on water, sediment, and pesticide transport in vegetative filter strips—Part 1: Nonuniform infiltration and soil water redistribution. Hydrol. Earth Syst. Sci. 2018, 22, 53–70. [Google Scholar] [CrossRef]
- Gowdish, L.C.; Muñoz-Carpena, R. 3DMGAR: A Transient Quasi-3D Point-Source Green–Ampt Infiltration and Redistribution Model. Vadose Zone J. 2018, 17, 180032. [Google Scholar] [CrossRef]
- Gowdish, L.; Muñoz-Carpena, R. An Improved Green–Ampt Infiltration and Redistribution Method for Uneven Multistorm Series. Vadose Zone J. 2009, 8, 470–479. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Doherty, J. PEST model-independent parameter estimation user manual. Watermark Numer. Comput. Brisb. Aust. 2004, 3338, 3349. [Google Scholar]
| Depth (cm) | Clay (-) | Silt (-) | (g/cm3) | (-) | Ks (cm/min) |
|---|---|---|---|---|---|
| 0–10 10–20 20–40 40–60 60–80 | 0.31 (0.27–0.34) 0.29 (0.26–0.34) 0.29 (0.26–0.32) 0.33 (0.30–0.35) 0.41 (0.38–0.43) | 0.57 (0.53–0.62) 0.61 (0.58–0.64) 0.63 (0.61–0.67) 0.61 (0.58–0.64) 0.54 (0.53–0.58) | 1.20 (1.10–1.28) 1.23 (1.05–1.50) 1.47 (1.41–1.50) 1.46 (1.35–1.53) 1.46 (1.41–1.50) | 0.55(0.52–0.58) 0.50(0.43–0.60) 0.45(0.43–0.47) 0.45(0.42–0.49) 0.45(0.42–0.47) | 0.07(0.02–0.25) 0.08(0.01–0.22) 0.07(0.02–0.13) 0.11(0.04–0.18) 0.03(0.01–0.05) |
| Homogeneous Case | Multilayered Case | ||||||
|---|---|---|---|---|---|---|---|
| Depth (cm) | (-) | S (cm) | Ks (cm/min) | Depth (cm) | (-) | S (cm) | Ks (cm/min) |
| 0–60 | 0.17 | 20 | 0.018 | 0–13 | 0.17 | 20 | 0.022 |
| 13–47 | 0.14 | 20 | 0.015 | ||||
| 47–60 | 0.12 | 20 | 0.012 | ||||
| Layer Number | Depth (cm) | M (-) | S (cm) | Ks (cm/min) |
|---|---|---|---|---|
| I | 0–5 | 0.130 | 20 | 0.018 |
| II | 5–19 | 0.062 | 20 | 0.015 |
| III | 19–39 | 0.028 | 20 | 0.015 |
| IV | 39–51 | 0.006 | 20 | 0.008 |
| Parameters | Main Field | Rill | Ditch |
|---|---|---|---|
| (/) | 0.6 | 0.15 | 0.25 |
| (cm) | 0 | −10 | −30 |
| (mm) | 5 | 4 | 3.5 |
| T(min) | 14 | 10 | 7 |
| Layer(cm) | I (0–10) | I (0–5) | I (0–5) |
| II (10–24) | II (5–14) | II (5–14) | |
| III (24–44) | III (14–34) | III (14–21) | |
| IV (44–51) | IV (34–41) | - |
| Parameter | Main Field | Rill | Ditch |
|---|---|---|---|
| WFD/UZT (cm) | 23/51 | 36/41 | 21/21 |
| Subunit infiltration (mm) | 21.1 | 18.1 | 13.8 |
| Subunit runoff (mm) | 2.6 | 5.6 | 9.9 |
| Area ratio (-) | 0.60 | 0.15 | 0.25 |
| Converted total runoff(mm) | 1.54 | 0.84 | 2.48 |
| Runoff ratio (-) | 0.32 | 0.17 | 0.51 |
| Runoff ratio/Area ratio (-) | 0.5 | 1.1 | 2.0 |
| Layer Number | Depth (cm) | M (-) | S (cm) | Ks (cm/min) |
|---|---|---|---|---|
| I | 0–5 | 0.094 | 20 | 0.018 |
| II | 5–19 | 0.029 | 20 | 0.015 |
| III | 19–34 | 0.035 | 20 | 0.015 |
| IV | 34–60 | 0.024 | 20 | 0.008 |
| V | 60–95 | 0.013 | 20 | 0.005 |
| Parameter | Main Field | Rill | Ditch |
|---|---|---|---|
| T(min) | 40 | 35 | 25 |
| Layers(cm) | I (0–5) | I (0–5) | I (0–5) |
| II (5–19) | II (5–9) | II (5–10) | |
| III (19–34) | III (9–24) | III (10–20) | |
| IV (34–60) | IV (24–50) | IV (20–30) | |
| V (60–95) | V (50–85) | V (30–65) |
| Parameter | Main Field | Rill | Ditch |
|---|---|---|---|
| WFD/UZT (cm) | 95/95 | 85/85 | 65/65 |
| Subunit infiltration (mm) | 40.0 | 36.8 | 35.1 |
| Subunit Runoff (mm) | 7.9 | 11.1 | 12.8 |
| Area ratio (-) | 0.6 | 0.15 | 0.25 |
| Converted total runoff (mm) | 4.7 | 1.7 | 3.2 |
| Runoff ratio (-) | 0.49 | 0.18 | 0.33 |
| Runoff ratio/Area ratio (-) | 0.8 | 1.2 | 1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Jiang, Y.; Zhou, Q.; Yang, H.; Ma, Q.; Zhang, C.; Wang, C. Effects of Microtopography on Runoff Generation in Plain Farmland: New Insights from an Event-Based Rainfall–Runoff Model. Water 2022, 14, 2686. https://doi.org/10.3390/w14172686
Yang H, Jiang Y, Zhou Q, Yang H, Ma Q, Zhang C, Wang C. Effects of Microtopography on Runoff Generation in Plain Farmland: New Insights from an Event-Based Rainfall–Runoff Model. Water. 2022; 14(17):2686. https://doi.org/10.3390/w14172686
Chicago/Turabian StyleYang, Hai, Yuehua Jiang, Quanping Zhou, Hui Yang, Qingshan Ma, Chengcheng Zhang, and Chuanhai Wang. 2022. "Effects of Microtopography on Runoff Generation in Plain Farmland: New Insights from an Event-Based Rainfall–Runoff Model" Water 14, no. 17: 2686. https://doi.org/10.3390/w14172686
APA StyleYang, H., Jiang, Y., Zhou, Q., Yang, H., Ma, Q., Zhang, C., & Wang, C. (2022). Effects of Microtopography on Runoff Generation in Plain Farmland: New Insights from an Event-Based Rainfall–Runoff Model. Water, 14(17), 2686. https://doi.org/10.3390/w14172686






