Transpiration Induced Changes in Atmospheric Water Vapor δ18O via Isotopic Non-Steady-State Effects on a Subtropical Forest Plantation
Abstract
:1. Introduction
2. Materials and Methods
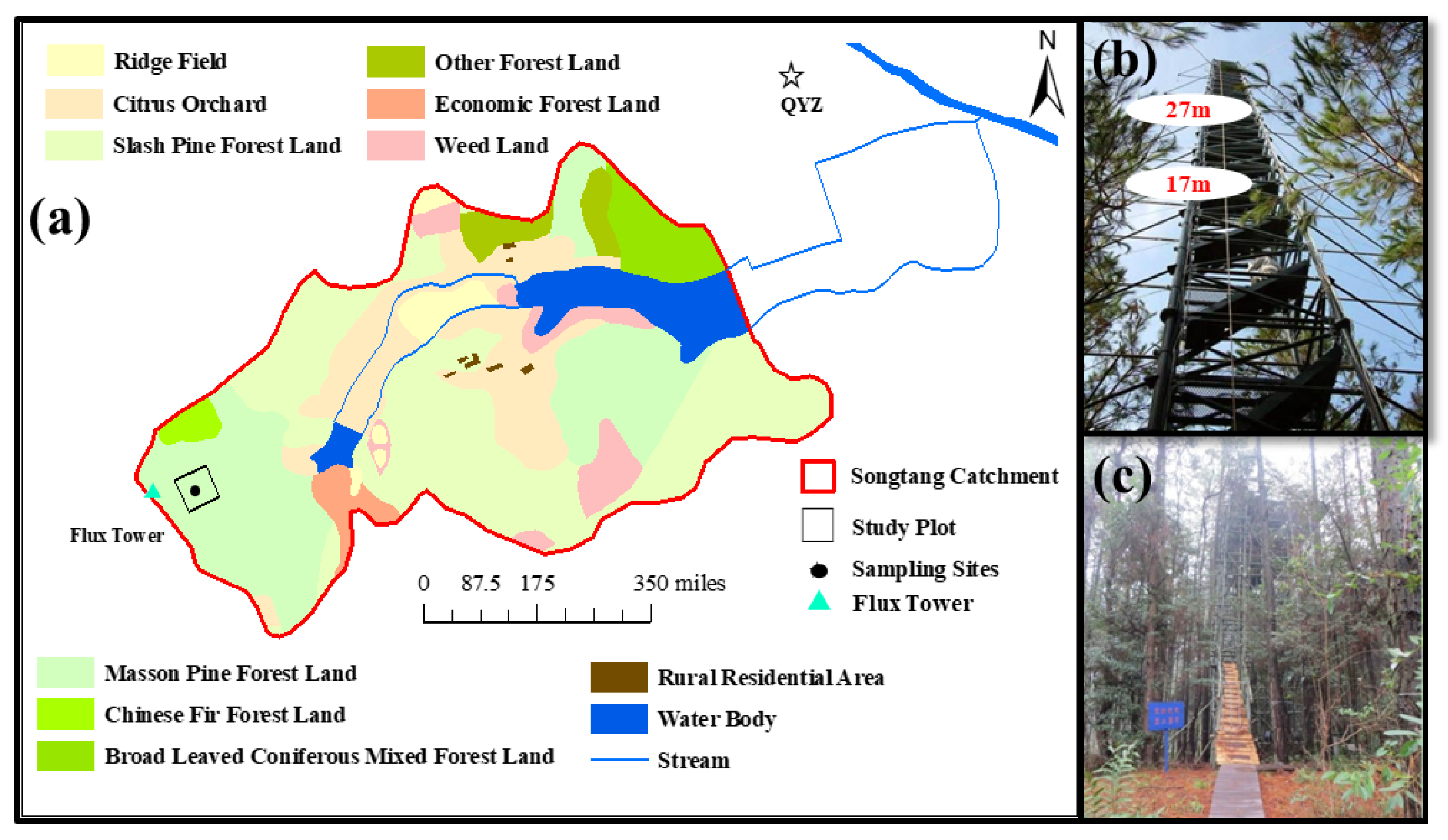
2.1. Study Site
2.2. In-Situ Measurements of Isotope Ratios in Water Vapor and Evapotranspiration
2.3. Measurement of Isotopic Compositions of Ecosystem Water Pools
2.4. Model and Statistical Methods
2.4.1. Simulation Models of Leaf Water, Transpiration, and Evaporation δ18O
2.4.2. Calculations of Transpiration, Evaporation, and Evapotranspiration Isoforcing
2.4.3. The Shuttleworth–Wallace Model: Estimates of Transpiration and Evaporation
2.4.4. Statistical Analyses
3. Results
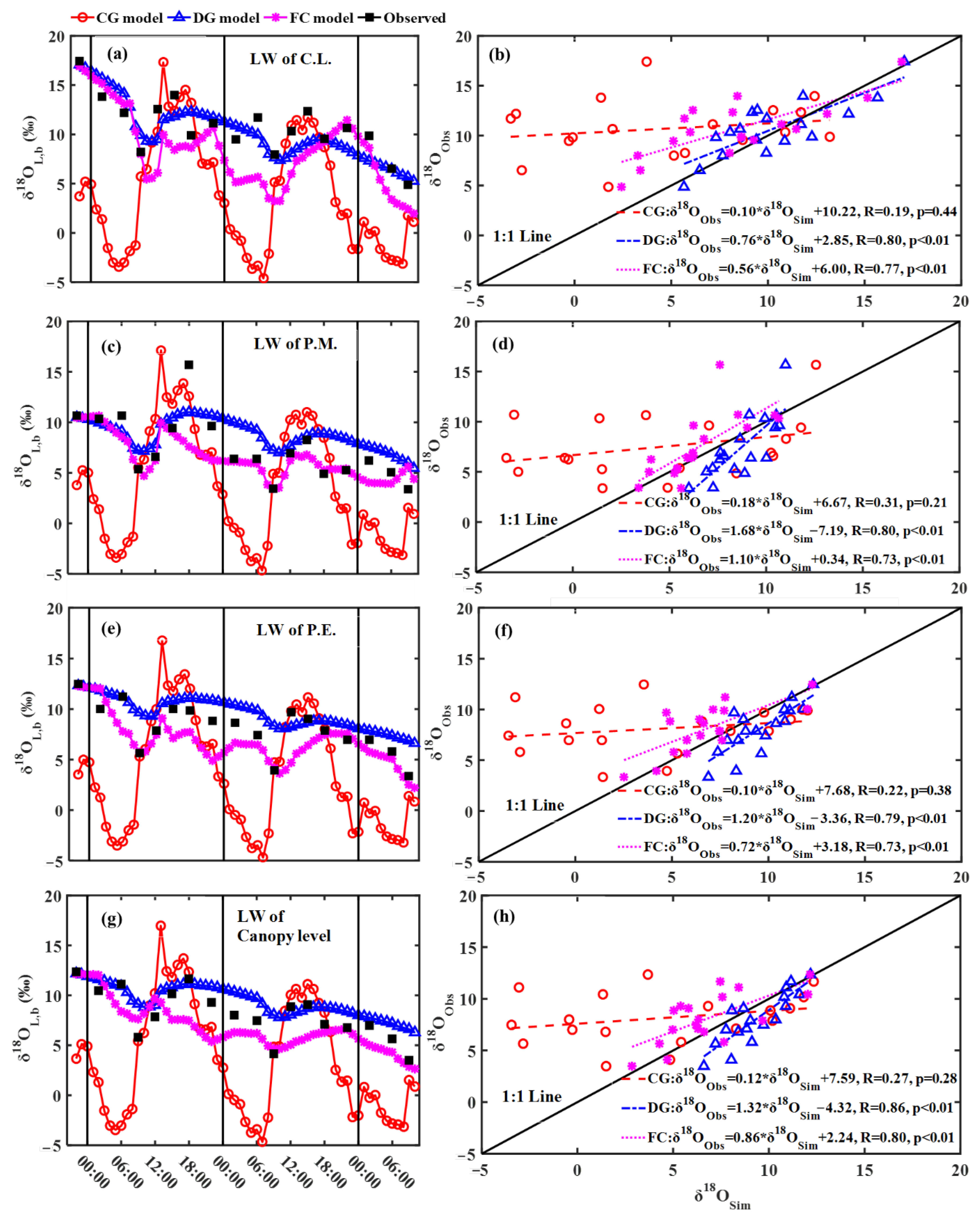
3.1. Observed and Modeling Results of Leaf Water δ18O
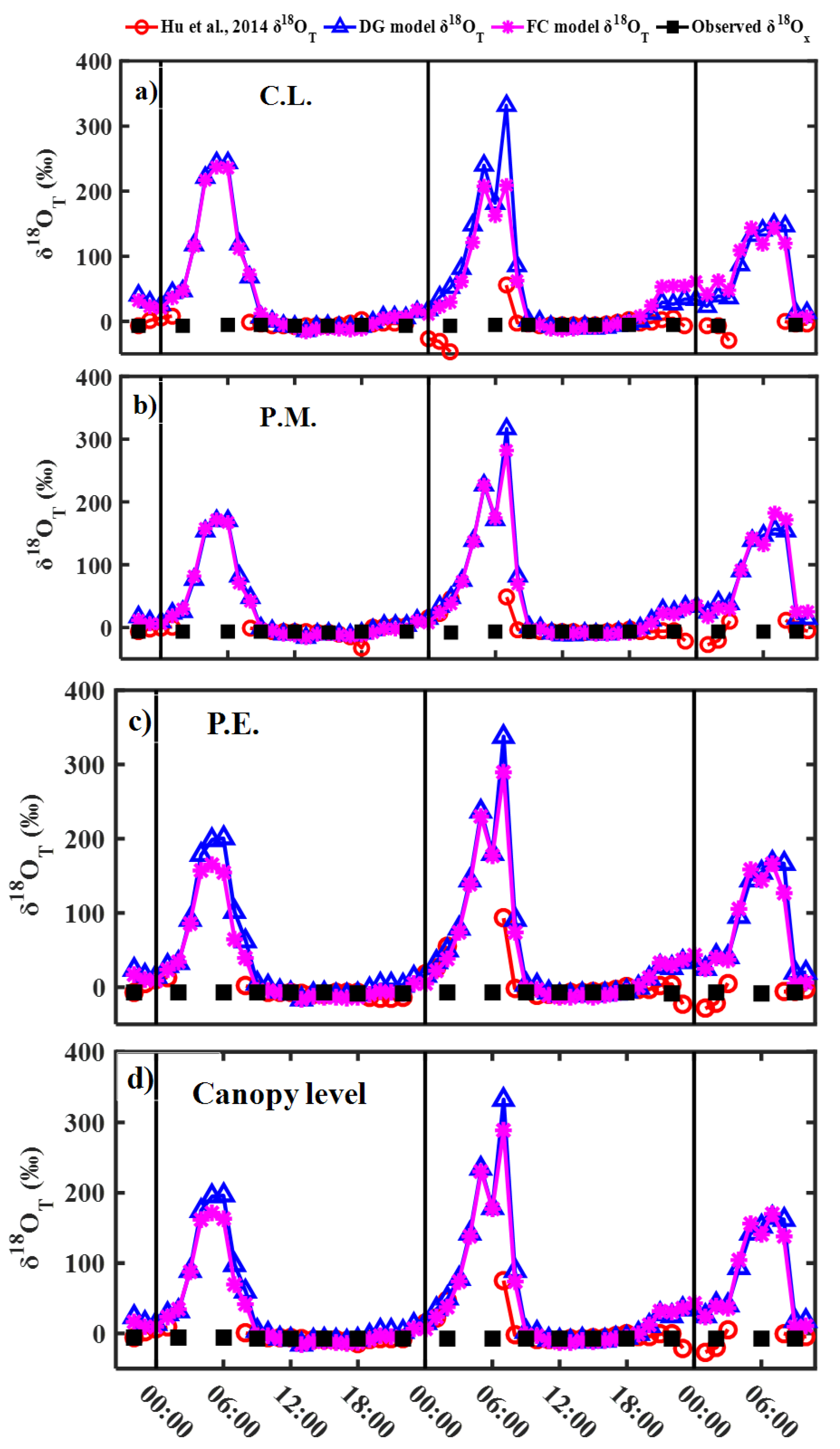
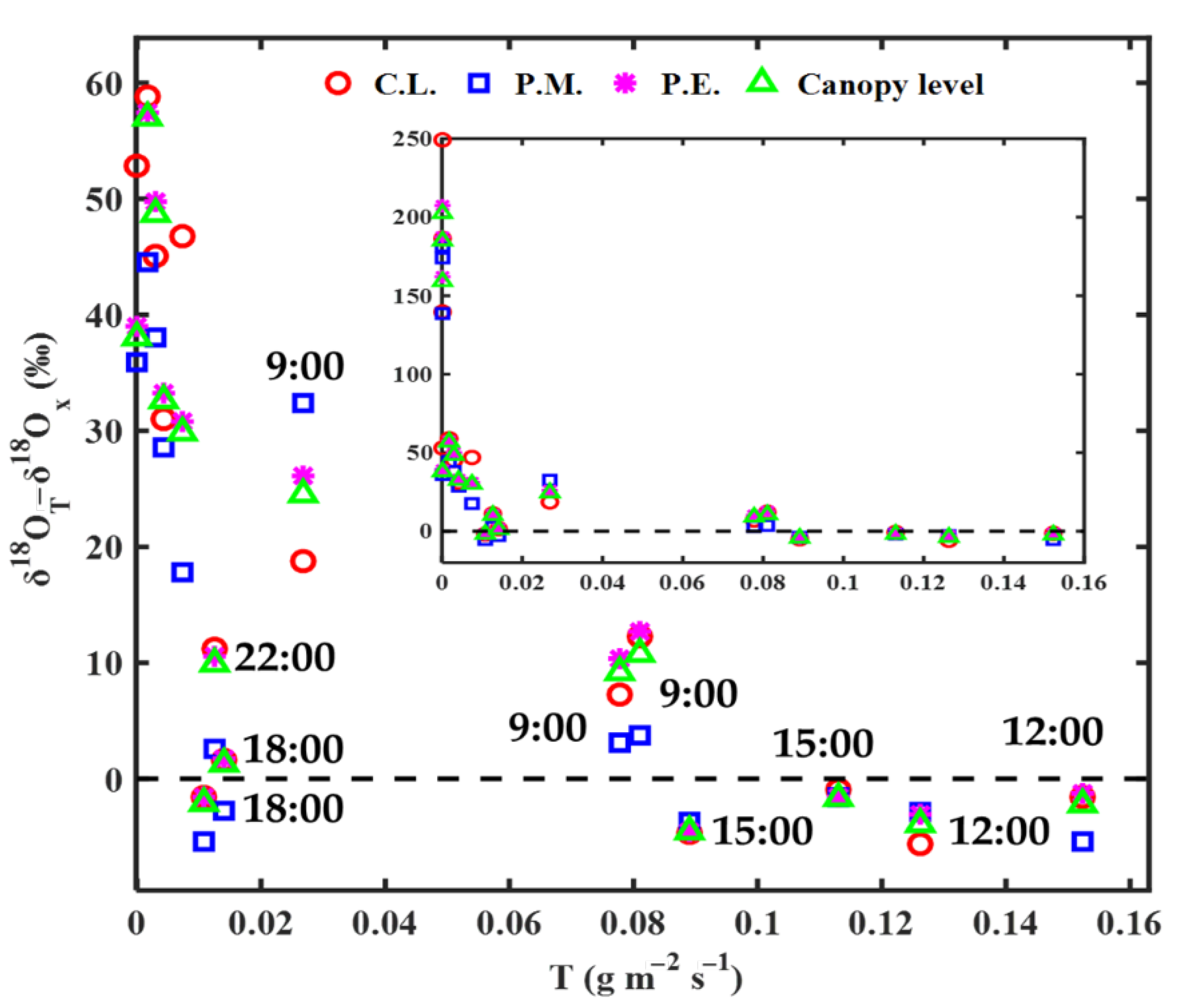
3.2. Modeling Results of Transpiration δ18O
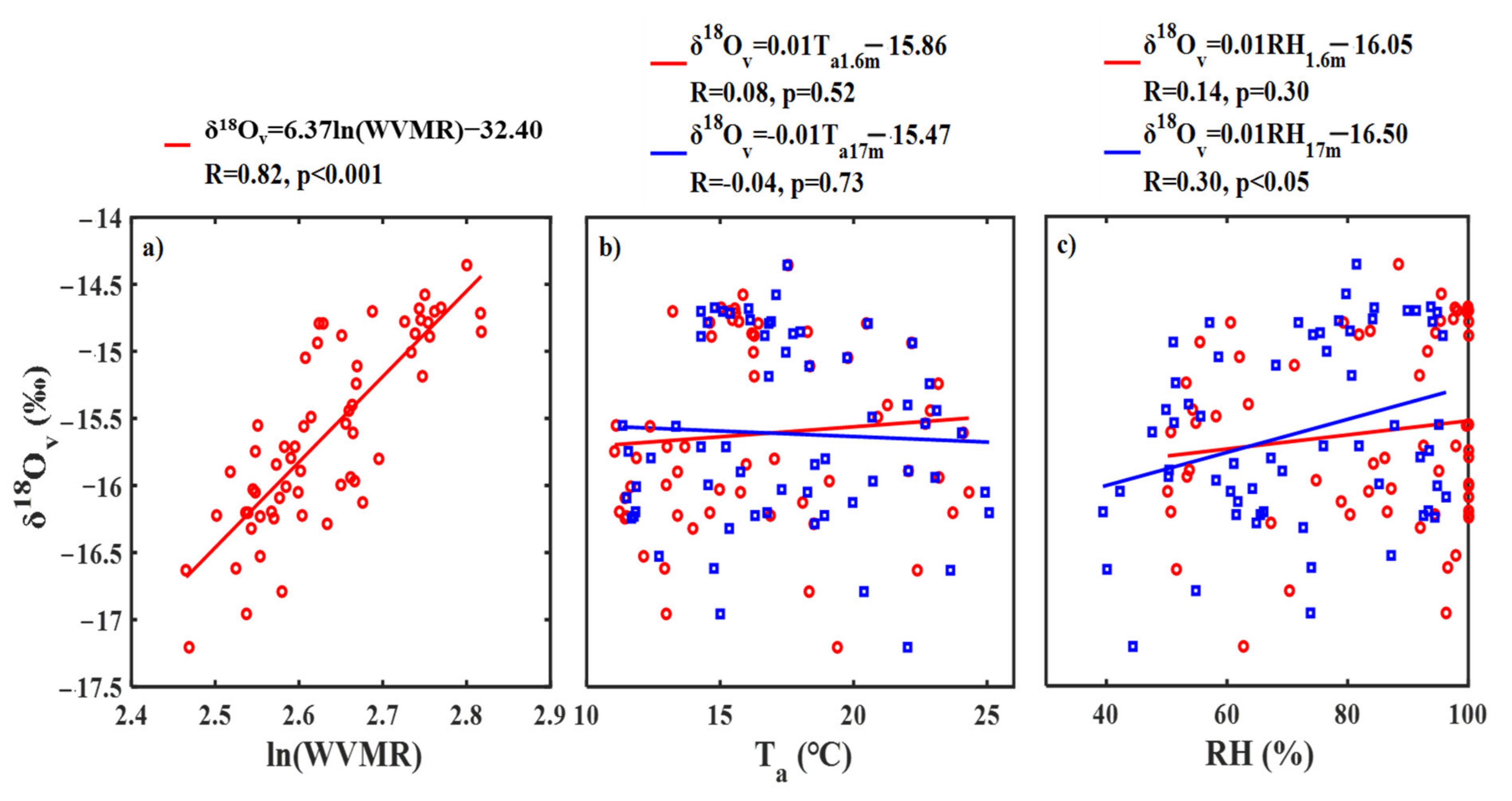
3.3. Diurnal Variability in Water Vapor δ18O and Its Controlling Factors
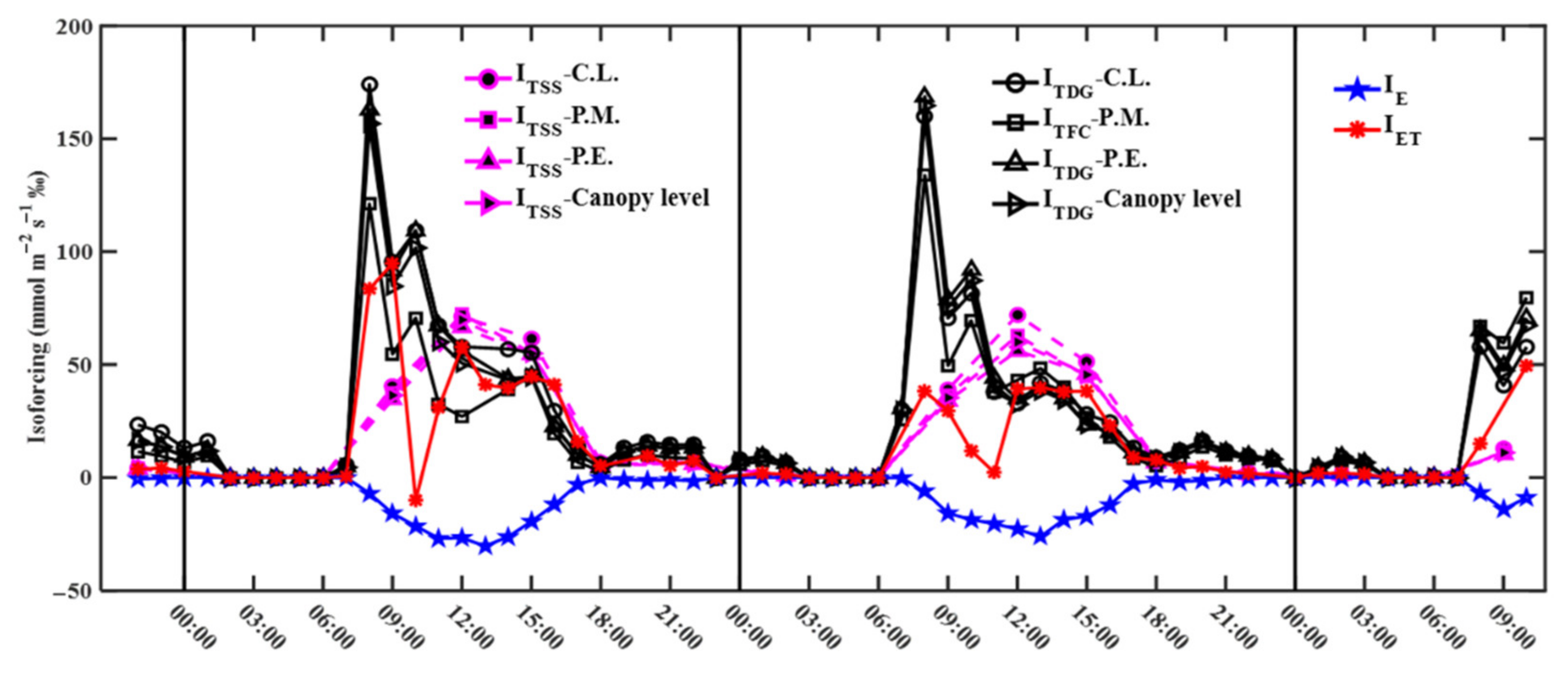
3.4. Transpiration, Evaporation, and Evapotranspiration Isoforcing
4. Discussion
4.1. Effects of Steady and Non-Steady-State Assumption, and the Péclet Effect on Estimating δ18OT
4.2. Effects of δ18OT with Non-Steady-State Assumption on Atmospheric Water Vapor δ18O
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brooks, J.R. Water, bound and mobile. Science 2015, 349, 138–139. [Google Scholar]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [PubMed]
- Xiao, W.; Wei, Z.; Wen, X. Evapotranspiration partitioning at the ecosystem scale using the stable isotope method—A review. Agric. For. Meteorol. 2018, 263, 346–361. [Google Scholar]
- Gat, J.R. Oxygen and hydrogen isotopes in the hydrologic cycle. Annu. Rev. Earth Planet. Sci. 1996, 24, 225–262. [Google Scholar]
- Sprenger, M.; Leistert, H.; Gimbel, K.; Weiler, M. Illuminating hydrological processes at the soil-vegetation-atmosphere interface with water stable isotopes. Rev. Geophys. 2016, 54, 674–704. [Google Scholar]
- Cernusak, L.A.; Barbour, M.M.; Arndt, S.K.; Cheesman, A.W.; English, N.B.; Feild, T.S.; Helliker, B.R.; Holloway-Phillips, M.M.; Holtum, J.A.M.; Kahmen, A.; et al. Stable isotopes in leaf water of terrestrial plants. Plant Cell Environ. 2016, 39, 1087–1102. [Google Scholar]
- Barbour, M.M.; Farquhar, G.D.; Buckley, T.N. Leaf water stable isotopes and water transport outside the xylem. Plant Cell Environ. 2017, 40, 914–920. [Google Scholar]
- Hu, Z.M.; Wen, X.F.; Sun, X.M.; Li, L.H.; Yu, G.R.; Lee, X.H.; Li, S.G. Partitioning of evapotranspiration through oxygen isotopic measurements of water pools and fluxes in a temperate grassland. J. Geophys. Res.-Biogeo. 2014, 119, 358–371. [Google Scholar]
- Lai, C.T.; Ehleringer, J.R.; Bond, B.J.; Paw, U.K. Contributions of evaporation, isotopic non-steady state transpiration and atmospheric mixing on the δ18O of water vapour in Pacific Northwest coniferous forests. Plant Cell Environ. 2006, 29, 77–94. [Google Scholar]
- Welp, L.R.; Lee, X.; Kim, K.; Griffis, T.J.; Billmark, K.A.; Baker, J.M. δ18O of water vapour, evapotranspiration and the sites of leaf water evaporation in a soybean canopy. Plant Cell Environ. 2008, 31, 1214–1228. [Google Scholar]
- Simonin, K.A.; Link, P.; Rempe, D.; Miller, S.; Oshun, J.; Bode, C.; Dietrich, W.E.; Fung, I.; Dawson, T.E. Vegetation induced changes in the stable isotope composition of near surface humidity. Ecohydrology 2014, 7, 936–949. [Google Scholar]
- Wei, Z.W.; Lee, X.H.; Wen, X.F.; Xiao, W. Evapotranspiration partitioning for three agro-ecosystems with contrasting moisture conditions: A comparison of an isotope method and a two-source model calculation. Agric. For. Meteorol. 2018, 252, 296–310. [Google Scholar]
- Xiao, W.; Lee, X.H.; Wen, X.F.; Sun, X.M.; Zhang, S.C. Modeling biophysical controls on canopy foliage water 18O enrichment in wheat and corn. Glob. Change Biol. 2012, 18, 1769–1780. [Google Scholar]
- Flanagan, L.B.; Ehleringer, J.R. Effects of mild water stress and diurnal changes in temperature and humidity on the stable oxygen and hydrogen isotopic composition of leaf water in Cornus stolonifera L. Plant Physiol. 1991, 97, 298–305. [Google Scholar] [CrossRef]
- Yakir, D. Variations in the natural abundance of 18O and deuterium in plant carbohydrates. Plant Cell Environ. 1992, 15, 1005–1020. [Google Scholar]
- Cernusak, L.A.; Pate, J.S.; Farquhar, G.D. Diurnal variation in the stable isotope composition of water and dry matter in fruiting Lupinus angustifolius under field conditions. Plant Cell Environ. 2002, 25, 893–907. [Google Scholar]
- Dongmann, G.; Nurnberg, H.W.; Forstel, H.; Wagener, K. Enrichment of H218O in leaves of transpiring plants. Radiat. Environ. Biophys. 1974, 11, 41–52. [Google Scholar]
- Farquhar, G.D.; Gan, K.S. On the progressive enrichment of the oxygen isotopic composition of water along a leaf. Plant Cell Environ. 2003, 26, 801–819. [Google Scholar]
- Farquhar, G.D.; Cernusak, L.A. On the isotopic composition of leaf water in the non-steady state. Funct. Plant Biol. 2005, 32, 293–303. [Google Scholar]
- Welp, L.R.; Lee, X.; Griffis, T.J.; Wen, X.F.; Xiao, W.; Li, S.; Sun, X.; Hu, Z.; Val Martin, M.; Huang, J. A meta-analysis of water vapor deuterium-excess in the midlatitude atmospheric surface layer. Glob. Biogeochem. Cycles 2012, 26, GB3021. [Google Scholar]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189, 115–117. [Google Scholar]
- Zhao, L.; Wang, L.; Liu, X.; Xiao, H.; Ruan, Y.; Zhou, M. The patterns and implications of diurnal variations in the d-excess of plant water, shallow soil water and air moisture. Hydrol. Earth Syst. Sci. 2014, 18, 4129–4151. [Google Scholar]
- Parkes, S.D.; McCabe, M.F.; Griffiths, A.D.; Wang, L.X.; Chambers, S.; Ershadi, A.; Williams, A.G.; Strauss, J.; Element, A. Response of water vapour D-excess to land-atmosphere interactions in a semi-arid environment. Hydrol. Earth Syst. Sci. 2017, 21, 533–548. [Google Scholar]
- Yang, B.; Wen, X.; Sun, X. Seasonal variations in depth of water uptake for a subtropical coniferous plantation subjected to drought in an East Asian monsoon region. Agric. For. Meteorol. 2015, 201, 218–228. [Google Scholar]
- Sun, X.; Wen, X.; Yu, G.; Liu, Y.; Liu, Q. Seasonal drought effects on carbon sequestration of a mid-subtropical planted forest of southeastern China. Sci. China Ser. D-Earth Sci. 2006, 49, 110–118. [Google Scholar]
- Yu, G.; Chen, Z.; Piao, S.; Peng, C.; Ciais, P.; Wang, Q.; Li, X.; Zhu, X. High carbon dioxide uptake by subtropical forest ecosystems in the East Asian monsoon region. Proc. Natl. Acad. Sci. USA 2014, 111, 4910–4915. [Google Scholar]
- Song, X.; Lyu, S.; Wen, X. Limitation of soil moisture on the response of transpiration to vapor pressure deficit in a subtropical coniferous plantation subjected to seasonal drought. J. Hydrol. 2020, 591, 125301. [Google Scholar]
- Song, X.W.; Lyu, S.D.; Sun, K.; Gao, Y.; Wen, X.F. Flux and source of dissolved inorganic carbon in a headwater stream in a subtropical plantation catchment. J. Hydrol. 2021, 600, 126511. [Google Scholar]
- Huang, L.; Wen, X. Temporal variations of atmospheric water vapor δD and δ18O above an arid artificial oasis cropland in the Heihe River Basin. J. Geophys. Res.-Atmos. 2014, 119, 11456–11476. [Google Scholar]
- Sturm, P.; Knohl, A. Water vapor δ2H and δ18O measurements using off-axis integrated cavity output spectroscopy. Atmos. Meas. Tech. 2010, 3, 67–77. [Google Scholar]
- Wen, X.F.; Lee, X.H.; Sun, X.M.; Wang, J.L.; Hu, Z.M.; Li, S.G.; Yu, G.R. Dew water isotopic ratios and their relationships to ecosystem water pools and fluxes in a cropland and a grassland in China. Oecologia 2012, 168, 549–561. [Google Scholar] [PubMed]
- Wen, X.F.; Sun, X.M.; Zhang, S.C.; Yu, G.R.; Sargent, S.D.; Lee, X.H. Continuous measurement of water vapor D/H and 18O/16O isotope ratios in the atmosphere. J. Hydrol. 2008, 349, 489–500. [Google Scholar]
- Lee, X.H.; Kim, K.; Smith, R. Temporal variations of the 18O/16O signal of the whole-canopy transpiration in a temperate forest. Glob. Biogeochem. Cycles 2007, 21, GB3013. [Google Scholar]
- Wen, X.F.; Yu, G.R.; Sun, X.M.; Li, Q.K.; Liu, Y.F.; Zhang, L.M.; Ren, C.Y.; Fu, Y.L.; Li, Z.Q. Soil moisture effect on the temperature dependence of ecosystem respiration in a subtropical Pinus plantation of southeastern China. Agric. For. Meteorol. 2006, 137, 166–175. [Google Scholar]
- Lyu, S.D.; Wang, J. Soil water stable isotopes reveal surface soil evaporation loss dynamics in a subtropical forest plantation. Forests 2021, 12, 1648. [Google Scholar]
- Querejeta, J.I.; Estrada-Medina, H.; Allen, M.F.; Jimenez-Osornio, J.J. Water source partitioning among trees growing on shallow karst soils in a seasonally dry tropical climate. Oecologia 2007, 152, 26–36. [Google Scholar]
- Lyu, S.D. Variability of δ2H and δ18O in soil water and its linkage to precipitation in an East Asian monsoon subtropical forest plantation. Water 2021, 13, 2930. [Google Scholar]
- Lyu, S.D.; Wang, J.; Song, X.W.; Wen, X.F. The relationship of δD and δ18O in surface soil water and its implications for soil evaporation along grass transects of Tibet, Loess, and Inner Mongolia Plateau. J. Hydrol. 2021, 600, 126533. [Google Scholar]
- Craig, H.; Gordon, L. Deuterium and oxygen-18 variations in the ocean and the marine atmosphere. In Stable Isotopes in Oceanographic Studies and Paleotemperatures; Tongiorgi, E., Ed.; Consiglio Nazionale delle Ricerche, Laboratorio di Geologia Nucleare: Spoleto, Italy, 1965. [Google Scholar]
- Merlivat, L. Molecular diffusivities of H216O, HD16O, and H218O in gases. J. Chem. Phys. 1978, 69, 2864–2871. [Google Scholar]
- Farquhar, G.D.; Ehleringer, J.R.; Hubick, K.T. Carbon isotope discrimination and photosynthesis. Annu. Rev. Plant Phys. 1989, 40, 503–537. [Google Scholar]
- Lee, X.H.; Griffis, T.J.; Baker, J.M.; Billmark, K.A.; Kim, K.; Welp, L.R. Canopy-scale kinetic fractionation of atmospheric carbon dioxide and water vapor isotopes. Glob. Biogeochem. Cycles 2009, 23, 15. [Google Scholar]
- Cernusak, L.A.; Farquhar, G.D.; Pate, J.S. Environmental and physiological controls over oxygen and carbon isotope composition of Tasmanian blue gum, Eucalyptus globulus. Tree Physiol. 2005, 25, 129–146. [Google Scholar] [PubMed]
- Helliker, B.R.; Ehleringer, J.R. Establishing a grassland signature in veins: 18O in the leaf water of C3 and C4 grasses. Proc. Natl. Acad. Sci. USA 2000, 97, 7894–7898. [Google Scholar] [PubMed]
- Yakir, D.; Sternberg, L.D.L. The use of stable isotopes to study ecosystem gas exchange. Oecologia 2000, 123, 297–311. [Google Scholar] [PubMed]
- Farquhar, G.D.; Lloyd, J. Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere. In Book Carbon and Oxygen Isotope Effects in the Exchange of Carbon Dioxide between Terrestrial Plants and the Atmosphere; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Cuntz, M.; Ogée, J.; Farquhar, G.D.; Peylin, P.; Cernusak, L.A. Modelling advection and diffusion of water isotopologues in leaves. Plant Cell Environ. 2007, 30, 892–909. [Google Scholar]
- Xiao, W.; Lee, X.H.; Griffis, T.J.; Kim, K.; Welp, L.R.; Yu, Q. A modeling investigation of canopy-air oxygen isotopic exchange of water vapor and carbon dioxide in a soybean field. J. Geophys. Res.-Biogeo. 2010, 115, G01004. [Google Scholar]
- Ron da, R.J.; de Bruin, H.A.R.; Holtslag, A.A.M. Representation of the canopy conductance in modeling the surface energy budget for low vegetation. J. Appl. Meteorol. 2001, 40, 1431–1444. [Google Scholar]
- Chakraborty, S.; Burman, P.K.D.; Sarma, D.; Sinha, N.; Datye, A.; Metya, A.; Murkute, C.; Saha, S.K.; Sujith, K.; Gogoi, N.; et al. Linkage between precipitation isotopes and biosphere-atmosphere interaction observed in northeast India. npj Clim. Atmos. Sci. 2022, 5, 10. [Google Scholar]
- Dubbert, M.; Werner, C. Water fluxes mediated by vegetation emerging isotopic insights at the soil and atmosphere interfaces. New Phytol. 2019, 221, 1754–1763. [Google Scholar]
- Yakir, D.; Wang, X.F. Fluxes of CO2 and water between terrestrial vegetation and the atmosphere estimated from isotope measurements. Nature 1996, 380, 515–517. [Google Scholar]
- Rothfuss, Y.; Javaux, M. Reviews and syntheses: Isotopic approaches to quantify root water uptake: A review and comparison of methods. Biogeosciences 2017, 14, 2199–2224. [Google Scholar]
- Li, Y.; Zhou, L.; Wang, S.; Chi, Y.; Chen, J. Leaf Temperature and Vapour Pressure Deficit (VPD) Driving Stomatal Conductance and Biochemical Processes of Leaf Photosynthetic Rate in a Subtropical Evergreen Coniferous Plantation. Sustainability 2018, 10, 4063. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, S.; Wang, J. Transpiration Induced Changes in Atmospheric Water Vapor δ18O via Isotopic Non-Steady-State Effects on a Subtropical Forest Plantation. Water 2022, 14, 2648. https://doi.org/10.3390/w14172648
Lyu S, Wang J. Transpiration Induced Changes in Atmospheric Water Vapor δ18O via Isotopic Non-Steady-State Effects on a Subtropical Forest Plantation. Water. 2022; 14(17):2648. https://doi.org/10.3390/w14172648
Chicago/Turabian StyleLyu, Sidan, and Jing Wang. 2022. "Transpiration Induced Changes in Atmospheric Water Vapor δ18O via Isotopic Non-Steady-State Effects on a Subtropical Forest Plantation" Water 14, no. 17: 2648. https://doi.org/10.3390/w14172648
APA StyleLyu, S., & Wang, J. (2022). Transpiration Induced Changes in Atmospheric Water Vapor δ18O via Isotopic Non-Steady-State Effects on a Subtropical Forest Plantation. Water, 14(17), 2648. https://doi.org/10.3390/w14172648






