Effects of Slide Shape on Impulse Waves Generated by a Subaerial Solid Slide
Abstract
:1. Introduction
2. Model Development
2.1. Numerical Model for Landslide Generated Waves
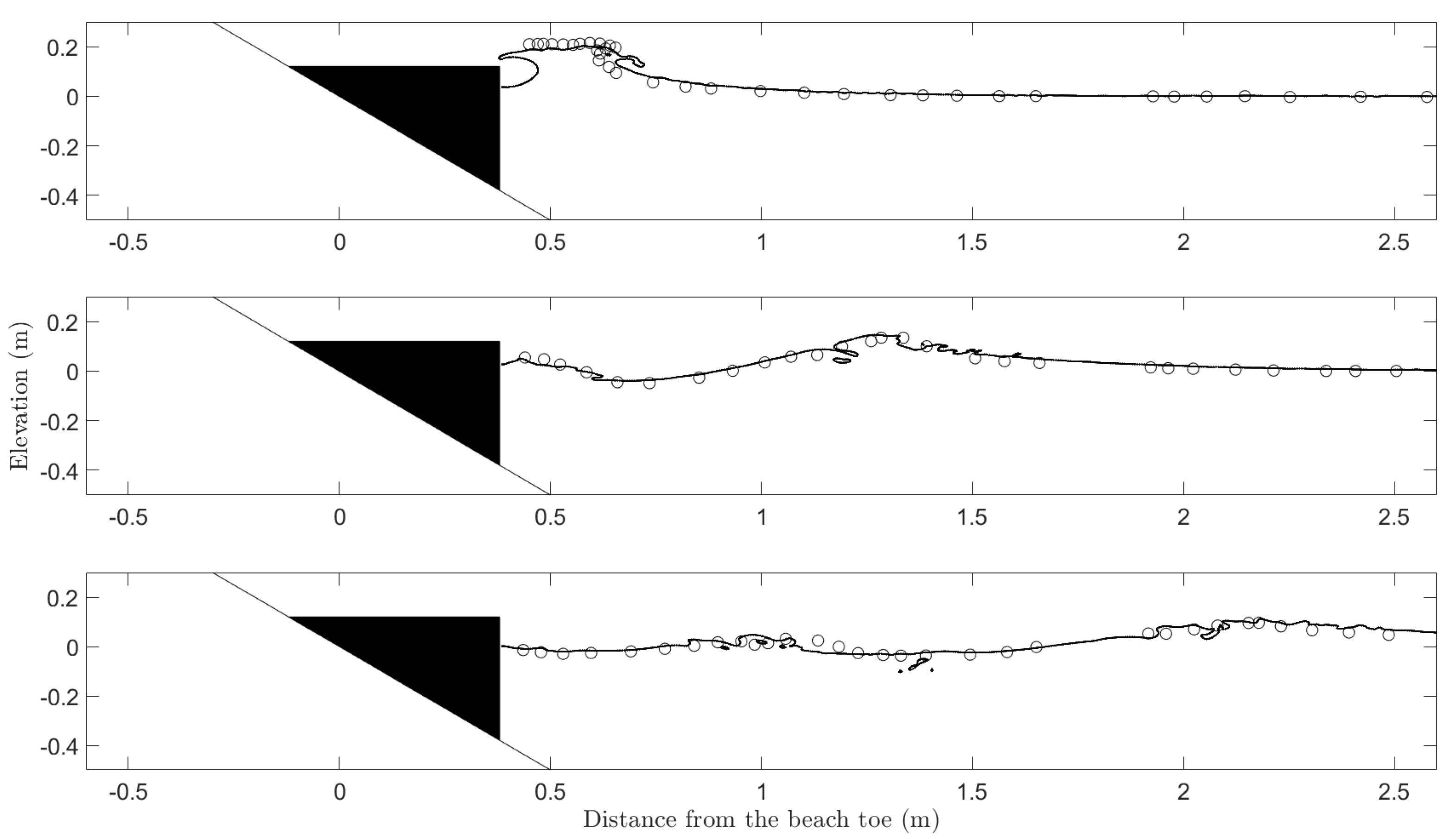
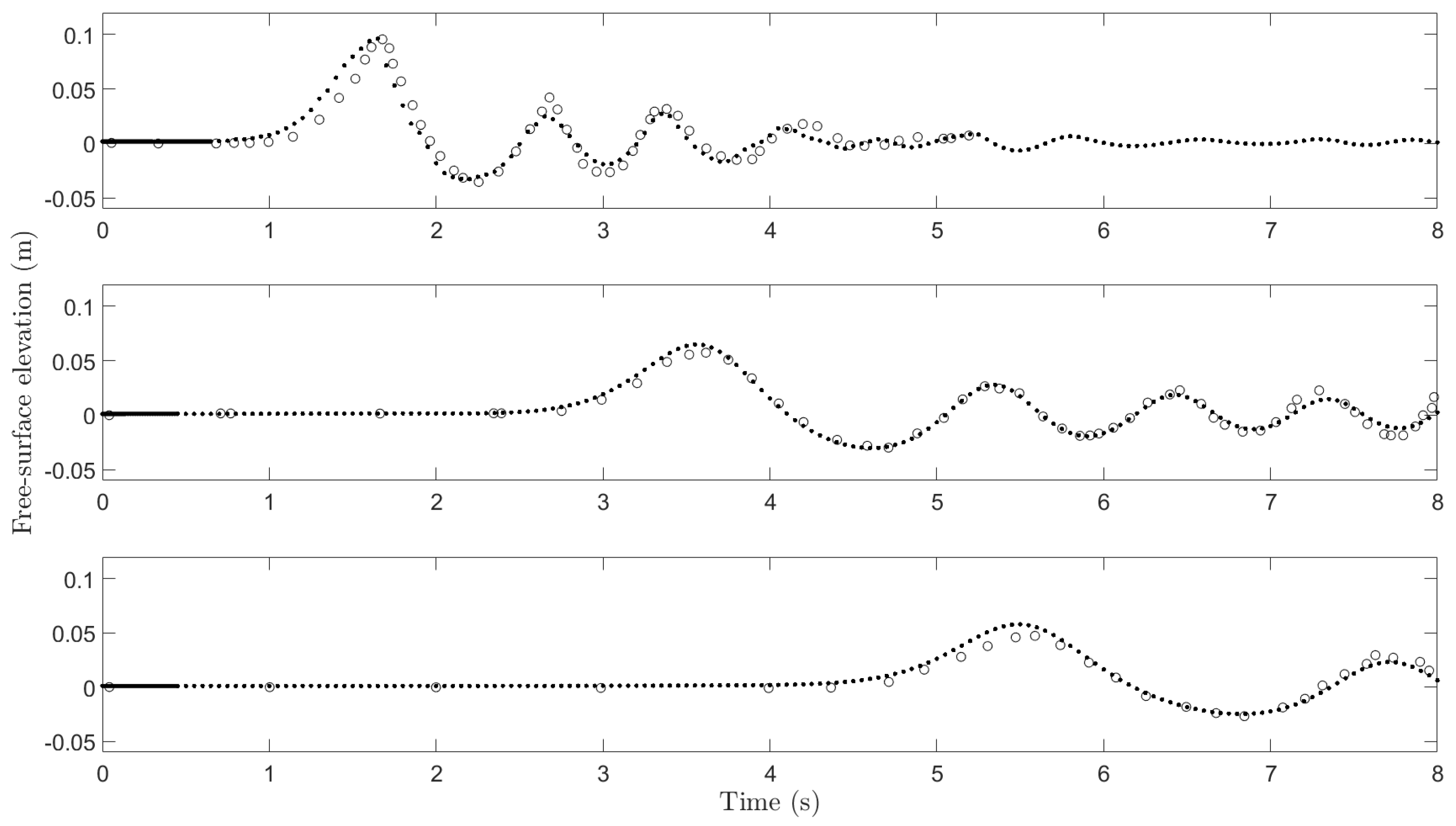
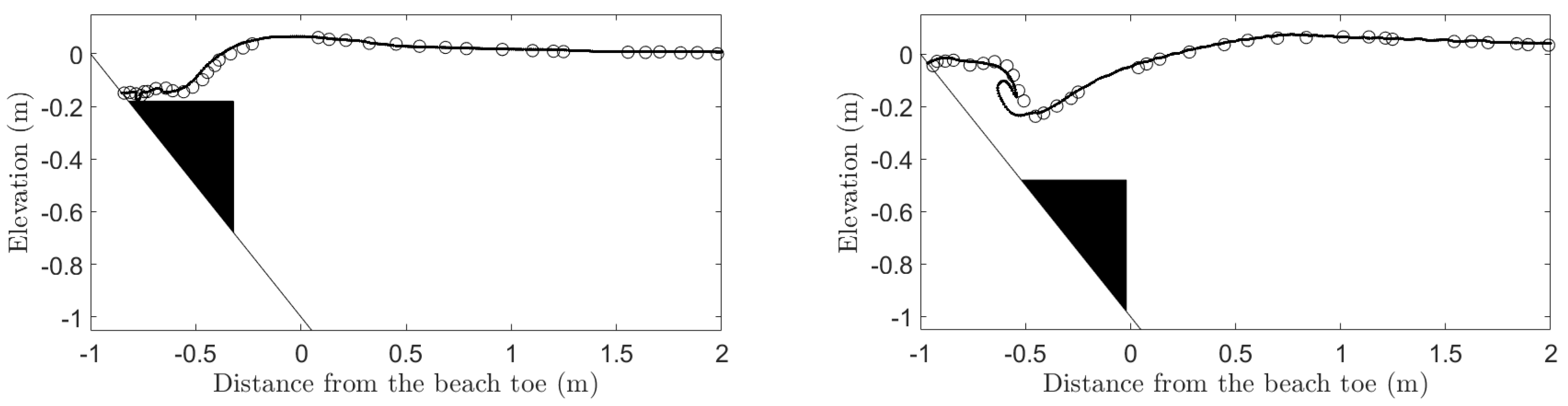
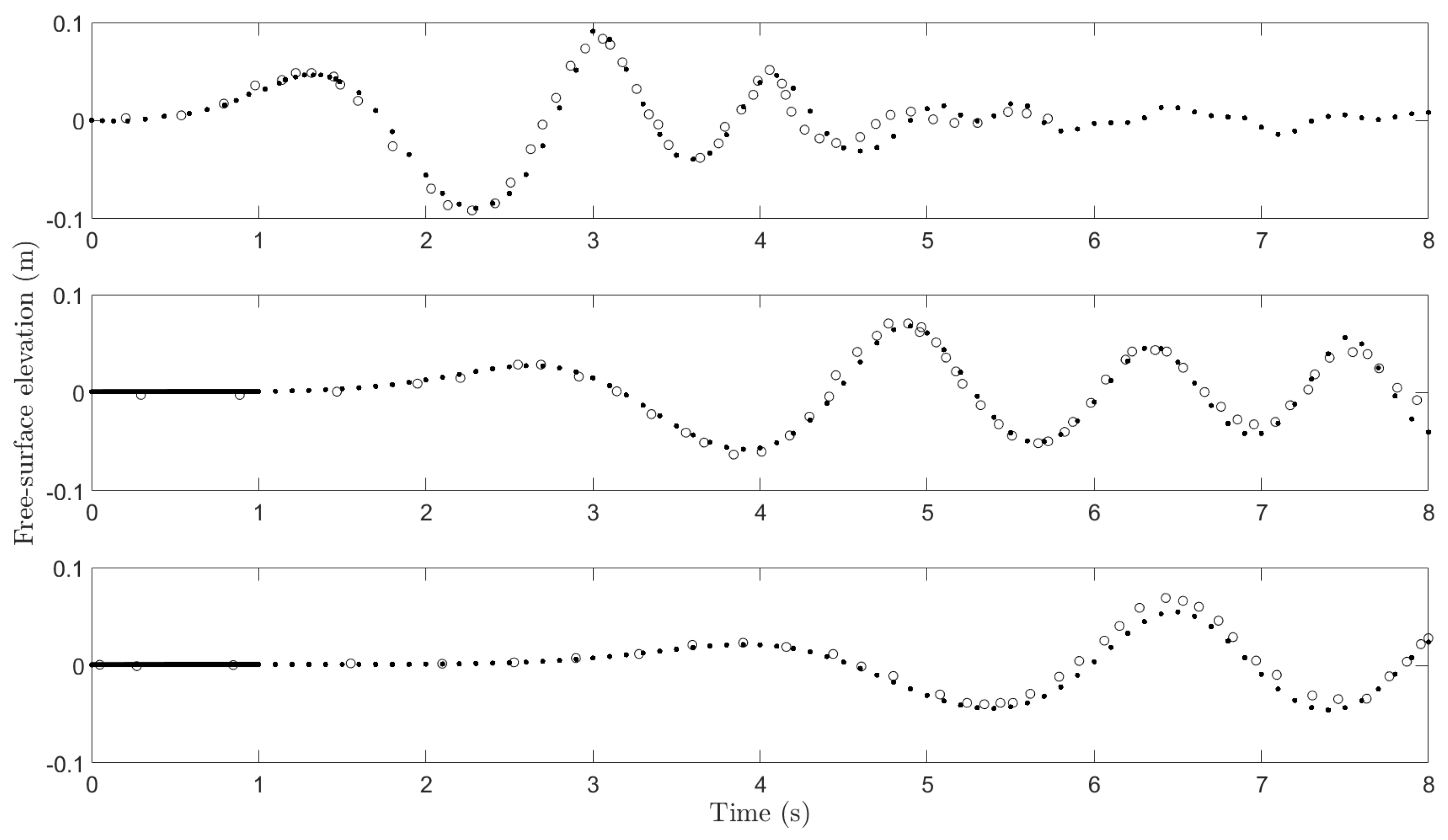
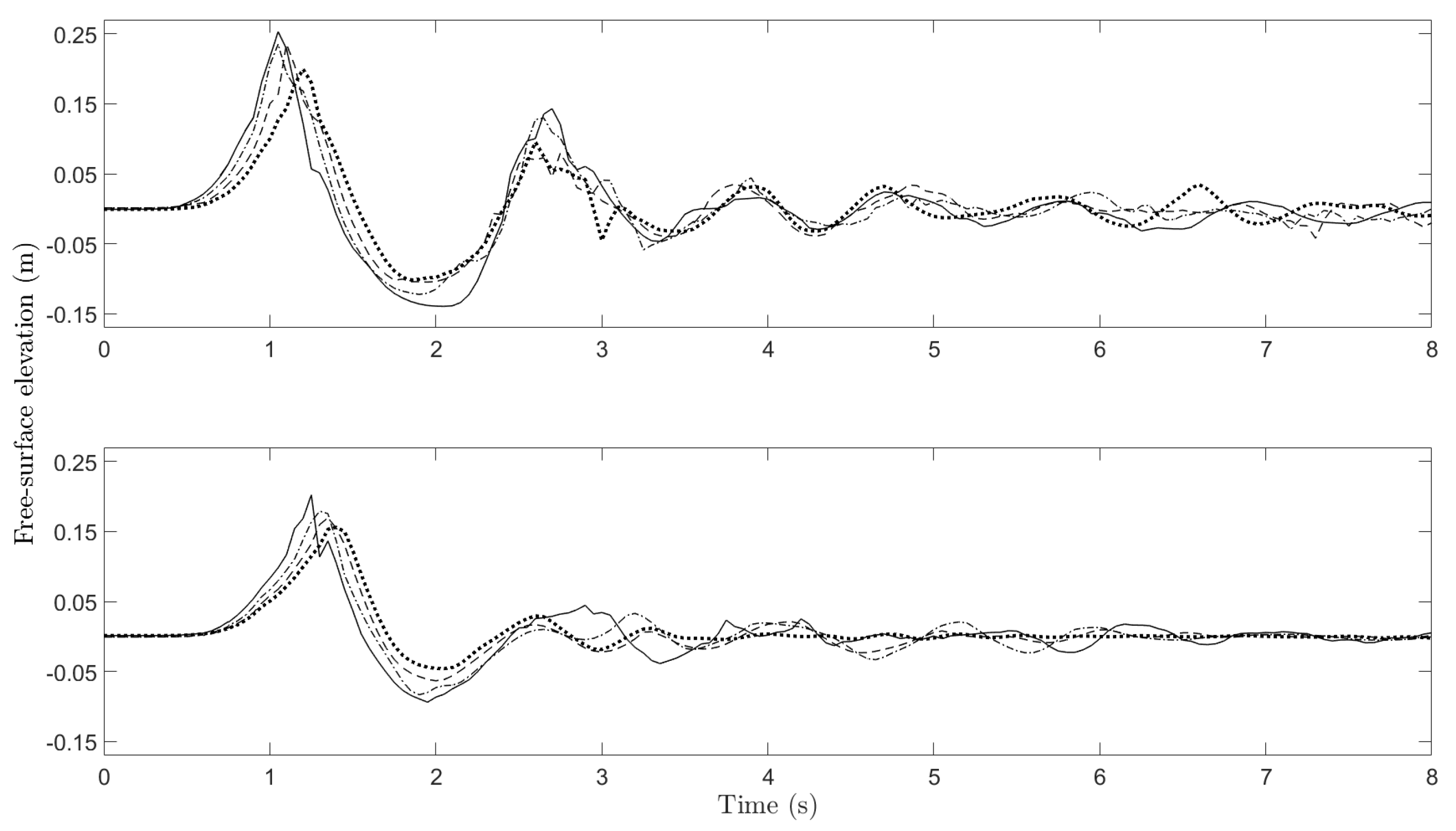
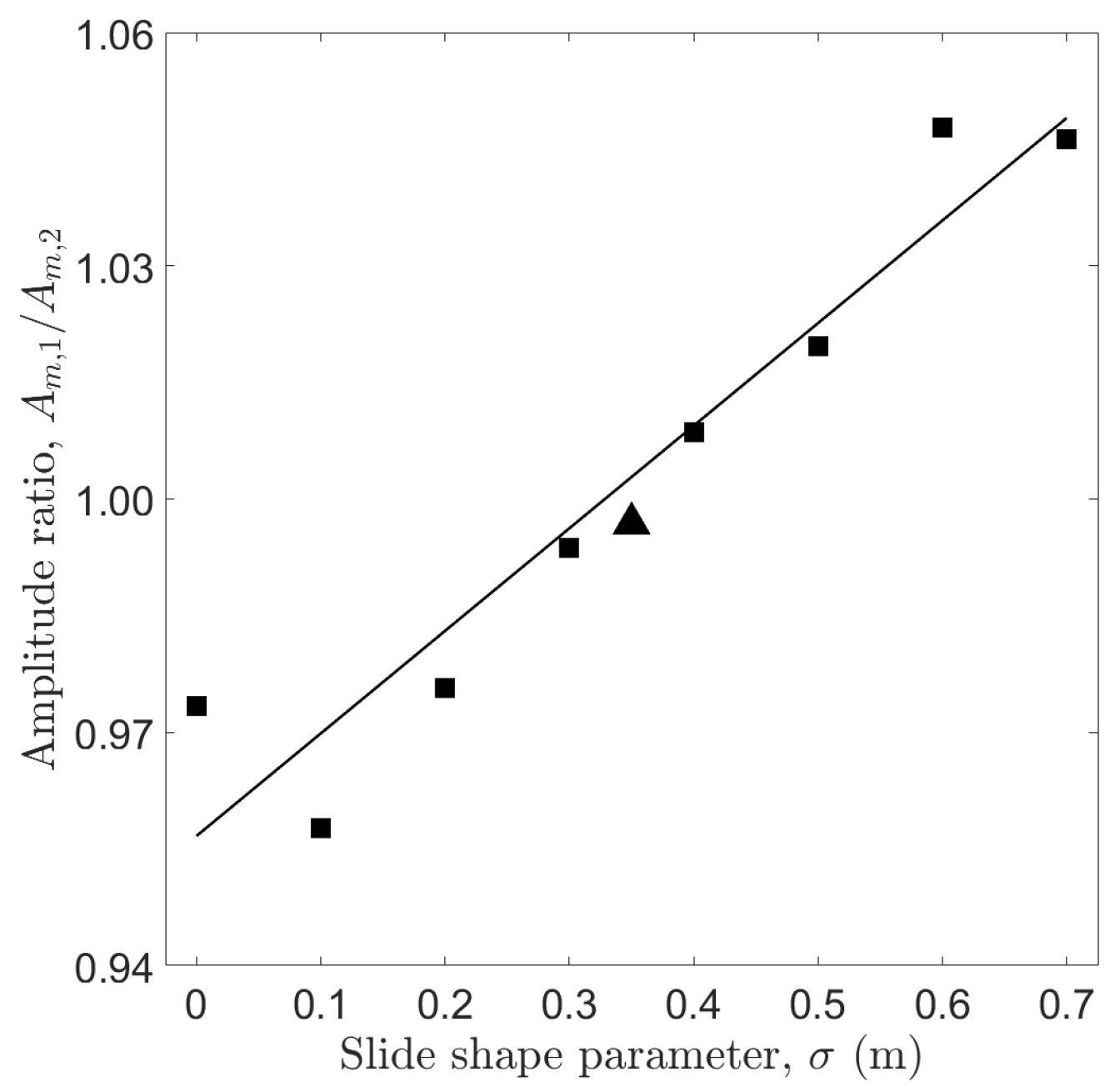
2.2. Model Validation
3. Numerical Experiments
3.1. Design of Numerical Experiments
3.2. Results and Discussions
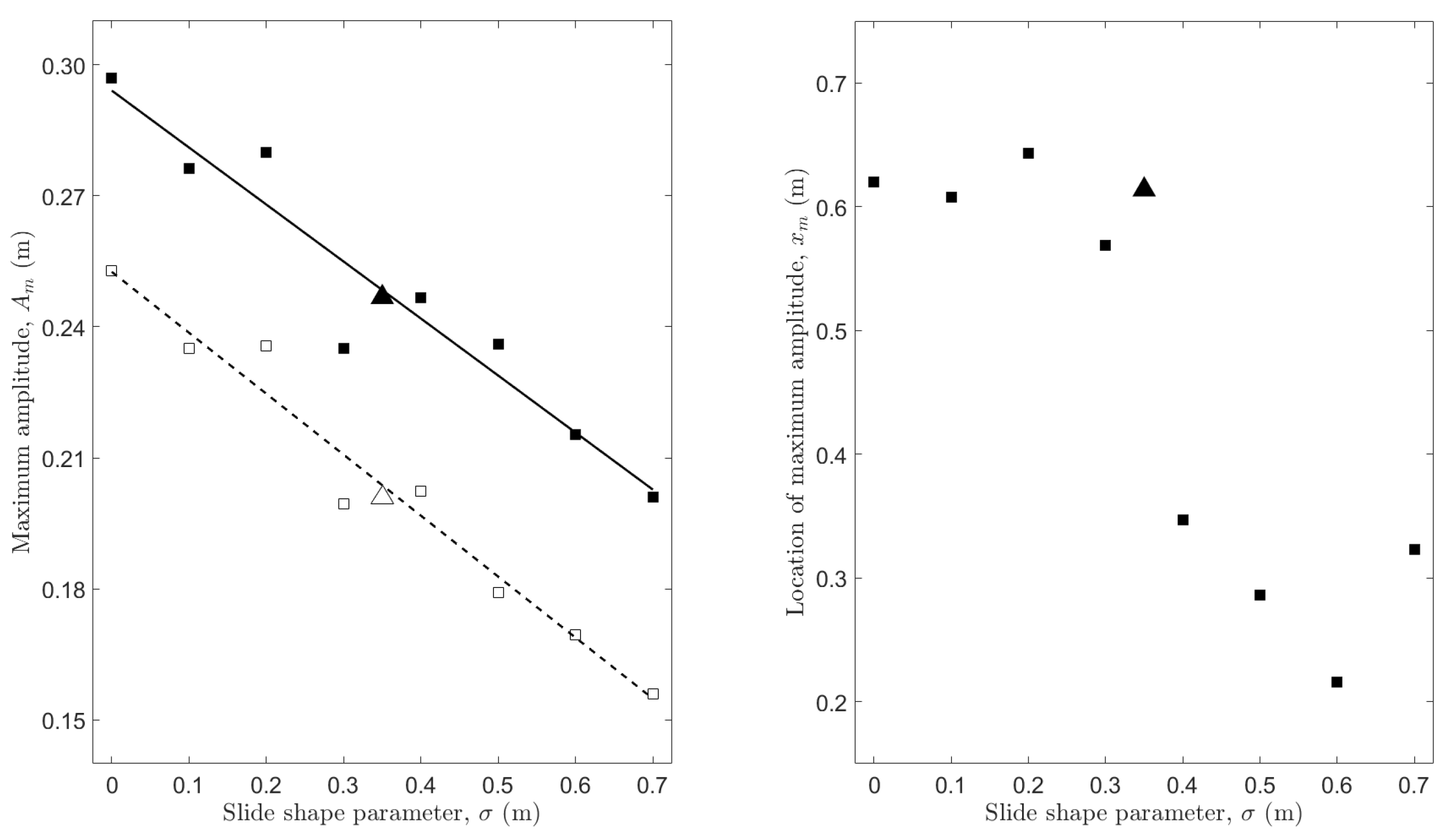
3.2.1. Maximum Amplitude and Its Location
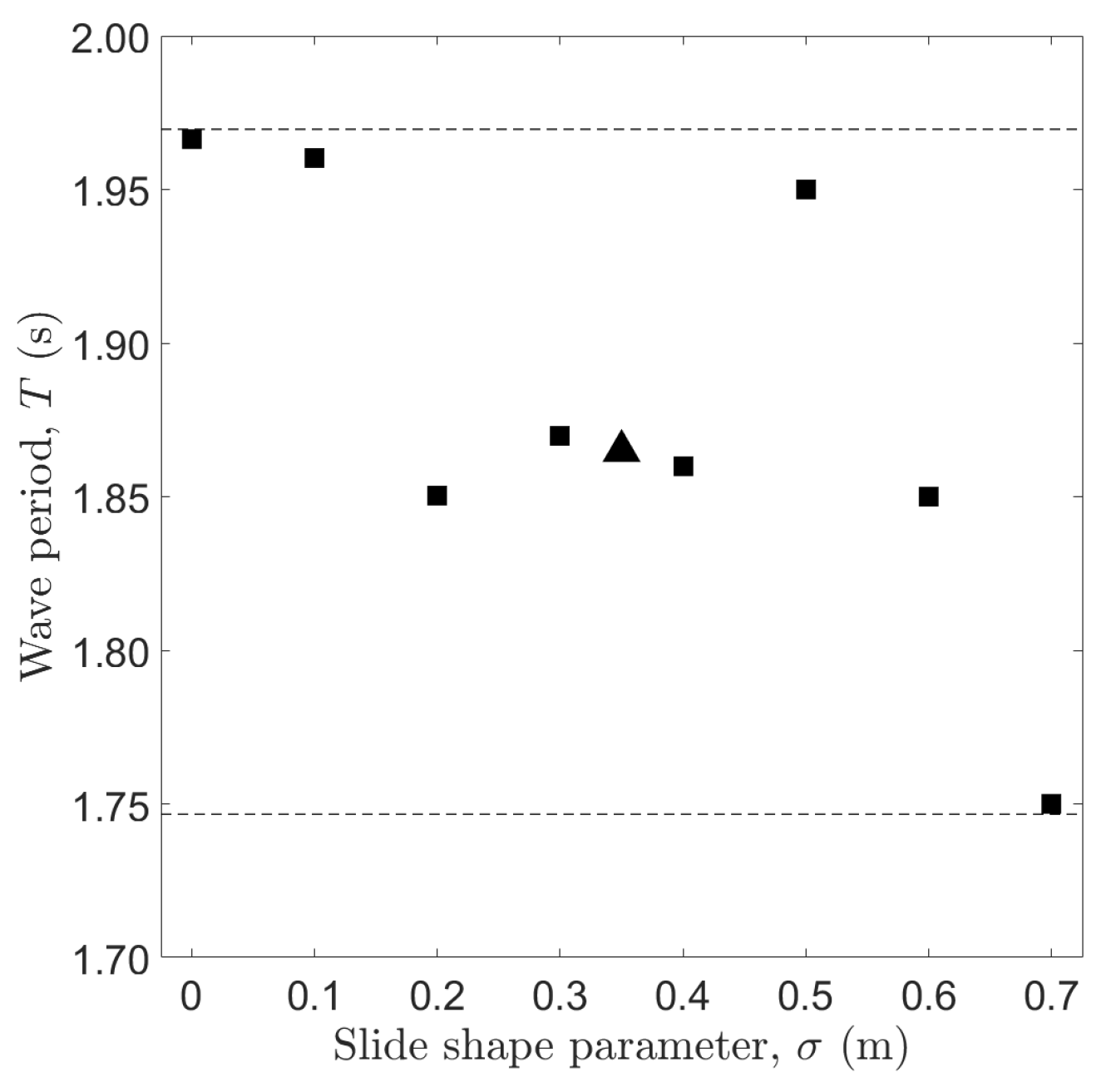
3.2.2. Wave Period
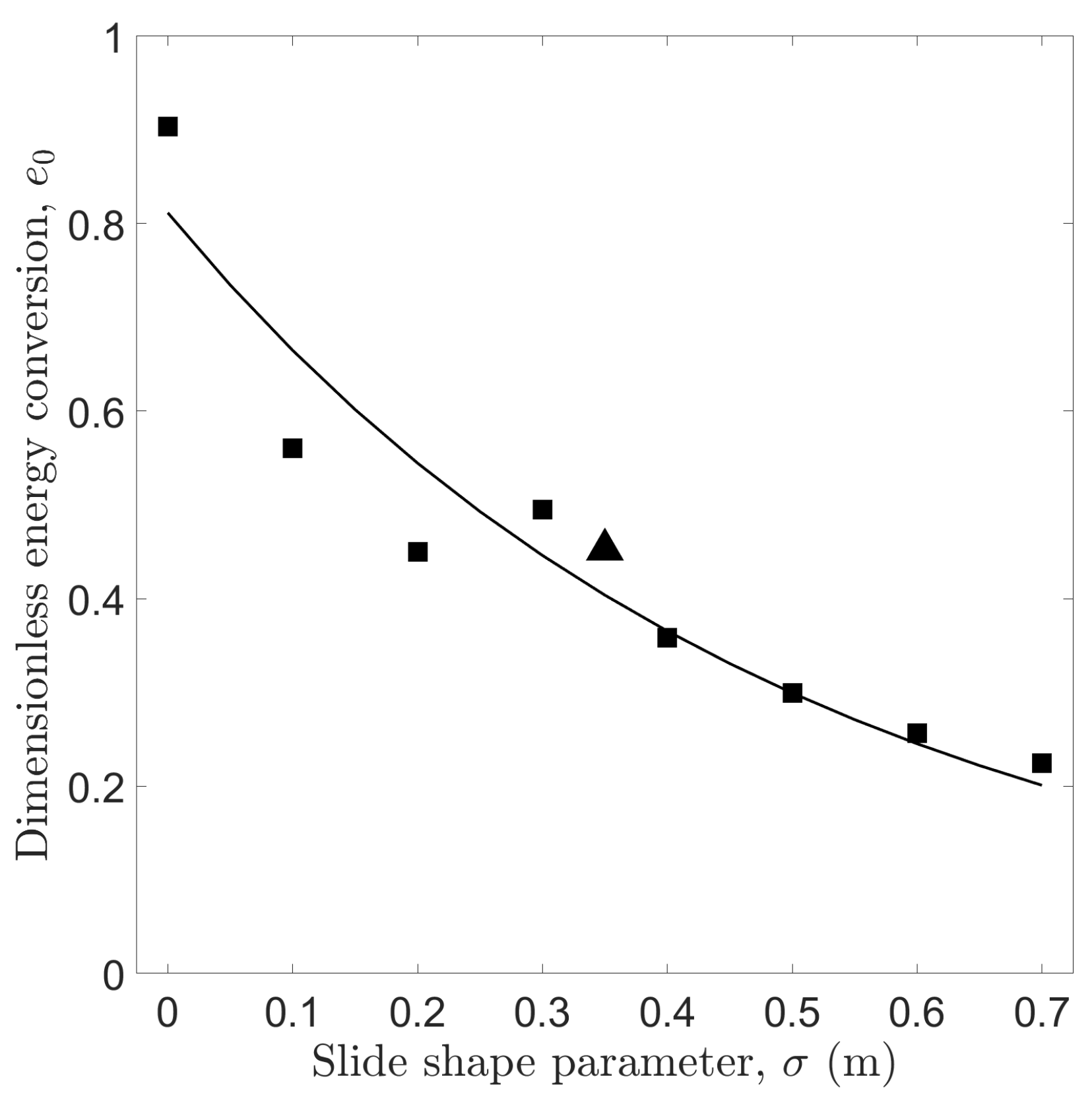
3.2.3. Impact Energy Conversion
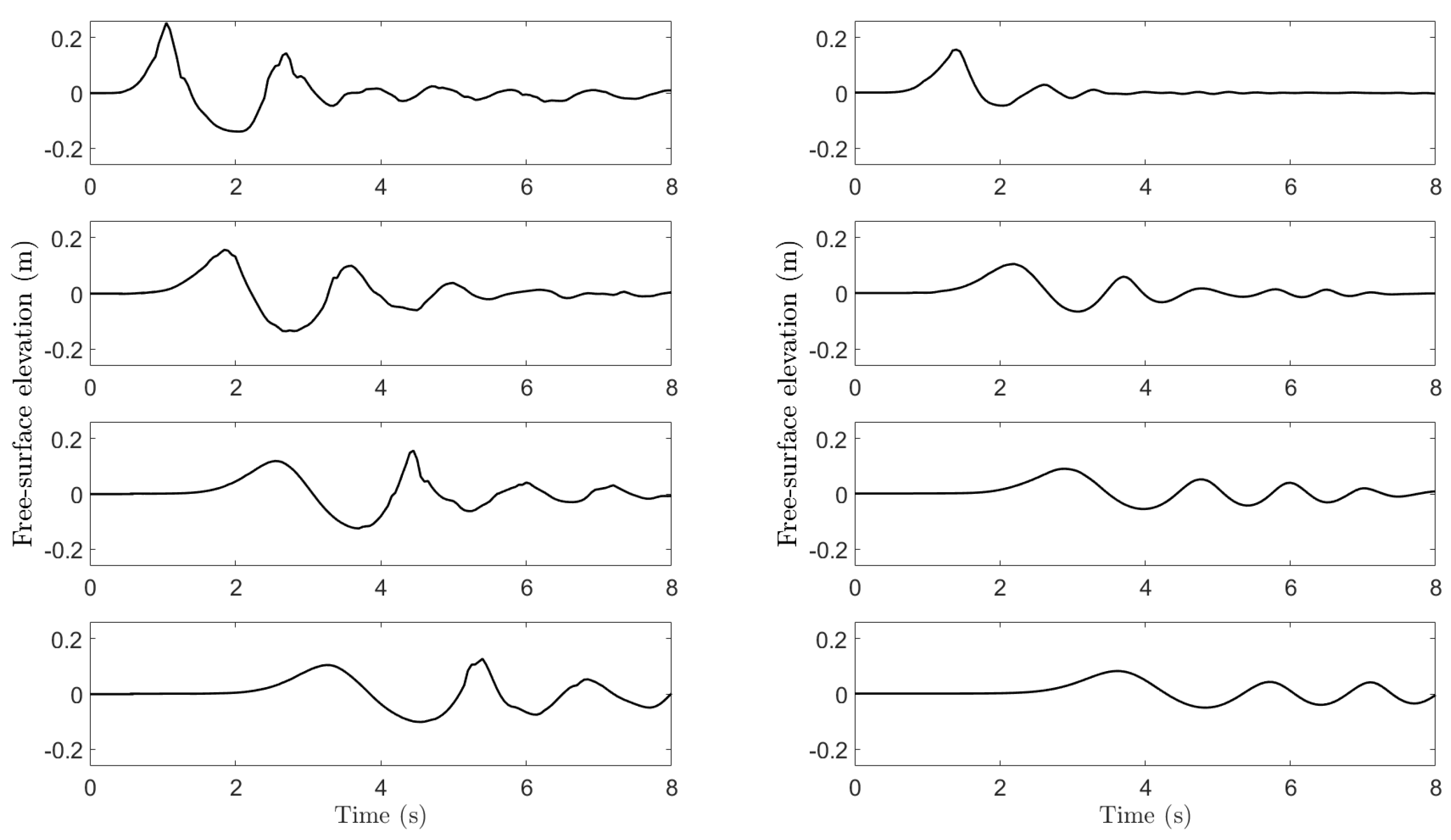
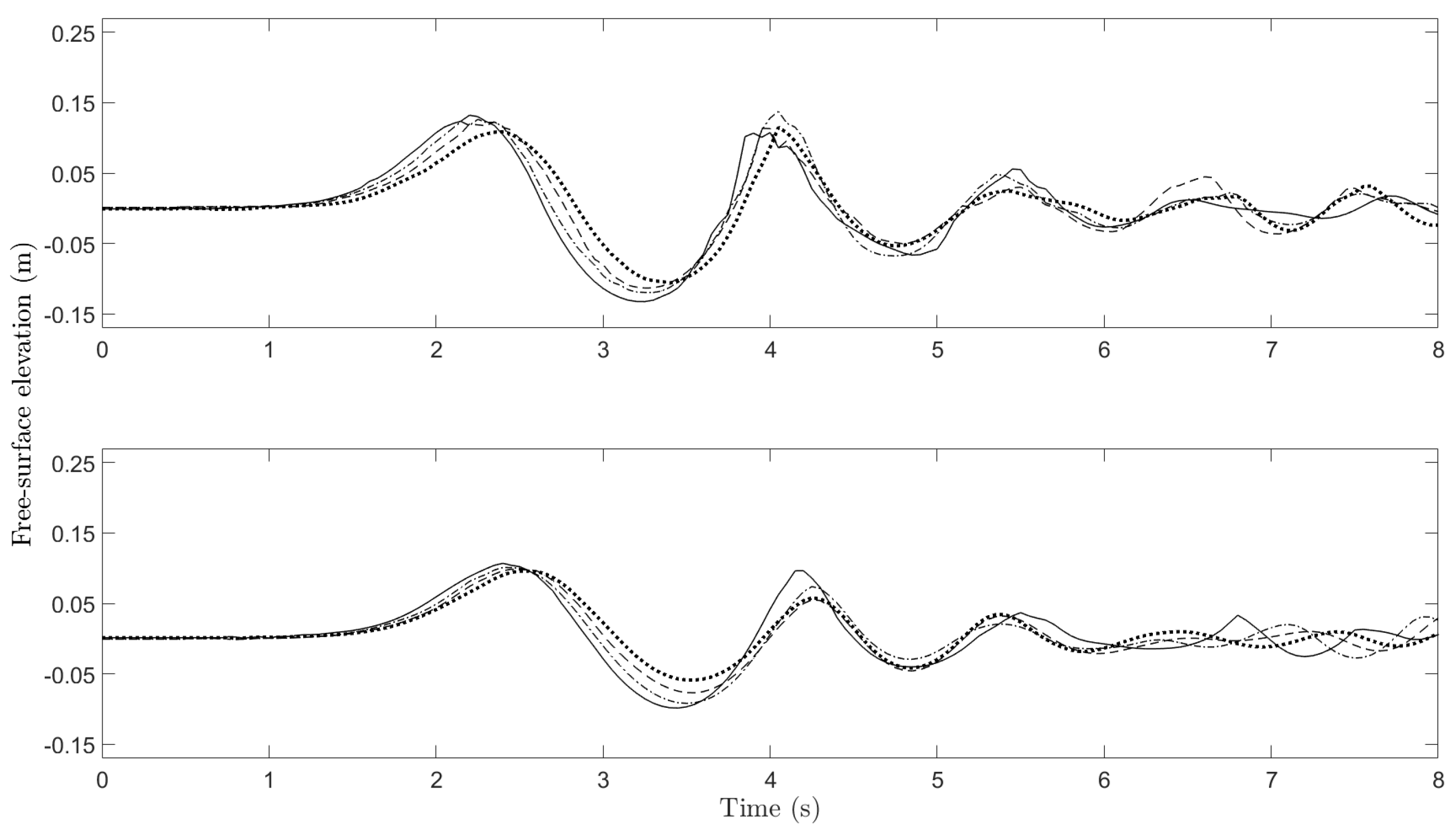
3.2.4. Evolution of Leading Waves
4. Concluding Remarks
- Maximum wave amplitude, , is inversely proportional to the slide shape parameter, . Location of the maximum amplitude, , also depends on (Section 3.2.1).
- Wave period, T, is almost independent of (Section 3.2.2).
- Impact energy conversion ratio, , decays exponential with (Section 3.2.3).
- The first crest always travels at the typical long wave speed while the second crest propagates at a speed about 15 to 25% slower depending on the value of (Section 3.2.4).
- In the far field, the second crest becomes larger than the first crest if is smaller (Section 3.2.4).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Slingerland, R.L.; Voight, B. Occurrences, properties and predictive models of landslide-generated impulse waves. In Rockslides and Avalanches; Voight, B., Ed.; Elsevier: Amsterdam, The Netherlands, 1979; Volume 2, pp. 317–397. [Google Scholar]
- Ward, S.N. Landslide tsunami. J. Geophys. Res. Solid Earth 2001, 106, 11201–11215. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.-E. Lituya Bay case: Rockslide impact and wave run-up. Sci. Tsunami Hazards 2001, 19, 3–22. [Google Scholar]
- Bardet, J.-P.; Synolakis, C.E.; Davies, H.L.; Imamura, F.; Okal, E.A. Landslide tsunamis: Recent findings and research directions. Pure Appl. Geophys. 2003, 160, 1793–1809. [Google Scholar] [CrossRef]
- Fritz, H.M.; Mohammed, F.; Yoo, J. Lituya Bay landslide impact generated mega-tsunami 50th anniversary. Pure Appl. Geophys. 2009, 166, 153–175. [Google Scholar] [CrossRef]
- Miller, D.J. Giant Waves in Lituya Bay, Alaska; Geological Survey Professional Paper 354-C; U.S. Government Printing Office: Washington, DC, USA, 1960.
- Higman, B.; Shugar, D.H.; Stark, C.P.; Ekström, G.; Koppes, M.N.; Lynett, P.; Dufresne, A.; Haeussler, P.J.; Geertsema, M.; Gulick, S.; et al. The 2015 landslide and tsunami in Taan Fiord, Alaska. Sci. Rep. 2018, 8, 12993. [Google Scholar] [CrossRef]
- Haeussler, P.J.; Gulick, S.P.S.; McCall, N.; Walton, M.; Reece, R.; Larsen, C.; Shugar, D.H.; Geertsema, M.; Venditti, J.G.; Labay, K. Submarine deposition of asubaerial landslide in Taan Fiord, Alaska. J. Geophys. Res. Earth Surf. 2018, 123, 2443–2463. [Google Scholar] [CrossRef]
- Ward, S.N.; Day, S. The 1958 Lituya Bay Landslide and Tsunami—A tsunami ball approach. J. Earthq. Tsunami 2010, 4, 285–319. [Google Scholar] [CrossRef]
- Franz, M.; Jaboyedoff, M.; Mulligan, R.P.; Podladchikov, Y.; Take, W.A. An efficient two-layer landslide-tsunami numerical model: Effects of momentum transfer validated with physical experiments of waves generated by granular landslides. Nat. Hazards Earth Syst. Sci. 2021, 21, 1229–1245. [Google Scholar] [CrossRef]
- L’Heureux, J.-S.; Hansen, L.; Longva, O.; Eilertsen, R.S. Landslides Along Norwegian Fjords: Causes and Hazard Assessment. In Landslide Science and Practice; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 5, pp. 317–397. [Google Scholar]
- Glimsdal, S.; L’Heureux, J.-S.; Harbitz, C.B.; Løvholt, F. The 29th January 2014 submarine landslide at Statland, Norway—Landslide dynamics, tsunami generation, and run-up. Landslides 2016, 13, 1435–1444. [Google Scholar] [CrossRef]
- Harbitz, C.B.; Pedersen, G.; Gjevik, B. Numerical simulations of large water waves due to landslides. J. Hydraul. Eng. 1993, 119, 1325–1342. [Google Scholar] [CrossRef]
- Harbitz, C.B.; Glimsdal, S.; Løvholt, F.; Kveldsvik, V.; Pedersen, G.K.; Jensen, A. Rockslide tsunamis in complex fjords: From an unstable rock slope at Åkerneset to tsunami risk in western Norway. Coast. Eng. 2014, 88, 101–122. [Google Scholar] [CrossRef]
- Dahl-Jensen, T.; Larsen, L.M.; Pedersen, S.A.S.; Pedersen, J.; Jepsen, H.F.; Pedersen, G.; Nielsen, T.; Pedersen, A.K.; Von Platen-Hallermund, F.; Weng, W. Landslide and Tsunami 21 November 2000 in Paatuut, West Greenland. Nat. Hazards 2004, 31, 277–287. [Google Scholar] [CrossRef]
- Gauthier, D.; Anderson, S.A.; Fritz, H.M.; Giachetti, T. Karrat Fjord (Greenland) tsunamigenic landslide of 17 June 2017: Initial 3D observations. Landslides 2018, 15, 327–332. [Google Scholar] [CrossRef]
- Couston, L.-A.; Mei, C.C.; Alam, M.-R. Landslide tsunamis in lakes. J. Fluid Mech. 2015, 772, 784–804. [Google Scholar] [CrossRef]
- Barla, G.; Paronuzzi, P. The 1963 Vajont Landslide: 50th Anniversary. Rock Mech. Rock Eng. 2013, 46, 1267–1270. [Google Scholar] [CrossRef]
- Waldmann, N.; Vasskog, K.; Simpson, G.; Chapron, E.; Støren, E.W.N.; Hansen, L.; Loizeau, J.-L.; Nesje, A.; Ariztegui, D. Anatomy of a catastrophe: Reconstructing the 1936 rock fall and tsunami event in Lake Lovatnet, Western Norway. Front. Earth Sci. 2021, 9, 671378. [Google Scholar] [CrossRef]
- Plafker, G.; Eyzaguirre, V.R. Rock Avalanche and Wave at Chungar, Peru. In Developments in Geotechnical Engineering; Voight, B., Ed.; Elsevier: Amsterdam, The Netherlands, 1979; Volume 14, pp. 269–279. [Google Scholar]
- Panizzo, A.; De Girolamo, P.; Di Risio, M.; Maistri, A.; Petaccia, A. Great landslide events in Italian artificial reservoirs. Nat. Hazards Earth Syst. Sci. 2005, 5, 733–740. [Google Scholar] [CrossRef]
- Kilburn, C.R.J.; Petley, D.N. Forecasting giant, catastrophic slope collapse: Lessons from Vajont, Northern Italy. Geomorphology 2003, 54, 21–32. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Bolla, A. The prehistoric Vajont rockslide: An updated geological model. Geomorphology 2012, 169, 165–191. [Google Scholar] [CrossRef]
- Delatte, N.J. Beyond Failure, Forensic Case Studies for Civil Engineers; ASCE Press: Reston, VA, USA, 2009; pp. 234–248. [Google Scholar]
- Lynett, P.J.; Borrero, J.C.; Liu, P.L.-F.; Synolakis, C.E. Field survey and numerical simulations: A review of the 1998 Papua New Guinea Tsunami. Pure Appl. Geophys. 2003, 160, 2119–2146. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Higuera, P.; Husrin, S.; Prasetya, G.S.; Prihantono, J.; Diastomo, H.; Pryambodo, D.G.; Susmoro, H. Coastal landslides in Palu Bay during 2018 Sulawesi earthquake and tsunami. Landslides 2020, 17, 2085–2098. [Google Scholar] [CrossRef]
- Grilli, S.T.; Tappin, D.R.; Carey, S.; Watt, S.F.L.; Ward, S.N.; Grilli, A.R.; Engwell, S.L.; Zhang, C.; Kirby, J.T.; Schambach, L.; et al. Modelling of the tsunami from the December 22, 2018 lateral collapse of Anak Krakatau volcano in the Sunda Straits, Indonesia. Sci. Rep. 2019, 9, 11946. [Google Scholar] [CrossRef] [PubMed]
- Masson, D.G.; Harbitz, C.B.; Wynn, R.B.; Pedersen, G.; Løvholt, F. Submarine landslides: Processes, triggers and hazard prediction. Phil. Trans. R. Soc. A 2006, 364, 2009–2039. [Google Scholar] [CrossRef] [PubMed]
- Harbitz, C.B.; Løvholt, F.; Bungum, H. Submarine landslide tsunamis: How extreme and how likely? Nat. Hazards 2014, 72, 1341–1374. [Google Scholar] [CrossRef]
- Parsons, T.; Geist, E.L.; Ryan, H.F.; Lee, H.J.; Haeussler, P.J.; Lynett, P.; Hart, P.E.; Sliter, R.; Rol, E. Source and progression of a submarine landslide and tsunami: The 1964 Great Alaska earthquake at Valdez. J. Geophys. Res. Solid Earth 2014, 119, 8502–8516. [Google Scholar] [CrossRef]
- Okal, E. Normal mode energetics for far-field tsunamis generated by dislocations and landslides. Pure Appl. Geophys. 2003, 160, 2189–2221. [Google Scholar] [CrossRef]
- Ruff, L.J. Some aspects of energy balance and tsunami generation by earthquakes and landslides. Pure Appl. Geophys. 2003, 160, 2155–2167. [Google Scholar] [CrossRef]
- Synolakis, C.E.; Bardet, J.-P.; Borrero, J.C.; Davies, H.L.; Okal, E.A.; Silver, E.A.; Sweet, S.; Tappin, D.R. The slump origin of the 1998 Papua New Guinea Tsunami. Proc. R. Soc. Lond. A 2002, 458, 763–789. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Wu, T.-R.; Raichlen, F.; Synolakis, C.E.; Borrero, J.C. Runup and rundown generated by three-dimensional sliding masses. J. Fluid Mech. 2005, 536, 107–144. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.-E. Near field characteristics of landslide generated impulse waves. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Watts, P. Tsunami features of solid block underwater landslides. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 144–152. [Google Scholar] [CrossRef]
- Liu, P.L.-F.; Lynett, P.; Synolakis, C.E. Analytical solutions for forced long waves on a sloping beach. J. Fluid Mech. 2003, 478, 101–109. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.L.-F.; Mei, C.C. Solid landslide generated waves. J. Fluid Mech. 2011, 675, 529–539. [Google Scholar] [CrossRef]
- Lee, C.-H.; Huang, Z. Multi-phase flow simulation of impulsive waves generated by a sub-aerial granular landslide on an erodible slope. Landslides 2020, 18, 881–895. [Google Scholar] [CrossRef]
- Synolakis, C.E. Tsunamis and seiches. In Earthquake Engineering Handbook; Chen, W.-F., Scawthorn, C., Eds.; CRC Press: Boca, FL, USA, 2003; pp. 1–90. [Google Scholar]
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Walder, J.S.; Watts, P.; Sorensen, O.E.; Janssen, K. Water waves generated by subaerial mass flows. J. Geophys. Res. Solid Earth 2003, 108, 226–2255. [Google Scholar]
- Ataie-Ashtiani, B.; Nik-Khah, A. Impulsive waves caused by subaerial landslides. Environ. Fluid Mech. 2008, 8, 263–280. [Google Scholar] [CrossRef]
- Watts, P.; Grilli, S.T.; Tappin, D.R.; Fryer, G.J. Tsunami generation by submarine mass failure. II: Predictive equations and case studies. J. Waterw. Port Coast. Ocean Eng. 2005, 131, 298–310. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Najafi-Jilani, A. Laboratory investigations on impulsive waves caused by underwater landslide. Coast. Eng. 2008, 55, 989–1004. [Google Scholar] [CrossRef]
- Madsen, P.A.; Schäffer, H.A. Analytical solutions for tsunami runup on a plane beach: Single waves, N-waves and transient waves. J. Fluid Mech. 2010, 645, 25–57. [Google Scholar] [CrossRef]
- Barranco, I.; Liu, P.L.-F. Run-up and inundation generated by non-decaying dam-break bores on a planar beach. J. Fluid Mech. 2021, 915, 1–29. [Google Scholar] [CrossRef]
- Zweifel, A.; Hager, W.H.; Minor, H.-E. Plane impulse waves in reservoirs. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 358–368. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Wave types of landslide generated impulse waves. Ocean Eng. 2011, 38, 630–640. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R.; Schäffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113, C12012. [Google Scholar] [CrossRef]
- Heinrich, P. Nonlinear water waves generated by submarine and aerial landslides. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 249–266. [Google Scholar] [CrossRef]
- Fine, I.V.; Rabinovich, A.B.; Thomson, R.E.; Kulikov, E.A. Numerical modeling of tsunami generation by submarine and subaerial landslides. In Submarine Landslides and Tsunamis; Yalçiner, A.C., Pelinovsky, E.N., Okal, E., Synolakis, C.E., Eds.; Springer: Dordrecht, The Netherlands, 2003; Volume 21, pp. 69–88. [Google Scholar]
- LeBlond, P.H.; Jones, A.T. Underwater landslides ineffective at tsunami generation. J. Waterw. Port Coast. Ocean Eng. 1995, 13, 25–26. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three–dimensional interaction of waves and porous coastal structures using OpenFOAM. Part II: Application. Coast. Eng. 2014, 83, 243–258. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Simulating coastal engineering processes with OpenFOAM. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Higuera, P.; Losada, I.J.; Lara, J.L. Three-dimensional numerical wave generation with moving boundaries. Coast. Eng. 2015, 101, 35–47. [Google Scholar] [CrossRef]
- Higuera, P.; Liu, P.L.-F.; Lin, C.; Wong, W.-Y.; Kao, M.-J. Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope. J. Fluid Mech. 2018, 847, 186–227. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. Tsunami wave interaction with mangrove forests: A 3-D numerical approach. Coast. Eng. 2015, 98, 33–54. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 45–65. [Google Scholar] [CrossRef]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equations. Phys. Rev. Lett. 1986, 56, 1505–1508. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Chandar, D.D.J.; Faedo, N.; Ringwood, J.V. Evaluation of the overset grid method for control studies of wave energy converters in OpenFOAM numerical wave tanks. J. Ocean Eng. Mar. Energy 2020, 6, 55–70. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Impulse product parameter in landslide generated impulse waves. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 145–155. [Google Scholar] [CrossRef]
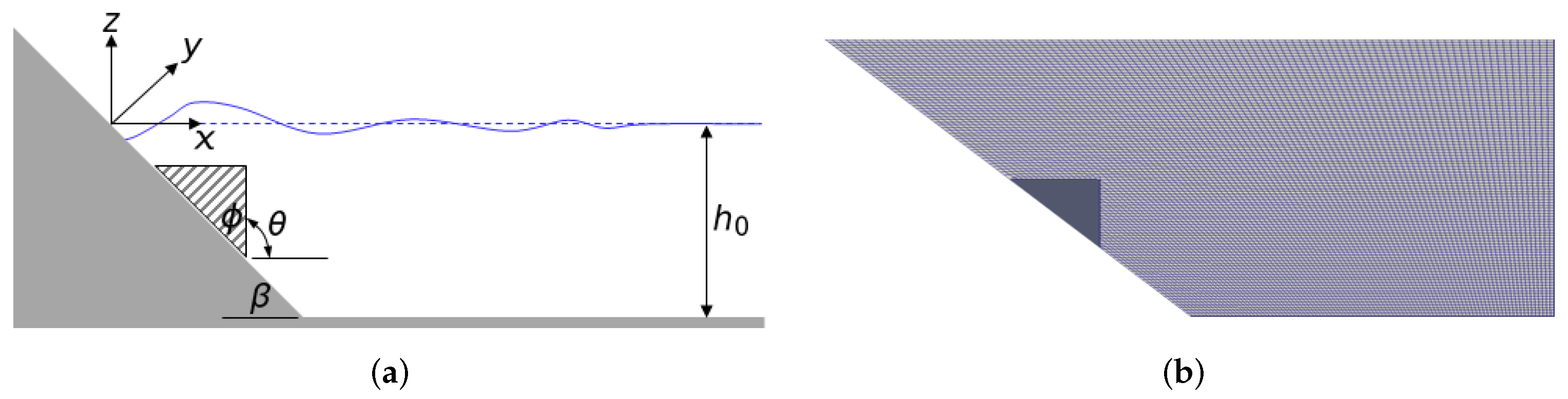
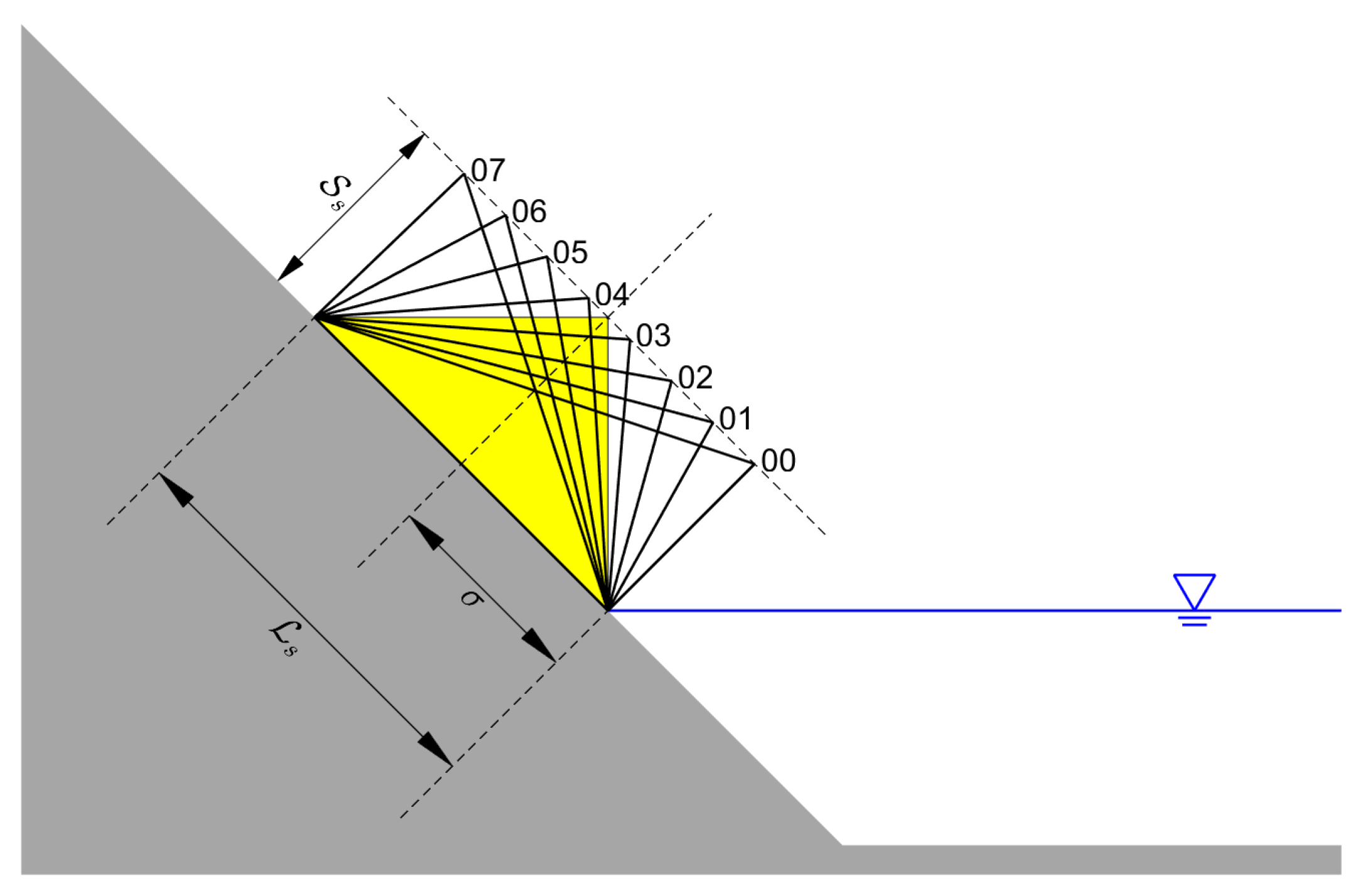
| Case # | (m) | (degree) |
|---|---|---|
| 00 | 0.0 | 90.0 |
| 01 | 0.1 | 74.2 |
| 02 | 0.2 | 60.5 |
| 03 | 0.3 | 50.0 |
| REF | 0.35 | 45.0 |
| 04 | 0.4 | 41.5 |
| 05 | 0.5 | 35.3 |
| 06 | 0.6 | 30.5 |
| 07 | 0.7 | 26.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-S.; Chan, I.-C. Effects of Slide Shape on Impulse Waves Generated by a Subaerial Solid Slide. Water 2022, 14, 2643. https://doi.org/10.3390/w14172643
Huang C-S, Chan I-C. Effects of Slide Shape on Impulse Waves Generated by a Subaerial Solid Slide. Water. 2022; 14(17):2643. https://doi.org/10.3390/w14172643
Chicago/Turabian StyleHuang, Chiung-Shu, and I-Chi Chan. 2022. "Effects of Slide Shape on Impulse Waves Generated by a Subaerial Solid Slide" Water 14, no. 17: 2643. https://doi.org/10.3390/w14172643
APA StyleHuang, C.-S., & Chan, I.-C. (2022). Effects of Slide Shape on Impulse Waves Generated by a Subaerial Solid Slide. Water, 14(17), 2643. https://doi.org/10.3390/w14172643






