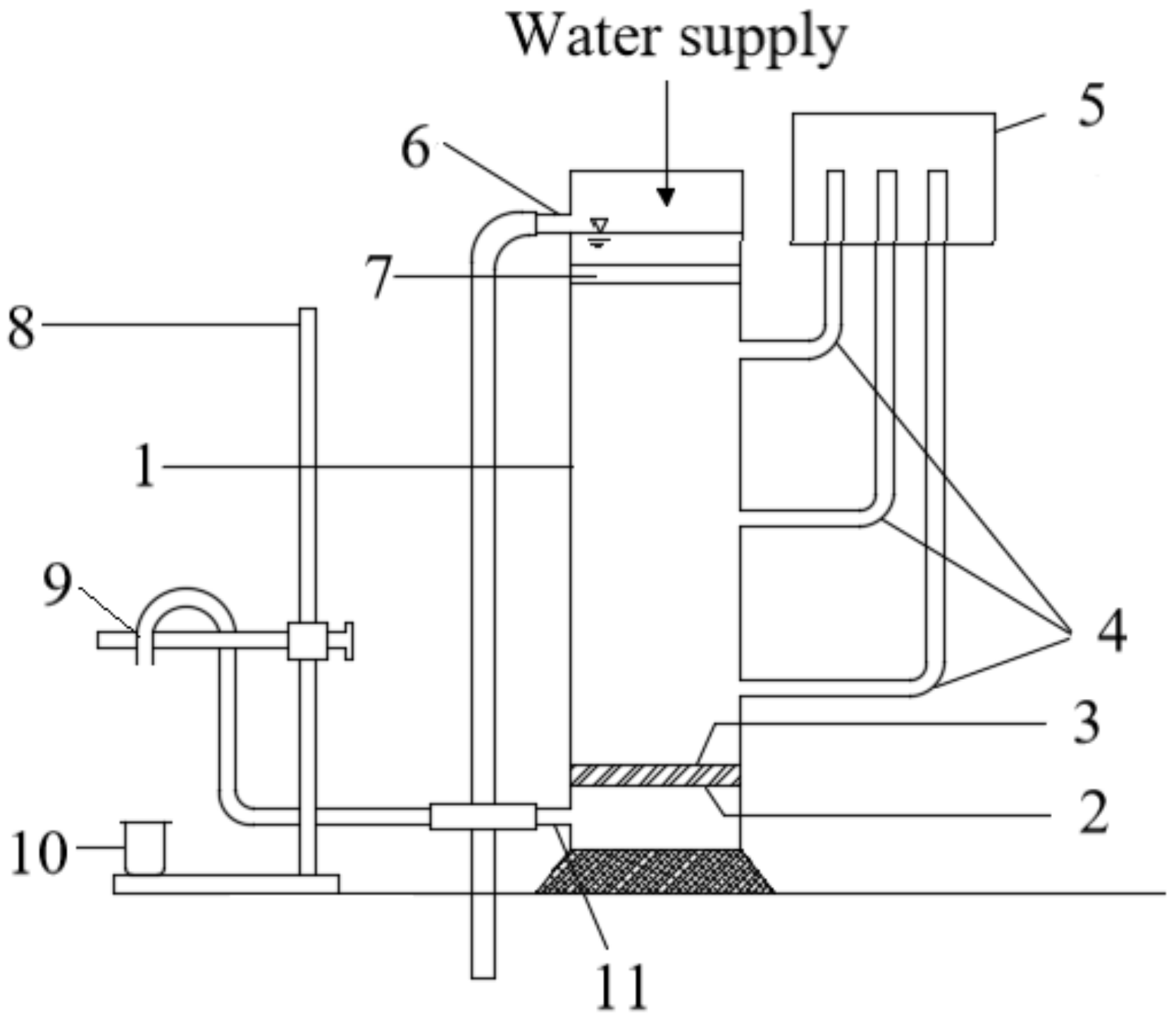
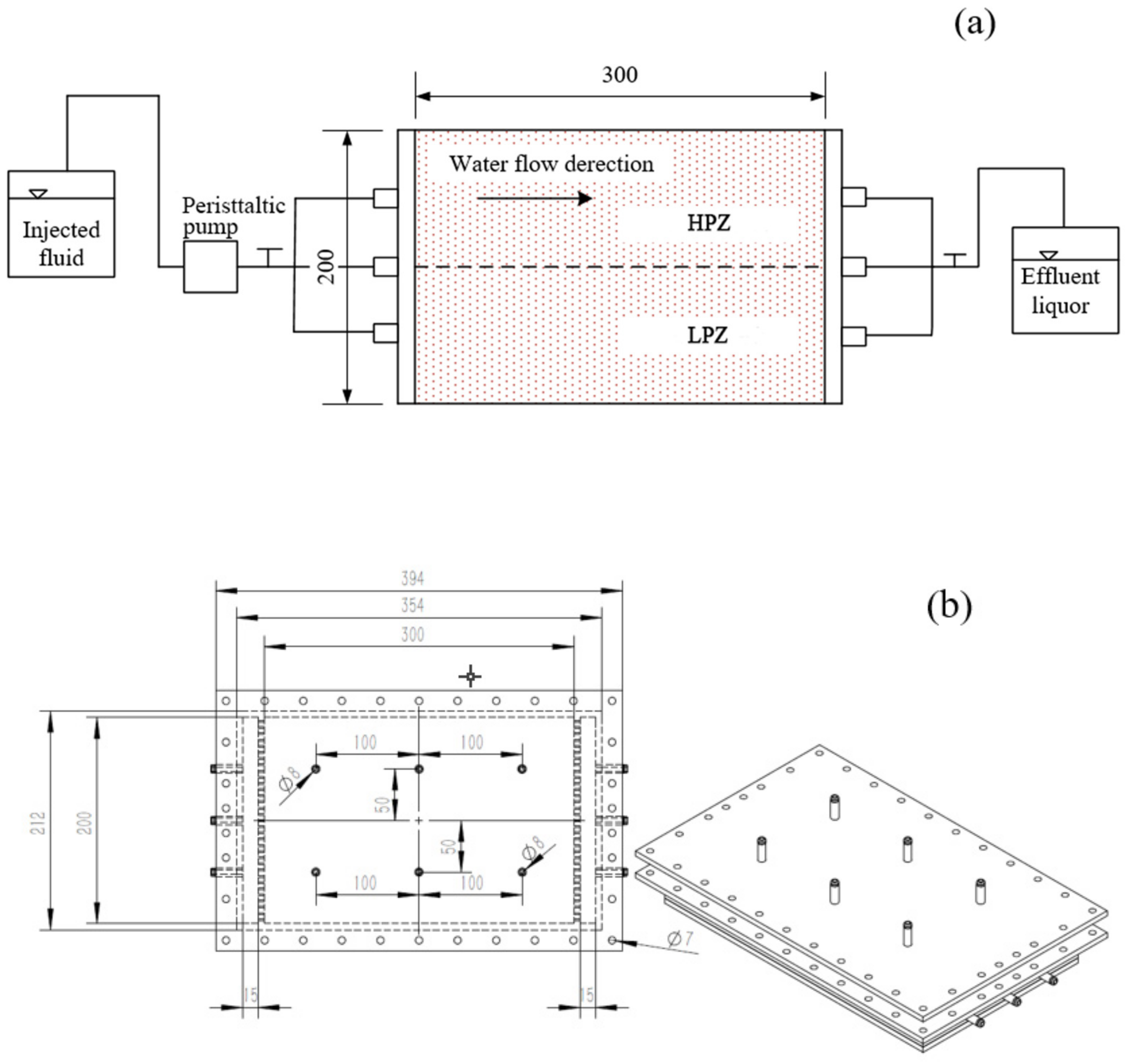
3.1. Factors Influencing U
3.1.1. Permeability Contrast
Permeability contrast (
, where
kb represents permeability values in more permeable media, and
ks represents less permeable media) indicates the distribution range and degree of permeability difference between media. The permeability contrasts of the media are listed in
Table 4 when injecting pure water, where
R0 and
U0 represent
R and
U under pure water injection.
3.1.2. Polymer Concentration
The
R and
U of the three combinations under different concentrations were calculated, and the results (
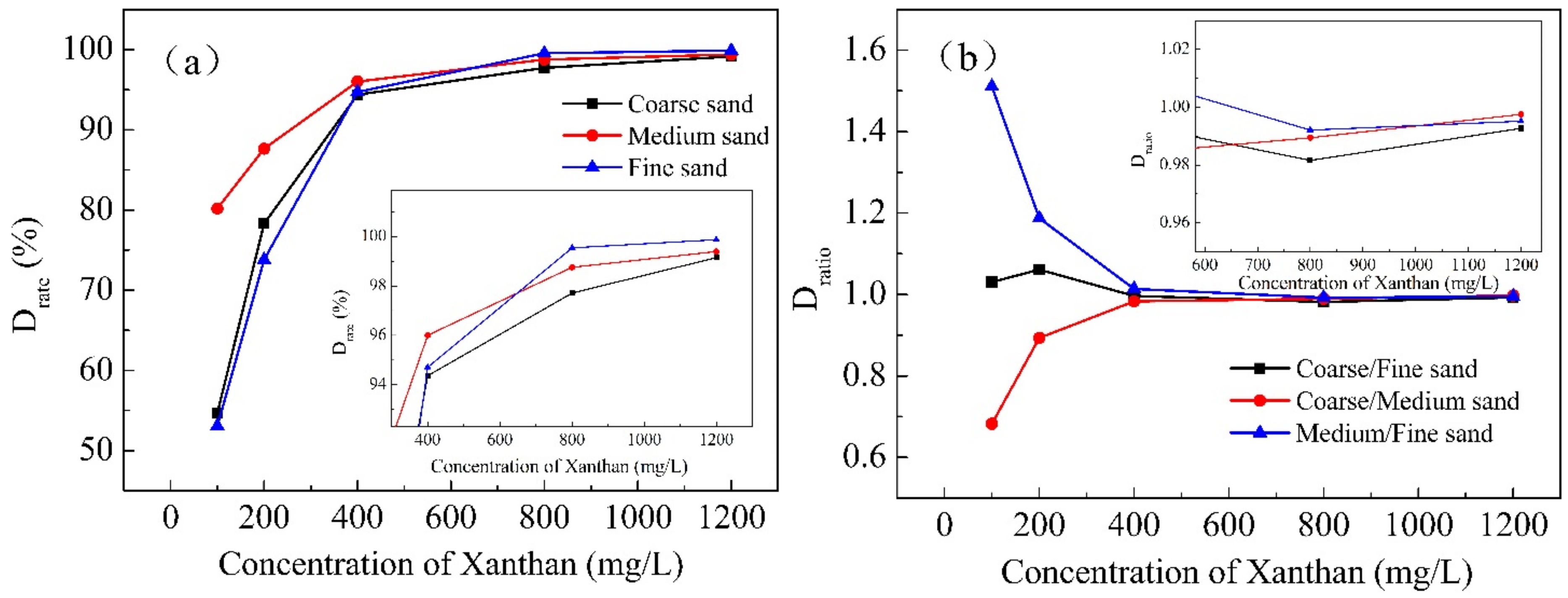
Table 5a) show that the order of
R between the three combinations is
Rcf >
Rcm >
Rmf when the concentration of xanthan gum was in the range of 100~800 mg/L, which was similar to the order of permeability contrast (
Table 4). However, when injecting pure water or xanthan gum at concentrations greater than 1200 mg/L,
Rcm <
Rmf, which is inversely related to the order of permeability contrast (
Rcf >
Rcm >
Rmf).
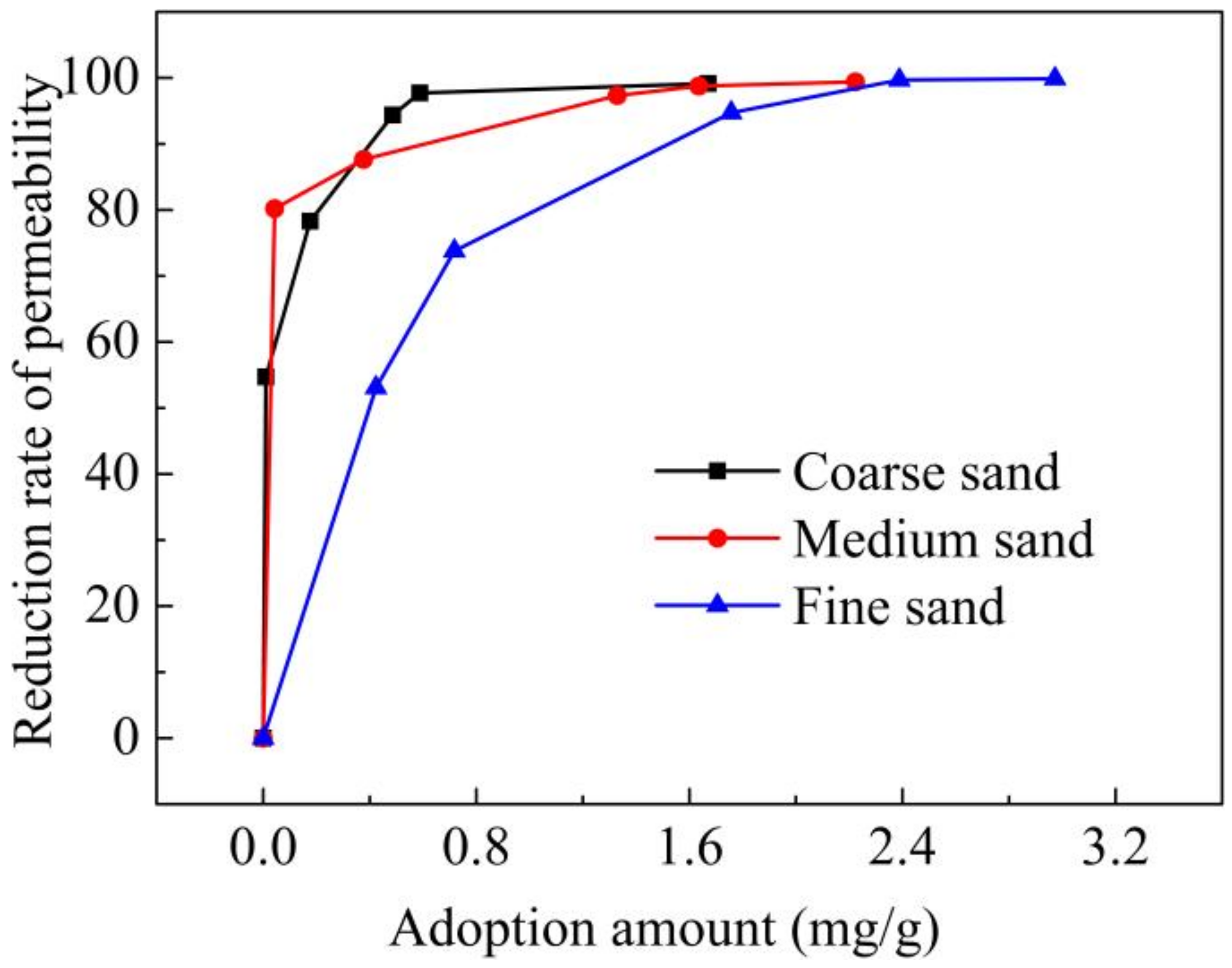
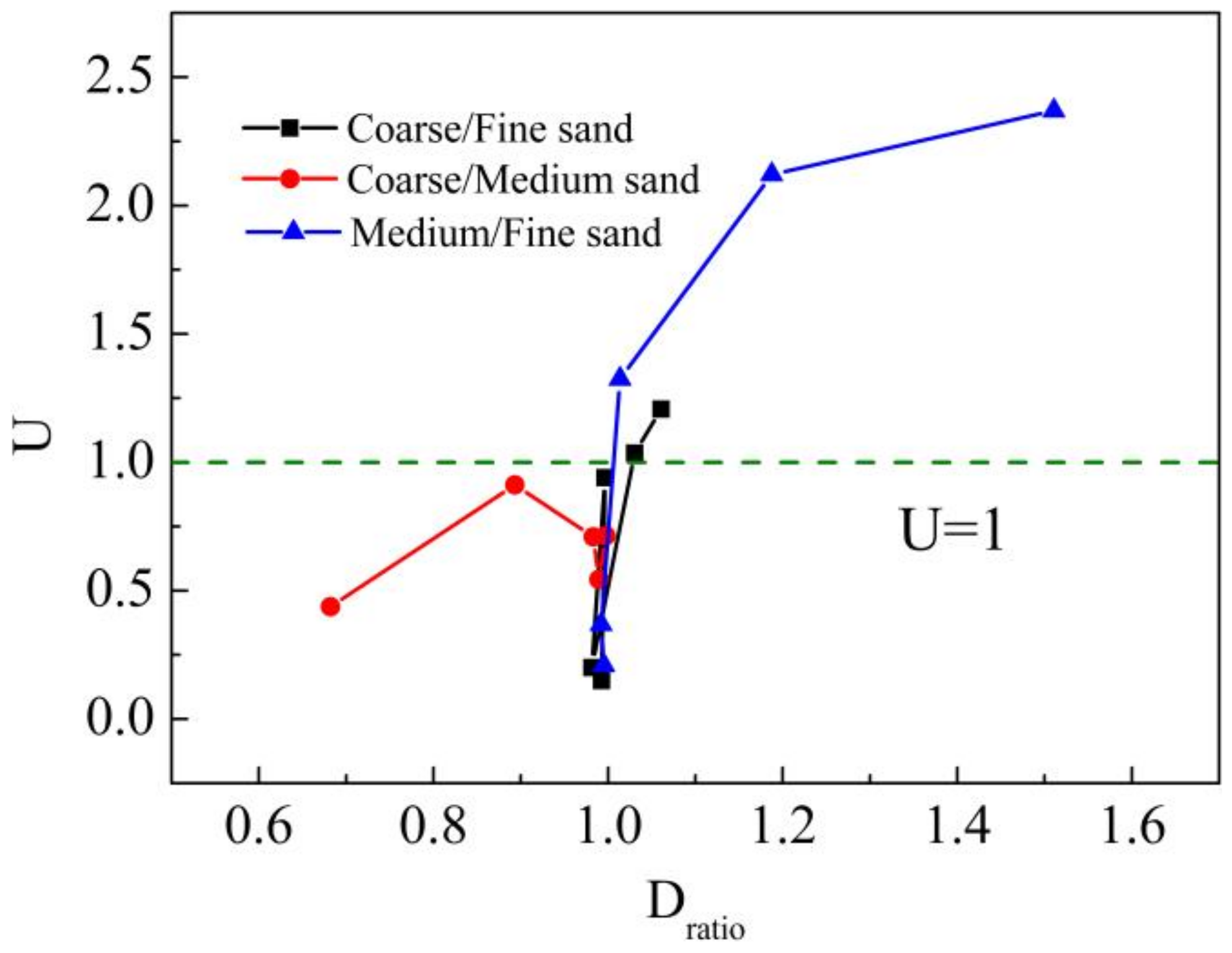
The order of U was Umf > Ucf > Ucm when the concentration of xanthan gum was in the range of 100~800 mg/L. In coarse sand/fine sand, when the concentration of xanthan gum was 200 mg/L, U (1.27) was greater than when the concentration was 100 mg/L (1.22). When the concentration was higher than 200 mg/L, U < 1, indicating that U first increased and then decreased with increasing xanthan gum concentration. Medium sand/fine sand presented a similar trend (the critical concentration is 400 mg/L). U of coarse sand/medium sand remained less than 1 throughout the entire concentration range, which may indicate that xanthan gum has a different degree of influence on different media combinations. Similarly, when the xanthan gum concentration was over 1200 mg/L, there was a reversal between the coarse sand/fine sand and medium sand/fine sand combinations (Ucf < Ucm).
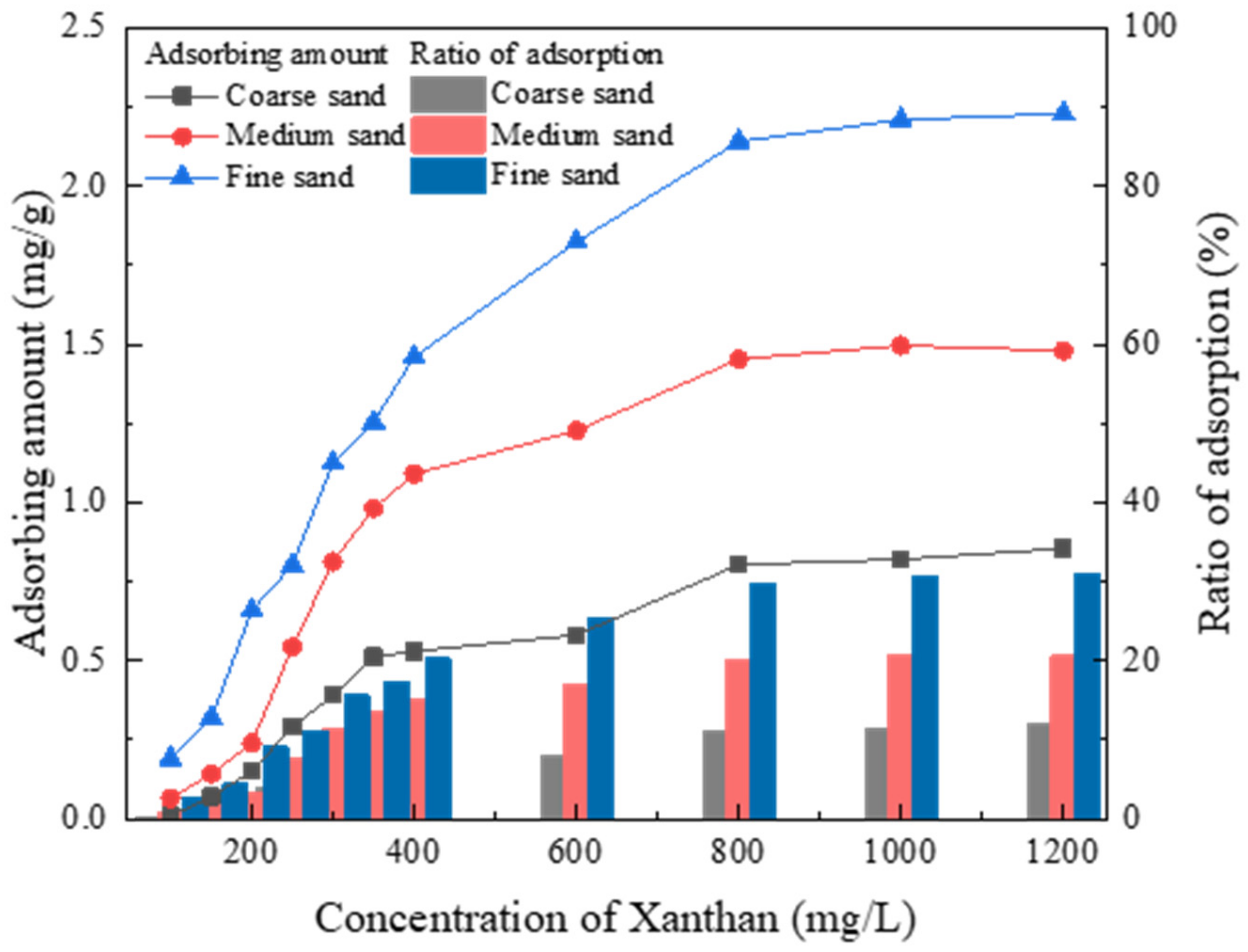
Generally, when the concentration of xanthan is relatively low and the permeability contrast is large, the enhancing effect of transmission uniformity in heterogeneous media is clearer. This possibly occurs because when xanthan gum of an appropriate concentration was injected, the viscosity of the solution increased, reducing the flow speed, improving the consistency of the amendment in the large and small pores, and leading to a more even transmission. As the concentration continued to increase, transmission was lower, which indicates that blockage may have occurred in the LPZ. The addition of xanthan gum with different concentrations showed different degrees of influence on hydraulic conductivities in coarse sand, medium sand and fine sand. According to Formula (2), the order in which media are affected the most was medium sand > coarse sand > fine sand. This explains why the U of coarse sand/medium sand remains less than 1; in this combination, xanthan gum had a much greater influence on medium sand than on fine sand, exacerbating uneven flow in the media. Thus, permeability contrast and polymer concentration jointly play a role in xanthan gum’s effect on flow uniformity.
3.3. Migration of Xanthan Gum
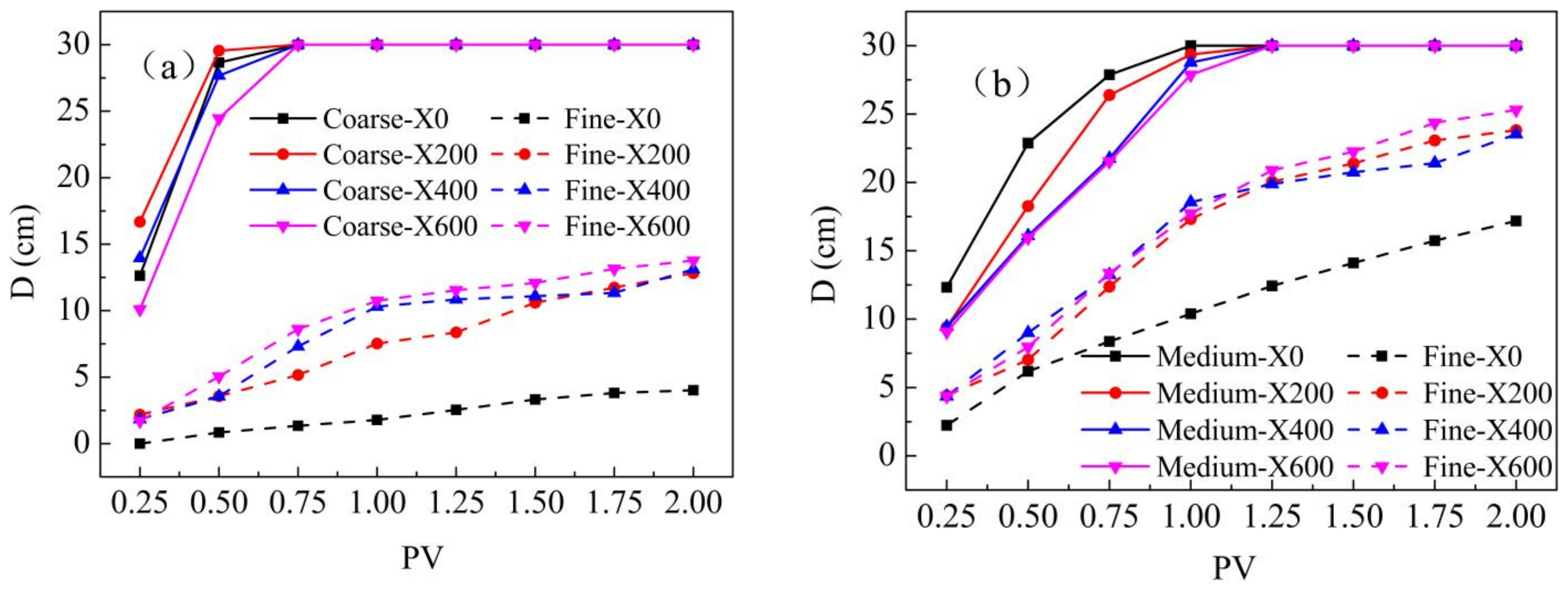
Figure 4 shows fluid migration in each medium during injection of xanthan solution into heterogeneous medium, where
D represents the migration distance. Generally, the maximum migration front in the heterogeneous medium was clearly uneven in different areas. According to
Figure 4a, when 0.75 PV solution was injected in a heterogeneous medium of combined coarse sand/fine sand, the average maximum migration distance reaches 30 cm in the HPZ, which shows little relation to the concentration of xanthan gum. On the other hand, the average maximum migration distance increased significantly in the LPZ; when the xanthan gum concentration was 200, 400 and 600 mg/L, the average maximum migration distance increased by 285.79%, 446.88% and 544.44%, respectively.
Additionally, due to the increase in viscosity, the migration speed in the HPZ decreased. Before 0.75 PV, the higher the concentration was, the slower the migration speed was, which improved the uniformity of solution transmission.
According to
Figure 4b, for the medium sand/fine sand combination, injection of xanthan solution also reduced the migration speed of the solution in the HPZ and increases the migration distance in the LPZ compared with pure water. When 1.0 PV of pure water was injected, the entire HPZ was filled with pure water, while 1.25 PV xanthan gum solution reached the same result. At the same time, the average maximum migration distance of xanthan gum solution in LPZ increased by 61.35%, 64.94% and 68.12% from low to high concentrations (200, 400 and 600 mg/L, respectively), and the difference between HPZ and LPZ decreased. Thus, the transmission of xanthan gum solution was different in heterogeneous media with different permeability contrasts. Compared with larger permeability contrast media, the solution was easier to transmit uniformly in heterogeneous media with smaller permeability contrast, i.e.,
U for the xanthan gum solution was larger in heterogeneous media with a low permeability contrast, which is consistent with the data in
Table 5a.
The data in
Table 5a are different from those shown in
Figure 4, in that when the concentration is increased from 200 to 400 mg/L,
Ucf is supposed to decrease, as is shown in
Table 5a, but
Figure 4 shows an even larger effect. This is because the peristaltic pump plays a pressurizing role in two-dimensional test. However, under specific conditions (PV > 1.25),
U still decreased with increasing polymer concentration. Therefore, the conclusions obtained using
U are still reasonable, and this error can be reduced by keeping the boundary conditions as consistent as possible during the experiment.
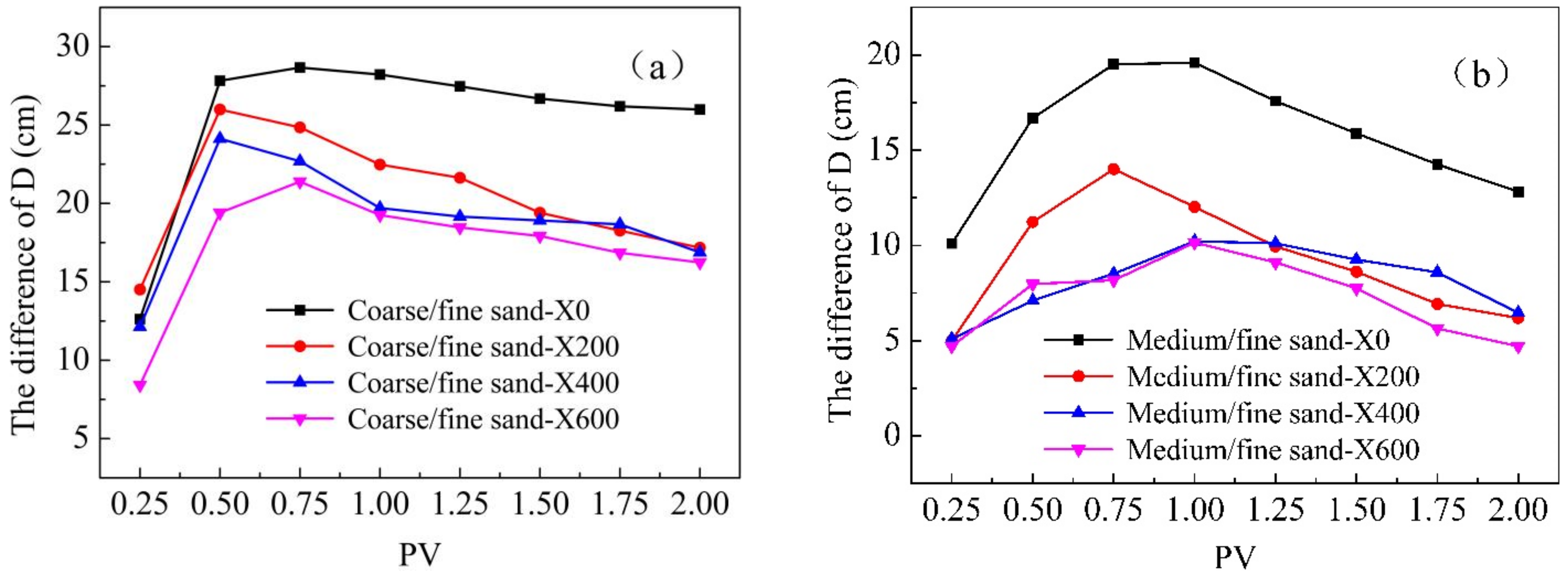
To more intuitively reflect the improvement of transmission uniformity under the injection of polymer solution, in this section, the displacement maximum migration front difference of the solution was calculated, and the results are shown in
Figure 5. The maximum migration front of the polymer solution in both the HPZ and LPZ is significantly decreased compared with that of pure water, which indicates a more uniform transmission in a heterogeneous medium.
The obtained results also show that the improvement effect on the front difference in heterogeneity is also related to permeability contrast, and the correlation law is similar to that of U in different permeability contrast combinations. Throughout the whole experimental process, the greater the concentration of xanthan gum solution was, the smaller the difference between the maximum migration fronts was. For coarse sand/fine sand, the differences in maximum migration fronts decreased by 13.33%, 20.84% and 25.99% when injected with concentrations of 200, 400 and 600 mg/L at 0.75 PV, respectively. For medium sand/fine sand, the polymer concentration showed a clearer effect on the maximum migration front difference when xanthan gum solution was injected at 1.25 PV, where the migration front differences of the three concentrations were reduced by 43.28%, 45.91% and 48.17%, respectively. The polymer solution in the LPZ had a greater shear effect, which reduced viscosity and finally weakened preferential flow and improved the transmission of the solution in a heterogeneous media.
In addition, the distribution of the repair agent in the low-permeability zone was very important for the removal of pollutants in the low-permeability zone. The improvement effect on the front difference in heterogeneity could also be related to the removal efficiency of pollutants [
18] and
U can also play a role in numerical models [
19] researching the enhancement of the sweeping efficiency of polymer solution.