Spatiotemporal Evaluation and Estimation of Precipitation of Multi-Source Precipitation Products in Arid Areas of Northwest China—A Case Study of Tianshan Mountains
Abstract
:1. Introduction
2. Materials and Methods
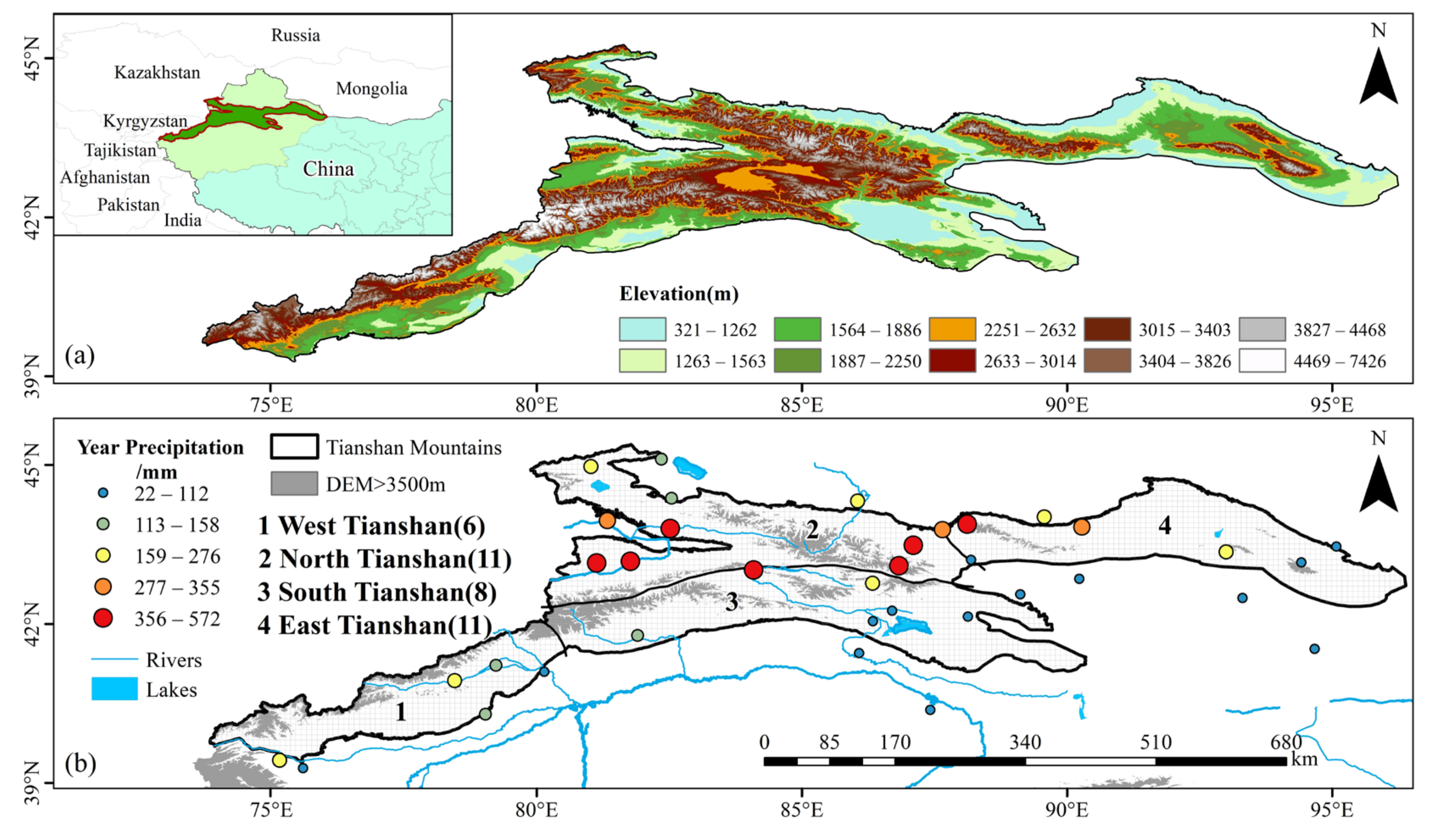
2.1. Study Region
2.2. Data
2.3. Research Methods
2.3.1. Temporal and Spatial Aggregation of Satellite Precipitation Products
2.3.2. Comparison of Applicability of Precipitation Products
2.3.3. Comparison Method between Satellite Data and Rainfall Station Data
3. Results
3.1. Precipitation Estimation Accuracy at Different Time Scales
3.1.1. Annual Scale Accuracy Assessment
3.1.2. Monthly Scale Accuracy Assessment
3.1.3. Daily Scale Accuracy Assessment
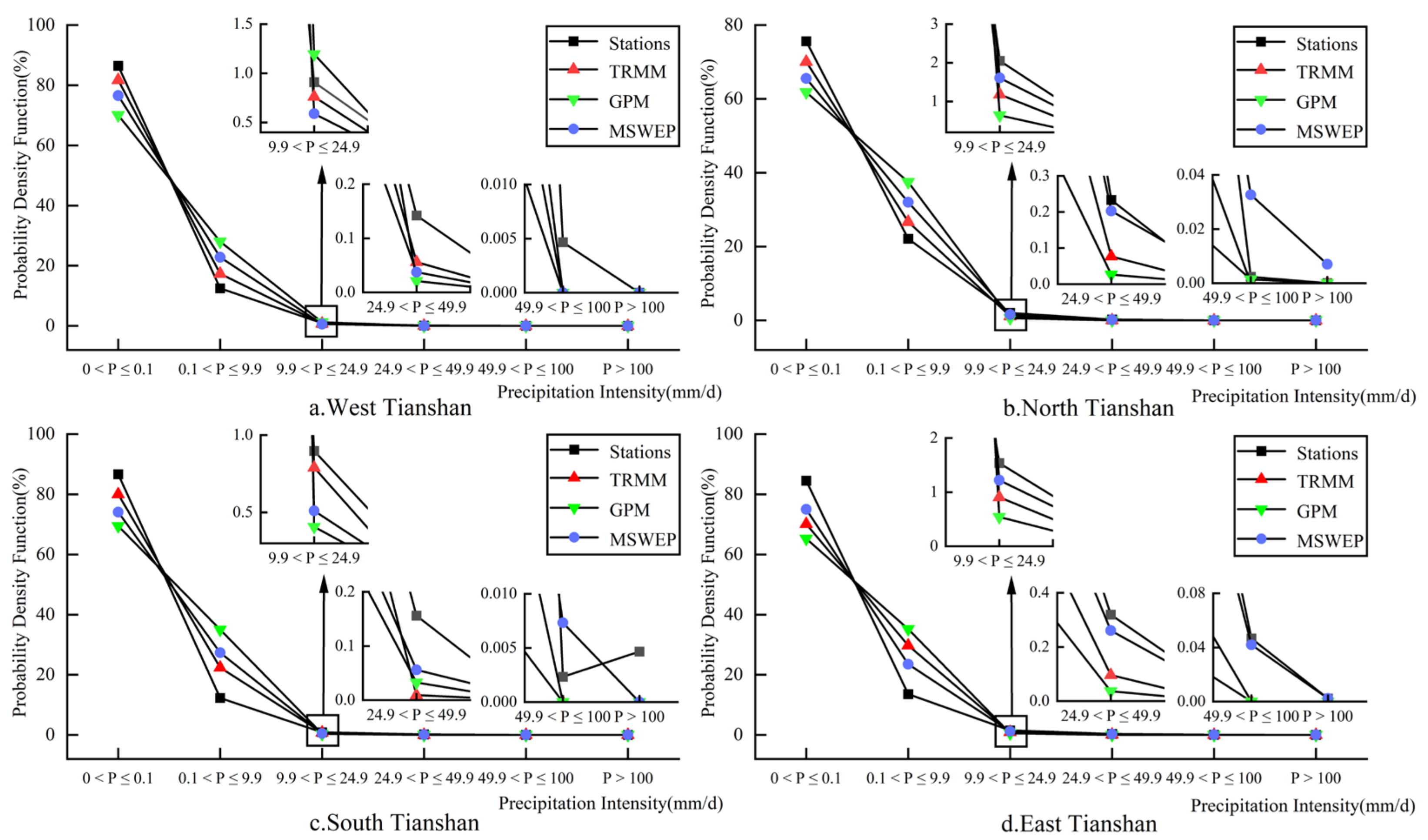
3.1.4. Comparison of Frequency Distribution of Precipitation Intensity
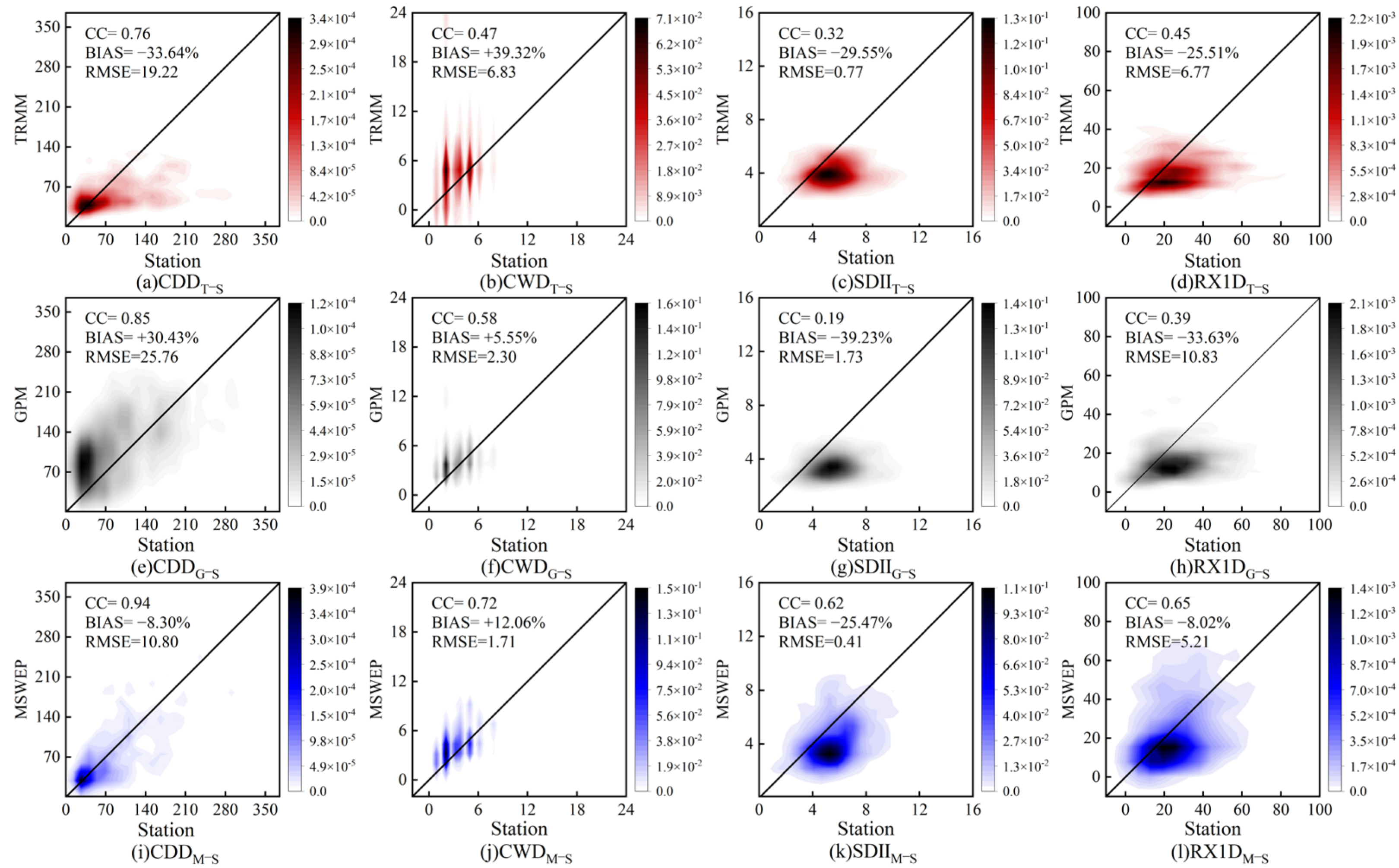
3.1.5. Evaluation of Extreme Precipitation Monitoring Capability
3.2. Precipitation Estimation Accuracy at Spatial Scale
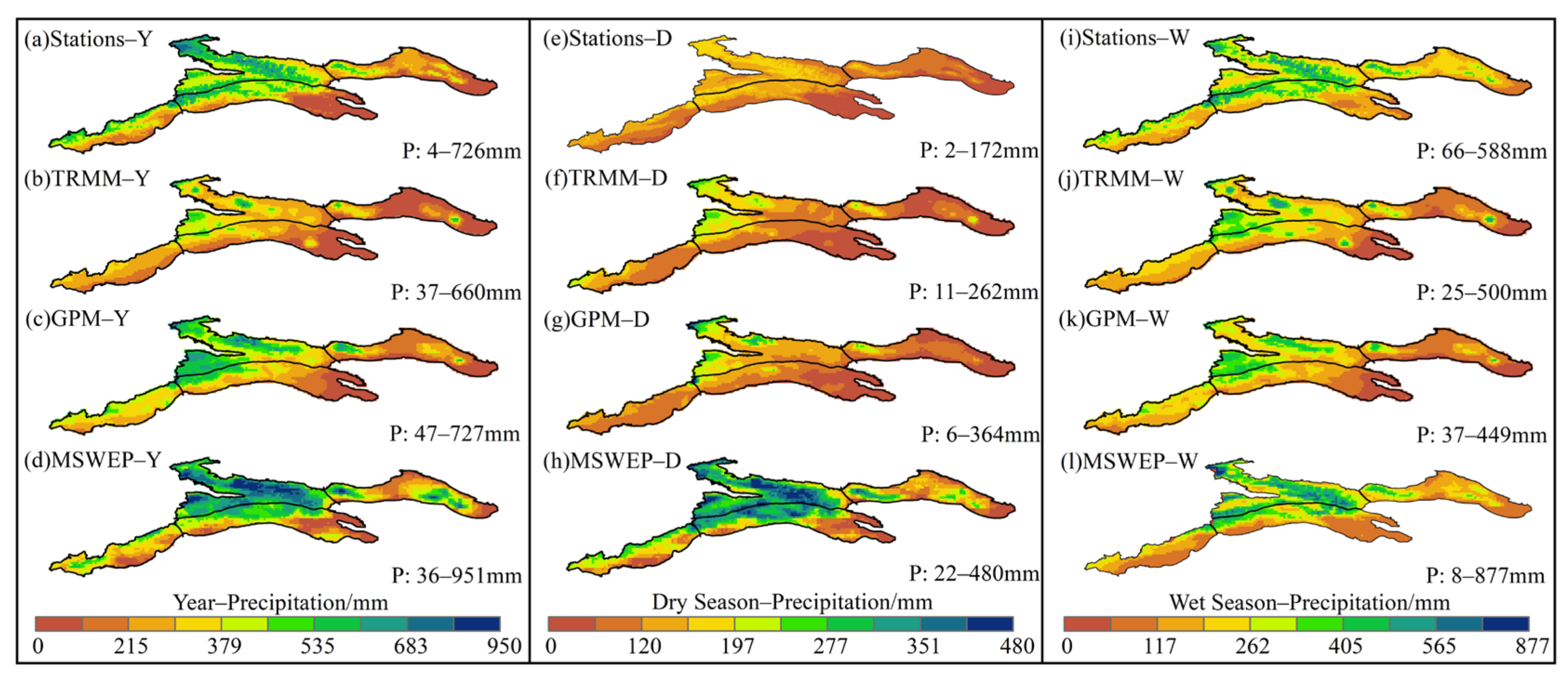
3.2.1. Spatial Distribution Characteristics of Precipitation in the Tianshan Mountains
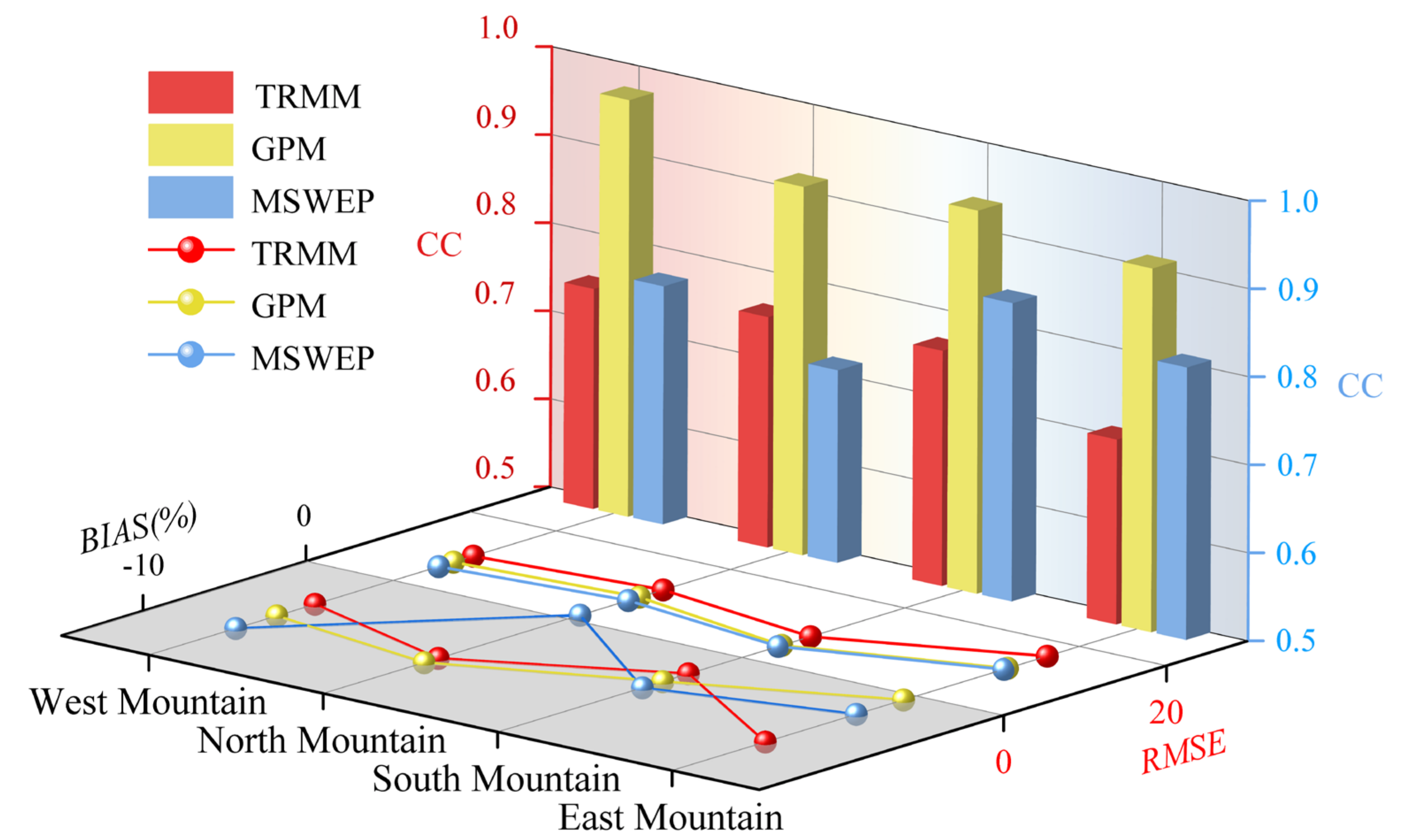
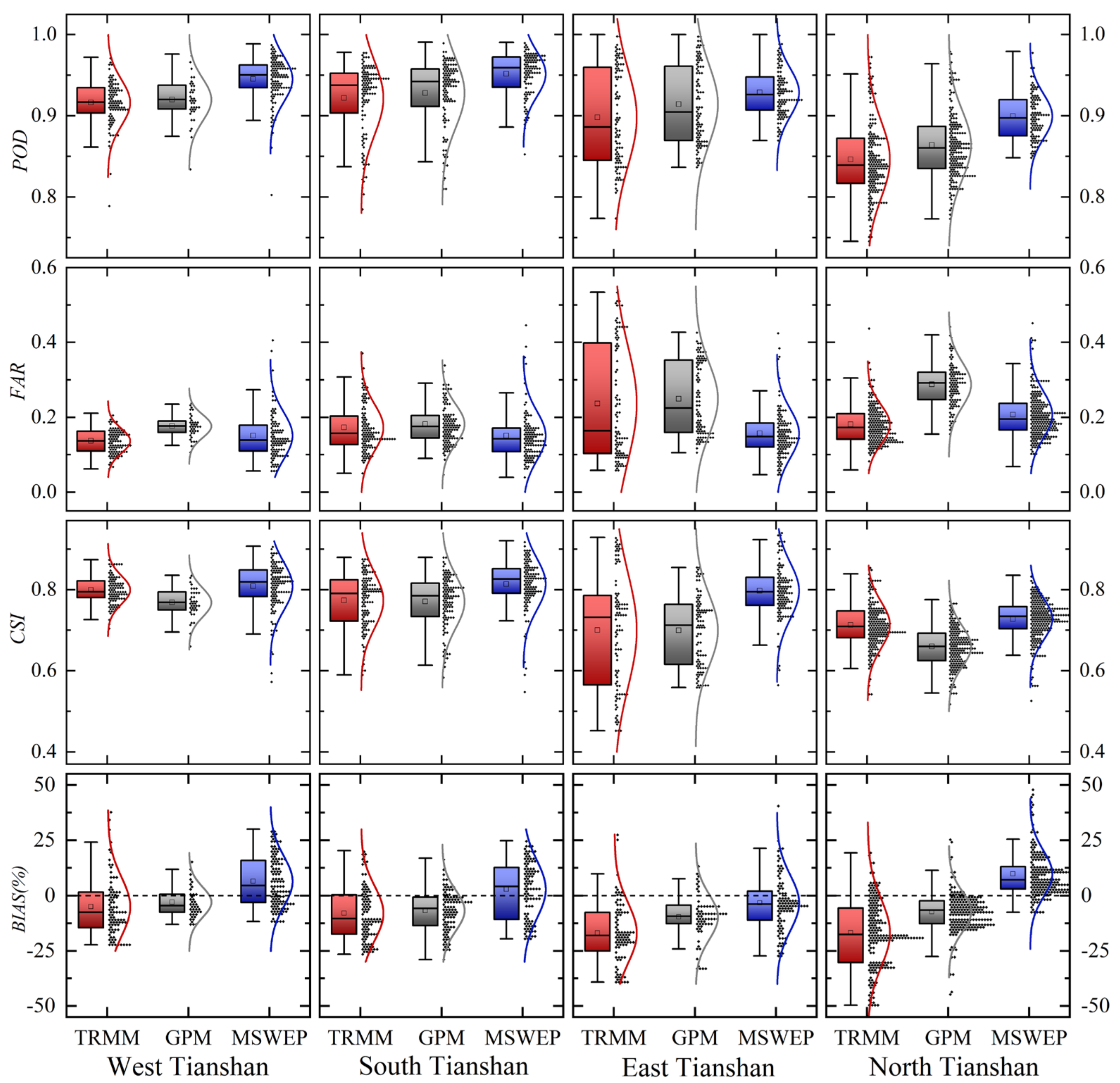
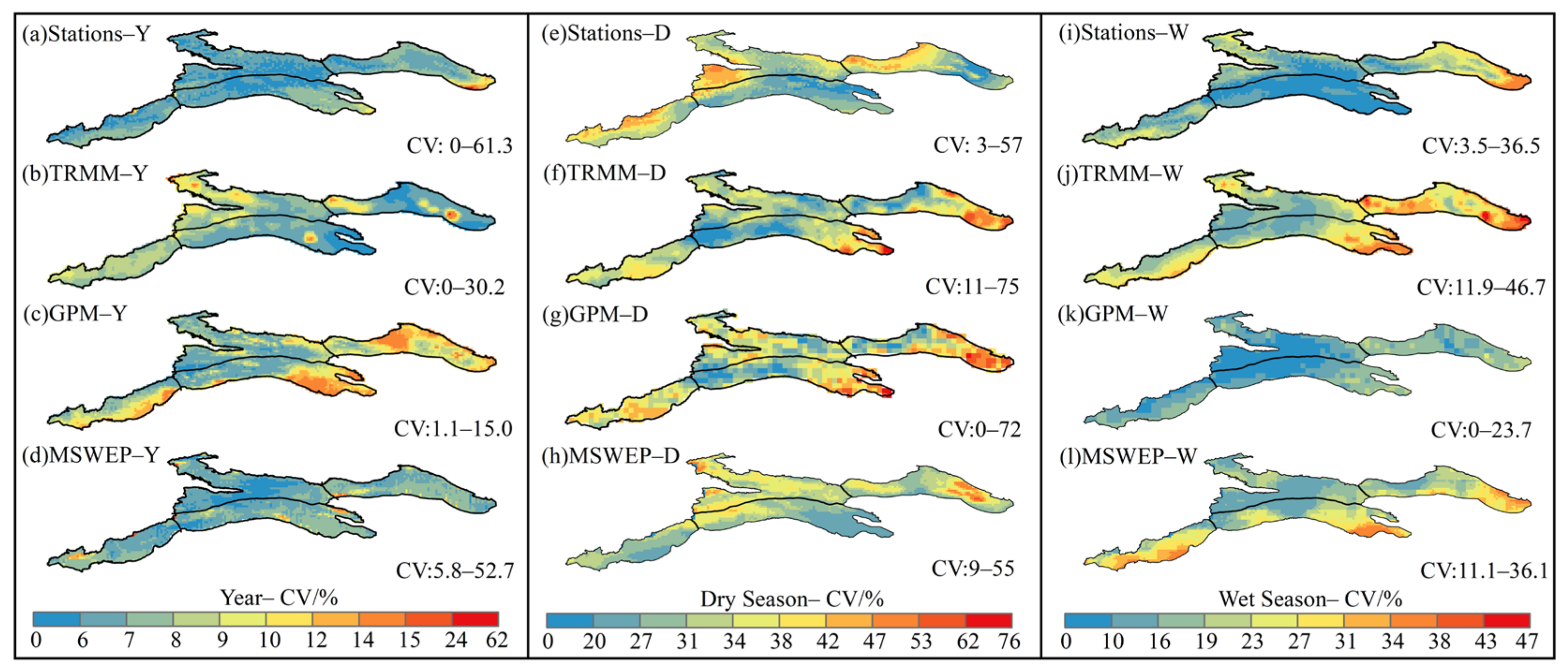
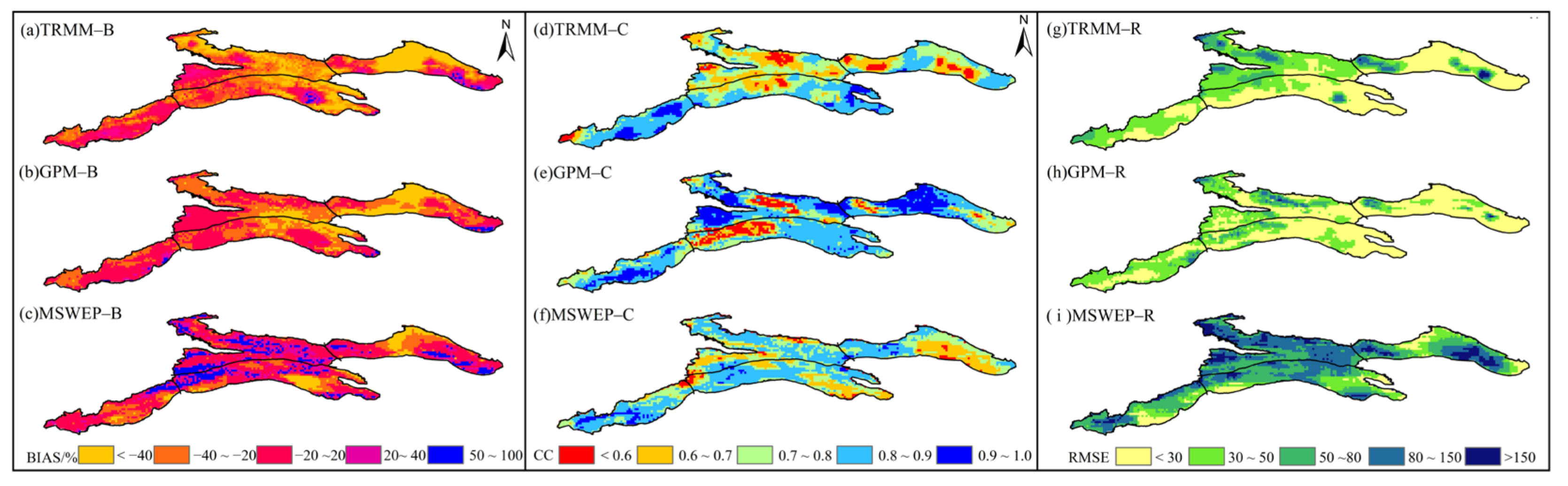
3.2.2. Spatial Accuracy Assessment of Precipitation in Tianshan Mountains
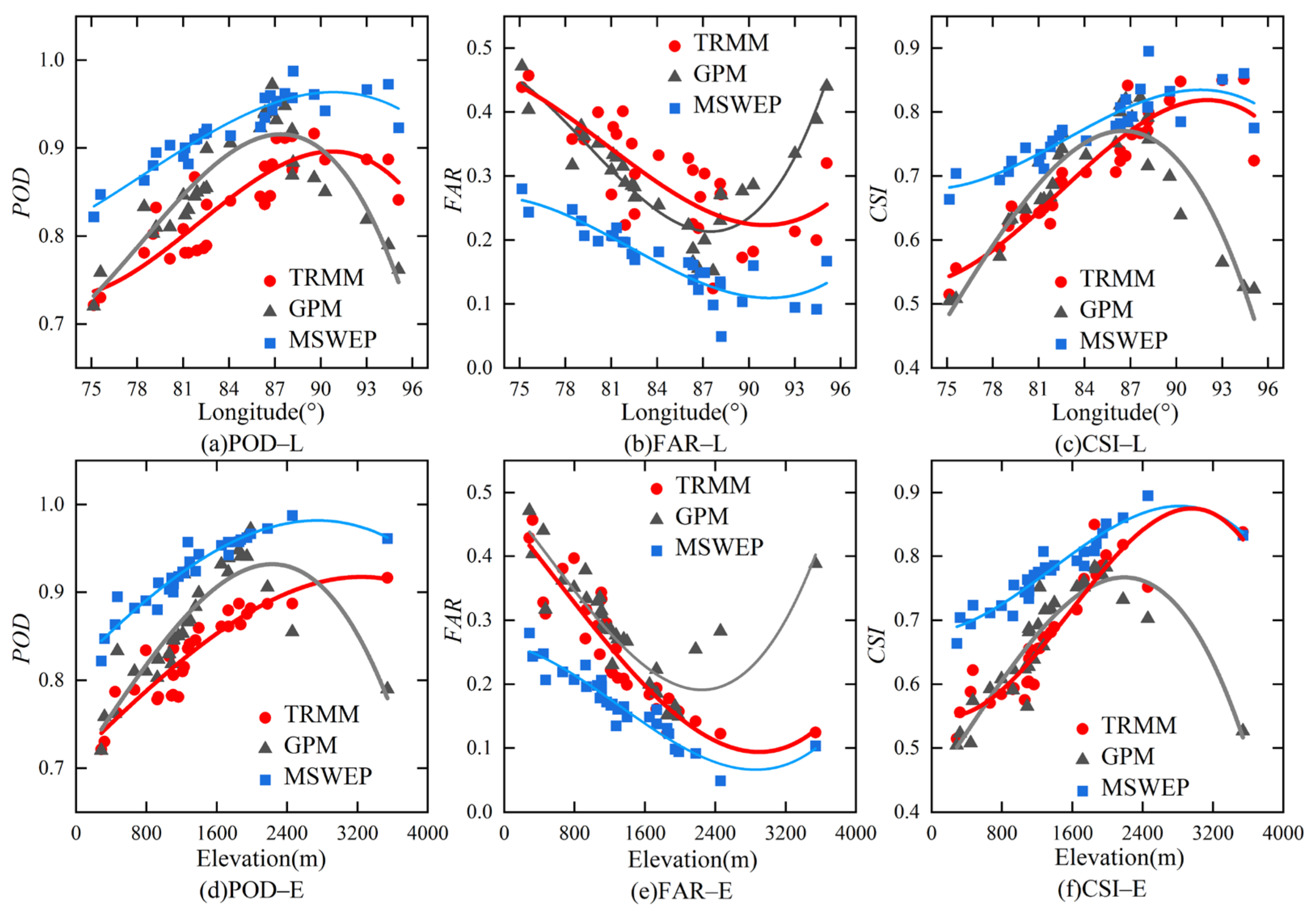
3.3. Factors Influencing the Accuracy of Satellite Precipitation Products
4. Discussion
4.1. Accuracy Difference between the Three Products
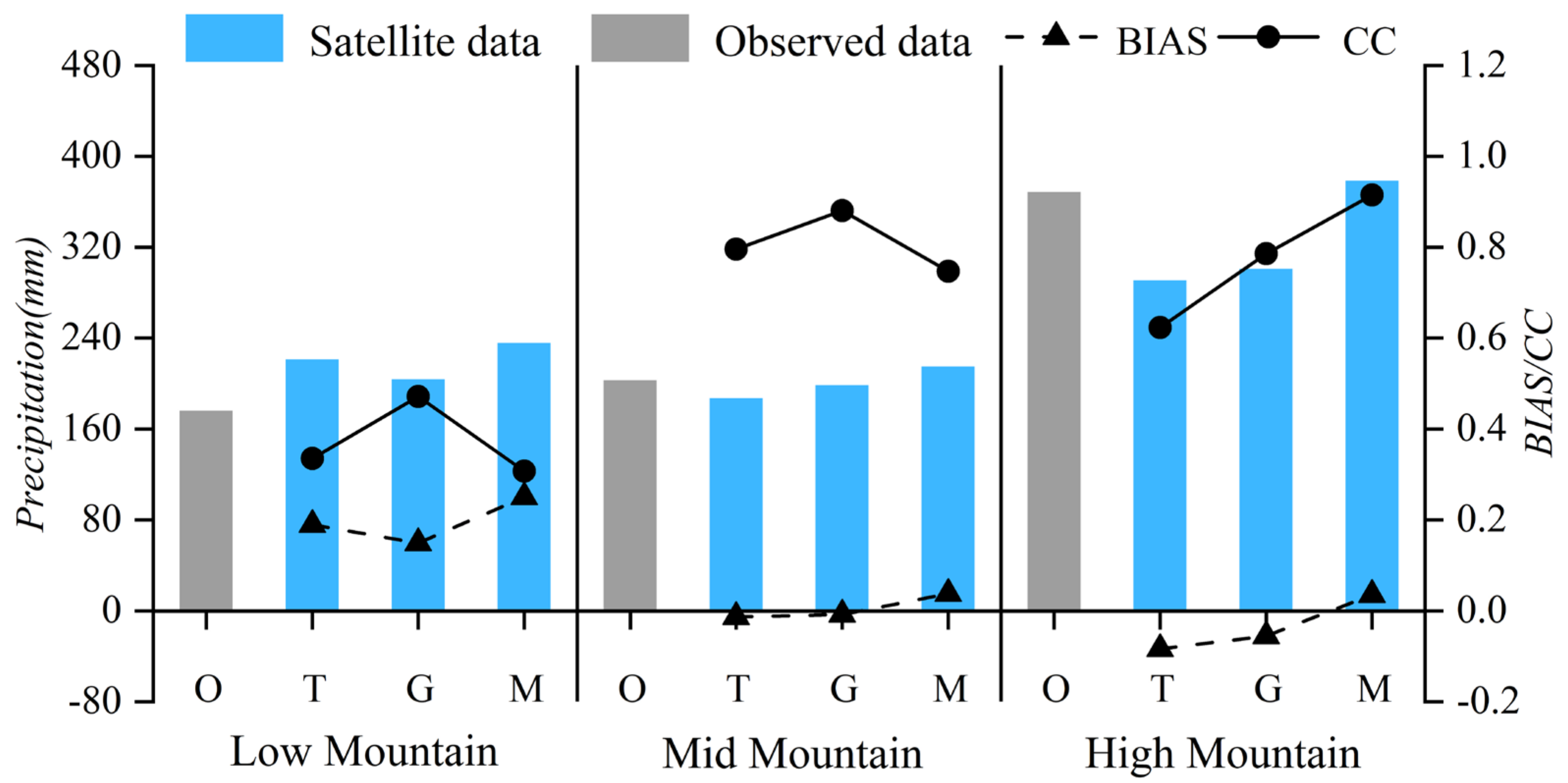
4.2. Precipitation Differences in Different Regions of the Tianshan Mountains
4.3. Application Prospect of Precipitation Products
5. Conclusions
- (1)
- At the annual scale, the three precipitation products showed a strong correlation with the measured precipitation; During the year, the estimation ability of precipitation in the wet season was stronger than that in the dry season. TRMM showed an underestimation of the measured precipitation, GPM improved the underestimation, and MSWEP showed an overestimation.
- (2)
- At the daily scale, TRMM and MSWEP had the best detection rates for light rain events and extreme precipitation events, respectively. The deviation between GPM and daily precipitation is the smallest.
- (3)
- At the spatial scale, the three precipitation products can roughly reflect the distribution characteristics of the measured precipitation, that is, the trend of decreasing from northwest to southeast, and the correlation between GPM and the measured precipitation is the best. In different regions, the detection rate of precipitation in the West region was the highest, and the detection rate of precipitation in the East region was the worst. MSWEP is the closest to the precipitation differentiation pattern in the Tianshan Mountains.
- (4)
- The three precipitation products showed high accuracy in low longitude areas and middle elevation mountain areas; In comparison, MSWEP has the highest applicability in high-altitude mountain areas.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Index Name | Formula | Ideal Value |
|---|---|---|
| Root Mean Square Error (RMSE) | 0 | |
| Mean Error (ME) | 0 | |
| Mean Absolute Error (MAE) | 0 | |
| Correlation Coefficient (CC) | 1 | |
| Frequency Bias (BIAS) | 0 | |
| Probability of Detection (POD) | 1 | |
| False Alarm Ratio (FAR) | 0 | |
| Critical Success Index (CSI) | 1 | |
| Standard Deviation Ratio (SDR) | 1 | |
| Coefficient of Variation (CV) | or | 100 |
| Name | Code | Definition | Unit |
|---|---|---|---|
| Consecutive Dry Days | CDD | The longest consecutive days with daily precipitation < 1 mm | d |
| Consecutive Wet Days | CWD | The longest consecutive days with daily precipitation ≥ 1 mm | d |
| Simple Daily Precipitation Intensity Index | SDII | The ratio of the total amount of precipitation ≥ 1 mm to the number of days | mm/d−1 |
| Annual Maximum 1-day Precipitation | RX1D | Annual maximum daily precipitation | mm |
References
- Qin, Y.; Chen, Z.; Shen, Y.; Zhang, S.; Shi, R. Evaluation of satellite rainfall estimates over the Chinese Mainland. Remote Sens. 2014, 6, 11649–11672. [Google Scholar] [CrossRef] [Green Version]
- Chung, C.T.; Power, S.B.; Arblaster, J.M.; Rashid, H.A.; Roff, G.L. Nonlinear precipitation response to El Niño and global warming in the Indo-Pacific. Clim. Dyn. 2014, 42, 1837–1856. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Assessment of satellite-based precipitation measurement products over the hot desert climate of Egypt. Remote Sens. 2019, 11, 555. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale comparative evaluation of the GPM IMERG v5 and TRMM 3B42 v7 precipitation products from 2015 to 2017 over a climate transition area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef] [Green Version]
- Liang-Liang, L.; Jian, L.; Ru-Cong, Y. Evaluation of CMIP6 HighResMIP models in simulating precipitation over Central Asia. Adv. Clim. Chang. Res. 2022, 13, 1–13. [Google Scholar] [CrossRef]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang. 2012, 112, 881–899. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Li, D.; Li, W.; Yang, Y. Identifying water vapor sources of precipitation in forest and grassland in the north slope of the Tianshan Mountains, Central Asia. J. Arid Land 2022, 14, 297–309. [Google Scholar] [CrossRef]
- Meng, X.; Long, A.; Wu, Y.; Yin, G.; Wang, H.; Ji, X. Simulation and spatiotemporal pattern of air temperature and precipitation in Eastern Central Asia using RegCM (Retraction of Vol 8, art no 3639, 2018). Sci. Rep. 2019, 18, 13674. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Wang, S.; Wang, L.; Zhang, M.; Argiriou, A.A.; Song, Y.; Lei, S. Isotopic evidence in modern precipitation for the westerly meridional movement in Central Asia. Atmos. Res. 2021, 259, 105698. [Google Scholar] [CrossRef]
- Xu, X.; Kleidon, A.; Miller, L.; Wang, S.; Wang, L.; Dong, G. Late Quaternary glaciation in the Tianshan and implications for palaeoclimatic change: A review. Boreas 2010, 39, 215–232. [Google Scholar] [CrossRef]
- Fan, M.; Xu, J.; Li, D.; Chen, Y. Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products. Remote Sens. 2022, 14, 519. [Google Scholar] [CrossRef]
- Yue, X.; Liu, G.; Chen, J.; Zhou, C. Synergistic regulation of the interdecadal variability in summer precipitation over the Tianshan Mountains by sea surface temperature anomalies in the high-latitude Northwest Atlantic Ocean and the Mediterranean Sea. Atmos. Res. 2020, 233, 104717. [Google Scholar] [CrossRef]
- Cai, P.; Hamdi, R.; Luo, G.; He, H.; Zhang, M.; Termonia, P.; De Maeyer, P. Agriculture intensification increases summer precipitation in Tianshan Mountains, China. Atmos. Res. 2019, 227, 140–146. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, P.; Li, J.; Singh, V.P.; Liu, J. Spatiotemporal properties of droughts and related impacts on agriculture in Xinjiang, China. Int. J. Climatol. 2015, 35, 1254–1266. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Malik, I.; Wistuba, M.; Cao, Y.; Hou, D.; Ta, Z.; He, J.; Zhang, L.; Yu, R. Spatiotemporal changes in water, land use, and ecosystem services in Central Asia considering climate changes and human activities. J. Arid Land 2021, 13, 881–890. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and intercomparison of high-resolution satellite precipitation estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Domrös, M.; Peng, G. The Climate of China; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hu, Z.; Hu, Q.; Zhang, C.; Chen, X.; Li, Q. Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in central Asia. J. Geophys. Res. Atmos. 2016, 121, 5648–5663. [Google Scholar] [CrossRef] [Green Version]
- Dinku, T.; Connor, S.J.; Ceccato, P.; Ropelewski, C.F. Comparison of global gridded precipitation products over a mountainous region of Africa. Int. J. Climatol. A J. R. Meteorol. Soc. 2008, 28, 1627–1638. [Google Scholar] [CrossRef]
- Gehne, M.; Hamill, T.M.; Kiladis, G.N.; Trenberth, K.E. Comparison of global precipitation estimates across a range of temporal and spatial scales. J. Clim. 2016, 29, 7773–7795. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavy precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Gebremichael, M.; Anagnostou, E.N.; Bitew, M.M. Critical steps for continuing advancement of satellite rainfall applications for surface hydrology in the Nile River basin 1. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 361–366. [Google Scholar] [CrossRef]
- Duan, Y.; Wilson, A.M.; Barros, A.P. Scoping a field experiment: Error diagnostics of TRMM precipitation radar estimates in complex terrain as a basis for IPHEx2014. Hydrol. Earth Syst. Sci. 2015, 19, 1501–1520. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Sun, Y.; Li, X.; Wang, T.; Wang, Y.; Qiu, Q.; Deng, Z. Evaluation and correction of GPM IMERG precipitation products over the capital circle in Northeast China at multiple spatiotemporal scales. Adv. Meteorol. 2018, 2018, 4714173. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Integrated Multi-satellitE Retrievals for GPM (IMERG) technical documentation. Nasa/Gsfc Code 2015, 612, 2019. [Google Scholar]
- Liu, Z. Comparison of integrated multisatellite retrievals for GPM (IMERG) and TRMM multisatellite precipitation analysis (TMPA) monthly precipitation products: Initial results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Win, K.W.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data-sparse mountainous watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y.; Wang, S.; Wang, X. Evaluation and comparison of CHIRPS and MSWEP daily-precipitation products in the Qinghai-Tibet Plateau during the period of 1981–2015. Atmos. Res. 2019, 230, 104634. [Google Scholar] [CrossRef]
- Xuan, D.; Hu, Q.; Wang, Y.; Yang, H.; Li, L.; Wang, L. Precipitation Characteristic Analysis of the Zhoushan Archipelago: From the View of MSWEP and Rainfall Merging. Water 2020, 12, 829. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Wu, J.; Bai, L.; Wang, B. Reliability of gridded precipitation products in the Yellow River Basin, China. Remote Sens. 2020, 12, 374. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Tian, F.; Khan, M.Y.A.; Xu, R.; He, Z.; Yang, L.; Lu, H.; Ma, Y. A high-accuracy rainfall dataset by merging multiple satellites and dense gauges over the southern Tibetan Plateau for 2014–2019 warm seasons. Earth Syst. Sci. Data 2021, 13, 5455–5467. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.K.; Dehghani, M. Evaluation of satellite rainfall climatology using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, X.; Xu, Y.-P.; Tian, Y. Merging multi-source precipitation products or merging their simulated hydrological flows to improve streamflow simulation. Hydrol. Sci. J. 2019, 64, 910–920. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, C.; Fu, G.; Sweetapple, C.; Zhou, H. Evaluation of global fine-resolution precipitation products and their uncertainty quantification in ensemble discharge simulations. Hydrol. Earth Syst. Sci. 2016, 20, 903–920. [Google Scholar] [CrossRef] [Green Version]
- Feng, K.; Hong, Y.; Tian, J.; Luo, X.; Tang, G.; Kan, G. Evaluating applicability of multi-source precipitation datasets for runoff simulation of small watersheds: A case study in the United States. Eur. J. Remote Sens. 2021, 54, 372–382. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Chen, Y.; Guo, H.; Wang, Y.; Lian, L. Applicability evaluation of multisource satellite precipitation data for hydrological research in arid mountainous areas. Remote Sens. 2020, 12, 2886. [Google Scholar] [CrossRef]
- Nepal, B.; Shrestha, D.; Sharma, S.; Shrestha, M.S.; Aryal, D.; Shrestha, N. Assessment of GPM-Era Satellite Products’(IMERG and GSMaP) ability to detect precipitation extremes over mountainous country Nepal. Atmosphere 2021, 12, 254. [Google Scholar] [CrossRef]
- Wei, L.; Jiang, S.; Ren, L.; Wang, M.; Zhang, L.; Liu, Y.; Yuan, F.; Yang, X. Evaluation of seventeen satellite-, reanalysis-, and gauge-based precipitation products for drought monitoring across mainland China. Atmos. Res. 2021, 263, 105813. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Bumke, K. Validation of ERA-Interim precipitation estimates over the Baltic Sea. Atmosphere 2016, 7, 82. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR downscaling method to reconstruct high-resolution precipitation dataset based on GSMaP-Gauge data: A case study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qin, X.; Liu, Y.; Jin, Z.; Liu, J.; Wang, L.; Chen, J. Evaluation of Long-Term and High-Resolution Gridded Precipitation and Temperature Products in the Qilian Mountains, Qinghai–Tibet Plateau. Front. Environ. Sci. 2022, 609, 906821. [Google Scholar] [CrossRef]
- Kumar, M.; Hodnebrog, Ø.; Daloz, A.S.; Sen, S.; Badiger, S.; Krishnaswamy, J. Measuring precipitation in Eastern Himalaya: Ground validation of eleven satellite, model and gauge interpolated gridded products. J. Hydrol. 2021, 599, 126252. [Google Scholar] [CrossRef]
- Hamm, A.; Arndt, A.; Kolbe, C.; Wang, X.; Thies, B.; Boyko, O.; Reggiani, P.; Scherer, D.; Bendix, J.; Schneider, C. Intercomparison of gridded precipitation datasets over a sub-region of the Central Himalaya and the Southwestern Tibetan Plateau. Water 2020, 12, 3271. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, G.; De Maeyer, P.; Cai, P.; Kurban, A. Improved atmospheric modelling of the oasis-desert system in Central Asia using WRF with actual satellite products. Remote Sens. 2017, 9, 1273. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.-Y.; Chen, Y.-Y.; Tang, G.-Q.; Wang, X.-Q.; Liu, Y.; Wei, M. Quantitative estimation of hourly precipitation in the Tianshan Mountains based on area-to-point kriging downscaling and satellite-gauge data merging. J. Mt. Sci. 2022, 19, 58–72. [Google Scholar] [CrossRef]
- Zhang, Y.; Hanati, G.; Danierhan, S.; Liu, Q.; Xu, Z. Evaluation and comparison of daily GPM/TRMM precipitation products over the Tianshan Mountains in China. Water 2020, 12, 3088. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ahmad, I.; Ding, Y.; Shangguan, D.; Zaman, M.; Ijaz, M.W.; Sarwar, K.; Han, H.; Yang, M. Assessment of IMERG-V06 precipitation product over different hydro-climatic regimes in the Tianshan Mountains, North-Western China. Remote Sens. 2019, 11, 2314. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Li, Z.; Anjum, M.N.; Gao, Y. Performance Evaluation of Version 5 (V05) of Integrated Multi-Satellite Retrievals for Global Precipitation Measurement (IMERG) over the Tianshan Mountains of China. Water 2019, 11, 1139. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.S.; Xue, X.; Zhang, X. Inter-comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Tang, G.; Wei, M.; Yang, L.; Zhang, Y. Evaluation of multi-satellite precipitation products in Xinjiang, China. Int. J. Remote Sens. 2018, 39, 7437–7462. [Google Scholar] [CrossRef]
- Palazzi, E.; Von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Ji, X.; Chen, Y. Characterizing spatial patterns of precipitation based on corrected TRMM 3B43 data over the mid Tianshan Mountains of China. J. Mt. Sci. 2012, 9, 628–645. [Google Scholar] [CrossRef]
- Zhao, C.; Yao, S.; Zhang, S.; Han, H.; Zhao, Q.; Yi, S. Validation of the accuracy of different precipitation datasets over Tianshan mountainous area. Adv. Meteorol. 2015, 2015, 617382. [Google Scholar] [CrossRef]
- Fan, M.; Xu, J.; Chen, Y.; Li, W. Simulating the precipitation in the data-scarce Tianshan Mountains, Northwest China based on the Earth system data products. Arab. J. Geosci. 2020, 13, 637. [Google Scholar] [CrossRef]
- Zhengyong, Z.; Xinlin, H.; Lin, L.; Zhongqin, L.; Puyu, W. Spatial distribution of rainfall simulation and the cause analysis in China’s Tianshan Mountains area. Adv. Water Sci. 2015, 26, 500–508. [Google Scholar]
- Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.; Stocker, E.; Adler, R.; Hou, A.; Kakar, R.; Wentz, F. The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar] [CrossRef]
- Sharifi, E.; Eitzinger, J.; Dorigo, W. Performance of the state-of-the-art gridded precipitation products over mountainous terrain: A regional study over Austria. Remote Sens. 2019, 11, 2018. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Zipser, E.J. Contribution of tropical cyclones to the global precipitation from eight seasons of TRMM data: Regional, seasonal, and interannual variations. J. Clim. 2010, 23, 1526–1543. [Google Scholar] [CrossRef]
- Scheel, M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, E.; Huffman, G. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Feng, A.; Liu, W.; Ma, X.; Dong, G. Variation of aridity index and the role of climate variables in the Southwest China. Water 2017, 9, 743. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W. Evaluation of version-7 TRMM multi-satellite precipitation analysis product during the Beijing extreme heavy rainfall event of 21 July 2012. Water 2013, 6, 32–44. [Google Scholar] [CrossRef] [Green Version]
- Ulloa, J.; Ballari, D.; Campozano, L.; Samaniego, E. Two-step downscaling of TRMM 3B43 V7 precipitation in contrasting climatic regions with sparse monitoring: The case of Ecuador in tropical South America. Remote Sens. 2017, 9, 758. [Google Scholar] [CrossRef] [Green Version]
- Price, D.T.; McKenney, D.W.; Nalder, I.A.; Hutchinson, M.F.; Kesteven, J.L. A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data. Agric. For. Meteorol. 2000, 101, 81–94. [Google Scholar] [CrossRef]
- Cressie, N.; Sainsbury-Dale, M.; Zammit-Mangion, A. Basis-Function Models in Spatial Statistics. arXiv 2022, arXiv:2202.03660. [Google Scholar] [CrossRef]
- Johannesson, G.; Cressie, N. Finding large-scale spatial trends in massive, global, environmental datasets. Env. Off. J. Int. Env. Soc. 2004, 15, 1–44. [Google Scholar] [CrossRef]
- Simeng, W.; Dazhao, W.; Chang, H. A comparative study of using ANUSPLIN and GWR models for downscaled GPM precipitation. In Proceedings of the 2019 8th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Istanbul, Turkey, 16–19 July 2019; pp. 1–5. [Google Scholar]
- Guo, B.; Zhang, J.; Meng, X.; Xu, T.; Song, Y. Long-term spatio-temporal precipitation variations in China with precipitation surface interpolated by ANUSPLIN. Sci. Rep. 2020, 10, 81. [Google Scholar] [CrossRef] [PubMed]
- Shu, S.; Liu, C.; Shi, R.; Gao, W. Research on spatial interpolation of meteorological elements in Anhui Province based on ANUSPLIN. In Proceedings of the Remote Sensing and Modeling of Ecosystems for Sustainability VIII, San Diego, CA, USA, 15 September 2011; pp. 183–194. [Google Scholar]
- An, Y.; Zhao, W.; Li, C.; Liu, Y. Evaluation of six satellite and reanalysis precipitation products using gauge observations over the Yellow River Basin, China. Atmosphere 2020, 11, 1223. [Google Scholar] [CrossRef]
- Vincent, L.A.; Peterson, T.; Barros, V.; Marino, M.; Rusticucci, M.; Carrasco, G.; Ramirez, E.; Alves, L.; Ambrizzi, T.; Berlato, M. Observed trends in indices of daily temperature extremes in South America 1960–2000. J. Clim. 2005, 18, 5011–5023. [Google Scholar] [CrossRef]
- Sorg, A.; Bolch, T.; Stoffel, M.; Solomina, O.; Beniston, M. Climate change impacts on glaciers and runoff in Tien Shan (Central Asia). Nat. Clim. Chang. 2012, 2, 725–731. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Sun, W.; Mu, X.; Song, X.; Wu, D.; Cheng, A.; Qiu, B. Changes in extreme temperature and precipitation events in the Loess Plateau (China) during 1960–2013 under global warming. Atmos. Res. 2016, 168, 33–48. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Asgari, A.; Fattahi, E. Variability of extreme temperature and precipitation in Iran during recent decades. Int. J. Climatol. A J. R. Meteorol. Soc. 2009, 29, 329–343. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Z.; Zhang, X.; Li, L.; Sun, Y. Additional risk in extreme precipitation in China from 1.5 °C to 2.0 °C global warming levels. Sci. Bull. 2018, 63, 228–234. [Google Scholar] [CrossRef] [Green Version]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
- Samel, A.N.; Wang, S.; Wang, W.-C. A comparison between observed and GCM-simulated summer monsoon characteristics over China. J. Clim. 1995, 8, 1690–1696. [Google Scholar] [CrossRef] [Green Version]
- Ni, F.; Cavazos, T.; Hughes, M.K.; Comrie, A.C.; Funkhouser, G. Cool-season precipitation in the southwestern USA since AD 1000: Comparison of linear and nonlinear techniques for reconstruction. Int. J. Climatol. A J. R. Meteorol. Soc. 2002, 22, 1645–1662. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Nakamura, K. Progress from TRMM to GPM. J. Meteorol. Soc. Jp. Ser. II 2021, 99, 697–729. [Google Scholar] [CrossRef]
- Zhang, Q.; Singh, V.P.; Li, J.; Jiang, F.; Bai, Y. Spatio-temporal variations of precipitation extremes in Xinjiang, China. J. Hydrol. 2012, 434, 7–18. [Google Scholar] [CrossRef]
- Lv, A.; Qi, S.; Wang, G. Multi-model driven by diverse precipitation datasets increases confidence in identifying dominant factors for runoff change in a subbasin of the Qaidam Basin of China. Sci. Total Environ. 2022, 802, 149831. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Dambul, R.; Jones, P. Trends of temperature extremes in Saudi Arabia. Int. J. Climatol. 2014, 34, 808–826. [Google Scholar] [CrossRef]
- Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol. A J. R. Meteorol. Soc. 2005, 25, 693–712. [Google Scholar] [CrossRef]
- Salio, P.; Hobouchian, M.P.; Skabar, Y.G.; Vila, D. Evaluation of high-resolution satellite precipitation estimates over southern South America using a dense rain gauge network. Atmos. Res. 2015, 163, 146–161. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Mitra, A.K.; Pai, D.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, C.K.; Bakimchandra, O.; Basistha, A. DEM-based delineation for improving geostatistical interpolation of rainfall in mountainous region of Central Himalayas, India. Theor. Appl. Climatol. 2017, 130, 51–58. [Google Scholar] [CrossRef]
- Yin, G.; Chen, X.; Tiyip, T. A comparison study between site-extrapolation-based and regional climate model-simulated climate datasets. Adv. Water Sci. 2015, 26, 631–643. [Google Scholar]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Liu, C.; Zipser, E.J. The global distribution of largest, deepest, and most intense precipitation systems. Geophys. Res. Lett. 2015, 42, 3591–3595. [Google Scholar] [CrossRef] [Green Version]
- Massari, C.; Crow, W.; Brocca, L. An assessment of the performance of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Gao, W.; Hu, J.; Du, L.; Du, L. Capability of imerg v6 early, late, and final precipitation products for monitoring extreme precipitation events. Remote Sens. 2021, 13, 689. [Google Scholar] [CrossRef]

| Dataset | Type | Time Resolution | Space Resolution | Time Range | Coverage | Source |
|---|---|---|---|---|---|---|
| Daily dataset of Surface Climatological Data for China (V3.0) | Observation data from ground stations | 1 d | - | 1951– | China | http://data.cma.cn/data/cdcdetail/dataCode/A.0012.0001.html (accessed on 12 August 2022) |
| TRMM3B42 | Combined measurements of satellite estimated precipitation | 3 h | 0.25 × 0.25° | 1998–2019 | Global | https://gpm.nasa.gov/data/directory (accessed on 12 August 2022) |
| GPM IMERG(V06) Final Run | Multi-satellite joint retrieval of precipitation data | 0.5 h | 0.1 × 0.1° | 2000– | Global | https://gpm.nasa.gov/data/directory (accessed on 12 August 2022) |
| MSWEP (V2.2) | Multi-source fusion of precipitation observation data | 3 h | 0.1 × 0.1° | 1979–2019 | Global | http://www.gloh2o.org (accessed on 12 August 2022) |
| Time Scale | Product | BIAS/% | MAE/mm | ||||||
|---|---|---|---|---|---|---|---|---|---|
| West | East | South | North | West | East | South | North | ||
| Wet Season | TRMM | −7.58 | −9.58 | −5.89 | −9.69 | 18.09 | 15.03 | 47.77 | 35.48 |
| GPM | −3.27 | −7.87 | −8.90 | −3.36 | 18.48 | 41.37 | 59.84 | 46.84 | |
| MSWEP | −9.22 | −5.82 | −4.83 | 2.99 | 20.53 | 41.36 | 66.24 | 66.75 | |
| Year | TRMM | −15.08 | −17.41 | −17.31 | −10.88 | 27.88 | 32.03 | 89.67 | 36.71 |
| GPM | −5.48 | −10.71 | −9.50 | −5.07 | 36.78 | 80.72 | 67.87 | 52.75 | |
| MSWEP | 1.23 | 10.95 | 15.33 | 19.66 | 41.71 | 62.38 | 69.79 | 68.48 | |
| Dry Season | TRMM | −18.25 | −20.82 | −19.86 | −15.67 | 68.15 | 128.35 | 107.84 | 92.46 |
| GPM | −14.56 | −15.36 | −15.78 | −10.85 | 56.55 | 126.95 | 175.88 | 98.76 | |
| MSWEP | 7.54 | 18.82 | 29.32 | 32.85 | 75.90 | 74.76 | 123.05 | 144.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; He, X.; Li, X.; Du, Y.; Yang, G.; Li, D.; Xu, W. Spatiotemporal Evaluation and Estimation of Precipitation of Multi-Source Precipitation Products in Arid Areas of Northwest China—A Case Study of Tianshan Mountains. Water 2022, 14, 2566. https://doi.org/10.3390/w14162566
Li X, He X, Li X, Du Y, Yang G, Li D, Xu W. Spatiotemporal Evaluation and Estimation of Precipitation of Multi-Source Precipitation Products in Arid Areas of Northwest China—A Case Study of Tianshan Mountains. Water. 2022; 14(16):2566. https://doi.org/10.3390/w14162566
Chicago/Turabian StyleLi, Xiaoqian, Xinlin He, Xiaolong Li, Yongjun Du, Guang Yang, Dongbo Li, and Wenhe Xu. 2022. "Spatiotemporal Evaluation and Estimation of Precipitation of Multi-Source Precipitation Products in Arid Areas of Northwest China—A Case Study of Tianshan Mountains" Water 14, no. 16: 2566. https://doi.org/10.3390/w14162566
APA StyleLi, X., He, X., Li, X., Du, Y., Yang, G., Li, D., & Xu, W. (2022). Spatiotemporal Evaluation and Estimation of Precipitation of Multi-Source Precipitation Products in Arid Areas of Northwest China—A Case Study of Tianshan Mountains. Water, 14(16), 2566. https://doi.org/10.3390/w14162566








