Assessment of Uncertainty in Grid-Based Rainfall-Runoff Model Based on Formal and Informal Likelihood Measures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
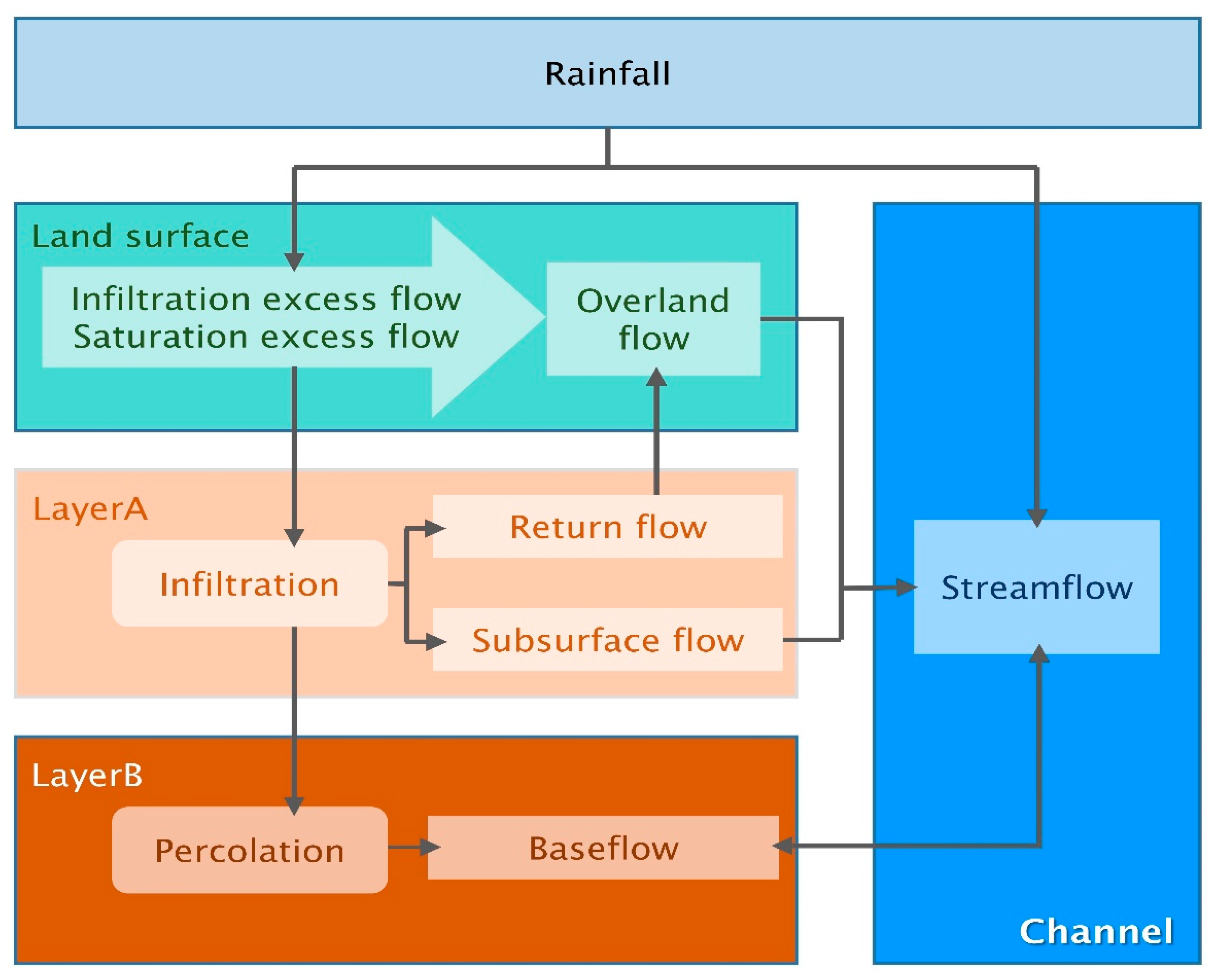
2.2. Grid-Based Rainfall-Runoff Model (GRM) Definition
2.3. Rainfall-Runoff Analysis
2.4. Uncertainty Analysis Using Generalized Likelihood Uncertified Estimation (GLUE)
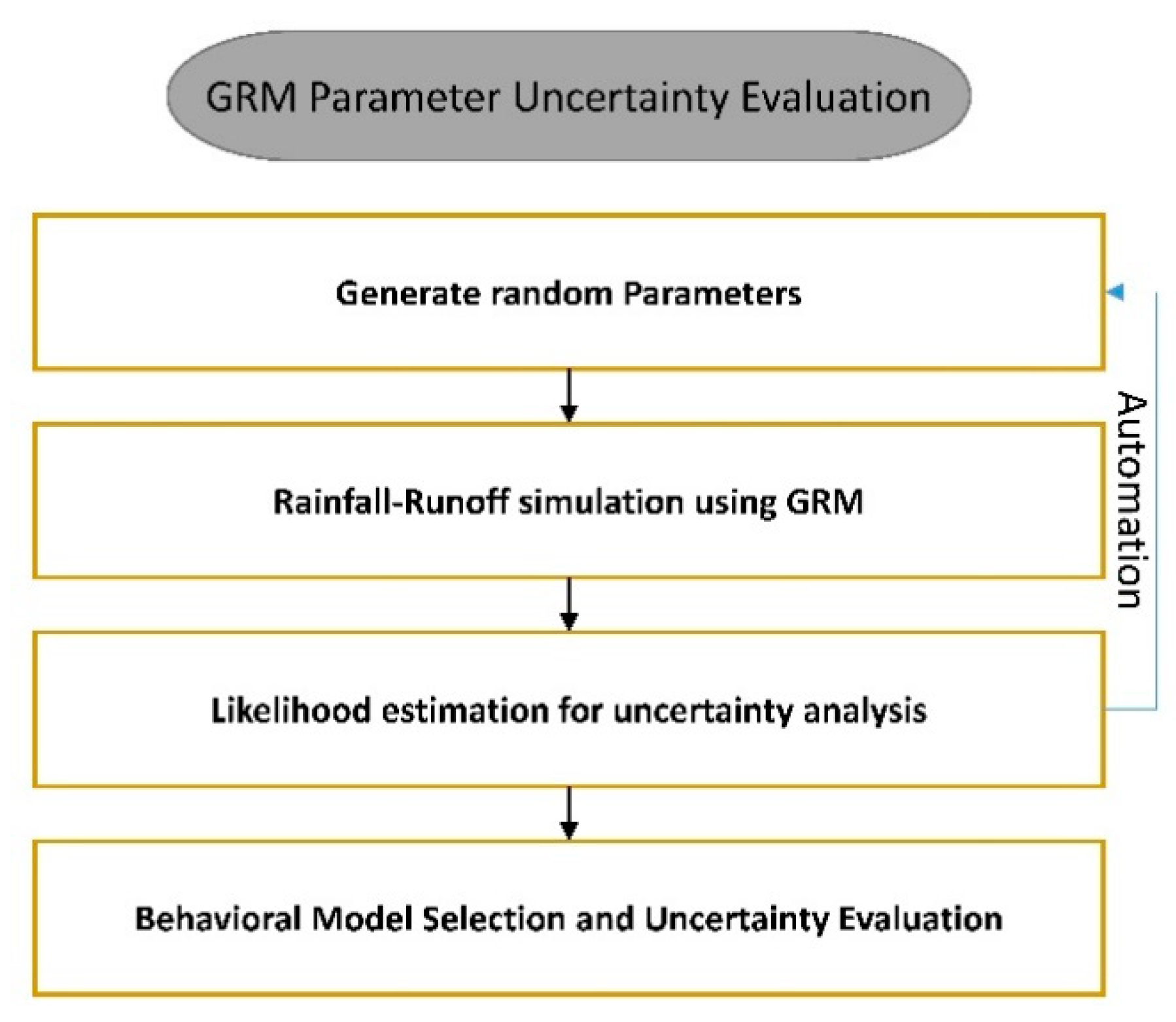
2.5. Automation Analysis and Parameter Setting of the GRM
3. Results
3.1. Distribution of Parameters According to Likelihood
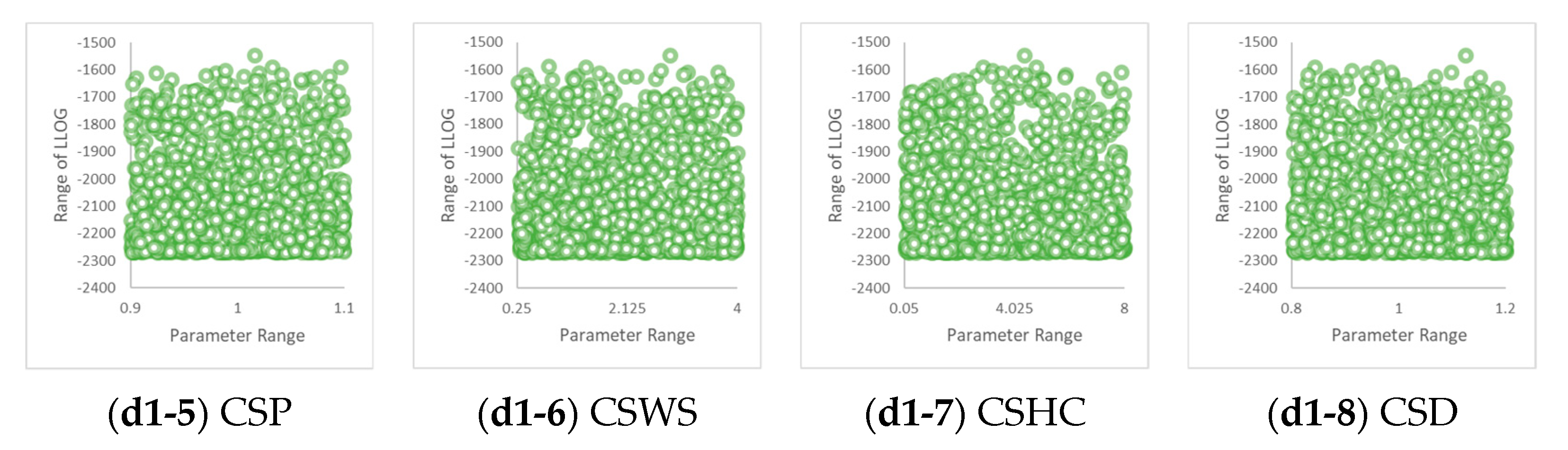
3.1.1. Event 1 Dotty Plot
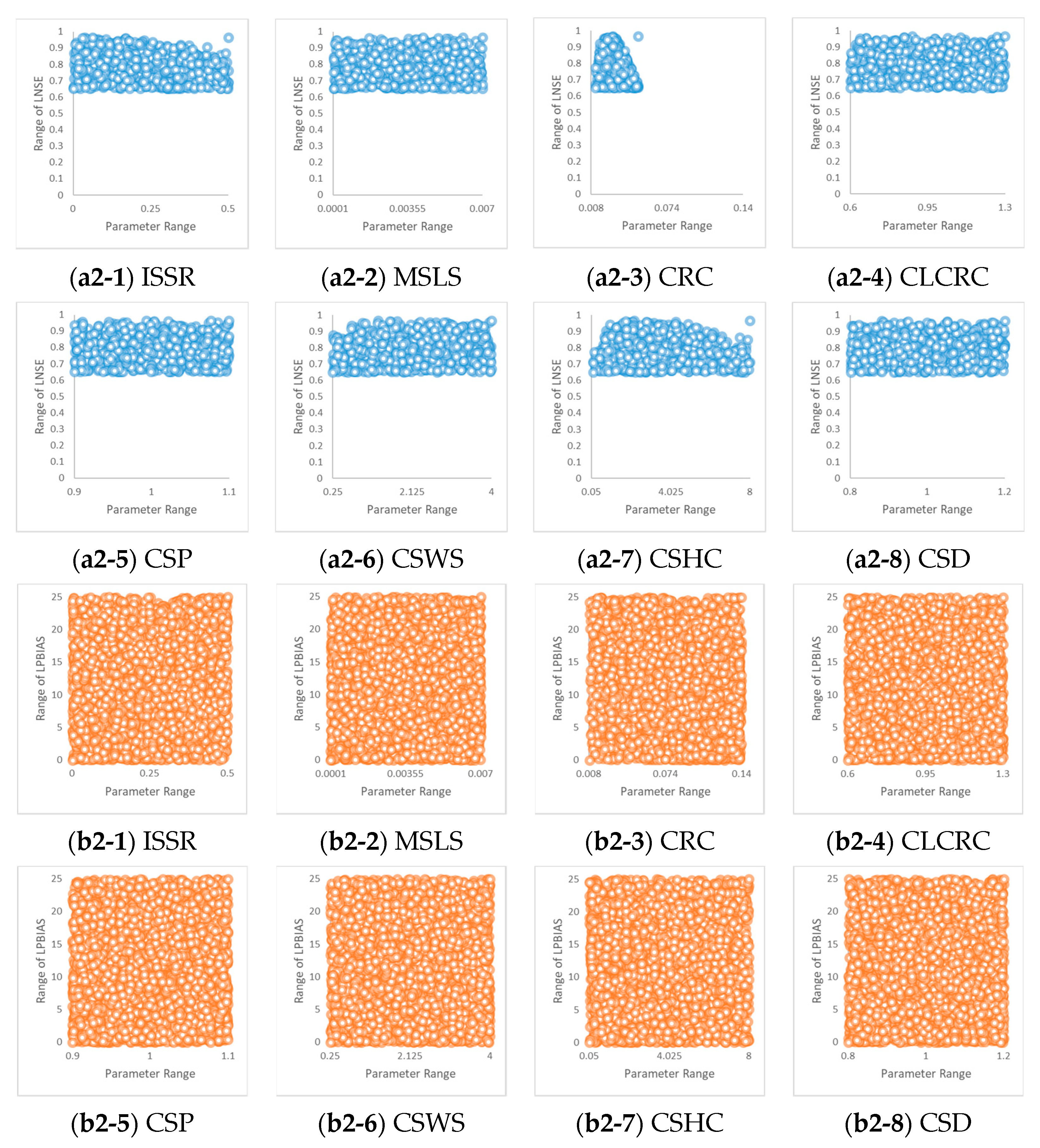
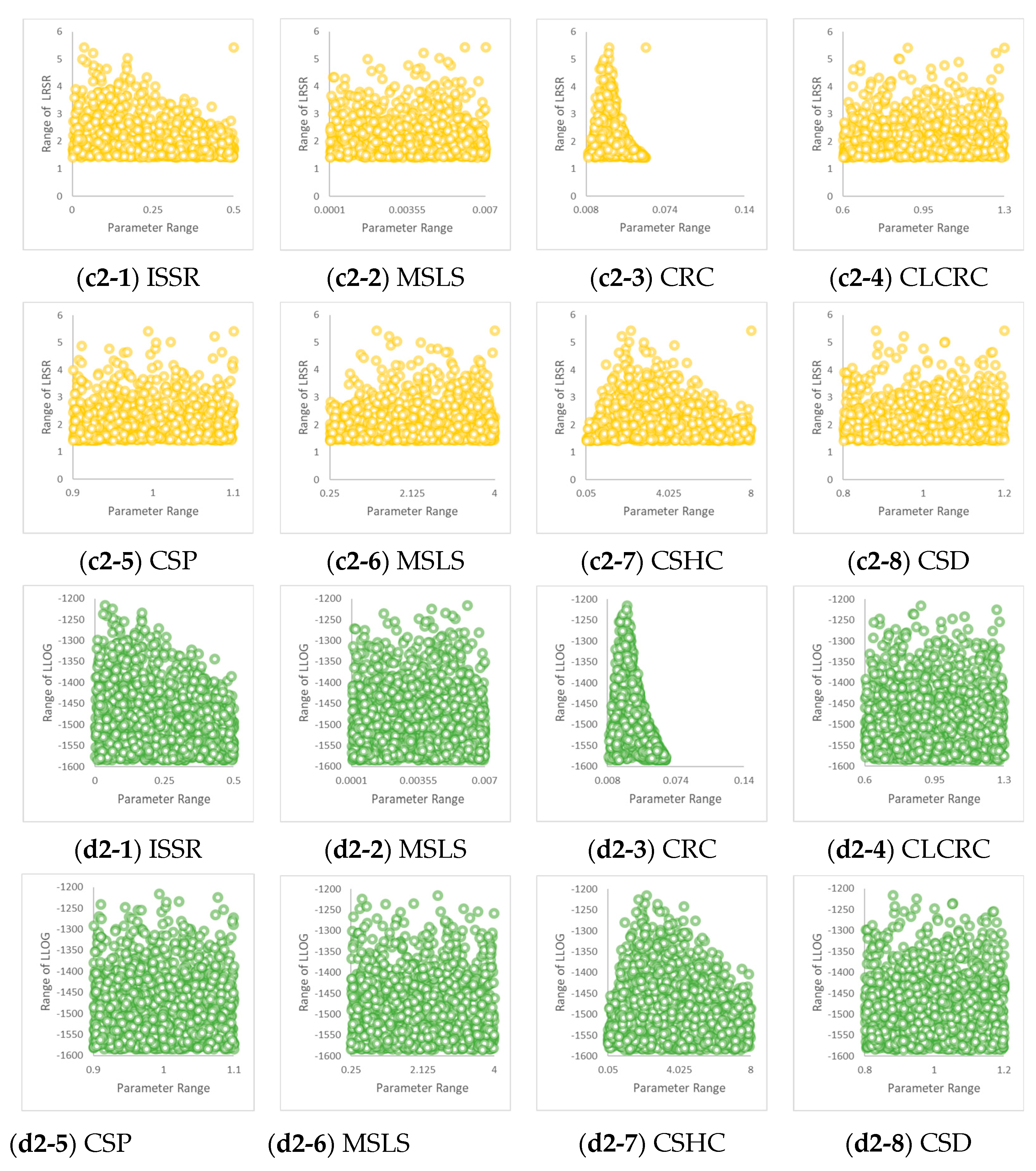
3.1.2. Event 2 Dotty Plot
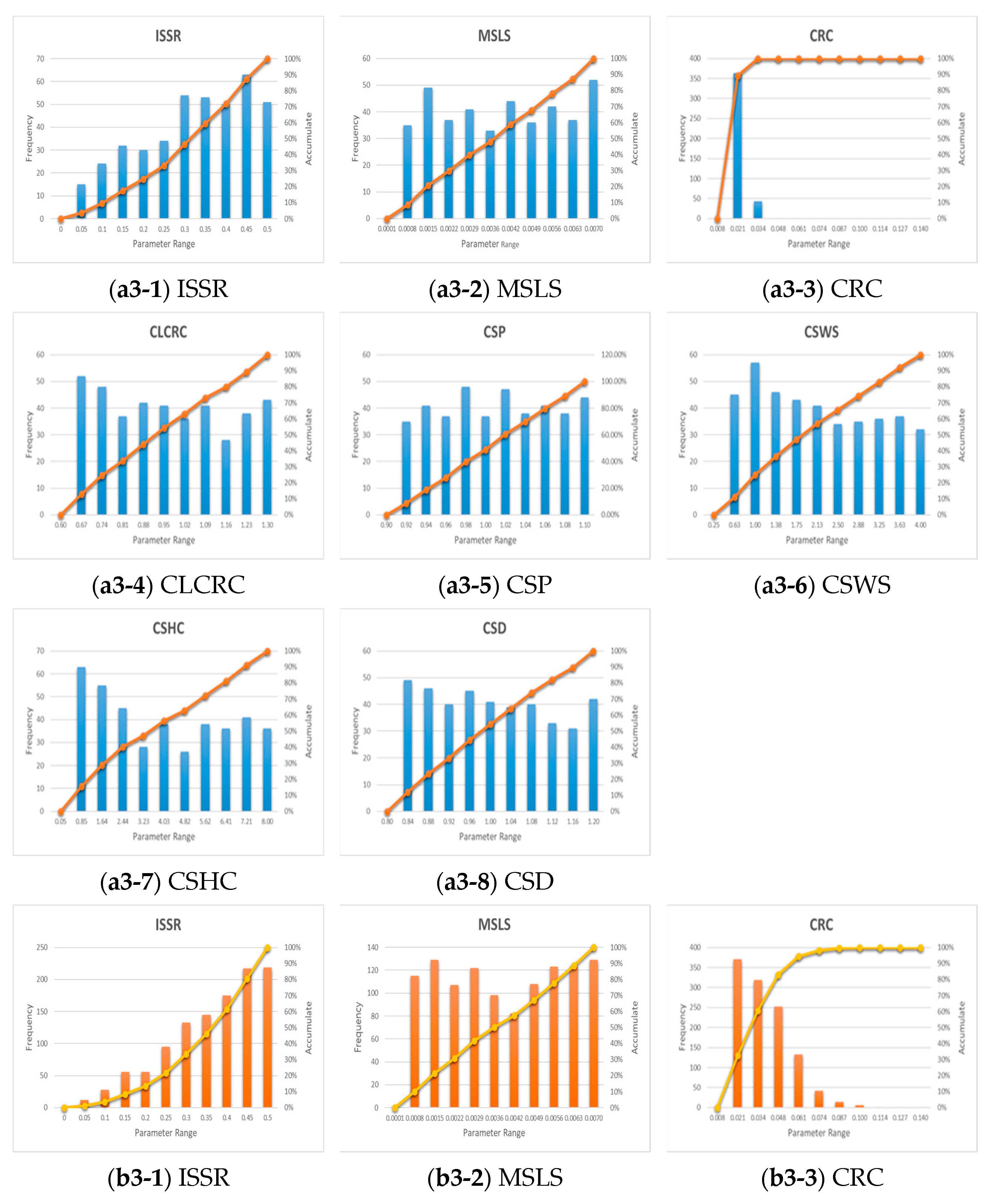
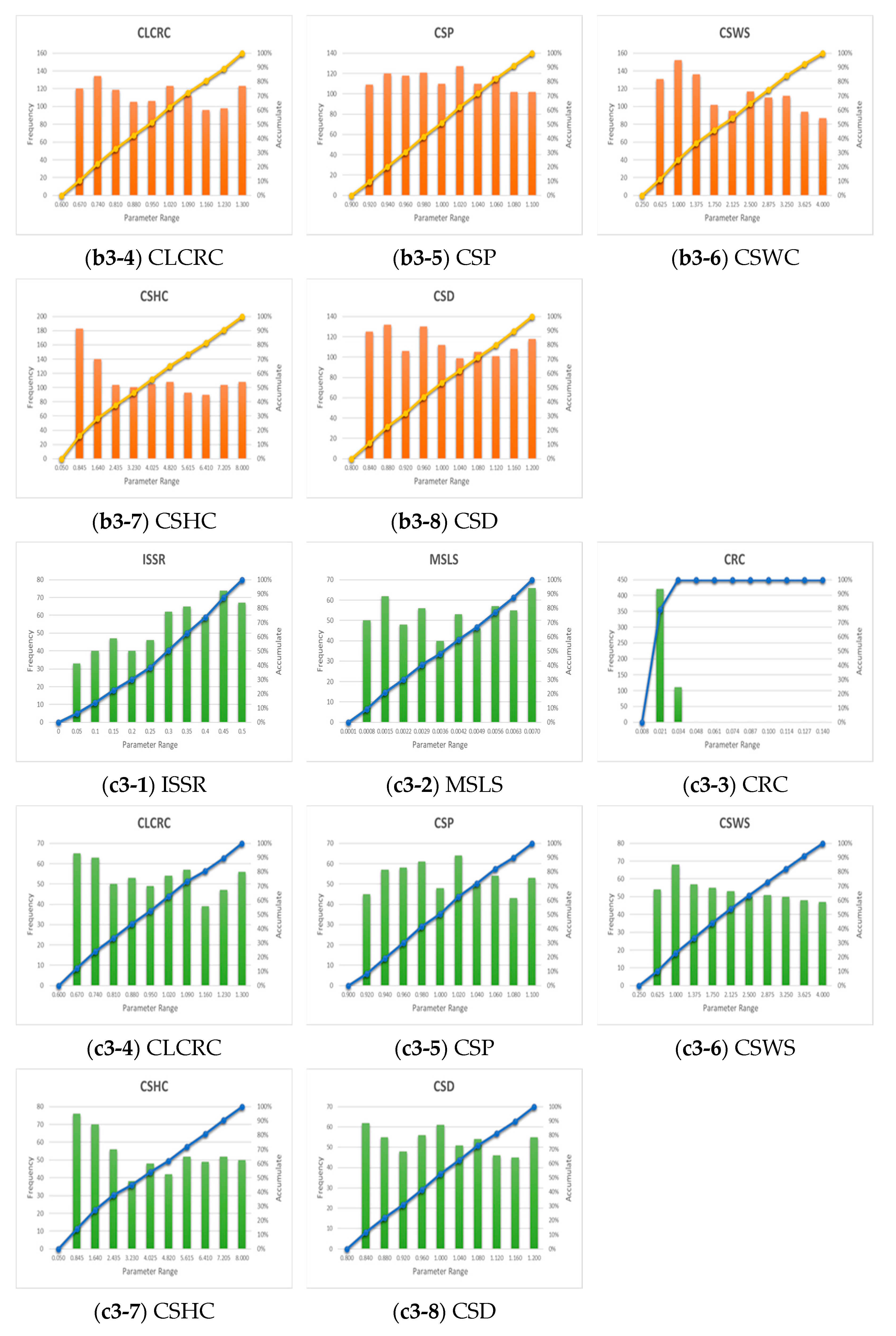
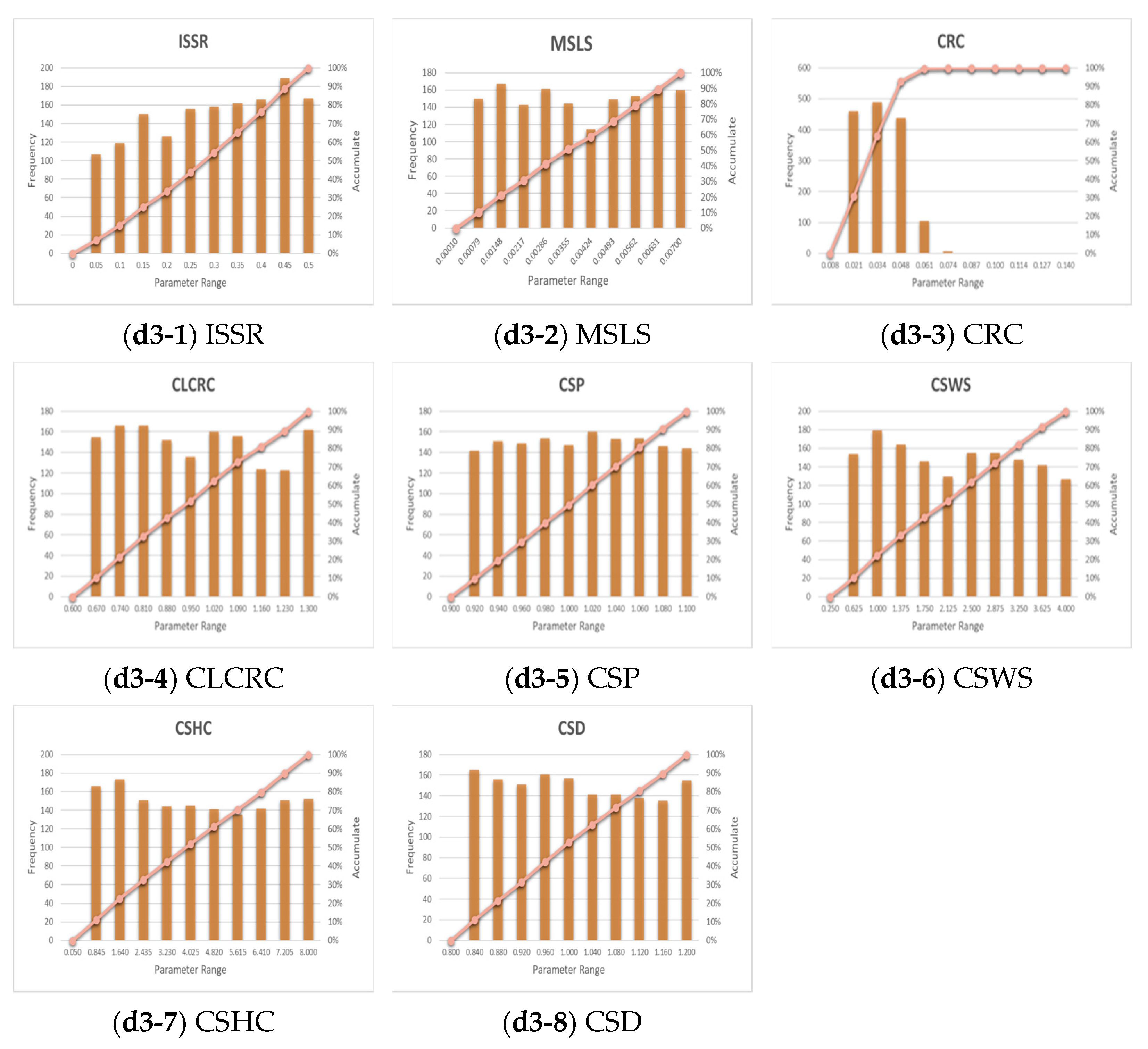
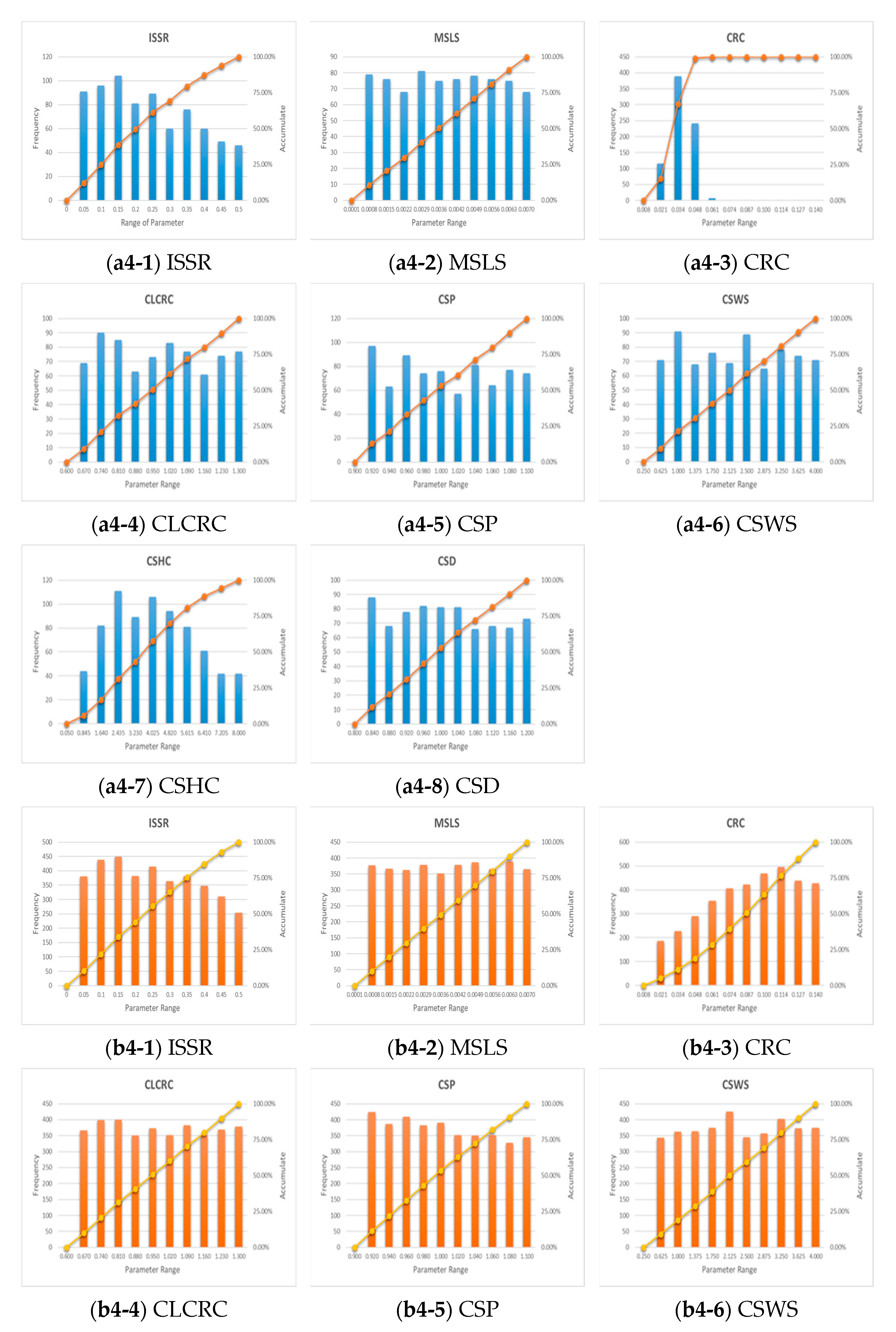
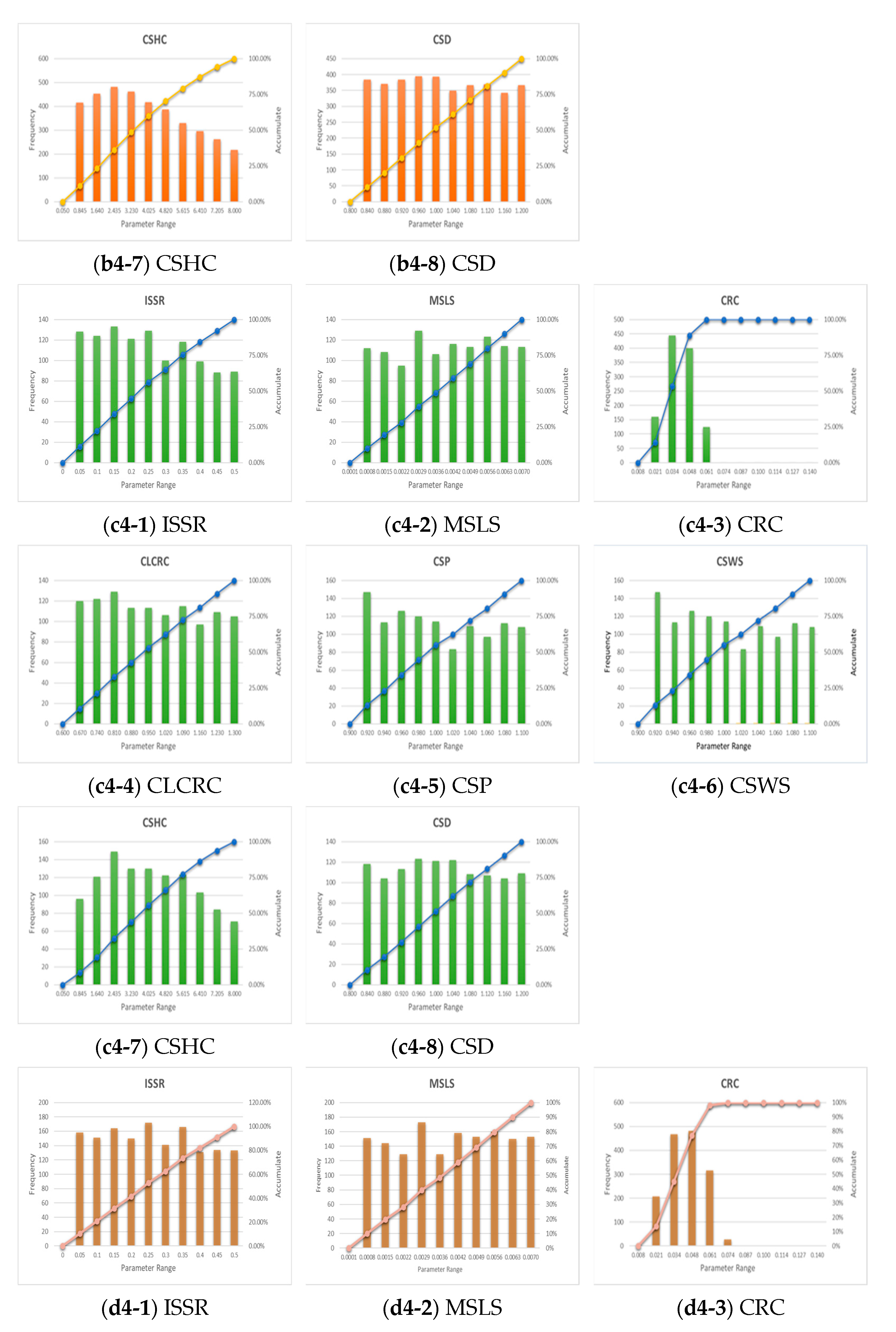
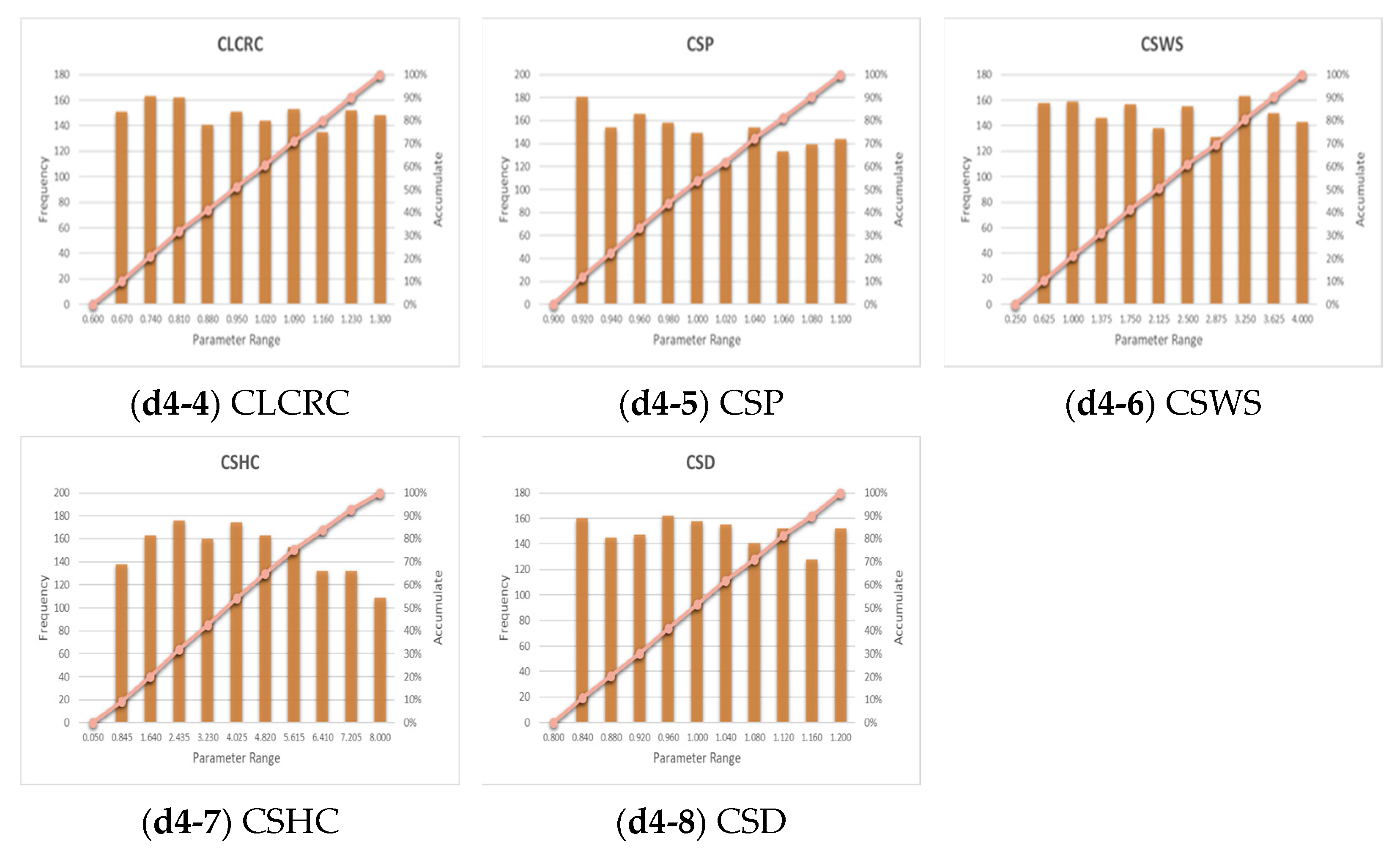
3.2. Posterior Distribution of GRM Parameters
3.2.1. Event 1 Parameter Sensitivity
3.2.2. Event 2 Parameter Sensitivity
3.3. Quantied Uncertainty in the GRM Model
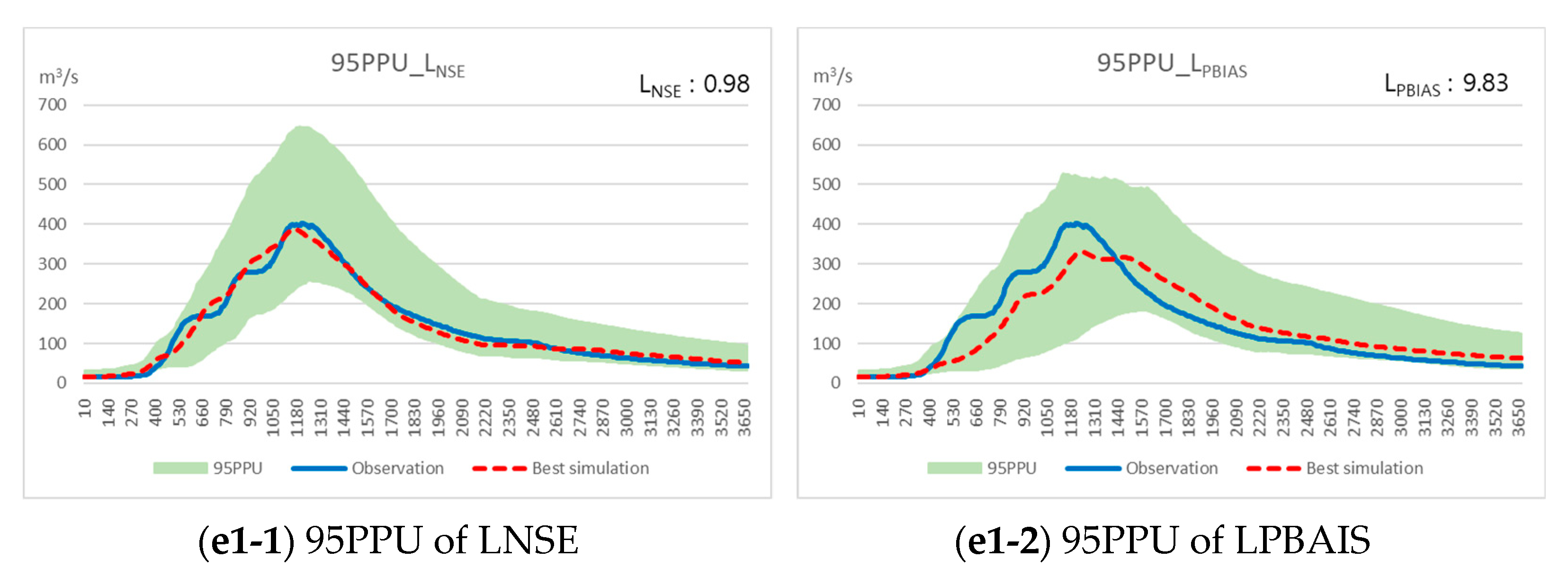
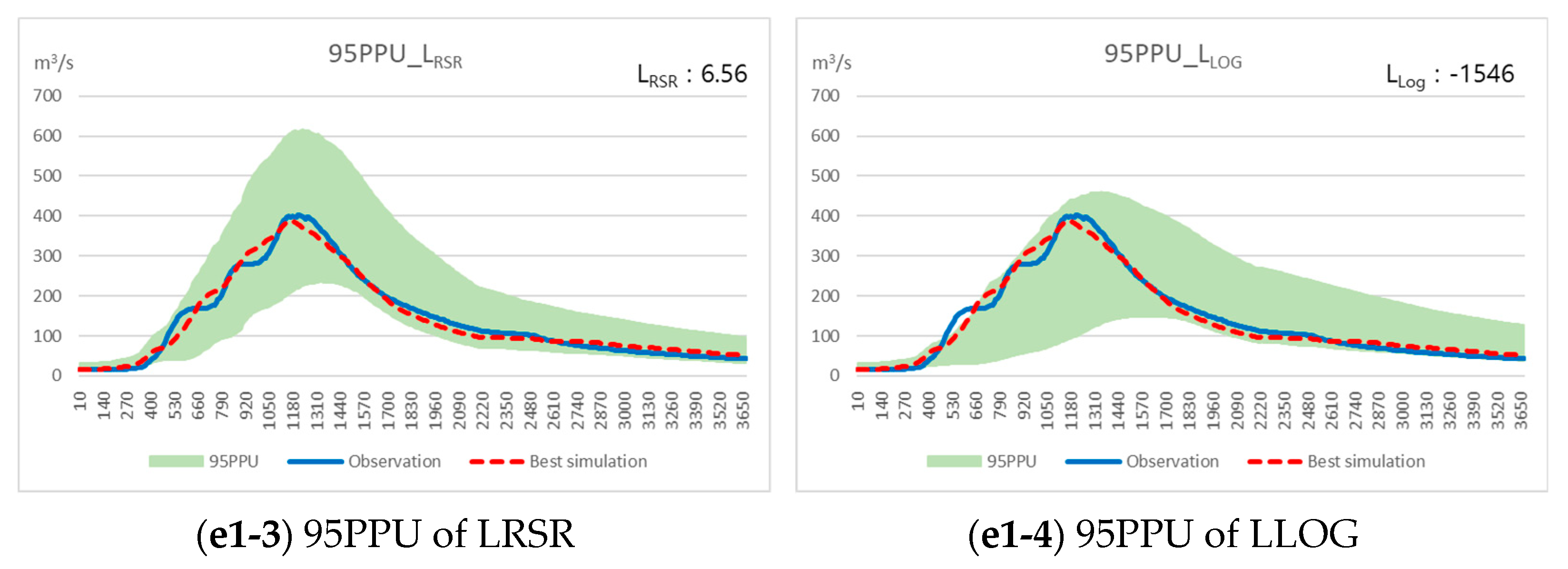
3.3.1. Event 1 95PPU
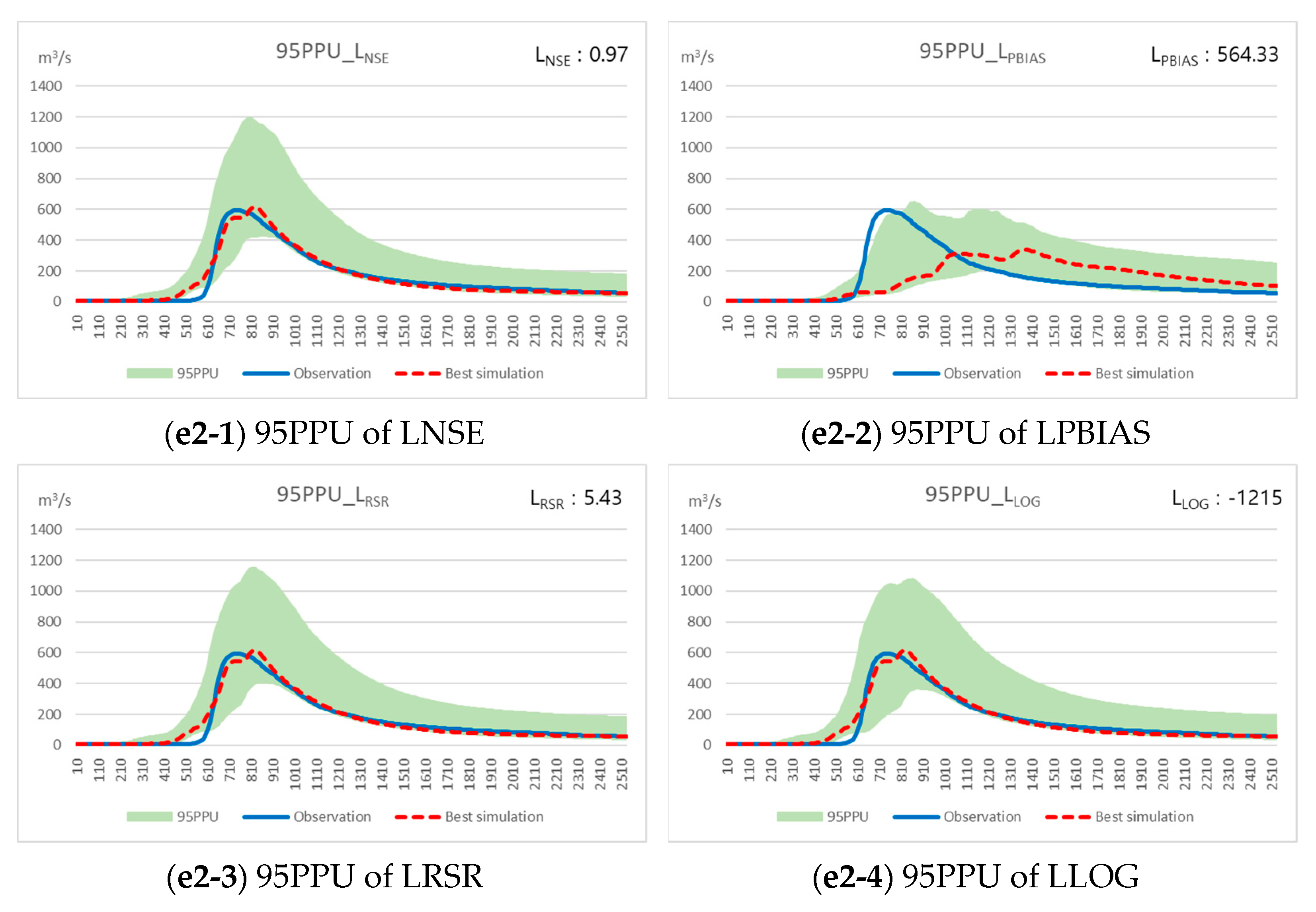
3.3.2. Event 2 95PPU
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tayfur, G.; Singh, V.P. ANN and Fuzzy Logic Models for Simulating Event−Based Rainfall−Runoff. J. Hydraul. Eng. 2006, 132, 1321–1330. [Google Scholar] [CrossRef] [Green Version]
- Tramblay, Y.; Bouvier, C.; Martin, C.; Didon−Lescot, J.F.; Todorovik, D.; Domergue, J.M. Assessment of initial soil moisture conditions for event−based rainfall–runoff modelling. J. Hydrol. 2010, 387, 176–187. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H. Influence of lag time on event−based rainfall–runoff modeling using the data driven approach. J. Hydrol. 2012, 438, 223–233. [Google Scholar] [CrossRef]
- Chang, T.K.; Talei, A.; Alaghmand, S.; Ooi, M.P.L. Choice of rainfall inputs for event−based rainfall−runoff modeling in a catchment with multiple rainfall stations using data−driven techniques. J. Hydrol. 2017, 545, 100–108. [Google Scholar] [CrossRef]
- Reshma, T.; Venkata Reddy, K.; Pratap, D.; Agilan, V. Parameters optimization using Fuzzy rule based multi−objective genetic algorithm for an event based rainfall−runoff model. Water Resour. Manag. 2018, 32, 1501–1516. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Geza, M.; McCray, J.E. Effects of soil data resolution on SWAT model stream flow and water quality predictions. J. Environ. Manag. 2008, 88, 393–406. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Hong, Q.; Yu, H.; Niu, J.F. Parameter uncertainty analysis of non−point source pollution from different land use types. Sci. Total Environ. 2010, 408, 1971–1978. [Google Scholar] [CrossRef]
- Zehe, E.; Becker, R.; Bárdossy, A.; Plate, E. Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation. J. Hydrol. 2005, 315, 183–202. [Google Scholar] [CrossRef]
- Mohamadi, M.A.; Kavian, A. Effects of rainfall patterns on runoff and soil erosion in field plots. J. Soil Water Conserv. 2015, 3, 273–281. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Zhang, J.; Wang, G.; Jin, J.; Liu, C.; Liu, Y.; He, R.; Bao, Z. Uncertainty Analysis of SWAT Modeling in the Lancang River Basin Using Four Different Algorithms. Water 2021, 13, 341. [Google Scholar] [CrossRef]
- Ebtehaj, M.; Moradkhani, H.; Gupta, H.V. Improving robustness of hydrologic parameter estimation by the use of moving block bootstrap resampling. Water Resour. Res. 2010, 46, 7. [Google Scholar] [CrossRef]
- Chaubey, I.; Haan, C.T.; Grunwald, S.; Salisbury, J.M. Uncertainty in the model parameters due to spatial variability of rainfall. J. Hydrol. 1999, 220, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Binley, A.M.; Beven, K.J.; Calver, A.; Watts, L.G. Changing responses in hydrology: Assessing the uncertainty in physically based model predictions. Water Resour. Res. 1991, 27, 1253–1261. [Google Scholar] [CrossRef]
- Melching, C.S. An improved first−order reliability approach for assessing uncertainties in hydrologic modeling. J. Hydrol. 1992, 132, 157–177. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N.; Bagtzoglou, A.C. On Latin Hypercube sampling for efficient uncertainty estimation of satellite rainfall observations in flood prediction. Comput. Geosci. 2006, 32, 776–792. [Google Scholar] [CrossRef]
- Durbin, J.; Koopman, S.J. Time Series Analysis by State Space Methods; OUP Oxford: Oxford, UK, 2012; Volume 38. [Google Scholar]
- Vrugt, J.A.; Braak, C.J.F.T.; Gupta, H.V.; Robinson, B.A. Response to comment by Keith Beven on “Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling?”. Stoch. Environ. Res. Risk Assess. 2009, 23, 1061–1062. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Wilson, J.L. First order analysis of uncertainty in numerical models of groundwater flow part: 1. Mathematical development. Water Resour. Res. 1981, 17, 149–161. [Google Scholar] [CrossRef] [Green Version]
- Townley, L.R.; Wilson, J.L. Computationally efficient algorithms for parameter estimation and uncertainty propagation in numerical models of groundwater flow. Water Resour. Res. 1985, 21, 1851–1860. [Google Scholar] [CrossRef]
- Nourali, M.; Ghahraman, B.; Pourreza−Bilondi, M.; Davary, K. Effect of formal and informal likelihood functions on uncertainty assessment in a single event rainfall−runoff model. J. Hydrol. 2016, 540, 549–564. [Google Scholar] [CrossRef]
- Hu, C.; Xia, J.; She, D.; Song, Z.; Zhang, Y.; Hong, S. A new urban hydrological model considering various land covers for flood simulation. J. Hydrol. 2021, 603, 126833. [Google Scholar] [CrossRef]
- Christensen, S. A synthetic groundwater modelling study of the accuracy of GLUE uncertainty intervals. Hydrol. Res. 2004, 35, 45–59. [Google Scholar] [CrossRef]
- Montanari, A. Large sample behaviors of the generalized likelihood uncertainty estimation (GLUE) in assessing the uncertainty of rainfall−runoff simulations. Water Resour. Res. 2005, 41, 8. [Google Scholar] [CrossRef]
- McMillan, H.; Clark, M. Rainfall−runoff model calibration using informal likelihood measures within a Markov chain Monte Carlo sampling scheme. Water Resour. Res. 2009, 45, 4. [Google Scholar] [CrossRef]
- Choi, Y.S.; Choi, C.K.; Kim, H.S.; Kim, K.T.; Kim, S. Multi−site calibration using a grid−based event rainfallrunoff model: A case study of the upstream areas of the Nakdong River basin in Korea. Hydrol. Process. 2015, 29, 2089–2099. [Google Scholar] [CrossRef]
- Shin, M.J.; Choi, Y.S. Sensitivity analysis to investigate the reliability of the grid−based rainfall−runoff model. Water 2018, 10, 1839. [Google Scholar] [CrossRef] [Green Version]
- Hornberger, G.M.; Spear, R.C. Approach to the preliminary analysis of environmental systems. J. Environ. Mgmt. 1981, 12, 7–18. [Google Scholar]
- Young, P. The Validity and Credibility of Models for Badly Defined Systems. In Uncertainty and Forecasting of Water Quality; Beck, M.B., Straten, G.V., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 69–98. [Google Scholar]
- Jin, X.; Xu, C.Y.; Zhang, Q.; Singh, V.P. Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. J. Hydrol. 2010, 383, 147–155. [Google Scholar] [CrossRef]
- Blasone, R.S.; Madsen, H.; Rosbjerg, D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling. J. Hydrol. 2008, 353, 18–32. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness−of−fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Beven, K. Environmental Modelling: An Uncertain Future? Routledge: New York, NY, USA, 2009. [Google Scholar]
- Ajmal, M.; Kim, T.W. Quantifying excess stormwater using SCS−CN–based rainfall runoff models and different curve number determination methods. J. Irrig Drain. Eng. 2015, 141, 04014058. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V. Uncertainty quantification in flood inundation mapping using generalized likelihood uncertainty estimate and sensitivity analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V.; Kim, S.; Kang, N.; Kim, Y.; Lee, K.; Kim, G.; Kim, H.S. Sensitivity of subjective decisions in the GLUE methodology for quantifying the uncertainty in the flood inundation map for Seymour reach in Indiana, USA. Water 2014, 6, 2104–2126. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, H.H.; Houseworth, J. Modified generalized likelihood uncertainty estimation (GLUE) methodology for considering the subjectivity of likelihood measure selection. J. Hydrol. Eng. 2011, 16, 558–561. [Google Scholar] [CrossRef]



| Rainfall Station Name | Rainfall Station Location | Station Weight (%) | |
|---|---|---|---|
| Latitude | Longitude | ||
| Samjuk | 37°4′36.36″ N | 127°22′7.03″ E | 26.13 |
| Geumdang Elementary School | 37°12′3.45″ N | 127°36′21.74″ E | 17.51 |
| Beopcheon | 37°12′16.31″ N | 127°44′52.87″ E | 15.78 |
| Yeoju Bridge | 37°17′43.27″ N | 127°38′31.92″ E | 14.03 |
| Wonsam | 37°10′6.32″ N | 127°18′15.06″ E | 9.01 |
| Seolseong | 37° 8′45.33″ N | 127°31′17.97″ E | 7.24 |
| Saenggeu | 37° 2′4.37″ N | 127°36′3.93″ E | 4.56 |
| Eumseong | 36°56′13.82″ N | 127°41′32.14″ E | 2.18 |
| Namgok | 37°13′53.30″ N | 127°16′41.07″ E | 1.71 |
| Angseong | 37° 5′11.35″ N | 127°44′43.87″ E | 1.50 |
| Oryu | 36°58′21.40″ N | 127°28′40.99″ E | 0.35 |
| Num | NAME | Start Date | End Date |
|---|---|---|---|
| 1 | Event 1 | 29 June 2011 (10:00:00) | 1 July 2011 (17:30:00) |
| 2 | Event 2 | 31 July 2017 (3:00:00) | 1 August 2012 (07:30:00) |
| Num | Parameters | Description | Range | Change Range | ||
|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | |||
| 1 | IniSaturation (ISSR) | Initial soil saturation ratio | 0 | 1 | 0 | 0.5 |
| 2 | MinSlopeOF (MSLS) | Minimum slope of land surface | 0.0001 | 0.01 | 0.0001 | 0.007 |
| 3 | ChRoughness (CRC) | Channel roughness coefficient | 0.008 | 0.2 | 0.008 | 0.14 |
| 4 | CalCoefLCRoughness (CLCRC) | Correction factor for land cover roughness coefficient | 0.6 | 1.3 | 0.6 | 1.3 |
| 5 | CalCoefSoilDepth (CSD) | Correction factor for soil depth | 0.8 | 1.2 | 0.9 | 1.1 |
| 6 | CalCoefPorosity (CSP) | Correction factor for soil porosity | 0.9 | 1.1 | 0.25 | 4 |
| 7 | CalCoefWFSuctionHead (CSWS) | Correction factor for soil wetting front suction head | 0.25 | 4 | 0.05 | 8 |
| 8 | CalCoefHydraulicK (CSHC) | Correction factor for soil hydraulic conductivity | 0.05 | 20 | 0.8 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seong, Y.; Choi, C.-K.; Jung, Y. Assessment of Uncertainty in Grid-Based Rainfall-Runoff Model Based on Formal and Informal Likelihood Measures. Water 2022, 14, 2210. https://doi.org/10.3390/w14142210
Seong Y, Choi C-K, Jung Y. Assessment of Uncertainty in Grid-Based Rainfall-Runoff Model Based on Formal and Informal Likelihood Measures. Water. 2022; 14(14):2210. https://doi.org/10.3390/w14142210
Chicago/Turabian StyleSeong, Yeonjeong, Cheon-Kyu Choi, and Younghun Jung. 2022. "Assessment of Uncertainty in Grid-Based Rainfall-Runoff Model Based on Formal and Informal Likelihood Measures" Water 14, no. 14: 2210. https://doi.org/10.3390/w14142210






