Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia
Abstract
:1. Introduction
2. Material and Methods
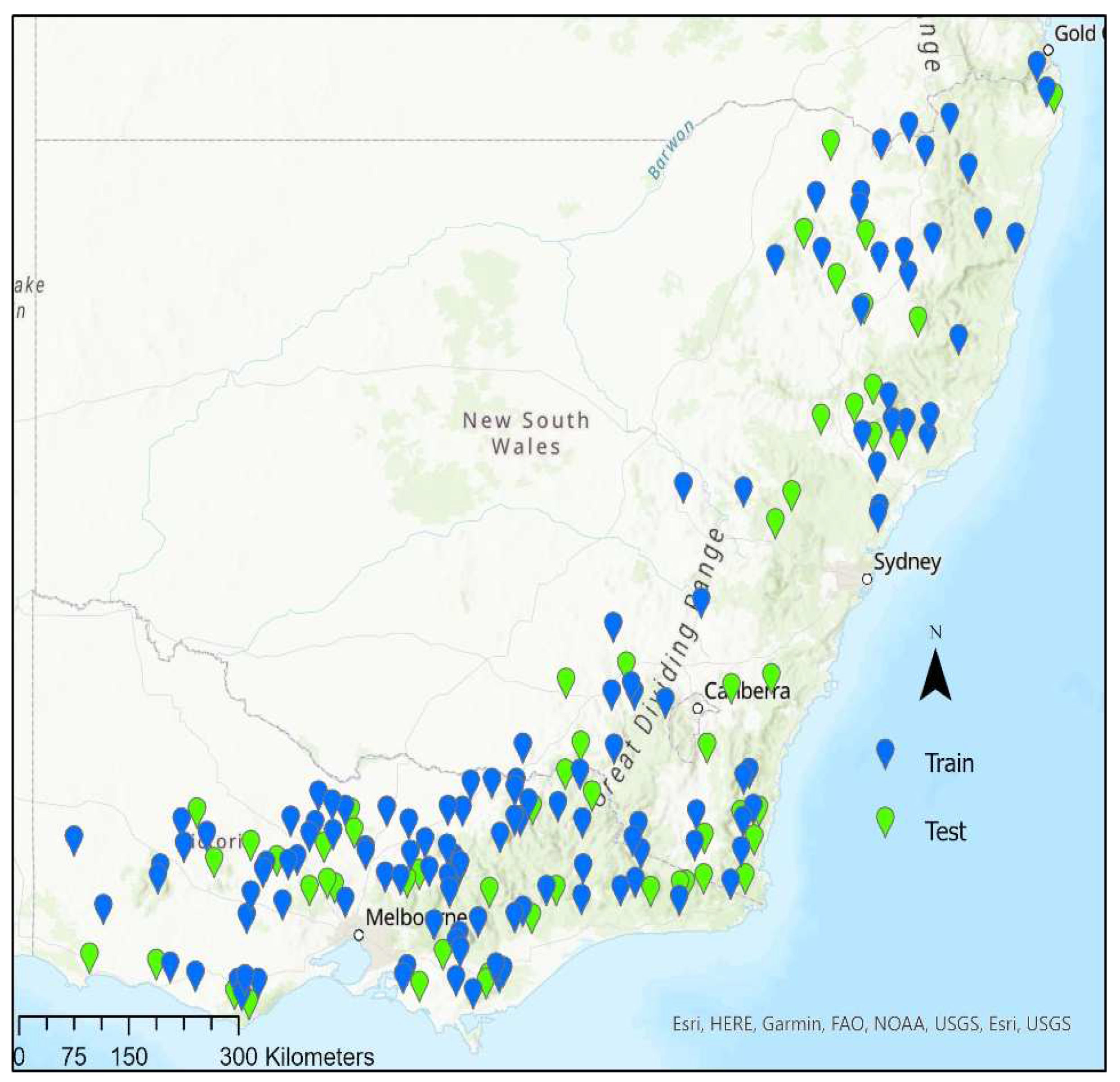
2.1. Study Area
2.1.1. Catchment Area (AREA)
2.1.2. Design Rainfall Intensity (I62)
2.1.3. Mean Annual Rainfall (MAR)
2.1.4. Shape Factor (SF)
2.1.5. Mean Annual Evapotranspiration (MAE)
2.1.6. Stream Density (SDEN)
2.1.7. S1085
2.1.8. Forest
2.2. Methodology
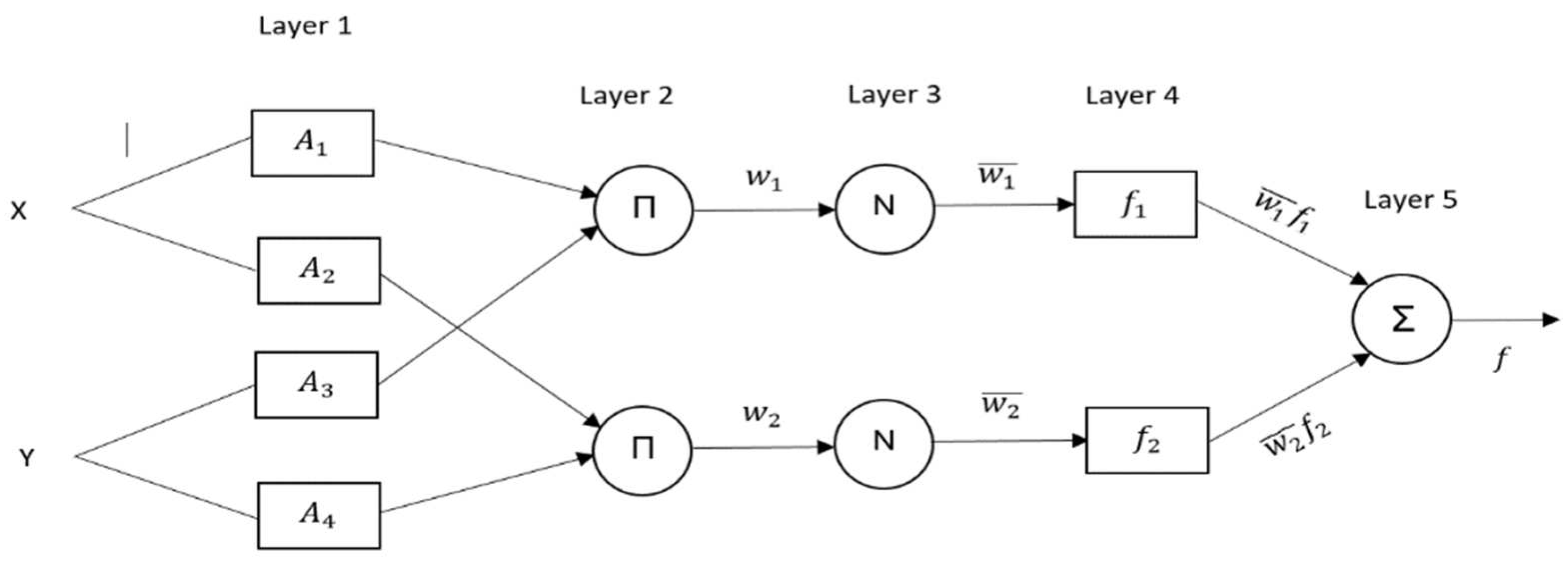
2.2.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2.2. Grid Partitioning (GP)
2.2.3. Subtractive Clustering (SC)
2.2.4. Fuzzy C-Means (FCM)
- Assuming initial locations for each cluster centre.
- Each data-point joins the cluster with the nearest cluster centre.
- New cluster centres are computed and considered the centroids of clusters.
- Terminate the process if the cluster partition is stable. If not, go to the second step.
2.2.5. Quantile Regression Technique (QRT)
2.2.6. Statistical Measures Used in Evaluation
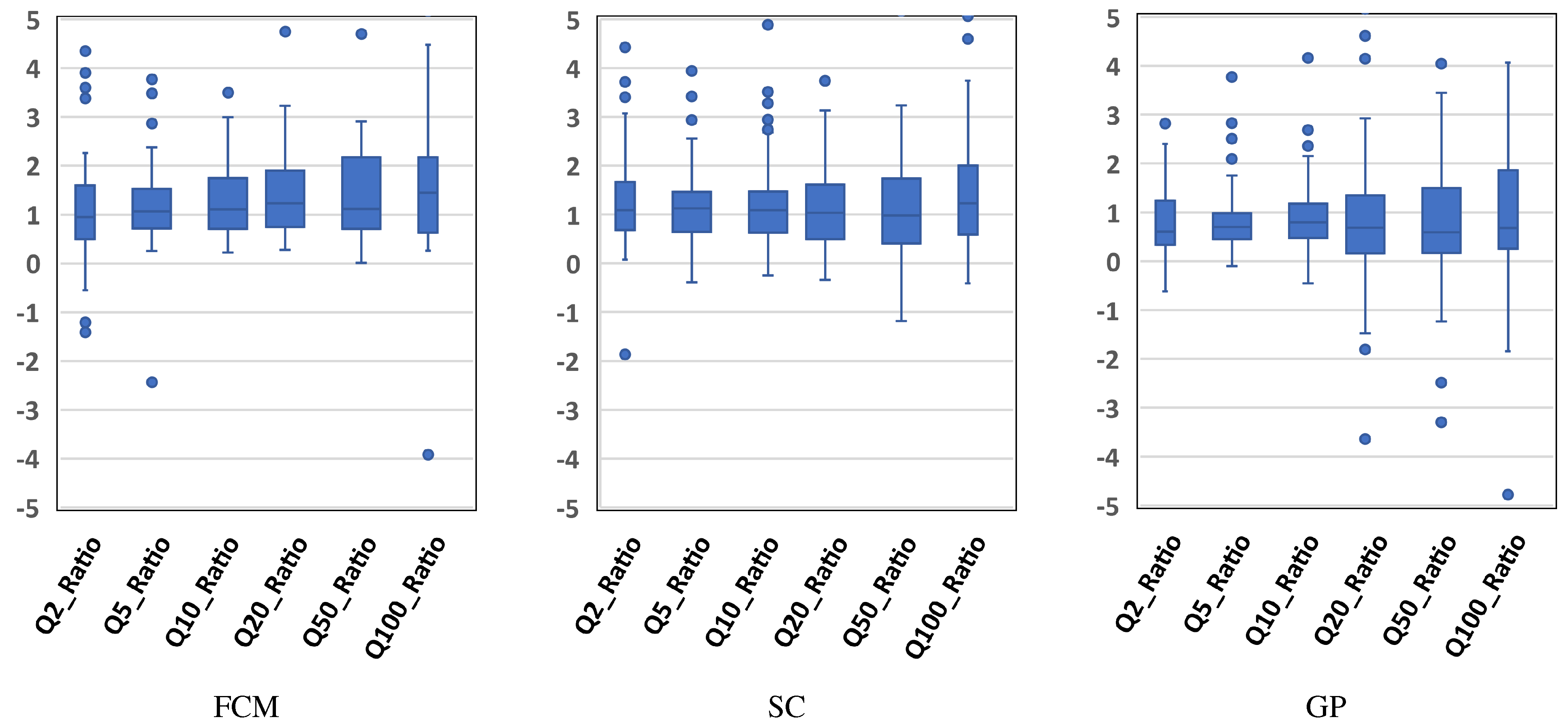
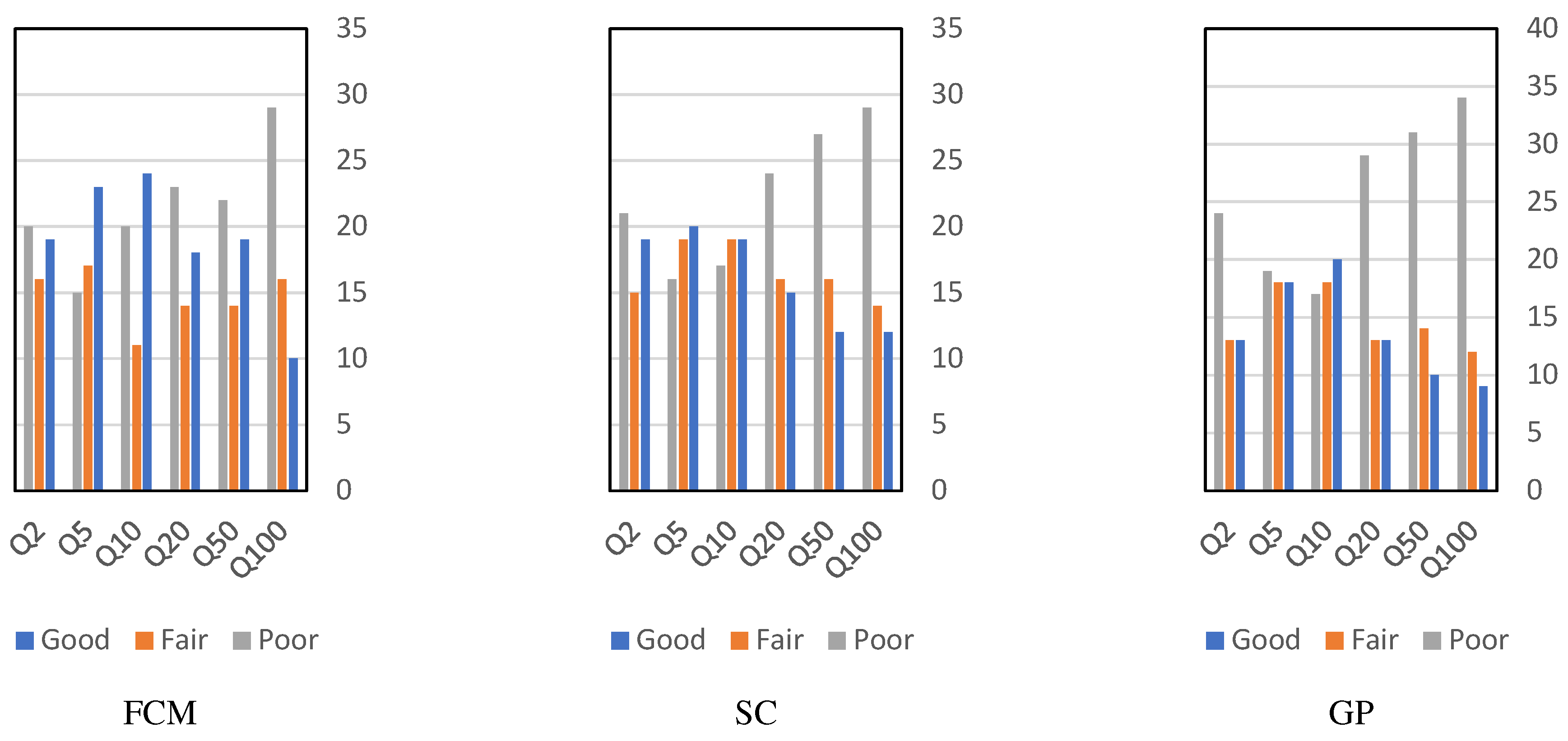
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hettiarachchi, S.; Wasko, C.; Sharma, A. Increase in Flood Risk Resulting from Climate Change in a Developed Urban Watershed—The Role of Storm Temporal Patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2041–2056. [Google Scholar] [CrossRef]
- Al-Sabhan, W.; Mulligan, M.; Blackburn, G.A. A Real-Time Hydrological Model for Flood Prediction using GIS and the WWW. Comput. Environ. Urban Syst. 2003, 27, 9–32. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional Flood Frequency Analysis in Eastern Australia: Bayesian GLS Regression-Based Methods within Fixed Region and ROI Framework–Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2012, 430, 142–161. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Ling, F. Regional Flood Frequency Analysis Method for Tasmania, Australia: A Case Study on the Comparison of Fixed Region and Region-Of-Influence Approaches. Hydrol. Sci. J. 2015, 60, 2086–2101. [Google Scholar] [CrossRef]
- Linh, N.T.T.; Ruigar, H.; Golian, S.; Bawoke, G.T.; Gupta, V.; Rahman, K.U.; Sankaran, A.; Pham, Q.B. Flood Prediction Based on Climatic Signals Using Wavelet Neural Network. Acta Geophys. 2021, 69, 1413–1426. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Nachtnebel, H.P.; Klik, A. Comparing the Index-Flood and Multiple-Regression Methods Using L-Moments. Phys. Chem. Earth Parts A/B/C 2011, 36, 54–60. [Google Scholar] [CrossRef]
- Rahman, A. Flood Estimation for Ungauged Catchments: A Regional Approach Using Flood and Catchment Characteristics. Ph.D. Thesis, Department of Civil Engineering, Monash University, Melbourne, Australia, 1997. [Google Scholar]
- Rahman, A. A Quantile Regression Technique to Estimate Design Floods for Ungauged Catchments in South-East Australia. Australas. J. Water Resour. 2005, 9, 81–89. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, E. Regional Flood Methods. In Australian Rainfall and Runoff: A Guide to Flood Estimation. Book 3, Peak Flow Estimation; Geoscience Australia: Canberra, Australia, 2019; pp. 105–146. [Google Scholar]
- Sahoo, A.; Samantaray, S.; Paul, S. Efficacy of ANFIS-GOA Technique in Flood Prediction: A Case Study of Mahanadi River Basin in India. H2Open J. 2021, 4, 137–156. [Google Scholar] [CrossRef]
- Wang, R.-Q. Chapter 13—Artificial Intelligence for Flood Observation. In Earth Observation for Flood Applications; Schumann, G.J.-P., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 295–304. [Google Scholar]
- Stedinger, J.R.; Lu, L.-H. Appraisal of Regional and Index Flood Quantile Estimators. Stoch. Hydrol. Hydraul. 1995, 9, 49–75. [Google Scholar] [CrossRef]
- Vafakhah, M.; Loor, S.M.H.; Pourghasemi, H.; Katebikord, A. Comparing Performance of Random Forest and Adaptive Neuro-Fuzzy Inference System Data Mining Models for Flood Susceptibility Mapping. Arab. J. Geosci. 2020, 13, 417. [Google Scholar] [CrossRef]
- Yang, L. Regional Flood Frequency Analysis for Newfoundland and Labrador Using the L-Moments Index-Flood Method. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2016. [Google Scholar]
- Zaman, M.A.; Rahman, A.; Haddad, K. Regional Flood Frequency Analysis in Arid Regions: A Case Study for Australia. J. Hydrol. 2012, 475, 74–83. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Zaman, M.; Kuczera, G.; Weinmann, P.E. Design Flood Estimation in Ungauged Catchments: A Comparison Between the Probabilistic Rational Method and Quantile Regression Technique for NSW. Australas. J. Water Resour. 2011, 14, 127–139. [Google Scholar] [CrossRef]
- Bates, B.C.; Rahman, A.; Mein, R.G.; Weinmann, P.E. Climatic and Physical Factors That Influence the Homogeneity of Regional Floods in South-Eastern Australia. Water Resour. Res. 1998, 34, 3369–3381. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual of Hydrology: Part 3. Retrieved from Flood-Frequency Analyses, Manual of Hydrology: Part 3. 1960. Available online: https://pubs.er.usgs.gov/publication/wsp1543A (accessed on 6 April 2022).
- Formetta, G.; Prosdocimi, I.; Stewart, E.; Bell, V. Estimating the Index Flood with Continuous Hydrological Models: An Application in Great Britain. Water Policy 2018, 49, 123–133. [Google Scholar] [CrossRef]
- Ishak, E.; Haddad, K.; Zaman, M.; Rahman, A. Scaling Property of Regional Floods in New South Wales Australia. Nat. Hazards 2011, 58, 1155–1167. [Google Scholar] [CrossRef]
- Kalai, C.; Mondal, A.; Griffin, A.; Stewart, E. Comparison of Nonstationary Regional Flood Frequency Analysis Techniques Based on the Index-Flood Approach. J. Hydrol. Eng. 2020, 25, 06020003. [Google Scholar] [CrossRef]
- Strnad, F.; Moravec, V.; Markonis, Y.; Máca, P.; Masner, J.; Stočes, M.; Hanel, M. An Index-Flood Statistical Model for Hydrological Drought Assessment. Water 2020, 12, 1213. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Palmer, R. Regional Flood Frequency Analysis Using Spatial Proximity and Basin Characteristics: Quantile Regression vs. Parameter Regression Technique. J. Hydrol. 2016, 540, 515–526. [Google Scholar] [CrossRef]
- Formetta, G.; Over, T.; Stewart, E. Assessment of Peak Flow Scaling and Its Effect on Flood Quantile Estimation in the United Kingdom. Water Resour. Res. 2021, 57, 1–21. [Google Scholar] [CrossRef]
- Rahman, A.S.; Khan, Z.; Rahman, A. Application of Independent Component Analysis in Regional Flood Frequency Analysis: Comparison between Quantile Regression and Parameter Regression Techniques. J. Hydrol. 2020, 581, 124372. [Google Scholar] [CrossRef]
- Thomas, D.M.; Benson, M.A. Generalization of Streamflow Characteristics from Drainage-Basin Characteristics; US Government Printing Office: Washington, DC, USA, 1970. [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Zahiri, A. Neuro-Fuzzy GMDH-Based Evolutionary Algorithms to Predict Flow Discharge in Straight Compound Channels. J. Hydrol. Eng. 2015, 20, 04015035. [Google Scholar] [CrossRef]
- Aziz, K.; Haque, M.M.; Rahman, A.; Shamseldin, A.Y.; Shoaib, M. Flood Estimation in Ungauged Catchments: Application of Artificial Intelligence Based Methods for Eastern Australia. Stoch. Hydrol. Hydraul. 2017, 31, 1499–1514. [Google Scholar] [CrossRef]
- Kordrostami, S.; Alim, M.A.; Karim, F.; Rahman, A. Regional Flood Frequency Analysis Using an Artificial Neural Network Model. Geosciences 2020, 10, 127. [Google Scholar] [CrossRef]
- Jajarmizadeh, M.; Lafdani, E.K.; Harun, S.; Ahmadi, A. Application of SVM and SWAT Models for Monthly Streamflow Prediction, a Case Study in South of Iran. KSCE J. Civ. Eng. 2014, 19, 345–357. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad-Shahidi, A.; Lim, S.Y. Scour Prediction in Long Contractions using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Allahbakhshian-Farsani, P.; Vafakhah, M.; Khosravi-Farsani, H.; Hertig, E. Regional Flood Frequency Analysis Through Some Machine Learning Models in Semi-arid Regions. Water Resour. Manag. 2020, 34, 2887–2909. [Google Scholar] [CrossRef]
- Bozchaloei, S.K.; Vafakhah, M. Regional Analysis of Flow Duration Curves Using Adaptive Neuro-Fuzzy Inference System. J. Hydrol. Eng. 2015, 20, 06015008. [Google Scholar] [CrossRef]
- Riahi-Madvar, H.; Dehghani, M.; Memarzadeh, R.; Gharabaghi, B. Short to Long-Term Forecasting of River Flows by Heuristic Optimization Algorithms Hybridized with ANFIS. Water Resour. Manag. 2021, 35, 1149–1166. [Google Scholar] [CrossRef]
- Garmdareh, E.S.; Vafakhah, M.; Eslamian, S.S. Regional Flood Frequency Analysis Using Support Vector Regression in Arid and Semi-arid Regions of Iran. Hydrol. Sci. J. 2018, 63, 426–440. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Regional Flood Frequency Analysis at Ungauged Sites Using the Adaptive Neuro-Fuzzy Inference System. J. Hydrol. 2008, 349, 31–43. [Google Scholar] [CrossRef]
- Mukerji, A.; Chatterjee, C.; Raghuwanshi, N.S. Flood Forecasting using ANN, Neuro-Guzzy, and Neuro-GA Models. J. Hydrol. Eng. 2009, 14, 647–652. [Google Scholar] [CrossRef]
- Aziz, K.; Rahman, A.; Shamseldin, A.; Shoaib, M. Co-Active Neuro Fuzzy Inference System for Regional Flood Estimation in Australia. J. Hydrol. Environ. Res. 2013, 1, 11–20. [Google Scholar]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D.; Cecilia, J.M. Estimation of Instantaneous Peak Flow Using Machine-Learning Models and Empirical Formula in Peninsular Spain. Water 2017, 9, 347. [Google Scholar] [CrossRef]
- Adikari, K.E.; Shrestha, S.; Ratnayake, D.T.; Budhathoki, A.; Mohanasundaram, S.; Dailey, M.N. Evaluation of Artificial Intelligence Models for Flood and Drought Forecasting in Arid and Tropical Regions. Environ. Model. Softw. 2021, 144, 105136. [Google Scholar] [CrossRef]
- Dawson, C.; Wilby, R. An Artificial Neural Network Approach to Rainfall-Runoff Modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Kuczera, G.; Franks, S. At-Site Flood Frequency Analysis. In Australian Rainfall and Runoff: A Guide to Flood Estimation. Book 3, Peak Flow Estimation; Geoscience Australia: Canberra, Australia, 2019; pp. 5–105. [Google Scholar]
- Anderson, H.W. Relating Sediment Yield to Watershed Variables. Trans. Am. Geophys. Union 1957, 38, 921–924. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]
- Assilian, S.; Mamdani, E. A Fuzzy Logic Controller for a Dynamic Plant; Queen Mary College: London, UK, 1973. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Bastian, A. Handling the Non-linearity of a Fuzzy Logic Controller at the Transition between Rules. Fuzzy Sets Syst. 1995, 71, 369–387. [Google Scholar] [CrossRef]
- Chiu, S.L. Fuzzy Model Identification Based on Cluster Estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Chiu, S. Method and Software for Extracting Fuzzy Classification Rules by Subtractive Clustering. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The Fuzzy C-Means Clustering Algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Bezdek, J.C. Models for Pattern Recognition. In Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: Berlin, Germany, 1981; pp. 1–13. [Google Scholar]
- Nourani, V.; Komasi, M. A Geomorphology-Based ANFIS Model for Multi-Station Modeling of Rainfall–Runoff Process. J. Hydrol. 2013, 490, 41–55. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M. A Possibilistic Approach to Clustering. IEEE Trans. Fuzzy Syst. 1993, 1, 98–110. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M. The Possibilistic C-Means Algorithm: Insights and Recommendations. IEEE Trans. Fuzzy Syst. 1996, 4, 385–393. [Google Scholar] [CrossRef]
- Gizaw, M.S.; Gan, T.Y. Regional Flood Frequency Analysis using Support Vector Regression under historical and future climate. J. Hydrol. 2016, 538, 387–398. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional Flood Estimation in New South Wales Australia Using Generalized Least Squares Quantile Regression. J. Hydrol. Eng. 2011, 16, 920–925. [Google Scholar] [CrossRef]
- Rahman, A.; Rahman, A. Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water 2020, 12, 781. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Shu, C. Regional Low-Flow Frequency Analysis Using Single and Ensemble Artificial Neural Networks. Water Resour. Res. 2009, 45, 1–16. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B.M.J. Regional Hydrological Frequency Analysis at Ungauged Sites with Random Forest Regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Aziz, K.; Rai, S.; Rahman, A. Design Flood Estimation in Ungauged Catchments Using Genetic Algorithm-Based Artificial Neural Network (GAANN) Technique for Australia. Nat. Hazards 2015, 77, 805–821. [Google Scholar] [CrossRef]
- Saberi-Movahed, F.; Najafzadeh, M.; Mehrpooya, A. Receiving More Accurate Predictions for Longitudinal Dispersion Coefficients in Water Pipelines: Training Group Method of Data Handling Using Extreme Learning Machine Conceptions. Water Resour. Manag. 2020, 34, 529–561. [Google Scholar] [CrossRef]




| Predictor Variable | Name of Variable | Unit | Statistical Parameter | ||
|---|---|---|---|---|---|
| Minimum | Maximum | Mean | |||
| AREA | Catchment area | km2 | 3.00 | 1010.00 | 349.06 |
| I62 | Design rainfall intensity with 6 h duration and 2 years return period | mm/h | 24.60 | 87.30 | 39.03 |
| MAR | Mean annual rainfall | mm | 484.39 | 1953.23 | 970.50 |
| SF | Shape factor | - | 0.25 | 1.62 | 0.78 |
| MAE | Mean annual evapo-transpiration | mm | 925.90 | 1543.30 | 1112.74 |
| SDEN | Stream density | km−1 | 0.51 | 5.47 | 2.06 |
| S1085 | Slope of central 75% of the mainstream | m/km | 0.80 | 69.90 | 13.02 |
| FOREST | Fraction forest | - | 0.00 | 1.00 | 0.55 |
| nCluster_FCM | Rad_SC | MF-Type and mf_n_GP | |
|---|---|---|---|
| Q2 | 8 | 0.76 | Trimf-2 |
| Q5 | 2 | 0.39 | Trimf-2 |
| Q10 | 5 | 0.37 | Trimf-2 |
| Q20 | 3 | 0.77 | Gauss2mf-5 |
| Q50 | 2 | 0.78 | Gauss2mf-5 |
| Q100 | 3 | 0.79 | Trimf-2 |
| Q2 | Q5 | Q10 | Q20 | Q50 | Q100 |
|---|---|---|---|---|---|
| Trimf-2 | Trimf-2 | Trimf-2 | Gauss2mf-5 | Gauss2mf-5 | Trimf-2 |
| Gauss2mf-5 | Trapmf-2 | Pimf-2 | Dsigmf-5 | Dsigmf-5 | Gauss2mf-5 |
| dsigmf-5 | Pimf-2 | Trapmf-2 | Trapmf-5 | Trapmf-5 | Trapmf-5 |
| Trapmf-5 | Gaussmf-2 | Dsigmf-2 | Trimf-2 | Gauss2mf-2 | Dsigmf-5 |
| Gbellmf-5 | Gbellmf-2 | Gauss2mf-2 | Gaussmf-2 | Trimf-2 | Pimf-5 |
| Gaussmf-2 | Gauss2mf-2 | Gbellmf-2 | Trapmf-2 | Gbellmf-5 | Gauss2mf-4 |
| Gauss2mf-2 | Dsigmf-2 | Gaussmf-2 | Gbellmf-2 | Gaussmf-5 | Trapmf-4 |
| Quantile | Q2 | Q5 | Q10 | Q20 | Q50 | Q100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistics | QRT | FCM | QRT | FCM | QRT | FCM | QRT | FCM | QRT | FCM | QRT | FCM |
| REr | 43.10 | 51.43 | 39.10 | 38.18 | 35.58 | 39.96 | 38.88 | 46.90 | 40.01 | 53.23 | 48.12 | 59.80 |
| QT_pred/QT_obs (Median) | 0.93 | 0.95 | 0.97 | 1.07 | 0.97 | 1.11 | 1.05 | 1.23 | 1.00 | 1.11 | 1.07 | 1.45 |
| RMSE | 49.91 | 50.88 | 115.46 | 119.05 | 190.22 | 206.06 | 289.55 | 315.90 | 507.50 | 531.49 | 749.58 | 845.69 |
| RBias | 31.76 | 44.60 | 32.32 | 67.60 | 38.23 | 87.67 | 41.72 | 53.66 | 46.43 | 44.29 | 57.25 | 61.43 |
| RMSNE | 1.13 | 2.06 | 1.32 | 2.64 | 1.50 | 3.02 | 1.61 | 2.34 | 1.78 | 1.85 | 2.09 | 2.90 |
| RRMSE | 0.82 | 0.84 | 0.75 | 0.78 | 0.77 | 0.84 | 0.79 | 0.87 | 0.88 | 0.93 | 1.01 | 1.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalnezhad, A.; Rahman, A.; Vafakhah, M.; Samali, B.; Ahamed, F. Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia. Water 2022, 14, 1608. https://doi.org/10.3390/w14101608
Zalnezhad A, Rahman A, Vafakhah M, Samali B, Ahamed F. Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia. Water. 2022; 14(10):1608. https://doi.org/10.3390/w14101608
Chicago/Turabian StyleZalnezhad, Amir, Ataur Rahman, Mehdi Vafakhah, Bijan Samali, and Farhad Ahamed. 2022. "Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia" Water 14, no. 10: 1608. https://doi.org/10.3390/w14101608
APA StyleZalnezhad, A., Rahman, A., Vafakhah, M., Samali, B., & Ahamed, F. (2022). Regional Flood Frequency Analysis Using the FCM-ANFIS Algorithm: A Case Study in South-Eastern Australia. Water, 14(10), 1608. https://doi.org/10.3390/w14101608








