A Medium and Long-Term Runoff Forecast Method Based on Massive Meteorological Data and Machine Learning Algorithms
Abstract
- (1)
- This study aims to summarize and compare the applicability and accuracy of different Feature Selection methods and Ensemble Learning models in medium and long-term runoff forecast.
- (2)
- Three typical methods (Filter, Wrapper, and Embedded) based on Feature Selection are employed to obtain predictors.
- (3)
- Two representative models (Bagging and Boosting) based on Ensemble Learning to realize the forecast.
1. Introduction
2. Methodology
2.1. Feature Selection
2.2. Filter
2.3. Wrapper
2.4. Embedded
2.5. Ensemble Learning
2.6. Classification and Regression Tree
2.7. Random Forest
2.8. Extreme Gradient Boosting
3. Case Study
3.1. Study Area
3.2. Predictors
3.3. Precision Evaluation Indexes
- (1)
- Square of correlation coefficient (R2)R2 is one of the most employed criteria to evaluate model efficiency. Its range between −1 and 1 (perfect fit) and it is defined as:
- (2)
- Relative Root Mean Square Error (RRMSE)RRMSE is based on RMSE which is not suitable for comparing different magnitudes of streamflow, i.e., RRMSE which ranges from −1 and 1 shows a good performance to compare runoff sequences in different river basins. RRMSE is calculated as [60]:
- (3)
- Relative Error (RE) and Mean Absolute Percentage Error (MAPE)RE and MAPE are conventional criteria to show the results in each data point. There are given by:
- (4)
- Nash-Sutcliffe Coefficient of Efficiency (NSE)
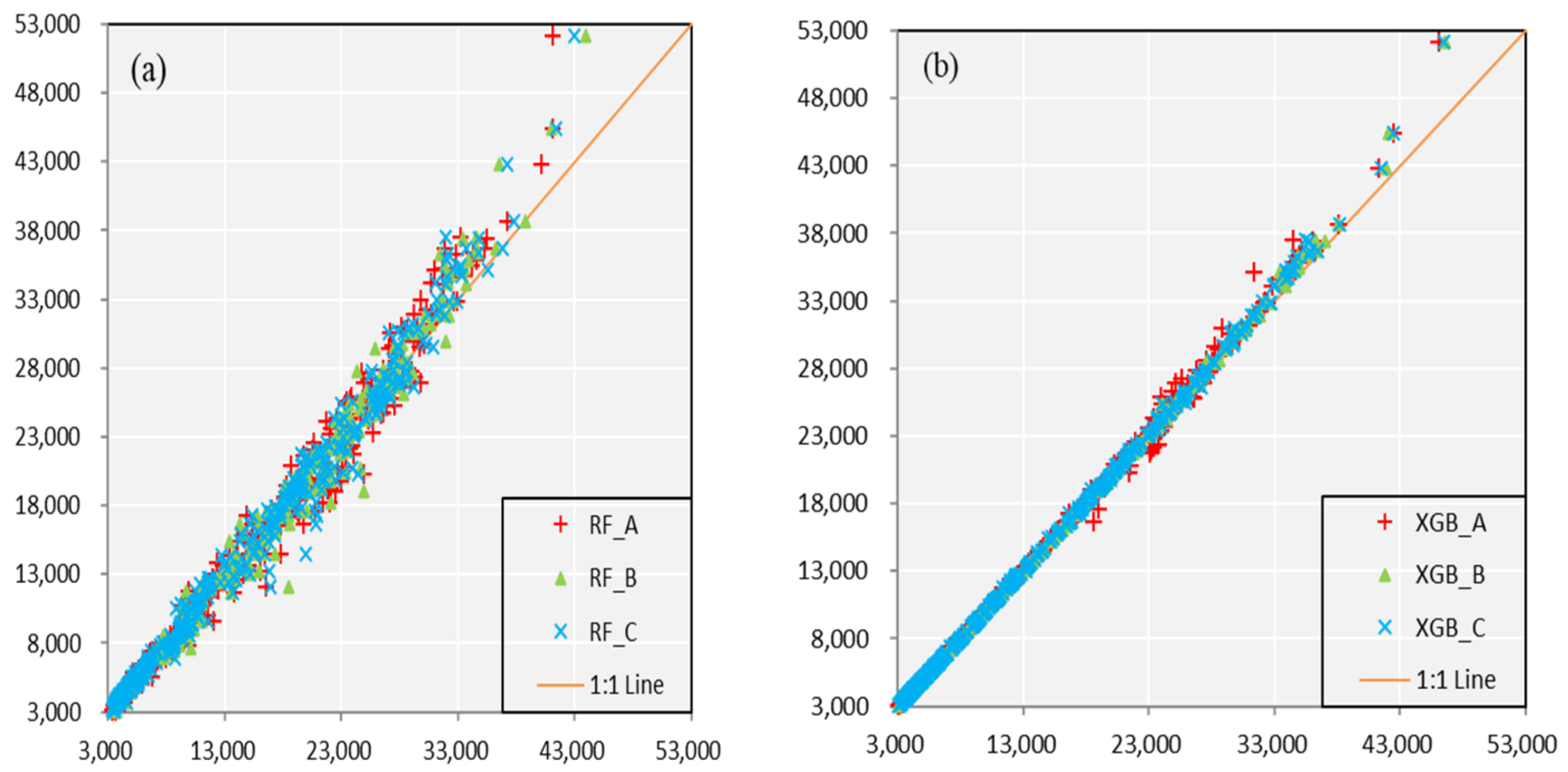
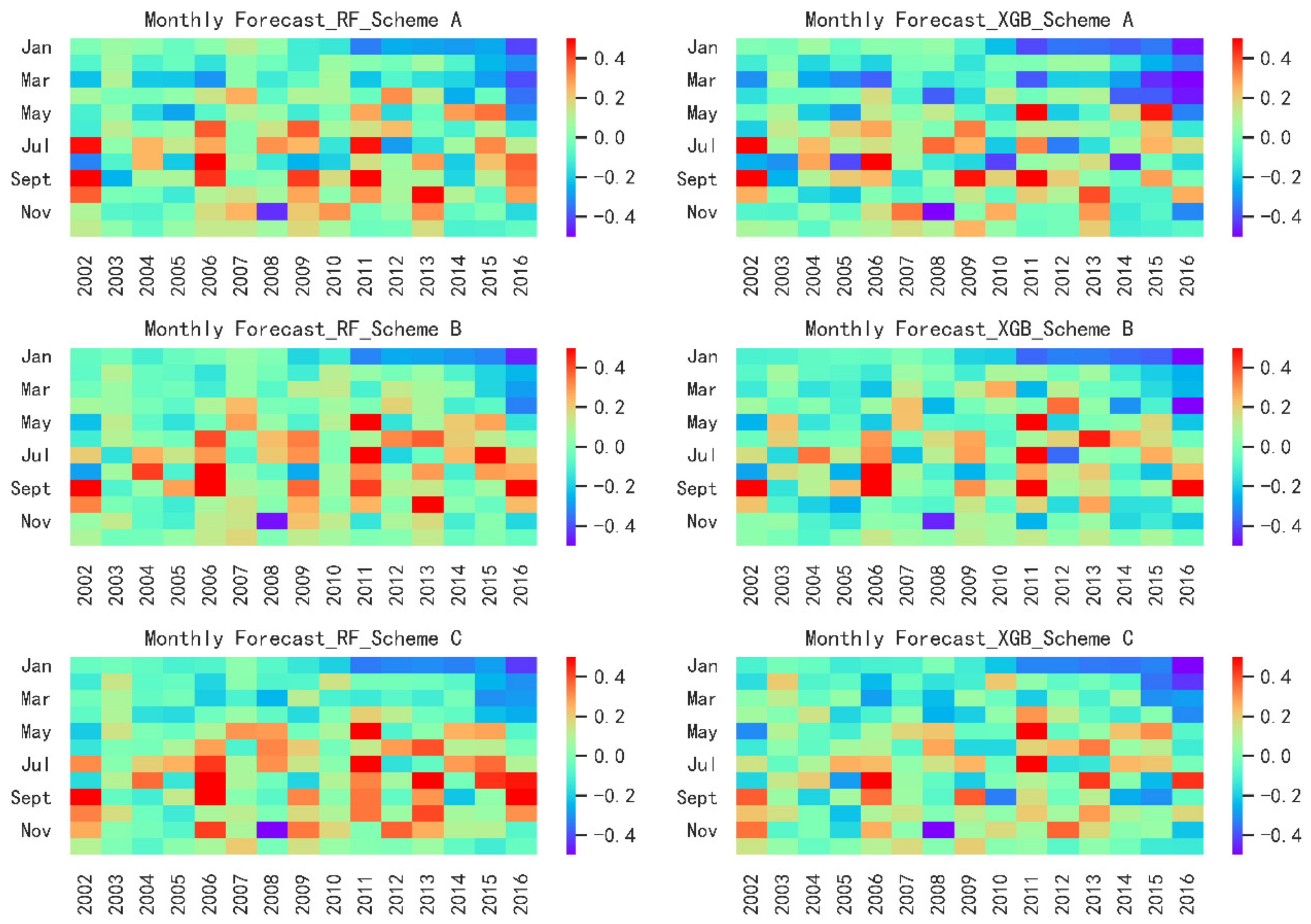
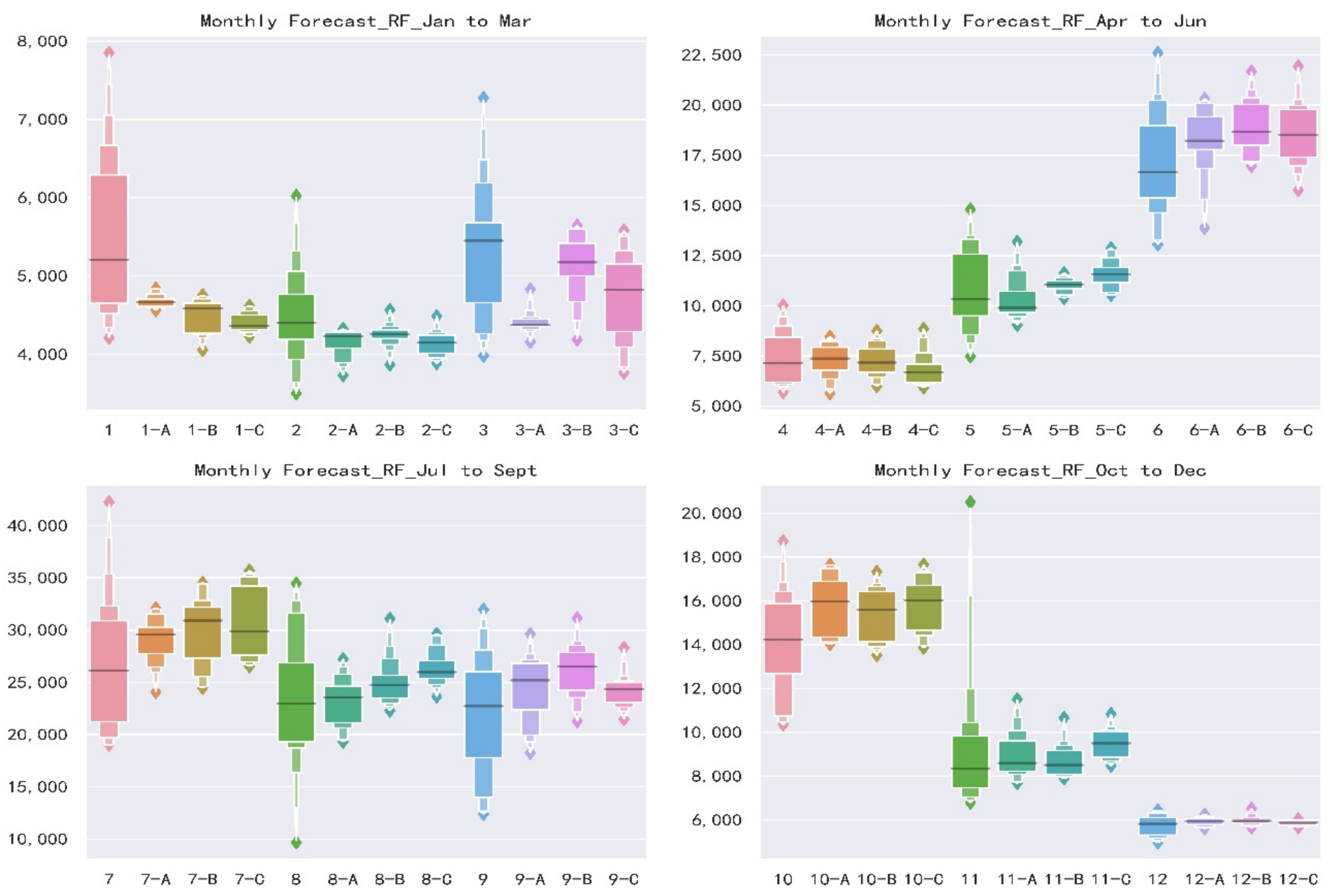
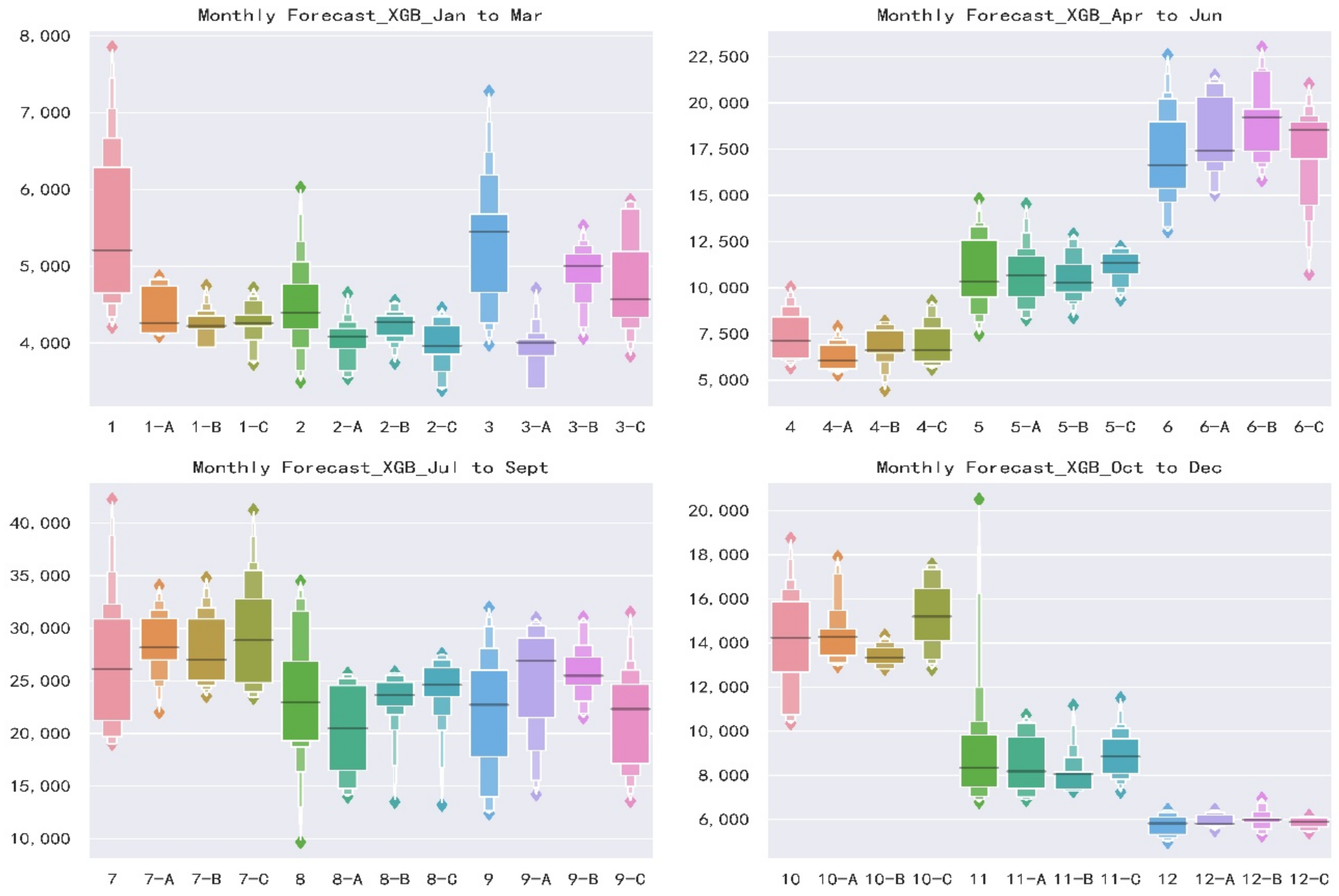
3.4. Monthly Forecast
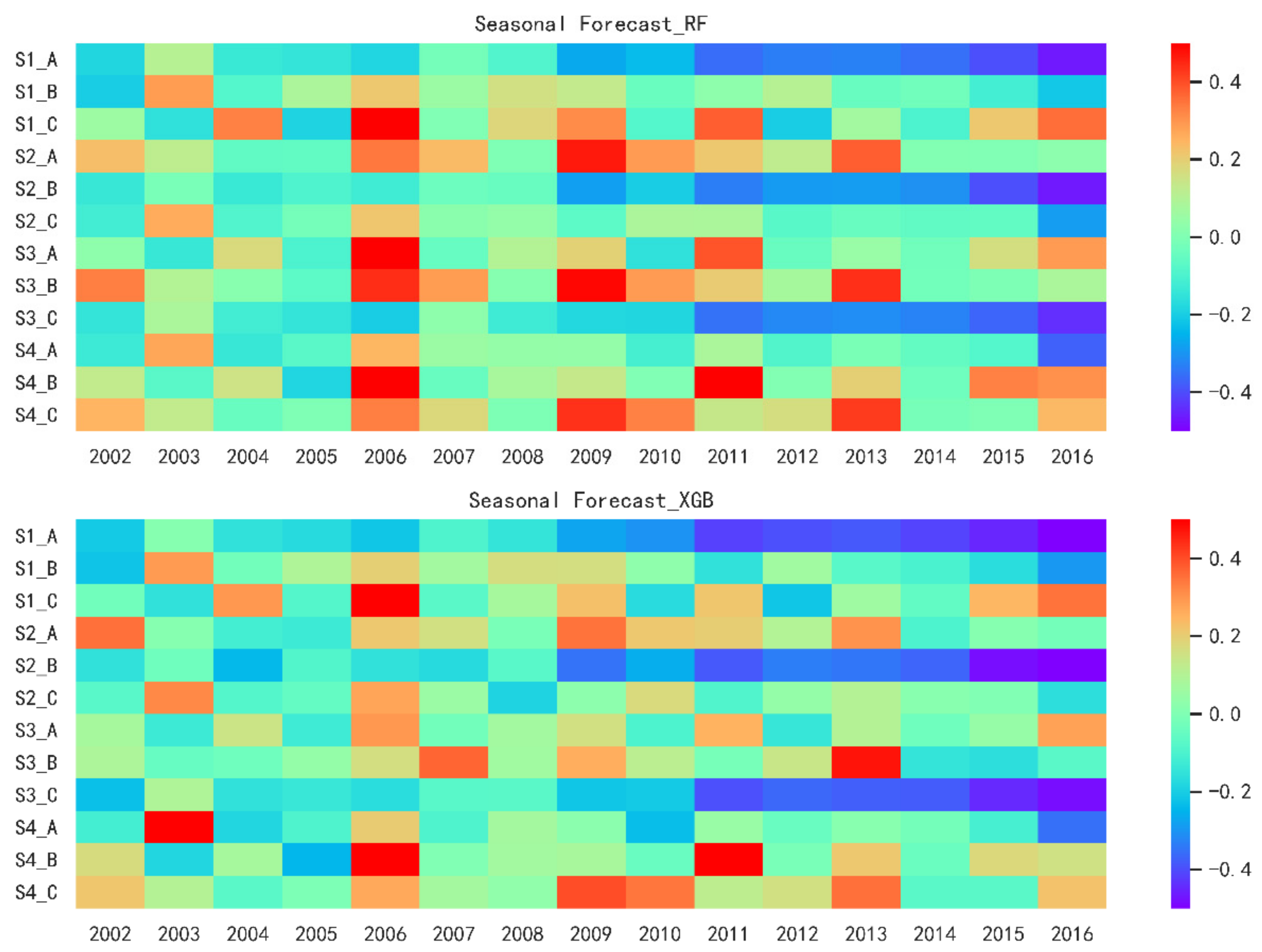
3.5. Seasonal Forecast
3.6. Annual Forecast
4. Conclusions
- (1)
- For three schemes, Scheme B shows the best forecast skills, highest accuracy and stability when comparing the same forecast lead time and models. Scheme A and Scheme C have similar results and are slightly inferior to Scheme B. It illustrates that taking the forecast performance of the learners to be used as the evaluation criterion for the FS is an effective and efficient approach.
- (2)
- For two models, XGB shows a better forecast result than RF model during the calibration period when comparing the same forecast lead time and predictors. Furthermore, in the validation period, XGB also shows a smaller forecast error if only taking Scheme B as a comparison. This is not to say that XGB is a better model than RF for two reasons. Firstly, it requires more basin data to verify whether there are differences in forecasting skill. Secondly, among some forecast factor schemes, RF displays a better performance. Therefore, the Ensemble Learning algorithms based on two different frameworks are suitable for medium and long-term runoff forecast.
- (3)
- For three different forecast lead time, it shows an interesting phenomenon. According to the most commonly used MAPE index, the annual runoff forecasting error is the smallest. MAPE is 8.34% and 7.11% in RF and XGB model, respectively, while the monthly and seasonal runoff forecast results are similar, and MAPE floats around 16%. This demonstrates that with the increase of the runoff magnitudes, the instability and non-uniformity of the distribution of the extreme value series are reduced, and the accuracy and stability of forecast are improved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennett, J.C.; Wang, Q.J.; Li, M.; Robertson, D.E.; Schepen, A. Reliable long-range ensemble streamflow forecasts: Combining calibrated climate forecasts with a conceptual runoff model and a staged error model. Water Resour. Res. 2016, 52, 8238–8259. [Google Scholar] [CrossRef]
- Bennett, J.C.; Wang, Q.J.; Robertson, D.E.; Schepen, A.; Li, M.; Michael, K. Assessment of an ensemble seasonal streamflow forecasting system for Australia. Hydrol. Earth Syst. Sci. 2017, 21, 6007–6030. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Decision Trees; Wadsworth Inc.: Belmont, CA, USA, 1984. [Google Scholar]
- Charles, S.P.; Wang, Q.J.; Ahmad, M.-U.-D.; Hashmi, D.; Schepen, A.; Podger, G.; Robertson, D.E. Seasonal streamflow forecasting in the upper Indus Basin of Pakistan: An assessment of methods. Hydrol. Earth Syst. Sci. 2018, 22, 3533–3549. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ang, J.C.; Mirzal, A.; Haron, H.; Hamed, H.N.A. Supervised, Unsupervised, and Semi-Supervised Feature Selection: A Review on Gene Selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 13, 971–989. [Google Scholar] [CrossRef] [PubMed]
- Choubin, B.; Zehtabian, G.; Azareh, A.; Rafiei-Sardooi, E.; Sajedi-Hosseini, F.; Kişi, Ö. Precipitation forecasting using classification and regression trees (CART) model: A comparative study of different approaches. Environ. Earth Sci. 2018, 77, 314. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Dai, Z.; Mei, X.; Darby, S.E.; Lou, Y.; Li, W. Fluvial sediment transfer in the Changjiang (Yangtze) river-estuary depositional system. J. Hydrol. 2018, 566, 719–734. [Google Scholar] [CrossRef]
- Erdal, H.I.; Karakurt, O. Advancing monthly streamflow forecast accuracy of CART models using ensemble learning paradigms. J. Hydrol. 2013, 477, 119–128. [Google Scholar] [CrossRef]
- Fernando, T.; Maier, H.; Dandy, G. Selection of input variables for data driven models: An average shifted histogram partial mutual information estimator approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Frederick, L.; Vanderslice, J.; Taddie, M.; Malecki, K.; Gregg, J.; Faust, N.; Johnson, W.P. Contrasting regionalgboost and national mechanisms for predicting elevated arsenic in private wells across the United States using classification and re-gression trees. Water Res. 2016, 91, 295–304. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.; Abe, N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 1612. [Google Scholar]
- Hadi, S.J.; Tombul, M. Monthly streamflow forecasting using continuous wavelet and multi-gene genetic pro-gramming combination. J. Hydrol. 2018, 561. [Google Scholar] [CrossRef]
- Han, J.; Mao, K.; Xu, T.; Guo, J.; Zuo, Z.; Gao, C. A Soil Moisture Estimation Framework Based on the CART Algo-rithm and Its Application in China. J. Hydrol. 2018, 563, 65–75. [Google Scholar] [CrossRef]
- Hofmann, H.; Wickham, H.; Kafadar, K. Letter-Value Plots: Boxplots for Large Data. J. Comput. Graph. Stat. 2017, 26, 469–477. [Google Scholar] [CrossRef]
- Hong, M.; Wang, D.; Wang, Y.; Zeng, X.; Ge, S.; Yan, H.; Singh, V.P. Mid- and long-term runoff forecasts by an improved phase-space reconstruction model. Environ. Res. 2016, 148, 560–573. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Koller, D.; Sahami, M. Toward optimal feature selection. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996. [Google Scholar]
- Liang, Z.; Li, Y.; Hu, Y.; Li, B.; Wang, J. A data-driven SVR model for long-term runoff forecast and uncertainty analysis based on the Bayesian framework. Theor. Appl. Climatol. 2017, 133, 137–149. [Google Scholar] [CrossRef]
- Liang, Z.; Tang, T.; Li, B.; Liu, T.; Wang, J.; Hu, Y. Long-term streamflow forecasting using SWAT through the in-tegration of the random forests precipitation generator: Case study of Danjiangkou Reservoir. Hydrol. Res. 2017, 49, 1513–1527. [Google Scholar] [CrossRef]
- Lin, G.-F.; Chen, L.-H. A non-linear rainfall-runoff model using radial basis function network. J. Hydrol. 2004, 289, 1–8. [Google Scholar] [CrossRef]
- Liu, H.; Setiono, R. A probabilistic approach to feature selection-a filter solution. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996. [Google Scholar]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, L.; Qin, H.; Hong, X.; Ye, J.; Yin, X. Monthly streamflow forecasting based on hidden Markov model and Gaussian Mixture Regression. J. Hydrol. 2018, 561, 146–159. [Google Scholar] [CrossRef]
- Lu, X.; Ju, Y.; Wu, L.; Fan, J.; Zhang, F.; Li, Z. Daily pan evaporation modeling from local and cross-station data using three tree-based machine learning models. J. Hydrol. 2018, 566, 668–684. [Google Scholar] [CrossRef]
- Lyu, Y.; Zheng, S.; Tan, G.; Shu, C. Effects of Three Gorges Dam operation on spatial distribution and evolution of channel thalweg in the Yichang-Chenglingji Reach of the Middle Yangtze River, China. J. Hydrol. 2018, 565, 429–442. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ng, A.Y. Feature Selection, L 1 vs. L 2 Regularization; Computer Science Department, Stanford University: Stanford, CA, USA, 2004. [Google Scholar]
- O’Neil, G.L.; Goodall, J.L.; Watson, L.T. Evaluating the potential for site-specific modification of LiDAR DEM derivatives to improve environmental planning-scale wetland identification using Random Forest classification. J. Hydrol. 2018, 559, 192–208. [Google Scholar] [CrossRef]
- Paradis, D.; Lefebvre, R.; Gloaguen, E.; Rivera, A. Predicting hydrofacies and hydraulic conductivity from direct-push data using a data-driven relevance vector machine approach: Motivations, algorithms, and application. Water Resour. Res. 2015, 51, 481–505. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; Samson, R.; Verhoest, N.E.C. Modelling groundwater-dependent vegetation patterns using ensemble learning. Hydrol. Earth Syst. Sci. 2008, 12, 603–613. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Kereszturi, G.; Yule, I. Integrating Airborne Hyperspectral, Topographic, and Soil Data for Estimating Pasture Quality Using Recursive Feature Elimination with Random Forest Regression. Remote. Sens. 2018, 10, 1117. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: Burlington, MA, USA, 1992. [Google Scholar]
- Rodriguez-Galiano, V.; Luque-Espinar, J.; Chica-Olmo, M.; Mendes, M. Feature selection approaches for predictive modelling of groundwater nitrate pollution: An evaluation of filters, embedded and wrapper methods. Sci. Total. Environ. 2018, 624, 661–672. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Schepen, A.; Zhao, T.; Wang, Q.; Zhou, S.; Feikema, P. Optimising seasonal streamflow forecast lead time for oper-ational decision making in Australia. Hydrol. Earth Syst. Sci. 2016, 20, 4117–4128. [Google Scholar] [CrossRef]
- Schick, S.; Rössler, O.; Weingartner, R. Monthly streamflow forecasting at varying spatial scales in the Rhine basin. Hydrol. Earth Syst. Sci. 2018, 22, 929–942. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 1—A strategy for system predictor identification. J. Hydrol. 2000, 239, 232–239. [Google Scholar] [CrossRef]
- Shen, K.-Q.; Ong, C.-J.; Li, X.-P.; Wilder-Smith, E.P.V. Feature selection via sensitivity analysis of SVM probabilistic outputs. Mach. Learn. 2007, 70, 1–20. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow forecast: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S.; Mohan, D. Evaluating influences of seasonal variations and anthropogenic activities on alluvial groundwater hydrochemistry using ensemble learning approaches. J. Hydrol. 2014, 511, 254–266. [Google Scholar] [CrossRef]
- Šípek, V.; Daňhelka, J. Modification of input datasets for the Ensemble Streamflow Forecast based on large-scale climatic indices and weather generator. J. Hydrol. 2015, 528, 720–733. [Google Scholar] [CrossRef]
- Sun, W.; Trevor, B. A stacking ensemble learning framework for annual river ice breakup dates. J. Hydrol. 2018, 561, 636–650. [Google Scholar] [CrossRef]
- Tang, G.; Long, D.; Behrangi, A.; Wang, C.; Hong, Y. Exploring Deep Neural Networks to Retrieve Rain and Snow in High Latitudes Using Multisensor and Reanalysis Data. Water Resour. Res. 2018, 54, 8253–8278. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J.F. An ensemble wavelet bootstrap machine learning approach to water demand forecasting: A case study in the city of Calgary, Canada. Urban Water J. 2017, 14, 185–201. [Google Scholar] [CrossRef]
- Wang, E.; Zhang, Y.; Luo, J.; Chiew, F.H.S.; Wang, Q.J. Monthly and seasonal streamflow forecasts using rain-fall-runoff modeling and historical weather data. Water Resour. Res. 2011, 47, 1296–1300. [Google Scholar] [CrossRef]
- Werbos, P.J. Applications of Advances in Nonlinear Sensitivity Analysis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 762–770. [Google Scholar]
- Woldemeskel, F.; McInerney, D.; Lerat, J.; Thyer, M.; Kavetski, D.; Shin, D.; Tuteja, N.; Kuczera, G. Evaluating post-processing approaches for monthly and seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2018, 22, 6257–6278. [Google Scholar] [CrossRef]
- Wood, A.W.; Hopson, T.; Newman, A.; Brekke, L.; Arnold, J.; Clark, M. Quantifying streamflow forecast skill elas-ticity to initial condition and climate forecast skill. J. Hydrometeorol. 2016, 17, 651–668. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Sorooshian, S.; Li, X. Simulating California reservoir operation using the classification and regres-sion-tree algorithm combined with a shuffled cross-validation scheme. Water Resour. Res. 2016, 52, 1626–1651. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Zaier, I.; Shu, C.; Ouarda, T.; Seidou, O.; Chebana, F. Estimation of ice thickness on lakes using artificial neural network ensembles. J. Hydrol. 2010, 383, 330–340. [Google Scholar] [CrossRef]
- Zhai, B.; Chen, J. Development of a stacked ensemble model for forecasting and analyzing daily average PM2.5 concentrations in Beijing, China. Sci. Total Environ. 2018, 635, 644–658. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Zhao, W.; Sánchez, N.; Lu, H.; Li, A. A spatial downscaling approach for the SMAP passive surface soil moisture product using random forest regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M. Investigating Chaos and Nonlinear Forecasting in Short Term and Mid-term River Discharge. Water Resour. Manag. 2016, 30, 1851–1865. [Google Scholar] [CrossRef]





| Scheme A | Scheme B | Scheme C |
|---|---|---|
| 5_Western Pacific Subtropical High Intensity Index | 11_Indian Ocean Basin-Wide Index | 8_Northern Hemisphere Subtropical High Ridge Position Index |
| 5_Pacific Subtropical High Intensity Index | 11_Pacific Subtropical High Area Index | 11_South China Sea Subtropical High Intensity Index |
| 11_Indian Ocean Warm Pool Strength Index | 11_Indian Ocean Warm Pool Area Index | 10_East Asian Trough Intensity Index |
| 10_Pacific Subtropical High Area Index | 10_Atlantic Meridional Mode SST Index | 11_Indian Ocean Warm Pool Area Index |
| 10_Indian Ocean Basin-Wide Index | 8_Atlantic Subtropical High Area Index | 8_South China Sea Subtropical High Ridge Position Index |
| 8_East Atlantic Pattern, EA | 10_Atlantic Multi-decadal Oscillation Index | 8_Eastern Pacific Subtropical High Northern Boundary Position Index |
| 11_Western Hemisphere Warm Pool Index | 10_Indian Ocean Basin-Wide Index | 7_Asia Polar Vortex Intensity Index |
| 10_Atlantic Multi-decadal Oscillation Index | 5_Pacific Subtropical High Intensity Index | 12_Northern Hemisphere Polar Vortex Central Intensity Index |
| 4_Western Pacific Warm Pool Strength index | 9_Pacific Subtropical High Northern Boundary Position Index | 5_Asian Zonal Circulation Index |
| 6_North Atlantic Subtropical High Intensity Index | 5_Western Pacific Subtropical High Intensity Index | 6_Antarctic Oscillation, AAO |
| RF | XGBoost | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| R2 | 0.992 | 0.993 | 0.993 | 0.999 | 0.999 | 0.999 |
| RRMSE | 0.072 | 0.068 | 0.070 | 0.019 | 0.012 | 0.013 |
| MAPE | 5.36% | 4.65% | 5.00% | 1.03% | 0.69% | 0.74% |
| NSE | 0.982 | 0.986 | 0.984 | 0.997 | 0.998 | 0.998 |
| RF | XGBoost | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| R2 | 0.924 | 0.930 | 0.926 | 0.907 | 0.923 | 0.921 |
| RRMSE | 0.226 | 0.231 | 0.258 | 0.238 | 0.211 | 0.229 |
| MAPE | 16.48% | 15.74% | 17.33% | 17.92% | 15.61% | 16.11% |
| NSE | 0.836 | 0.837 | 0.814 | 0.805 | 0.844 | 0.832 |
| RF | XGBoost | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| R2 | 0.995 | 0.996 | 0.994 | 0.998 | 0.999 | 0.998 |
| RRMSE | 0.057 | 0.053 | 0.058 | 0.026 | 0.022 | 0.025 |
| MAPE | 4.27% | 4.00% | 4.39% | 1.60% | 1.40% | 1.53% |
| NSE | 0.989 | 0.992 | 0.987 | 0.993 | 0.995 | 0.993 |
| RF | XGBoost | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| R2 | 0.921 | 0.946 | 0.923 | 0.931 | 0.940 | 0.925 |
| RRMSE | 0.238 | 0.219 | 0.251 | 0.231 | 0.209 | 0.247 |
| MAPE | 18.89% | 16.71% | 18.51% | 18.98% | 15.89% | 18.82% |
| NSE | 0.813 | 0.881 | 0.804 | 0.848 | 0.872 | 0.830 |
| RF | XGBoost | |||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| MAPE (Calibration) | 3.32% | 2.56% | 2.49% | 4.23% | 3.97% | 3.94% |
| MAPE (Validation) | 8.84% | 8.34% | 9.79% | 8.99% | 7.11% | 7.54% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wei, J.; Wang, D.; Li, B.; Huang, H.; Xu, B.; Xu, Y. A Medium and Long-Term Runoff Forecast Method Based on Massive Meteorological Data and Machine Learning Algorithms. Water 2021, 13, 1308. https://doi.org/10.3390/w13091308
Li Y, Wei J, Wang D, Li B, Huang H, Xu B, Xu Y. A Medium and Long-Term Runoff Forecast Method Based on Massive Meteorological Data and Machine Learning Algorithms. Water. 2021; 13(9):1308. https://doi.org/10.3390/w13091308
Chicago/Turabian StyleLi, Yujie, Jing Wei, Dong Wang, Bo Li, Huaping Huang, Bin Xu, and Yueping Xu. 2021. "A Medium and Long-Term Runoff Forecast Method Based on Massive Meteorological Data and Machine Learning Algorithms" Water 13, no. 9: 1308. https://doi.org/10.3390/w13091308
APA StyleLi, Y., Wei, J., Wang, D., Li, B., Huang, H., Xu, B., & Xu, Y. (2021). A Medium and Long-Term Runoff Forecast Method Based on Massive Meteorological Data and Machine Learning Algorithms. Water, 13(9), 1308. https://doi.org/10.3390/w13091308






