Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop
Abstract
1. Introduction
Necessity of the Research and Novelty
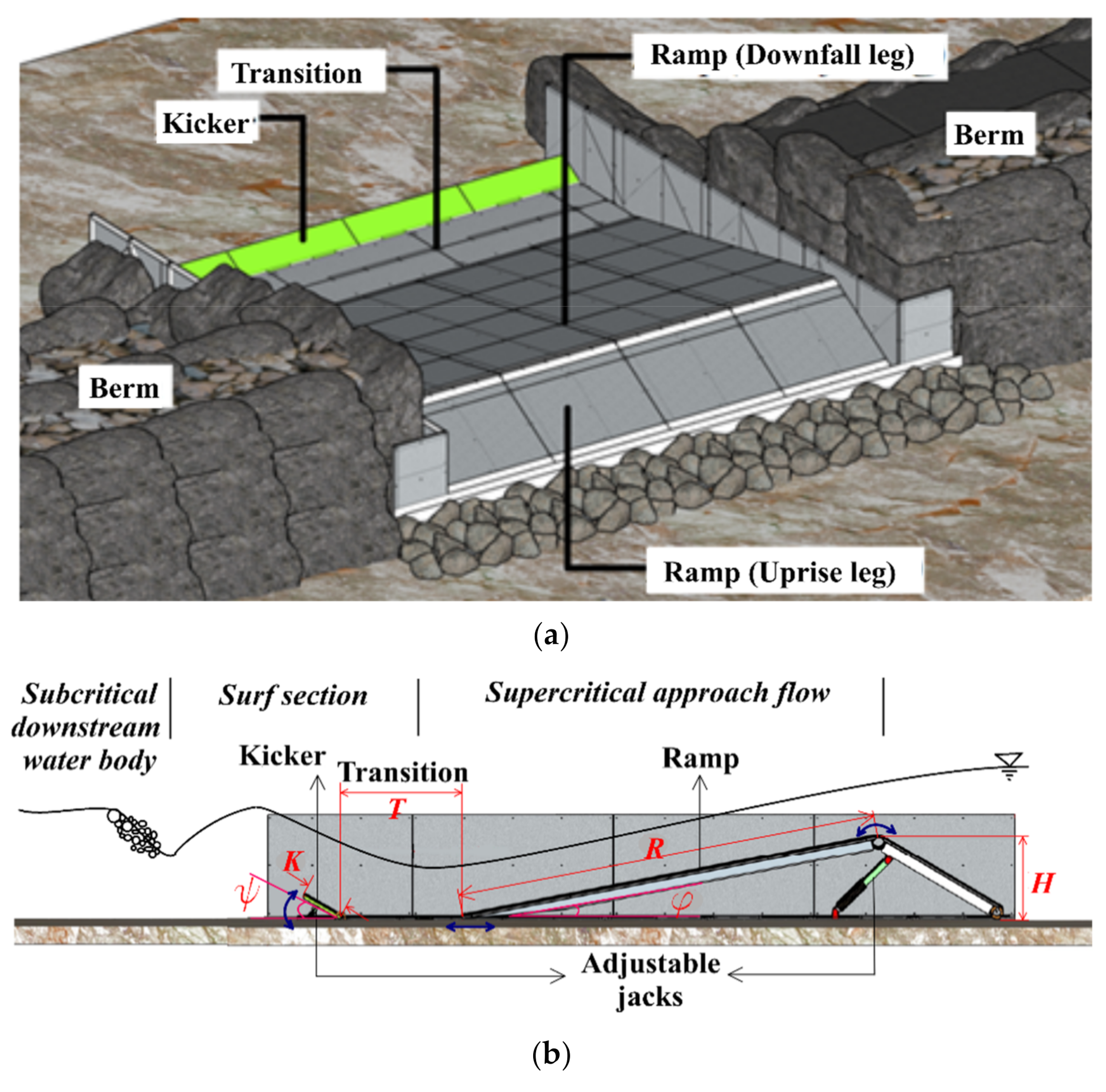
2. Methodology
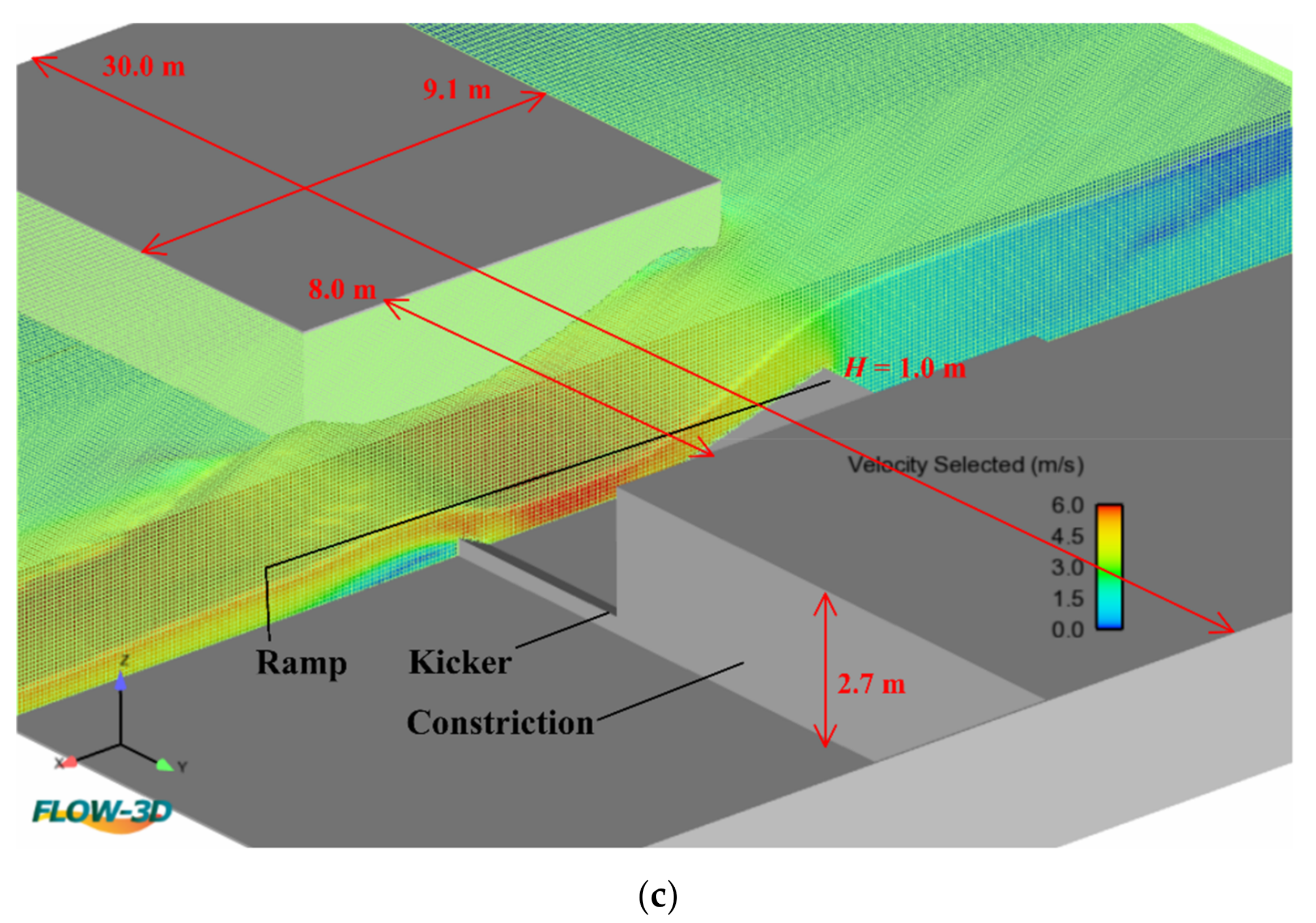
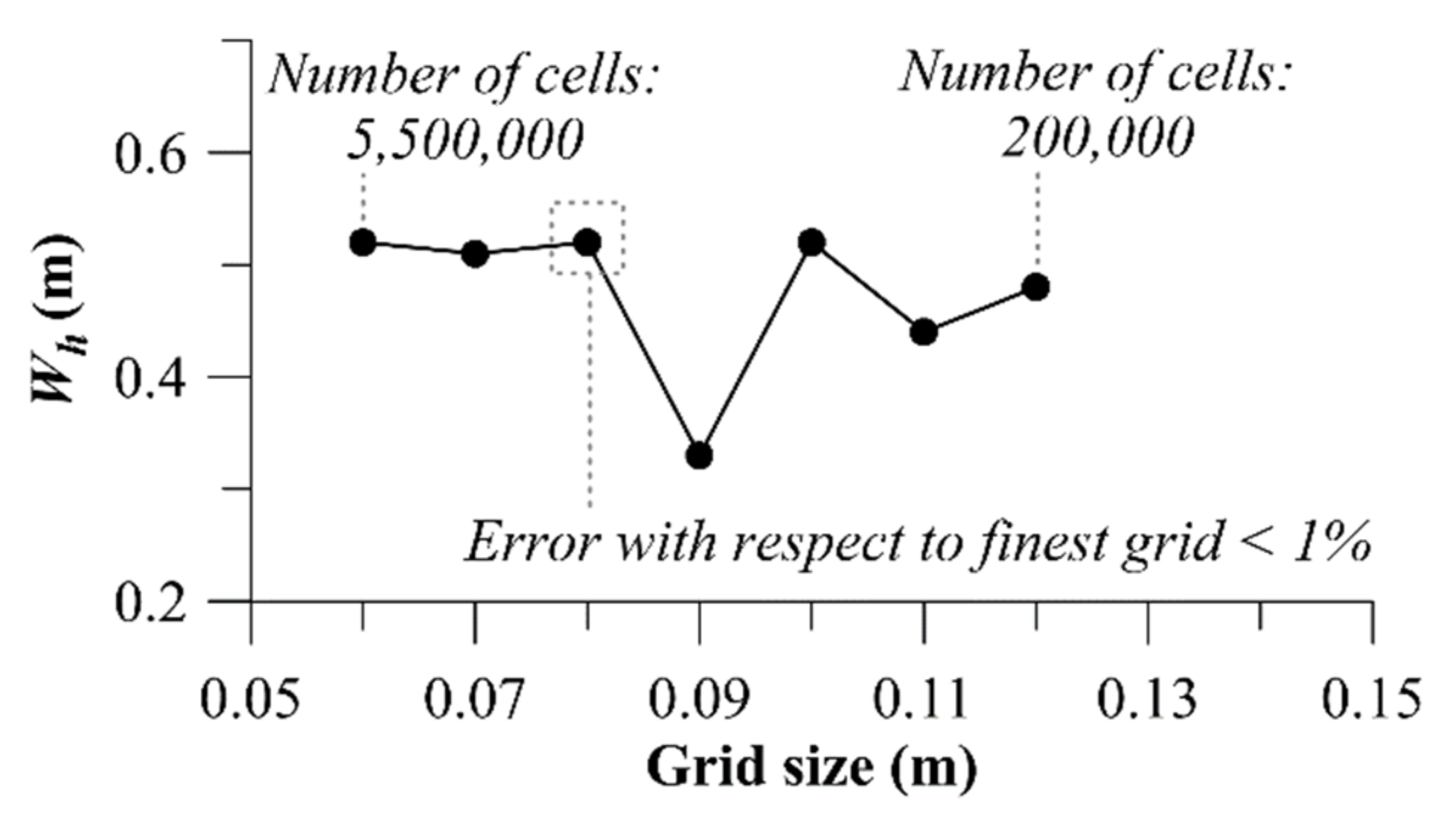
2.1. Mathematical Model and Numerical Solver
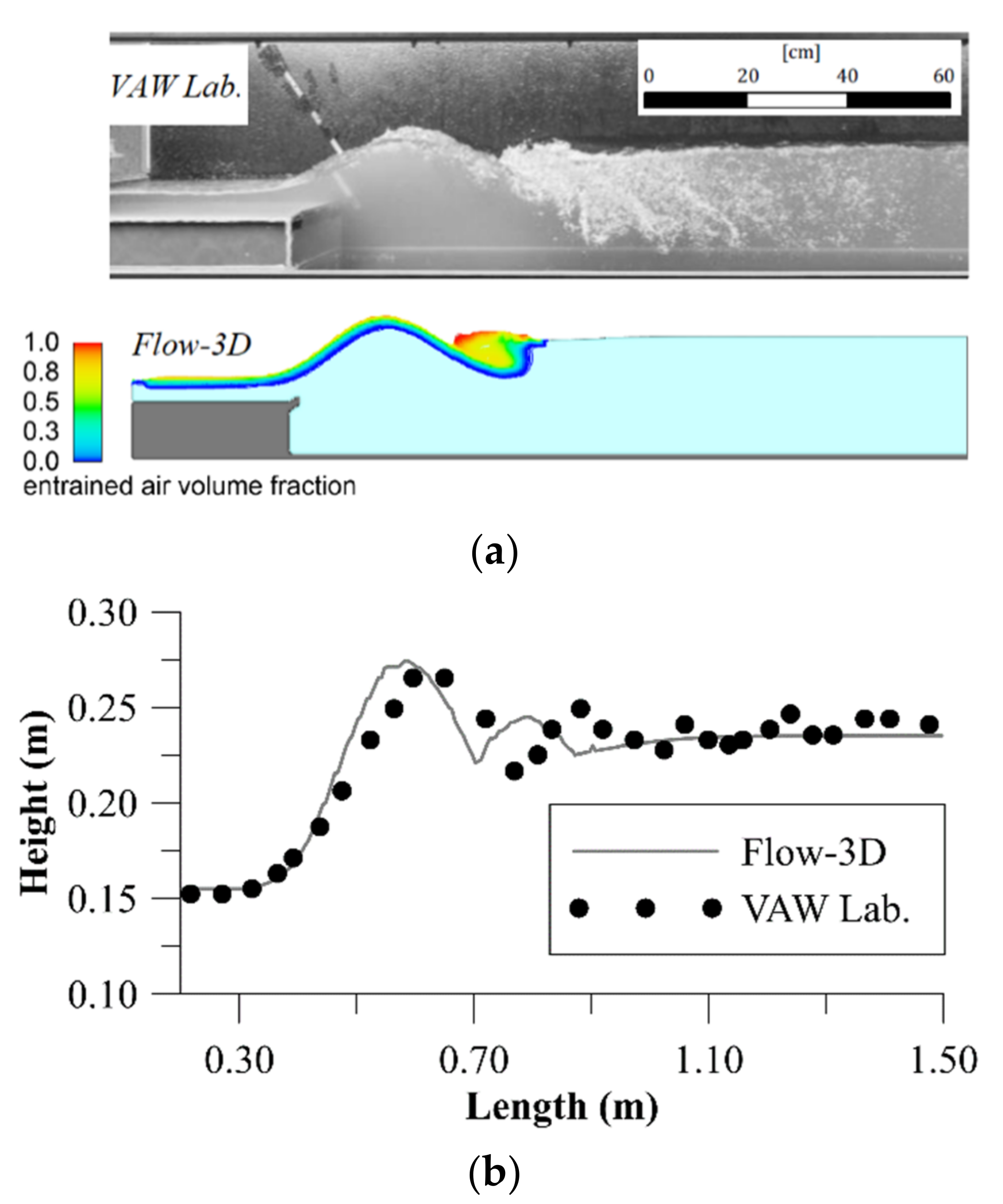
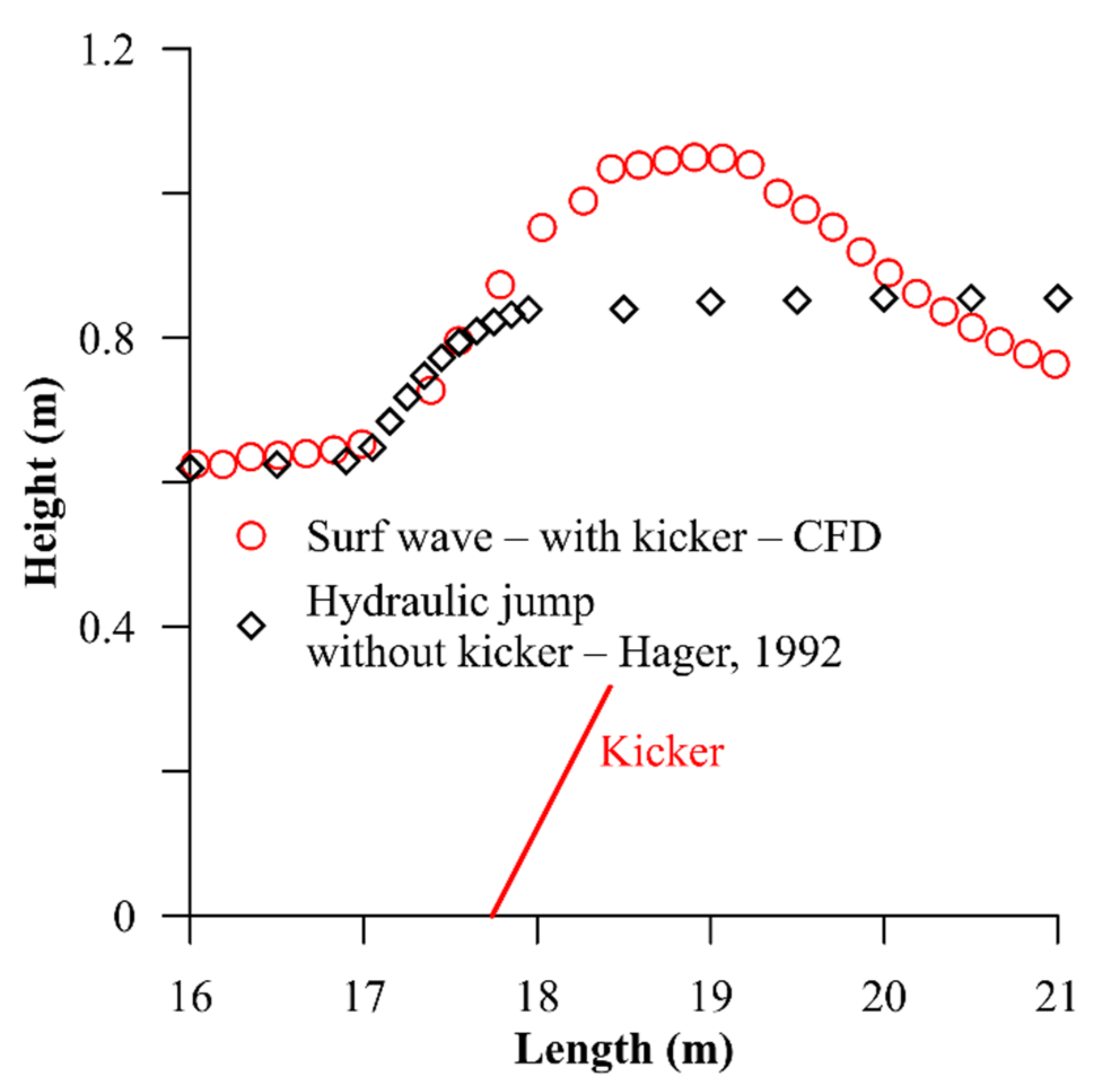
2.2. Calibration
2.3. Parametric Analysis
3. Results
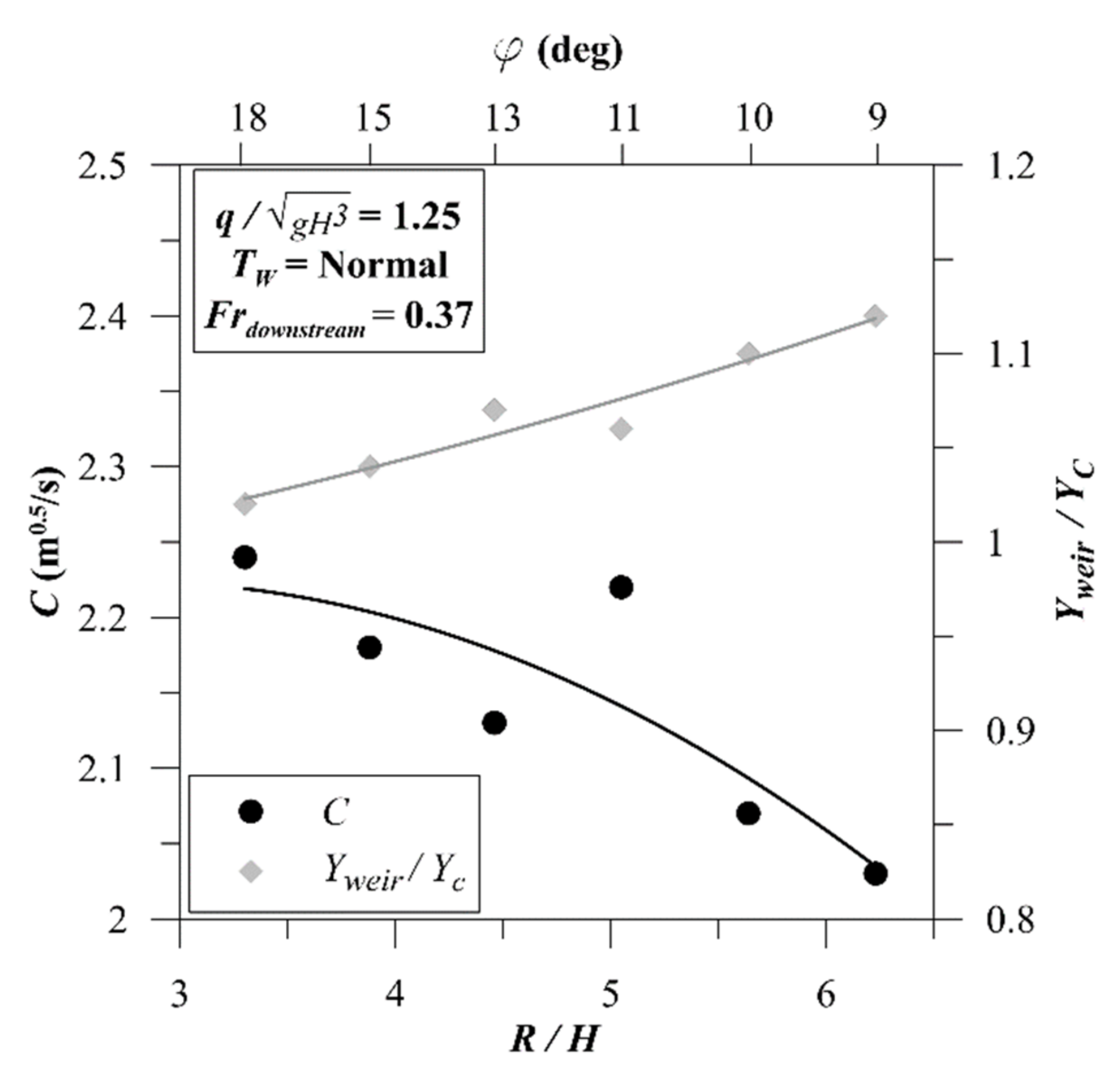
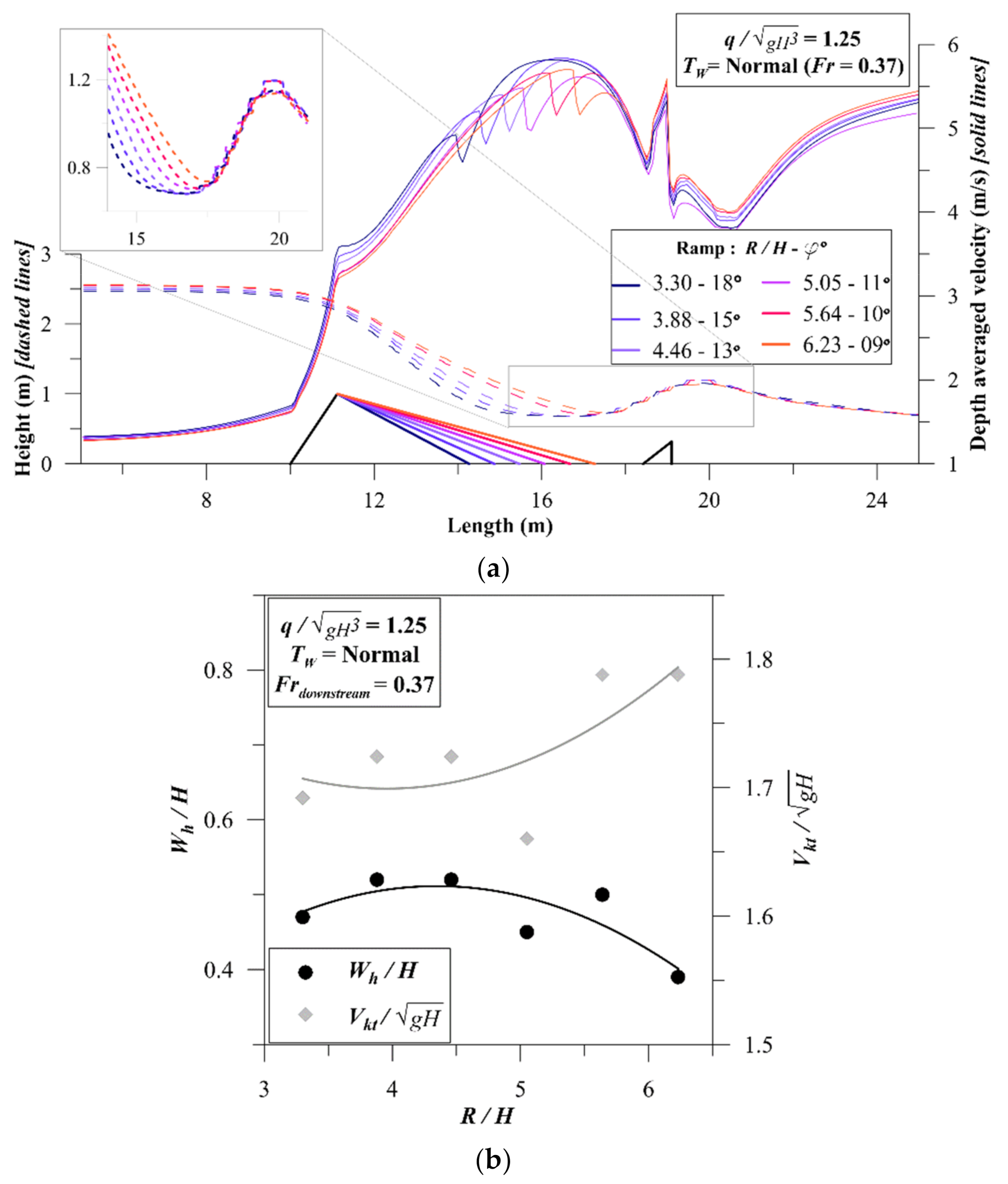
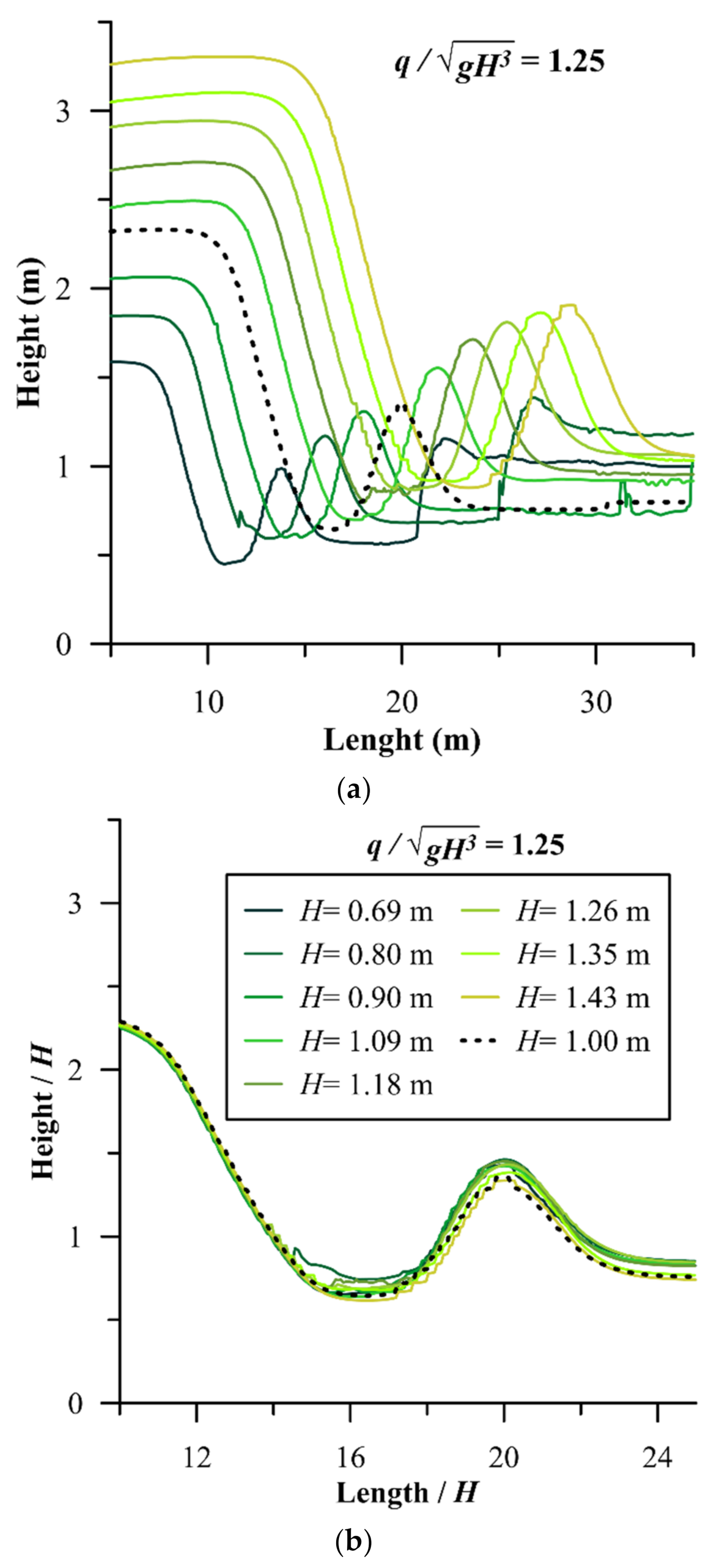
3.1. Ramp
3.2. Transition
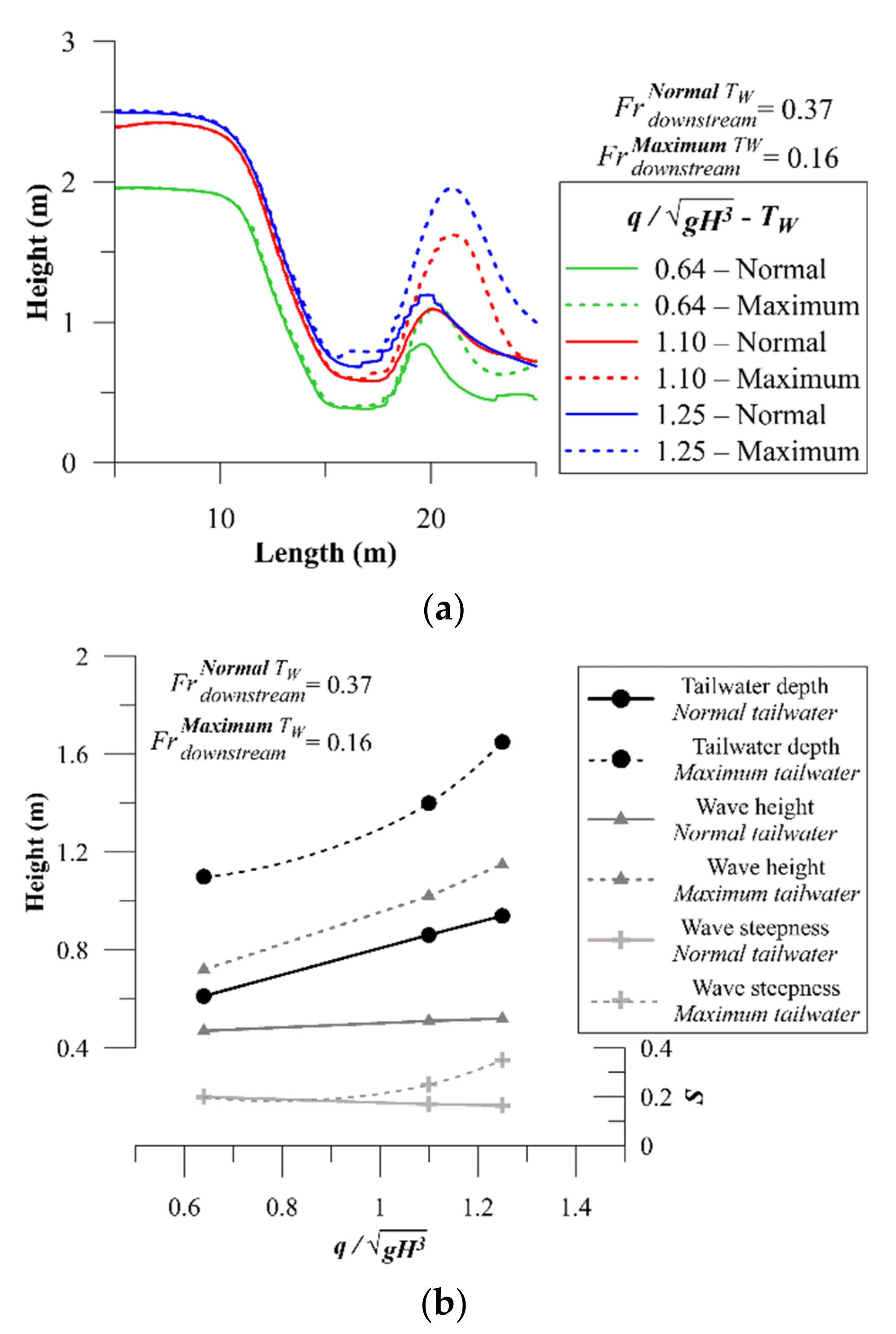
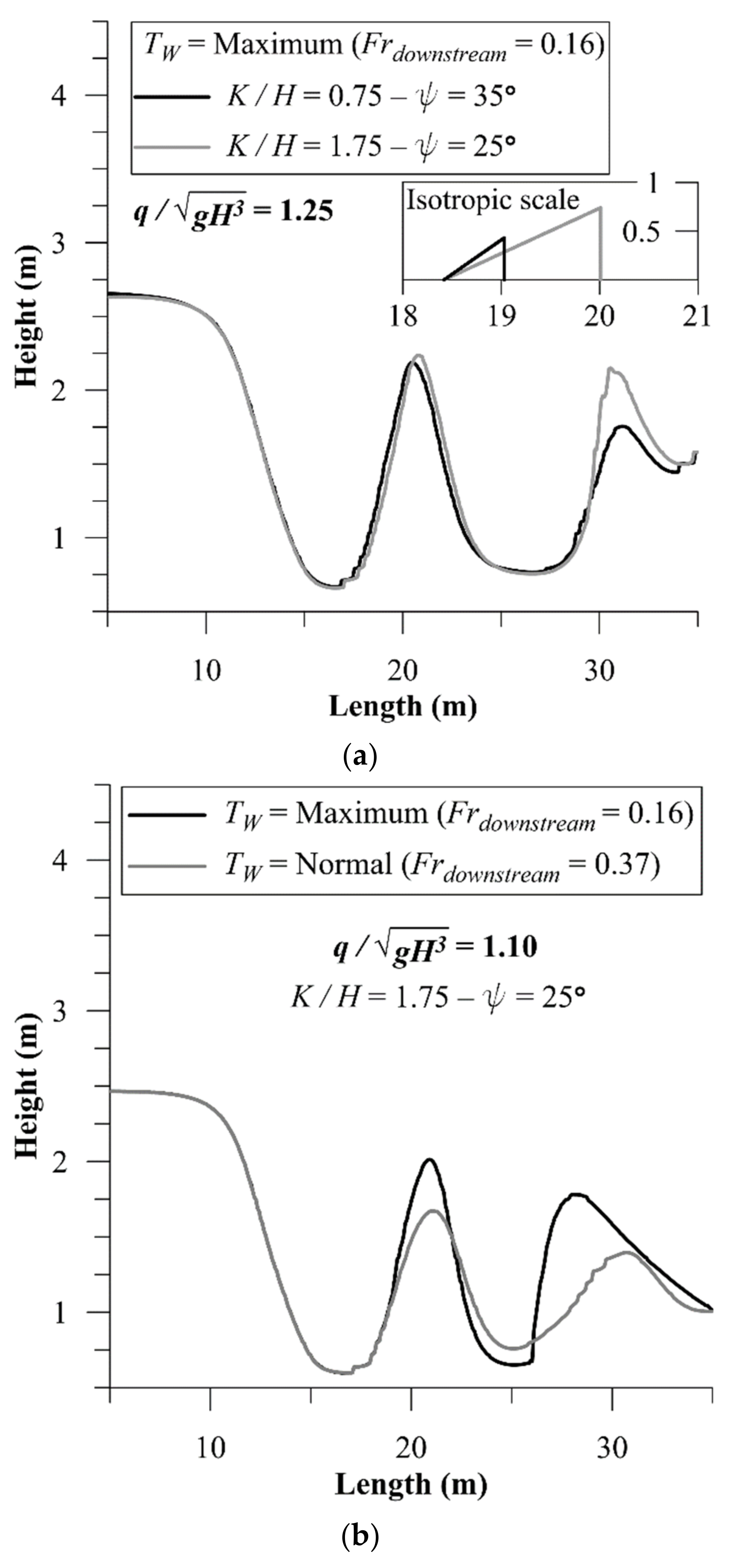
3.3. Tailwater Depth
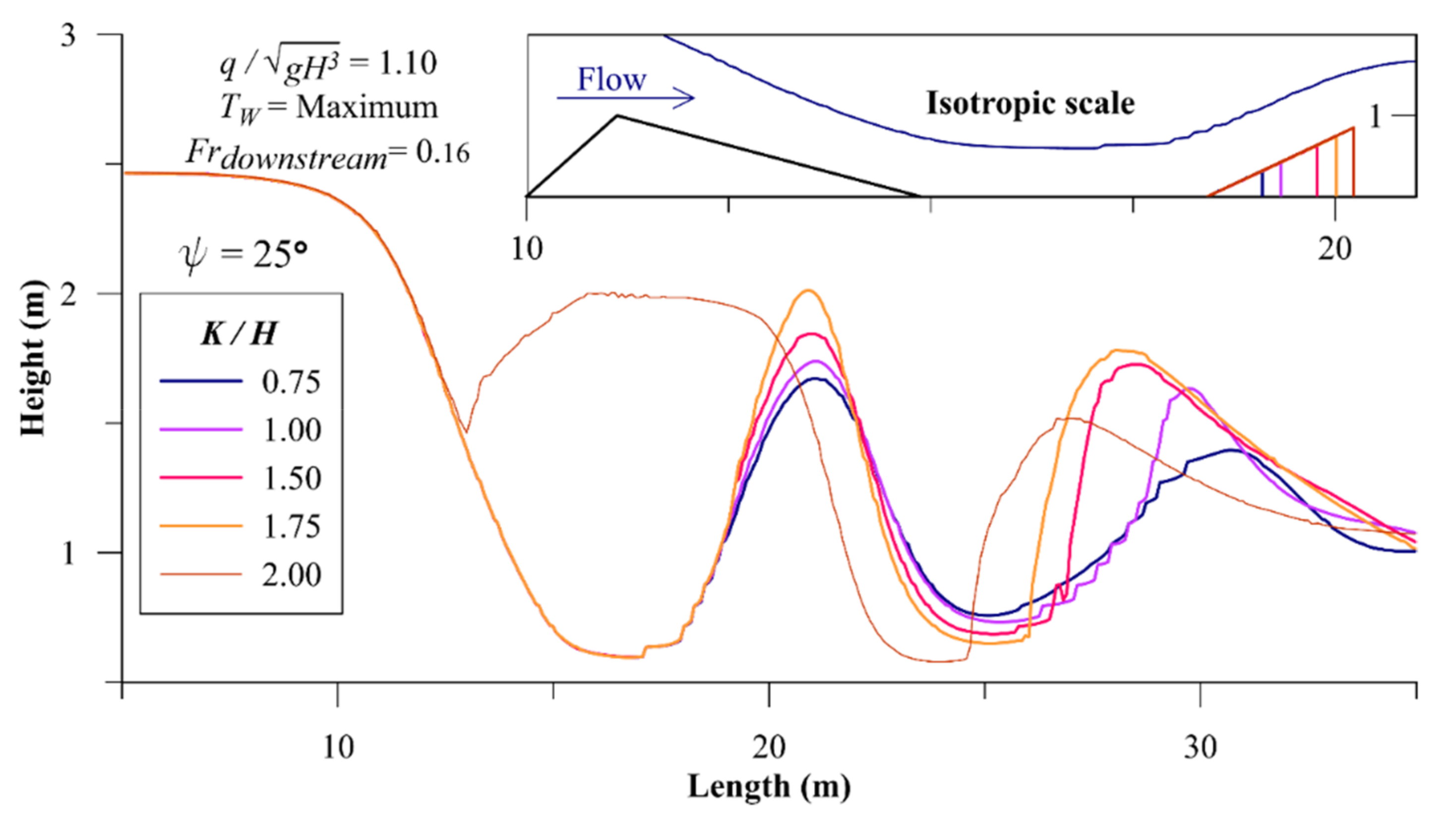
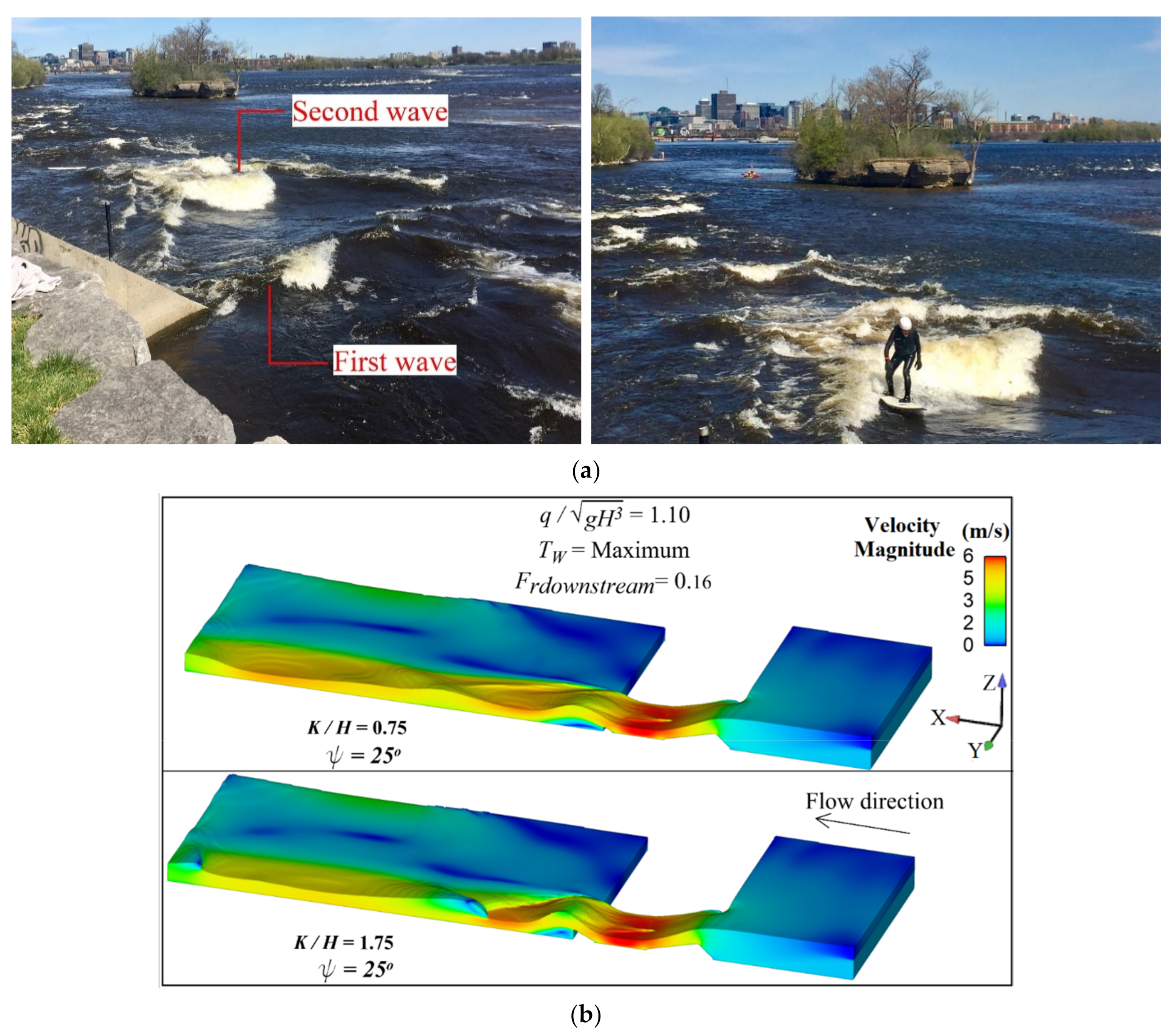
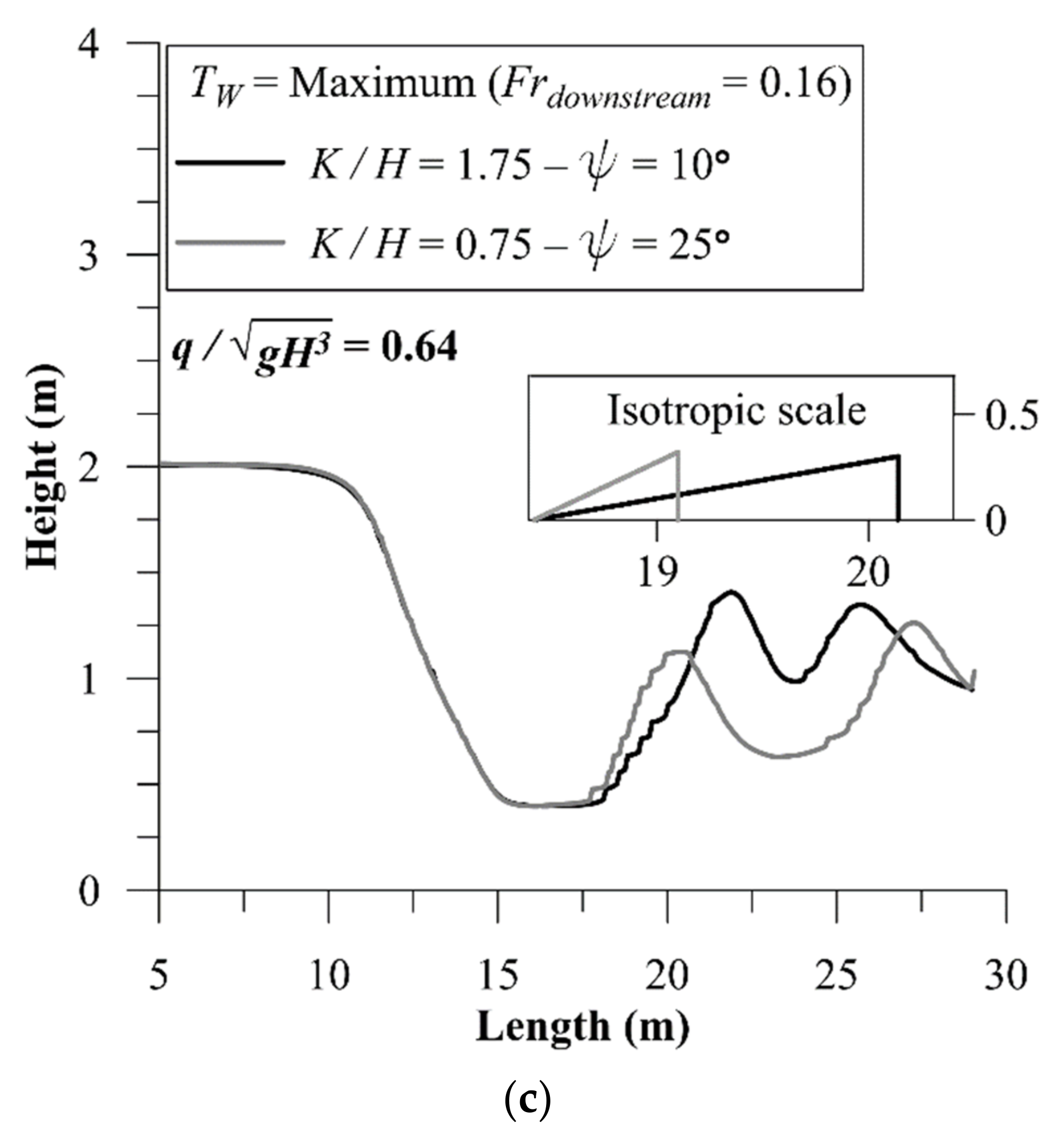
3.4. Kicker Geometry
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| weir coefficient | |
| distance from the wall | |
| water head over the weir; | |
| component of rate of deformation; | |
| body forces; | |
| Froude number of the flow downstream of the wave; | |
| gravitational acceleration; | |
| ramp height; | |
| kicker length; | |
| turbulent kinetic energy; | |
| weir length; | |
| pressure; | |
| flowrate; | |
| flowrate per unit width of the wave structure; | |
| ramp length; | |
| wave slope; | |
| transition length; | |
| tailwater depth; | |
| time; | |
| velocity; | |
| velocity component in each direction; | |
| depth averaged velocity at kicker tip; | |
| shear velocity; | |
| wave height; | |
| dimensionless wall coordinate; | |
| critical depth; | |
| depth over the weir crest; | |
| volume fraction (water toair ration); | |
| density; | |
| dynamic viscocity; | |
| eddy viscosity; | |
| turbulent dissipation rate; | |
| ϕ | ramp acute angle with respect to horizon; |
| ψ | kicker acute angle with respect to horizon; |
References
- Addicks, R. Catch a Wave in Wyoming. CNN 2010. Available online: http://www.cnn.com/2010/TRAVEL/08/09/wyoming.river.surfing/ (accessed on 9 August 2010).
- Hjort, B. “Nidelva II”. Elveguide. Available online: http://elveguide.netrunner.nu/guider/soer-troendelag/nidelva-ii (accessed on 10 December 2020).
- Bung, D.B.; Hildebrandt, A.; Oertel, M.; Schlenkhoff, A.; Schlurmann, T.; Smith, J.M. Bore Propagation over a Submerged Horizontal Plate by Physical and Numerical Simulation; ICCE: Hamburg, Germany, 2009; pp. 3542–3553. [Google Scholar]
- Whitley, D. “Riding the Wave of Change on Munich’s Eisbach”. BBC Travel. 2013. Available online: http://www.bbc.com/travel/feature/20130517-riding-the-wave-of-change-on-munichs-eisbach/1 (accessed on 20 September 2020).
- Falk, S.; Kniesburges, S.; Janka, R.; O’Keefe, T.; Grosso, R.; Döllinger, M. Numerical Investigation of the Hydrodynamics of Changing Fin Positions within a 4-Fin Surfboard Configuration. Appl. Sci. 2020, 10, 816. [Google Scholar] [CrossRef]
- D’Ambrosio, D. Hydrodynamic Characterization of Planing Surfboards Using CFD. Proceedings 2020, 49, 68. [Google Scholar] [CrossRef]
- Shormann, D.; Oggiano, L.; Panhuis, M.I.H. Numerical CFD Investigation of Shortboard Surfing: Fin Design vs. Cutback Turn Performance. Proceedings 2020, 49, 132. [Google Scholar] [CrossRef]
- Scarfe, B.E.; Elwany, M.H.S.; Mead, S.T.; Black, K.P. The Science of Surfing Waves and Surfing Breaks: A Review; Technical Report, 1–12. Scripps Inst. of Oceanography; University of California: La Jolla, CA, USA, 2003. [Google Scholar]
- Cáceres, I.; Trung, L.H.; Van Ettinger, H.D.; Reniers, A.; Uijttewaal, W. Wave and Flow Response to an Artificial Surf Reef: Laboratory Measurements. J. Hydraul. Eng. 2010, 136, 299–310. [Google Scholar] [CrossRef]
- Carmo, J.S.A.D.; Neves, M.G.; Voorde, M.T. Designing a multifunctional artificial reef: Studies on the influence of parameters with most influence in the vertical plane. J. Coast. Conserv. 2010, 15, 99–112. [Google Scholar] [CrossRef]
- Voorde, M.T.; Carmo, J.S.A.D.; Neves, M.G. Designing a Preliminary Multifunctional Artificial Reef to Protect the Portuguese Coast. J. Coast. Res. 2009, 251, 69–79. [Google Scholar] [CrossRef]
- Black, K.; Mead, S. Design of surfing reefs. Reef J. 2009, 1, 177–191. [Google Scholar]
- Hornung, H.G.; Killen, P. A stationary oblique breaking wave for laboratory testing of surfboards. J. Fluid Mech. 1976, 78, 459–480. [Google Scholar] [CrossRef]
- Oertel, M.; Mönkemöller, J.; Schlenkhoff, A. Artificial stationary breaking surf waves in a physical and numerical model. J. Hydraul. Res. 2012, 50, 338–343. [Google Scholar] [CrossRef]
- Bauer, J. Lessons from Cunovo. TEC21 2015, 141, 34–36. [Google Scholar]
- Puckert, D.K.; Mester, B.; Noack, M.; Wieprecht, S. Neckarwelle: A River Surfing Wave Facility in the Heart of the City of Stuttgart. Hydrolink 2018, 2, 38–40. [Google Scholar]
- Aufleger, M.; Neisch, V. Stationary Surf Waves in Rivers. Hydrolink 2018, 2, 36–37. [Google Scholar]
- Chanson, H. Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. Eur. J. Mech. B Fluids 2009, 28, 191–210. [Google Scholar] [CrossRef]
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Mahtabi, G.; Chaplot, B.; Azamathulla, H.M.; Pal, M. Classification of Hydraulic Jump in Rough Beds. Water 2020, 12, 2249. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; Vallés-Morán, F.J.; Sánchez-Gómez, S.; Estrada, M.D.R.; García-Bartual, R. Experimental Characterization of the Hydraulic Jump Profile and Velocity Distribution in a Stilling Basin Physical Model. Water 2020, 12, 1758. [Google Scholar] [CrossRef]
- Hassanpour, N.; Dalir, A.H.; Bayon, A.; Abdollahpour, M. Pressure Fluctuations in the Spatial Hydraulic Jump in Stilling Basins with Different Expansion Ratio. Water 2020, 13, 60. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Transition from supercritical to subcritical flow at an abrupt drop. J. Hydraul. Res. 1991, 29, 309–328. [Google Scholar] [CrossRef]
- Koch, K. Influence of the Flap on Surfablility of Waves. Master’s Thesis, ETH Zurich, Zurich, Switzerland, 2016. [Google Scholar]
- Fuchs, H. Effect of Adjustable Flaps on River Surf Waves at Abrupt Drops. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Retsinis, E.; Papanicolaou, P. Numerical and Experimental Study of Classical Hydraulic Jump. Water 2020, 12, 1766. [Google Scholar] [CrossRef]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2018, 11, 28. [Google Scholar] [CrossRef]
- Kawagoshi, N.; Hager, W.H. Wave type flow at abrupt drops. J. Hydraul. Res. 1990, 28, 235–252. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows; Butterworth-Heinemann: Burlington, VT, USA, 2007. [Google Scholar]
- Wyl, R.V. Influence of the Flap on Surfablility of Waves. Master’s Thesis, ETH Zurich, Zurich, Switzerland, 2015. [Google Scholar]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Discussion of “particle image velocity measurements of undular and hydraulic jumps”. J. Hydraul. Eng. 2009, 135, 434–436. [Google Scholar] [CrossRef]
- Fakhari, Z.; Kabiri-Samani, A. Scour in the transition from super- to subcritical flow without a hydraulic jump. J. Hydraul. Res. 2017, 55, 470–479. [Google Scholar] [CrossRef]
- Surf Anywhere Consulting Inc. Available online: https://www.surfanywhere.ca/ (accessed on 30 April 2021).
- Hager, W.H. Classical hydraulic jump: Free surface profile. Can. J. Civ. Eng. 1993, 20, 536–539. [Google Scholar] [CrossRef]
- Chanson, H. Development of the Bélanger Equation and Backwater Equation by Jean-Baptiste Bélanger (1828). J. Hydraul. Eng. 2009, 135, 159–163. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Rabiei, M.H.; Safavi, H.; Borghei, S.M. Experimental–analytical investigation of super- to subcritical flow transition without a hydraulic jump. J. Hydraul. Res. 2013, 52, 129–136. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.; Naderi, S. Turbulent structure in the transition from super- to subcritical flow without a hydraulic jump. J. Hydraul. Res. 2016, 55, 1–13. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asiaban, P.; Rennie, C.D.; Egsgard, N. Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop. Water 2021, 13, 1287. https://doi.org/10.3390/w13091287
Asiaban P, Rennie CD, Egsgard N. Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop. Water. 2021; 13(9):1287. https://doi.org/10.3390/w13091287
Chicago/Turabian StyleAsiaban, Puria, Colin D. Rennie, and Neil Egsgard. 2021. "Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop" Water 13, no. 9: 1287. https://doi.org/10.3390/w13091287
APA StyleAsiaban, P., Rennie, C. D., & Egsgard, N. (2021). Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop. Water, 13(9), 1287. https://doi.org/10.3390/w13091287




