Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand
Abstract
1. Introduction
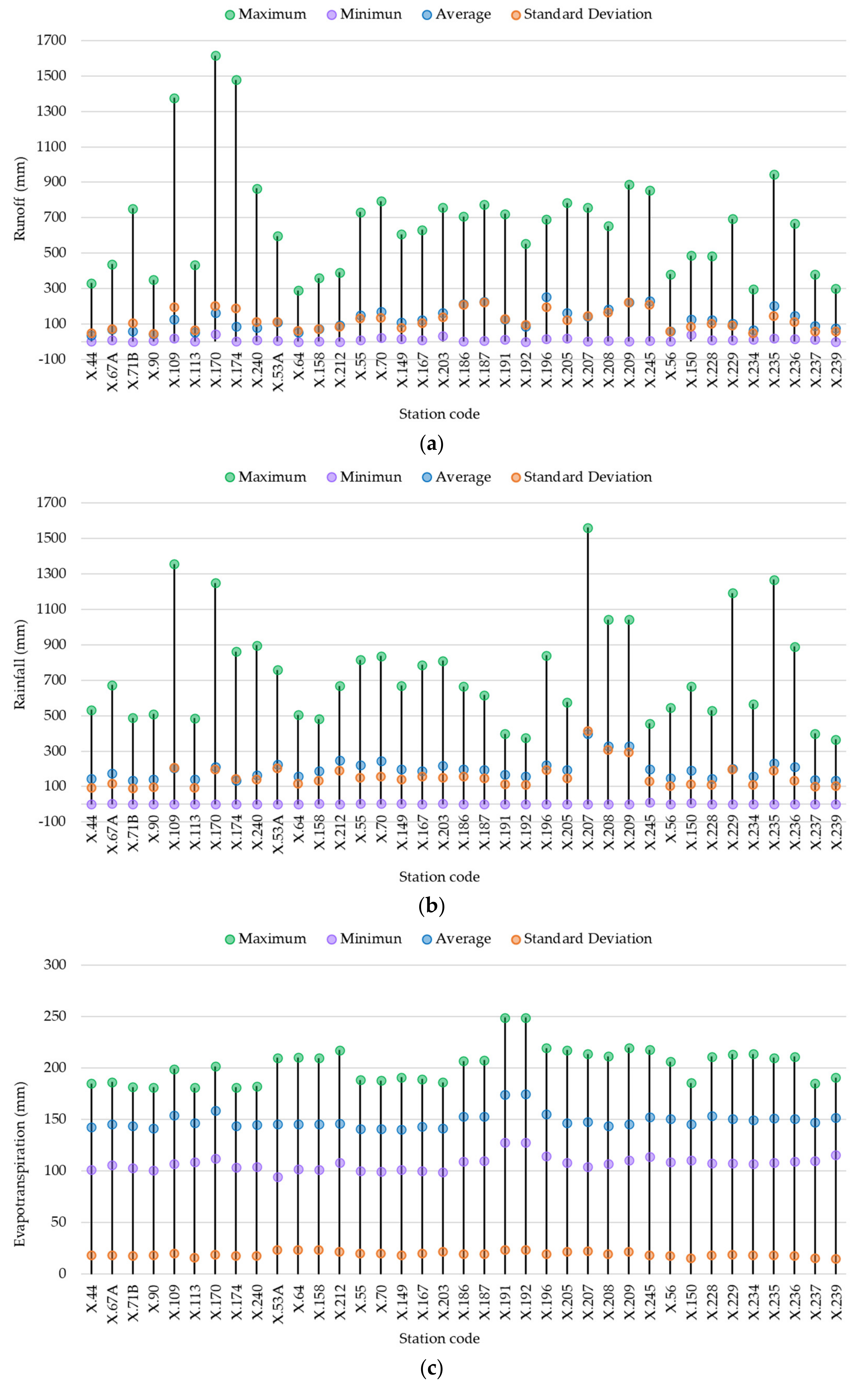
2. Study Area and Data Analysis
- Monthly values of the heat index
- Annual temperature efficiency index
- Evapotranspiration
- The C value can be obtained from:
- Potential Evapotranspirationwhere = Monthly average temperature (°C), = PET constants at different latitudes.
3. GR2M Model
4. Model’s Calibration and Verification
4.1. Warm-Up Period
4.2. Calibrating and Verifying the GR2M Model
5. Performance Criteria for Evaluating the Applicability of the GR2M Model
6. Results and Discussion
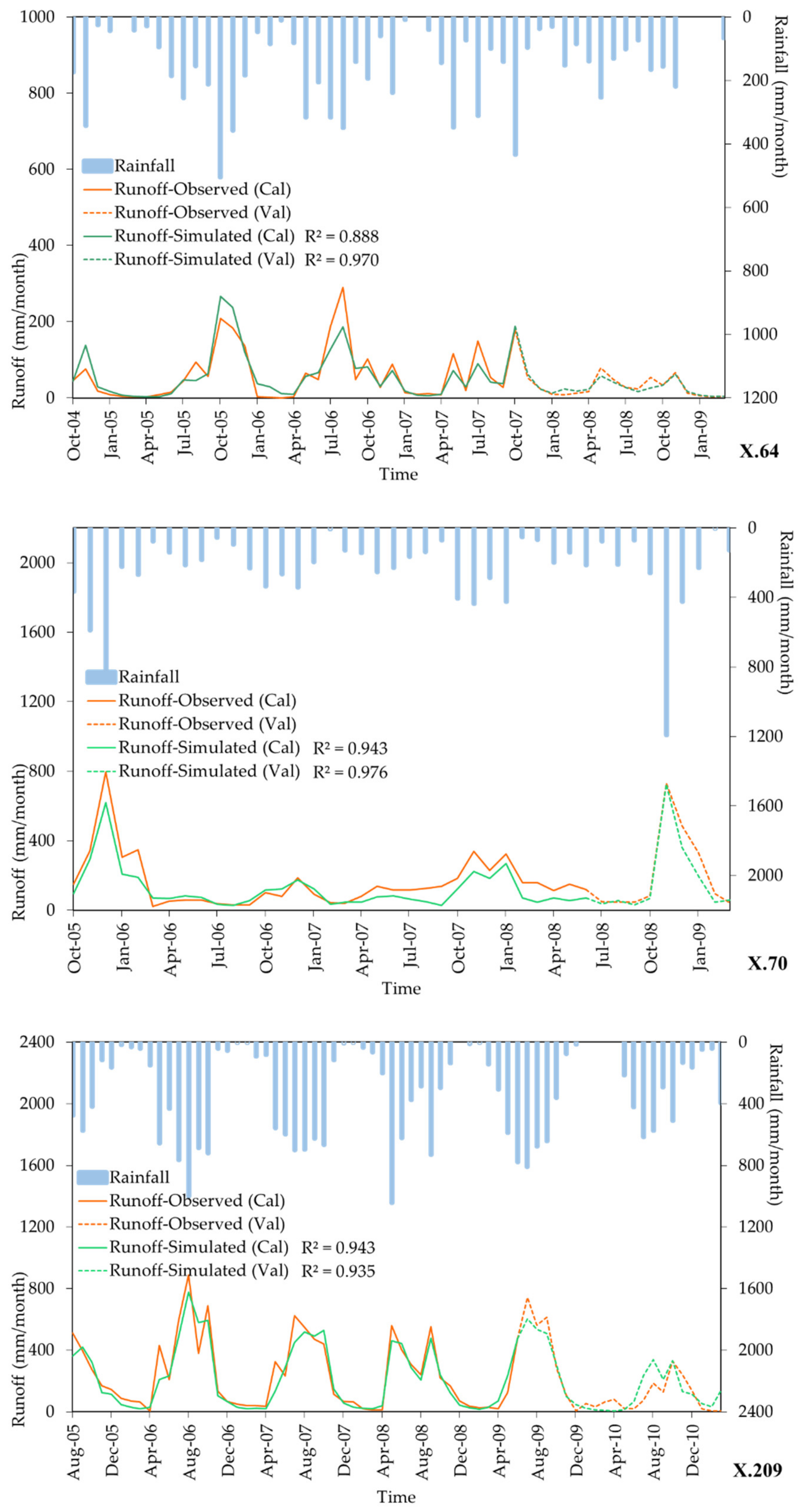
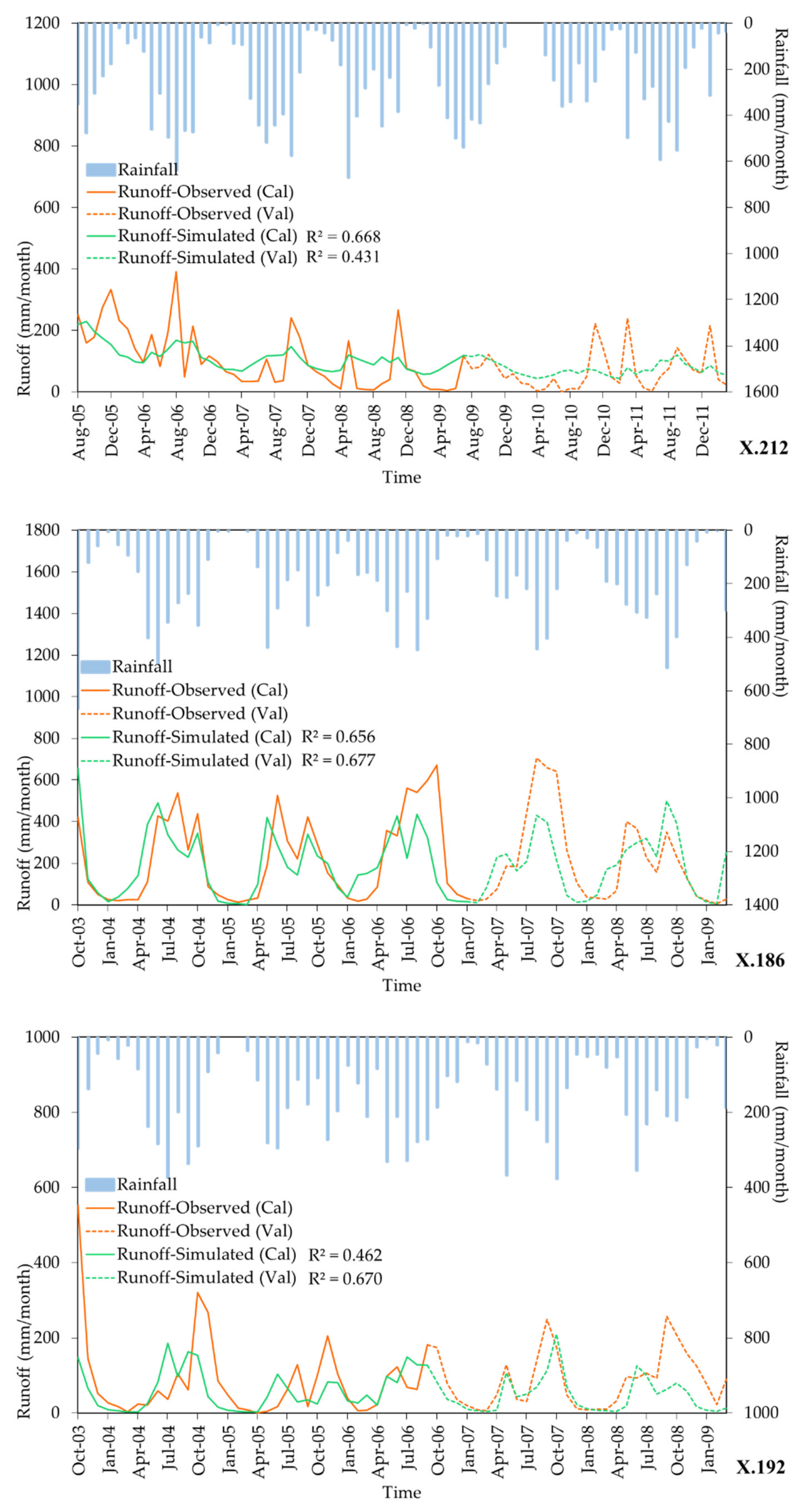
6.1. The Results of Calibrating and Verifying the GR2M Model
6.2. The Optimal Values of Production Store Capacity (X1) and Groundwater Exchange Rate (X2)
6.3. The Spatial Distribution of X1 and X2 Values Using the Inverse Distance Weighting (IDW) Method
7. Sensitivity Analysis
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vaze, J.; Chiew, F.; Perraud, J.; Viney, N.; Post, D.; Teng, J.; Wang, B.; Lerat, J.; Goswami, M. Rainfall-runoff Modelling across Southeast Australia: Datasets, Models and Results. Australas. J. Water Resour. 2010, 14, 101–116. [Google Scholar] [CrossRef]
- Suwal, N.; Kuriqi, A.; Huang, X.; Delgado, J.; Młyński, D.; Walega, A. Environmental Flows Assessment in Nepal: The Case of Kaligandaki River. Sustainability 2020, 12, 8766. [Google Scholar] [CrossRef]
- Ahmad, M.-U.-D.; Peña-Arancibia, J.L.; Stewart, J.P.; Kirby, J.M. Water balance trends in irrigated canal commands and its implications for sustainable water management in Pakistan: Evidence from 1981 to 2012. Agric. Water Manag. 2021, 245, 106648. [Google Scholar] [CrossRef]
- López-Lambraño, A.; Martínez-Acosta, L.; Gámez-Balmaceda, E.; Medrano-Barboza, J.; López, J.R.; López-Ramos, A. Supply and Demand Analysis of Water Resources. Case Study: Irrigation Water Demand in a Semi-Arid Zone in Mexico. Agriculture 2020, 10, 333. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, P.; Zhang, F.; Liu, X.; Yue, Q.; Wang, Y. Optimal irrigation water allocation in Hetao Irrigation District con-sidering decision makers’ preference under uncertainties. Agric. Water Manag. 2021, 246, 106670. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Wang, J.; Zhao, Y.; Chen, J.; Xu, C. Impacts of Climate Change and Land-Use Change on Hydrological Extremes in the Jinsha River Basin. Water 2019, 11, 1398. [Google Scholar] [CrossRef]
- Kabiri, R.; Bai, V.R.; Chan, A. Assessment of hydrologic impacts of climate change on the runoff trend in Klang Watershed, Malaysia. Environ. Earth Sci. 2015, 73, 27–37. [Google Scholar] [CrossRef]
- Lin, B.; Chen, X.; Yao, H.; Chen, Y.; Liu, M.; Gao, L.; James, A. Analyses of landuse change impacts on catchment runoff using different time indicators based on SWAT model. Ecol. Indic. 2015, 58, 55–63. [Google Scholar] [CrossRef]
- Kwak, J.; Lee, J.; Jung, J.; Kim, H.S. Case Study: Reconstruction of Runoff Series of Hydrological Stations in the Nakdong River, Korea. Water 2020, 12, 3461. [Google Scholar] [CrossRef]
- Ballinas-González, H.A.; Alcocer-Yamanaka, V.H.; Canto-Rios, J.J.; Simuta-Champo, R. Sensitivity Analysis of the Rainfall–Runoff Modeling Parameters in Data-Scarce Urban Catchment. Hydrology 2020, 7, 73. [Google Scholar] [CrossRef]
- Lerat, J.; Thyer, M.; McInerney, D.; Kavetski, D.; Woldemeskel, F.; Pickett-Heaps, C.; Shin, D.; Feikema, P. A robust approach for calibrating a daily rainfall-runoff model to monthly streamflow data. J. Hydrol. 2020, 591, 125129. [Google Scholar] [CrossRef]
- Abdessamed, D.; Abderrazak, B. Coupling HEC-RAS and HEC-HMS in rainfall–runoff modeling and evaluating floodplain inundation maps in arid environments: Case study of Ain Sefra city, Ksour Mountain. SW of Algeria. Environ. Earth Sci. 2019, 78, 586. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, R.-B.; Meng, Q.-X. Calibration of Conceptual Rainfall-Runoff Models Using Global Optimization. Adv. Meteorol. 2015, 2015, 545376. [Google Scholar] [CrossRef]
- Khazaei, M.R.; Zahabiyoun, B.; Saghafian, B.; Ahmadi, S. Development of an Automatic Calibration Tool Using Genetic Algorithm for the ARNO Conceptual Rainfall-Runoff Model. Arab. J. Sci. Eng. 2013, 39, 2535–2549. [Google Scholar] [CrossRef]
- Dezetter, A.; Girard, S.; Paturel, J.; Mahé, G.; Ardoin-Bardin, S.; Servat, E. Simulation of runoff in West Africa: Is there a single data-model combination that produces the best simulation results? J. Hydrol. 2008, 354, 203–212. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O. Evaluating climate change effects on runoff by statistical downscaling and hydrological model GR2M. Theor. Appl. Clim. 2014, 117, 343–361. [Google Scholar] [CrossRef]
- Lyon, S.W.; King, K.; Polpanich, O.-U.; Lacombe, G. Assessing hydrologic changes across the Lower Mekong Basin. J. Hydrol. Reg. Stud. 2017, 12, 303–314. [Google Scholar] [CrossRef]
- Zamoum, S.; Souag-Gamane, D. Monthly streamflow estimation in ungauged catchments of northern Algeria using regional-ization of conceptual model parameters. Arab. J. Geosci. 2019, 12, 342. [Google Scholar] [CrossRef]
- Boulariah, O.; Longobardi, A.; Meddi, M. Statistical comparison of nonlinear rainfall-runoff models for simulation in Africa North-West semi-arid areas. In Proceedings of the 15th International Conference on Environment Science and Technology, Rhodes, Greece, 31 August–2 September 2017. [Google Scholar]
- Topalović, Ž.; Todorović, A.; Plavšić, J. Evaluating the transferability of monthly water balance models under changing climate conditions. Hydrol. Sci. J. 2020, 65, 928–950. [Google Scholar] [CrossRef]
- Hadour, A.; Mahé, G.; Meddi, M. Watershed based hydrological evolution under climate change effect: An example from North Western Algeria. J. Hydrol. Reg. Stud. 2020, 28, 100671. [Google Scholar] [CrossRef]
- Rintis, H.; Suyanto; Setyoasri, Y.P. Rainfall-Discharge Simulation in Bah Bolon Catchment Area by Mock Method, NRECA Method, and GR2M Method. Appl. Mech. Mater. 2016, 845, 24–29. [Google Scholar] [CrossRef]
- O’Connor, P.; Murphy, C.; Matthews, T.; Wilby, R.L. Reconstructed monthly river flows for Irish catchments 1766–2016. Geosci. Data J. 2020, 1766–2016. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Paturel, J.E.; Servat, E.; Vassiliadis, A. Sensitivity of conceptual rainfall-runoff algorithms to errors in input data—Case of the GR2M model. J. Hydrol. 1995, 168, 111–125. [Google Scholar] [CrossRef]
- Kabouya, M. Modélisation Pluie-Débit aux Pas de Temps Mensuel et Annuel en Algérie Septentrionale. Ph.D. Thesis, Université Paris Sud Orsay, Orsay, France, 1990. [Google Scholar]
- Makhlouf, Z.; Michel, C. A two-parameter monthly water balance model for French watersheds. J. Hydrol. 1994, 162, 299–318. [Google Scholar] [CrossRef]
- Mouelhi, S. Vers Une Chaîne Cohérente de Modèles Pluie-Débit Conceptuels Globaux aux Pas de Temps Pluriannuel, Annuel, Mensuel et Journalier. Ph.D. Thesis, ENGREF Paris, Paris, France, 2003. [Google Scholar]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Fathi, M.M.; Awadallah, A.G.; Abdelbaki, A.M.; Haggag, M. A new Budyko framework extension using time series SARIMAX model. J. Hydrol. 2019, 570, 827–838. [Google Scholar] [CrossRef]
- Bachir, S.; Nouar, B.; Hicham, C.; Azzedine, H.; Larbi, D. Application of GR2M for rainfall-runoff modeling in Kébir Rhumel Watershed, north east of Algeria. World Appl. Sci. J. 2015, 33, 1623–1630. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Mahdavi, M.; Rezaei, A.; Salajegheh, A. Evaluating GR2M model in some small watersheds of Iran (Case study Gilan and Mazandaran Provinces). J. Basic Appl. Sci. Res. 2013, 3, 463–472. [Google Scholar]
- Kunnath-Poovakka, A.; Eldho, T.I. A comparative study of conceptual rainfall-runoff models GR4J, AWBM and Sacramento at catchments in the upper Godavari river basin, India. J. Earth Syst. Sci. 2019, 128, 33. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Sarzaeim, P.; Bozorg-Haddad, O.; Bozorgi, A.; Loáiciga, H.A. Runoff projection under climate change conditions with data-mining methods. J. Irrig. Drain. Eng. 2017, 143, 04017026. [Google Scholar] [CrossRef]
- Alazba, A.A.; Mattar, M.A.; El-Nesr, M.N.; Amin, M.T. Field assessment of friction head loss and friction correction factor equations. J. Irrig. Drain. Eng. ASCE 2012, 138, 166–176. [Google Scholar] [CrossRef]
- Lian, Y.; Chan, I.-C.; Singh, J.; Demissie, M.; Knapp, V.; Xie, H. Coupling of hydrologic and hydraulic models for the Illinois River Basin. J. Hydrol. 2007, 344, 210–222. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Arashloo, S.R.; Danandeh Mehr, A. Rainfall-runoff modeling through regression in the reproducing kernel Hilbert space algorithm. J. Hydrol. 2020, 587, 125014. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Ladoy, P. Fractal characterization of inhomogeneous geophysical measuring networks. Nature 1986, 319, 43–44. [Google Scholar] [CrossRef]
- Mazzarella, A.; Tranfaglia, G. Fractal Characterisation of Geophysical Measuring Networks and its Implication for an Optimal Location of Additional Stations: An Application to a Rain-Gauge Network. Theor. Appl. Climatol. 2000, 65, 157–163. [Google Scholar] [CrossRef]
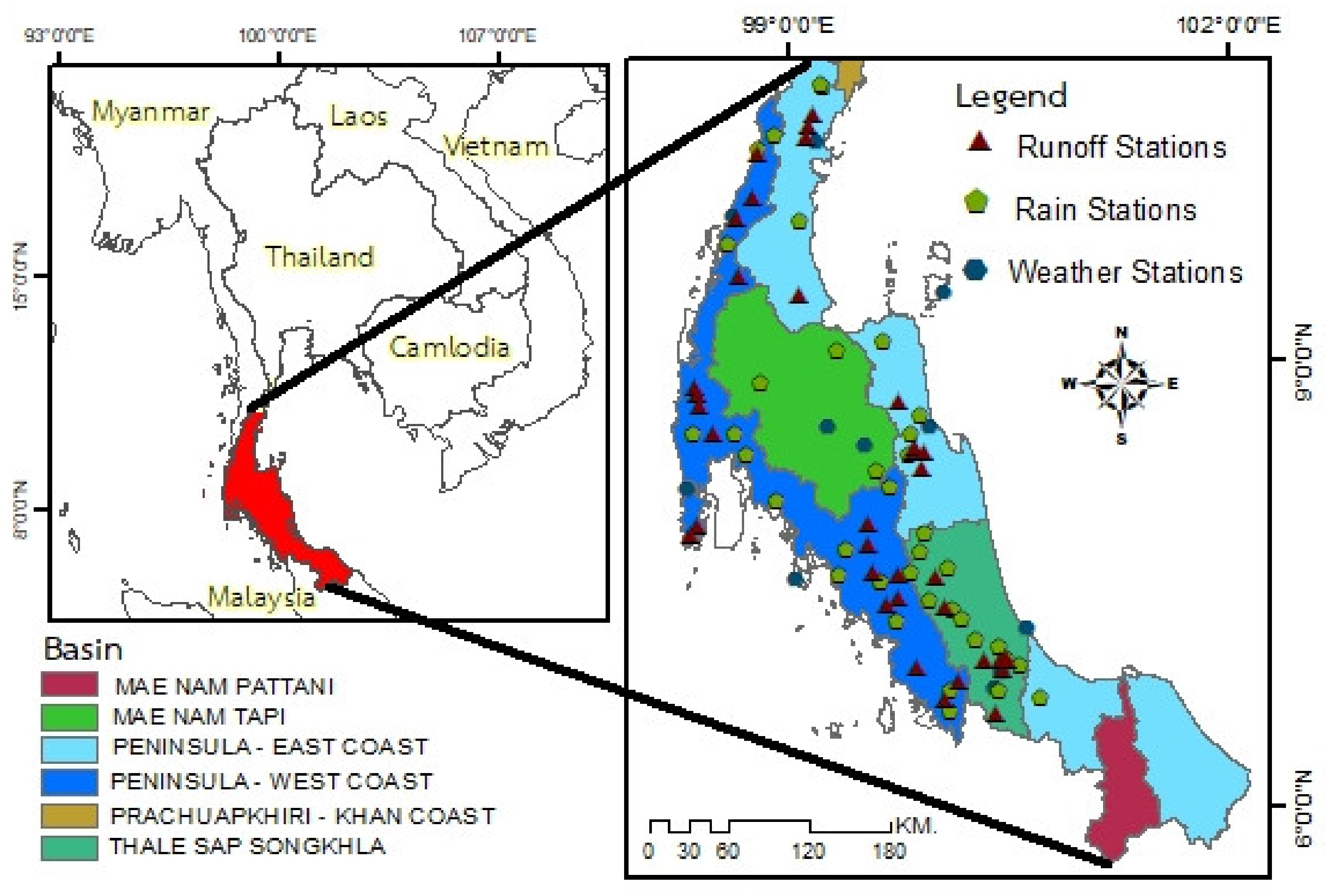

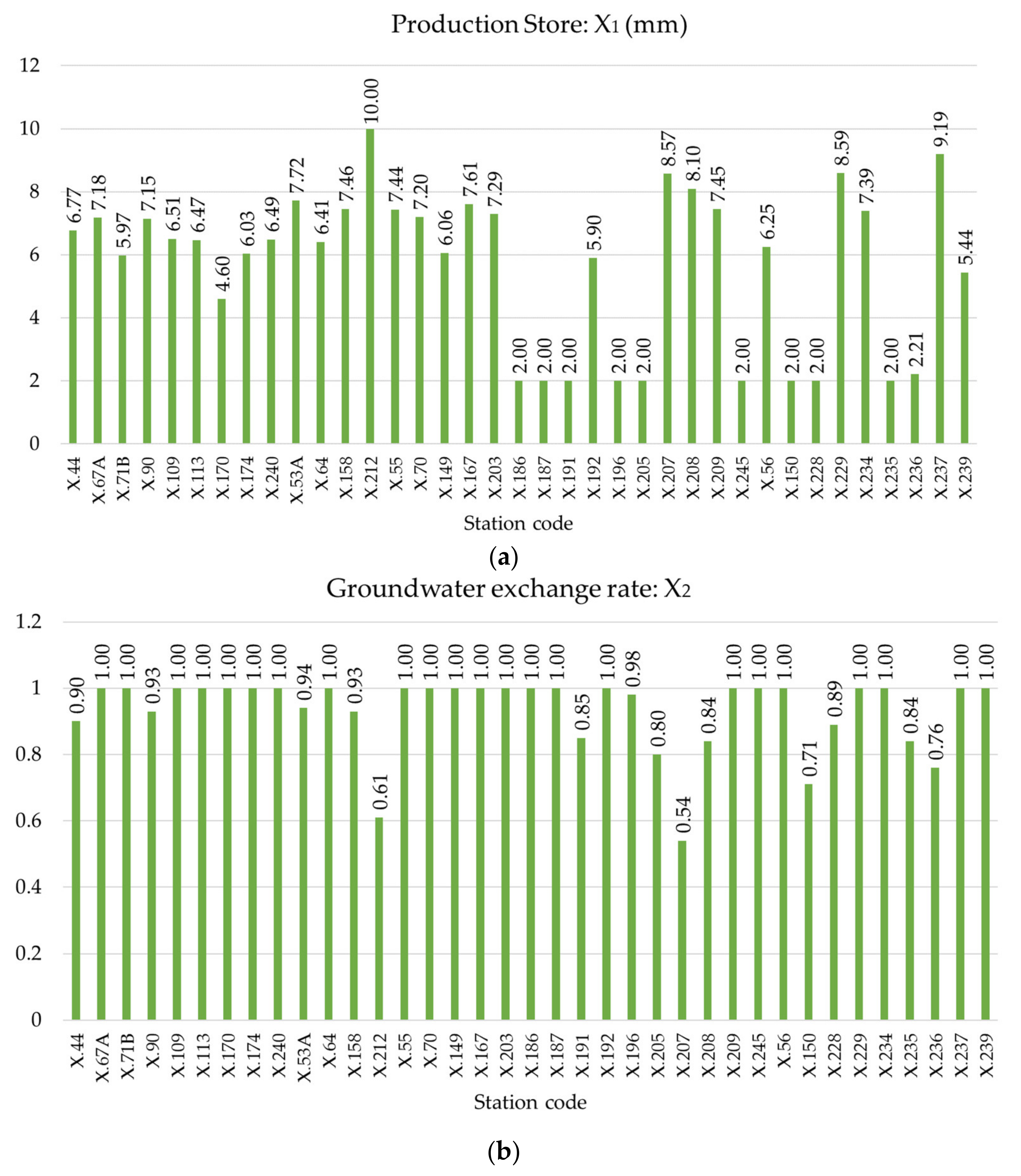
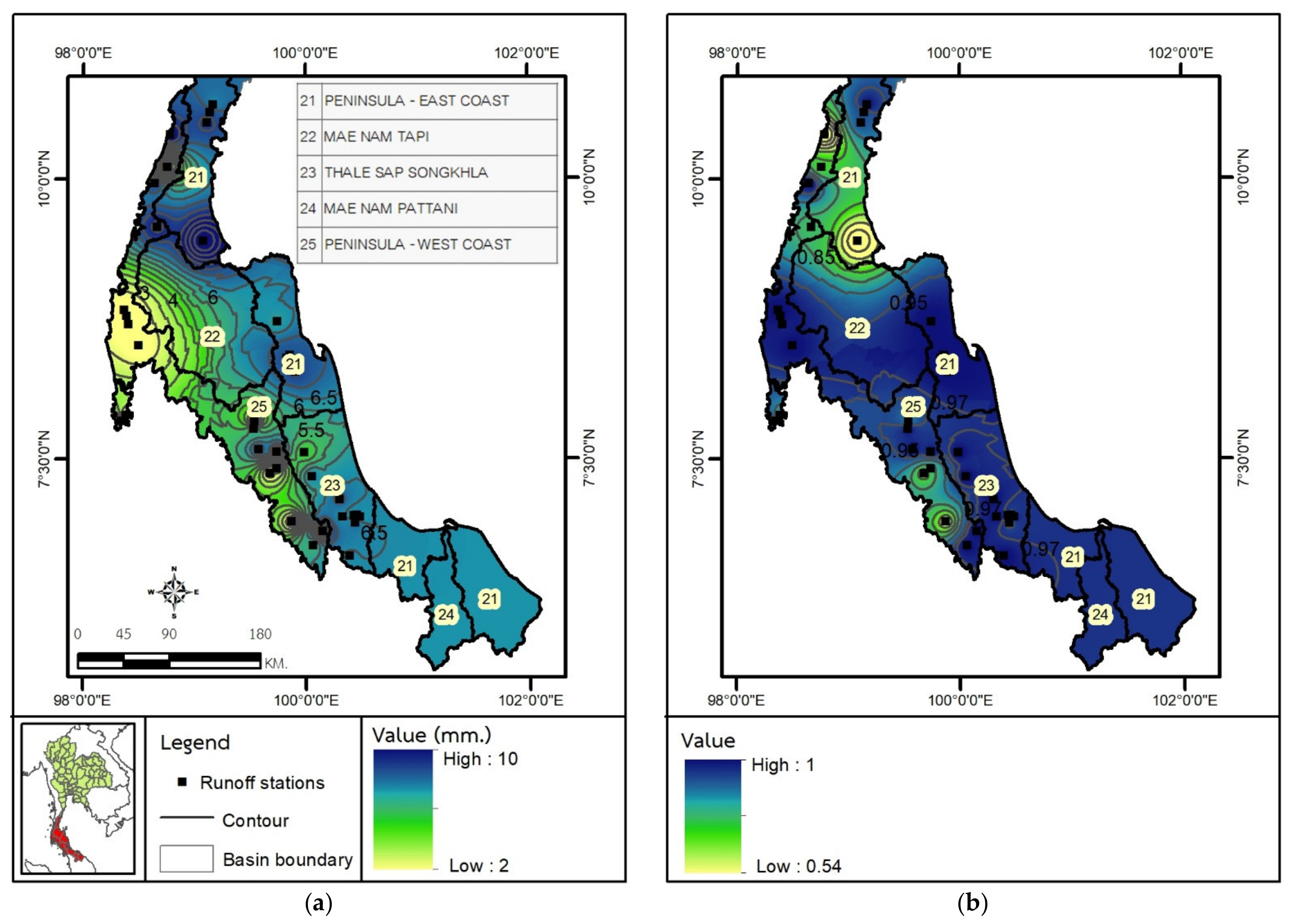
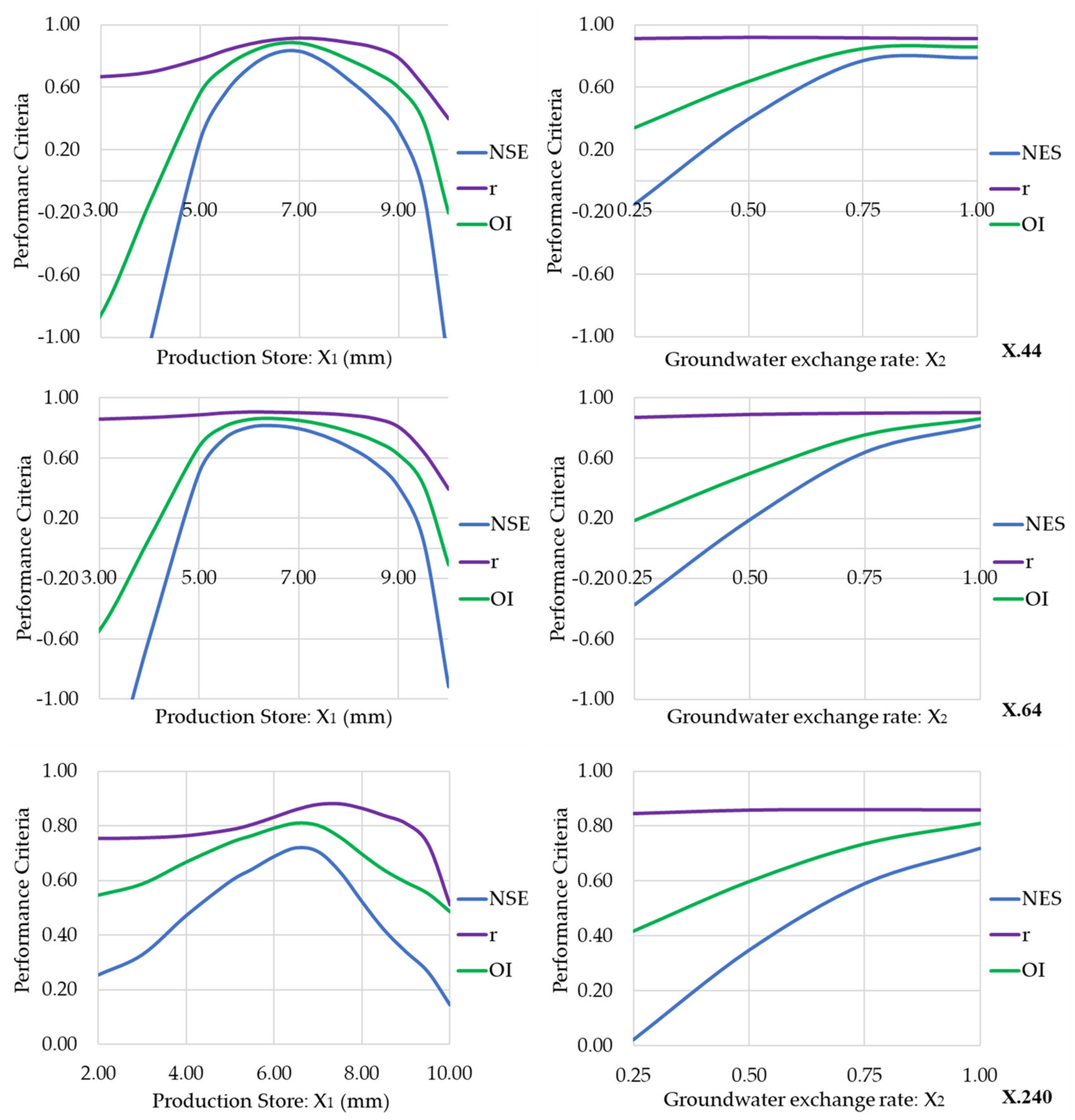
| No. | Code | Basin Name | Period | |||
|---|---|---|---|---|---|---|
| All | Warm-Up | Calibration | Validation | |||
| 1 | X.44 | TSS | April 2004–March 2009 | April 2004–September 2004 | October 2004–February 2007 | March 2007–March 2009 |
| 2 | X.67A | TSS | April 2005–March 2009 | April 2005–October 2005 | November 2005–September 2007 | October 2007–March 2009 |
| 3 | X.71B | TSS | April 2004–March 2009 | April 2004–October 2004 | November 2004–April 2007 | May 2007–March 2009 |
| 4 | X.90 | TSS | April 2003–March 2009 | April 2003–October 2003 | November 2003–July 2007 | August 2007–March 2009 |
| 5 | X.109 | TSS | April 2003–March 2008 | April 2003–October 2003 | November 2003–December 2006 | January 2007–March 2008 |
| 6 | X.113 | TSS | April 2003–March 2009 | April 2003–October 2003 | November 2003–November 2006 | December 2006–March 2009 |
| 7 | X.170 | TSS | April 2003–March 2009 | April 2003–October 2003 | November 2003–February 2007 | March 2007–March 2009 |
| 8 | X.174 | TSS | April 2003–March 2009 | April 2003–October 2003 | November 2003–January 2007 | February 2007–March 2009 |
| 9 | X.240 | TSS | April 2004–March 2009 | April 2004–September 2004 | October 2004–February 2007 | March 2007–March 2009 |
| 10 | X.53A | PEC | April 2003–March 2010 | April 2003–July 2003 | August 2003–December 2006 | January 2007–March 2010 |
| 11 | X.64 | PEC | April 2004–March 2009 | April 2004–September 2004 | October 2004–September 2007 | October 2007–March 2009 |
| 12 | X.158 | PEC | April 2004–March 2009 | April 2004–August 2004 | September 2004–September 2007 | October 2007–March 2009 |
| 13 | X.212 | PEC | April 2005–March 2012 | April 2005–July 2005 | August 2005–June 2009 | July 2009–March 2012 |
| 14 | X.55 | PEC | April 2005–March 2009 | April 2005–October 2005 | November 2005–November 2007 | December 2007–March 2009 |
| 15 | X.70 | PEC | April 2005–March 2009 | April 2005–September 2005 | October 2005–May 2008 | June 2008–March 2009 |
| 16 | X.149 | PEC | April 2005–March 2009 | April 2005–October 2005 | November 2005–April 2008 | May 2008–March 2009 |
| 17 | X.167 | PEC | April 2003–March 2009 | April 2003–October 2003 | November 2003–October 2006 | November 2006–March 2009 |
| 18 | X.203 | PEC | April 2005–March 2009 | April 2005–October 2005 | November 2005–December 2007 | January 2008–March 2009 |
| 19 | X.186 | PWC | April 2003–March 2009 | April 2003–September 2003 | October 2003–December 2006 | January 2007–March 2009 |
| 20 | X.187 | PWC | April 2003–March 2009 | April 2003–August 2003 | September 2003–August 2006 | September 2006–March 2009 |
| 21 | X.191 | PWC | April 2003–March 2009 | April 2003–August 2003 | September 2003–May 2007 | June 2007–March 2009 |
| 22 | X.192 | PWC | April 2003–March 2009 | April 2003–September 2003 | October 2003–August 2006 | September 2006–March 2009 |
| 23 | X.196 | PWC | April 2003–March 2009 | April 2003–August 2003 | September 2003–August 2006 | September 2006–March 2009 |
| 24 | X.205 | PWC | April 2005–March 2012 | April 2005–August 2005 | September 2005–May 2009 | June 2009–March 2012 |
| 25 | X.207 | PWC | April 2003–March 2010 | April 2003–August 2003 | September 2003–September 2007 | October 2007–March 2010 |
| 26 | X.208 | PWC | April 2005–March 2009 | April 2005–July 2005 | August 2005–September 2007 | October 2007–March 2009 |
| 27 | X.209 | PWC | April 2005–March 2011 | April 2005–July 2005 | August 2005–May 2009 | June 2009–March 2011 |
| 28 | X.245 | PWC | April 2005–March 2009 | April 2005–July 2005 | August 2005–June 2007 | July 2007–March 2009 |
| 29 | X.56 | PWC | April 2004–March 2009 | April 2004–August 2004 | September 2004–August 2007 | September 2007–March 2009 |
| 30 | X.150 | PWC | April 2005–March 2009 | April 2005–September 2005 | October 2005–July 2007 | August 2007–March 2009 |
| 31 | X.228 | PWC | April 2003–March 2009 | April 2003–October 2003 | November 2003–September 2006 | October 2006–March 2009 |
| 32 | X.229 | PWC | April 2003–March 2009 | April 2003–October 2003 | November 2003–March 2007 | April 2007–March 2009 |
| 33 | X.234 | PWC | April 2004–March 2009 | April 2004–September 2004 | October 2004–August 2007 | September 2007–March 2009 |
| 34 | X.235 | PWC | April 2004–March 2009 | April 2004–September 2004 | October 2004–September 2007 | October 2007–March 2009 |
| 35 | X.236 | PWC | April 2004–March 2009 | April 2004–July 2004 | August 2004–December 2006 | January 2007–March 2009 |
| 36 | X.237 | PWC | April 2004–March 2009 | April 2004–August 2004 | September 2004–January 2007 | February 2007–March 2009 |
| 37 | X.239 | PWC | April 2004–March 2009 | April 2004–July 2004 | August 2004–December 2007 | January 2007–March 2009 |
| No. | Code | Performance Criteria | No. | Code | Performance Criteria | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | ||||||||||||
| NSE | r | OI | NSE | r | OI | NSE | r | OI | NSE | r | OI | ||||
| 1 | X.44 | 0.942 | 0.973 | 0.949 | 0.465 | 0.705 | 0.657 | 20 | X.187 | 0.563 | 0.756 | 0.668 | 0.349 | 0.654 | 0.548 |
| 2 | X.67A | 0.978 | 0.99 | 0.974 | 0.719 | 0.852 | 0.795 | 21 | X.191 | 0.177 | 0.492 | 0.505 | 0.664 | 0.831 | 0.749 |
| 3 | X.71B | 0.688 | 0.954 | 0.793 | 0.605 | 0.797 | 0.733 | 22 | X.192 b | 0.165 | 0.462 | 0.493 | 0.167 | 0.670 | 0.451 |
| 4 | X.90 | 0.772 | 0.887 | 0.85 | 0.468 | 0.502 | 0.478 | 23 | X.196 | 0.333 | 0.691 | 0.544 | 0.283 | 0.691 | 0.505 |
| 5 | X.109 | 0.925 | 0.987 | 0.94 | 0.577 | 0.849 | 0.696 | 24 | X.205 c | 0.518 | 0.755 | 0.693 | −0.119 | 0.663 | 0.289 |
| 6 | X.113 | 0.736 | 0.91 | 0.821 | 0.479 | 0.796 | 0.648 | 25 | X.207 | 0.758 | 0.878 | 0.798 | 0.836 | 0.920 | 0.856 |
| 7 | X.170 | 0.805 | 0.903 | 0.867 | 0.038 | 0.451 | 0.392 | 26 | X.208 | 0.796 | 0.906 | 0.838 | 0.751 | 0.894 | 0.808 |
| 8 | X.174 | 0.725 | 0.975 | 0.821 | 0.385 | 0.731 | 0.61 | 27 | X.209 a | 0.880 | 0.943 | 0.896 | 0.870 | 0.935 | 0.883 |
| 9 | X.240 | 0.975 | 0.993 | 0.973 | 0.511 | 0.735 | 0.687 | 28 | X.245 | 0.476 | 0.715 | 0.636 | 0.199 | 0.503 | 0.457 |
| 10 | X.53A | 0.822 | 0.908 | 0.868 | 0.714 | 0.847 | 0.793 | 29 | X.56 | 0.813 | 0.911 | 0.868 | 0.676 | 0.866 | 0.746 |
| 11 | X.64 a | 0.787 | 0.888 | 0.838 | 0.941 | 0.970 | 0.942 | 30 | X.150 | 0.833 | 0.915 | 0.871 | 0.226 | 0.623 | 0.461 |
| 12 | X.158 | 0.573 | 0.759 | 0.714 | 0.752 | 0.869 | 0.818 | 31 | X.228 | 0.111 | 0.527 | 0.450 | 0.346 | 0.702 | 0.554 |
| 13 | X.212 b | 0.383 | 0.668 | 0.594 | 0.173 | 0.431 | 0.467 | 32 | X.229 c | 0.564 | 0.794 | 0.730 | −0.437 | 0.407 | 0.120 |
| 14 | X.55 | 0.654 | 0.903 | 0.761 | 0.987 | 0.996 | 0.980 | 33 | X.234 | 0.854 | 0.934 | 0.890 | 0.713 | 0.882 | 0.773 |
| 15 | X.70 a | 0.780 | 0.943 | 0.845 | 0.923 | 0.976 | 0.916 | 34 | X.235 | 0.430 | 0.758 | 0.648 | 0.404 | 0.679 | 0.596 |
| 16 | X.149 | 0.557 | 0.912 | 0.702 | 0.957 | 0.986 | 0.950 | 35 | X.236 | 0.801 | 0.896 | 0.857 | 0.513 | 0.719 | 0.647 |
| 17 | X.167 | 0.892 | 0.973 | 0.912 | 0.278 | 0.803 | 0.534 | 36 | X.237 c | 0.734 | 0.277 | 0.411 | −0.305 | 0.497 | 0.202 |
| 18 | X.203 | 0.732 | 0.970 | 0.809 | 0.897 | 0.973 | 0.904 | 37 | X.239 | 0.376 | 0.754 | 0.602 | 0.055 | 0.673 | 0.388 |
| 19 | X.186 b | 0.400 | 0.660 | 0.580 | 0.405 | 0.680 | 0.620 | ||||||||
| Maximum | 0.978 | 0.993 | 0.974 | 0.987 | 0.996 | 0.980 | |||||||||
| Minimum | 0.111 | 0.277 | 0.411 | −0.437 | 0.407 | 0.120 | |||||||||
| Average | 0.657 | 0.825 | 0.757 | 0.472 | 0.750 | 0.639 | |||||||||
| Standard Deviation | 0.233 | 0.170 | 0.153 | 0.350 | 0.166 | 0.213 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ditthakit, P.; Pinthong, S.; Salaeh, N.; Binnui, F.; Khwanchum, L.; Kuriqi, A.; Khedher, K.M.; Pham, Q.B. Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand. Water 2021, 13, 1226. https://doi.org/10.3390/w13091226
Ditthakit P, Pinthong S, Salaeh N, Binnui F, Khwanchum L, Kuriqi A, Khedher KM, Pham QB. Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand. Water. 2021; 13(9):1226. https://doi.org/10.3390/w13091226
Chicago/Turabian StyleDitthakit, Pakorn, Sirimon Pinthong, Nureehan Salaeh, Fadilah Binnui, Laksanara Khwanchum, Alban Kuriqi, Khaled Mohamed Khedher, and Quoc Bao Pham. 2021. "Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand" Water 13, no. 9: 1226. https://doi.org/10.3390/w13091226
APA StyleDitthakit, P., Pinthong, S., Salaeh, N., Binnui, F., Khwanchum, L., Kuriqi, A., Khedher, K. M., & Pham, Q. B. (2021). Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand. Water, 13(9), 1226. https://doi.org/10.3390/w13091226









