Abstract
With the aim of building more compact fishways and adapting them to field conditions to improve their location by fish, it is common to use turning pools, reducing the longitudinal development of the construction. However, depending on their design, turning pools may affect the hydraulic performance of the fishway and consequently the fish passage. To study these phenomena, turning pools in a vertical slot and in different configurations of submerged notches with bottom orifice fishway types were assessed. Both types of fishways were studied using numerical 3D models via OpenFOAM, a computational fluid dynamics software, in combination with fish responses, assessed with PIT (Passive Integrated Transponder) tag telemetry for three different species of potamodromous cyprinids in several fishways. Results show differences between the hydrodynamics of straight and turning pools, with lower values in the hydrodynamic variables in turning pools. Regarding fish behavior, the ascent was slower in turning pools but with no effect on passage success and without being a problem for fish migration. This information validates the use of turning pools as a key design component for fishways for studied species.
1. Introduction
The most widespread solution to allow natural movements of fish in river barriers (e.g., dams and gauging weirs) are fishways or fish passages [1]. However, there are still many uncertainties to prove that they can effectively fulfill their objective [2]. There is a great diversity of fishway designs, one or more for each circumstance or scenario (e.g., stepped fishways, nature-like fishways, fish lifts, fish locks, etc.), but stepped or pool-type fishways are the most common ones [3,4]. Stepped fishways consist of a sloped channel divided by cross-walls that generate a succession of pools. Each cross-wall connects the pools by slots, notches, or orifices, allowing the water to flow and the fish to pass. According to the connections between pools, the most common stepped fishways are the single vertical slot fishway (VS) and the submerged notch with bottom orifice fishway (SNBO) [1,5,6].
The design of fishways is a multidisciplinary task, where hydraulic and civil engineering meets biology. On one side, fishways must meet some hydraulic and dimensional requirements that allow the location, passage, and exit by fish, and, on the other, they must satisfy the requisites of their placement. The biological requirements (slope, discharge, and volume of the pool) usually provoke large longitudinal extensions in fishways and, to fulfill the entrance and location requirements as well as geometrical constraints of the obstacle, it is common to fold them out in a zigzag arrangement/pattern, where straight sections are joined by 180° turning pools. Most studies on fishway hydraulics are focused on and defined for straight sections [5,7,8,9,10,11], and the effect of including turning pools remains poorly explored. Turning pools suppose a discontinuity in the overall performance of the fishway (due to their different geometry), which provokes a differentiated flow pattern and hydraulic performance. Moreover, there are few guidelines to design them, showing a great variability between different fishway designs [12,13], from different morphology of corners (right angles, chamfers, curves) or the presence of baffles to the location of the entering and exiting connections. Thus, the presence of a turning pool introduces in the fishway a new hydrodynamic scenario that fish will need to overcome [14,15] and that could affect even the uniformity of adjacent straight sections [9]. On the other hand, turning pools are assumed to behave as resting pools due to their higher water volume [3,12,16]. In this regard, design guidelines recommend their installation every two meters of water level height [3], with a low volumetric power dissipation (<50 W/m3) and with chamfered or rounded corners [5,15].
Fishways’ success depends on interactions between fish behavior and their swimming ability with hydraulic characteristics [17,18,19,20]. Therefore, it is crucial to study the influence of turning pools in fishway usage, although these studies are still scarce. The paper by Marriner et al. [13] simulated the hydraulics of different turning pool configurations, showing that their hydrodynamics were different from those of the straight sections and that they could influence the fish movements. Studies focused on fish behavior in turning pools show slower passage times during the upstream movement through these types of pools [16,21,22,23,24,25]. However, only Thiem et al. [24,25] reported passage problems for sturgeon due to the higher energetic cost when traversing turning pools. Thus, the influence of turning pools in fishway efficiency is still unclear for most fish species. To clarify this, efforts in the last decade notably increased looking for fishway passage metrics [26,27,28] with some specific standardized proposals, such as passage success and transit time [20], that could help to give answers to this question.
Considering the above, the main goal of this paper is to analyze the effect of turning pools in the ascent of fish through stepped fishways, using transit time and passage success as standardized metrics. To achieve this, four different configurations of turning pools were studied and analyzed in combination with numerical 3D models, using three potamodromous fish under two different trial conditions. The results show that transit time through turning pools was higher than in straight sections, but neither affecting the passage success nor supposing an important delay in the overall migration.
2. Materials and Methods
2.1. Study Sites
Data for this study were collected in four different field fishways, all of them associated with hydropower plants and located in the center and southeast of Spain. Previous research on general fishway passage success on these sites can be found in the papers by Bravo-Córdoba et al. and Sanz-Ronda et al. [29,30,31]. All of them are stepped fishways, one with single vertical slot connections (VS type) between pools—the El Jarral weir (38°12′2.80″ N 1°23′40.30″ W; Abarán, Murcia)—and the other three with a submerged notch and bottom orifice connections (SNBO type)—the Postrasvase weir (38°15′42.50″ N 1°41′57.63″ W; Calasparra, Murcia), the San Miguel weir (41°30′20.24″ N 4° 54′57.00″ W; San Miguel del Pino, Valladolid), and the Guma weir (41°38′13.60″ N 3°32′37.15″ W; Guma, Burgos) (Figure 1).
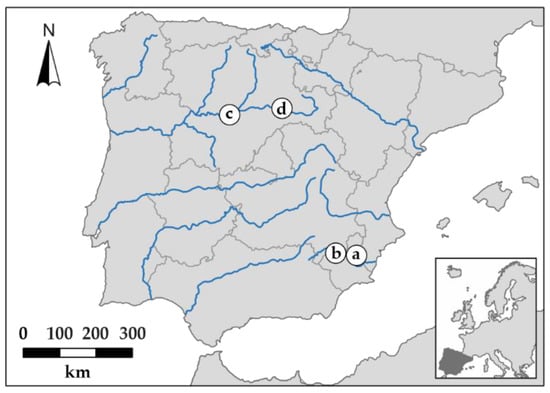
Figure 1.
Location in the Iberian Peninsula of the study sites. (a) El Jarral (VS); (b) Postrasvase (SNBO); (c) San Miguel (SNBO); (d) Guma (SNBO).
All fishways were designed and constructed following the standard design guidelines [3,5] and considering the geometrical and hydraulic recommendations for cyprinids (Table 1 and Figure 2). Furthermore, in all of them, the discharges can be regulated by sluice gates located in the most upstream cross-walls.

Table 1.
Mean value of the geometric variables for the studied fishways. Vertical Slot (VS); Submerged Notch with Bottom Orifice (SNBO). NA: Not Applicable.
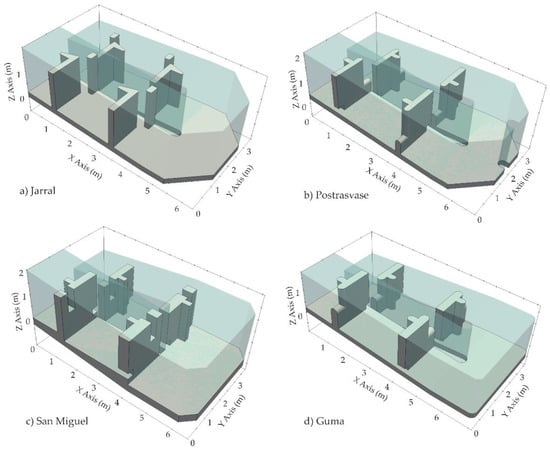
Figure 2.
3D scheme of the turning pools under study. (a) El Jarral (VS); (b) Postrasvase (SNBO); (c) San Miguel (SNBO); (d) Guma (SNBO).
It is worth mentioning that during field trials water levels downstream of the studied rivers were higher than those calculated during design conditions, affecting the boundary conditions in the entrance of the fishways. These conditions produced non-uniform profiles in the first pools of the fishways, that is to say, backwater profiles that increased the water depth and reduced the water drops in few centimeters between the most downstream pools of the fishway [10,32]. Due to the small influence of these conditions on the overall performance of the fishways, they were excluded from the analysis.
2.2. 3D Numerical Model
To relate biological results in straight sections and turning pools with hydraulic conditions, eight CFD (Computational Fluid Dynamics) models were developed. Two models (straight section and turning pool) were developed for each of the fishways under study. Figure 2 illustrates the simulated turning pools. In both cases, straight sections and turning pools, an extra pool upstream, and an extra pool downstream were included in the simulated scenarios to remove the possible influence of inlet and outlet conditions. This ensures the full development of the hydraulic conditions in the target pool.
2.2.1. CFD Methods
The 3D models were implemented using the open source numerical C++ toolbox OpenFOAM (release 3.0.1). OpenFOAM uses a tensorial approach and finite volume method (FVM) for the resolution of CFD problems. The resolution of the transient flow of two fluids separated by a sharp interface (water-air) is achieved with the prebuilt Eulerian solver interFoam [32], an implementation of the classical VOF (Volume of Fluid Method) method [33]. A detailed description of the procedure and methods used (flow equations, boundary conditions, and the simulation process applied) for modeling can be found in Fuentes-Pérez et al. [34].
To solve turbulence, in all the models, Reynolds-Averaged Navier-Stokes (RANS) turbulence modelling methods were used (k-ε turbulent model). To date, RANS turbulence modelling techniques are the most popular alternative for fishway modelling [13,14,35]. This is motivated by their possible application in a wide range of flows and their accurate predictions of time-averaged velocity distribution [13,36,37]. Compared with other methods, RANS methods demonstrated a good accuracy/computational cost ratio [34].
2.2.2. Mesh, Boundary Conditions, and Time Sensitivity Analysis
All studied meshes were generated using a two-step procedure [34]. First, the block-Mesh utility [38] was used to create a structured hexahedral mesh of the channel without considering the cross-walls. Next, the snappyHexMesh utility [38] was applied to define cross-walls, creating a high quality hex-dominant mesh. After a mesh independency analysis, the mesh size used to perform the simulations was 0.04 m, which is in accordance with other CFD fishway studies [13,14,34,39].
The overall performance of each scenario was controlled by defining a constant flow rate at the inlet (variableHeightFlowRateInletVelocity), enabling the free water level oscillation (VariableHeightFlowRate) and a constant mean velocity in the outlet (OutletPhaseMeanVelocity) [34]. These boundary conditions were iteratively varied until the observed behavior matched the conditions observed in the field. In all cases, final results were in accordance with field observations, that is to say, velocities in slots and notches in the range of field measurements, and water levels and discharges in accordance with field measurements and 1D equations used in fishway design [40].
In all the simulations, the differences between time-steps on water levels and mass flow were monitored to ensure that an asymptotic behavior was reached. To report the simulation results, 50 time steps after the asymptotic behavior were averaged.
2.2.3. CFD Data Treatment and Hydraulic Variables
CFD data from OpenFOAM was plotted, visualized, and exported to text format with Paraview software (version 5.8.0). Final analysis, visualization, and comparisons were performed in Matlab R2019a. For visual comparison, contour plots parallel to the bottom were plotted. For SNBO fishways, two plots were done, one in the middle of upstream cross-wall orifice and another in the middle of the water height of the notch ((h1 − p)/2; where h1: height difference between the top of the notch and the water level in the upstream pool; p: sill height), and for the VS fishway, only one plot was done in the middle of the water height of the upstream cross-wall slot.
Three main variables were considered to perform the contour comparison between fishways and between straight sections and turning pools: velocity (u), turbulent kinetic energy (k), and vorticity in the vertical plane (ωxy). The formal definition of these variables can be found in Appendix B. All these variables were pointed out as relevant in previous turning pool and fish movement analyses [13,18,19]. Finally, to compare the frequency distribution of these variables in the full volume between straight and turning pools as well as for different fishways, Kruskal-Wallis tests were applied.
2.3. Fish Response
2.3.1. Fish Collection and Tagging
All experiments were carried out during the season with strong migratory activity, which corresponds to between May and July for Iberian potamodromous cyprinids (Iberian barbel Luciobarbus bocagei, Southern Iberian barbel Luciobarbus sclateri, and Iberian straight-mouth nase Pseudochondrostoma polylepis) [41,42,43]. Barbels and nases are rheophilic fish, and they coexist in the same river reaches, though they do not show the same swimming performance [31,44,45].
Fish were captured by electrofishing (Erreka model 2000 W or Hans-Grassl ELT60II backpack equipment; 180–250 V and 1.5–3 A) in an upstream river section close to each fishway. Within two hours after capture, fish were transported to the vicinity of the corresponding fishway in 100 L aerated tanks. They were held in acclimation tanks or enclosed by a net in one of the pools of the fishways at ambient temperatures and with a direct supply of water from the river.
All fish were anesthetized with MS-222 (100 mg/L) or eugenol (50 mg/L diluted in ethanol in proportion 1:10), measured (fork length (FL), ±0.1 cm), weighted (±1 g), and tagged intraperitoneally with a HDX (Half Duplex) passive integrated transponder (PIT) tag by an incision posterior to the left pectoral fin. Two tag sizes were used, a small one (length: 12 mm; diameter: 2.12 mm; weight: 0.1 g) and a larger one (length: 23 mm; diameter: 3.65 mm; weight: 0.6 g). In all cases, a relationship of tag weight/fish weight lower than 2% was considered. After tagging, fish were acclimated to the experimental environment for at least two hours, always after visual evidence of recovery from anesthetic. Two different trial conditions were used depending on the study case (Table 2): (a) free experiments, where fish were released downstream the fishway into the river, and (b) confined experiments, where fish were released in a downstream pool of the fishway, avoiding fish entrance or exit by mean of meshes in the uppermost and lowermost cross-walls.

Table 2.
Fish samples. N: number of fish. FL: Fork length; C.I.: Confidence Interval (95%); Range: Minimum and maximum FL. VS: Vertical Slot; SNBO: Submerged Notch with Bottom Orifice.
2.3.2. Data Collection
In each fishway, a series of pass-through antennas were used to record the movements of the tagged fish. The antennas covered the slots in the VS fishway and the notch and the orifice in the SNBO fishways. Each antenna was connected to a reader (Half Duplex multiplexer reader, ORFID, Portland, OR, USA), programmed to send and receive information at 14 Hz (3.5 Hz or 0.29 s per antenna). Three antennas were placed in each test case, two located at the entrance and exit of the turning pool (antenna 1 and 2) and the other covering the straight section upstream of the turning pool (antenna 2 to 3). The straight section before the turning pool was not considered because their hydraulic conditions change greatly due to the tailwater level oscillations (non-uniform scenario).
When collecting the data recorded by antennas, the following data selection criteria and metric-calculation procedures were considered:
- Only those fish with attempts (i.e., at least with one record on the first antenna) were included.
- For transit time calculation, only ascent events with success were taken into account (a successful event was considered when a fish reached the uppermost antenna).
- Transit time in each section was calculated as the time taken from the first detection on the most downstream antenna to the first detection on the most upstream antenna (from antenna 1 to 2 for turning pools and from antenna 2 to 3 for straight sections).
- To avoid the possible effect of fish with multiple events (mainly in free trials related to fish that used the fishway as a daily habitat), when a fish had more than one successful event, only the one with the fastest transit time was selected, resulting in one event per fish.
- To make possible the comparisons among both fishway sections (straight section vs. turning pool) and different field test cases, data of transit time were relativized by the water height difference between antennas, resulting in a transit time per meter of height ascended (min/m).
Passage success in the turning pools was calculated as the proportion of fish that ascended the turning pool over the total number of fish that reached it.
2.3.3. Data Analysis
All fish response data analyses were performed in Statgraphics Centurion statistical software (Statgraphics Technologies, Inc., The Plains, VA, USA; Version 18.1).
Mann-Whitney (MW) tests were carried out to evaluate if there were significant differences in transit time between fishway sections. Comparisons of transit time between different fishway types were done separately depending on whether they were confined or free trials.
The chi-square test of independence was used to check the differences between the passage success through the turning pools in the different test cases.
3. Results
3.1. 3D Numerical Models
The simulated 1D variables match the field observations (Table 3). In general, the higher the water drop between pools, the higher the maximum velocity. The VPDs are lower in all turning pools when comparing with the straight sections. This is due to their higher water volume, and it is in accordance with resting pool recommendations.

Table 3.
Summary of 1D classical hydraulic variables. Q: Flow discharge (m3/s); h0: Mean water depth in a pool (m); ΔH: Difference in water level between pools or head drop (m); umax: Maximum water velocity in the slot/notch/orifice (m/s); VPD: Volumetric power dissipation (W/m3).
For clarity reasons, all the 3D simulations and 2D contour plots are attached in Appendix A (Figure A1, Figure A2, Figure A3, Figure A4, Figure A5 and Figure A6). As a summary of hydrodynamic variable distributions inside turning pools and straight sections, Figure 3 illustrates the frequency distributions of hydrodynamic variables by different study cases. Regarding u and k, it is possible to see that higher values are more probable in straight sections, which is confirmed when comparing the overall mean values. The ωxy probability distribution does not show a clear differentiation; however, in all cases the sign switches between turning pools and straight sections. For all fishways, the Kruskal-Wallis test indicates that straight sections and turning pools have the same frequency distribution in any of the variables (p-value < 0.001). Similar results are obtained for the comparison among all straight sections as well as among all turning pools (both global and paired comparison; all p-value < 0.001).
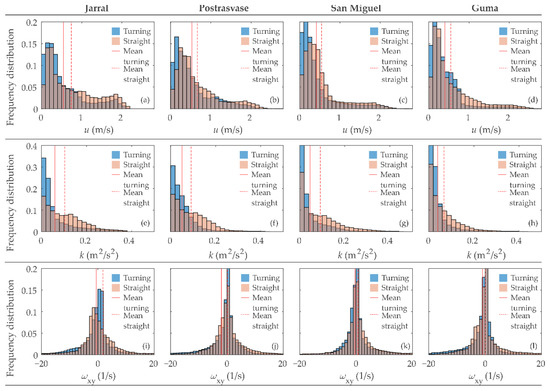
Figure 3.
Normalized frequency distribution of different hydrodynamic variables considered for different study cases. u: Velocity, k: turbulent kinetic energy, and ωxy: vorticity in the vertical plane.
3.2. Fish Response
The Mann-Whitney test revealed that all studied cases showed significant differences in standardized transit time when comparing turning pool and straight section (Figure 4). In all cases, the passage was slower through the turning pools.
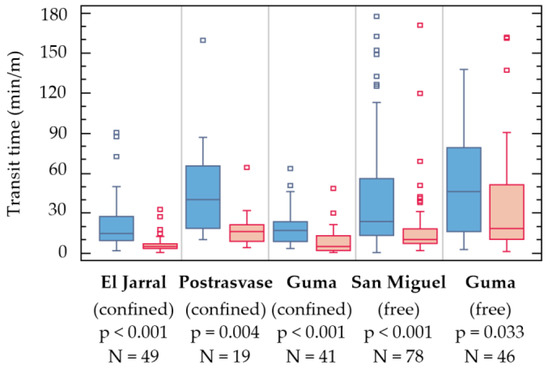
Figure 4.
Box-plot distribution of transit time (standardized to minutes per meter of height ascended) for turning pools (blue box) and straight sections (red box), for barbels. p-value refers to the MW test comparison of median values between turning and straight sections of the same field test case. N = number of events.
Transit time also showed significant differences between turning pools and straight sections when comparing by species (P. polylepis and L. sclateri in Postrasvase and El Jarral weirs) (Figure 5). In both study cases and for both species, the passage was slower through turning pools.
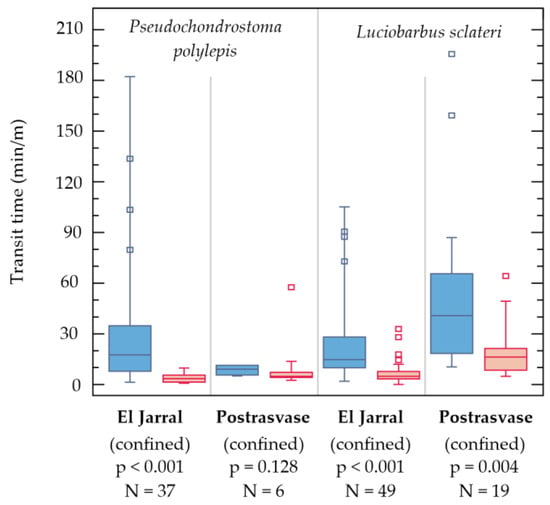
Figure 5.
Box-plot distribution of transit time (standardized to minutes per meter of height ascended) for turning pools (blue box) and straight sections (red box), separately by species (left: P. polylepis; right: L. sclateri). p-value refers to the comparison of median values between turning and straight sections of the same field test case. N = number of events.
When comparing transit time between the different test cases, species, and trial conditions, the Postrasvase test case showed a significantly slower passage for barbel in the turning pool and the straight section (Table 4). In addition, the Guma test case also showed a significantly slower passage under free trial conditions in the straight section.

Table 4.
Passage success in turning pools and Transit time in the different sections (median and InterQuartile Range, standardized to minutes per meter of height ascended). Superscript letters indicating significant differences between the different fishways for a given metric (p-value < 0.05; analysis done separately by species and trial condition).
Regarding passage success in turning pools, it exceeds 85% for all test cases and with no significant differences between them (p-value > 0.800 in all cases; comparisons based on species and trial condition).
4. Discussion
The use of turning pools is a common practice in the design of fishways, but, to date, there are few studies and many uncertainties about their hydraulic and biological performance. The present study provides new insights regarding some of the main hydraulic variables affecting fish passage when crossing turning pools, as well as passage performance for different designs of turning pools and potamodromous fish species in field conditions. The fish ascent was slower through the turning pools, but without evidence that suggested a problem for passage success or a relevant migration delay. The relationship between fish passage and hydraulic parameters seems to be related to the different hydrodynamic scenarios present in turning pools, which may suggest that fish use them for resting, or that they delay when they face this new hydrodynamic environment (when compared with the overall hydrodynamic performance of the fishway).
4.1. Numerical Models
Hydraulic variables showed differences between straight sections and turning pools, and between the different study cases. Recirculation areas, the main jet region, as well as the frequency distribution of the analyzed variables, showed a significantly different pattern between all studied cases and sections, providing differentiated hydrodynamic conditions that could have a relevant influence on swimming performance [46,47] and pool usage [19]. Considering fishway classical design guides [3,5,6], VPD (Volumetric Power Dissipation) is considered one of the main design parameters due to its simplicity and wide application. This variable is often related to the easiness for fish to pass through a pool, as well as its comfortability for fish. In all the studied cases and sections, VPD was within the recommended limits (less than 200–150 W/m3 [3,5]), with a much lower value in turning pools due to their higher water volume. However, VPD could sometimes be a conflicting variable [48], as it simplifies the local hydrodynamic performance of a fishway. For instance, two fishways with the same VPD but different geometrical characteristics will present different flow patterns that could have a direct impact on their suitability for fish. This is the case of VS connections vs. SNBO connections, and while the first is characterized by almost a 2D flow pattern (Appendix A), the latest shows a complete 3D development. This reinforces the need to relate more complex hydrodynamic analyses to the effective fish performance of fishways [18,34].
Regarding water velocity, all maximum values were located immediately after the connections (slot, notch, or orifice), and they were compatible with the maximum swimming performances of the studied species (greater than 3.0 m/s [44,45]), and most of them were below 2 m/s, in line with general recommendations [3]. The frequency distribution of this variable reveals that the areas of low velocity (<0.5 m/s) were more frequent than those with high velocities (>1.5 m/s), and these differences were higher in turning pools than straight pools. This suggests that, in both cases, the area of high velocities was concentrated in the jet, while in the rest of the volume of the pool, velocity ranges were lower, possibly allowing fish to rest. The same analysis can be done for turbulent kinetic energy. High values (“low” for k ≤ 0.05 m2/s2 and “high” for k > 0.05 m2/s2 [18]) were concentrated near the jet region, while most of the volume of the pools was dominated by low values, which are preferred by fish [4,19,49]. Regarding vorticity, vortices with length and width greater than fish can potentially disorient or destabilize the individuals [13,18,50,51], while vortices lower than the size range of fish and with a certain periodicity may enhance their swimming and passage [52]. In this sense, Marriner et al. [13] suggested that the addition of baffles in turning pools could split the large vortices observed in fishway pools into smaller vortexes more compatible with fish. Nevertheless, vorticity is a complex variable that can be measured by different metrics [28], and its relationship with fishway passage efficiency is still unclear. In our case and considering our experimental design, it was no possible to relate vorticity in turning pools and fish passage clearly.
4.2. Fish Responses
Some authors detected passage problems in turning pools for American shad and lake sturgeon [24,53], probably caused by suboptimal hydraulic conditions, which disorient fish and dislike or exceed swimming performance. White et al. [54] explored the possible bottleneck effect of turning pools via the analysis of fish accumulation in turning pools, although without conclusive results. None of the above was detected in our study. In general, standardized transit time in turning pools was between two and three times greater than in the straight sections. It could be related to the exploration of a new hydraulic environment, a reduction of the motivation, or the possible use of turning pools as resting areas [12,16]. In any case, considering that the total time expended in turning pools is negligible compared to the total time expended in straight sections, it only supposes an overall delay of a few minutes, which does not seem to generate a problem (an important migration delay).
Passage success in turning pools reinforces our previous conclusion. The obtained results were similar in all test cases and always higher than 80%, which suggests that, despite a small delay, fish can overcome turning pools. The overall success rates of these fishways are between 73% and 100% [20], and similar ranges suggest that turning pools are not the cause of failure.
Even though differences were found in the hydraulic parameters studied in both turning and straight pools, all of them are within the recommended values in these types of structures, and none seem to limit the ascent of the fish.
Regarding the different geometry of turning pools (chamfered, curved, right-angled; internal/external notches and with or without baffles), the studied designs did not show relevant differences that help to choose the best design for fish. In all cases, there were differences for transit time between turning and straight pools but, in general, there were no relevant differences between the types of turning pools, apart from Postrasvase. This test case is characterized mainly by the presence of a baffle in the turning pool (Figure 2). The installation of baffles in turning pools was first analyzed in the serial hydraulic study performed by Marriner et al. [13], suggesting that they could reduce the vortex size in favor of fish and generate an acceptable resting area downstream the baffle. Nevertheless, the obtained results do not allow for the conclusion of which is the best fishway performance with the presence of baffles in turning pools. It is worth mentioning that there are relevant differences between the studied geometries by Marriner et al. [13] and the Postrasvase fishway; thus, further biological research is necessary with regard to the presence of baffles in turning pools.
The effect of fish species and trial conditions was reported as relevant factors affecting fishway passage [20]. In the present work, none of these variables show significant clear relation with passage success or transit time.
5. Summary and Conclusions
Considering the above analysis, it is possible to conclude that the different hydrodynamics conditions of turning pools provoke a slower transit of fish through them, but without affecting neither the passage success nor migration delay. The effect of turning pool hydrodynamics on fish remains unclear, even considering that the frequency distribution of hydrodynamic variables seems more favorable in turning pools than in straight sections. Therefore, the present study validates the usage of turning pools as a key design element to develop more compact fishways and to optimize their location. However, it is worth mentioning that all the turning pools studied here were designed considering the recommendations for resting pools, that is to say, with at least twice the volume of a straight pool; thus, until further studies are conducted, a similar approach is recommended for new designs.
Future research about the use of turning pools as a resting area and the influence of hydraulic parameters in passage time considering other turbulence parameters is recommended, with the aim of clarifying fish passage performance through fishways. For this, it would also be advisable to compare e.g., the ascent between similar stepped fishways with and without turning pools, and the ascent between straight sections prior and after turning pools, as well as to relate results to fish physiology.
Author Contributions
Conceptualization: F.J.S.-R., F.J.B.-C. and J.F.F.-P.; methodology: J.F.F.-P. and F.J.B.-C.; validation: F.J.S.-R., F.J.B.-C. and J.F.F.-P.; field experiments: F.J.S.-R., F.J.B.-C., J.F.F.-P. and J.V.-C.; data curation: F.J.B.-C. and J.V.-C.; writing—original draft preparation: F.J.B.-C. and J.F.F.-P.; writing—review and editing: F.J.S.-R., A.M.d.A.-P. and J.V.-C.; supervision: A.M.d.A.-P.; project administration: F.J.S.-R.; funding acquisition: F.J.S.-R. All authors have read and agreed to the published version of the manuscript.
Funding
Contributions of Juan Francisco Fuentes-Pérez and Francisco Javier Bravo Cordoba were partly financed by a Torres Quevedo grant, PTQ2018-010162 and PTQ2016-08494, respectively. This project has received funding from the European Union’s H2020 research and innovation program under grant agreement No. 727830, FIThydro.
Institutional Review Board Statement
The study was conducted according to the European Union ethical guidelines (Directive 2010/63/UE) and Spanish Act RD 53/2013 for the protection of animals used for scientific purposes, with the favorable report from the Animal Research Ethics Committee from the University of Valladolid as well as the approval of the competent authorities, i.e., Regional Government on Natural Resources (Junta de Castilla y León and Gobierno de Murcia) and Water Management Authority (Confederación Hidrográfica del Duero y del Segura).
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon reasonable request to the corresponding author.
Acknowledgments
We specifically thank Juan Carlos Romeral de la Puente (SAVASA) for letting us use his installations in Guma HPP. We would also like to thank the GEA staff and Itagra.ct tech-nological centre for logistical support, as well as the fishing services of the Regional Government on Natural Resources (Castilla y León) and the Water Management Authority (Confederación Hidrográfica del Duero).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Velocity Contours
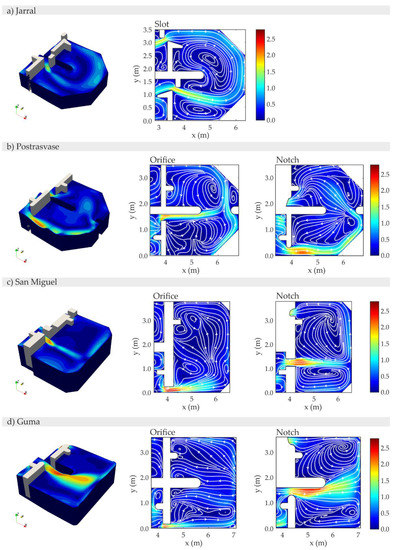
Figure A1.
u (m/s) turning pool contours in the middle section of the orifice, notch, and slot.
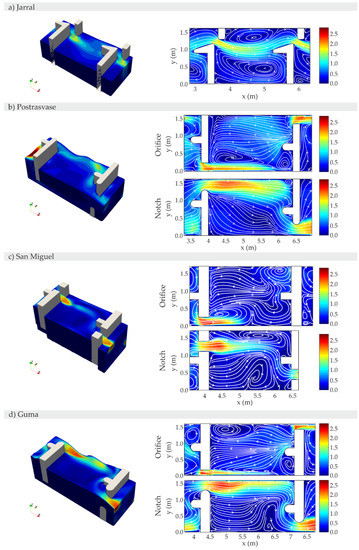
Figure A2.
u (m/s) straight section contours in the middle section of the orifice, notch, and slot.
Appendix A.2. Turbulent Kinetic Energy Contours
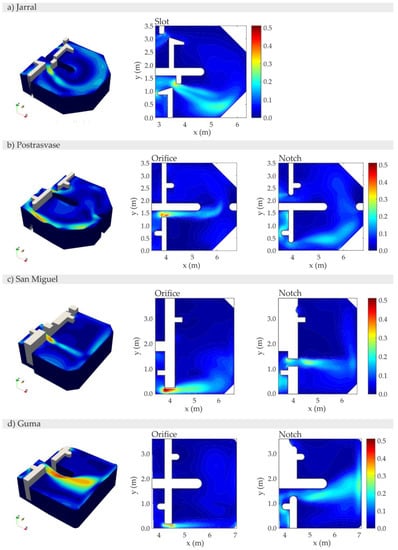
Figure A3.
k (J/kg) turning pool contours in the middle section of the orifice, notch, and slot.
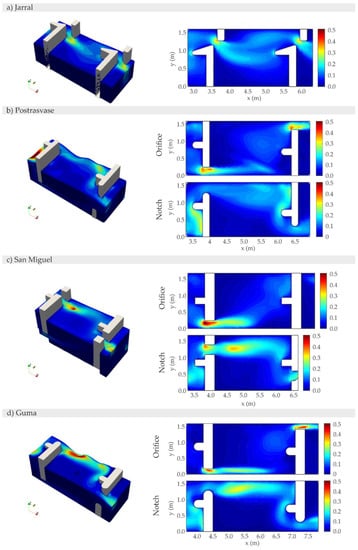
Figure A4.
k (J/kg) straight section contours in the middle section of the orifice, notch, and slot.
Appendix A.3. Vorticity Contours
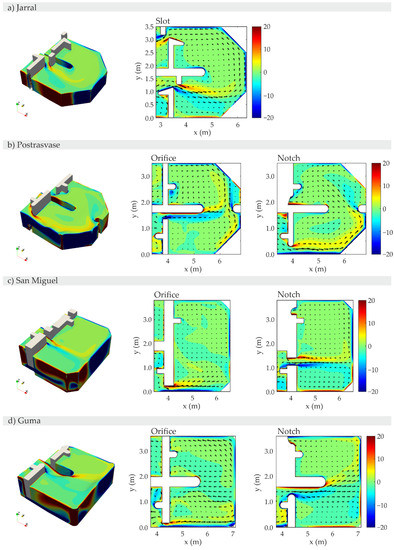
Figure A5.
ωxy (1/s) turning pool contours in the middle section of the orifice, notch, and slot.
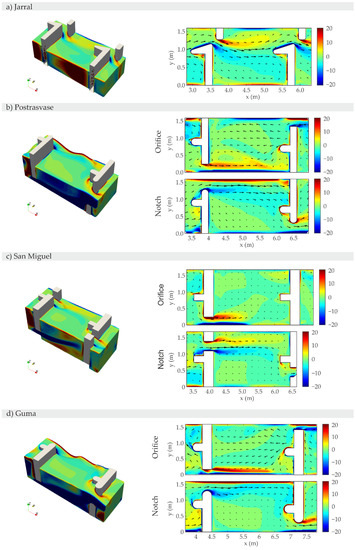
Figure A6.
ωxy (1/s) straight section contours in the middle section of the orifice, notch, and slot.
Appendix B
Appendix B.1. Velocity (m/s)
Appendix B.2. Turbulence kinetic energy definition (m2/s2 = J/kg)
Appendix B.3. Vorticity definition (s−1)
References
- Clay, C.H.; Eng, P. Design of Fishways and Other Fish. Facilities; Apple Academic Press: Palm Bay, FL, USA, 2017. [Google Scholar]
- Silva, A.T.; Lucas, M.C.; Castro-Santos, T.; Katopodis, C.; Baumgartner, L.J.; Thiem, J.D.; Aarestrup, K.; Pompeu, P.S.; O’Brien, G.C.; Braun, D.C.; et al. The future of fish passage science, engineering, and practice. Fish. Fish. 2018, 19, 340–362. [Google Scholar] [CrossRef]
- FAO/DVWK Fish Passes: Design, Dimensions, and Monitoring; FAO: Rome, Italy, 2002; ISBN 9251048940.
- Santos, J.M.; Silva, A.; Katopodis, C.; Pinheiro, P.; Pinheiro, A.; Bochechas, J.; Ferreira, M.T. Ecohydraulics of pool-type fishways: Getting past the barriers. Ecol. Eng. 2012, 48, 38–50. [Google Scholar] [CrossRef]
- Larinier, M. Pool Fishways, Pre-Barrages and Natural Bypass Channels. Bull. Fr. Pêche Piscic. 2002, 364, 54–82. [Google Scholar] [CrossRef]
- Martínez de Azagra, A. Escalas Para Peces; ETSIIAA; Universidad de Valladolid: Palencia, Spain, 1999. [Google Scholar]
- Rajaratnam, N.; Katopodis, C.; Solanki, S. New designs for vertical slot fishways. Can. J. Civ. Eng. 1992, 19, 402–414. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.F.; Sanz-Ronda, F.J.; Paredes, A.M.D.A.; García-Vega, A. Modeling Water-Depth Distribution in Vertical-Slot Fishways under Uniform and Nonuniform Scenarios. J. Hydraul. Eng. 2014, 140, 06014016. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.F.; Sanz-Ronda, F.J.; De Azagra, A.M.; García-Vega, A. Non-uniform hydraulic behavior of pool-weir fishways: A tool to optimize its design and performance. Ecol. Eng. 2016, 86, 5–12. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Van Der Vinne, G.; Katopodis, C. Hydraulics of Vertical Slot Fishways. J. Hydraul. Eng. 1986, 112, 909–927. [Google Scholar] [CrossRef]
- Puertas, J.; Pena, L.; Teijeiro, T. Experimental Approach to the Hydraulics of Vertical Slot Fishways. J. Hydraul. Eng. 2004, 130, 10–23. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Katopodis, C.; Wu, S.; Sabur, M.A. Hydraulics of Resting Pools for Denil Fishways. J. Hydraul. Eng. 1997, 123, 632–638. [Google Scholar] [CrossRef]
- Marriner, B.A.; Baki, A.B.M.; Zhu, D.Z.; Thiem, J.D.; Cooke, S.J.; Katopodis, C. Field and numerical assessment of turning pool hydraulics in a vertical slot fishway. Ecol. Eng. 2014, 63, 88–101. [Google Scholar] [CrossRef]
- Marriner, B.A.; Baki, A.B.; Zhu, D.Z.; Cooke, S.J.; Katopodis, C. The hydraulics of a vertical slot fishway: A case study on the multi-species Vianney-Legendre fishway in Quebec, Canada. Ecol. Eng. 2016, 90, 190–202. [Google Scholar] [CrossRef]
- Fish, U.S.; Service, W. Fish Passage Engineering Design Criteria; USFWS Northeast Reg.: Hadley, MA, USA, 2017.
- Cooke, S.J.; Cech, J.J.; Glassman, D.M.; Simard, J.; Louttit, S.; Lennox, R.J.; Cruz-Font, L.; O’Connor, C.M. Water resource development and sturgeon (Acipenseridae): State of the science and research gaps related to fish passage, entrainment, impingement and behavioural guidance. Rev. Fish. Biol. Fish. 2020, 30, 219–244. [Google Scholar] [CrossRef]
- Wang, R.; David, L.; Larinier, M. Contribution of experimental fluid mechanics to the design of vertical slot fish passes. Knowl. Manag. Aquat. Ecosyst. 2010, 396, 2. [Google Scholar] [CrossRef]
- Silva, A.T.; Katopodis, C.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N. Cyprinid swimming behaviour in response to turbulent flow. Ecol. Eng. 2012, 44, 314–328. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.F.; Eckert, M.; Tuhtan, J.A.; Ferreira, M.T.; Kruusmaa, M.; Branco, P. Spatial preferences of Iberian barbel in a vertical slot fishway under variable hydrodynamic scenarios. Ecol. Eng. 2018, 125, 131–142. [Google Scholar] [CrossRef]
- Bravo-Córdoba, F.J.; Valbuena-Castro, J.; García-Vega, A.; Fuentes-Pérez, J.F.; Ruiz-Legazpi, J.; Sanz-Ronda, F.J. Fish passage assessment in stepped fishways: Passage success and transit time as standardized metrics. Ecol. Eng. 2021, 162, 106172. [Google Scholar] [CrossRef]
- Bunt, C.M.; Cooke, S.J.; McKinley, R.S. Assessment of the Dunnville Fishway for Passage of Walleyes from Lake Erie to the Grand River, Ontario. J. Great Lakes Res. 2000, 26, 482–488. [Google Scholar] [CrossRef]
- Pon, L.B.; Cooke, S.J.; Hinch, S.G. Passage Efficiency and Migration Behaviour of Salmonid Fishes at the Seton Dam Fishway; Department of Forest Sciences: Vancouver, BC, Canada, 2006. [Google Scholar]
- Silva, A.T.; Hatry, C.; Thiem, J.D.; Gutowsky, L.F.G.; Hatin, D.; Zhu, D.Z.; Dawson, J.W.; Katopodis, C.; Cooke, S.J. Behaviour and Locomotor Activity of a Migratory Catostomid during Fishway Passage. PLoS ONE 2015, 10, e0123051. [Google Scholar] [CrossRef] [PubMed]
- Thiem, J.D.; Dawson, J.W.; Hatin, D.; Danylchuk, A.J.; Dumont, P.; Gleiss, A.C.; Wilson, R.P.; Cooke, S.J. Swimming activity and energetic costs of adult lake sturgeon during fishway passage. J. Exp. Biol. 2016, 219, 2534–2544. [Google Scholar] [CrossRef] [PubMed]
- Thiem, J.; Binder, T.; Dawson, J.; Dumont, P.; Hatin, D.; Katopodis, C.; Zhu, D.; Cooke, S.; Thiem, J. Behaviour and passage success of upriver-migrating lake sturgeon Acipenser fulvescens in a vertical slot fishway on the Richelieu River, Quebec, Canada. Endanger. Species Res. 2011, 15, 1–11. [Google Scholar] [CrossRef]
- Noonan, M.J.; Grant, J.W.; Jackson, C.D. A quantitative assessment of fish passage efficiency. Fish. Fish. 2011, 13, 450–464. [Google Scholar] [CrossRef]
- Bunt, C.M.; Castro-Santos, T.; Haro, A. Reinforcement and Validation of the Analyses and Conclusions Related to Fishway Evaluation Data from Bunt Performance of Fish Passage Structures at Upstream Barriers to Migratio. River Res. Appl. 2016, 32, 2125–2137. [Google Scholar] [CrossRef]
- Castro-Santos, T.; Cotel, A.; Webb, P. Fishway Evaluations for Better Bioengineering: An Integrative Approach A Framework for Fishway. Am. Fish. Soc. Symp. 2009, 69, 557–575. [Google Scholar]
- Bravo-Córdoba, F.J.; Sanz-Ronda, F.J.; Ruiz-Legazpi, J.; Valbuena-Castro, J.; Makrakis, S. Vertical slot versus submerged notch with bottom orifice: Looking for the best technical fishway type for Mediterranean barbels. Ecol. Eng. 2018, 122, 120–125. [Google Scholar] [CrossRef]
- Córdoba, F.J.B.; Sanz-Ronda, F.; Navas-Pariente, A.; Valbuena-Castro, J. Comportamiento del barbo ibérico (Luciobarbus bocagei) en una escala de peces de vertedero sumergido con orificio de fondo. Cuad. Soc. Esp. Cienc. For. 2019, 45, 231–240. [Google Scholar] [CrossRef]
- Sanz-Ronda, F.J.; Bravo-Córdoba, F.J.; Sánchez-Pérez, A.; García-Vega, A.; Valbuena-Castro, J.; Fernandes-Celestino, L.; Torralva, M.; Oliva-Paterna, F.J. Passage Performance of Technical Pool-Type Fishways for Potamodromous Cyprinids: Novel Experiences in Semiarid Environments. Water 2019, 11, 2362. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces; University of London: London, UK, 1997. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.; Silva, A.; Tuhtan, J.; García-Vega, A.; Carbonell-Baeza, R.; Musall, M.; Kruusmaa, M. 3D modelling of non-uniform and turbulent flow in vertical slot fishways. Environ. Model. Softw. 2018, 99, 156–169. [Google Scholar] [CrossRef]
- Barton, A.F.; Keller, R.J.; Katopodis, C. Verification of a numerical model for the prediction of low slope vertical slot fishway hydraulics. Australas. J. Water Resour. 2009, 13, 53–60. [Google Scholar] [CrossRef]
- Bombač, M.; Novak, G.; Rodic, P.; Četina, M. Numerical and physical model study of a vertical slot fishway. J. Hydrol. Hydromech. 2014, 62, 150–159. [Google Scholar] [CrossRef]
- Cea, L.; Pena, L.; Puertas, J.; Vázquez-Cendón, M.E.; Peña, E. Application of Several Depth-Averaged Turbulence Models to Simulate Flow in Vertical Slot Fishways. J. Hydraul. Eng. 2007, 133, 160–172. [Google Scholar] [CrossRef]
- Greenshields, C.J. The Open Source CFD Toolbox User Guide; OpenFOAM Foundation Ltd.: London, UK, 2015. [Google Scholar]
- Quaresma, A.L.; Romão, F.; Branco, P.; Ferreira, M.T.; Pinheiro, A.N. Multi slot versus single slot pool-type fishways: A modelling approach to compare hydrodynamics. Ecol. Eng. 2018, 122, 197–206. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.F.; García-Vega, A.; Sanz-Ronda, F.J.; Paredes, A.M.D.A. Villemonte’s approach: A general method for modeling uniform and non-uniform performance in stepped fishways. Knowl. Manag. Aquat. Ecosyst. 2017, 418, 23. [Google Scholar] [CrossRef]
- Doadrio, I. Atlas y Libro Rojo de los Peces Continentales de España; Ministerio de Medio Ambiente: Madrid, Spain, 2002; ISBN 84-8014-313-4.
- Rodriguez-Ruiz, A.; Granado-Lorencio, C. Spawning period and migration of three species of cyprinids in a stream with Mediterranean regimen (SW Spain). J. Fish. Biol. 1992, 41, 545–556. [Google Scholar] [CrossRef]
- García-Vega, A.; Fuentes-Pérez, J.F.; Bravo-Córdoba, F.J.; Ruiz-Legazpi, J.; Valbuena-Castro, J.; Sanz-Ronda, F.J. Pre-reproductive movements of potamodromous cyprinids in the Iberian Peninsula: When environmental variability meets semipermeable barriers. Hydrobiology 2021, 1–22. [Google Scholar] [CrossRef]
- Sanz-Ronda, F.J.; Ruiz-Legazpi, J.; Bravo-Córdoba, F.J.; Makrakis, S.; Castro-Santos, T. Sprinting performance of two Iberian fish: Luciobarbus bocagei and Pseudochondrostoma duriense in an open channel flume. Ecol. Eng. 2015, 83, 61–70. [Google Scholar] [CrossRef]
- Ruiz-Legazpi, J.; Sanz-Ronda, F.J.; Bravo-córdoba, F.J.; Fuentes-Pérez, J.F.; Castro-Santos, T. Influence of environmental and biometric factors on the swimming capacity of the Iberian barbel (Luciobarbus bocageiSteindachner, 1864), an endemic po-tamodromous cyprinid of the Iberian Peninsula. Limnetica 2018, 37, 251–265. [Google Scholar] [CrossRef]
- Tarrade, L.; Texier, A.; David, L.; Larinier, M. Topologies and measurements of turbulent flow in vertical slot fishways. Hydrobiology 2008, 609, 177–188. [Google Scholar] [CrossRef]
- Liao, J.C. A review of fish swimming mechanics and behaviour in altered flows. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1973–1993. [Google Scholar] [CrossRef] [PubMed]
- Towler, B.; Mulligan, K.; Haro, A. Derivation and application of the energy dissipation factor in the design of fishways. Ecol. Eng. 2015, 83, 208–217. [Google Scholar] [CrossRef]
- Alexandre, C.; Quintella, B.; Silva, A.; Mateus, C.; Romão, F.; Branco, P.; Ferreira, M.; Almeida, P. Use of electromyogram telemetry to assess the behavior of the Iberian barbel (Luciobarbus bocagei Steindachner, 1864) in a pool-type fishway. Ecol. Eng. 2013, 51, 191–202. [Google Scholar] [CrossRef]
- Pavlov, D.; Lupandin, A.; Skorobogatov, M. The Effects of Flow Turbulence on the Behavior and Distribution of Fish. J. Ich-thyol. 2000, 20, 232–261. [Google Scholar]
- Tritico, H.M.; Cotel, A.J. The effects of turbulent eddies on the stability and critical swimming speed of creek chub (Semotilus atromaculatus). J. Exp. Biol. 2010, 213, 2284–2293. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.C. Neuromuscular control of trout swimming in a vortex street: Implications for energy economy during the Karman gait. J. Exp. Biol. 2004, 207, 3495–3506. [Google Scholar] [CrossRef] [PubMed]
- Haro, A.; Castro-Santos, T. Passage of American Shad: Paradigms and Realities. Mar. Coast. Fish. 2012, 4, 252–261. [Google Scholar] [CrossRef]
- White, L.J.; Harris, J.H.; Keller, R.J. Movement of three non-salmonid fish species through a low-gradient vertical-slot fishway. River Res. Appl. 2011, 27, 499–510. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).