The Identification of Fouling in Reverse Osmosis in the Treatment of Water with Petroleum Substances
Abstract
1. Introduction
1.1. Theoretical Background
Constant Pressure Pore-Blocking Model (Hermia Model)
2. Materials and Methods
2.1. Analytical Methodology
GC–MS BTEX Chromatographic Analysis
3. Results and Discussion
Hermia Model
4. Conclusions
- The model developed by J. Hermia made it possible to determine the pore blocking mechanisms for the membrane during surface and surface water treatment with BTEX. The concentration of BTEX in the water did not affect the blocking mechanism of the diaphragm. The research confirmed a good agreement between the experimental and theoretical results.
- Based on the comparison of the results obtained experimentally with the results obtained based on the Hermia model analysis, we showed that the dominant membrane blocking mechanism in the studied process was the formation of a filter cake.
- This means that polyamide membrane fouling by BTEX and mono-aromatic hydrocarbons in surface water followed a sequence of mechanisms with an initial flux decline due to an internal pore blocking mechanism, followed by complete pore blocking with subsequent intermediate pore blocking. Finally, it should be pointed out that both resistance-in-series analysis as well as fouling mechanism identification led to consistent conclusions: the membrane fouling was of external type; the two identified pore blocking mechanisms (complete and intermediate) were also external types.
- The fouling of the membrane was of the external type; we identified two pore blocking mechanisms (n = 0, cake blocking; and n = 1, temporary blocking).
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammadi, T.; Kazemimoghadam, M.; Saadabadi, M. Modeling of membrane fouling and flux decline in reverse osmosis during separation of oil in water emulsions. Desalination 2003, 157, 369–375. [Google Scholar] [CrossRef]
- Kargol, A. A mechanistic model of transport processes in porous membranes generated by osmotic and hydrostatic pressure. J. Membr. Sci. 2001, 191, 61–69. [Google Scholar] [CrossRef]
- Cwirko, K.; Tomczak, E.; Szaniawska, D. Membrane fouling in the ultrafiltration of water–protein–sodium chloride model systems. Chem. Process. Eng. 2018, 39, 185–196. [Google Scholar]
- Yeit, H.T.; Zhong, Z.W.; Mohd, S.T.; Abdul, W.M. Fouling behaviours of two stages microalgae/membrane filtration system applied to palm oil mill effluent treatment. Membr. Water Treat. 2018, 9, 373–383. [Google Scholar]
- Piekutin, J.; Skoczko, I. Use of stripping tower and reverse osmosis in removal of petroleum hydrocarbons from water. Desalination Water Treat. 2013, 52, 3714–3718. [Google Scholar] [CrossRef]
- Hermia, J. Constant pressure blocking filtration laws. Inst. Chem. Eng. 1982, 60, 183–187. [Google Scholar]
- Liang, S.; Lian, T.; Jian, Z.; Xuan, Z.; Shipeng, S.; Yan, W. Developing high–performance thin–film composite forward osmosis membranes by various tertiary amine catalysts for desalination. Adv. Compos. Hybrid. Mater. 2019, 2, 51–69. [Google Scholar]
- Konieczny, K.; Rajca, M.; Bodzek, M.; Gambołyś, B. Influence of NOM properties on the fouling of ultrafiltration membranes. Environ. Pollut. 2008, 30, 3–8. [Google Scholar]
- Mielczarek, K.; Bohdziewicz, J. Performance prediction of ultrafiltration Treatment of post–process coke wastewater based on the assumptions of hydraulic filtration resistance model. Arch. Environ. Prot. 2011, 37, 107–118. [Google Scholar]
- Szaniawska, D.; Kuca, M. Fouling of ceramic membranes in the ultrafiltration process of protein and sodium chloride solutions. Inż. Ap. Chem. 2010, 49, 109–110. [Google Scholar]
- Piekutin, J. Estimate of possibilities removal of selected nitrogen forms from infiltration water and optimization of reversed osmosis system. ECE 2008, 15, 9–16. [Google Scholar]
- Guo, J.; Bao, H.; Zhang, Y.; Shen, X.; Kim, J.K.; Ma, J.; Shao, L. Unravelling intercalation–regulated nanoconfinement for durably ultrafast sieving graphene oxide membranes. J. Membr. Sci. 2021, 619, 118791. [Google Scholar] [CrossRef]
- Lee, S.; Lueptow, R.M. Rotating reverse osmosis: A dynamic model for flux and rejection. J. Membr. Sci. 2001, 192, 129–143. [Google Scholar] [CrossRef]
- Konieczny, K.; Rafa, J. Modeling of the membrane filtration process of natural waters. Pol. J. Environ. Stud. 2000, 9, 57–64. [Google Scholar]
- Jamal, K.; Khan, M.A.; Kamil, M. Mathematical modeling of reverse osmosis systems. Desalination 2004, 160, 29–42. [Google Scholar] [CrossRef]
- Setareh, H.; Mehdi, A.; Hamed, J. Investigation of Fouling Mechanisms Using Surface Morphology and Physicochemical Membrane Features. Chem. Eng. Technol. 2019, 42, 1310–1320. [Google Scholar]
- Salahi, A.; Abbasi, M.; Mohammadi, T. Permeate flux decline during UF of oily wastewater: Experimental and modeling. Desalination 2010, 251, 153–160. [Google Scholar] [CrossRef]
- Piekutin, J.; Skoczko, I.; Ignatowicz, K. Use of integrated process of petroleum removal from water. Desalination Water 2016, 57, 1593–1597. [Google Scholar] [CrossRef]
- Chang, E.E.; Yang, S.Y.; Huang, C.P.; Liang, C.H.; Chiang, P.C. Assessing the fouling mechanisms of high–pressure nanofiltration membrane using the modified Hermia model and the resistance–in–series model. Sep. Purif. Technol. 2011, 79, 329–336. [Google Scholar] [CrossRef]
- Shalana, L.B.; Kathleen, M.L.; Sherri, L.M. Evaluation of Ozone Pretreatment on Flux Parameters of Reverse Osmosis for Surface Water Treatment. Ozone Sci. Eng. 2008, 30, 152–164. [Google Scholar]
- Konieczny, K. Ultrafiltration and microfiltration in water treatment for municipal purposes. SJSUTST 2002, 42, 36–44, [In Polish]. [Google Scholar]
- Razi, B.; Aroujalian, A.; Fathizadeh, M. Modeling of fouling layer deposition in cross–flow microfiltration durint tomato juice clarification. Food Bioprod. Process. 2012, 90, 841–848. [Google Scholar] [CrossRef]
- Haigang, L.; Huanjin Xia, H.; Yingxin, M. Modeling organic fouling of reverse osmosis membrane: From adsorption to fouling layer formation. Desalination 2016, 386, 25–31. [Google Scholar]
- ASTM. Standard Test Method for Silt Density Index (SDI) of Water, in Designation: D 4189—95 (Reapproved 2002); ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Li, Q.; Elimelech, M. Organic fouling and chemical cleaning of nanofiltration membranes: Measurements and mechanisms. Environ. Sci. Technol. 2004, 38, 4683–4693. [Google Scholar] [CrossRef]
- Bodzek, M.; Konieczny, K. Membrane Techniques in the Removal of Inorganic Anionic Micropollutants from Water Environment State of the Art. Arch. Environ. Prot. 2011, 37, 15–22. [Google Scholar]
- Sioutopoulos, D.C.; Karabelas, A.J. Correlation of organic fouling resistances in RO and UF membrane filtration under constant flux and constant pressure. J. Membr. Sci. 2012, 34, 407–408. [Google Scholar] [CrossRef]
- Bellona, C.; Drewes, J.E.; Xu, P.; Amy, G. Factors affecting the rejection of organic solutes during NF/RO treat;ment—A literature review. Water Res. 2004, 38, 2795. [Google Scholar] [CrossRef]
- Wenten, I.G.; Khoiruddin, M. Reverse osmosis applications: Prospect and challenges. Desalination 2016, 391, 112–125. [Google Scholar] [CrossRef]
- Yorgun, M.S.; Balcioglu, I.A.; Saygin, O. Performance comparison of ultrafiltration, nanofiltration and reverse osmosis on whey treatment. Desalination 2008, 229, 204–216. [Google Scholar] [CrossRef]
- Bird, M.R.; Bartlett, M. Measuring and modeling flux recovery during the chemical cleaning of MF membranes for the processing of whey protein concentrate. J. Food Eng. 2002, 53, 143–152. [Google Scholar] [CrossRef]
- Chen, K.L.; Song, L.; Ong, S.L.; Ng, W.J. The development of membrane fouling in full–scale RO processes. J. Membr. Sci. 2004, 232, 63–72. [Google Scholar] [CrossRef]
- Košutić, K.; Kunst, B. RO and NF membrane fouling and cleaning and pore size distribution variations. Desalination 2002, 150, 113–120. [Google Scholar] [CrossRef]
- Amiri, M.C.; Samiei, M. Enhancing permeate flux in a RO plant by controlling membrane fouling. Desalination 2007, 207, 361–369. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Melián-Martel, N.; Nuez, I. Short Review on Predicting Fouling in RO desalination. Membranes 2017, 7, 62. [Google Scholar] [CrossRef]
- Jepsen, K.L.; Bram, M.V.; Pedersen, S.; Yang, Z. Membrane Fouling for Produced Water Treatment: A Review Study from a Process Control Perspective. Water 2018, 10, 847. [Google Scholar] [CrossRef]
- Kostogloua, M.; Karabelasb, A.J. A mathematical study of the evolution of fouling and operating parameters throughout membrane sheets comprising spiral wound modules. Chem. Eng. J. 2012, 187, 222–231. [Google Scholar] [CrossRef]
- Pascuala, X.; Gub, H.; Bartmanb, A.R.; Zhub, A.; Rahardiantob, A.; Giralta, J.; Ralloc, R.; Christofidesb, P.D.; Cohenb, Y. Data-driven models of steady state and transient operations of spiral–wound RO plant. Desalination 2013, 316, 154–161. [Google Scholar] [CrossRef]
- Weinrich, L.; Haas, C.N.; LeChevallier, M.W. Recent advances in measuring and modeling reverse osmosis membrane fouling in seawater desalination: A review. J. Water Reuse Desalination 2013, 3, 85–101. [Google Scholar] [CrossRef][Green Version]
- Hadadian, Z.; Zahmatkesh, S.; Ansari, M.; Haghighi, A.; Moghimipour, E. Mathematical and experimental modeling of reverse osmosis (RO) process. Sep. Technol. Thermodyn. 2021, 38, 366–379. [Google Scholar]
- Xianhui, L.; Danyan, Y.; Genghong, A.; Dawei, J.; Jianxin, L. Fouling and Cleaning of Reverse Osmosis Membranes duing Municipal Tap Water Treatment on a Pilot–Scale Plant. J. Water Sustain. 2011, 1, 139–151. [Google Scholar]
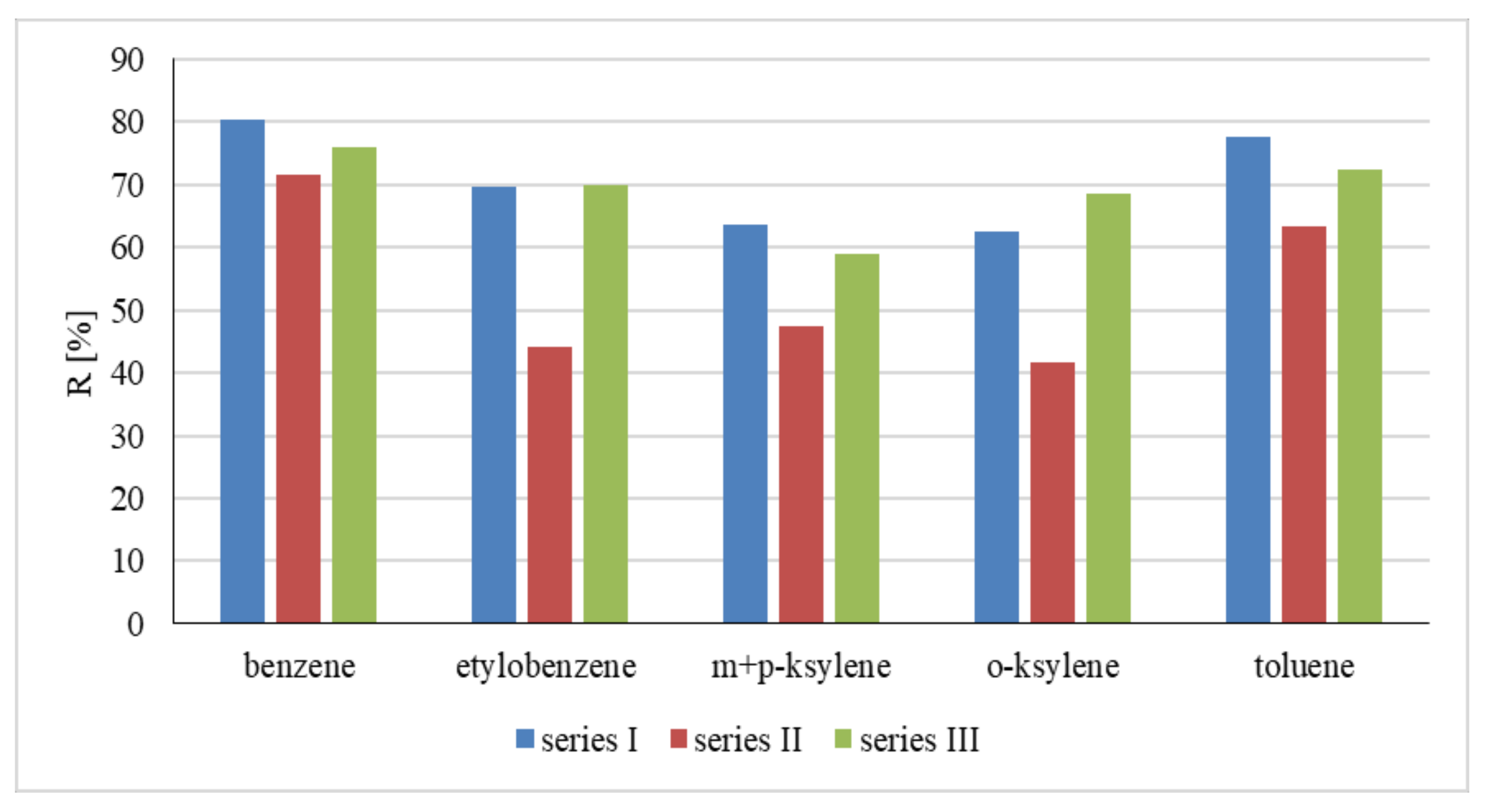
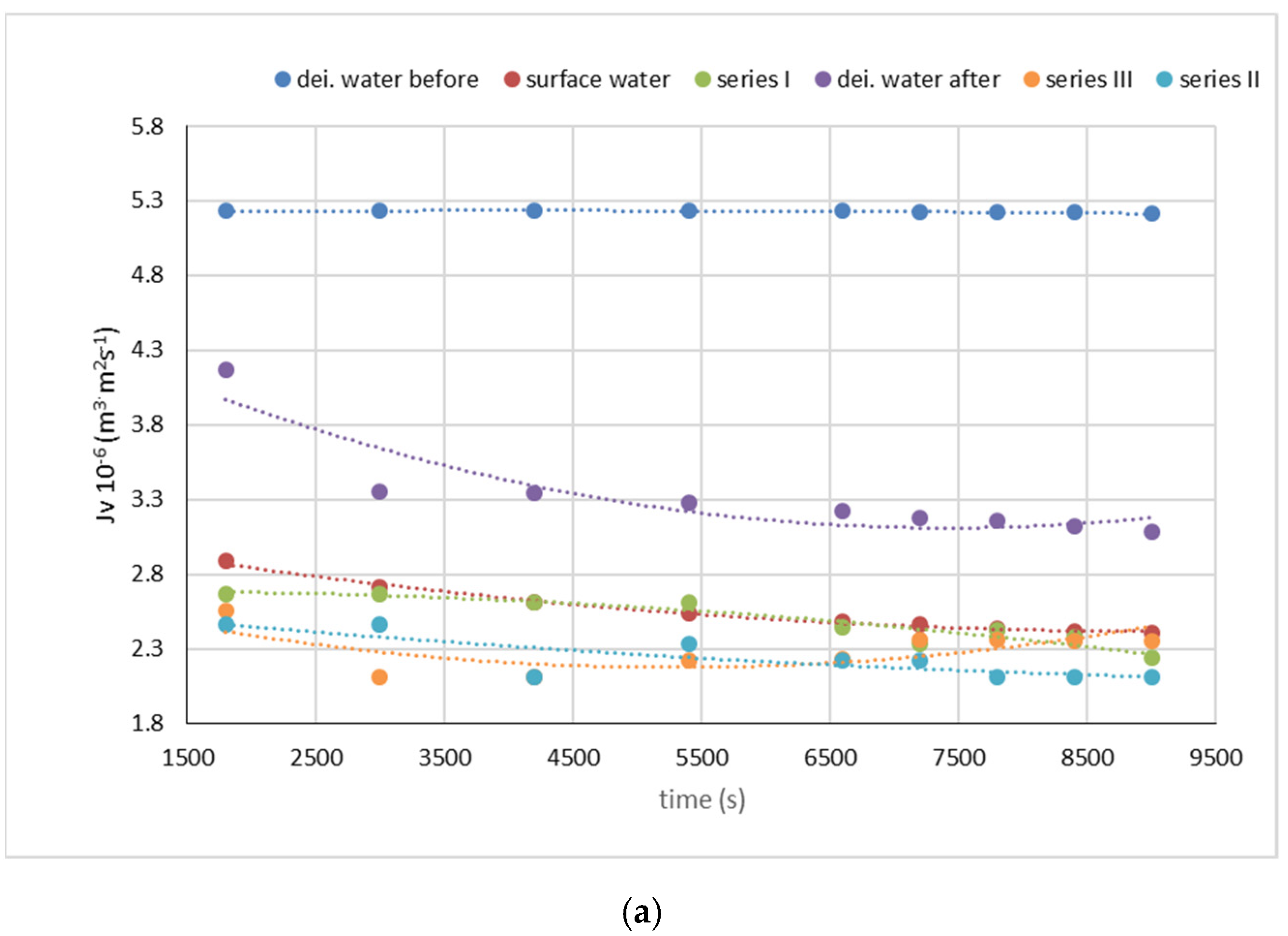
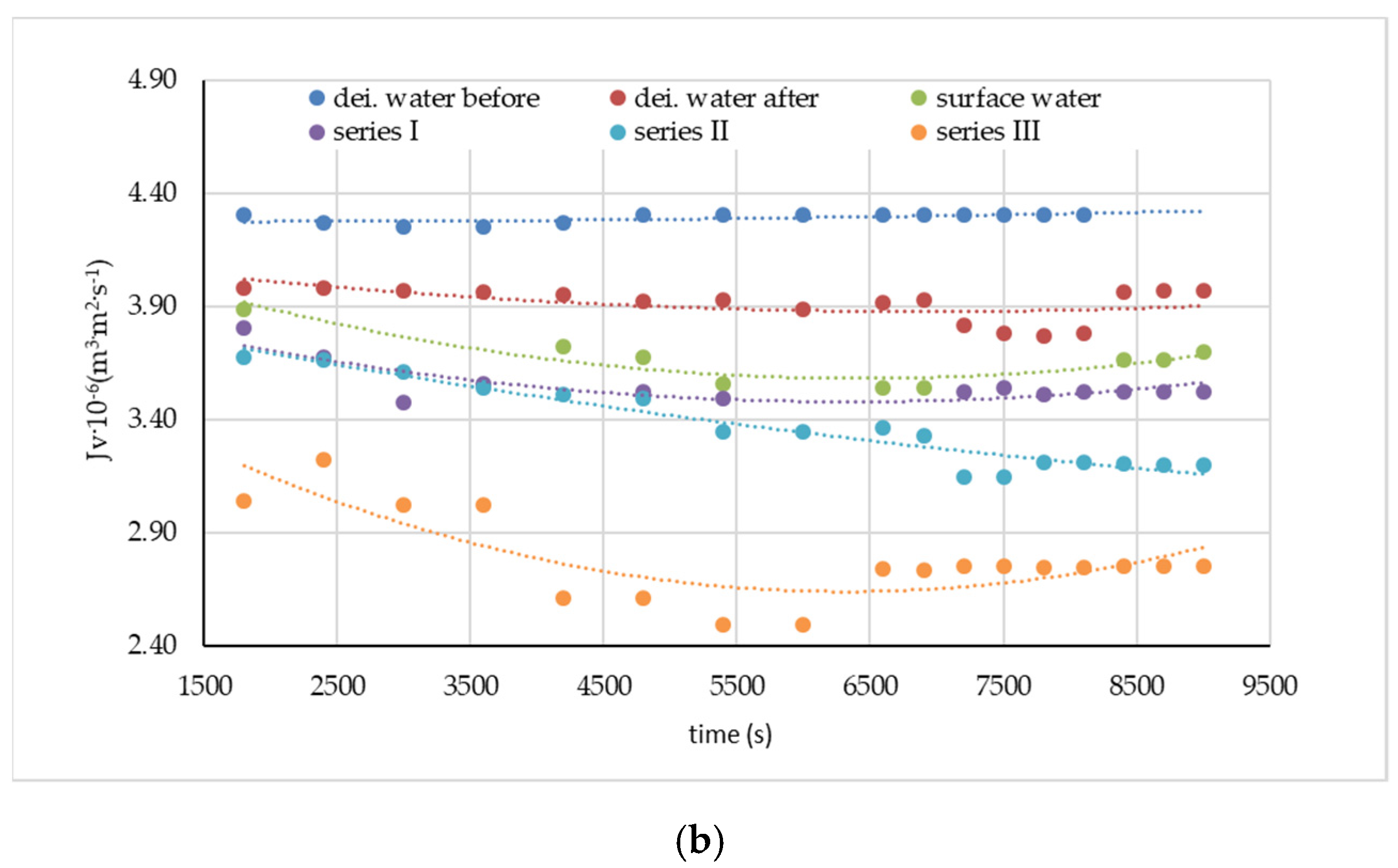
| Water Type | Symbol | Absorbance (UV254) 1/cm | ΣBTEX | ||
|---|---|---|---|---|---|
| mg dm−3 | |||||
| Min | Max | ||||
| Surface | Water 2 | 0.097 | 0.122 | 0.000 | 1.700 |
| Surface + MP * | Water 3 | 0.202 | 0.511 | 0.800 | 17.00 |
| Mono-Aromatic Hydrocarbons (mg dm−3) | |||
|---|---|---|---|
| series I | series II | series III | |
| C6H6—benzene | 0.033 | 0.326 | 1.724 |
| C6H5−C2H5—ethylbenzene | 0.083 | 0.888 | 2.119 |
| C6H4(CH3)2—m+p-xylene | 0.270 | 3.960 | 5.148 |
| C6H4(CH3)2—o-xylene | 0.105 | 1.090 | 1.416 |
| C6H5CH3—toluene | 0.311 | 3.234 | 5.356 |
| ΣBTEX | 0.802 | 9.498 | 15.76 |
| Parameter | Unit | Surface Water | R (%) | ||||
|---|---|---|---|---|---|---|---|
| Values | Standard Deviation | ||||||
| Min | Max | Mean | Median | ||||
| Color | mg Pt dm−3 | 10.00 | 22.00 | 16.91 | 12.00 | 1.774 | 96.00 |
| Turbidity | NTU | 0.900 | 2.000 | 1.200 | 1.30 | 0.793 | 100.0 |
| Conductivity | µS/cm | 360.0 | 410.0 | 379.1 | 388.0 | 21.76 | 98.00 |
| pH | 7.190 | 7.600 | 7.270 | 7.260 | 0.110 | ||
| Calcium | mg Ca2+ dm−3 | 79.20 | 89.51 | 83.53 | 84.10 | 2.701 | 96.00 |
| Manganese | mg Mn dm−3 | 0.020 | 0.040 | 0.017 | 0.018 | 0.052 | 84.00 |
| Iron | mg Fe dm−3 | 0.080 | 0.190 | 0.13 | 0.38 | 0.161 | 78.00 |
| CODMn | mg O2 dm−3 | 6.600 | 14.60 | 10.53 | 10.40 | 1.965 | 92.00 |
| ΣBTEX | µg dm−3 | 0.010 | 1.700 | 0.05 | 0.05 | 0.075 | 81.00 |
| Water Type | Correlation Coefficient r | ||||
|---|---|---|---|---|---|
| n = 0 | n = 1 | n = 3/2 | n = 2 | Maximum Value of Correlation Coefficient | |
| Surface | 0.9976 | 0.9996 | 0.9994 | 0.9995 | 0.9996 |
| Surface, Enriched with BTEX 0.802 mg dm−3 | 0.9979 | 0.9887 | 0.9842 | 0.9754 | 0.9979 |
| Surface, Enriched with BTEX 9.49 mg dm−3 | 0.9988 | 0.9868 | 0.9925 | 0.9807 | 0.9988 |
| Surface, Enriched with BTEX 15.76 mg dm−3 | 0.9989 | 0.9985 | 0.9983 | 0.9955 | 0.9989 |
| Water Type | Correlation Coefficient r | Fisher’s Test Value |
|---|---|---|
| Hermia Model | FH | |
| Surface, BTEX 0.802 mg dm−3 | 0.9999 | 665.70 |
| Surface, BTEX 9.49 mg dm−3 | 0.9998 | 332.30 |
| Surface, BTEX 15.76 mg dm−3 | 0.9999 | 665.70 |
| Surface | 0.9996 | 165.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piekutin, J. The Identification of Fouling in Reverse Osmosis in the Treatment of Water with Petroleum Substances. Water 2021, 13, 1092. https://doi.org/10.3390/w13081092
Piekutin J. The Identification of Fouling in Reverse Osmosis in the Treatment of Water with Petroleum Substances. Water. 2021; 13(8):1092. https://doi.org/10.3390/w13081092
Chicago/Turabian StylePiekutin, Janina. 2021. "The Identification of Fouling in Reverse Osmosis in the Treatment of Water with Petroleum Substances" Water 13, no. 8: 1092. https://doi.org/10.3390/w13081092
APA StylePiekutin, J. (2021). The Identification of Fouling in Reverse Osmosis in the Treatment of Water with Petroleum Substances. Water, 13(8), 1092. https://doi.org/10.3390/w13081092






