1. Introduction
Emerging markets as marine wind energy are imposing new challenges to the offshore industry; marine wind energy business competitiveness is strongly related to offshore substructures and their logistics. With the aim of reducing installation costs, new or unusual operations are being planned and executed in an effort to avoid the use of specialized and expensive vessels [
1,
2]. One of these cases is the DEMOGRAVI3 project, a Horizon 2020 funded effort to prove the feasibility of a singular gravity based foundation (GBF) design through the construction, transportation, installation, and exploitation of a full-scale prototype. One of the singularities of this design, also one of its main advantages, is the capability of transport, self-installation, and decommissioning with the sole assistance of regular tugs. This avoids the need for specialized heavy-lift vessels or tailored built craft, thus reducing both costs and economic uncertainties related to installation and decommissioning phases.
Self-installing foundations, such as the ones mentioned before, also use tugs as external assistance for precise positioning over the seabed; this approach motivates the design of operations that conjugate several vessels or floating structures joined together by mooring and anchoring lines. In the context of cost reduction, vessel size and linking elements must be optimized according to operational requirements [
3]. Ideally, operators will pursue the use of the smaller tug, avoid the use of complex and heavy towing line set-ups, like clump weights, and have the best control possible by using the shortest possible distance between tugs and the structure. All the listed elements lead to taught-slack events on the mooring/towing lines. On the other hand, installation crews also need operational windows to be as wide as possible. In this context, line tension analysis and prediction must be assessed. Snap-load events are complex to model, and maximum achievable loads depend on the system stiffness as a whole, and that is both difficult to model and to achieve. The aim of this work is to define a maximum set-up load in order to avoid the occurrence of such events due to the uncertainty associated with loads during installation.
A definition of what can be considered a snap-load event on vertical cables with hanging loads can be found on [
4,
5], and it is also well-described in Det Norske Veritas (DNV-GL) recommended practices [
6].
Several authors have worked on the subject, modelling the phenomena both numerically and using physical scale models, obtaining good agreement between experimental and numerical results. Numerical models are usually formulated by allowing, as an example, the following [
7,
8]:
Three-dimensional motion;
Large displacements;
Inclusion of forces due to the weight of the cable, buoyancy, drag, and added mass;
Non-uniform cables—capacity to include any subsystems, such as hanging clump weights; and
Axial stiffness of the cable operating in alternating taut-slack conditions.
However, taut-slack events imply high transverse velocities of the line at mid-point, thus increasing relevance of the drag and added mass forces on the maximum tension values. Viscous drag coefficients are affected by scale effects often found in Froude models. Given that drag coefficients are driven by the Reynolds number and the scaling factor between the model and prototype is 2/3λ, tension values for impulsive load processes need to be adjusted for each event. This individual analysis is outside the scope of these tests. Moreover, peak load values due to snap events are dependent on the stiffness of the structure and every single element forced by cable tension. Model tugboats are where an in-line element between the anchoring line and the mooring line connects the tug to the structure. This was outside the scope of the project to model the stiffness of the tug as part of the system; instead, the tug had similar stiffness to the equivalent length of the cable. While this approach may have an impact on the magnitude of the peak value, it did not prevent its occurrence.
This work approaches the analysis of mooring line tension as a key aspect on the loop around optimization of positioning means for the design, costs, operational requirements, and climatic windows.
This paper reviews present strategies to analyze mooring line tension and identify impulsive or snap load occurrence; the authors also propose a methodology to define the maximum load thresholds for a given line set-up and compare it to the methodology found in DNV-GL standards [
6,
9].
2. Materials and Methods
2.1. Physical Modeling
The experiment was carried out within the framework of the H2020 DEMOGRAVI3 project; the Technical University of Madrid was in charge of simulating installation scenarios and providing data for operational window analysis and optimization. For this purpose, a 1:50 scale simulator of a multi-floater system was used, following the work described in [
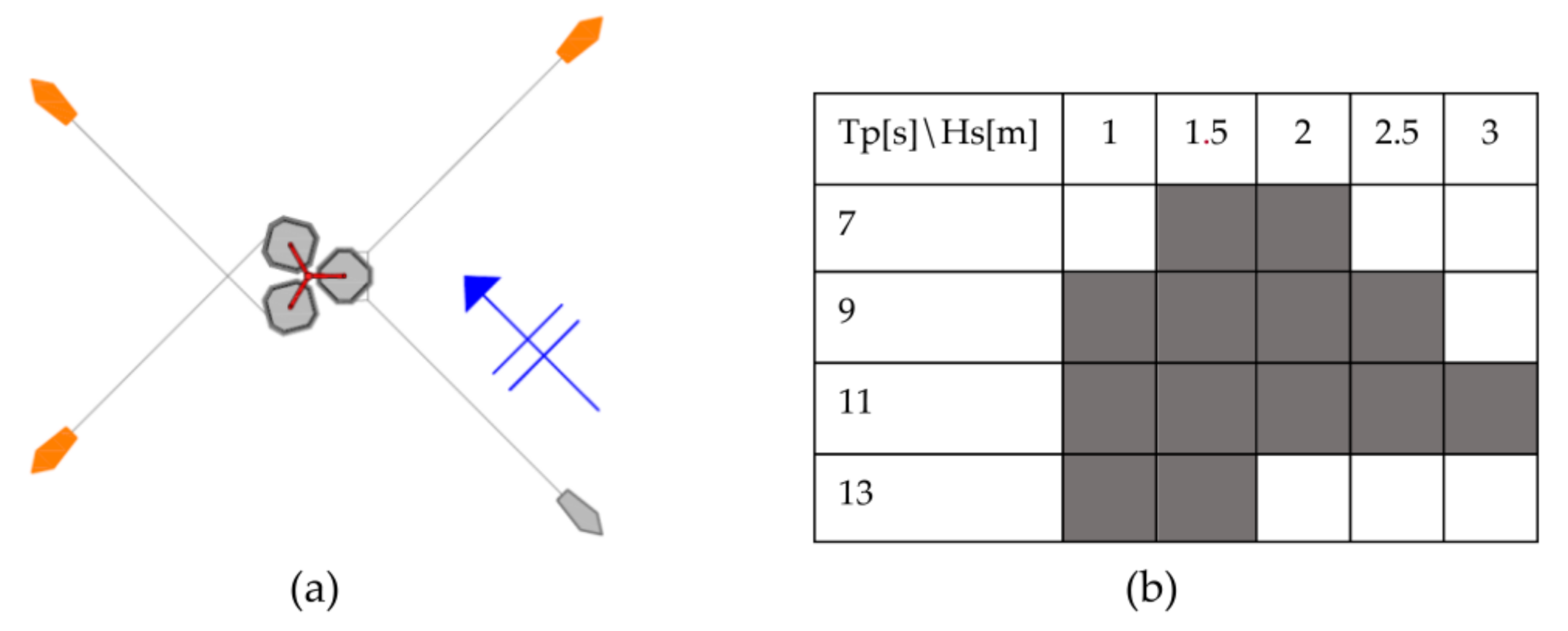
10]. The set-up comprises the GBF linked to four tugboats anchored to the seafloor (
Figure 1). The system is forced with spectral sea states (Hs[m], Tp[s] and Dir[°]) according to the wave climate at the location. The test matrix can be found in
Figure 1.
Six orientations were considered in pre-installation tests to study the influence of wave incidence in the structure response, and the orientation presented in
Figure 1a registered the worst-case scenario for the mooring line design based on maximum cable tension measured on the tugboats’ winches. It was found that due to drift caused by wave action, the vessel facing incoming waves registers the higher loads. This work focused on the loads registered by that tugboat. Further details can be found in [
11].
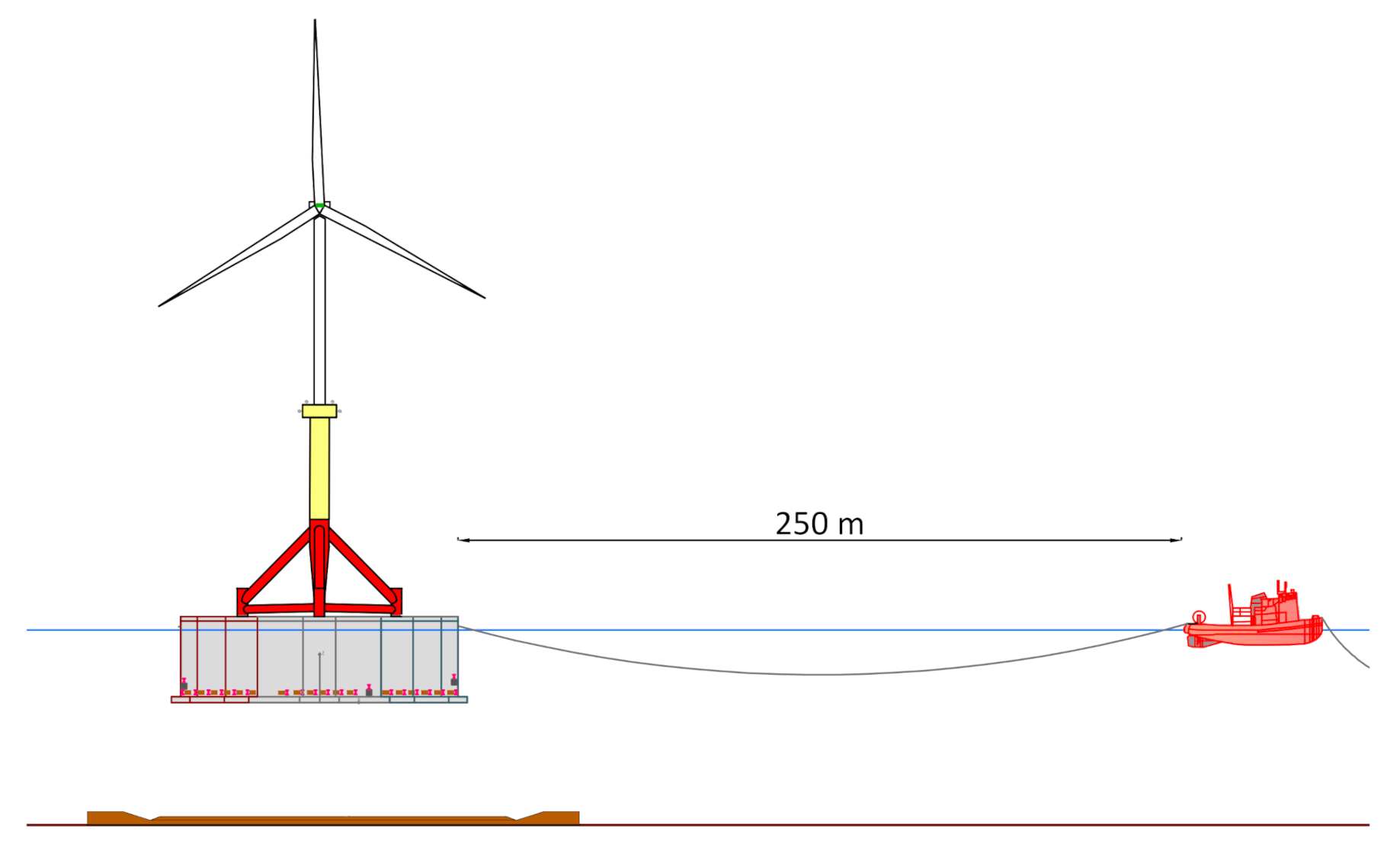
Tugs were placed at a 250 m distance and anchored to the sea floor (
Figure 2); because of size restrictions inside the wave basin, the anchor line was modelled using the SMART system for modelling anchoring lines, as described in [
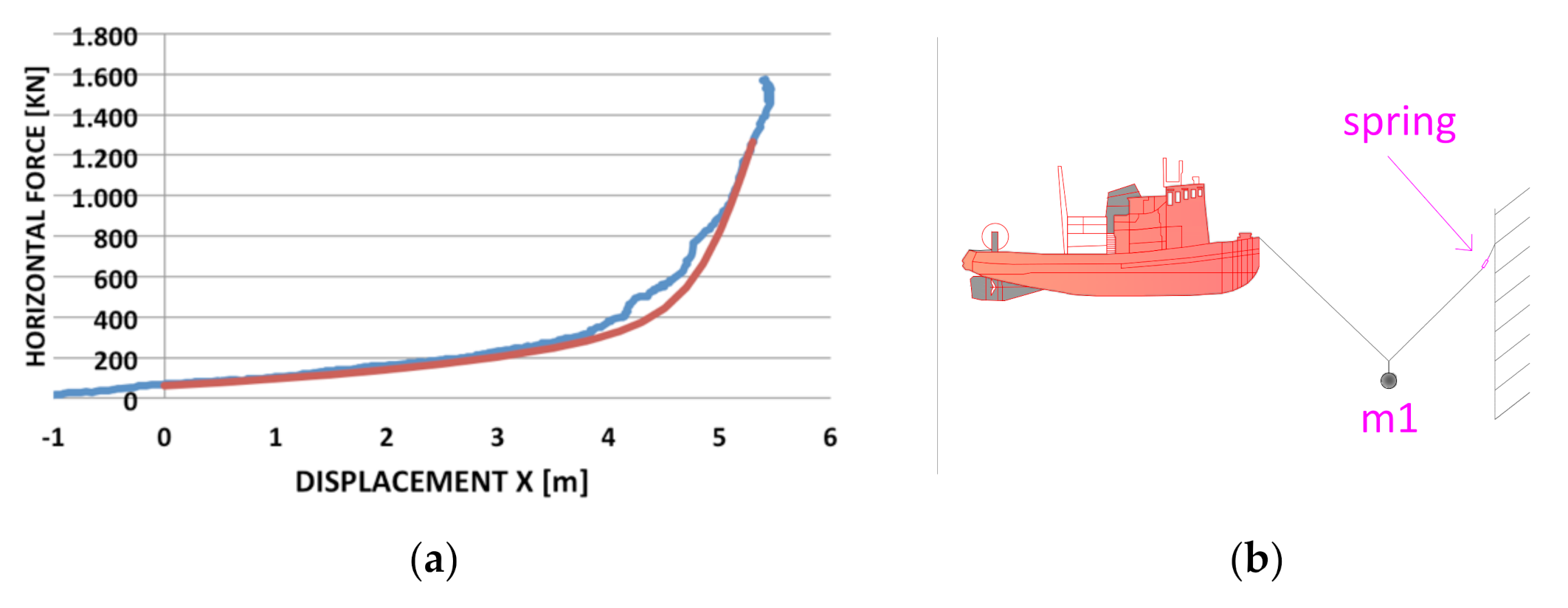
12]. Due to the need for extending the calibrated range of the anchoring lines beyond catenary-related stiffness, an appropriate spring was also included between the clump weight and the fixed point in the smart system modeling axial stiffness of the anchoring line. The set-up and calibration results are shown in
Figure 3.
2.2. Methods of Analysis
Data sets for towing line tension were analyzed under three perspectives.
The first was to find a threshold value for tension on each test condition that could help define an operational window for installation. This was initially approached by applying basic statistical analysis focusing on maximum tension values registered during the test. Moreover, Offshore Standard DNV-OS-E301 describes a methodology for mooring line design for floating moored structures. This methodology identifies local maxima values as the maximum value between two successive global mean up-crossings, and assumes them to be independent stochastic variables that fit to three parameter Weibull distributions and approach a Gumbel for an increasing number of maxima.
The second procedure is to identify snap-load events as a threshold indicator. A snap load is defined as a spike in tension as a mooring line re-engages immediately following a slack condition, typically of very short duration. This can occur due to a combination of light pre-tension, shallow water depth, and large platform motions in response to a survival storm condition, or in our particular case, due to coupled tugboat and DEMOGRAVI3 motions. In the context of marine operations, [
6] defines a criterion to avoid snap conditions on crane wire lifting or when lowering an object into the sea, as:
where
F denotes the line tension and subscripts denote dynamic or static components, given that the total force on the wire is
From Hsu et al., a snap condition implies a slack condition, that is, the total force on the line becomes zero. A revision of the rules by DNV (DNV 2011) modifies Equation (1) to allow for a 10% margin for safety, thus,
Therefore, to identify slack events, load time series have been analyzed using 0.9 Fst criteria.
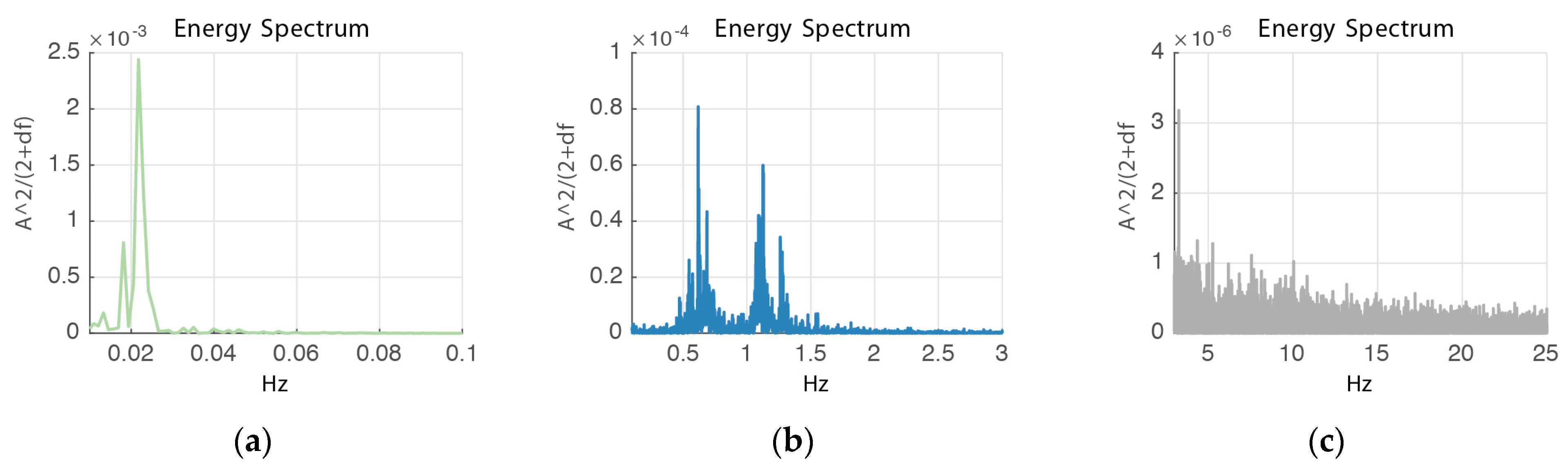
Since this methodology is mainly formulated for hanging loads where the mean tension value is equal to the suspended load, some signal conditioning was needed. Load time-series were found to be the response to different sources (see
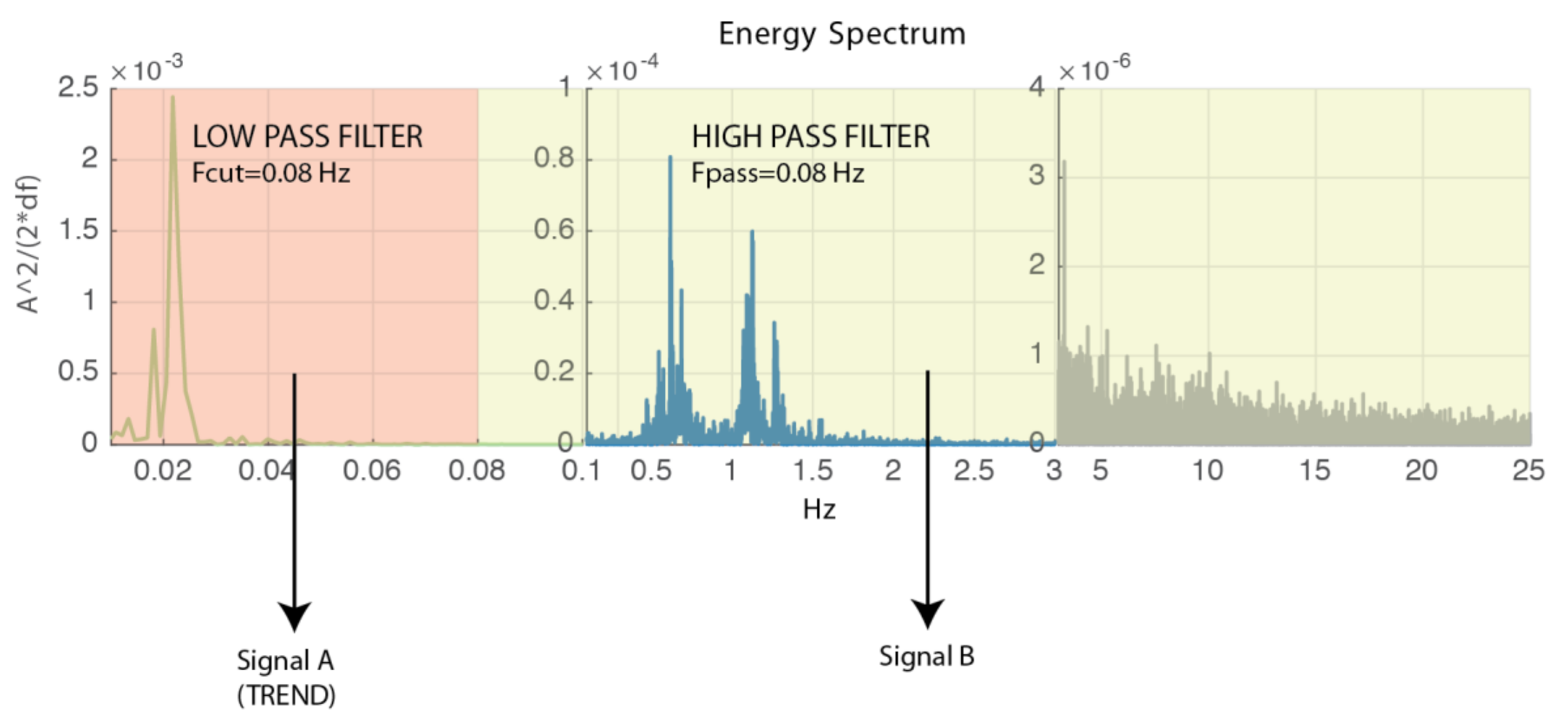
Figure 4). When analyzing a low-energy sea-state test, three different frequency response ranges were found, where the first one, from 0 to 0.1 Hertz (model time), contains the lower frequency related to sway or drift displacement of the whole system forced by waves, having a peak at 0.02 Hertz. The second range goes from 0.1 to 3 Hertz, and matches with the wave period and tugboat pitch movement. All energy above 5 Hertz can be considered as white noise, provided it is an almost flat spectrum.
To be able to apply the snap load criteria as per DNV OS-E301, the raw signal has been filtered to subtract the low-frequency (trend) signal and white noise (See
Figure 5).
Once the trend is defined (see
Figure 6), the method is applied as described in
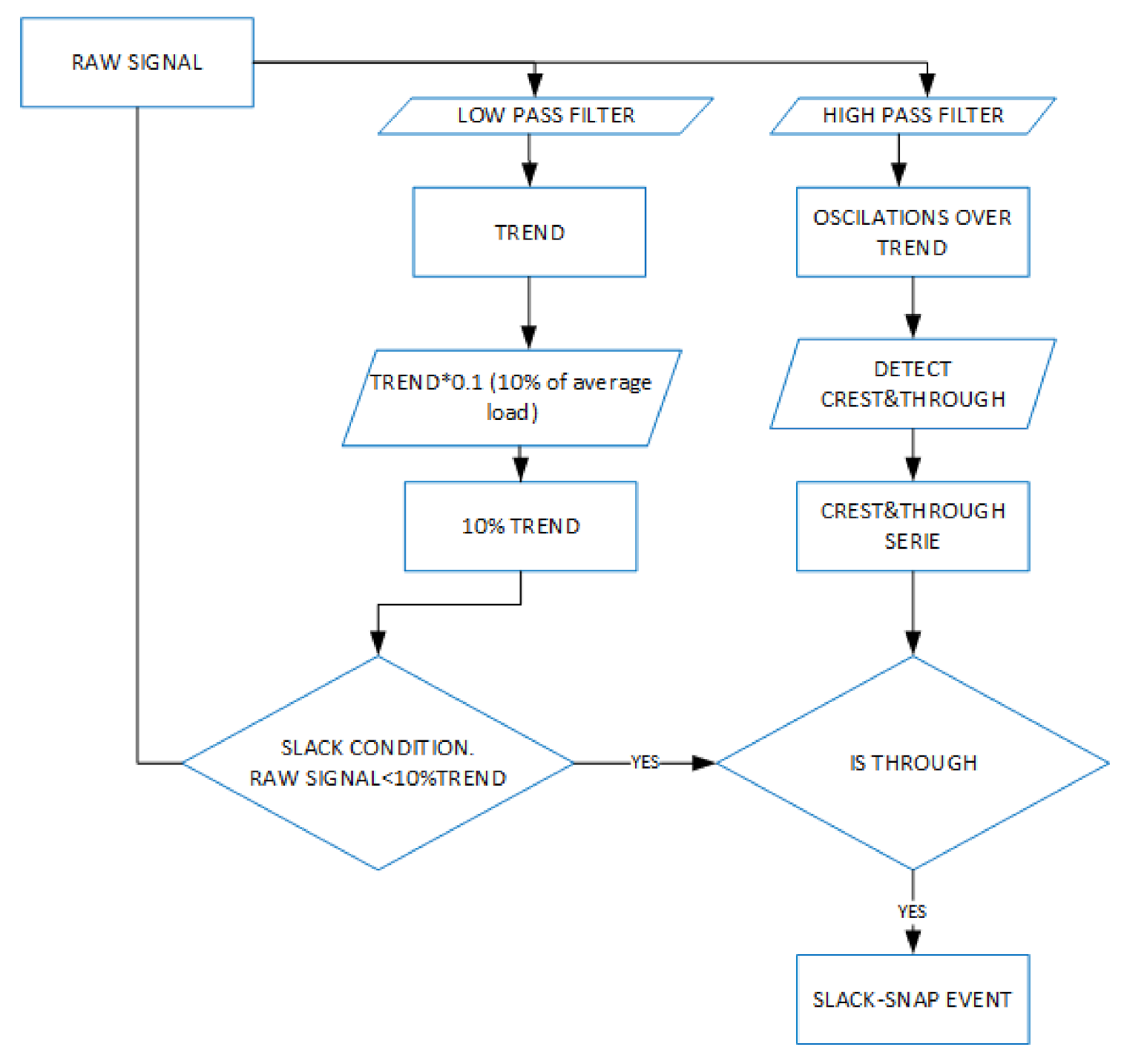
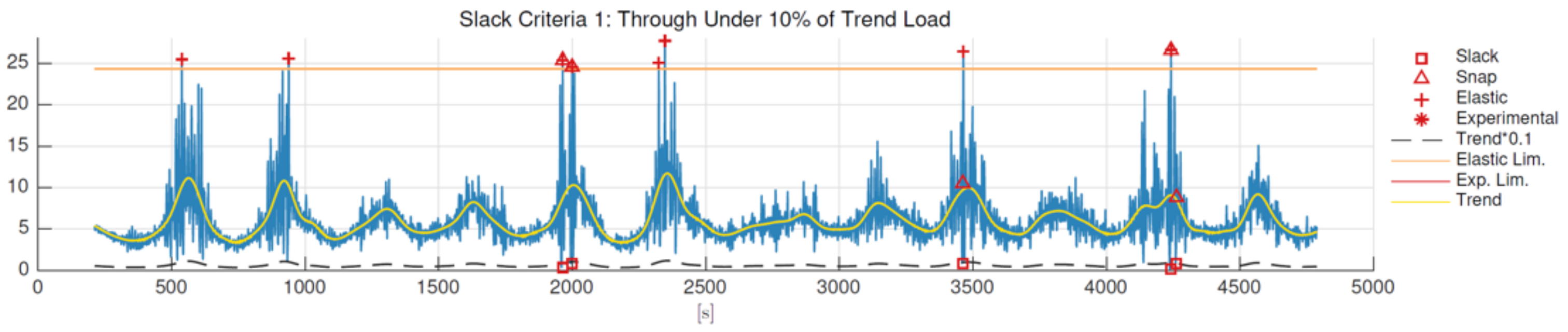
Figure 7. The signal is compared to 10% of the trend load, and every local minimum under that threshold is considered as a slack event, while if the following local maximum is over the trend, the load oscillation is accounted as a slack-snap event. A graphic example is shown in Figure 9.
The last method was derived after extensive analysis of mooring line systems employed on the simulations and registered load data.
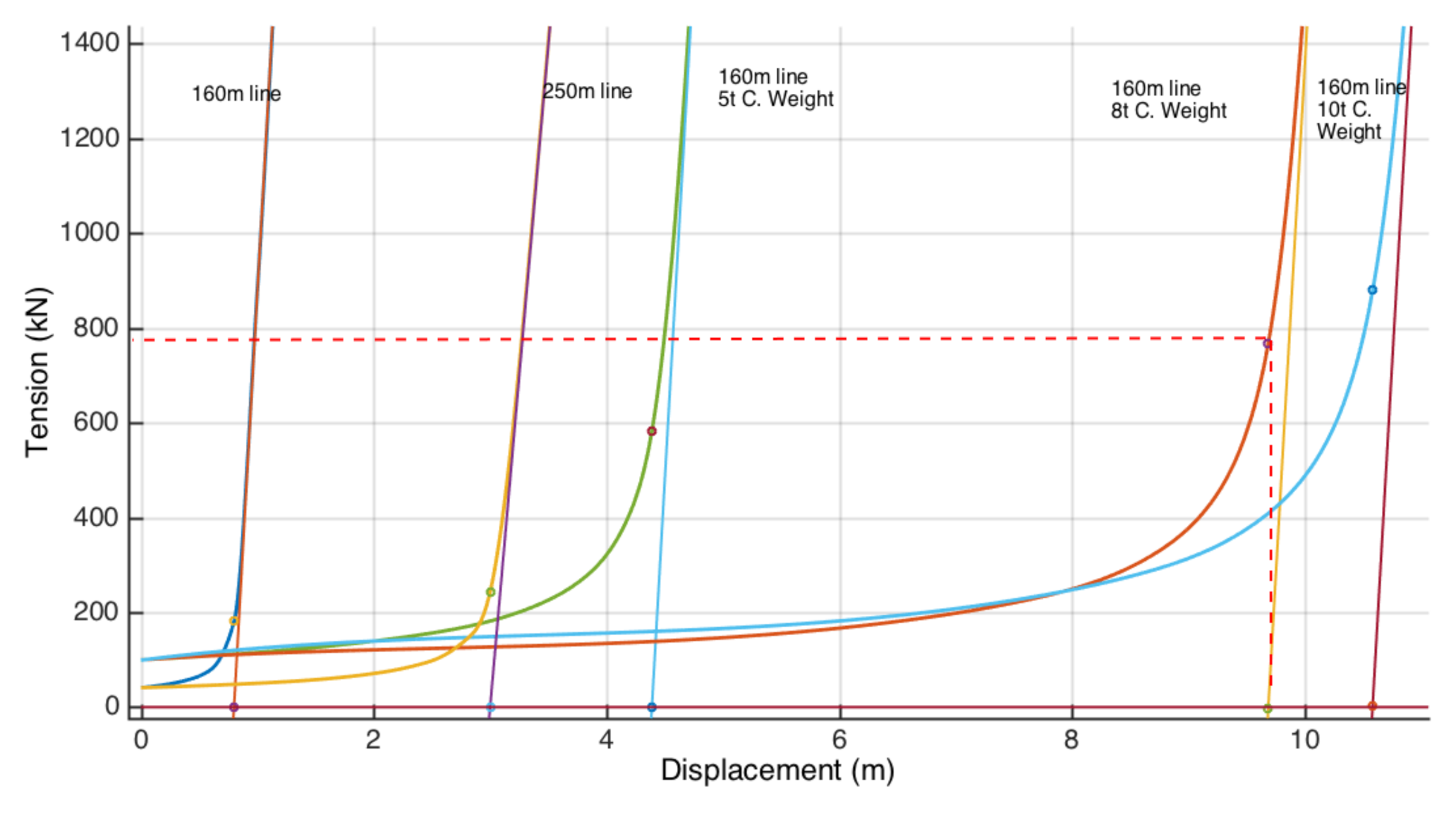
Mooring line set-up stiffness can be considered to be the sum of axial stiffness due to the length (L) and EA of each particular cable, plus a geometrical or catenary component due to the weight of the cable and/or the added clump weight. Analysis of any mooring line’s tension/elongation diagram shows two different behaviors, so for lower elongation values, tension is mainly due to the geometrical condition of the line, while for higher elongations and load values, the line gets straightened, and the response can be considered linear and a function of L and EA.
This is shown in
Figure 8, where the load versus horizontal displacement of the mooring points is plotted.
To define this limit, the linear response of the line was fitted to a straight line (similar to EA) in order to define the mooring line deflection for T = 0 ton. Even though it is clear that cable elongation is present for the whole range of use of the line, this value is used as a criterion to define the limit between geometrical stiffness predominance and in axial stiffness of the cable. Tension values above these thresholds must be further analyzed, since small displacement is likely to result in snap loads.
Figure 9 shows an example of the last two methods applied to a load time-series.
3. Results
3.1. Mooring Line Set-Up Analysis
The mooring line response to structure displacement was analyzed, where the tension was related to sway displacement (prototype) from the equilibrium position of the structure connected to four tugs. As it is shown in
Figure 1, significant differences in initial tension values can be found for simple lines (40–50 kN) versus those with a clump weight (100 kN). A mooring line that is 250 m long is able to cope with 3 m of displacement before changing the principal source of its elastic behavior from geometry to axial stiffness (EA).
In the case of clump weight-equipped lines, its “geometrical” stiffness behavior copes with sway displacement from 4–10 m, and the transition to axial elasticity happens along a larger displacement (2–4 m in case of clump weight lines versus 0.2–0.5 m in case of simple lines), thus allowing for a longer, higher damped response.
3.2. Design Load Analysis
The following results use a particular orientation and towing line configuration as being representative of the methodology. The particular case is the same as described before: 45 orientation, mooring line length of 250 m, and no clump weight.
3.2.1. Statistical Analysis
The maximum value for the registered load series does not provide sufficient data to allow for proper comprehension of how the system behaves as a whole (see
Figure 10). During tests, particularly those of higher energy sea states, mean or base loads were found to be smaller. Therefore, the statistical analysis of the time-series was completed with percentile 98 and mean descriptors in an attempt to provide a global overview of a complex system composed of five floating bodies of different masses and dynamic responses connected to each other and the seabed.
Mean values increase as expected when the tested sea state energy and wave steepness increases (see
Figure 11). As in the previous result, the loads correspond to the mooring line between the structure and the tug facing the incoming waves. The drift of the whole system is responsible for the mean value figures.
A comparison of this statistical descriptor takes a factor of 2 upfront between maximum and percentile 98 values for the same tests (see
Figure 12). This leads us to think that high snap loads correspond to maximum recorded values.
3.2.2. DNV-OS-E301
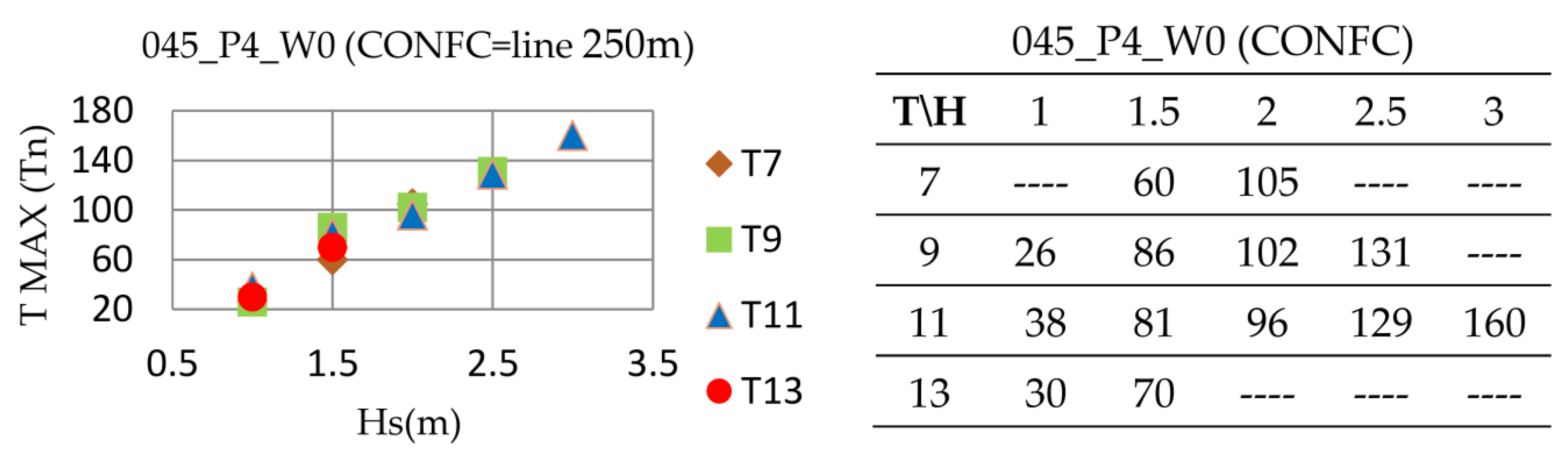
Most probable maximum (MPM) values obtained applying this methodology were found to be between four and eight times smaller than maxima values registered (see
Figure 13 and
Figure 14). The procedure described in DNV-OS-E301 to calculate mooring line load value to use for design and verification purposes does not take into account snap loads.
3.3. Snap Load Identification Results (DNV-RP-H103) and Geometrical Stiffness Criteria
For the same test as above, the following
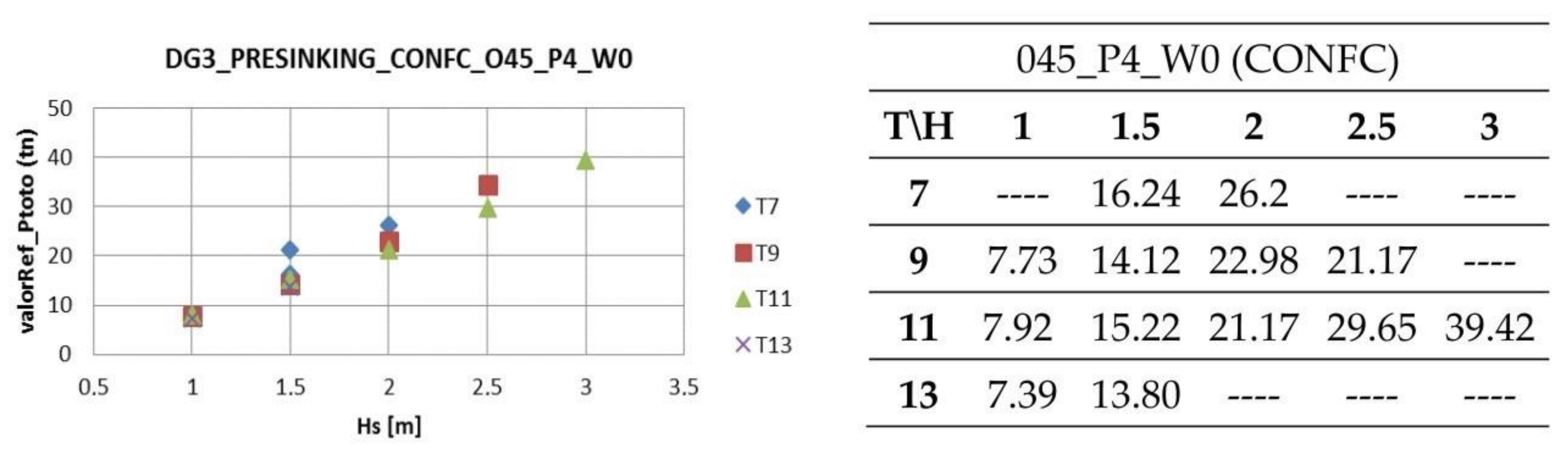
Table 1 gathers the number of events identified by slack-snap criteria and those load events with crests above the geometrical stiffness threshold.
The evaluation of these analyses follows a similar pattern to what can be found on the analysis of maximum tension values. The number of identified events for each parameter increases as the significant wave height (Hs[m]) and peak wave period (Tp[s]) are increased.
In the same way, as the global elasticity of the line is increased (in terms of elastic limit and its related deformation, see
Figure 8), identified events decrease.
As it can be noted, the number of identified events is significantly larger for DNV criteria, and in particular, for smaller wave periods. In the way that DNV methodology is applied, slack -snap events are accounted for regardless of how high the local peak values are.
4. Discussion
Multiple tests for different mooring line configurations and 45° incident wave angles have been run. Analysis of tension time-series by simple statistical analysis shows mooring lines’ output maximum values in excess of 120 t before reaching DESIRED operational thresholds (Hs[m] ≥ 2 m, Tp[s] = (7–13). These are due to the presence of impulsive loads promoted by insufficient capacity of the mooring lines to stop the structure’s sway displacement before extinguishing its geometrical elasticity. This elasticity is due to cable mass and mooring line geometry (catenary).
Analysis of different mooring line designs is presented, showcasing the impact of clump weights on the drift/load behavior.
It has been found that statistical analysis provides a clear description of the different phenomena that take place during tests in relation to mooring line loads; however, it does not offer a simple design tool for defining operational thresholds.
For this reason, the time-series were evaluated under different impulsive load cycle detection criteria to help the design team define operational thresholds during the pre-installation stage. To be able to apply the different criteria, the raw signal was filtered to subtract low-frequency (trend) signals and white noise.
Because statistical analysis does not provide satisfactory information about the mooring line snap-loading process, impulsive load detection criteria were applied. The results after this further analysis verify the presence of an impulsive response in time series and reinforces the need for added geometrical elasticity of mooring lines.
The DNV-GL approach to identifying slack-snap events has proven to be very accurate; however, it does not take into account the maximum value of the snap event, thus requiring further filtering to be useful as a tool to define load test thresholds.
The proposed methodology has been successfully applied to define operational thresholds of a particular mooring line design. This same value has been used as a threshold to tag trespassing local maxima as snap loads.
5. Conclusions
Modelling and analysis of a mooring line dynamic response has been the subject of permanent scientific revision for the last 40 years. This matter is particularly important in the Demogravi3 project during two main stages in the project’s life span: the transport afloat, and the installation phase.
Work Package 5.2 is mainly focused on the modelling and instrumental development of the system composed by auxiliary tug vessels, the Demogravi3 structure, and mooring/anchoring lines.
For this reason, an extensive review has taken place about impulsive load treatment for a similar offshore mooring line configuration, including physical and numerical modelling as well as analytic approaches, and common recommendations and guidelines; unfortunately, none of the approaches found in the literature are of direct application to the complex mooring set-up design for Demogravi3 installation. This has led us to implement those approaches that offer applicable solutions to characterize impulsive load occurrence on mooring line tensions during pre-installation tests. Moreover, a new criterion has been suggested (geometrical elasticity limit) due to the simplicity of its concept and ease of application.
When impulsive loads occur, scale effects foul the registered value of tension, and this is due to vertical/transverse drag loads on the cable due to its high transverse velocity during impulsive events and the impossibility to properly reproduce the elasticity of all the involved components (i.e., winch and tug-boat stiffness). This suggests that those tests where impulsive loads are detected should be analyzed accordingly.
From data measured of the tests conducted, an analysis of the mooring lines’ response against 45° was carried out using several approaches. Firstly, the tension-displacement response of mooring lines was analyzed for the different line configurations. Thus, a statistical analysis was performed, providing typical descriptors such as the maximum value and 98th percentile, in addition to a maxima analysis from a DNV methodology which fits data to a Gumbel distribution. Finally, a dynamic response analysis based on impulsive loads was included, such as impulsive load detection and the number of events which occurred. Because impulsive load events induce the already-mentioned uncertainty to peak values, this analysis provides a tool to help decision-making related to mooring line design and its associated uncertainty level.
In the same way, as anchoring lines are designed to not to make use of axial elasticity of the anchoring line, thus relying on the geometrical capacity of the line, the elasticity limit for mooring line tension defines a limit at which impulsive, or slack-taught, events start to be present. The proposed methodology allows to define a threshold load to avoid such events.
Author Contributions
Conceptualization, M.C.-M. and R.M.-S.; methodology, M.C.-M. and R.M.-S.; formal analysis, M.C.-M.; investigation, M.C.-M.; data curation, M.C.-M.; writing—original draft preparation, M.C.-M.; writing—review and editing, M.C.-M., R.M.-S. and L.P.-R.; supervision, L.P.-R.; project administration, R.M.-S.; funding acquisition, R.M.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by Horizon 2020 framework program, grant number DEMOGRAVI3-GAT-691717-1. The authors also acknowledge the support of the Spanish Ministry for Science, Innovation and Universities (MCIU) under grant RTI2018-096791-B-C21 “Hidrodinamica de elementos de amortiguamiento del movimiento de aerogeneradoresflotantes (FOWT-DAMP)”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Monobasewind. Available online: https://www.monobasewind.com (accessed on 10 February 2021).
- Gravi3. Available online: https://www.gravi3.com (accessed on 10 February 2021).
- IRENA. Innovation Outlook: Offshore Wind; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2016. [Google Scholar]
- Niedzwecki, J.M.; Thampi, S.K. Snap Loading of Marine Cable Systems. Appl. Ocean Res. 1991, 13, 210–219. [Google Scholar] [CrossRef]
- Weiting, H.; Krish, T.; Lance, M. Snap Load Criteria for Mooring Lines of a Floating Offshore Wind Turbine. In Proceedings of the ASME 1st International Offshore Wind Technical Conference, San Francisco, CA, USA, 4–7 November 2018. [Google Scholar] [CrossRef]
- DNV-OS-E301. Offshore Standards. Position mooring. Det Norske Veritas AS. 2018. Available online: http://rules.dnvgl.com/docs/pdf/dnvgl/os/2018-07/dnvgl-os-e301.pdf (accessed on 12 April 2021).
- Huang, S.; Vassalos, D. A Numerical Method for Predicting Snap Loading of Marine Cables. Appl. Ocean Res. 1993, 15, 235–242. [Google Scholar] [CrossRef]
- Shah, A.A.; Umar, A.; Siddiqui, N.A. A methodology for assessing the reliability of taut and slack mooring systems against instability. Ocean Eng. 2005, 32, 1216–1234. [Google Scholar] [CrossRef]
- DNV Recommendation RP-H103 Modelling and Analysis of Marine Operations Det Norske Veritas AS. 2011. Available online: https://rules.dnvgl.com/docs/pdf/DNV/codes/docs/2011-04/RP-H103.pdf (accessed on 12 April 2021).
- Cabrerizo, M.A.; Molina, R.J.; Vaquero, S.; Borromeo, M.C.; Rodriguez-Sanchez, A.; Rodriguez, A.; Camarero, A. Non intrusive approach to floating structures simulation: Small Scale Real-Time Caisson Monitoring & Control System. In Proceedings of the 4th International Conference on the Application of Physical Modelling to Port and Coastal Protection, Coastlab 2012, Gent, Belgium, 17–20 September 2012. [Google Scholar]
- Cabrerizo-Morales, M.A.; Molina, R.; Valdecasas, J.G.; Abanades, J.; Pérez-Rojas, L.A. Mooring line load thresholds definition based on impulsive load analysis during wind turbine + GBF instalation. H2020-Demogravi3. In Proceedings of the International Conference on the Application of Physical Modelling to Port and Coastal Protection, Coastlab 2018, Santander, Spain, 22–26 May 2018. [Google Scholar]
- Subrata, K.; Chakrabarti, C. Physical Modelling of Offshore Structures, Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1001–1054. [Google Scholar]
Figure 1.
(a) GBF (center) and tugboats (4) set-up for commissioning. (b) Wave conditions test matrix.
Figure 1.
(a) GBF (center) and tugboats (4) set-up for commissioning. (b) Wave conditions test matrix.
Figure 2.
Towing line configuration, as studied in this work.
Figure 2.
Towing line configuration, as studied in this work.
Figure 3.
(a) Calibration results for the modified smart system on the anchoring line of tugboats. Red: theoretical load versus horizontal sway displacement of the tug; blue: registered load on calibration test. (b) Modified smart set-up.
Figure 3.
(a) Calibration results for the modified smart system on the anchoring line of tugboats. Red: theoretical load versus horizontal sway displacement of the tug; blue: registered load on calibration test. (b) Modified smart set-up.
Figure 4.
Energy spectrum of test load data. (a) 0–0.1 Hz zoom, (b) 0.01–3 Hz Zoom, (c) f > 3 Hz zoom.
Figure 4.
Energy spectrum of test load data. (a) 0–0.1 Hz zoom, (b) 0.01–3 Hz Zoom, (c) f > 3 Hz zoom.
Figure 5.
Filters applied to the raw signal.
Figure 5.
Filters applied to the raw signal.
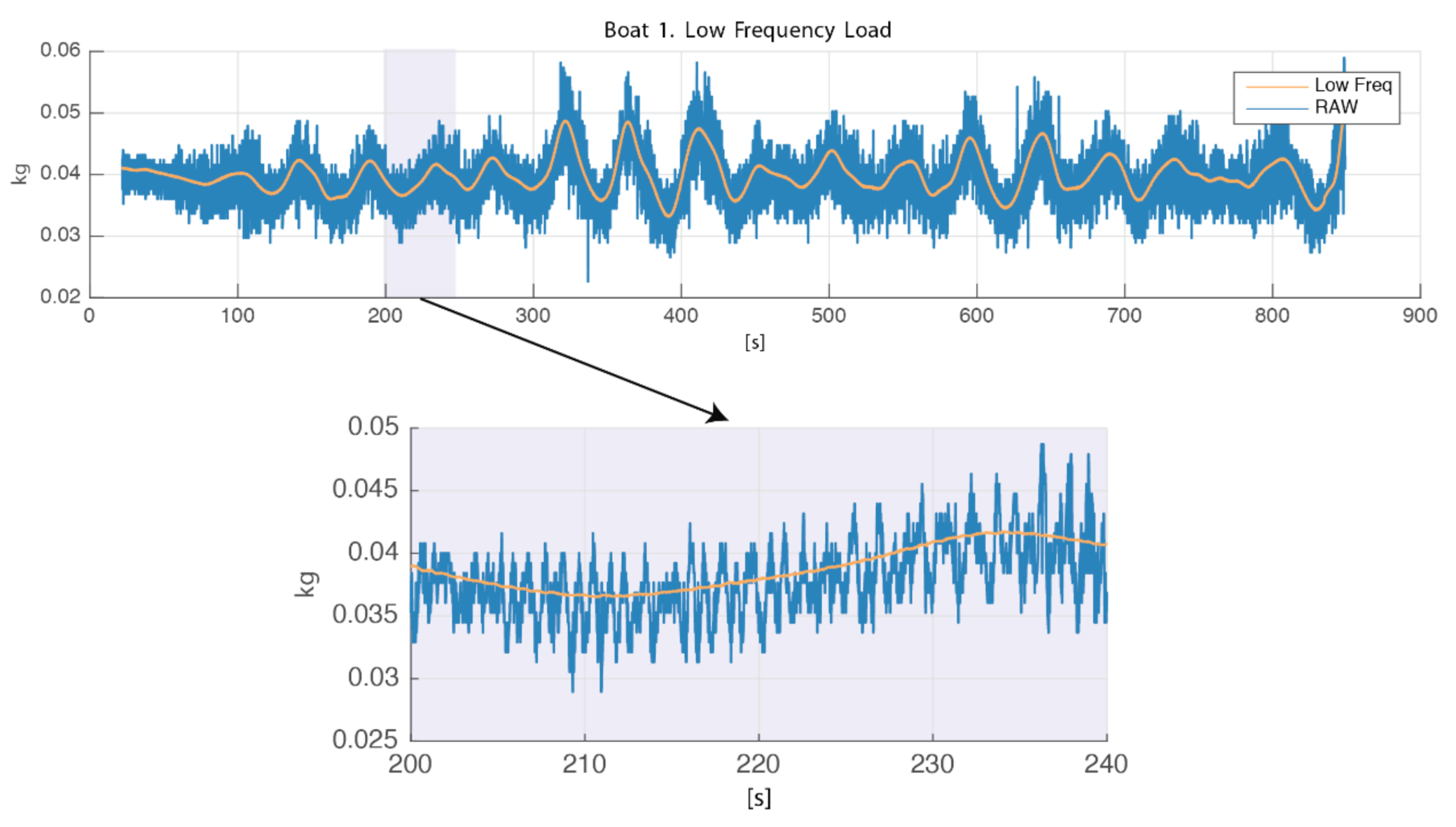
Figure 6.
Low-frequency trend over raw signal for (Hs[m] = 1, Tp[s] = 11).
Figure 6.
Low-frequency trend over raw signal for (Hs[m] = 1, Tp[s] = 11).
Figure 7.
Slack detection flow chart for 10% of the mean load.
Figure 7.
Slack detection flow chart for 10% of the mean load.
Figure 8.
Horizontal displacement versus load for different towing line set-ups used on the simulation. The geometrical stiffness limit for different configurations is noted with a small circle for each configuration. Dotted red line indicates the value for 8 t clump weight (CW) configuration.
Figure 8.
Horizontal displacement versus load for different towing line set-ups used on the simulation. The geometrical stiffness limit for different configurations is noted with a small circle for each configuration. Dotted red line indicates the value for 8 t clump weight (CW) configuration.
Figure 9.
Time-series showing mean trend, 0.1 trend threshold, geometrical stiffness threshold, and detected events.
Figure 9.
Time-series showing mean trend, 0.1 trend threshold, geometrical stiffness threshold, and detected events.
Figure 10.
Maxima values registered for test case.
Figure 10.
Maxima values registered for test case.
Figure 11.
Mean values registered for test case.
Figure 11.
Mean values registered for test case.
Figure 12.
Percentile 98 values registered for test case.
Figure 12.
Percentile 98 values registered for test case.
Figure 13.
Local max data for load distribution. Bottom: Local max. mooring load data fit to Gumbel distribution. MPM for 0.128 kgf model value (aprox. 16.37 t. prototype). Test case: CONFD_H2T9_O45_P4_W0. Hs[m]:2; Tp[s]:9.
Figure 13.
Local max data for load distribution. Bottom: Local max. mooring load data fit to Gumbel distribution. MPM for 0.128 kgf model value (aprox. 16.37 t. prototype). Test case: CONFD_H2T9_O45_P4_W0. Hs[m]:2; Tp[s]:9.
Figure 14.
Most probable maximum (MPM) values obtained for the registered data.
Figure 14.
Most probable maximum (MPM) values obtained for the registered data.
Table 1.
Number of snap events identified applying [
9] (DNV) and the Geometrical Stiffness Threshold (GSTh) proposed in this work.
Table 1.
Number of snap events identified applying [
9] (DNV) and the Geometrical Stiffness Threshold (GSTh) proposed in this work.
| (DNV) 045_P4_W0 (CONFC) |
|---|
| T\H | 1 | 1.5 | 2 | 2.5 | 3 |
|---|
| 7 | ---- | 117 | 313 | ---- | ---- |
| 9 | 8 | 112 | 351 | 528 | ---- |
| 11 | 2 | 157 | 321 | 534 | 596 |
| 13 | 12 | 146 | ---- | ---- | ---- |
| (GSTh) 045_P4_W0 (CONFC) |
| T\H | 1 | 1.5 | 2 | 2.5 | 3 |
| 7 | ---- | 1 | 11 | ---- | ---- |
| 9 | 5 | 13 | 60 | 107 | ---- |
| 11 | 13 | 71 | 117 | 144 | 130 |
| 13 | 28 | 72 | ---- | ---- | ---- |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).