India’s Commitments to Increase Tree and Forest Cover: Consequences for Water Supply and Agriculture Production within the Central Indian Highlands
Abstract
1. Introduction
2. Materials and Methods
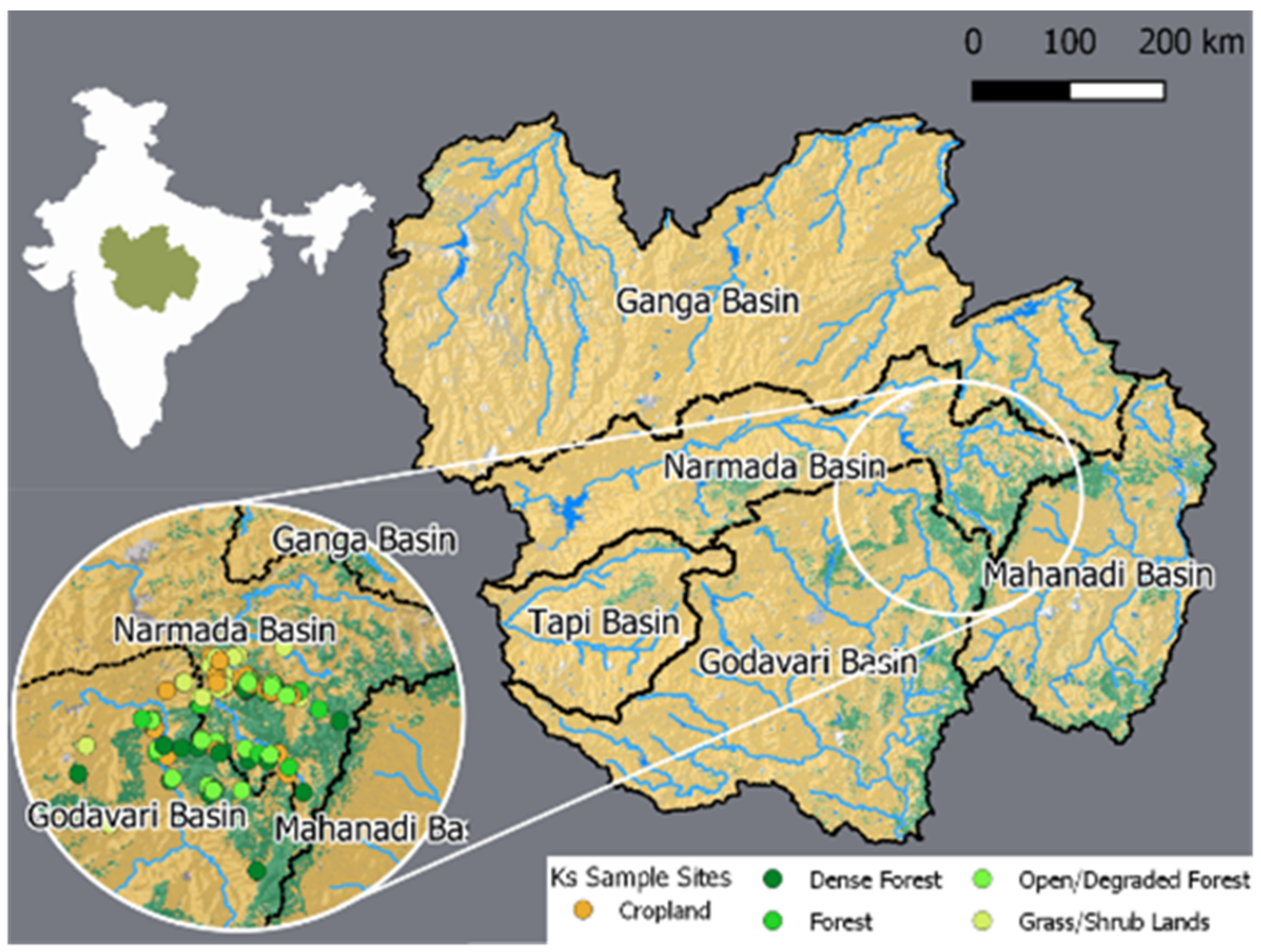
2.1. Study Area
2.2. Land Cover Saturated Hydraulic Conductivity
2.3. SPHY Hydrological Modeling
2.4. Forest Cover Scenarios
3. Results
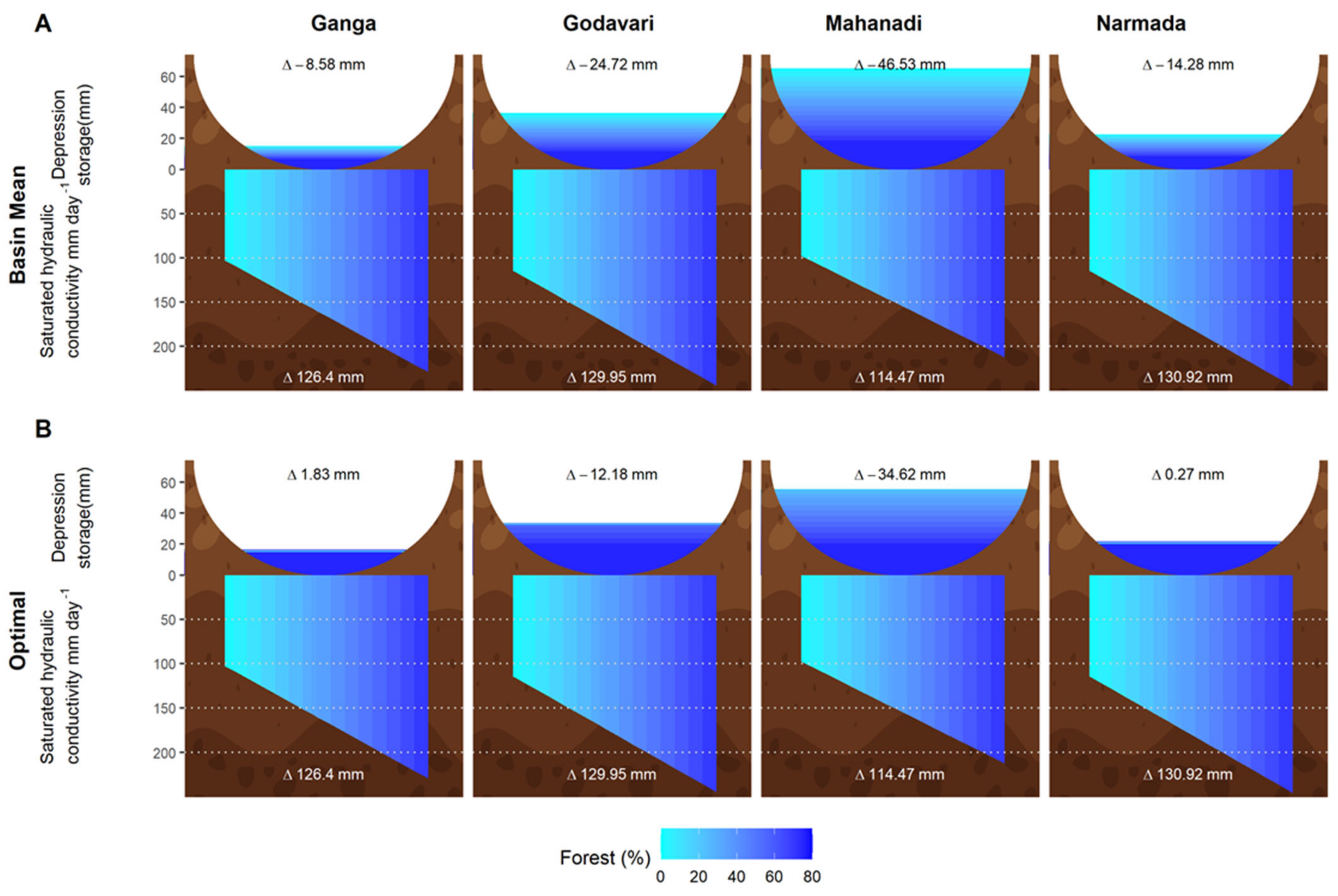
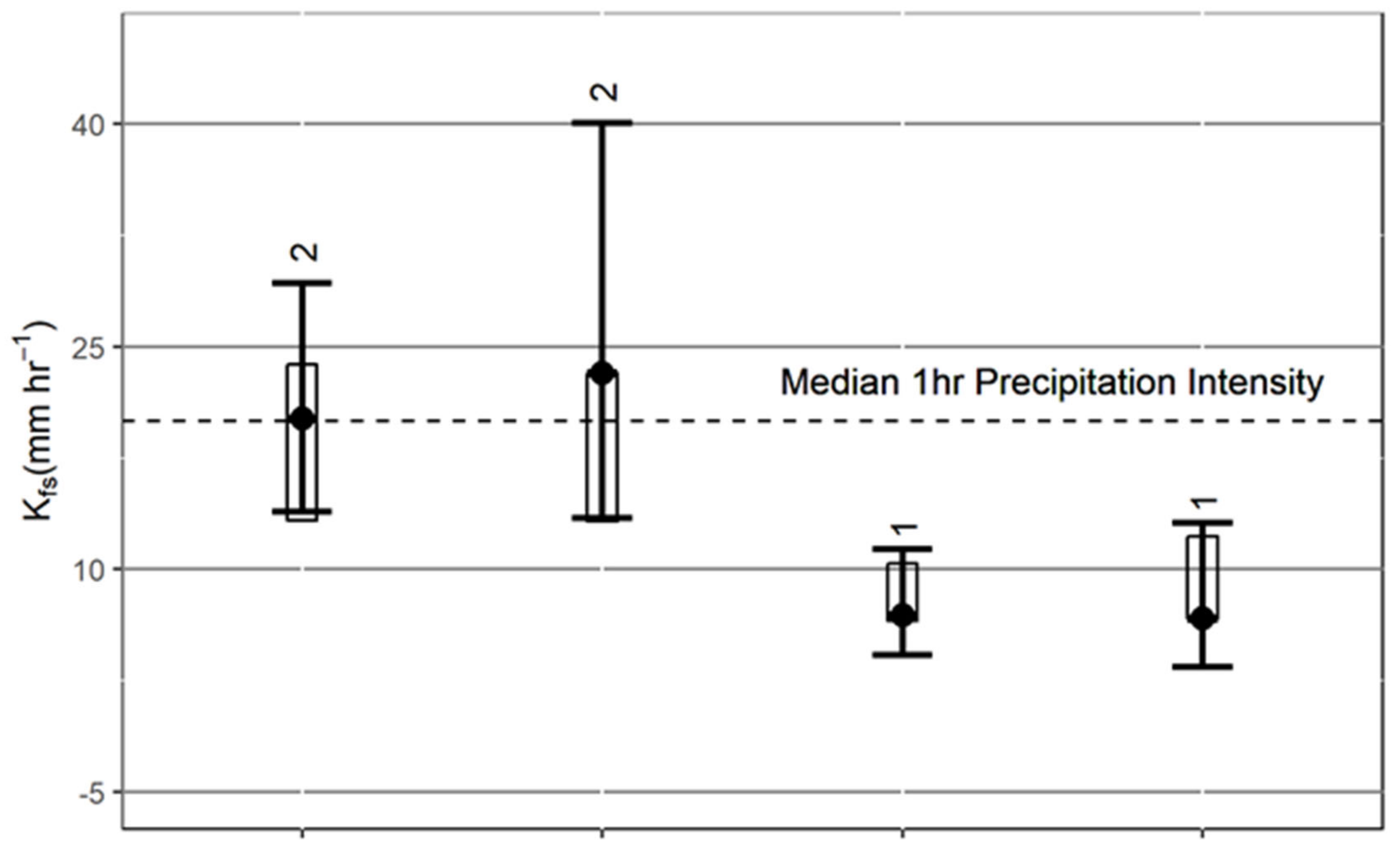
3.1. Land Cover Saturated Hydraulic Conductivity
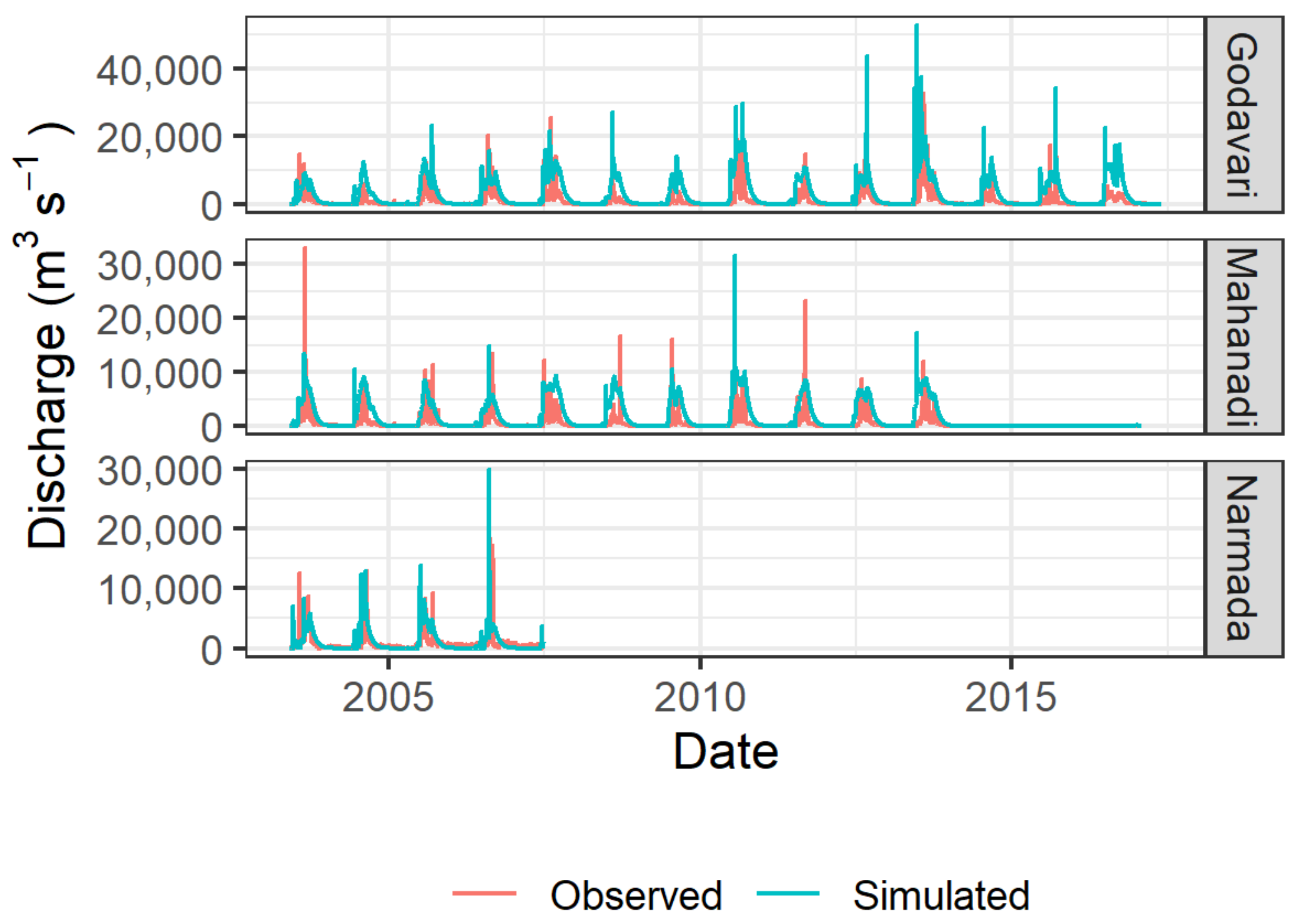
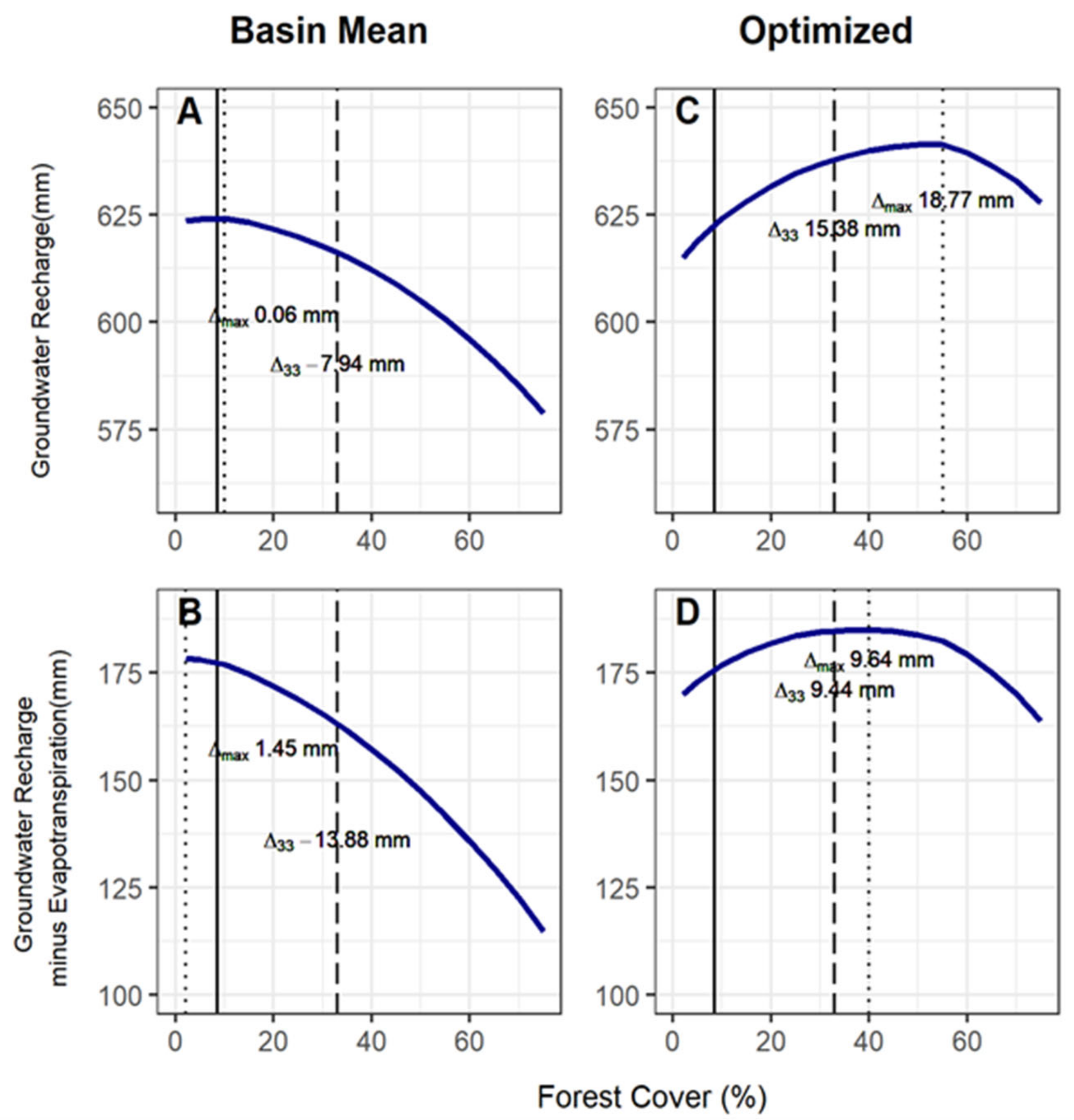
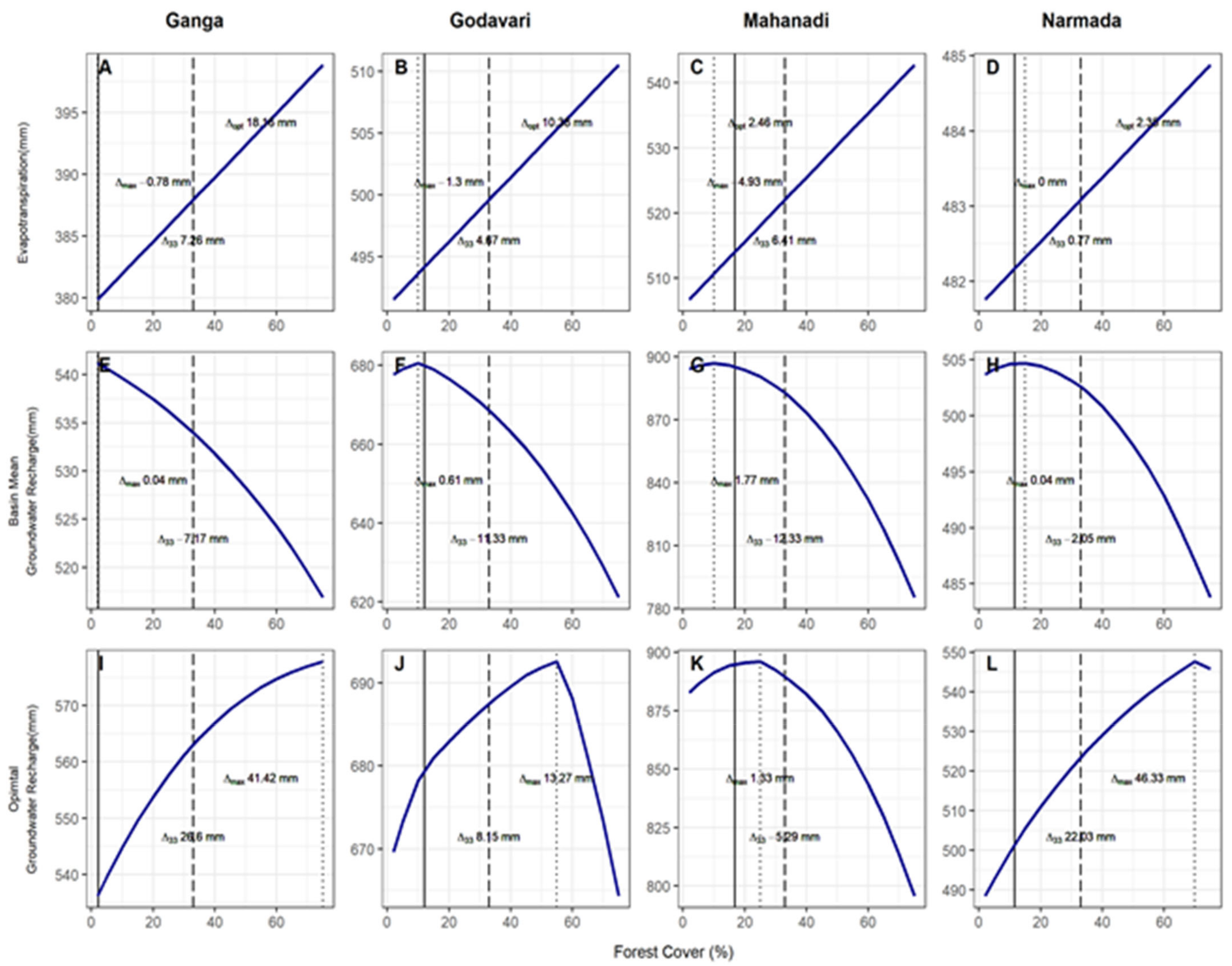
3.2. Hydrological Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Environment and Forests, Government of India: National Mission for a Green India. Available online: http://www.jkforest.gov.in/pdf/gim/GIM_Mission-Document-1.pdf (accessed on 31 March 2021).
- Singh, V.P.; Sinha, R.B.; Nayak, D.; Neufeldt, H.; van Noordwijk, M.; Rizvi, J. The National Agroforestry Policy of India: Experiential Learning in Development and Delivery Phases; ICRAF Working Paper No. 240; World Agroforestry Centre: New Delhi, India, 2016; pp. 1–40. Available online: http://apps.worldagroforestry.org/downloads/Publications/PDFS/WP16143.pdf (accessed on 31 March 2021).
- Dhyani, S.K. National Agroforestry Policy 2014 and the need for area estimation under agroforestry. Curr. Sci. 2014, 107, 9–10. [Google Scholar]
- Chavan, S.B.; Keerthika, A.; Dhyani, S.K.; Handa, A.K.; Newaj, R.; Rajarajan, K. National Agroforestry Policy in India, a low hanging fruit. Curr. Sci. 2015, 108, 1826–1834. [Google Scholar]
- Bremer, L.L.; Farley, K.A. Does plantation forestry restore biodiversity or create green deserts? A synthesis of the effects of land-use transitions on plant species richness. Biodivers. Conserv. 2010, 19, 3893–3915. [Google Scholar]
- Iezzi, M.; De Angelo, C.; Di Bitetti, M. Tree plantations replacing natural grasslands in high biodiversity areas: How do they affect the mammal assemblage? Ecol. Manag. 2020, 473, 118303. [Google Scholar] [CrossRef]
- Bond, W.J.; Parr, C.L. Beyond the forest edge, Ecology, diversity and conservation of the grassy biomes. Biol. Conserv. 2010, 143, 2395–2404. [Google Scholar] [CrossRef]
- Clark, B.; DeFries, R.; Krishnaswamy, J. Intra-annual dynamics of water stress in the central Indian Highlands from 2002 to 2012. Reg. Environ. Chang. 2016, 16, 83–95. [Google Scholar] [CrossRef]
- Roxy, M.K.; Ghosh, S.; Pathak, A.; Athulya, R.; Mujumdar, M.; Murtugudde, R.; Terray, P.; Majeevan, M. A threefold rise in widespread extreme rain events over central India. Nat. Commun. 2017, 8, 708. [Google Scholar] [CrossRef] [PubMed]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing Trend of Extreme Rain Events Over India in a Warming Environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- The World Bank. World Development Indicators, Rural Environment and Land Use; The World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Ministry of Environment and Forests. Forest Survey of India; Ministry of Environment and Forests: Dehra Dun, India, 2019. [Google Scholar]
- Ministry of Environment and Forests. Forest Survey of India; Ministry of Environment and Forests: Dehra Dun, India, 1997. [Google Scholar]
- Krishnaswamy, J.; Kelkar, N.; Birkel, C. Positive and neutral effects of forest cover on dry-season stream flow in Costa Rica identified from Bayesian regression models with informative prior distributions. Hydrol. Process. 2018, 32, 3604–3614. [Google Scholar] [CrossRef]
- Krishnaswamy, J.; Bonell, M.; Venkatesh, B.; Purandara, B.K.; Rakesh, K.N.; Lele, S.; Kiran, M.C.; Reddy, V.; Badiger, S. The groundwater recharge response and hydrologic services of tropical humid forest ecosystems to use and reforestation: Support for the “infiltration-evapotranspiration trade-off hypothesis”. J. Hydrol. 2013, 498, 191–209. [Google Scholar] [CrossRef]
- Maréchal, J.-C.; Varma, M.R.; Riotte, J.; Vouillamoz, J.-M.; Kumar, M.M.; Ruiz, L.; Sekhar, M.; Braun, J.-J. Indirect and direct recharges in a tropical forested watershed: Mule Hole, India. J. Hydrol. 2009, 364, 272–284. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests, not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Krishnaswamy, J.; Bonell, M.; Venkatesh, B.; Purandara, B.K.; Lele, S.; Kiran, M.; Reddy, V.; Badiger, S.; Rakesh, K. The rain–runoff response of tropical humid forest ecosystems to use and reforestation in the Western Ghats of India. J. Hydrol. 2012, 472–473, 216–237. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; Bruijnzeel, L.A.; Mulligan, M.; van Dijk, A.I. Forests as ‘sponges’ and ‘pumps’: Assessing the impact of deforestation on dry-season flows across the tropics. J. Hydrol. 2019, 574, 946–963. [Google Scholar] [CrossRef]
- International Union of Forest Research Organizations (IUFRO). Forest and Water on a Changing Planet: Vulnerability, Adaptation and Governance Opportunities; A Global Assessment Report IUFRO World Series Volume 38; Creed, I.F., van Noordwijk, M., Eds.; International Union of Forest Research Organizations (IUFRO): Vienna, Austria, 2018; pp. 1–190. ISBN 978-3-902762-95-5. [Google Scholar]
- Creed, I.F.; Jones, J.A.; Archer, E.; Claassen, M.; Ellison, D.; McNulty, S.G.; Van Noordwijk, M.; Vira, B.; Wei, X.; Bishop, K.; et al. Managing Forests for Both Downstream and Downwind Water. Front. Glob. Chang. 2019, 2, 2. [Google Scholar] [CrossRef]
- Roa-García, M.C.; Brown, S.; Schreier, H.; Lavkulich, L.M. The role of land use and soils in regulating water flow in small headwater catchments of the Andes. Water Resour. Res. 2011, 47, 47. [Google Scholar] [CrossRef]
- Brown, A.E.; Zhang, L.; McMahon, T.A.; Western, A.W.; Vertessy, R.A. A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation. J. Hydrol. 2005, 310, 28–61. [Google Scholar] [CrossRef]
- Task Committee on Revision of Manual 70. Evaporation, Evapotranspiration, and Irrigation Water Requirements; Jensen, M.E., Allen, R.G., Eds.; Society of Civil Engineers: Reston, VA, USA, 2015. [Google Scholar]
- Liu, C.-W.; Tan, C.-H.; Huang, C.-C. Determination of the magnitudes and values for groundwater recharge from Taiwan’s paddy field. Paddy Water Environ. 2005, 3, 121–126. [Google Scholar] [CrossRef]
- Tanaka, K.; Funakoshi, Y.; Hokamura, T.; Yamada, F. The role of paddy rice in recharging urban groundwater in the Shira River Basin. Paddy Water Environ. 2010, 8, 217–226. [Google Scholar] [CrossRef]
- Brown, A.E.; Western, A.W.; McMahon, T.A.; Zhang, L. Impact of forest cover changes on annual streamflow and flow duration curves. J. Hydrol. 2013, 483, 39–50. [Google Scholar] [CrossRef]
- Webb, A.A.; Kathuria, A. Response of streamflow to afforestation and thinning at Red Hill, Murray Darling Basin, Australia. J. Hydrol. 2012, 412–413, 133–140. [Google Scholar] [CrossRef]
- Dung, B.X.; Gomi, T.; Miyata, S.; Sidle, R.C.; Kosugi, K.; Onda, Y. Runoff responses to forest thinning at plot and catchment scales in a headwater catchment draining Japanese cypress forest. J. Hydrol. 2012, 444–445, 51–62. [Google Scholar] [CrossRef]
- Huang, X.-D.; Shi, Z.-H.; Fang, N.-F.; Li, X. Influences of Land Use Change on Baseflow in Mountainous Watersheds. Forests 2016, 7, 16. [Google Scholar] [CrossRef]
- Trabucco, A.; Zomer, R.J.; Bossio, D.A.; van Straaten, O.; Verchot, L.V. Climate change mitigation through afforestation/reforestation: A global analysis of hydrologic impacts with four case studies. Agric. Ecosyst. Environ. 2008, 126, 81–97. [Google Scholar] [CrossRef]
- Van Meerveld, H.J.; Zhang, J.; Tripoli, R.; Bruijnzeel, L.A. Effects of Reforestation of a Degraded Imperata Grassland on Dominant Flow Pathways and Streamflow Responses in Leyte, the Philippines. Water Resour. Res. 2019, 55, 4128–4148. [Google Scholar] [CrossRef]
- Ilstedt, U.; Malmer, A.; Verbeeten, E.; Murdiyarso, D. The effect of afforestation on water infiltration in the tropics: A systematic review and meta-analysis. Ecol. Manag. 2007, 251, 45–51. [Google Scholar] [CrossRef]
- Zhang, J.; Bruijnzeel, L.A.; Quiñones, C.M.; Tripoli, R.; Asio, V.B.; Van Meerveld, H.J. Soil physical characteristics of a degraded tropical grassland and a ‘reforest’, Implications for runoff generation. Geoderma 2019, 333, 163–177. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, X.; Zeng, Z.; Liu, Y.; Peng, S.; Zhu, Z.; Piao, S. The Effect of Afforestation on Soil Moisture Content in Northeastern China. PLoS ONE 2016, 11, e0160776. [Google Scholar] [CrossRef] [PubMed]
- Patil, N.G.; Tiwary, P.; Pal, D.K.; Bhattacharyya, T.; Sarkar, D.; Mandal, C.; Mandal, D.K.; Chandran, P.; Ray, S.K.; Prasad, J.; et al. Soil Water Retention Characteristics of Black Soils of India and Pedotransfer Functions Using Different Approaches. J. Irrig. Drain. Eng. 2013, 139, 313–324. [Google Scholar] [CrossRef]
- Ghimire, C.P.; Bonell, M.; Bruijnzeel, L.A.; Coles, N.A.; Lubczynski, M.W. Reforesting severely degraded grassland in the Lesser Himalaya of Nepal: Effects on soil hydraulic conductivity and overland flow production. J. Geophys. Res. Earth Surf. 2013, 118, 2528–2545. [Google Scholar] [CrossRef]
- Ghimire, C.P.; Bruijnzeel, L.A.; Lubczynski, M.W.; Bonell, M. Negative trade-off between changes in vegetation water use and infiltration recovery after reforesting degraded pasture land in the Nepalese Lesser Himalaya. Hydrol. Earth Syst. Sci. 2014, 18, 4933–4949. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X.; Ning, D.; Hou, Y.; Liu, S. A global review on hydrological responses to forest change across multiple spatial scales: Importance of scale, climate, forest type and hydrological regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- Ilstedt, U.; Tobella, A.B.; Bazié, H.R.; Bayala, J.; Verbeeten, E.; Nyberg, G.; Sanou, J.; Benegas, L.; Murdiyarso, D.; Laudon, H.; et al. Intermediate tree cover can maximize groundwater recharge in the seasonally dry tropics. Sci. Rep. 2016, 6, 21930. [Google Scholar] [CrossRef]
- The World Bank. World Development Indicators, 2018. Agricultural Land (% of Land Area). Available online: https://data.worldbank.org/indicator/AG.LND.AGRI.ZS (accessed on 31 March 2021).
- Kumar, M.D.; Scott, C.A.; Singh, O.P. Inducing the shift from flat-rate or free agricultural power to metered supply, Implications for groundwater depletion and power sector viability in India. J. Hydrol. 2011, 409, 382–394. [Google Scholar] [CrossRef]
- Shiferaw, B.; Reddy, V.; Wani, S. Watershed externalities, shifting cropping patterns and groundwater depletion in Indian semi-arid villages, The effect of alternative water pricing policies. Ecol. Econ. 2008, 67, 327–340. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Shukla, S.; Graham, W.D.; Wani, S.P.; Jones, J.W.; Heaney, J. Current and future groundwater withdrawals: Effects, management and energy policy options for a semi-arid Indian watershed. Adv. Water Resour. 2017, 110, 459–475. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Central Ground Water Board. Ground Water Year Book—India 2016–2017; Central Ground Water Board Ministry of Water Resources Government of India: Faridabad, India, 2017. [Google Scholar]
- Mandal, D.K.; Mandal, C.; Singh, S.K. Delineating Agro-Ecological Regions. Available online: https://www.nbsslup.in/assets/uploads/clinks/Delineating%20Agro-Ecological%20Regions.pdf (accessed on 31 March 2021).
- Defourny, P.; Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C.; Schlerf, M.; Santoro, M. Land Cover CCI, Product User Guide Version 2, 2016; UCL-Geomatics: London, UK, 2016. [Google Scholar]
- Central Ground Water Board Ministry of Water Resources Government of India. Ground Water Scenario of India 2009–2010; Central Ground Water Board Ministry of Water Resources Government of India: Faridabad, India, 2010; pp. 1–46. [Google Scholar]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.; Velpuri, M.; Gumma, M.; Gangalakunta, O.R.P.; Turral, H.; Cai, X.; et al. Global irrigated area map (GIAM), derived from remote sensing, for the end of the last millennium. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Agarwala, M. Forest Degradation and Governance in Central India, Evidence from Ecology, Remote Sensing and Political Ecology. Ph.D. Thesis, Columbia University, New York, NY, USA, 2015. [Google Scholar]
- Shekhar, S.; Kumar, S.; Densmore, A.L.; Van Dijk, W.M.; Sinha, R.; Kumar, M.; Joshi, S.K.; Rai, S.P.; Kumar, D. Modelling water levels of northwestern India in response to improved irrigation use efficiency. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Malakar, P.; Mukherjee, A.; Bhanja, S.N.; Saha, D.; Ray, R.K.; Sarkar, S.; Zahid, A. Importance of spatial and depth-dependent drivers in groundwater level modeling through machine learning. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–22. [Google Scholar]
- Water Resources Department, Directorate of Irrigation Research & Development. Laboratory Testing Procedure for Soil & Water Sample Analysis; Directorate of Irrigation Research & Development: Pune, India, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Searle, S.; Speed, F.; Milliken, G. Population Marginal Means in the Linear Model: An Alternative to Least Squares Means. Am. Stat. 1980, 34, 216–221. [Google Scholar] [CrossRef]
- Lenth, R.V. Least-Squares Means: The R Packagelsmeans. J. Stat. Softw. 2016, 69, 1–33. [Google Scholar] [CrossRef]
- Terink, W.; Khanal, S. SPHY, Spatial Processes in Hydrology. Advanced Training, Input Data, Sensitivity Analysis, Model Calibration, and Scenario Analyses; FutureWater: Wageningen, The Netherlands, 2016. [Google Scholar]
- Terink, W.; Terink, W.; Lutz, A.F.; Simons, G.W.H.; Immerzeel, W.W.; Droogers, P. Sphy V2.0. Spat. Process. Hydrol. Geosci. Model. Dev. 2015, 8, 2009–2034. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995. [Google Scholar]
- Saxton, K.E.; Rawls, W.; Romberger, J.S.; Papendick, R.I. Estimating Generalized Soil-water Characteristics from Texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived from Spaceborne Elevation Data. EosTrans. Am. Geophys. Union 2011, 89, 93–94. [Google Scholar] [CrossRef]
- Horn, B. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. Extraction of Drainage Networks from Digital Elevation Data. Comput. Vis. Graph. Image Process. 1984, 28, 328–344. [Google Scholar] [CrossRef]
- Barnes, R. RichDEM: Terrain Analysis Software. Available online: http://github.com/r-barnes/richdem (accessed on 31 March 2021).
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Campbell, G.S.; Shiozawa, S. Prediction of Hydraulic Properties of Soils Using Particle-Size Distribution and Bulk Density Data. In Proceedings of the International Workshop on Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils, Riverside, CA, USA, 11–13 October 1989; pp. 317–329. [Google Scholar]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef]
- Jabro, J.D. Estimation of Saturated Hydraulic Conductivity of Soils from Particle Size Distribution and Bulk Density Data. Trans. ASAE 1992, 35, 557–560. [Google Scholar] [CrossRef]
- Puckett, W.E.; Dane, J.H.; Hajek, B.F. Physical and Mineralogical Data to Determine Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 1985, 49, 831–836. [Google Scholar] [CrossRef]
- Dane, J.H.; Puckett, E.W.; Hajek, B.F. Field Soil Hydraulic Properties Based on Physical and Mineralogical Information. In Proceedings of the International Workshop on Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils, Riverside, CA, USA, 11–13 October 1989; pp. 389–403. [Google Scholar]
- Chakraborty, D.; Mazumdar, S.P.; Garg, R.N.; Banerjee, S.; Santra, P.; Singh, R.; Tomar, R.K. Pedotransfer functions for predicting points on the moisture retention curve of Indian soils. Indian J. Agric. Sci. 2011, 81I, 1031. [Google Scholar]
- Chakraborty, D.; Chakraborty, A.; Santra, P.; Tomar, R.K.; Garg, R.N.; Sahoo, R.N.; Choudhury, S.G.; Bhavanarayana, M.; Kalra, N. Prediction of hydraulic conductivity of soils from particle-size distribution. Curr. Sci. 2006, 90, 1526–1531. [Google Scholar]
- Gupta, S.C.; Larson, W.E. Estimating soil water retention characteristics from particle size distribution, organic matter percent, and bulk density. Water Resour. Res. 1979, 15, 1633–1635. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Tomasella, J.; Hodnett, M.G. Estimating Soil Water Retention Characteristics from Limited Data in Brazilian Amazonia. Soil Sci. 1998, 163, 190–202. [Google Scholar] [CrossRef]
- Hodnett, M.G.; Tomasella, J. Marked differences between van Genuchten soil water-retention parameters for temperate and tropical soils, a new water-retention pedo-transfer functions developed for tropical soils. Geoderma 2002, 108, 155–180. [Google Scholar] [CrossRef]
- Varallyay, G.; Rajkai, K.; Pachepsky, Y.A.; Shcherbakov, R.A. Mathematical description of soil water retention curve. Pochvovedenie 1982, 4, 77–89. [Google Scholar]
- Wösten, J.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Vereecken, H.; Maes, J.; Feyen, J.; Darius, P. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content. Soil Sci. 1989, 148, 389–403. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500 m SIN Grid V006 [Data Set]. Available online: https://lpdaac.usgs.gov/products/mod16a2v006/ (accessed on 31 March 2021).
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006. Available online: https://lpdaac.usgs.gov/products/mod15a2hv006/ (accessed on 31 March 2021).
- Hong, Y.; Gochis, D.; Cheng, J.-T.; Hsu, K.-L.; Sorooshian, S. Evaluation of PERSIANN-CCS Rainfall Measurement Using the NAME Event Rain Gauge Network. J. Hydrometeorol. 2007, 8, 469–482. [Google Scholar] [CrossRef]
- Mahrooghy, M.; Anantharaj, V.G.; Younan, N.H.; Aanstoos, J.; Hsu, K.-L. On an Enhanced PERSIANN-CCS Algorithm for Precipitation Estimation. J. Atmos. Ocean. Technol. 2012, 29, 922–932. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.D. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Robinson, M.; Cognard-Plancq, A.-L.; Cosandey, C.; David, J.; Durand, P.; Führer, H.-W.; Hall, R.; Hendriques, M.; Marc, V.; McCarthy, R.; et al. Studies of the impact of forests on peak flows and baseflows: A European perspective. Ecol. Manag. 2003, 186, 85–97. [Google Scholar] [CrossRef]
- Van Noordwijk, M.; Tanika, L.; Lusiana, B. Flood risk reduction and flow buffering as ecosystem services—Part 1, Theory on flow persistence, flashiness and base flow. Hydrol. Earth Syst Sci. 2017, 21, 2321–2340. [Google Scholar] [CrossRef]
- Van Noordwijk, M. Agroforestry as part of climate change response; IOP Conference Series. Earth Environ. Sci. 2018, 200, 012002. [Google Scholar]
- Paul, S.; Ghosh, S.; Rajendran, K.; Murtugudde, R. Moisture Supply from the Western Ghats Forests to Water Deficit East Coast of India. Geophys. Res. Lett. 2018, 45, 4337–4344. [Google Scholar] [CrossRef]
- Agus, F.; Irawan, I.; Suganda, H.; Wahyunto, W.; Setiyanto, A.; Kundarto, M. Environmental multifunctionality of Indonesian agriculture. Paddy Water Environ. 2006, 4, 181–188. [Google Scholar] [CrossRef]
- Wangpakapattanawong, P.; Finlayson, R.; Öborn, I.; Roshetko, J.M.; Sinclair, F.; Shono, K.; Borelli, S.; Hillbrand, A.; Conigliaro, M. Agroforestry in Rice-Production Landscapes in Southeast Asia: A Practical Manual. Available online: http://www.fao.org/3/i7137e/i7137e.pdf (accessed on 31 March 2021).
- Spracklen, D.V.; Arnold, S.R.; Taylor, C.M. Observations of increased tropical rainfall preceded by air passage over forests. Nature 2012, 489, 282–285. [Google Scholar] [CrossRef]
- Davis, K.F.; Chiarelli, D.D.; Rulli, M.C.; Chhatre, A.; Richter, B.; Singh, D.; DeFries, R. Alternative cereals can improve water use and nutrient supply in India. Sci. Adv. 2018, 4, 1108. [Google Scholar] [CrossRef] [PubMed]
- Pandey, D.N. Multifunctional agroforestry systems in India. Curr. Sci. 2007, 92, 455–463. [Google Scholar]
- Viswanath, S.; Lubina, P.A.; Subbanna, S.; Sandhya, M.C. Traditional Agroforestry systems and practices. A review . Adv. Agric. Res. Technol. 2018, 2, 18–19. [Google Scholar]
- Chinnamani, S. Agroforestry research in India: A brief review. Agrofor. Syst. 1993, 23, 253–259. [Google Scholar] [CrossRef]
- Santoro, A.; Venturi, M.; Bertani, R.; Agnoletti, M. A Review of the Role of Forests and Agroforestry Systems in the FAO Globally Important Agricultural Heritage Systems (GIAHS) Programme. Forests 2020, 11, 860. [Google Scholar] [CrossRef]
| Basin | Area (km2) | Forest | Cropland |
|---|---|---|---|
| Ganga | 175,883 | 2.23% | 92.22% |
| Godavari | 107,679 | 12.06% | 85.01% |
| Mahanadi | 58,772 | 16.75% | 80.55% |
| Narmada | 66,398 | 11.63% | 83.66% |
| Tapi | 29,661 | 3.00% | 92.25% |
| CIH | 438,393 | 8.07% | 87.59% |
| Input Parameter | Source | (%) Spatial Resolution | (%) Temporal Resolution | Processing |
|---|---|---|---|---|
| Precipitation time series | PERSIANN CCS | 0.04° | Daily | (%) Re-sampled to 250 m |
| Evapotranspiration time series | MOD16A2 | 500 m | 8-day | (%) Re-sampled to 250 m and temporally interpolate to daily images |
| Leaf Area Index time series | MOD15A2H | 500 m | 8-day | (%) Re-sampled to 250 m and temporally interpolate to daily images |
| Digital Elevation Data | HydroSHED | 90 m | (%) Re-sampled to 250 m, processed to delineate basins, create a slope map and D8 drainage direction map and flow accumulation map | |
| Land Cover | ESA CCI Land cover 2010 | 300 m | 2010 | Re-sampled to 250 m with classes simplified into Forest, Shrubland, Grassland, Agriculture, Built area, Bare Soil, Water, Snow/Ice |
| Clay Content (%) | SoilGrids: CLYPPT | 250 m | The SoilGrids Layers 1 through 7 were used to computer saturated hydraulic conductivity, saturated soil water content, water content at pF2 (field capacity), pF3 (wilting point) and pF4.2 (permanent wilting point). The 7 layers were then averaged into topsoil and subsoil layers weighted by layer thickness and land cover. | |
| Silt Content (%) | SoilGrids: SLTPPT | 250 m | ||
| Sand Content (%) | SoilGrids: SNDPPT | 250 m | ||
| Organic Carbon Content (%) | SoilGrids: ORCDRC | 250 m | ||
| pH x 10 in H2O | SoilGrids: PHIHOX | 250 m | ||
| Cation Exchange Capacity | SoilGrids: CECSOL | 250 m | ||
| Bulk Density | SoilGrids: BLDFIE | 250 m |
| Nash Sutcliffe Efficiency Index | |||
|---|---|---|---|
| Basin | Calibration | Validation | Full Period |
| Godavari | 0.48 | 0.36 | 0.43 |
| Mahanadi | 0.35 | −1.05 | 0.09 |
| Narmada | 0.29 | −1.19 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clark, B.; DeFries, R.; Krishnaswamy, J. India’s Commitments to Increase Tree and Forest Cover: Consequences for Water Supply and Agriculture Production within the Central Indian Highlands. Water 2021, 13, 959. https://doi.org/10.3390/w13070959
Clark B, DeFries R, Krishnaswamy J. India’s Commitments to Increase Tree and Forest Cover: Consequences for Water Supply and Agriculture Production within the Central Indian Highlands. Water. 2021; 13(7):959. https://doi.org/10.3390/w13070959
Chicago/Turabian StyleClark, Benjamin, Ruth DeFries, and Jagdish Krishnaswamy. 2021. "India’s Commitments to Increase Tree and Forest Cover: Consequences for Water Supply and Agriculture Production within the Central Indian Highlands" Water 13, no. 7: 959. https://doi.org/10.3390/w13070959
APA StyleClark, B., DeFries, R., & Krishnaswamy, J. (2021). India’s Commitments to Increase Tree and Forest Cover: Consequences for Water Supply and Agriculture Production within the Central Indian Highlands. Water, 13(7), 959. https://doi.org/10.3390/w13070959






