Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants
Abstract
1. Introduction
1.1. Nature of Contaminants in Sewers
1.2. Polluting Sources Identification
1.3. Optimal Sensor Location
2. Materials and Methods
2.1. Hydraulic Simulation Model
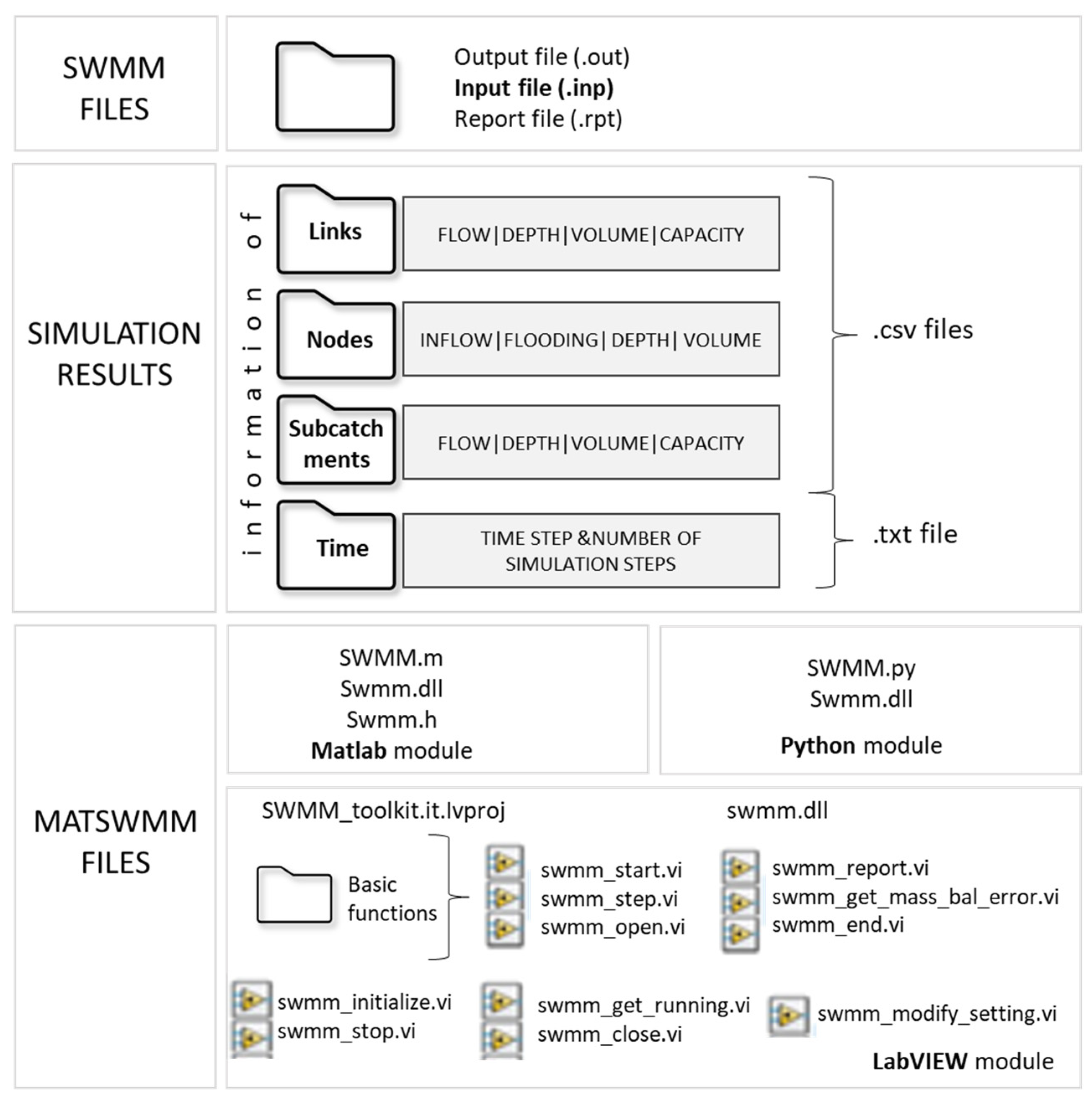
2.2. Structure of the MatSWMM Toolbox
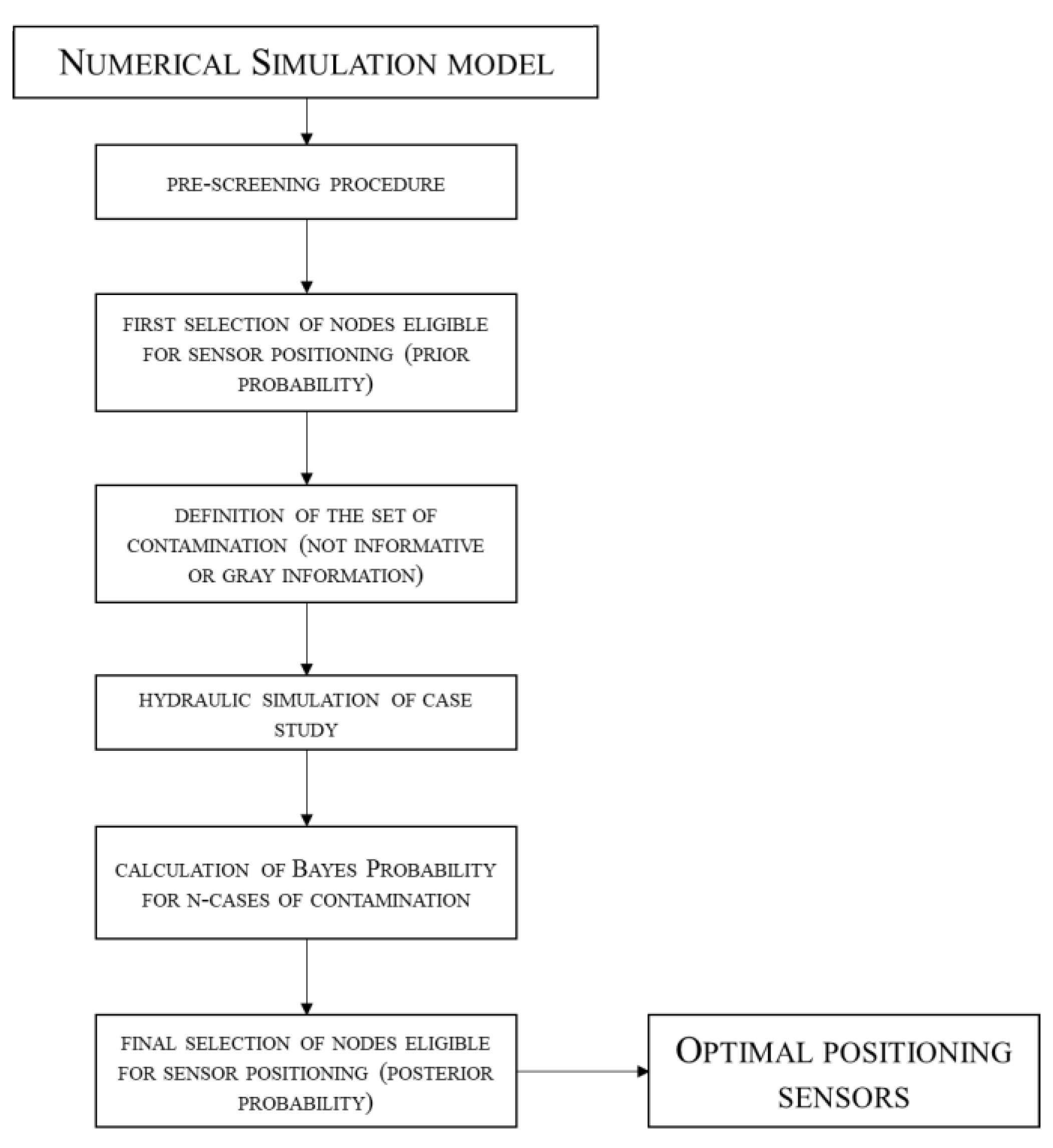
2.3. Bayesian Solver
- Outfall nodes, because clearly positioning a sensor in the terminal nodes does not give me any advantage for the purposes of rapid interception and containment of contamination;
- Head nodes, since positioning the sensors in those nodes would give a 1:1 information, i.e., it would mark a trace of contamination only if it started from that node so it would not be of help in all those other cases in which the source of contamination has started or it has moved somewhere else.
- P[A|B] is the conditional probability of A, known B. It is also called posterior probability, because it depends on the specific value of B;
- P[B|A] is the conditional probability of B, known A;
- P[A] is the prior probability or marginal probability of A. “A priori” means that it does not consider any information about B;
- P[B] is the prior probability B and acts as a normalizing constant.
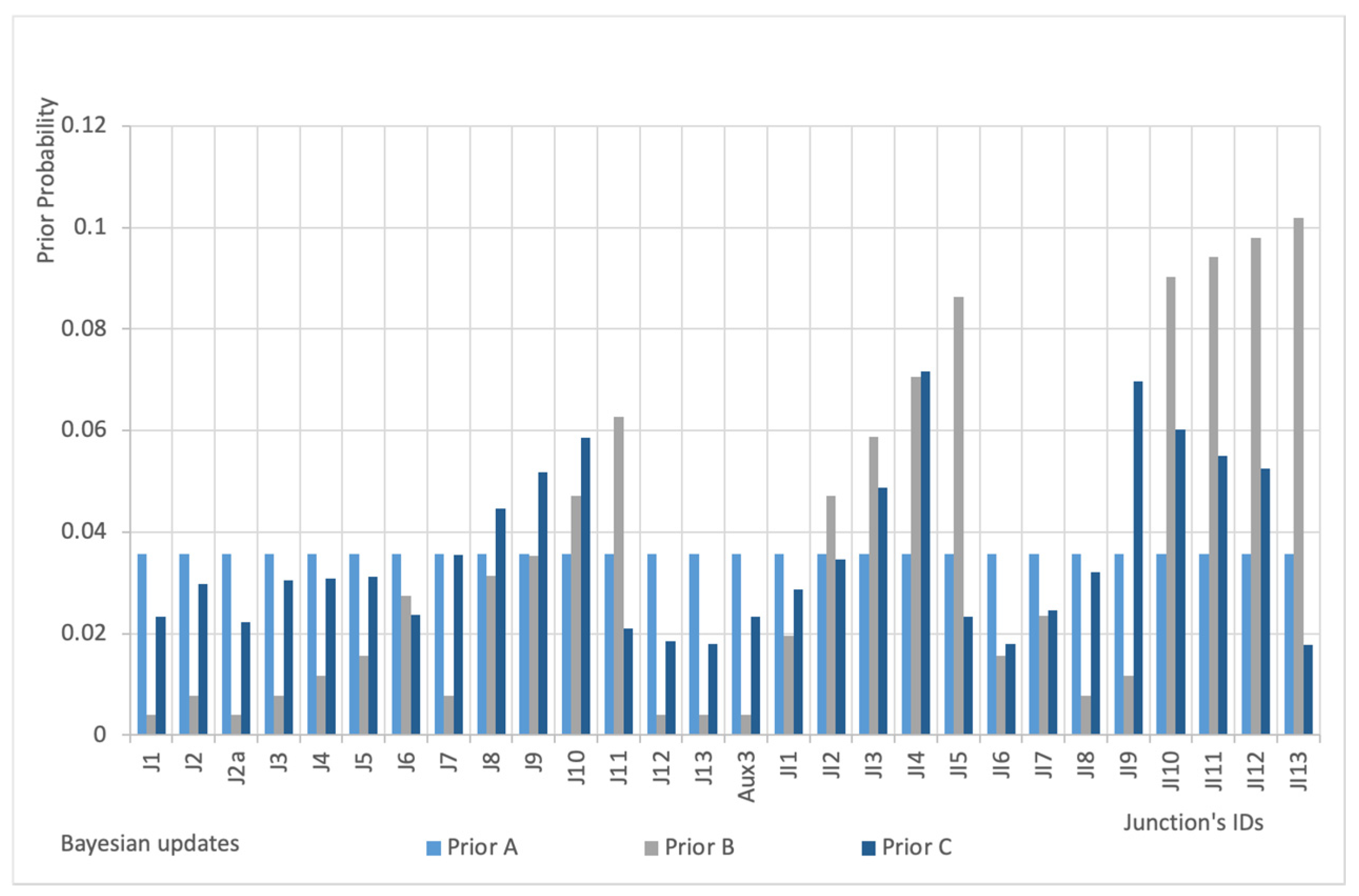
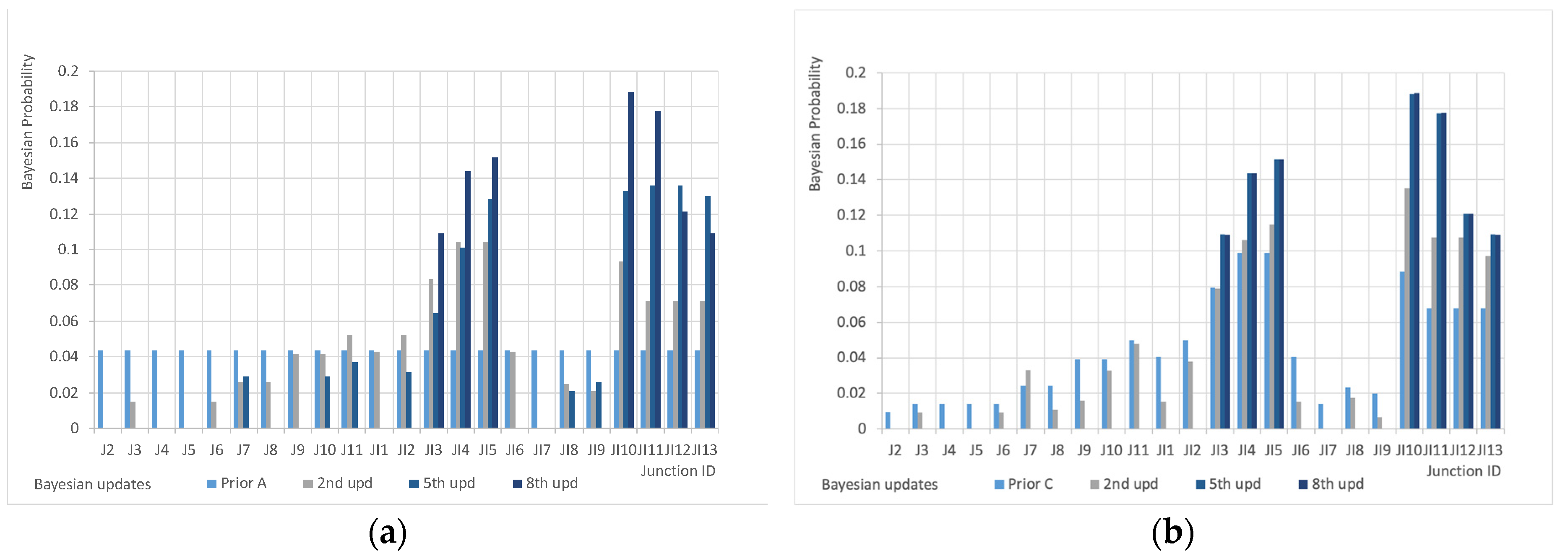
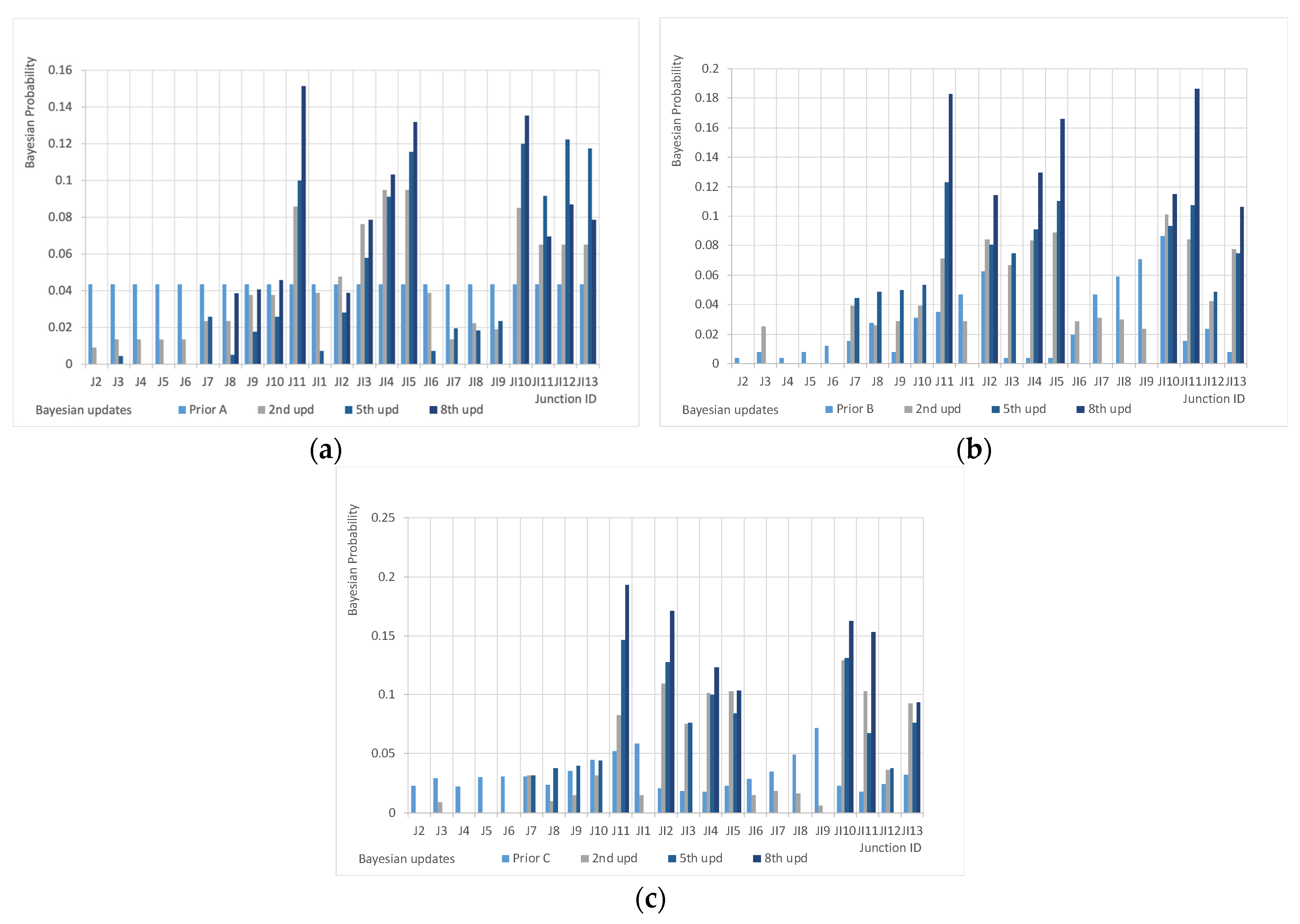
- Prior A: no pre-screening procedure and no prior knowledge (each node has an equal initial probability to be the location of a sensor).
- Prior B: no prior knowledge and pre-screening procedure based on network topology.
- Prior C: pre-screening procedure and prior knowledge based on water fluxes.
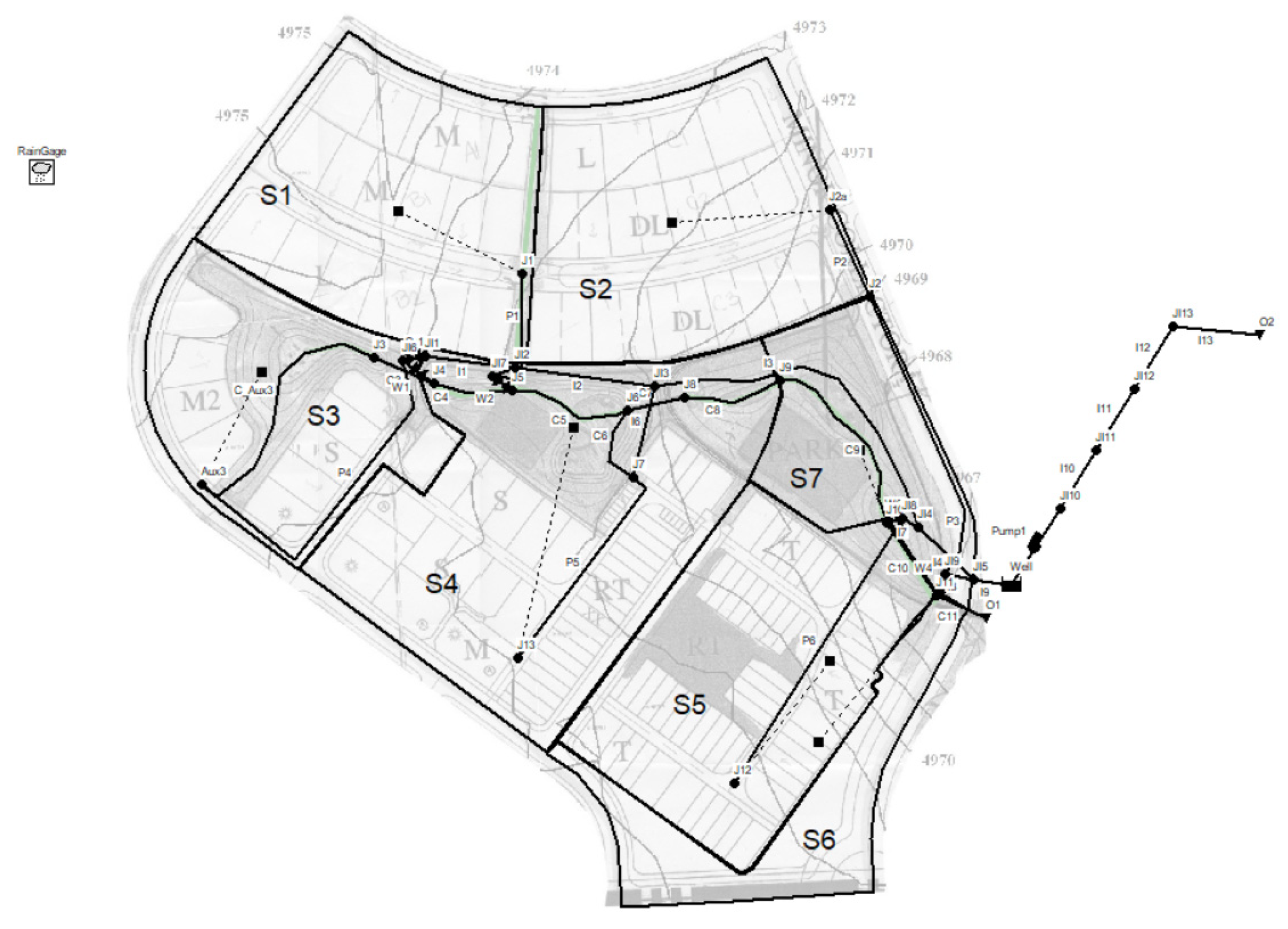
2.4. Case Study
3. Results and Discussion
- O1 and O2 which are the outfalls nodes;
- J1, J2a, Aux3, J12 and J13 which are the head nodes;
- Sensor deployment is dependent on contaminant kinetics and detectability with respect to background concentration so that more dense and uniformly distributed networks are expected when degradable and immanent contaminants need to be investigated;
- Xenobiotic conservative contaminations are easier to be located provided that sensor technology is sufficiently reliable and that networks can be deployed in downstream nodes so a smaller number of sensors is able to investigate large portions of the drainage system;
- The Bayesian approach gives its best in this type of problem, in which the initial database is small and only general and non-formal information is available about polluting sources; the method is able to introduce information coming from the initial detection exercises to improve the network in time thus allowing for deploying an initial sensor network configuration to be updated once a sufficient number of events are detected.
4. Conclusions
- The selection of prior distribution is irrelevant for the selection of the optimal sensor configuration in the conservative scenario while affects results in the non-conservative case; differences are not great (with the Prior B outperforming the others) but they are not negligible.
- Prior C based on flows probably does not adequately address the fact that with bigger flows, the sensor may be unable to detect the contamination due to the masking effect of distributed discharges of the same chemical.
- The number of steps needed to achieve the optimal configuration is much higher in the non-conservative case, showing the presence of greater uncertainties, and results are worse even if still largely acceptable.
- The two sensor configurations are different with the conservative case privileging the downstream nodes and the non-conservative one suggesting a more balanced configuration. This demonstrates that the nature of contaminant is a relevant information for deploying the best possible sensing strategy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Passerat, J.; Ouattara, N.K.; Mouchel, J.-M.; Rocher, V. Impact of an intense combined sewer overflow event on the microbiological water quality of the Seine River. Water Res. 2011, 45, 893–903. [Google Scholar] [CrossRef] [PubMed]
- Piazza, S.; Mirjam Blokker, E.J.; Freni, G.; Puleo, V.; Sambito, M. Impact of diffusion and dispersion of contaminants in water distribution networks modelling and monitoring. Water Sci. Technol. Water Supply 2020, 20, 46–58. [Google Scholar] [CrossRef]
- Francés-Chust, J.; Carpitellan, S.; Herrera, M.; Izquierdo, J.; Montalvo, I. Optimal placement of quality sensors in water distribution systems. In Proceedings of the Conference: Mathematical Modelling Conference in Engineering & Human Behaviour, Valencia, Spain, 10–12 July 2019. [Google Scholar]
- Lifshitz, R.; Ostfeld, A. Clustering for real time response to water distribution system contamination event intrusion. J. Water Resour. Plan. Manag. 2019, 145, 04018091. [Google Scholar] [CrossRef]
- Piazza, S.; Sambito, M.; Feo, R.; Freni, G.; Puleo, V. Optimal positioning of water quality sensors in water distribution networks: Comparison of numerical and experimental results. In Proceedings of the CCWI 2017—15th International Conference on Computing and Control for the Water Industry, Sheffield, UK, 5–7 September 2017. [Google Scholar]
- Bourgeois, W.; Burgess, J.E.; Stuetz, R.M. On-line monitoring of wastewater quality: A review. J. Chem. Technol. Biotechnol. 2001, 76, 337–348. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Brochu, E.; Brochu, T.; de Freitas, N. A Bayesian interactive optimization approach to procedural animation design. In Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Madrid, Spain, 2–4 July 2010; pp. 103–112. [Google Scholar]
- Lizotte, D.; Wang, T.; Bowling, M.; Schuurmans, D. Automatic gait optimization with Gaussian process regression. In Proceedings of the 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007; pp. 944–949. [Google Scholar]
- Martinez-Cantin, R.; de Freitas, N.; Doucet, A.; Castellanos, J.A. Active policy learning for robot planning and exploration under uncertainty. Proc. Robot. Sci. Syst. 2007, 3, 321–328. [Google Scholar]
- Marchant, R.; Ramos, F. Bayesian optimization for intelligent environmental monitoring. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2242–2249. [Google Scholar] [CrossRef]
- Wang, Z.; Shakibi, B.; Jin, L.; de Freitas, N. Bayesian multi-scale optimistic optimization. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics (AISTATS), Reykjavic, Iceland, 22–25 April 2014; pp. 1005–1014. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-based Optimization for General Algorithm Configuration, Learning and Intelligent Optimization; Springer: Berlin, Germany, 2011; pp. 507–523. [Google Scholar]
- Wang, Z.; Zoghi, M.; Matheson, D.; Hutter, F.; de Freitas, N. Bayesian optimization in high dimensions via random embeddings. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 1778–1784. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kegl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), Granada, Spain, 12–17 December 2011; pp. 2546–2554. [Google Scholar]
- Hoffman, M.; Shahriari, B.; de Freitas, N. On correlation and budget constraints in model-based bandit optimization with application to automatic machine learning. In Proceedings of the 17th International Conference on Artificial Intelligence and Statistics (AISTATS), Reykjavic, Iceland, 22–25 April 2014; pp. 365–374. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, New York, NY, USA, 3–6 December 2012; Volume 2, pp. 2951–2959. [Google Scholar]
- Swersky, K.; Snoek, J.; Adams, R.P. Multi-task Bayesian optimization. In Proceedings of the Neural Information Processing Systems, Harrahs and Harveys, Lake Tahoe, CA, USA, 5–10 December 2013; pp. 2004–2012. [Google Scholar]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11 August 2013; pp. 847–855. [Google Scholar]
- Garnett, R.; Osborne, M.A.; Roberts, S.J. Bayesian optimization for sensor set selection. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks; Association for Computing Machinery: New York, NY, USA, 2010; pp. 209–219. [Google Scholar]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M. Gaussian process optimization in the bandit setting: No regret and experimental design. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 1015–1022. [Google Scholar]
- Mahendran, N.; Wang, Z.; Hamze, F.; de Freitas, N. Adaptive MCMC with Bayesian optimization. J. Mach. Learn. Res. 2012, 22, 751–760. [Google Scholar]
- Azimi, J.; Jalali, A.; Fern, X. Hybrid batch Bayesian optimization. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 1215–1222. [Google Scholar]
- Brochu, E.; Cora, V.M.; de Freitas, N. A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning; Technical Report UBC TR-2009-23; Department of Computer Science, University of British Columbia: Vancouver, BC, Canada, 2009. [Google Scholar]
- Marsalek, J.; Rochfort, Q. Urban wet-weather flows: Sources of fecal contamination impacting on recreational waters and threatening drinking-water sources. J. Toxicol. Environ. Health A 2004, 67, 1765–1777. [Google Scholar] [CrossRef] [PubMed]
- Nawrot, N.; Wojciechowska, E.; Rezania, S.; Walkusz-Miotk, J.; Pazdro, K. The effects of urban vehicle traffic on heavy metal contamination in road sweeping waste and bottom sediments of retention tanks. Sci. Total Environ. 2020, 749, 141511. [Google Scholar] [CrossRef] [PubMed]
- Cryder, Z.; Greenberg, L.; Richards, J.; Wolf, D.; Luo, Y.; Gan, J. Fiproles in urban surface runoff: Understanding sources and causes of contamination. Environ. Pollut. 2019, 250, 754–761. [Google Scholar] [CrossRef] [PubMed]
- Ghane, E.; Ranaivoson, A.Z.; Feyereisen, G.W.; Rosen, C.J.; Moncrief, J.F. Comparison of Contaminant Transport in Agricultural Drainage Water and Urban Stormwater Runoff. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Sutarlie, L.; Loh, X.J. Sensors, Biosensors, and Analytical Technologies for Aquaculture Water Quality. Research 2020, 8272705. [Google Scholar] [CrossRef] [PubMed]
- Pasika, S.; Gandla, S.T. Smart water quality monitoring system with cost-effective using IoT. Heliyon 2020, 6, e04096. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.C.; Tsai, M.Y.; Tsai, Y.C.; You, J.J.; Cheng, C.L.; Wang, J.H.; Li, S.J. Development of Miniaturized Water Quality Monitoring System Using Wireless Communication. Sensors 2019, 19, 3758. [Google Scholar] [CrossRef] [PubMed]
- Sambito, M.; Di Cristo, C.; Freni, G.; Leopardi, A. Optimal water quality sensor positioning in urban drainage systems. J. Hydroinform. 2020, 22, 46–60. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Davis, J.; Rossman, L.A.; Supply, W. Storm Water Management Model Applications Manual; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2009.
- Riano-Briceno, G.; Barreiro-Gomeza, J.; Ramirez-Jaimea, A.; Quijanoa, N.; Ocampo-Martinez, C. MatSWMM—An Open-Source Toolbox for Designing Real-Time Control of Urban Drainage Systems. Environ. Model. Softw. 2016, 83, 143–154. [Google Scholar] [CrossRef]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
| Pressurized Distribution Networks | Free Surface Networks | |
|---|---|---|
| Contamination episodes | Water leak from loss of pressure or household pipes/hospitals/etc. and voluntary contamination. | Illicit discharges from private or industrial and commercial activities, in sewer systems. |
| Contaminants | Microbial pathogens from fecal contamination, aquatic microorganisms and their toxins, chemical contaminants. | Untreated domestic and industrial waste, toxic materials and debris. |
| Modelling | The solutions space is known a priori, it may be a backward contamination and the flow has low variations. | The solutions space is not known a priori, it cannot be a backward contamination and the flow has high variations. |
| Impact of contamination | Resources and public health. | Sewer system, wastewater treatment plant and water body. |
| Sensor technology | Fixed type sensors. | Fixed, mobile type sensors or sampling. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambito, M.; Freni, G. Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants. Water 2021, 13, 934. https://doi.org/10.3390/w13070934
Sambito M, Freni G. Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants. Water. 2021; 13(7):934. https://doi.org/10.3390/w13070934
Chicago/Turabian StyleSambito, Mariacrocetta, and Gabriele Freni. 2021. "Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants" Water 13, no. 7: 934. https://doi.org/10.3390/w13070934
APA StyleSambito, M., & Freni, G. (2021). Strategies for Improving Optimal Positioning of Quality Sensors in Urban Drainage Systems for Non-Conservative Contaminants. Water, 13(7), 934. https://doi.org/10.3390/w13070934







