An Integrated Bottom-Up Approach for Leak Detection in Water Distribution Networks Based on Assessing Parameters of Water Balance Model
Abstract
1. Introduction
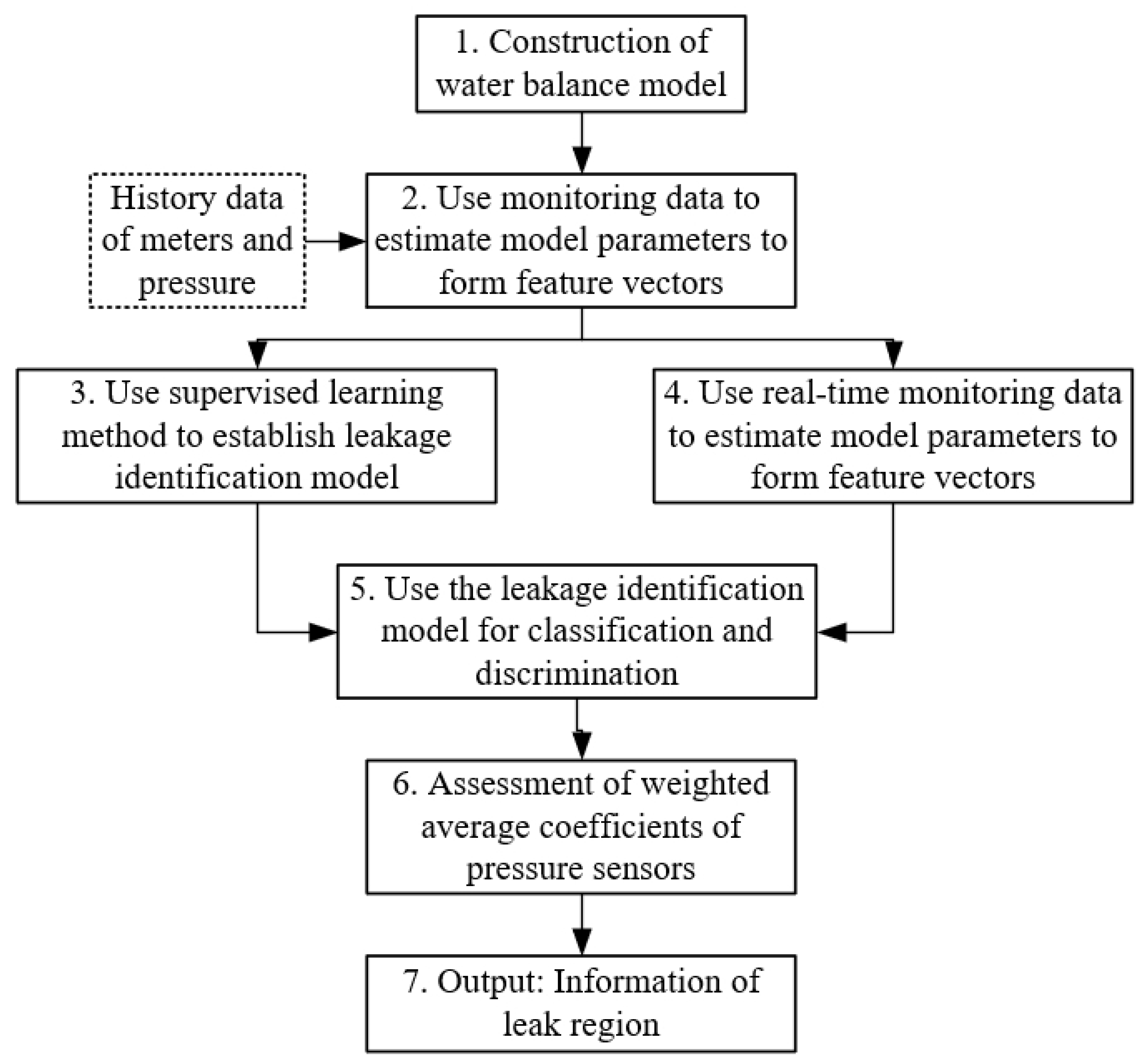
2. Methodology
2.1. Construction of Water Balance Model
2.1.1. Authorized Consumptions
2.1.2. Apparent Losses
2.1.3. Real Losses
2.1.4. Water Balance Model
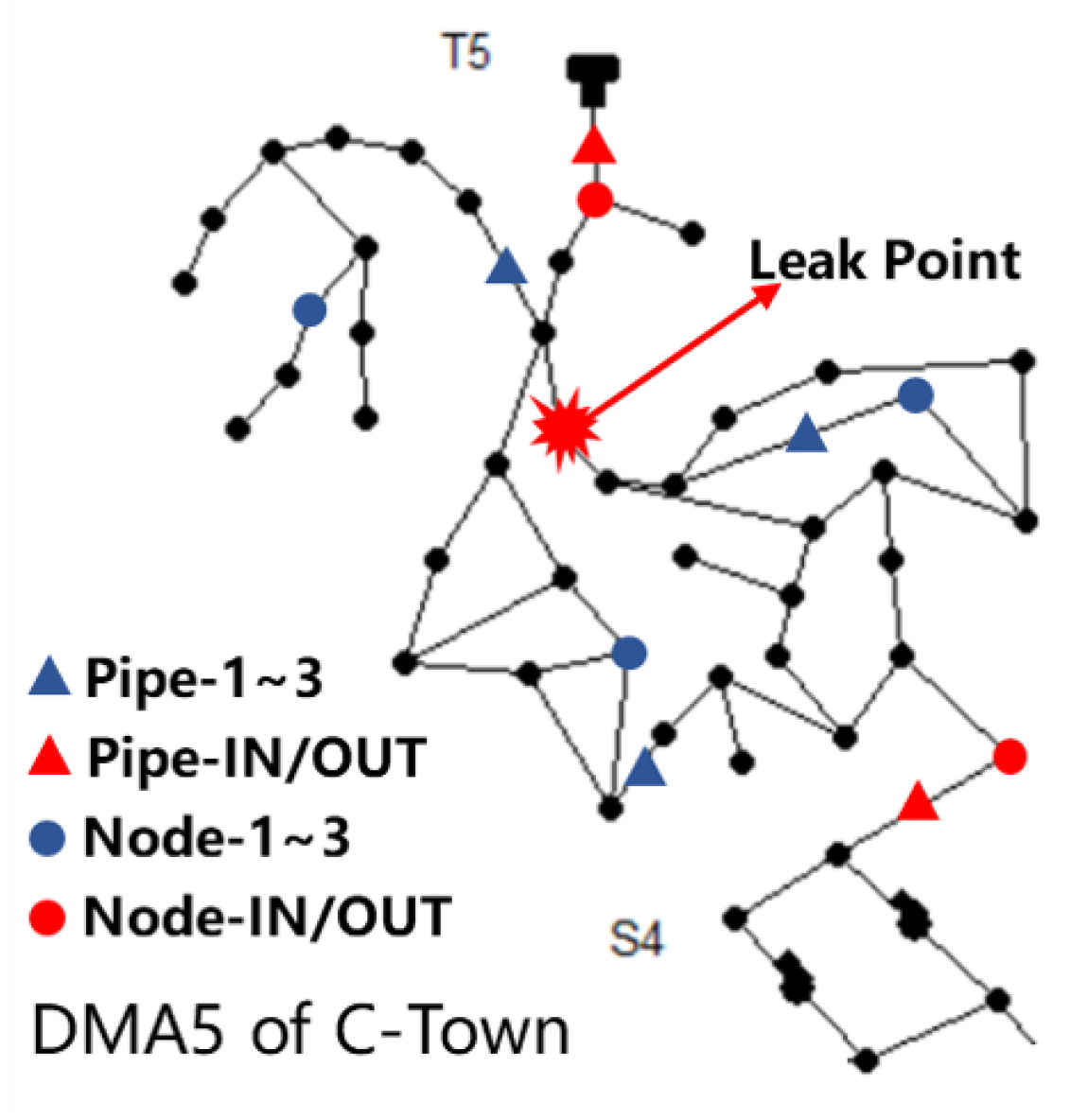
2.2. Approximate Location Information of Leak
2.3. Parameters Assessment
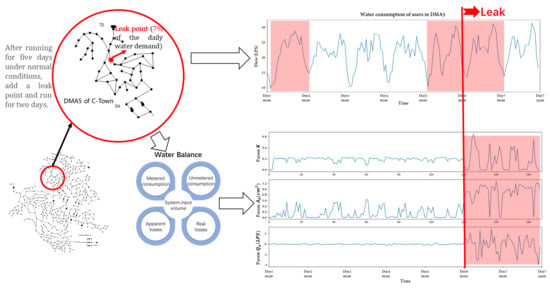
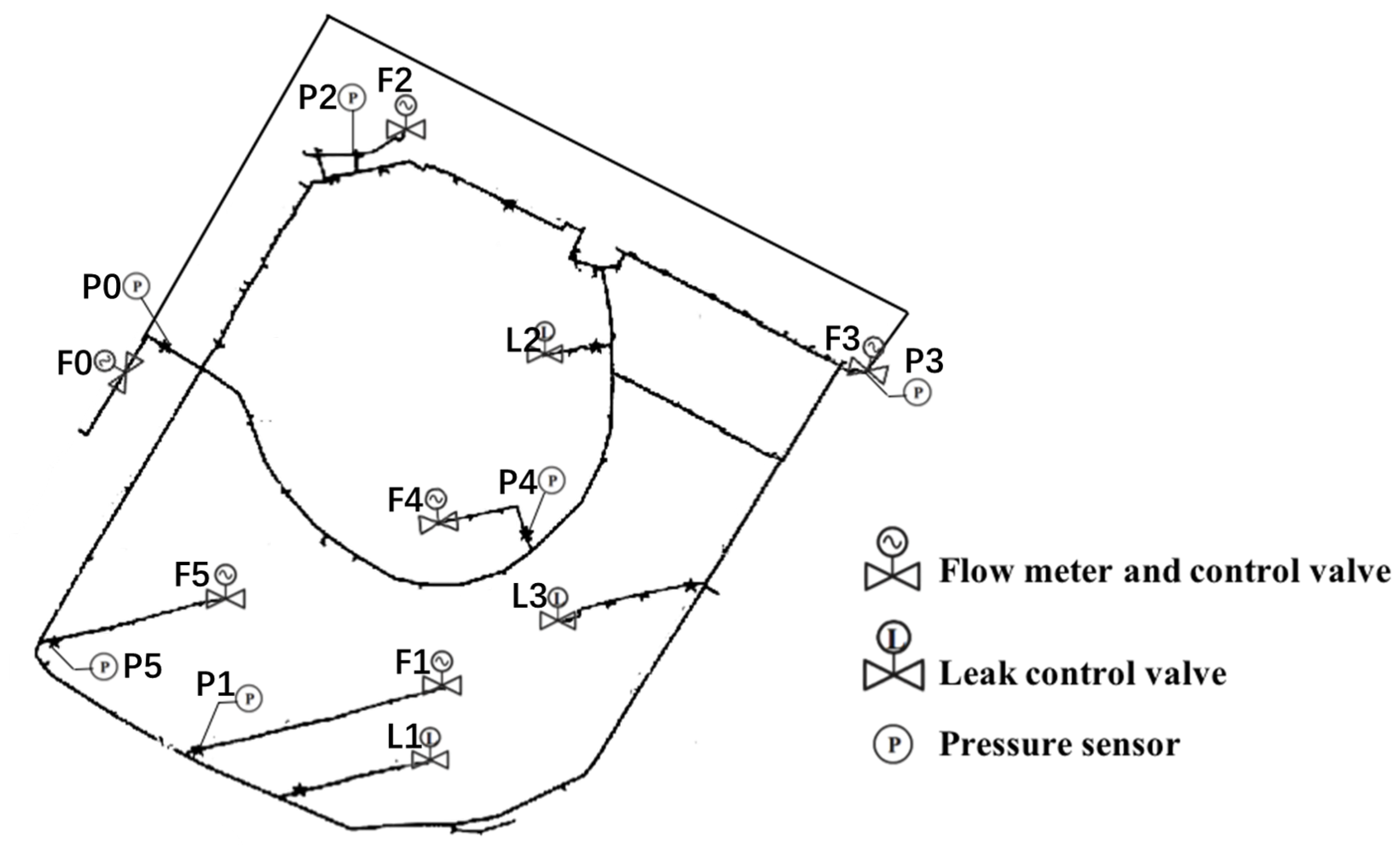
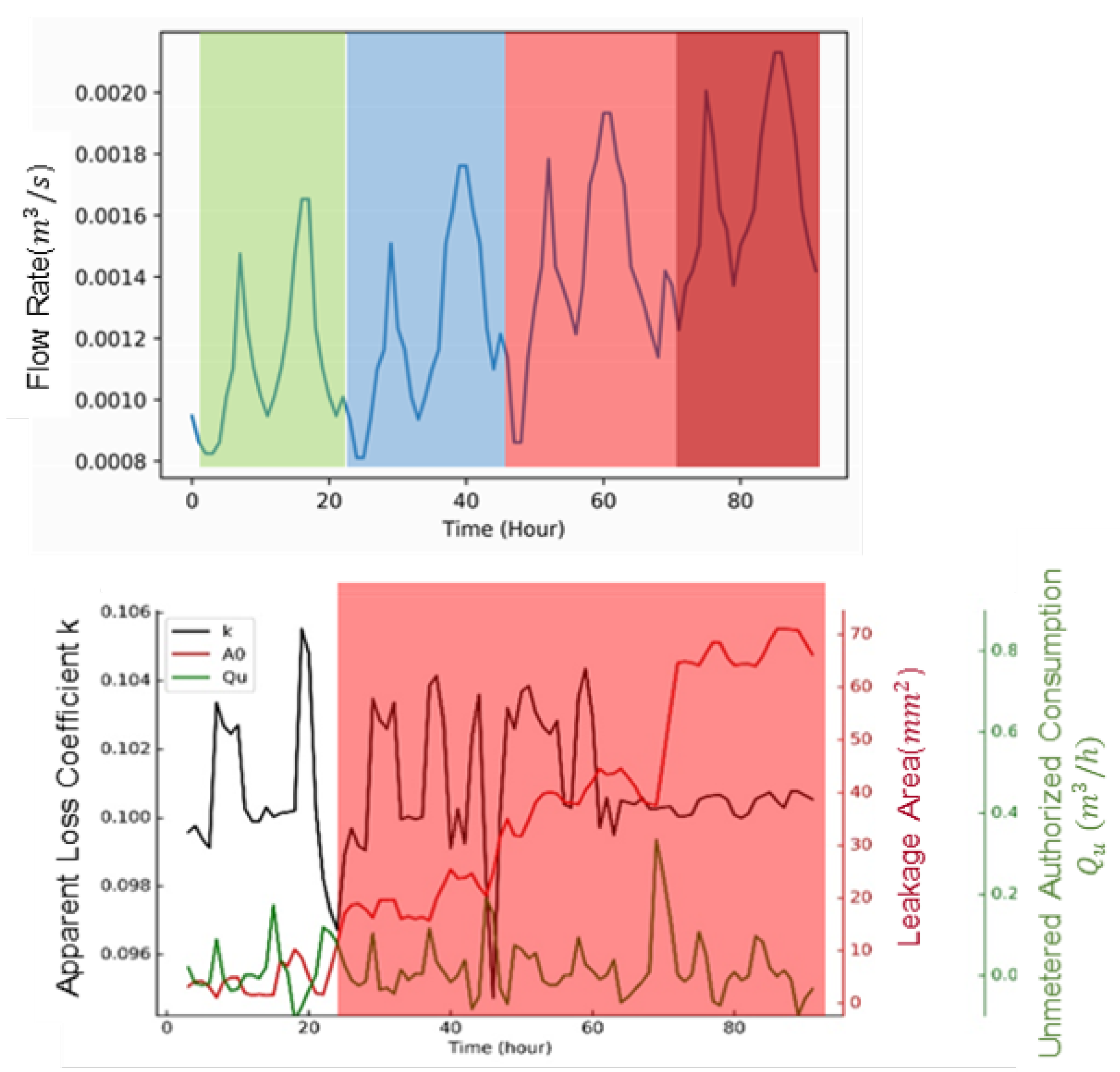
3. Case Study
3.1. Case 1
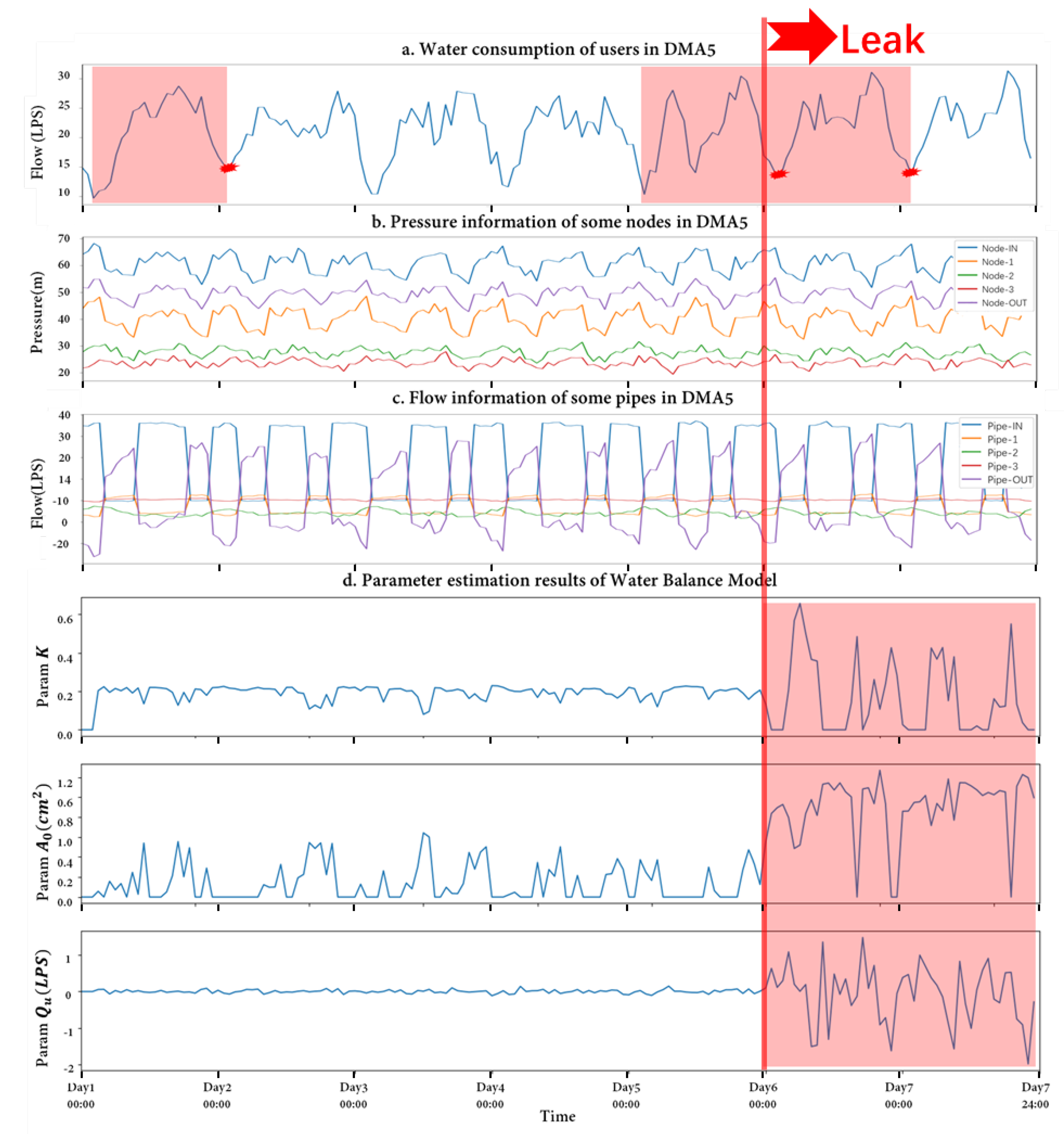
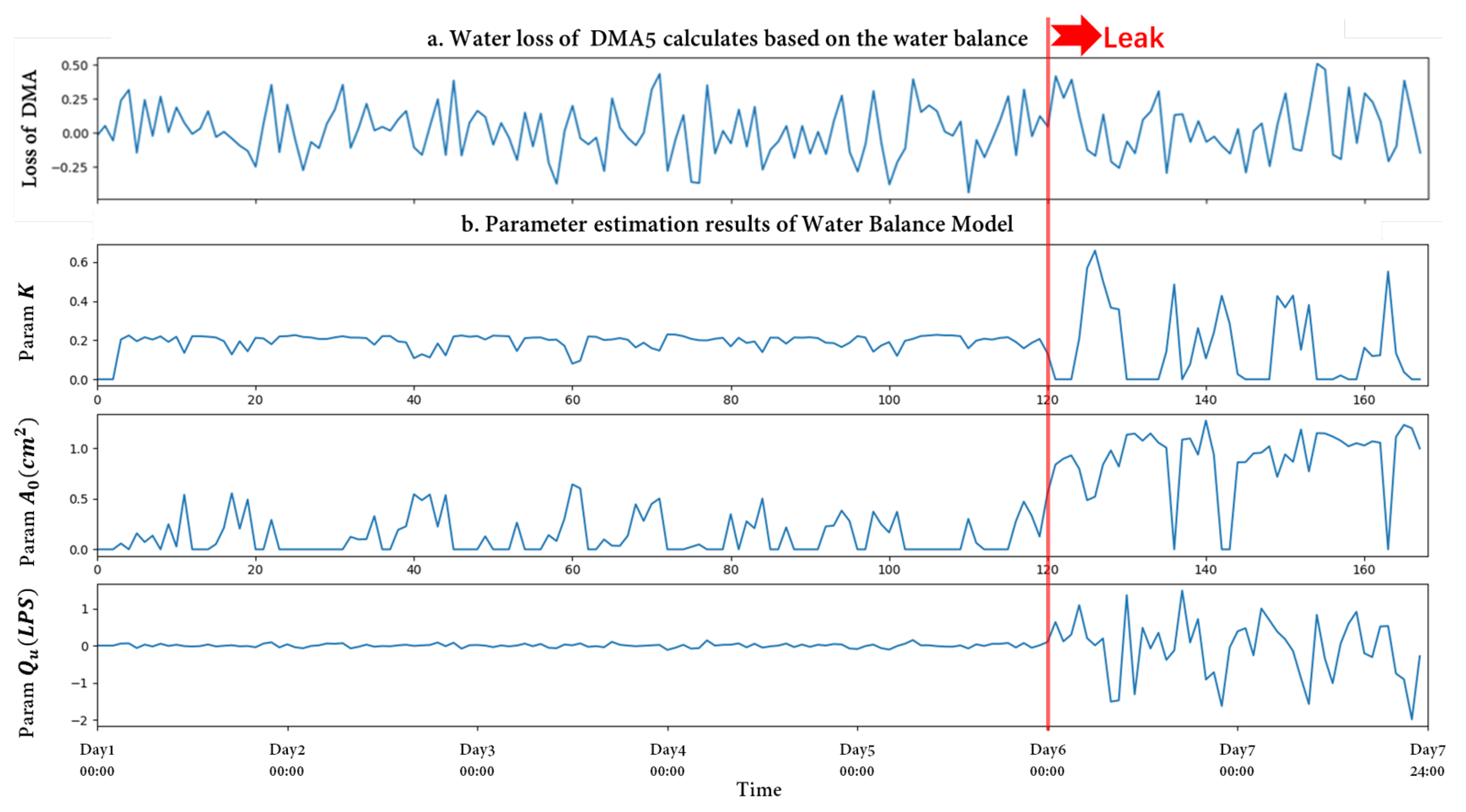
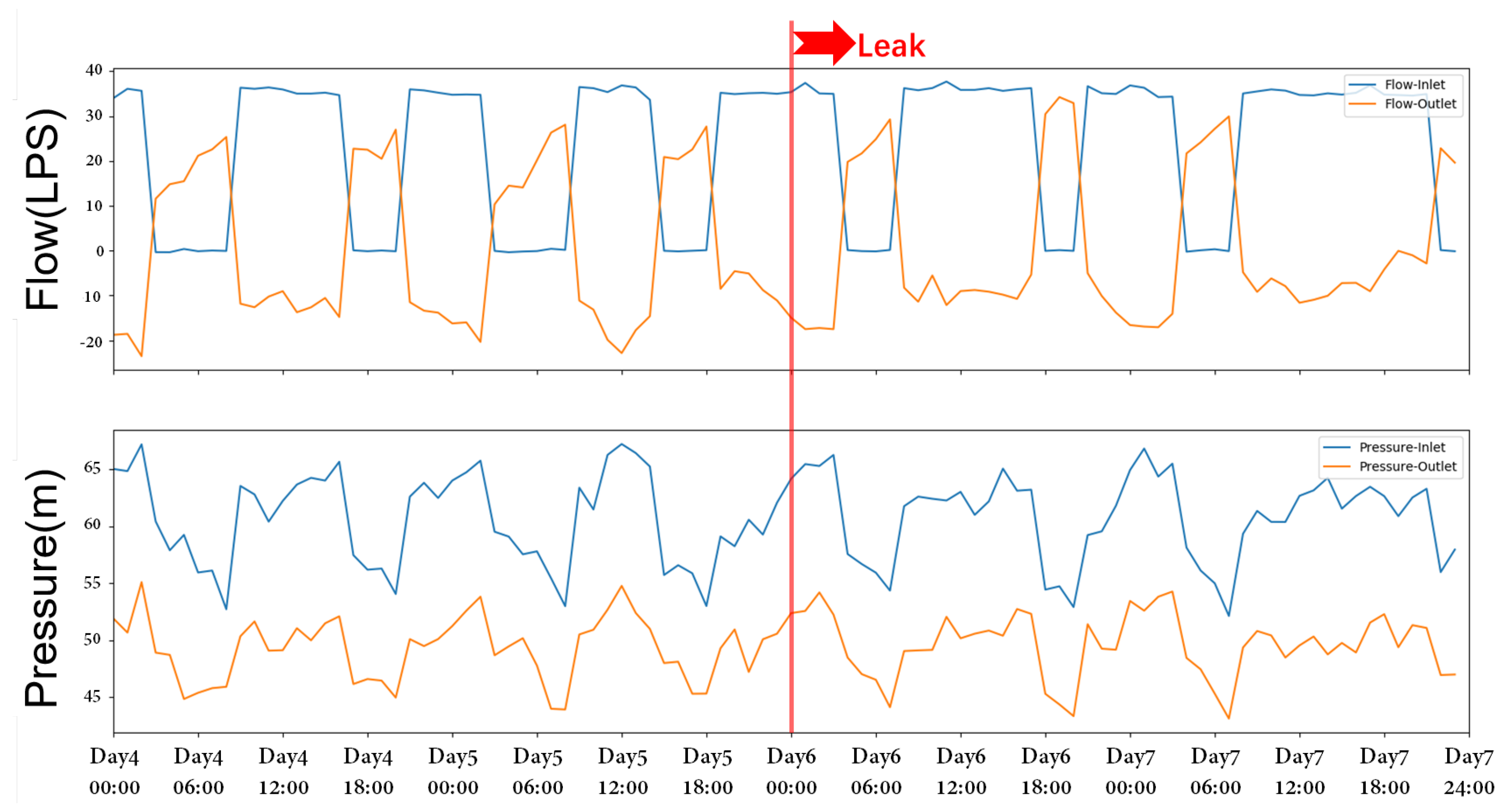
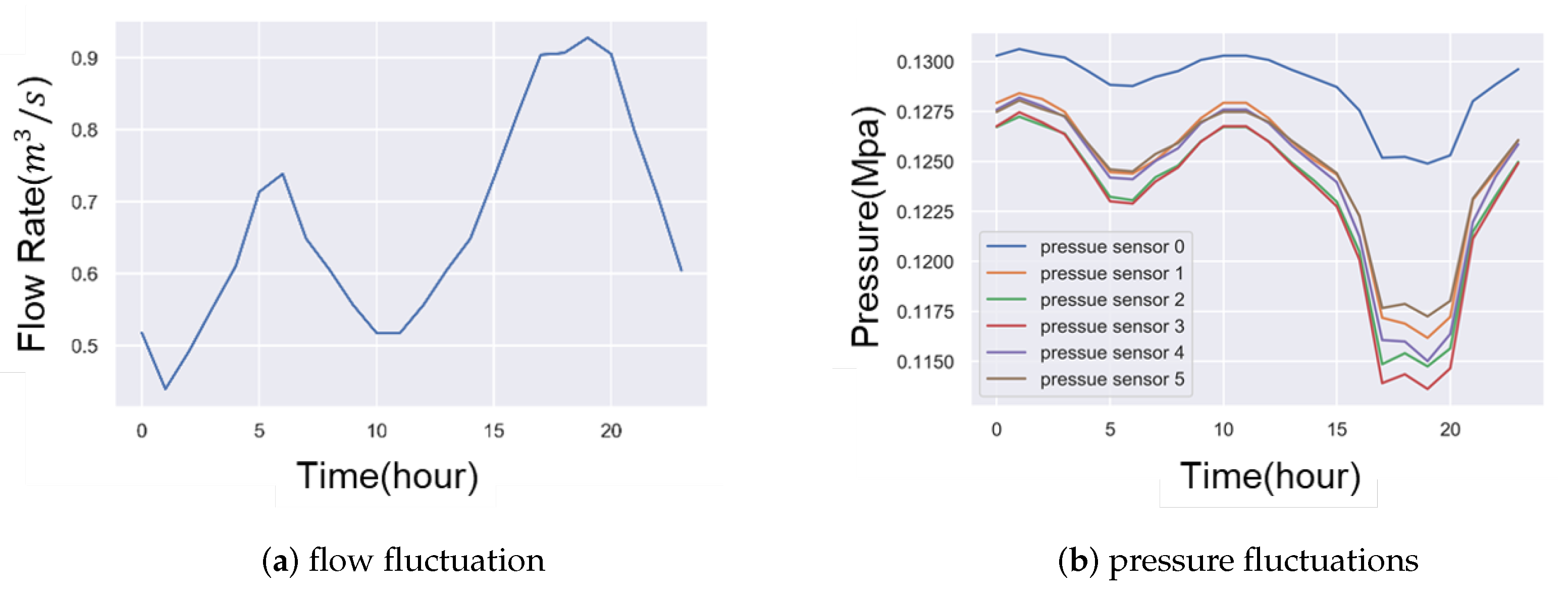
3.1.1. Leak Detection Bases on Proposed Method
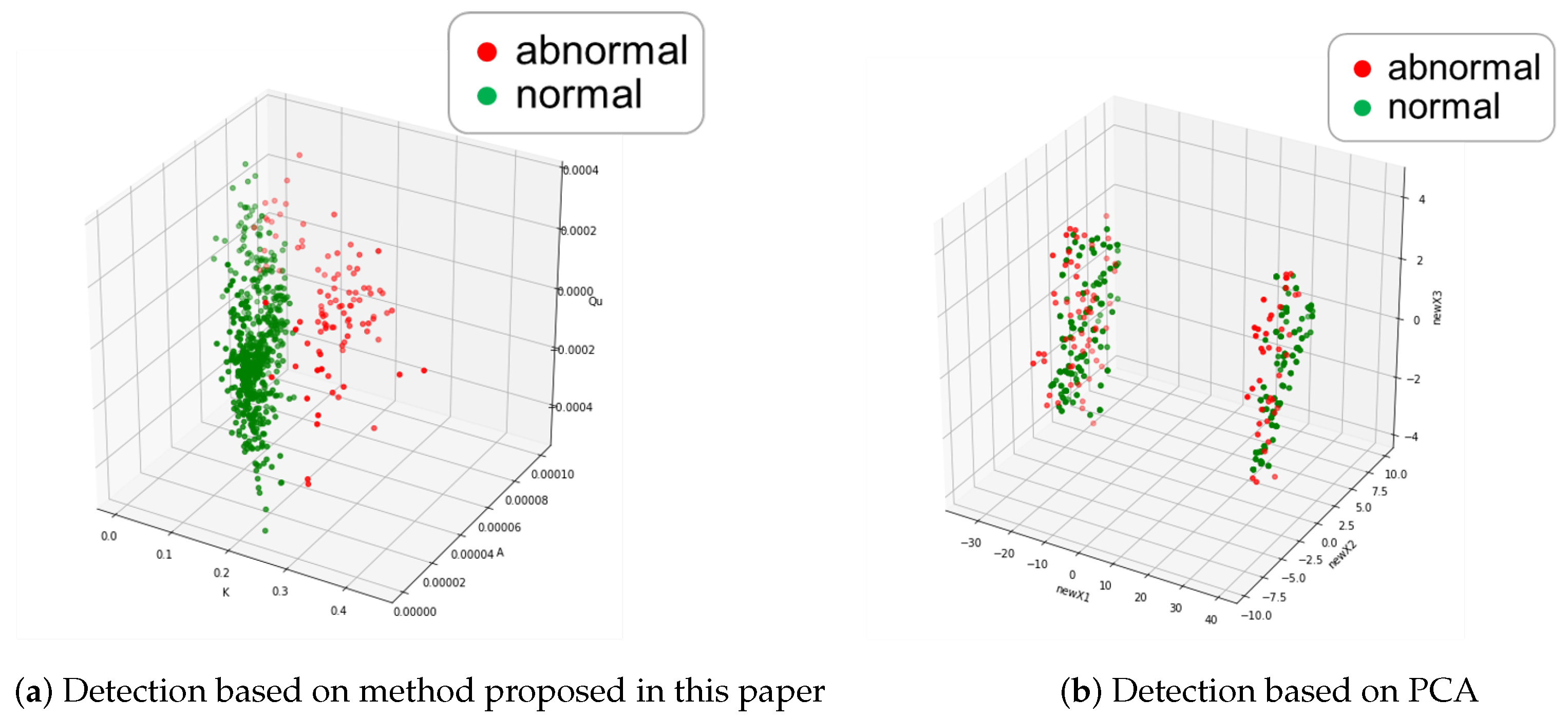
3.1.2. Leak Detection Performance Validation
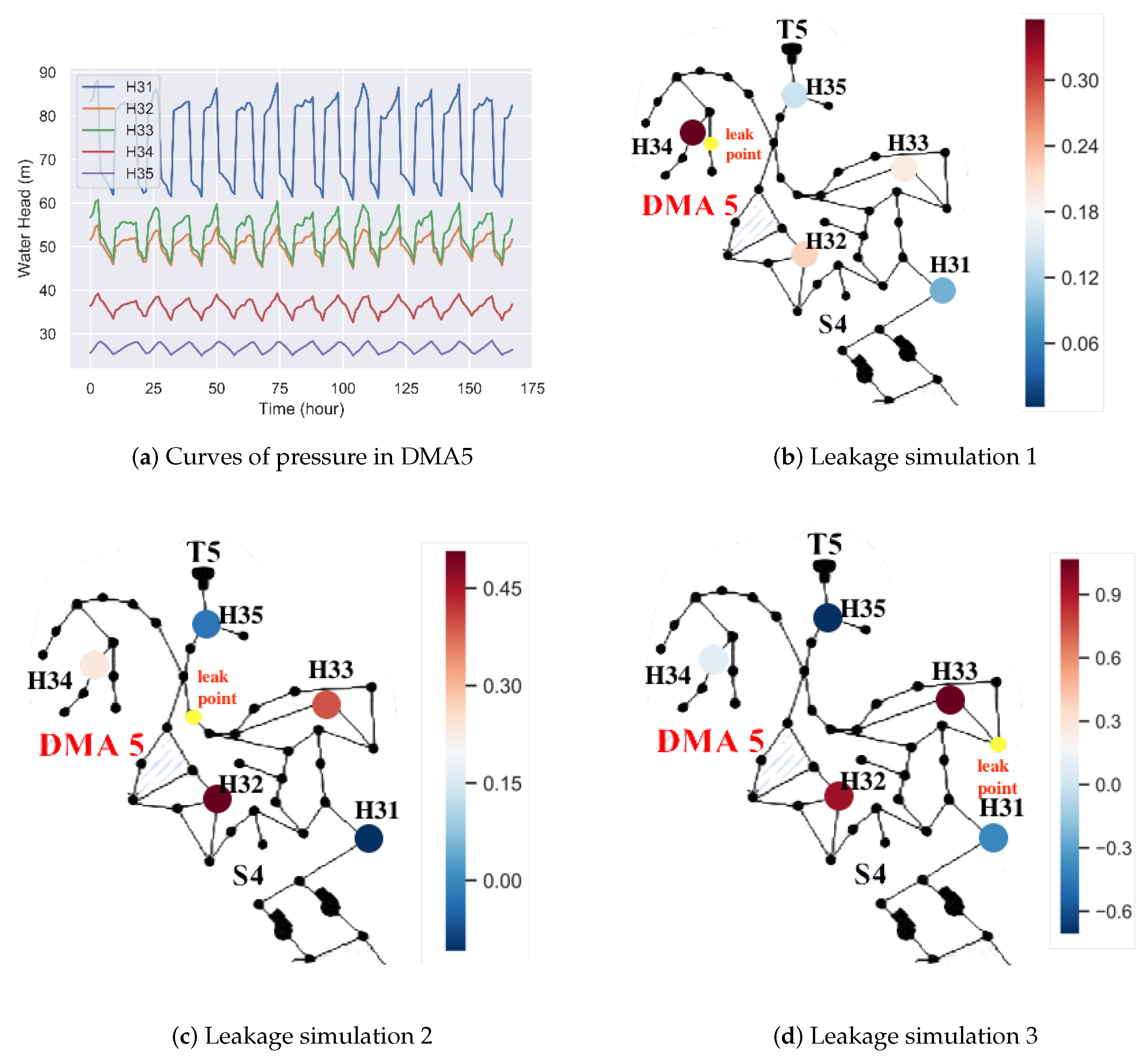
3.1.3. Approximate Location Information of Leakage
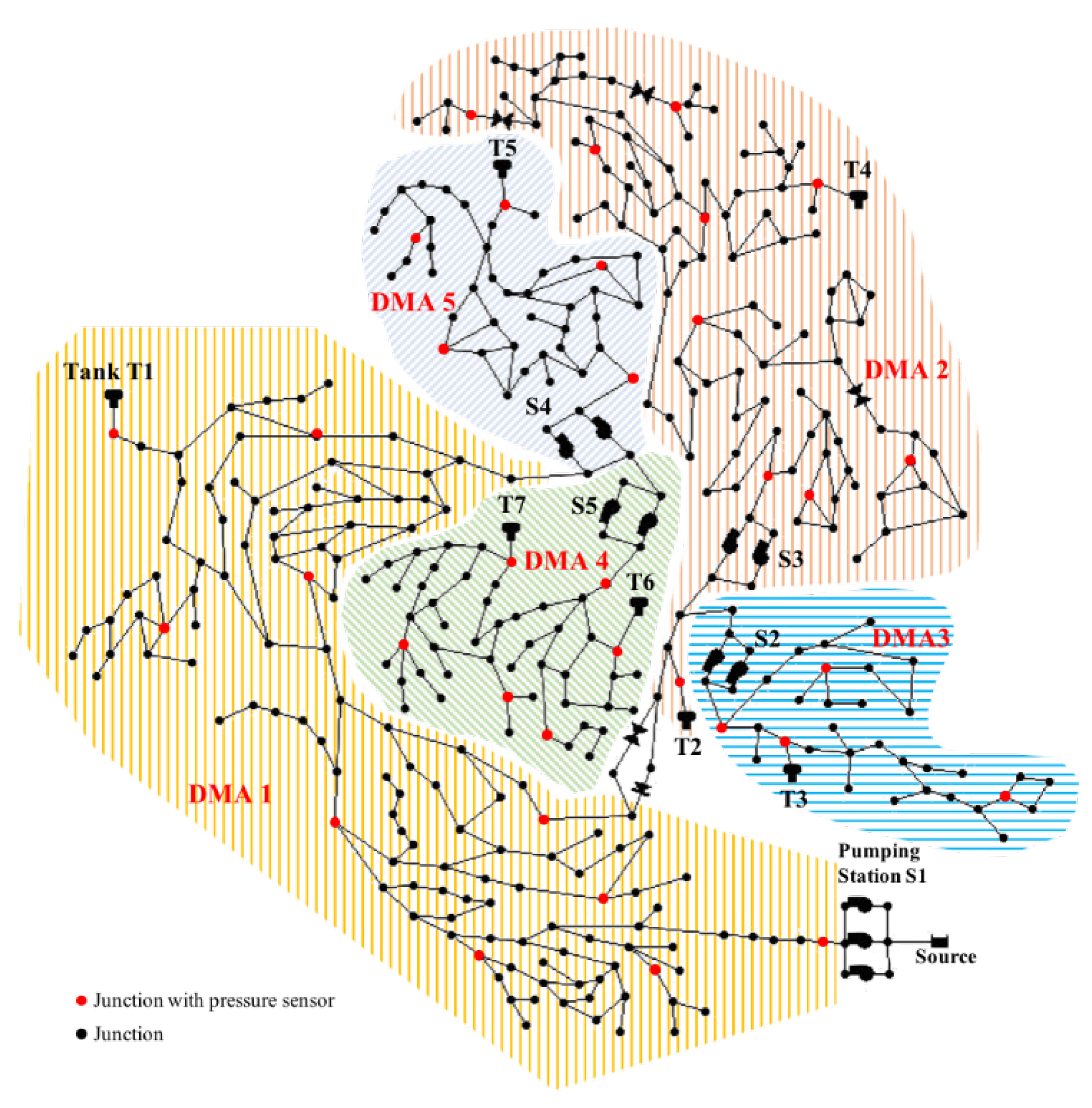
3.2. Case 2
3.2.1. Parameters Assessment
3.2.2. Approximate Location Information of Leak
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WDNs | water distribution networks |
| Adam | Adaptive moment estimation |
| MNF | minimum night flow |
| SCADA | supervisory control and data acquisition |
| DMAs | district metering areas |
| FAVAD | fixed and variable area discharge |
References
- Fontanazza, C.M.; Notaro, V.; Puleo, V.; Nicolosi, P.; Freni, G. Contaminant Intrusion through Leaks in Water Distribution System: Experimental Analysis. Procedia Eng. 2015, 119, 426–433. [Google Scholar] [CrossRef]
- Liu, H.; Yan, Z. Pipeline small leak detection based on PSO-SVM. Oil Gas Field Surf. Eng. 2019, 38, 105–110. [Google Scholar]
- Fei, L.; Tao, T. Leakage assessment and control method of water supply pipe network. China Water Wastewater 2012, 28, 35–39. [Google Scholar]
- Lambert, A. Assessing Non-Revenue Water and its Components: A Practical Approach. Water 2003, 21, 50–51. [Google Scholar]
- Oberascher, M.; Möderl, M.; Sitzenfrei, R. Water Loss Management in Small Municipalities: The Situation in Tyrol. Water 2020, 12, 3446. [Google Scholar] [CrossRef]
- Van den Berg, C. Drivers of non-revenue water: A cross-national analysis. Util. Policy 2015, 36, 71–78. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Using the bimonthly water balance of a non-fully monitored water distribution network with seasonal water demand peaks to define its actual NRW level: The case of Kos town, Greece. Urban Water J. 2014, 11, 348–360. [Google Scholar] [CrossRef]
- Lenzi, C.; Bragalli, C.; Bolognesi, A.; Fortini, M. Infrastructure Leakage Index Assessment in Large Water Systems. Procedia Eng. 2014, 2014, 1017–1026. [Google Scholar] [CrossRef]
- McKenzie, R.; Seago, C. Assessment of real losses in potable water distribution systems: Some recent developments. Water Sci. Technol. Water Supply 2005, 5, 33–40. [Google Scholar] [CrossRef]
- Adedeji, K.B.; Hamam, Y.; Abu-Mahfouz, A.M. Impact of Pressure-Driven Demand on Background Leakage Estimation in Water Supply Networks. Water 2019, 11, 1600. [Google Scholar] [CrossRef]
- Alvisi, S.; Luciani, C.; Franchini, M. Using water consumption smart metering for water loss assessment in a DMA: A case study. Urban Water J. 2019, 16, 77–83. [Google Scholar] [CrossRef]
- Xin, K.; Tao, T.; Lu, Y.; Xiong, X.; Li, F. Apparent Losses Analysis in District Metered Areas of Water Distribution Systems. Water Resour. Manag. 2014, 28, 683–696. [Google Scholar] [CrossRef]
- Mutikanga, H.; Sharma, S.; Vairavamoorthy, K. Assessment of apparent losses in urban water systems. Water Environ. J. 2011, 25, 327–335. [Google Scholar] [CrossRef]
- Marzola, I.; Alvisi, S.; Franchini, M. Analysis of MNF and FAVAD Models for Leakage Characterization by Exploiting Smart-Metered Data: The Case of the Gorino Ferrarese (FE-Italy) District. Water 2021, 13, 643. [Google Scholar] [CrossRef]
- Hutton, C.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D. Dealing with uncertainty in water distribution system models: A framework for real-time modeling and data assimilation. Water Resour. Plan. Manag. 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Van Zyl, J.; Clayton, C. The effect of pressure on leakage in water distribution systems. Proc. Inst. Civ. Eng. Water Manag. 2007, 160, 109–114. [Google Scholar] [CrossRef]
- Sanz, G.; Perez, R.; Kapelan, Z.; Savic, D. Leak detection and localization through demand components calibration. J. Water Resour. Plan. Manag. 2016, 142, 1097–1098. [Google Scholar] [CrossRef]
- Xie, X.; Hou, D.; Tang, X.; Zhang, H. Leakage Identification in Water Distribution Networks with Error Tolerance Capability. Water Resour. Manag. 2019, 33, 1233–1247. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Wu, X.; Liu, Y.; Guan, Y. Burst detection in district metering areas using a data driven clustering algorithm. Water Res. 2016, 100, 28–37. [Google Scholar] [CrossRef]
- Romano, M.; Kapelan, Z.; Savic, D. Automated detection of pipe bursts and other events in water distribution systems. J. Water Resour. Plan. Manag. 2014, 140, 457–467. [Google Scholar] [CrossRef]
- Laucelli, D.; Romano, M.; Savic, D.; Giustolisi, O. Detecting anomalies in water distribution networks using EPR modelling paradigm. J. Hydroinform. 2016, 18, 409–427. [Google Scholar] [CrossRef]
- Palau, C.; Arregui, F.; Carlos, M. Burst detection in water networks using principal component analysis. J. Water Resour. Plan. Manag. 2012, 138, 47–54. [Google Scholar] [CrossRef]
- Ye, G.; Fenner, R. Kalman filtering of hydraulic measurements for burst detection in water distribution systems. J. Pipeline Syst. Eng. Pract. 2011, 2, 14–22. [Google Scholar] [CrossRef]
- Huang, P.; Zhu, N.; Hou, D.; Chen, J.; Xiao, Y.; Yu, J.; Zhang, G.; Zhang, H. Real-Time Burst Detection in District Metering Areas in Water Distribution System Based on Patterns of Water Demand with Supervised Learning. Water 2018, 10, 1765. [Google Scholar] [CrossRef]
- Soldevila, A.; Fernandez-Canti, R.; Blesa, J.; Tornil-Sin, S.; Puig, V. Leak localization in water distribution networks using Bayesian classifiers. J. Process Control 2017, 55, 1–9. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Wang, X. Distance-based burst detection using multiple pressure sensors in district metering areas. J. Water Resour. Plan. Manag. 2018, 144, 06018009. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Tabesh, M.; Yekta, A.A.; Burrows, R. An integrated model to evaluate losses in water distribution systems. Water Resour. Manag. 2009, 23, 477–492. [Google Scholar] [CrossRef]
- Farah, E.; Shahrour, I. Leakage detection using smart water system: Combination of water balance and automated minimum night flow. Water Resour. Manag. 2017, 31, 4821–4833. [Google Scholar] [CrossRef]
- Schwaller, J.; van Zyl, J.; Kabaasha, A. Characterising the pressure-leakage response of pipe networks using the FAVAD equation. Water Sci. Technol. Water Supply 2015, 15, 1373–1382. [Google Scholar] [CrossRef]
- Chen, X.; Hou, B.; Xiao, W.; Hou, X.; Wang, L. Research on Intelligent Measurement and Leakage Diagnosis System and Method of Industrial Enterprise Dynamic Water Balance. Sci. Technol. Innov. Appl. 2020, 26, 6–9. [Google Scholar]
- Farley, M.; Trow, S. Losses in Water Distribution Networks: A Practitioners’ Guide to Assessment, Monitoring and Control. Water Intell. Online 2005. [Google Scholar] [CrossRef]
- Almandoz, J.; Cabrera, E.; Arregui, F.; Cabrera, E.; Cobacho, R. Leakage assessment through water distribution network simulation. J. Water Resour. Plan. Manag. 2005, 131, 458–466. [Google Scholar] [CrossRef]
- Kabaasha, A.; Piller, O.; van Zyl, J. Incorporating the Modified Orifice Equation into Pipe Network Solvers for More Realistic Leakage Modeling. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Schwaller, J.; van Zyl, J. Modeling the pressure-leakage response of water distribution systems based on individual leak behavior. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Cassa, A.; van Zyl, J.; Laubscher, R. A numerical investigation into the effect of pressure on holes and cracks in water supply pipes. Urban Water J. 2010, 7, 109–120. [Google Scholar] [CrossRef]
- Cassa, A.; Van Zyl, J.; Laubscher, R. Predicting the pressure-leakage slope of cracks in pipes subject to elastic deformations. J. Water Supply Res. Technol. AQUA 2013, 62, 214. [Google Scholar] [CrossRef]
- Kingma, D.; Jimmy, B. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]


| System input volume | Authorized consumptions | Metered consumption |
| Unmetered consumption | ||
| Water losses | Apparent losses | |
| Real losses |
| Detection Method | Recall Rates |
|---|---|
| WB-Method | 94.59% |
| PCA | 45.83% |
| Detection Method | ||||
|---|---|---|---|---|
| WB-Method | 89.19% | 94.73% | 98.95% | 100% |
| PCA | 23.53% | 33.33% | 36.84% | 48.15% |
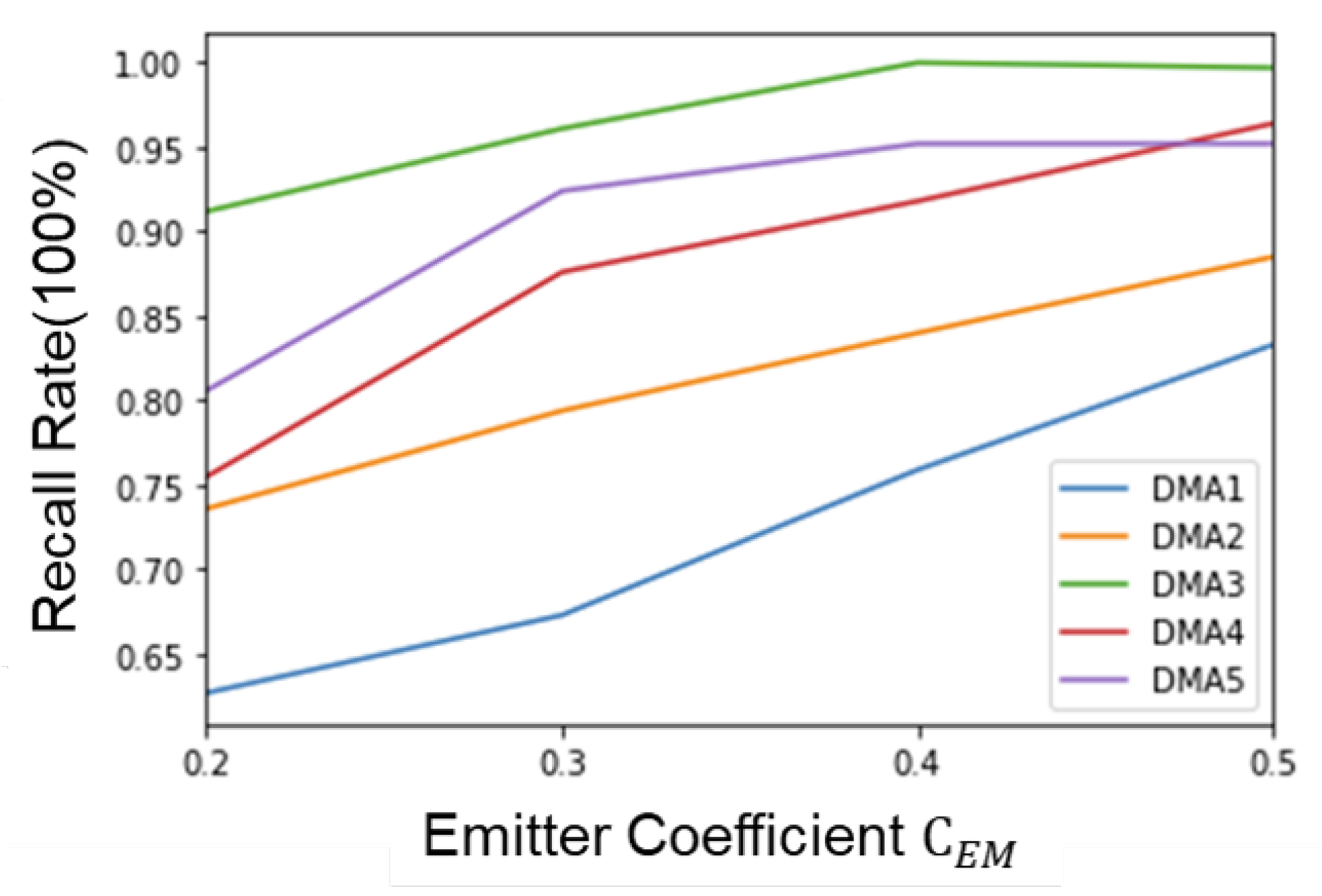
| Time Window Length | 4 | 6 | 8 |
|---|---|---|---|
| DMA1 | 78.4% | 83.8% | 86.5% |
| DMA2 | 85.7% | 92.9% | 96.4% |
| DMA3 | 94.6% | 97.3% | 97.3% |
| DMA4 | 94.1% | 97.1% | 100% |
| DMA5 | 96.4% | 96.4% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhang, L.; Chen, J.; Xiao, Y.; Hou, D.; Huang, P.; Zhang, G.; Zhang, H. An Integrated Bottom-Up Approach for Leak Detection in Water Distribution Networks Based on Assessing Parameters of Water Balance Model. Water 2021, 13, 867. https://doi.org/10.3390/w13060867
Yu J, Zhang L, Chen J, Xiao Y, Hou D, Huang P, Zhang G, Zhang H. An Integrated Bottom-Up Approach for Leak Detection in Water Distribution Networks Based on Assessing Parameters of Water Balance Model. Water. 2021; 13(6):867. https://doi.org/10.3390/w13060867
Chicago/Turabian StyleYu, Jie, Li Zhang, Jinyu Chen, Yao Xiao, Dibo Hou, Pingjie Huang, Guangxin Zhang, and Hongjian Zhang. 2021. "An Integrated Bottom-Up Approach for Leak Detection in Water Distribution Networks Based on Assessing Parameters of Water Balance Model" Water 13, no. 6: 867. https://doi.org/10.3390/w13060867
APA StyleYu, J., Zhang, L., Chen, J., Xiao, Y., Hou, D., Huang, P., Zhang, G., & Zhang, H. (2021). An Integrated Bottom-Up Approach for Leak Detection in Water Distribution Networks Based on Assessing Parameters of Water Balance Model. Water, 13(6), 867. https://doi.org/10.3390/w13060867