Technical Note: On the Production and Accuracy of CNC-Manufactured Hydraulic Scale Models
Abstract
1. Introduction
2. Material and Methods
3. Results
3.1. Comparison of Point Clouds and Meshes
3.2. Accuracy Assessment Based on Statistical Parameters
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ettema, R. Role of hydraulic experiments. In Experimental Hydraulics, Volume I: Fundamentals and Methods; Section 1.2; Muste, M., Lyn, D.A., Admiraal, D.M., Ettema, R., Nikora, V., Garcia, M.H., Eds.; Taylor & Francis Group: London, UK, 2017. [Google Scholar]
- Hughes, S. Physical Models and Laboratory Techniques in Coastal Engineering; Advanced Series on Ocean Engineering; World Scientific Publishing: Singapore, 1993; Volume 7. [Google Scholar]
- Novak, P.; Guinot, V.; Jeffrey, A.; Reeve, D.E. Hydraulic Modelling—An Introduction; Spon Press: London, UK; New York, NY, USA, 2010. [Google Scholar]
- Muste, M.; Aberle, J.; Admiraal, D.; Ettema, R.; Garcia, M.; Lyn, D.; Nikora, V.; Rennie, C. (Eds.) Experimental Hydraulics: Methods, Instrumentation, Data Processing and Management; CRC Press: London, UK, 2017. [Google Scholar]
- Rowiński, P.M. (Ed.) Experimental Methods in Hydraulic Research; GeoPlanet: Earth and Planetary Sciences; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Baynes, E.R.C.; van de Lageweg, W.I.; McLelland, S.J.; Parsons, D.R.; Aberle, J.; Dijkstra, J.; Henry, P.-Y.; Rice, S.P.; Thom, M.; Moulin, F. Beyond equilibrium: Re-evaluating physical modelling of fluvial systems to represent climate changes. Earth-Sci. Rev. 2018, 181, 82–97. [Google Scholar] [CrossRef]
- Addis, W. (Ed.) Physical Models: Their Historical and Current Use in Civil and Building Engineering Design; Ernst & Sohn: Berlin, Germany, 2021. [Google Scholar]
- Henry, P.Y.; Aberle, J.; Anquetin, P.-G.; Grasso, F.; Bodewes, B.; Fernadez, R.L.; McLelland, S.; Vettori, D.; Caceres, I.; Marzeddu, A.; et al. Hydralab+ Deliverable D8.III Protocols for Scaling Morphodynamics in Time. Zenodo 2018. [Google Scholar] [CrossRef]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Henry, P.-Y.; Aberle, J.; Navaratnam, C.U.; Rüther, N. Hydraulic physical model production with Computer Numerically Controlled (CNC) manufacturing techniques. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 40, p. 05065. [Google Scholar] [CrossRef]
- Webb, C.B.; Barfuss, S.L.; Johnson, M.C. Modelling roughness in scale models. J. Hydraul. Res. 2010, 48, 260–264. [Google Scholar] [CrossRef]
- Chandler, J.H.; Buffin-Bélanger, T.; Rice, S.; Reid, I.; Graham, D.I. The accuracy of a river bed moulding/casting system and the effectiveness of a low-cost digital camera for recording river bed fabric. Photogramm. Rec. 2003, 18, 209–223. [Google Scholar] [CrossRef]
- Buffin-Bélanger, T.; Reid, I.; Rice, S.; Chandler, J.H.; Lancaster, J. A casting procedure for reproducing coarse-grained sedimentary surfaces. Earth Surf. Process. Landf. 2003, 28, 787–796. [Google Scholar] [CrossRef]
- Buffin-Bélanger, T.; Rice, S.; Reid, I.; Lancaster, J. Spatial heterogeneity of near-bed hydraulics above a patch of river gravel. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Rice, S.P.; Buffin-Bélanger, T.; Reid, I. Sensitivity of interfacial hydraulics to the microtopographic roughness of water-lain gravels. Earth Surf. Process. Landf. 2014, 39, 184–199. [Google Scholar] [CrossRef]
- Spiller, S.; Rüther, N.; Friedrich, H. Dynamic lift on an artificial static armor layer during highly unsteady open channel flow. Water 2015, 7, 4951–4970. [Google Scholar] [CrossRef]
- Cooper, J.R.; Ockleford, A.; Rice, S.P.; Powell, D.M. Does the permeability of gravel river beds affect near-bed hydrodynamics? Earth Surf. Process. Landf. 2018, 43, 943–955. [Google Scholar] [CrossRef]
- Navaratnam, C.U.; Aberle, J.; Qin, J.; Henry, P.-Y. Influence of gravel-bed porosity and grain orientation on bulk flow resistance. Water 2018, 10, 561. [Google Scholar] [CrossRef]
- Bertin, S.; Friedrich, H.; Delmas, P.; Chan, E.; Gimel’farb, G. Digital stereo photogrammetry for grain-scale monitoring of fluvial surfaces: Error evaluation and workflow optimisation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 193–208. [Google Scholar] [CrossRef]
- Brasington, J. Terrestrial Laser Scanning: Topographic measurement and modelling. In Experimental Hydraulics, Volume II: Instrumentation and Measurement Techniques; Section 4.2; Aberle, J., Rennie, C.D., Admiraal, D.M., Muste, M., Eds.; Taylor & Francis: New York, NY, USA, 2017. [Google Scholar]
- Henning, M.; Detert, M.; Aberle, J. Photogrammetry. In Experimental Hydraulics, Volume II: Instrumentation and Measurement Techniques; Section 4.4; Aberle, J., Rennie, C.D., Admiraal, D.M., Muste, M., Eds.; Taylor & Francis: New York, NY, USA, 2017. [Google Scholar]
- Stewart, M.T.; Cameron, S.M.; Nikora, V.I.; Zampiron, A.; Marusic, I. Hydraulic resistance in open-channel flows over self-affine rough beds. J. Hydraul. Res. 2019, 57, 183–196. [Google Scholar] [CrossRef]
- Nikora, V.; Stoesser, T.; Cameron, S.; Stewart, M.; Papadopoulos, K.; Ouro, P.; McSherry, R.; Zampiron, A.; Marusic, I.; Falconer, R. Friction factor decomposition for rough-wall flows: Theoretical background and application to open-channel flows. J. Fluid Mech. 2019, 872, 626–664. [Google Scholar] [CrossRef]
- Chua, C.K.; Leong, K.F. 3D Printing and Additive Manufacturing: Principles and Applications, 5th ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2017. [Google Scholar]
- Liaw, C.-Y.; Guvendiren, M. Current and emerging applications of 3D printing in medicine. Biofabrication 2017, 9, 024102. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.; Wang, L. 3D printing of biomimetic composites with improved fracture toughness. Acta Mater. 2019, 173, 61–73. [Google Scholar] [CrossRef]
- Mohammed, J.S. Applications of 3D printing technologies in oceanography. Methods Oceanogr. 2016, 17, 97–117. [Google Scholar] [CrossRef]
- Bhattacharjee, N.; Urrios, A.; Kang, S.; Folch, A. The upcoming 3D-printing revolution in microfluidics. Lab Chip 2016, 16, 1720–1742. [Google Scholar] [CrossRef]
- Kloft, H.; Hack, N.; Lindemann, H.; Mainka, J. Shotcrete 3D printing (SC3DP)—3D-Drucken von großformatigen Betonbauteilen. Dtsch. Bauz. 2019, 2, 54–57. [Google Scholar]
- Bertin, S.; Friedrich, H.; Delmas, P.; Chan, E.; Gimel’farb, G. DEM quality assessment with a 3d printed gravel bed applied to stereo photogrammetry. Photogramm. Rec. 2014, 29, 241–264. [Google Scholar] [CrossRef]
- Hodge, R.A.; Hoey, T.B. A Froude-scaled model of a bedrock-alluvial channel reach: 1. Hydraulics. J. Geophys. Res. Earth Surf. 2016, 121, 1578–1596. [Google Scholar] [CrossRef]
- Pedersen, Ø.; Aberle, J.; Rüther, N. Hydraulic scale modelling of the rating curve for a gauging station with challenging geometry. Hydrol. Res. 2019, 50, 825–836. [Google Scholar] [CrossRef]
- Andersson, L.; Larsson, I.; Hellstrom, J.; Andreasson, P.; Andersson, A. Experimental Study of Head Loss over Laser scanned Rock Tunnel. In Hydraulic Structures and Water System Management, Proceedings of the 6th IAHR International Symposium on Hydraulic, Portland, OR, USA, 27–30 June 2016; Crookston, B.M., Tullis, B., Eds.; Utah State University: Logan, UT, USA, 2016; pp. 22–29. [Google Scholar] [CrossRef]
- Aberle, J.; Henry, P.-Y.; Kleischmann, F.; Navaratnam, C.U.; Vold, M.; Eikenberg, R.; Olsen, N.R.B. Experimental and numerical determination of the head loss of a pressure driven flow through an unlined rock-blasted tunnel. Water 2020, 12, 3492. [Google Scholar] [CrossRef]
- Aberle, J.; Branß, T.; Eikenberg, R.; Henry, P.-Y.; Olsen, N.R.B. Directional dependency of flow resistance in an unlined rock blasted hydropower tunnel. J. Hydraul. Res. 2021. under review. [Google Scholar]
- Mainka, J. Non-Waste-Wachsschalungen—Entwicklung Einer Wachsschalungstechnologie Für Geometrisch Komplexe Betonbauteile (Non-Waste-Wax-Formwork Technology). Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2019. [Google Scholar] [CrossRef]
- CloudCompare. Available online: https://www.cloudcompare.org/doc/wiki/index.php?title=ICP (accessed on 10 February 2021).
- Zang, Y.; Yang, B.; Li, J.; Guan, H. An Accurate TLS and UAV Image Point Clouds Registration Method for Deformation Detection of Chaotic Hillside Areas. Remote Sens. 2019, 11, 647. [Google Scholar] [CrossRef]
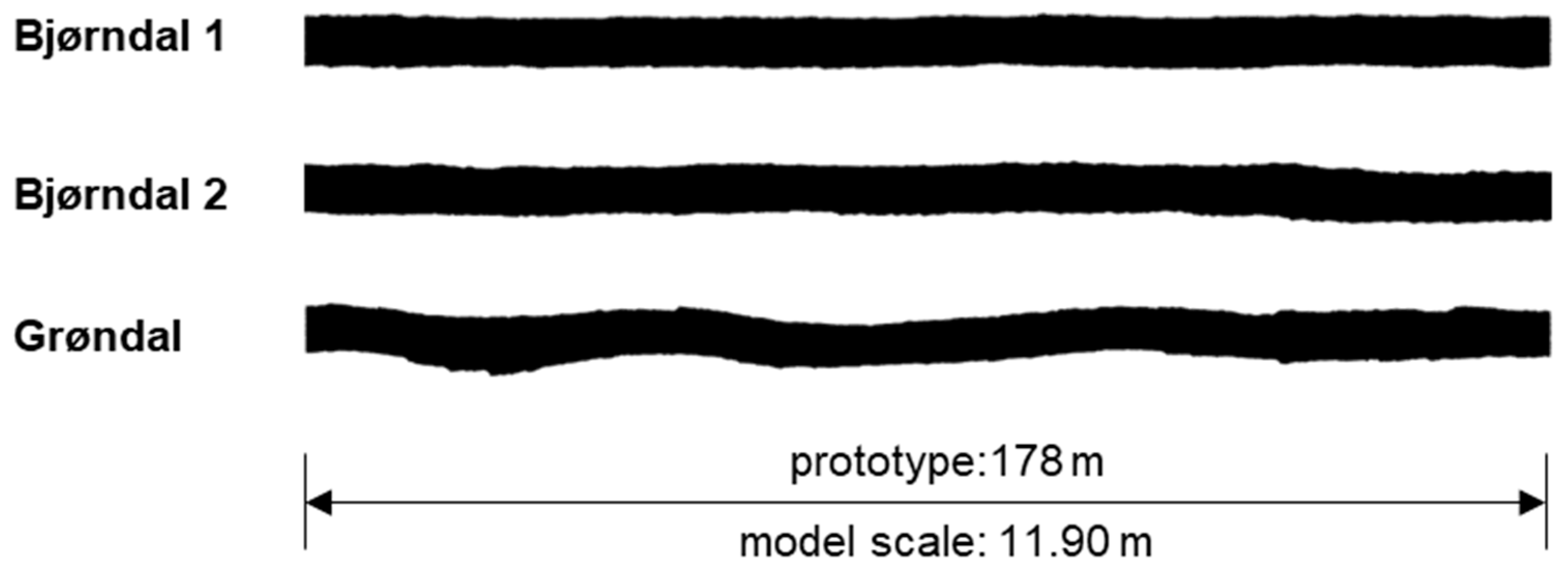

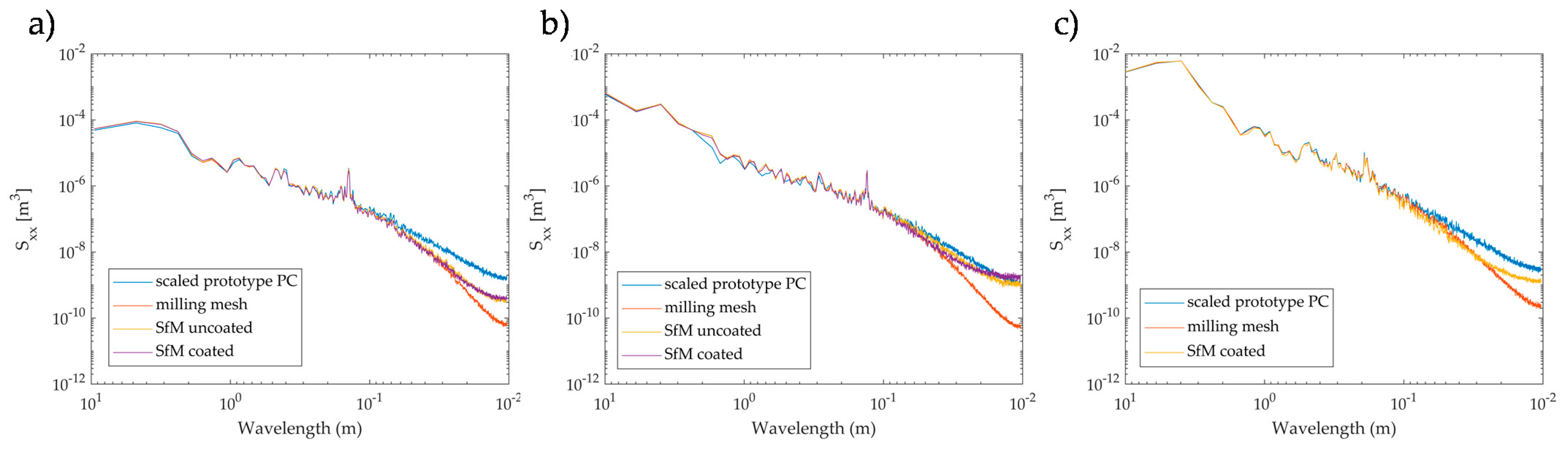
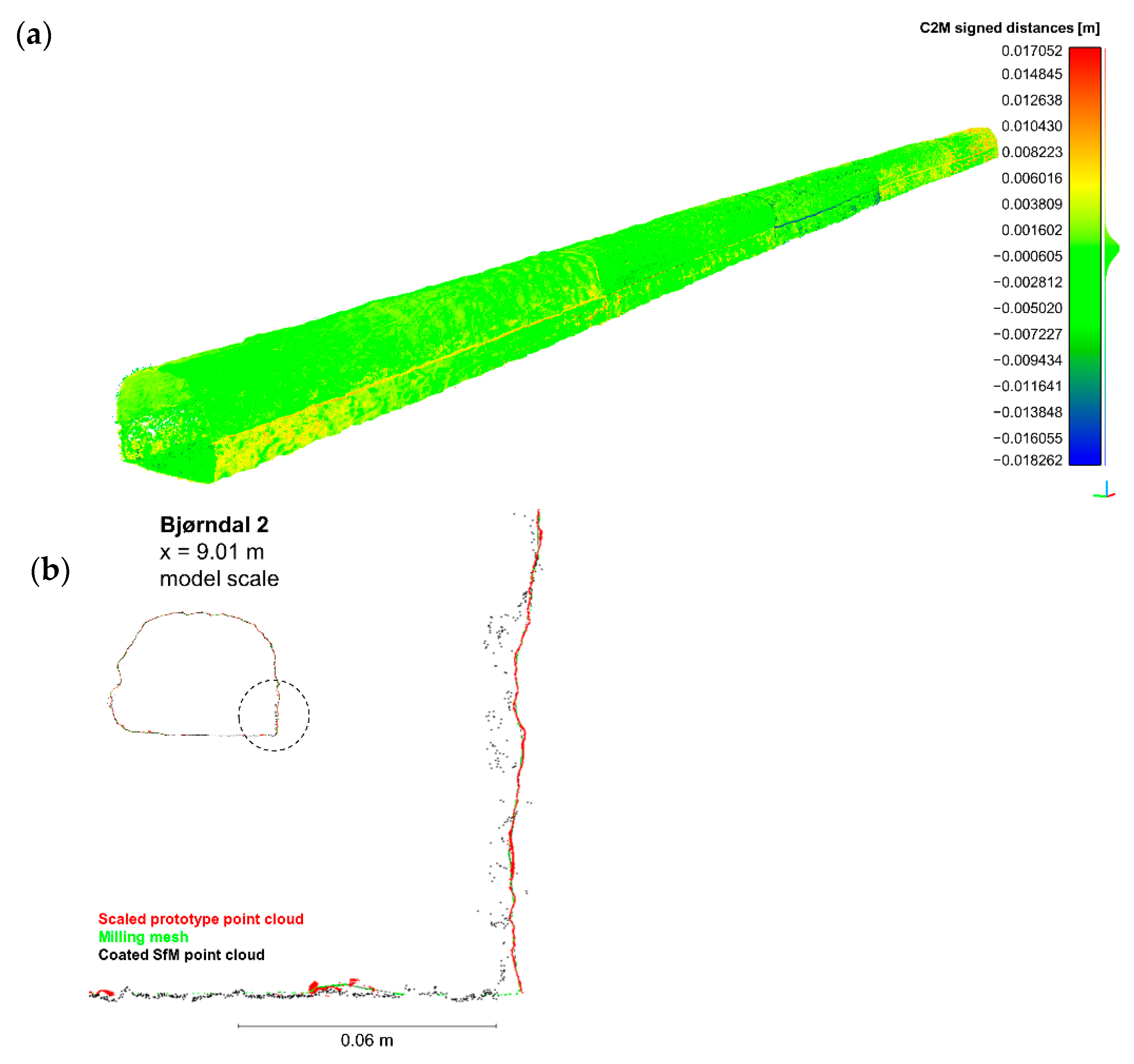
| Steps | Total Length (m) | Total Points (-) | Total Surface Area (m²) | Point Density (pts/m²) | |
|---|---|---|---|---|---|
| Bjørndal 1 | Prototype point cloud (2) | 178.50 | 344,817,314 | 4,001 | 86,191 |
| Milling mesh | 11.90 | 684,515 | 17.78 | 38,498 | |
| SfM point cloud uncoated (3) | 9.52 | 97,791,710 | 14.21 | 6,880,408 | |
| SfM point cloud coated | 11.91 (4) | 82,556,506 | 17.78 | 4,643,094 | |
| Bjørndal 2 | Prototype point cloud (2) | 178.36 | 386,099,896 | 3,962 | 97,459 |
| Milling mesh | 11.90 | 703,182 | 17.61 | 39,937 | |
| SfM point cloud uncoated | 11.90 | 251,039,847 | 17.61 | 14,257,657 | |
| SfM point cloud coated | 11.91 | 78,743,193 | 17.61 | 4,472,172 | |
| Grøndal | Prototype point cloud (2) | 178.56 | 282,057,286 | 4,221 | 66,816 |
| Milling mesh | 11.89 (5) | 719,253 | 18.76 | 38,336 | |
| SfM point cloud uncoated | (1) | (1) | (1) | (1) | |
| SfM point cloud coated | 11.89 | 45,075,401 | 18.76 | 2,402,538 |
| Comparison of | Bjørndal 1 | Bjørndal 2 | Grøndal | |
|---|---|---|---|---|
| Scaled prototype point cloud * and milling mesh | mean deviation (m) | 7.5 × 10−4 | 9.3 × 10−4 | 7.9 × 10−4 |
| standard deviation (m) | 6.9 × 10−4 | 8.8 × 10−4 | 7.7 × 10−4 | |
| 5th percentile (m) | 1.1 × 10−4 | 1.7 × 10−4 | 1.2 × 10−4 | |
| 95th percentile (m) | 2.1 × 10−3 | 2.3 × 10−3 | 2.1 × 10−3 | |
| Milling mesh * and SfM point cloud uncoated | mean deviation (m) | 1.6 × 10−4 | −3.4 × 10−5 | N/A |
| standard deviation (m) | 2.0 × 10−3 | 1.2 × 10−3 | N/A | |
| 5th percentile (m) | 1.6 × 10−3 | −1.8 × 10−3 | N/A | |
| 95th percentile (m) | 2.0 × 10−3 | 1.6 × 10−3 | N/A | |
| Milling mesh * and SfM point cloud coated | mean deviation (m) | −5.4 × 10−6 | −9.7 × 10−5 | 1.1 × 10−4 |
| standard deviation (m) | 1.2 × 10−3 | 1.5 × 10−3 | 1.4 × 10−3 | |
| 5th percentile (m) | −1.7 × 10−3 | −2.4 × 10−3 | −2.1 × 10−3 | |
| 95th percentile (m) | 1.7 × 10−3 | 1.9 × 10−3 | 2.3 × 10−3 | |
| Scaled prototype point cloud * and SfM point cloud coated | mean deviation (m) | 4.2 × 10−3 | 5.3 × 10−3 | 3.5 × 10−3 |
| standard deviation (m) | 9.9 × 10−3 | 1.2 × 10−2 | 9.6 × 10−3 | |
| 5th percentile (m) | 1.6 × 10−4 | 1.8 × 10−4 | 1.7 × 10−4 | |
| 95th percentile (m) | 2.5 × 10−2 | 2.8 × 10−2 | 1.7 × 10−2 | |
| SfM point cloud uncoated * and SfM point cloud coated | mean deviation (m) | 4.8 × 10−4 | 9.6 × 10−4 | N/A |
| standard deviation (m) | 4.4 × 10−4 | 1.0 × 10−3 | N/A | |
| 5th percentile (m) | 1.3 × 10−4 | 1.3 × 10−4 | N/A | |
| 95th percentile (m) | 1.2 × 10−3 | 2.8 × 10−3 | N/A |
| Tunnel | CDEM | σ (m) | Sk | Ku | A (m²) | W (m) | H (m) |
|---|---|---|---|---|---|---|---|
| Bjørndal 1 | Scaled prototype | 7.92 × 10−3 | 1.11 × 10−1 | 3.06 | 0.1406 | 0.463 | 0.369 |
| Milling mesh | 8.30 × 10−3 | 8.60 × 10−3 | 3.09 | 0.1405 | 0.460 | 0.368 | |
| Uncoated | 8.10 × 10−3 | −8.93 × 10−2 | 3.22 | 0.1403 | 0.460 | 0.368 | |
| Coated | 8.20 × 10−3 | 2.86 × 10−2 | 3.15 | 0.1405 | 0.461 | 0.369 | |
| Bjørndal 2 | Scaled prototype | 1.73 × 10−2 | −1.09 × 10−1 | 2.55 | 0.1338 | 0.459 | 0.346 |
| Milling mesh | 1.88 × 10−2 | −1.50 × 10−1 | 2.33 | 0.1337 | 0.458 | 0.345 | |
| Uncoated | 1.89 × 10−2 | −1.16 × 10−1 | 2.45 | 0.1334 | 0.458 | 0.346 | |
| Coated | 1.86 × 10−2 | −1.62 × 10−1 | 2.34 | 0.1332 | 0.458 | 0.345 | |
| Grøndal | Scaled prototype | 4.56 × 10−2 | −3.65 × 10−1 | 2.80 | 0.1458 | 0.440 | 0.408 |
| Milling mesh | 4.61 × 10−2 | −3.64 × 10−1 | 2.79 | 0.1455 | 0.440 | 0.406 | |
| Coated | 4.57 × 10−2 | −3.25 × 10−1 | 2.83 | 0.1442 | 0.437 | 0.406 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aberle, J.; Eikenberg, R.; Branß, T.; Henry, P.-Y. Technical Note: On the Production and Accuracy of CNC-Manufactured Hydraulic Scale Models. Water 2021, 13, 916. https://doi.org/10.3390/w13070916
Aberle J, Eikenberg R, Branß T, Henry P-Y. Technical Note: On the Production and Accuracy of CNC-Manufactured Hydraulic Scale Models. Water. 2021; 13(7):916. https://doi.org/10.3390/w13070916
Chicago/Turabian StyleAberle, Jochen, Ralph Eikenberg, Till Branß, and Pierre-Yves Henry. 2021. "Technical Note: On the Production and Accuracy of CNC-Manufactured Hydraulic Scale Models" Water 13, no. 7: 916. https://doi.org/10.3390/w13070916
APA StyleAberle, J., Eikenberg, R., Branß, T., & Henry, P.-Y. (2021). Technical Note: On the Production and Accuracy of CNC-Manufactured Hydraulic Scale Models. Water, 13(7), 916. https://doi.org/10.3390/w13070916







