An Enhanced Innovative Triangular Trend Analysis of Rainfall Based on a Spectral Approach
Abstract
:1. Introduction
2. Materials and Methods
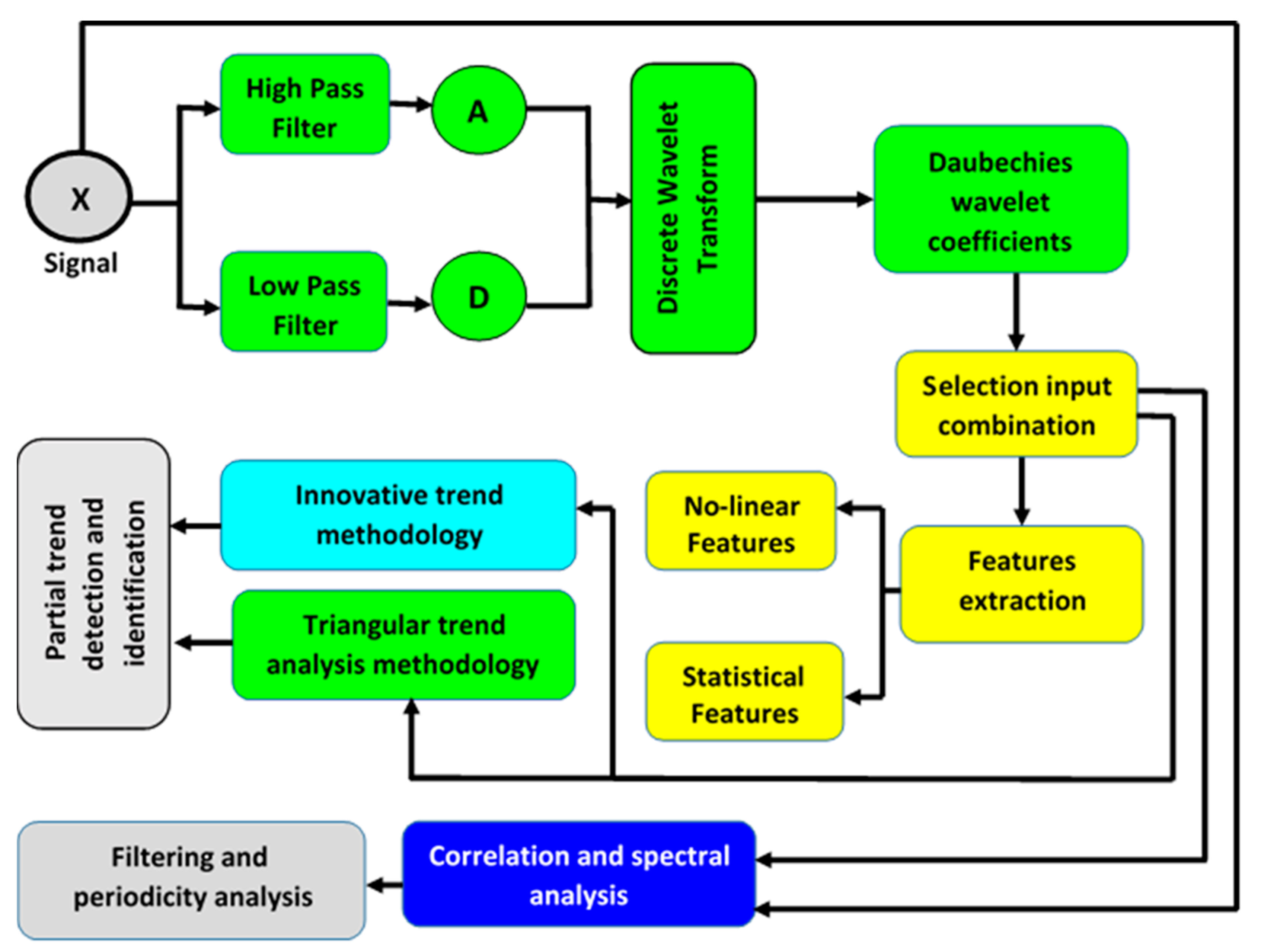
- Pretreatment of the input rainfall signal X(t).
- Using filter bank includes high pass filter (A) and low pass filter (D) for signal filtering.
- The outputs of A and D are downsampled by the DWT scale coefficient (factor of 2).
- Choosing the adequate sub-band signal or the scale of decomposition for downsampling based on the time series length.
- Selecting the mother- and daughter-wavelet, e.g., Daubechies mother-wavelet (db20).
- After step 5, the wavelet coefficients are obtained.
- From the wavelet coefficients (approximations and details), 24 models were proposed (Table 2), assessed, and analyzed using correlation and spectral analyses for assessing the periodicity and to perform the filtering
- The 24 proposed models were used as input time series into the ITTA.
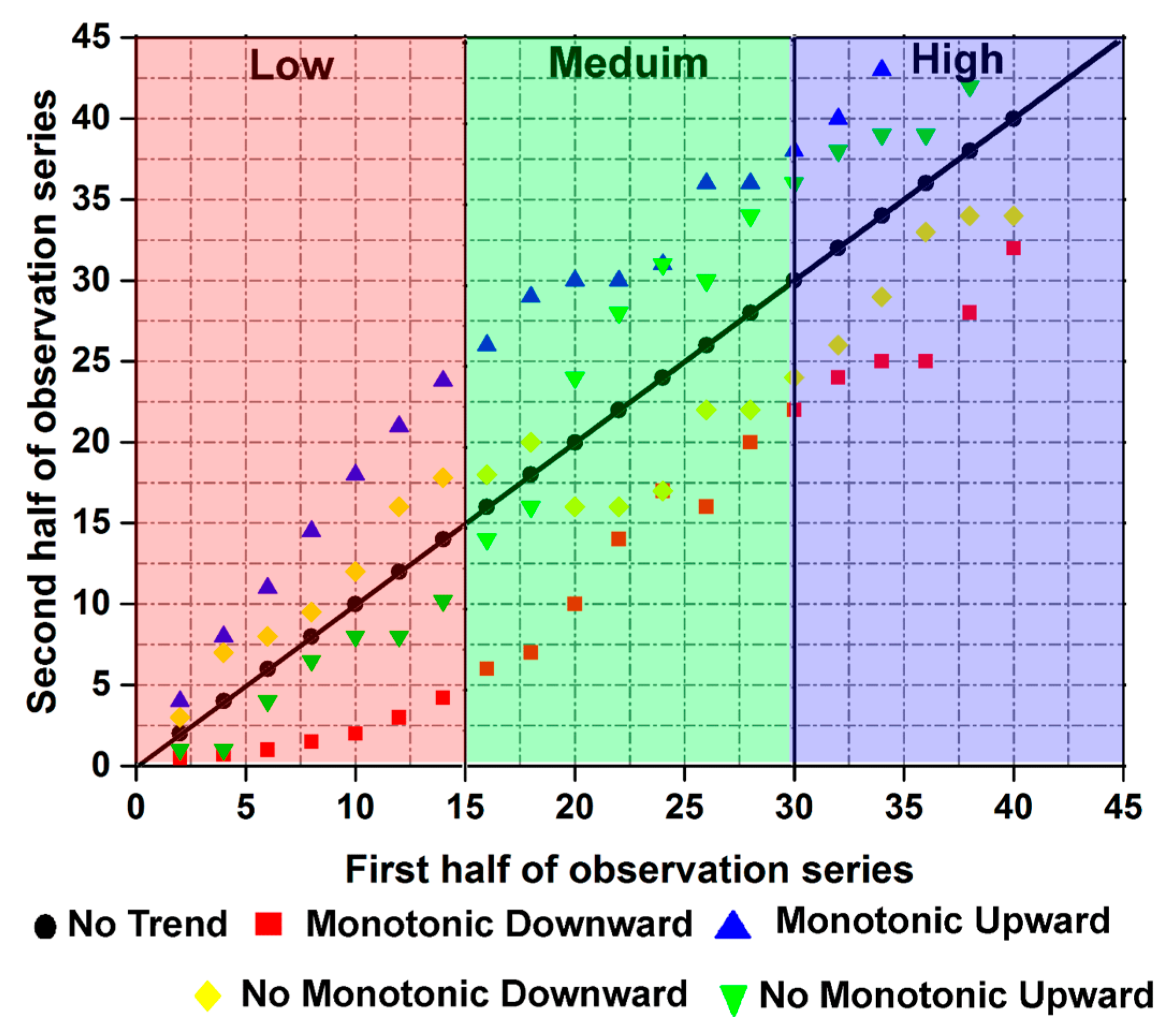
2.1. Triangular Trend Analysis Methodology
- To exploit the entire available time series.
- To always stay within the original methodology (same template) and for comparative purposes.
- To extract and detect long-term and significant partial trends.
2.2. Discrete Wavelet Transform
2.3. Correlation and Spectral Analysis
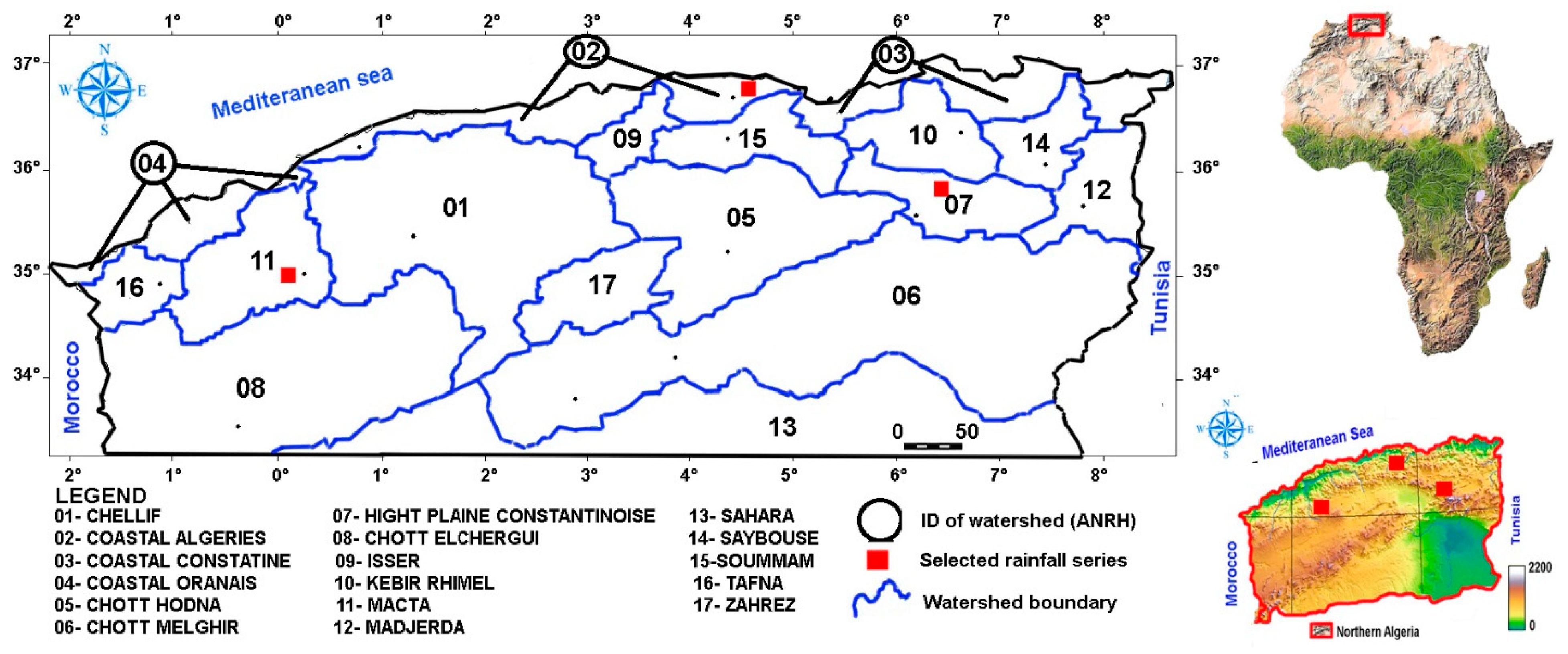
2.4. Study Area and Collected Data
3. Results and Discussion
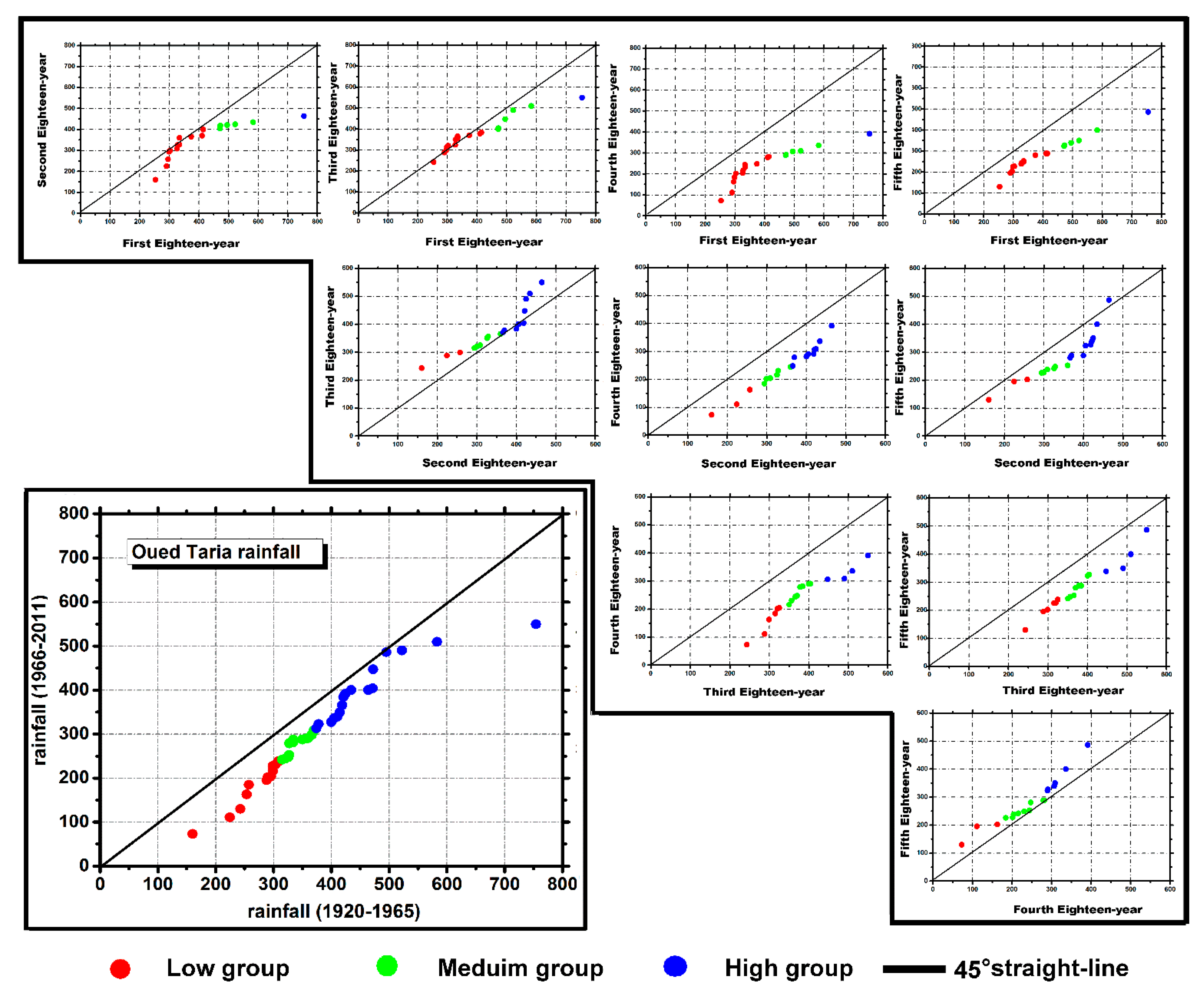
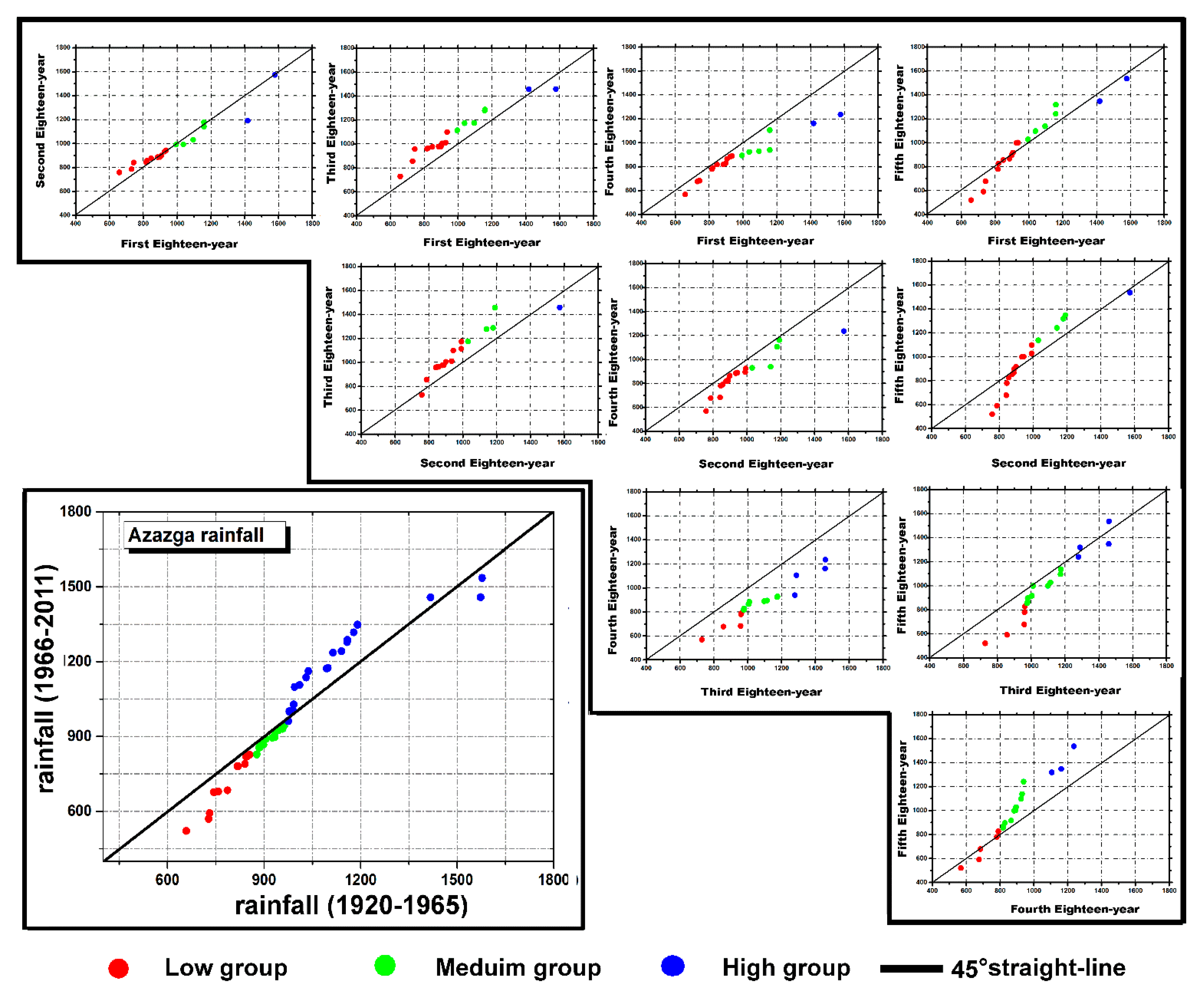
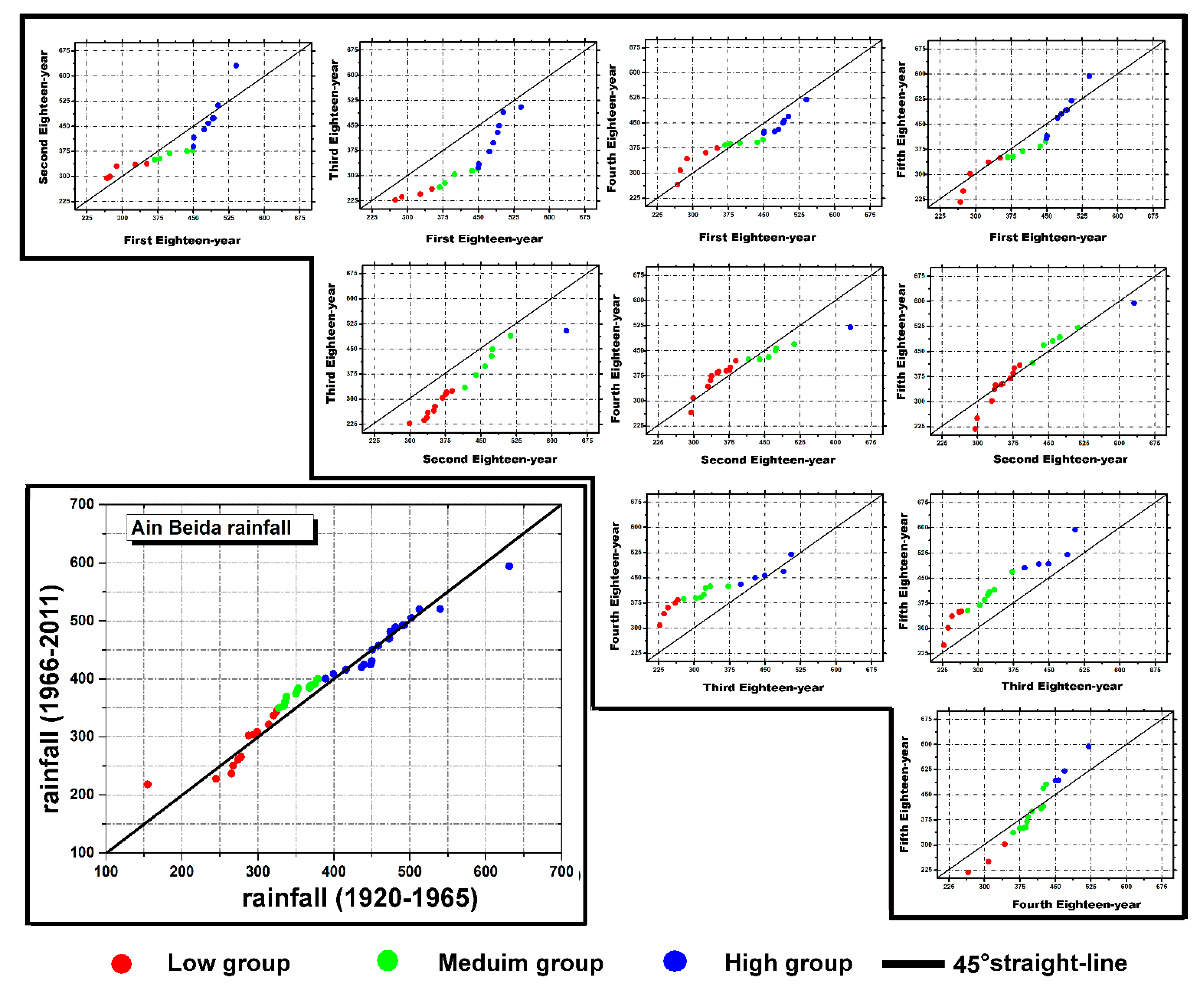
3.1. Triangular Trend Analysis Methodology
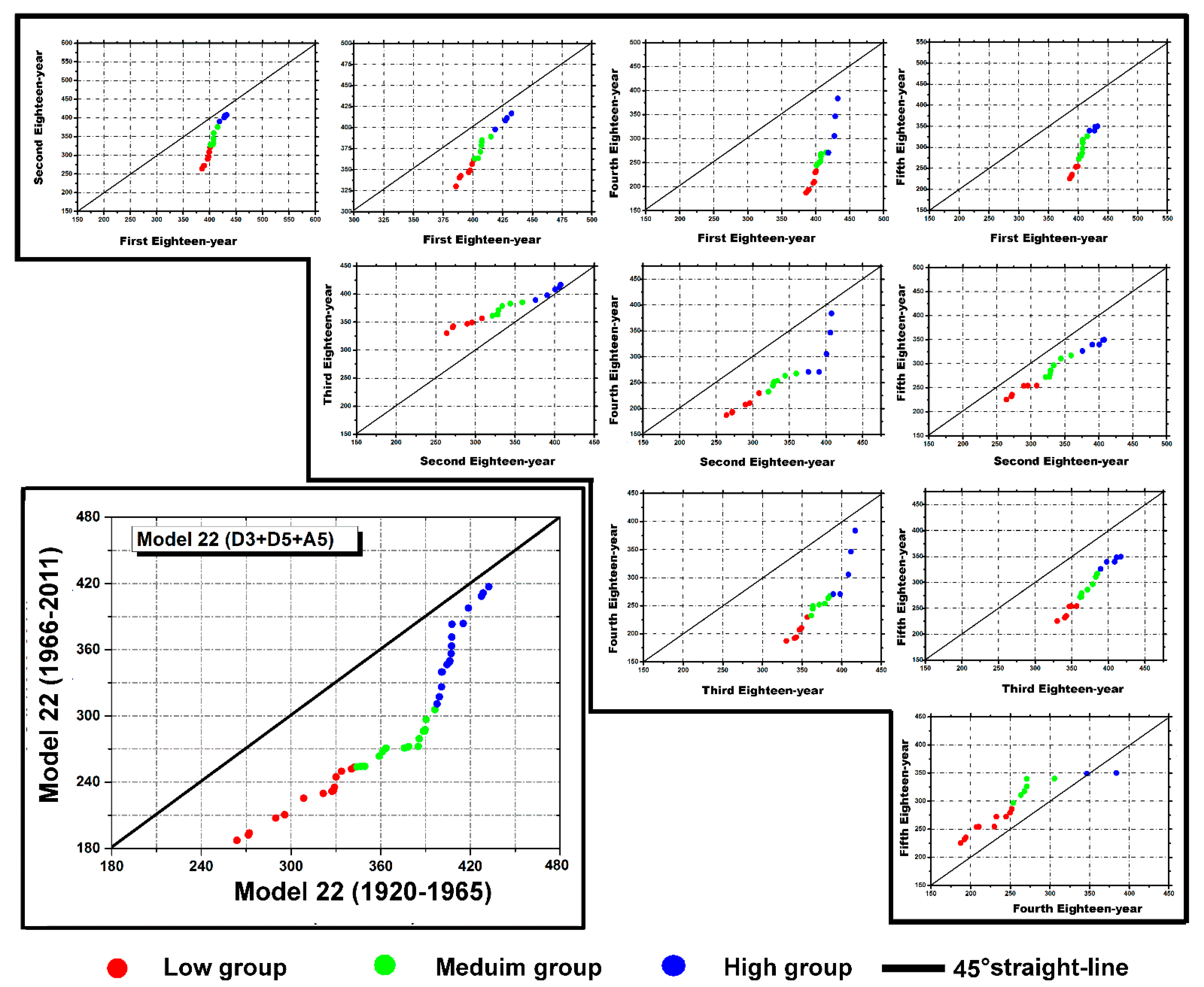
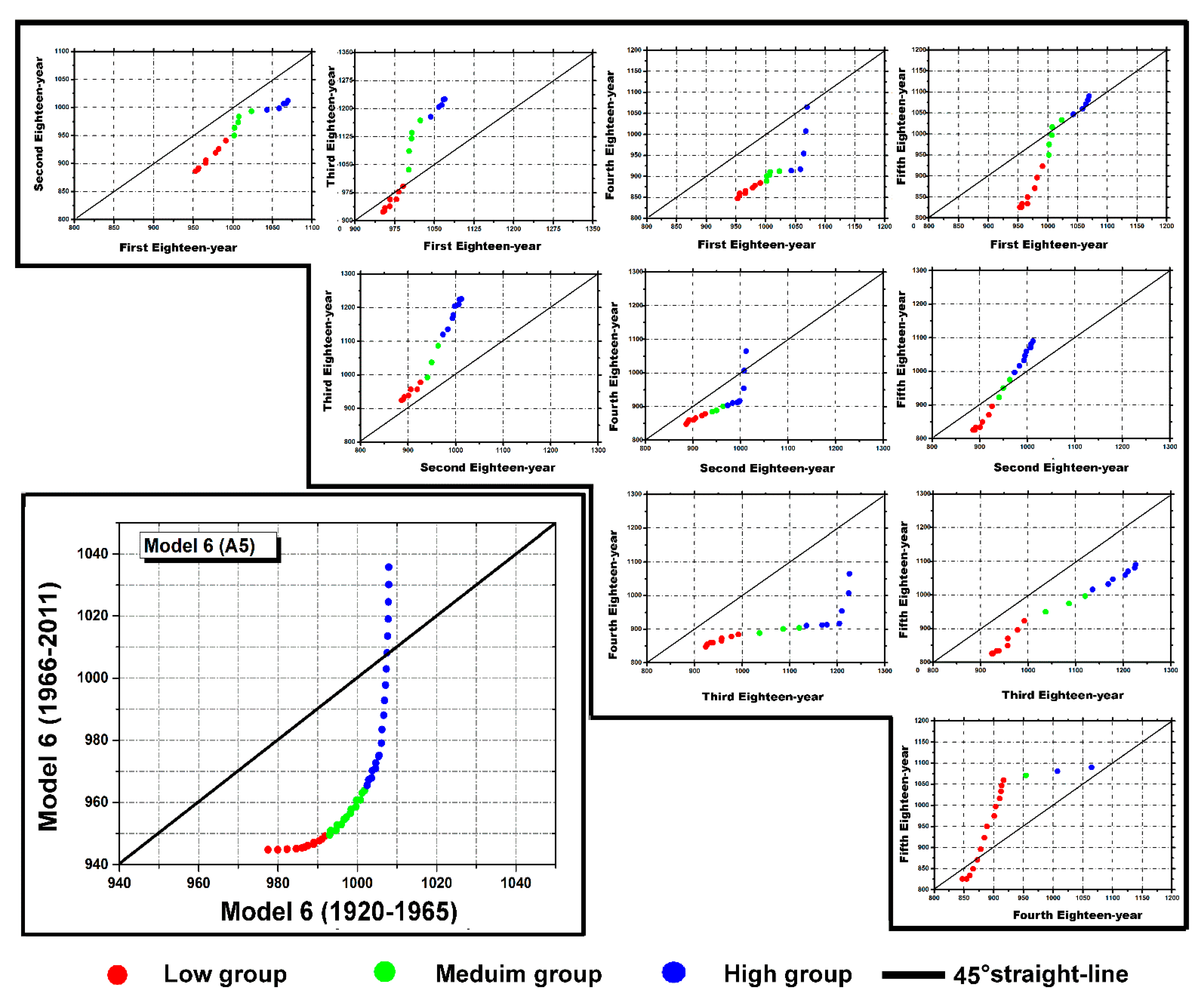
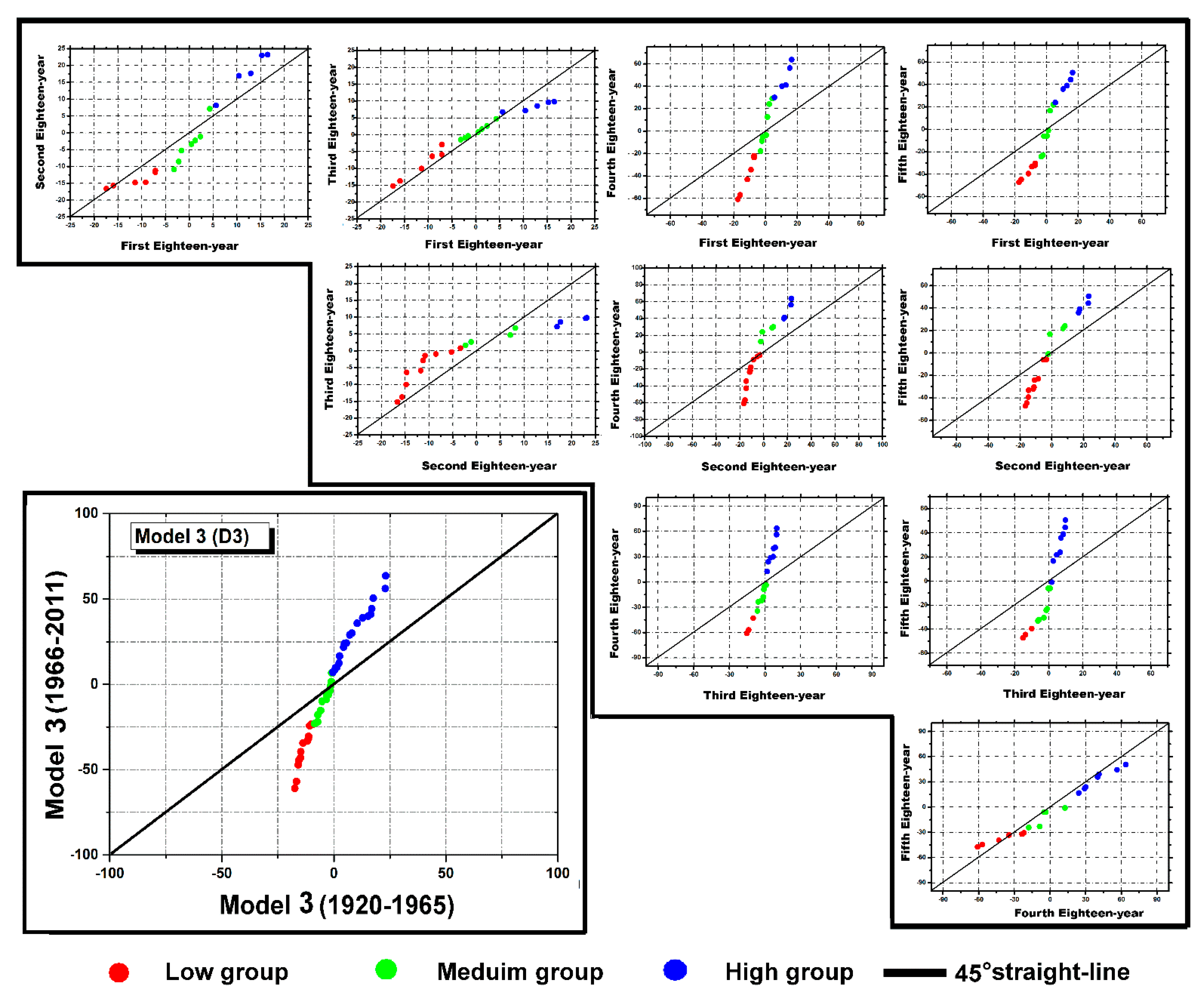
3.2. Combining Triangular Trend Analysis Methodology with Discrete Wavelet Transform
- A partial trend toward drier conditions occurred between 1920 and 1950.
- A partial trend toward humid conditions occurred from 1950 to 1975.
- A partial negative trend extended in northern Algeria from the years 1975.
- A partial trend with a non−significant increase occurred from the end of the 1990s.
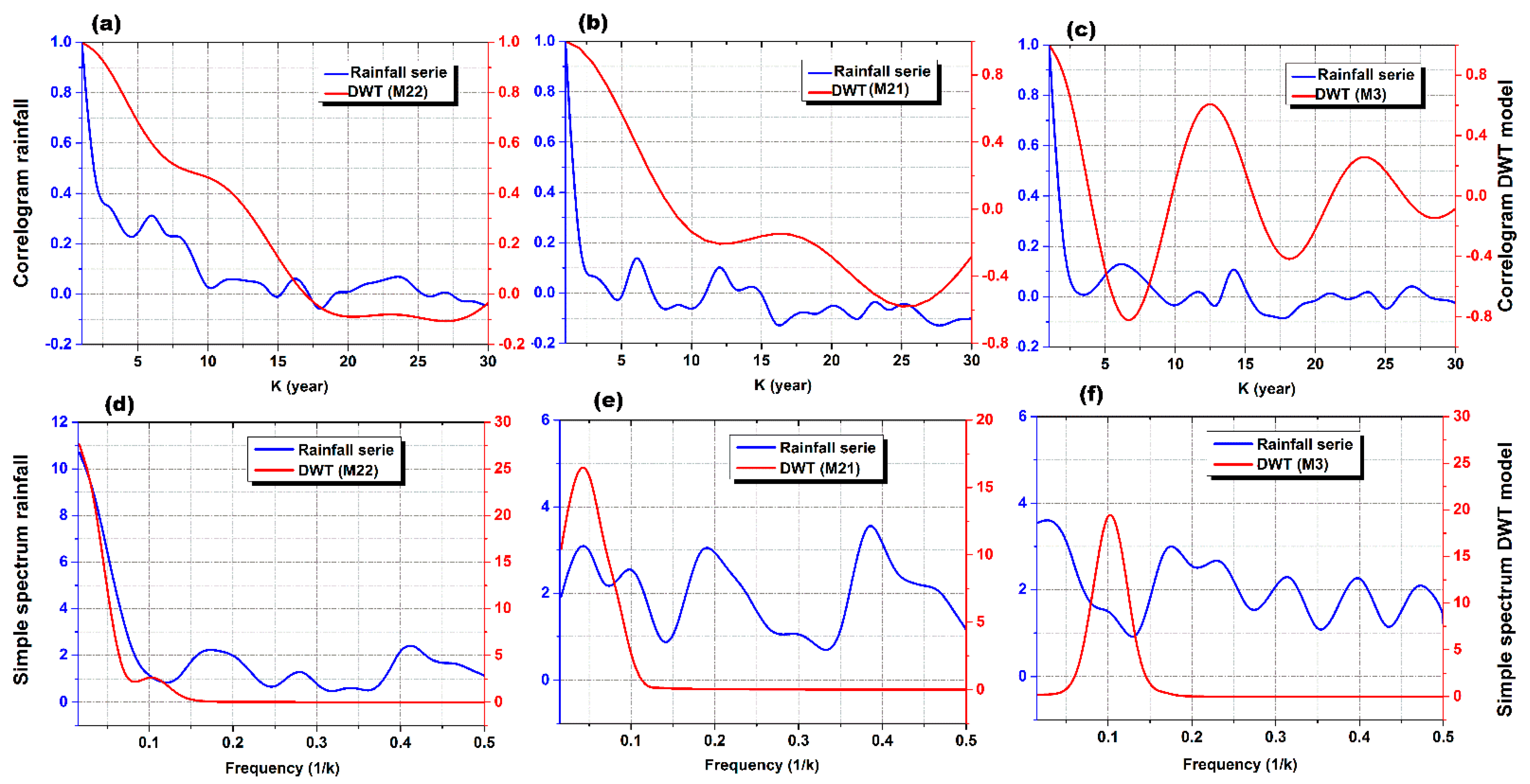
- The short and medium-term processes, and less than decadal periodicity, dominate the high variability of rainfall. This masks the partial trend and change points presented in the rainfall series and makes it hard to identify. In southwestern Europe, between 1850 and 2018, the authors in [21] linked the lack of substantially declining or growing patterns to the long-term rainfall series, to the predominance of inter-annual variability, making trend identification difficult. Thus, spectral analysis as a time–frequency-based method, and a first assessment tool to diagnose and characterize climatic series’ high variability before inserting in trend method analyses, is indispensable.
4. Conclusions
- According to the analysis, the ITTA−DWT successfully detected the partial patterns in the studied rainfall time series.
- The analysis revealed the alternate long-term dry and wet periods, where most components of wet periods occurred between 1950 and 1975, with a non−significant increase in rainy episodes observed from the end of the 1990s. The dry periods were observed from 1975 to the end of the 1990s.
- The analysis indicated an increase in the occurrence of heavy rainfalls compared to low and medium intensity rainfalls, in the study area, which can infer the risk of occurrence of torrential rainfalls, which can generate floods.
- The analysis proved DWT’s efficiency as a coupling method that can improve ITTA accuracy for partial trend component identification.
- The analysis proved the effectiveness of DWT as a filtering and denoising method for climatic time series.
- The inter-annual to multiannual of the short to medium processes dominate the high variability of rainfall, masking the partial trend components existing in the rainfall series, making it hard for identification.
- Before inducing the climatic time series in the trend analysis methods, the diagnosis of its behavior, and removing some components, can improve the accuracy of the analysis.
- The obtained results indicated that combining ITA, D–ITA, T–ITA, ITTA, and some input combination models resulting from the DWT is very promising, relative to those of the initial rainfall sequence. Those results corroborate the results obtained by [14]. The ITA–DWT, D–ITA–DWT, T–ITA–DWT, ITTA–DWT methods outperformed the ITA, D–ITA, T–ITA, ITTA methods for partial trend identification.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verbist, K.M.J.; Maureira, H.; Rojas, P.; Vicuna, S. A stress test for climate change impacts on water security: A CRIDA case study. Clim. Risk Manag. 2020, 28, 100222. [Google Scholar] [CrossRef]
- Khan, I.; Waqas, T.; Samiullah; Ullah, S. Precipitation variability and its trend detection for monitoring of drought hazard in northern mountainous region of Pakistan. Arab. J. Geosci. 2020, 13, 698. [Google Scholar] [CrossRef]
- Almazroui, M.; Sen, Z.; Mohorji, A.M.; Islam, M.N. Impacts of Climate Change on Water Engineering Structures in Arid Regions: Case Studies in Turkey and Saudi Arabia. Earth Syst. Environ. 2018, 3, 43–57. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; da Silva, R.M.; Costa, S.G.F. Cluster analysis applied to spatiotemporal variability of monthly precipitation over Paraíba state using tropical rainfall measuring mission (TRMM) data. Remote Sens. 2019, 11, 637. [Google Scholar] [CrossRef] [Green Version]
- Santos, C.A.; Freire, P.K.; Silva, R.M.D.; Akrami, S.A. Hybrid wavelet neural network approach for daily inflow forecasting using tropical rainfall measuring mission data. J. Hydrol. Eng. 2019, 24, 04018062. [Google Scholar] [CrossRef]
- Caloiero, T.; Caloiero, P.; Frustaci, F. Long-term precipitation trend analysis in Europe and in the Mediterranean basin. Water Environ. J. 2018, 32, 433–445. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using discrete wavelet transforms to analyse trends in streamflow and precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Kendall, A.; Spang, E.S. The role of industrial ecology in food and agriculture’s adaptation to climate change. J. Ind. Ecol. 2020, 24, 313–317. [Google Scholar] [CrossRef]
- Xian, M.; Liu, X.; Yin, M.; Song, K.; Zhao, S.; Gao, T. Rainfall Monitoring Based on Machine Learning by Earth-Space Link in the Ku Band. IEEE J. Sel. Top Appl. Earth Obs. Remote Sens. 2020, 13, 3656–3668. [Google Scholar] [CrossRef]
- Achour, K.; Meddi, M.; Zeroual, A.; Bouabdelli, S.; Maccioni, P.; Moramarco, T. Spatio-temporal analysis and forecasting of drought in the plains of northwestern Algeria using the standardized precipitation index. J. Earth Syst. Sci. 2020, 129, 42. [Google Scholar] [CrossRef]
- Neama, M.A.; Attia, M.; Negm, A.; Nasr, M. Overview of Water Resources, Quality, and Management in Algeria. In The Handbook of Environmental Chemistry; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Hallouz, F.; Meddi, M.; Mahé, G.; Rahmani, S.A.; Karahacane, H.; Brahimi, S. Analysis of meteorological drought sequences at various timescales in semi-arid climate: Case of the Cheliff watershed (northwest of Algeria). Arab. J. Geosci. 2020, 13, 280. [Google Scholar] [CrossRef]
- Boudiaf, B.; Dabanli, I.; Boutaghane, H.; Şen, Z. Temperature and Precipitation Risk Assessment Under Climate Change Effect in Northeast Algeria. Earth Syst. Environ. 2020, 4, 1–14. [Google Scholar] [CrossRef]
- Zerouali, B.; Chettih, M.; Abda, Z.; Mesbah, M.; Djemai, M. The use of hybrid methods for change points and trends detection in rainfall series of northern Algeria. Acta Geophys. 2020, 68, 1443–1460. [Google Scholar] [CrossRef]
- Achite, M.; Buttafuoco, G.; Toubal, K.A.; Luca, F. Precipitation spatial variability and dry areas temporal stability for different elevation classes in the Macta basin (Algeria). Environ. Earth Sci. 2017, 76, 458. [Google Scholar] [CrossRef]
- Taibi, S.; Meddi, M.; Mahé, G.; Assani, A. Relationships between atmospheric circulation indices and rainfall in Northern Algeria and comparison of observed and RCM-generated rainfall. Theor. Appl. Climatol. 2017, 127, 241–257. [Google Scholar] [CrossRef]
- Meddi, M.M.; Assani, A.A.; Meddi, H. Temporal Variability of Annual Rainfall in the Macta and Tafna Catchments, Northwestern Algeria. Water Resour. Manag. 2010, 24, 3817–3833. [Google Scholar] [CrossRef]
- Zeroual, A.; Assani, A.A.; Meddi, M.; Alkama, R. Assessment of climate change in Algeria from 1951 to 2098 using the Köppen-Geiger climate classification scheme. Clim. Dyn. 2019, 52, 227–243. [Google Scholar] [CrossRef]
- Bouabdelli, S.; Meddi, M.; Zeroual, A.; Alkama, R. Hydrological drought risk recurrence under climate change in the karst area of Northwestern Algeria. J. Water Clim. Chang. 2020, jwc2020207. [Google Scholar] [CrossRef]
- Öztopal, A.; Şen, Z. Innovative Trend Methodology Applications to Precipitation Records in Turkey. Water Resour. Manag. 2017, 31, 727–737. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Vicente-Serrano, S.M.; Domínguez-Castro, F.; Murphy, C.; Reig, F.; Tramblay, Y.; Luna, M.Y.; Turco, M.; Noguera, I.; Aznárez-Balta, M.; et al. Long-term precipitation in Southwestern Europe reveals no clear trend attributable to anthropogenic forcing. Environ. Res. Lett. 2020, 15, 094070. [Google Scholar] [CrossRef]
- Zerouali, B.; Mesbah, M.; Chettih, M.; Djemai, M.; Abda, Z. Hydrogeological System of Sebaou River Watershed (Northern Central Algeria): An Assessment of Rainfall-Runoff Relationship. In Advances in Sustainable and Environmental Hydrology, Hydrogeology, Hydrochemistry and Water Resources; Springer: Cham, Switzerland, 2019; pp. 29–31. [Google Scholar] [CrossRef]
- Modi, A.; Tare, V.; Chaudhuri, C. Usage of long-term river discharge data in water balance model for assessment of trends in basin storages. Model. Earth Syst. Environ. 2020. [Google Scholar] [CrossRef]
- Singh, V.P. Hydrologic modeling: Progress and future directions. Geosci. Lett. 2018, 5, 15. [Google Scholar] [CrossRef]
- Silva, R.M.; Silva, J.F.C.B.C.; Santos, C.A.G.; Brasil Neto, R.M. Spatial distribution and estimation of rainfall trends and erosivity in the Epitácio Pessoa reservoir catchment, Paraíba—Brazil. Nat. Hazards 2020, 102, 829–849. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; Silva, R.M.; Passos, J.S.A. Integrated spatiotemporal trends using TRMM 3B42 data for the Upper São Francisco River basin, Brazil. Environ. Monit. Assess 2018, 190, 175. [Google Scholar] [CrossRef] [PubMed]
- Santos, C.A.G.; Kisi, O.; da Silva, R.M.; Zounemat-Kermani, M. Wavelet-based variability on streamflow at 40-year timescale in the Black Sea region of Turkey. Arab. J. Geosci. 2018, 11, 169. [Google Scholar] [CrossRef]
- Atta-ur-Rahman; Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar] [CrossRef]
- Rashid, M.M.; Beecham, S.; Chowdhury, R.K. Assessment of trends in point rainfall using continuous wavelet transforms. Adv. Water Resour. 2015, 82, 1–15. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Santos, C.A.G.; Moreira, M.; Moreira, M.; Corte-Real, J.; Silva, V.C.L.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Abungba, J.A.; Khare, D.; Pingale, S.M.; Adjei, K.A.; Gyamfi, C.; Odai, S.N. Assessment of hydro-climatic trends and variability over the black volta basin in Ghana. Earth Syst. Environ. 2020, 4, 739–755. [Google Scholar] [CrossRef]
- Ajayi, V.O.; Ilori, O.W. Projected drought events over West Africa using RCA4 regional climate model. Earth Syst. Environ. 2020, 4, 329–348. [Google Scholar] [CrossRef]
- Ilori, O.W.; Ajayi, V.O. Change detection and trend analysis of future temperature and rainfall over west Africa. Earth Syst. Environ. 2020, 4, 493–512. [Google Scholar] [CrossRef]
- Faramarzi, N.; Sadeghnejad, S. Fluid and rock heterogeneity assessment of gas condensate reservoirs by wavelet transform of pressure-transient responses. J. Nat. Gas Sci. Eng. 2020, 81, 103469. [Google Scholar] [CrossRef]
- Bolzan, M.J.A.; Franco, A.M.S.; Echer, E. A wavelet based method to remove the long term periodicities of geophysical time series. Adv. Space Res. 2020, 66, 299–306. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J. A stochastic wavelet-based data-driven framework for forecasting uncertain multiscale hydrological and water resources processes. Environ. Model. Softw. 2020, 130, 104718. [Google Scholar] [CrossRef]
- Joshi, N.; Gupta, D.; Suryavanshi, S.; Adamowski, J.; Madramootoo, C.A. analysis of trends and dominant periodicities in drought variables in India: A wavelet transform based approach. Atmos. Res. 2016, 182, 200–220. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. An evaluation of statistical, NMME and hybrid models for drought prediction in China. J. Hydrol. 2018, 566, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Valipour, M. Optimization of neural networks for precipitation analysis in a humid region to detect drought and wet year alarms. Meteorol. Appl. 2016, 23, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Şen, Z. An innovative trend analysis methodology. ASCE J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Assessment of seasonal and annual rainfall trend in Calabria (southern Italy) with the ITA method. J. Hydroinform. 2020, 22, 738–748. [Google Scholar] [CrossRef]
- Sezen, C.; Partal, T. Wavelet combined innovative trend analysis for precipitation data in the Euphrates-Tigris basin, Turkey. Hydrol. Sci. J. 2020, 65, 1909–1927. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Multiple Şen-innovative trend analyses and partial Mann-Kendall test. J. Hydrol. 2018, 566, 685–704. [Google Scholar] [CrossRef]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-term trends and seasonality detection of the observed flow in Yangtze River using Mann-Kendall and Sen’s innovative trend method. Water 2019, 11, 1855. [Google Scholar] [CrossRef] [Green Version]
- Malik, A.; Kumar, A.; Guhathakurta, P.; Kisi, O. Spatial-temporal trend analysis of seasonal and annual rainfall (1966–2015) using innovative trend analysis method with significance test. Arab. J. Geosci. 2019, 12, 328. [Google Scholar] [CrossRef]
- Mohorji, A.M.; Şen, Z.; Almazroui, M. Trend Analyses Revision and Global Monthly Temperature Innovative Multi-Duration Analysis. Earth Syst. Environ. 2017, 1, 9. [Google Scholar] [CrossRef] [Green Version]
- Şen, Z. Global warming quantification by innovative trend template method. Int. J. Global. Warm. 2017, 12, 499–512. [Google Scholar] [CrossRef]
- Dabanlı, İ.; Şen, Z.; Yeleğen, M.Ö.; Şişman, E.; Selek, B.; Güçlü, Y.S. Trend Assessment by the Innovative-Şen Method. Water Resour. Manag. 2016, 30, 5193–5203. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kisi, O. Trend analysis of maximum hydrologic drought variables using Mann–Kendall and Şen’s innovative trend method. River Res. Appl. 2017, 33, 597–610. [Google Scholar] [CrossRef]
- Elouissi, A.; Şen, Z.; Habi, M. Algerian rainfall innovative trend analysis and its implications to Macta watershed. Arab. J. Geosci. 2016, 9, 303. [Google Scholar] [CrossRef]
- Nourani, V.; Nezamdoost, N.; Samadi, M.; Daneshvar Vousoughi, F. Wavelet-based trend analysis of hydrological processes at different timescales. J. Water Clim. Chang. 2015, 6, 414–435. [Google Scholar] [CrossRef]
- Şen, Z. Trend identification simulation and application. J. Hydrol. Eng. 2013, 19, 635–642. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend significance test and applications. Theor. Appl. Climatol. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Kisi, O. An innovative method for trend analysis of monthly pan evaporations. J. Hydrol. 2015, 527, 1123–1129. [Google Scholar] [CrossRef]
- Alashan, S. An improved version of innovative trend analyses. Arab. J. Geosci. 2018, 11, 50. [Google Scholar] [CrossRef]
- Sişman, E. Discussion of “Critical Values for Şen’s Trend Analysis” by Richard, H. McCuen. J. Hydrol. Eng. 2020, 25, 07019004. [Google Scholar] [CrossRef] [Green Version]
- Güçlü, Y.S.; Şişman, E.; Dabanlı, İ. Innovative triangular trend analysis. Arab. J. Geosci. 2020, 13, 27. [Google Scholar] [CrossRef]
- Ruggieri, E.; Antonellis, M. An exact approach to Bayesian sequential change point detection. Comput. Stat. Data Anal. 2016, 97, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern. Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; p. 357. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Analyse multirésolution croisée de pluies et débits de sources karstiques. C. R. Geosci. 2020, 334. [Google Scholar] [CrossRef]
- Mangin, A. Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Amraoui, F.; Razack, M.; Bouchaou, L. Comportement d’une source karstique soumise à une sécheresse prolongée: La source Bittit (Maroc). C. R. Geosci. 2004, 336, 1099–1109. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, Revised ed.; Holden-Day: Toronto, ON, Canada, 1976. [Google Scholar]
- Padilla, A.; Pulido-Bosch, A. Study of hydrographs of karstic aquifers by means of correlation and cross spectral analysis. J. Hydrol. 1995, 168, 73–89. [Google Scholar] [CrossRef]
- Hamlaoui-Moulai, L.; Mesbah, M.; Souag-Gamane, D.; Medjerab, A. Detecting Hydro-Climatic Change Using Spatiotemporal Analysis of Rainfall Time Series in Western Algeria. Nat. Hazards 2013, 65, 1293–1311. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Nadal-Romero, E.; González-Hidalgo, J.C.; Albaladejo, J.; Andreu, V.; Bagarello, V.; Barhi, H.; Batalla, R.J.; Bernal, S.; Campo, J.; et al. Spatial variability of the relationships of runoff and sediment yield with weather types throughout the Mediterranean basin. J. Hydrol. 2019, 571, 390–405. [Google Scholar] [CrossRef] [Green Version]
- Xoplaki, E.; González-Rouco, J.F.; Luterbacher, J.; Wanner, H. Wet season Mediterranean precipitation variability: Influence of large-scale dynamics and trends. Clim. Dynam. 2004, 23, 63–78. [Google Scholar] [CrossRef] [Green Version]
- Feki, H.; Hermassi, T.; Soualhia, N. Characterisation of mean monthly rainfall variability over mellegue catchment—Tunisia. In Proceedings of the Euro-Mediterranean Conference for Environmental Integration, Sousse, Tunisia, 20–25 November 2017; Springer: Cham, Switzerland, 2017; pp. 793–795. [Google Scholar]
- Chargui, S.; Jaberi, A.; Cudennec, C.; Lachaal, F.; Calvez, R.; Slimani, M. Statistical detection and no-detection of rainfall change trends and breaks in semiarid Tunisia—50+ years over the Merguellil agro-hydro-climatic reference basin. Arab. J. Geosci. 2018, 11, 675. [Google Scholar] [CrossRef]
- Gader, K.; Gara, A.; Vanclooster, M.; Khlifi, S.; Slimani, M. Drought assessment in a south Mediterranean transboundary catchment. Hydrol. Sci. J. 2020, 65, 1300–1315. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Nadal-Romero, E.; González-Hidalgo, J.C.; Albaladejo, J.; Andreu, V.; Bahri, H.; Bernal, S.; Biddoccu, M.; Bienes, R.; Campo, J.; et al. Relationship of Weather Types on the Seasonal and Spatial Variability of Rainfall, Runoff, and Sediment Yield in the Western Mediterranean Basin. Atmosphere 2020, 11, 609. [Google Scholar] [CrossRef]
- Lopez-Bustins, J.A.; Lemus-Canovas, M. The influence of the Western Mediterranean Oscillation upon the spatio-temporal variability of precipitation over Catalonia (northeastern of the Iberian Peninsula). Atmos. Res. 2020, 236, 104819. [Google Scholar] [CrossRef]
- Ellouze, M.; Azri, C.; Abida, H. Spatial variability of monthly and annual rainfall data over Southern Tunisia. Atmos. Res. 2009, 93, 832–839. [Google Scholar] [CrossRef]
- Vaseghi, S.V. Advanced Digital Signal Processing and Noise Reduction; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kim, S.; Noh, H.; Kang, N.; Lee, K.; Kim, Y.; Lim, S.; Lee, D.R.; Kim, H.S. Noise reduction analysis of radar rainfall using chaotic dynamics and filtering techniques. Adv. Meteorol. 2014, 2014, 517571. [Google Scholar] [CrossRef] [Green Version]
- Jayawardena, A.W.; Gurung, A.B. Effect of Noise in Nonlinear Hydrological Time Series Analysis and Prediction; No. 255; International Association of Hydrological Sciences Publication: Wallingford, UK, 1999; pp. 121–128. [Google Scholar]
- Adamowski, K.; Prokoph, A.; Adamowski, J. Development of a new method of wavelet aided trend detection and estimation. Hydrol. Process. 2009, 23, 2686–2696. [Google Scholar] [CrossRef]
- Palizdan, N.; Falamarzi, Y.; Huang, Y.F.; Lee, T.S. Precipitation trend analysis using discrete wavelet transform at the Langat River Basin, Selangor, Malaysia. Stoch. Environ. Res. Risk A 2017, 31, 853–877. [Google Scholar] [CrossRef]
- Pandey, B.; Tiwari, H.; Khare, D. Trend analysis using discrete wavelet transform (DWT) for long-term precipitation (1851–2006) over India. Hydrolog. Sci. J. 2017, 62, 2187–2208. [Google Scholar] [CrossRef]
- Pathak, P.; Kalra, A.; Ahmad, S.; Bernardez, M. Wavelet-aided analysis to estimate seasonal variability and dominant periodicities in temperature, precipitation, and streamflow in the Midwestern United States. Water Resour. Manag. 2016, 30, 4649–4665. [Google Scholar] [CrossRef]
- Partal, T. Multi-annual analysis and trends of the temperatures and precipitations in West Anatolia. J. Water Clim. Chang. 2017, jwc2017109. [Google Scholar] [CrossRef]
- Sang, Y.F.; Sun, F.; Singh, V.P.; Xie, P.; Sun, J. A discrete wavelet spectrum approach for identifying non-monotonic trends in hydroclimate data. Hydrol. Earth Syst. Sci. 2018, 22, 757–766. [Google Scholar] [CrossRef] [Green Version]
- Freire, P.K.D.M.M.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl. Soft. Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- Abda, Z.; Chettih, M.; Zerouali, B. Assessment of neuro-fuzzy approach based different wavelet families for daily flow rates forecasting. Model. Earth Syst. Environ. 2020. [Google Scholar] [CrossRef]
- Kisi, O.; Alizamir, M.; Shiri, J. Conjunction Model Design for Intermittent Streamflow Forecasts: Extreme Learning Machine with Discrete Wavelet Transform. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation; Springer: Singapore, 2020; pp. 171–181. [Google Scholar] [CrossRef]
- Pal, L.; Ojha, C.S.P.; Chandniha, S.K.; Kumar, A. Regional scale analysis of trends in rainfall using nonparametric methods and wavelet transforms over a semi-arid region in India. Int. J. Climatol. 2019, 39, 2737–2764. [Google Scholar] [CrossRef]
- Adarsh, S.; Janga Reddy, M. Trend analysis of rainfall in four meteorological subdivisions of southern India using nonparametric methods and discrete wavelet transforms. Int. J. Climatol. 2015, 35, 1107–1124. [Google Scholar] [CrossRef]
- Araghi, A.; Baygi, M.M.; Adamowski, J.; Malard, J.; Nalley, D.; Hasheminia, S.M. Using wavelet transforms to estimate surface temperature trends and dominant periodicities in Iran based on gridded reanalysis data. Atmos. Res. 2015, 155, 52–72. [Google Scholar] [CrossRef]
- Gómez Navarro, L. Aproximación Metodológica al Estudio de Secuencias Secas de Larga Duración: El Caso de las Islas Baleares; Publicaciones de la Asociación Española de Climatología: Zaragoza, Spain, 2002. [Google Scholar]
- Khoualdia, W.; Djebbar, Y.; Hammar, Y. Caractérisation de la variabilité climatique: Cas du bassin versant de la Medjerda (Nord-Est algérien). Synthèse Revue Sci. Technol. 2014, 29, 6–23. [Google Scholar]
- Khedimallah, A.; Meddi, M.; Mahé, G. Characterization of the interannual variability of precipitation and runoff in the Cheliff and Medjerda basins (Algeria). J. Earth Syst. Sci. 2020, 129, 134. [Google Scholar] [CrossRef]
- Zerouali, B.; Mesbah, M.; Chettih, M.; Djemai, M. Contribution of cross time-frequency analysis in assessment of possible relationships between large-scale climatic fluctuations and rainfall of northern central Algeria. Arab. J. Geosci. 2018, 11, 392. [Google Scholar] [CrossRef]
- Elmeddahi, Y.; Issaadi, A.; Mahmoudi, H.; Tahar Abbes, M.; Goosen Mattheus, F.A. Effect of climate change on water resources of the Algerian Middle Cheliff basin. Desalination Water Treat. 2014, 52, 2073–2081. [Google Scholar] [CrossRef]
- Mrad, D.; Dairi, S.; Boukhari, S.; Djebbar, Y. Applied multivariate analysis on annual rainfall in the northeast of Algeria. J. Water Clim Chang. 2019. [Google Scholar] [CrossRef]
- Sangüesa-Barreda, G.; Camarero, J.J.; Sánchez-Salguero, R.; Gutiérrez, E.; Linares, J.C.; Génova, M.; Ribas, M.; Tíscar, P.A.; López-Sáez, J.A. Droughts and climate warming desynchronize Black pine growth across the Mediterranean Basin. Sci. Total Environ. 2019, 697, 133989. [Google Scholar] [CrossRef] [PubMed]
- Ouatiki, H.; Boudhar, A.; Ouhinou, A.; Arioua, A.; Hssaisoune, M.; Bouamri, H.; Benabdelouahab, T. Trend analysis of rainfall and drought over the Oum Er-Rbia River Basin in Morocco during 1970–2010. Arab. J. Geosci. 2019, 12, 128. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef] [Green Version]
- Coll, J.R.; Aguilar, E.; Ashcroft, L. Drought variability and change across the Iberian Peninsula. Theor. Appl. Climatol. 2017, 130, 901–916. [Google Scholar] [CrossRef] [Green Version]
- Achite, M.; Ouillon, S. Recent changes in climate, hydrology and sediment load in the Wadi Abd, Algeria (1970–2010). Hydrol. Earth Syst. Sci. 2016, 20, 1355–1372. [Google Scholar] [CrossRef] [Green Version]
- Jemai, H.; Ellouze, M.; Abida, H.; Laignel, B. Spatial and temporal variability of rainfall: Case of Bizerte-Ichkeul Basin (Northern Tunisia). Arab. J. Geosci. 2018, 11, 177. [Google Scholar] [CrossRef]
- Meddi, H.; Meddi, M.; Assani, A.A. Study of Drought in Seven Algerian Plains. Arab. J. Sci. Eng. 2014, 39, 339–359. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Ruiz Sinoga, J.D.; León Gross, T. Droughts and their social perception in the mass media (southern Spain). Int. J. Climatol. 2013, 33, 709–724. [Google Scholar] [CrossRef]
- Derdous, O.; Bouamrane, A.; Mrad, D. Spatiotemporal analysis of meteorological drought in a Mediterranean dry land: Case of the Cheliff basin–Algeria. Model. Earth Syst. Environ. 2020. [Google Scholar] [CrossRef]
- Piccarreta, M.; Pasini, A.; Capolongo, D.; Lazzari, M. Changes in Daily Precipitation Extremes in the Mediterranean from 1951 to 2010: The Basilicata Region, Southern Italy. Int. J. Climatol. 2013, 33, 3229–3248. [Google Scholar] [CrossRef]
- Khezazna, A.; Amarchi, H.; Derdous, O.; Bousakhria, F. Drought monitoring in the Seybouse basin (Algeria) over the last decades. Water Land. Dev. 2017, 33, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Zeineddine, N.; Ovidiu, M. Rainfall Variability and Trend Analysis of Annual Rainfall in North Africa. Int. J. Earth Atmos. Sci. 2016, 2016, 7230450. [Google Scholar] [CrossRef]
- Philandras, C.M.; Nastos, P.T.; Kapsomenakis, J.; Douvis, K.C.; Tselioudis, G.; Zerefos, C.S. Long term precipitation trends and variability within the Mediterranean region. Nat. Hazard Earth Sys. 2011, 11, 3235–3250. [Google Scholar] [CrossRef] [Green Version]
- Ozer, P.; Erpicum, M.; Demarée, G.; Vandiepenbeeck, M. The Sahelian drought may have ended during the 1990s. Hydrolog. Sci. J. 2003, 48, 489–492. [Google Scholar] [CrossRef]
| Sub-Series | 1st | 2nd | 3rd | 4th | (n/t)th |
|---|---|---|---|---|---|
| 1st | 1 | 1st–2nd | 1st–3rd | 1st–4th…. | 1th–(n/t)th |
| 2nd | 1 | 2nd–3rd | 2nd–4th…. | 2nd–(n/t)th | |
| 3rd | Meaningless | 1 | 3rd–4th…. | 3rd–(n/t)th | |
| 4th | 1 | 4th–(n/t)th | |||
| (n/t)th | 1 | ||||
| Oued Taria Station X = 274.4 km Y = 176.4 km Z = 1000 m | Azazga Station X = 649.6 km Y = 383.9 km Z = 430 m | Ain Beida Station X = 924.15 km Y = 288 km Z = 1004 m | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model (M) | Combination | R12 | Min | Max | CTV (%) | R22 | Min | Max | CTV (%) | R32 | Min | Max | CTV (%) |
| OS | - | 1.00 | 72 | 754 | 100 | 1.00 | 521 | 1577 | 100 | 1.00 | 155 | 631 | 100 |
| M 1 | D1 | 0.30 | −169 | 195 | 30.6 | 0.43 | −398 | 360 | 43.1 | 0.42 | −154 | 152 | 41.4 |
| M 2 | D2 | 0.22 | −124 | 139 | 20.7 | 0.28 | −364 | 288 | 29.8 | 0.32 | −94 | 89 | 30.3 |
| M 3 | D3 | 0.05 | −51 | 55 | 5.6 | 0.07 | −149 | 165 | 11.2 | 0.06 | −61 | 64 | 7.0 |
| M 4 | D4 | 0.09 | −68 | 66 | 9.5 | 0.06 | −118 | 126 | 6.3 | 0.09 | −64 | 40 | 10.6 |
| M 5 | D5 | 0.08 | −68 | 82 | 13.7 | 0.10 | −113 | 134 | 11.0 | 0.05 | −16 | 10 | 0.8 |
| M 6 | A5 | 0.20 | 278 | 423 | 24.5 | 0.01 | 945 | 1036 | 1.2 | 0.09 | 350 | 437 | 7.6 |
| M 7 | D1+A5 | 0.50 | 179 | 618 | 54.9 | 0.44 | 585 | 1363 | 44.4 | 0.51 | 242 | 546 | 49.2 |
| M 8 | D2+A5 | 0.40 | 174 | 561 | 45.5 | 0.29 | 642 | 1291 | 31.1 | 0.40 | 256 | 494 | 38.1 |
| M 9 | D3+A5 | 0.25 | 228 | 451 | 30.4 | 0.09 | 799 | 1110 | 12.1 | 0.16 | 332 | 461 | 14.0 |
| M10 | D4+A5 | 0.29 | 220 | 445 | 34.2 | 0.07 | 849 | 1092 | 7.7 | 0.19 | 287 | 465 | 17.3 |
| M 11 | D5+A5 | 0.33 | 213 | 417 | 32.9 | 0.12 | 835 | 1104 | 12.4 | 0.10 | 339 | 443 | 11.4 |
| M 12 | D1+D2+A5 | 0.71 | 140 | 732 | 76.1 | 0.72 | 591 | 1650 | 74.3 | 0.81 | 223 | 617 | 80.0 |
| M 13 | D1+D2+D3+A5 | 0.76 | 100 | 753 | 81.9 | 0.82 | 530 | 1602 | 82.9 | 0.88 | 210 | 616 | 87.0 |
| M 14 | D1+D2+D3+D4+A5 | 0.86 | 54 | 769 | 91.7 | 0.88 | 530 | 1627 | 89.0 | 0.99 | 163 | 625 | 96.3 |
| M 15 | D1+D2+D3+D5+A5 | 0.90 | 119 | 738 | 90.2 | 0.93 | 519 | 1594 | 93.9 | 0.89 | 198 | 622 | 90.7 |
| M 16 | D1+D3+D4+D5+A5 | 0.79 | 149 | 640 | 78.9 | 0.70 | 482 | 1434 | 71.9 | 0.69 | 194 | 560 | 68.9 |
| M 17 | D1+D3+D4+A5 | 0.65 | 130 | 655 | 70.6 | 0.61 | 512 | 1480 | 62.2 | 0.68 | 187 | 554 | 65.1 |
| M 18 | D1+D4+D5+A5 | 0.74 | 175 | 619 | 73.1 | 0.71 | 512 | 1480 | 62.2 | 0.62 | 227 | 561 | 62.7 |
| M 19 | D2+D4+D5+A5 | 0.63 | 80 | 571 | 63.7 | 0.45 | 644 | 1374 | 49.3 | 0.51 | 190 | 525 | 51.4 |
| M 20 | D3+D4+D5+A5 | 0.48 | 178 | 472 | 48.3 | 0.27 | 729 | 1253 | 28.6 | 0.27 | 276 | 480 | 27.2 |
| M 21 | D4+D5+A5 | 0.43 | 192 | 451 | 42.6 | 0.18 | 826 | 1226 | 18.9 | 0.20 | 276 | 469 | 21.1 |
| M 22 | D3+D5+A5 | 0.39 | 187 | 432 | 38.7 | 0.20 | 686 | 1165 | 22.7 | 0.17 | 337 | 471 | 17.8 |
| M 23 | D2+D5+A5 | 0.54 | 132 | 549 | 53.9 | 0.20 | 605 | 1328 | 42.6 | 0.41 | 248 | 500 | 41.8 |
| M 24 | D1+D5+A5 | 0.64 | 158 | 603 | 63.3 | 0.55 | 558 | 1356 | 55.6 | 0.51 | 226 | 551 | 53.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zerouali, B.; Al-Ansari, N.; Chettih, M.; Mohamed, M.; Abda, Z.; Santos, C.A.G.; Zerouali, B.; Elbeltagi, A. An Enhanced Innovative Triangular Trend Analysis of Rainfall Based on a Spectral Approach. Water 2021, 13, 727. https://doi.org/10.3390/w13050727
Zerouali B, Al-Ansari N, Chettih M, Mohamed M, Abda Z, Santos CAG, Zerouali B, Elbeltagi A. An Enhanced Innovative Triangular Trend Analysis of Rainfall Based on a Spectral Approach. Water. 2021; 13(5):727. https://doi.org/10.3390/w13050727
Chicago/Turabian StyleZerouali, Bilel, Nadhir Al-Ansari, Mohamed Chettih, Mesbah Mohamed, Zaki Abda, Celso Augusto Guimarães Santos, Bilal Zerouali, and Ahmed Elbeltagi. 2021. "An Enhanced Innovative Triangular Trend Analysis of Rainfall Based on a Spectral Approach" Water 13, no. 5: 727. https://doi.org/10.3390/w13050727










