Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses
Abstract
1. Introduction
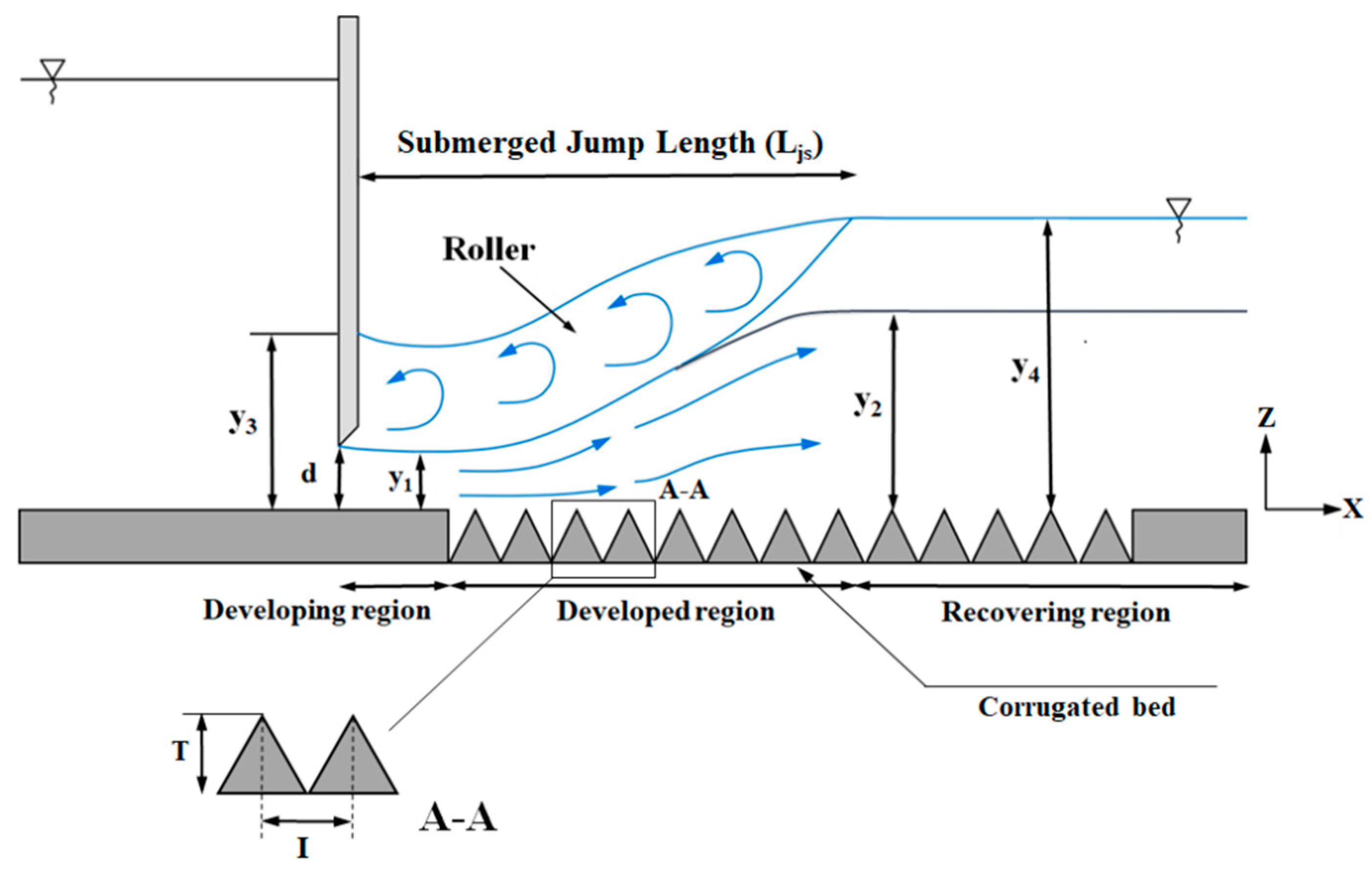
2. Submerged Hydraulic Jump
3. Materials and Methods
3.1. Input Parameters for Numerical Models
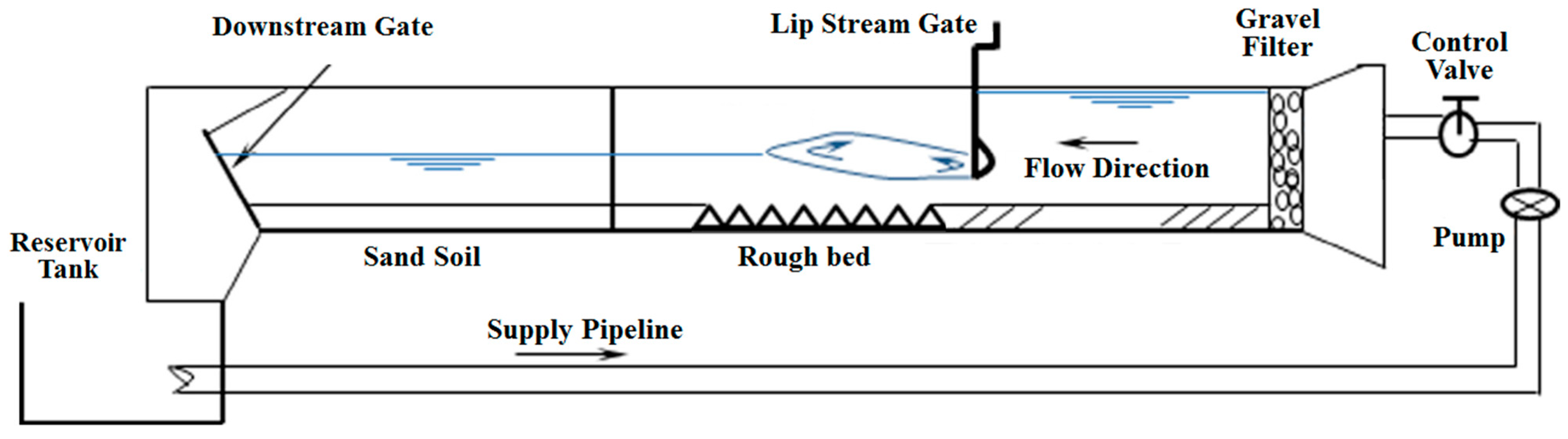
3.2. Experimental Model
3.3. CFD Analysis
3.4. Turbulence Model
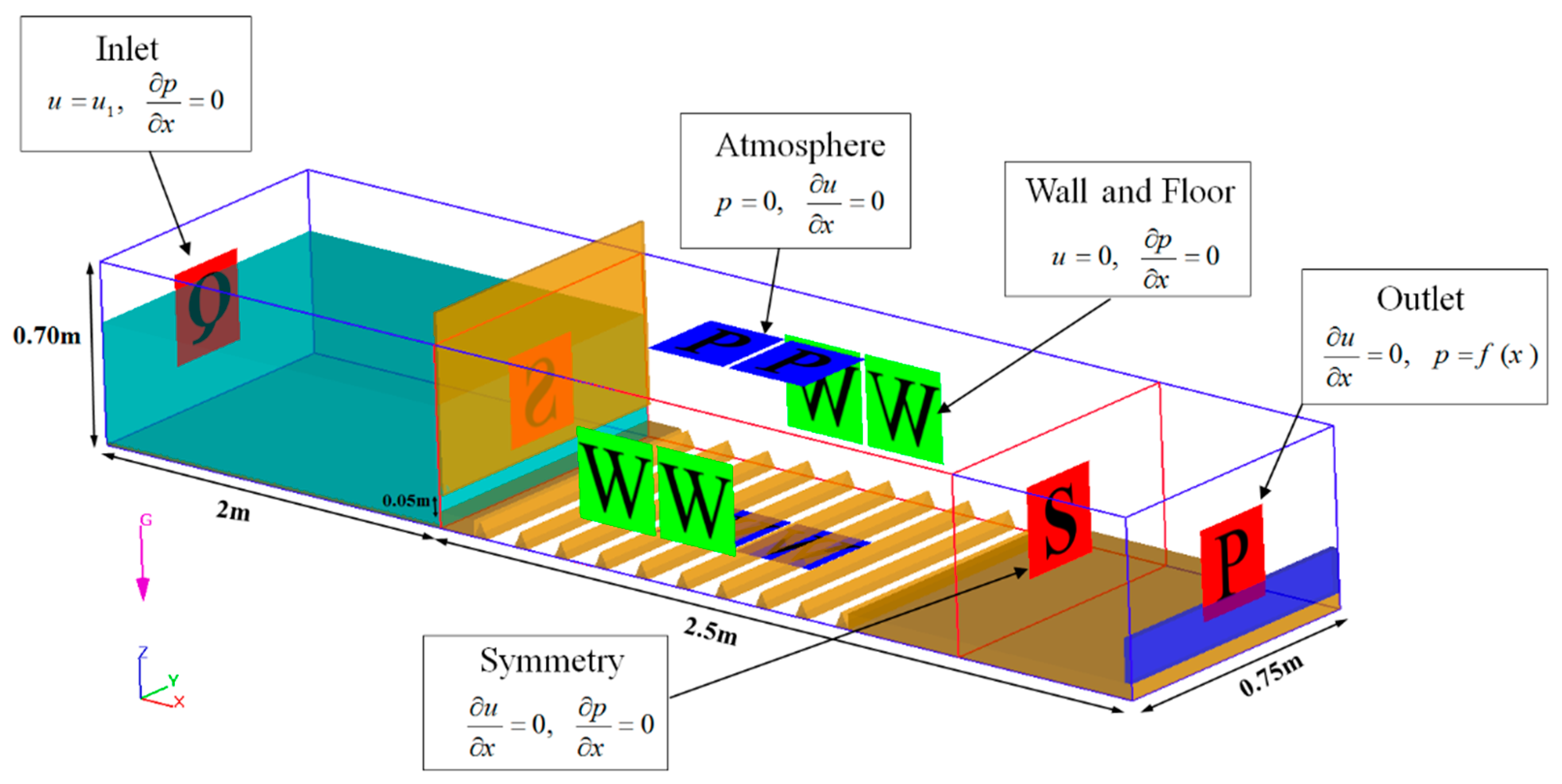
3.5. Boundary Conditions in the Computational Domain
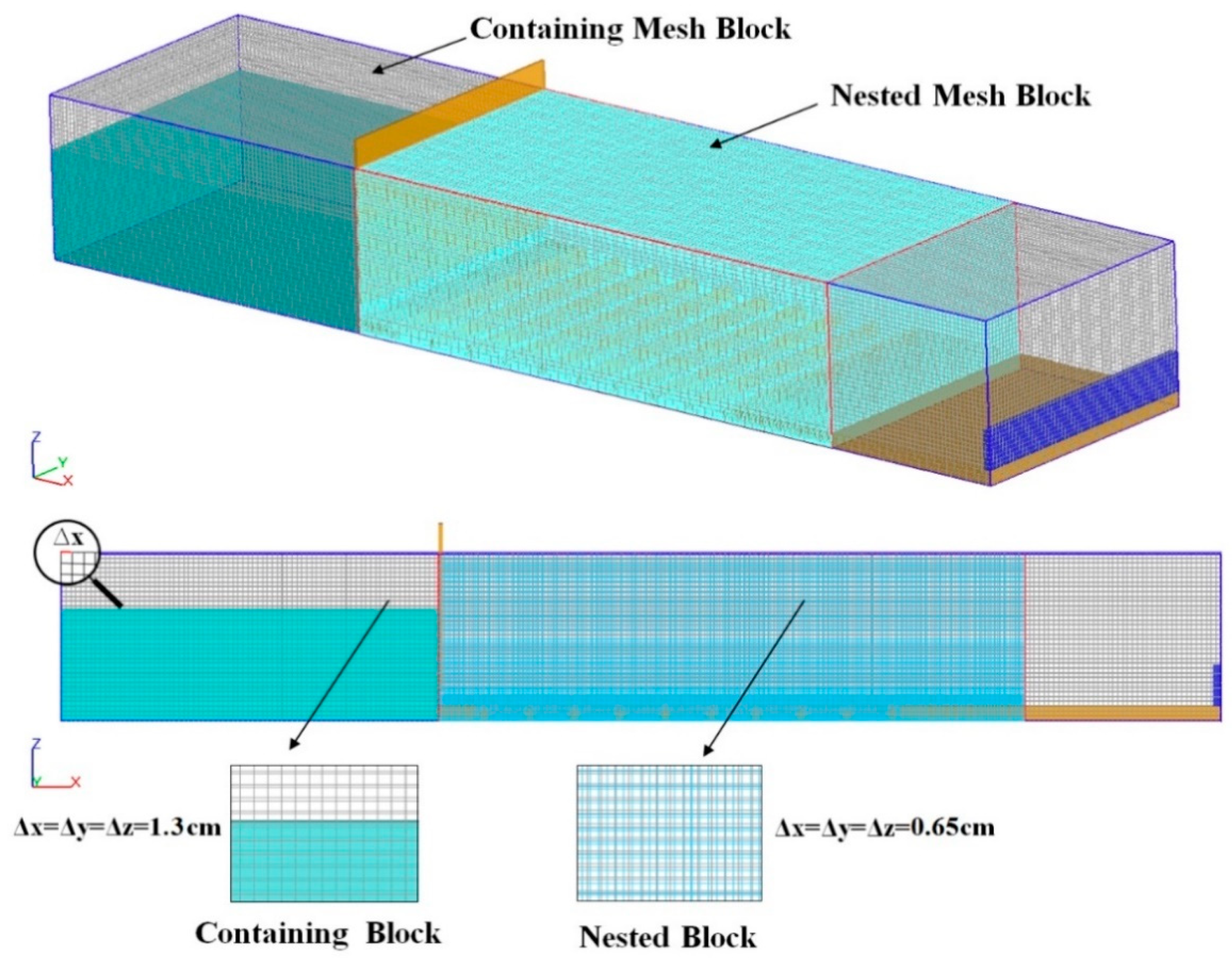
3.6. Computational Grid and Grid Convergence Analysis
4. Results and Discussions
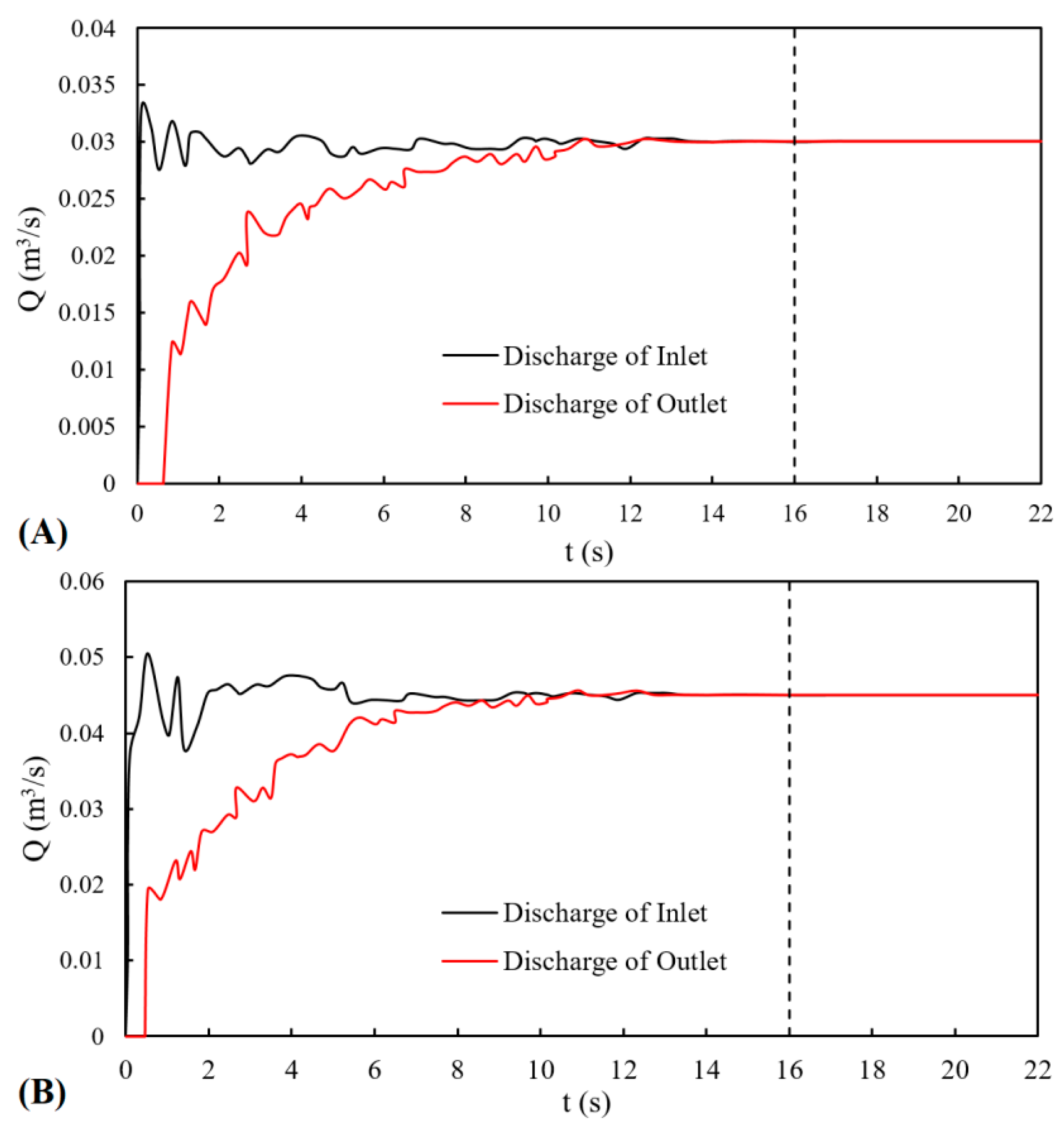
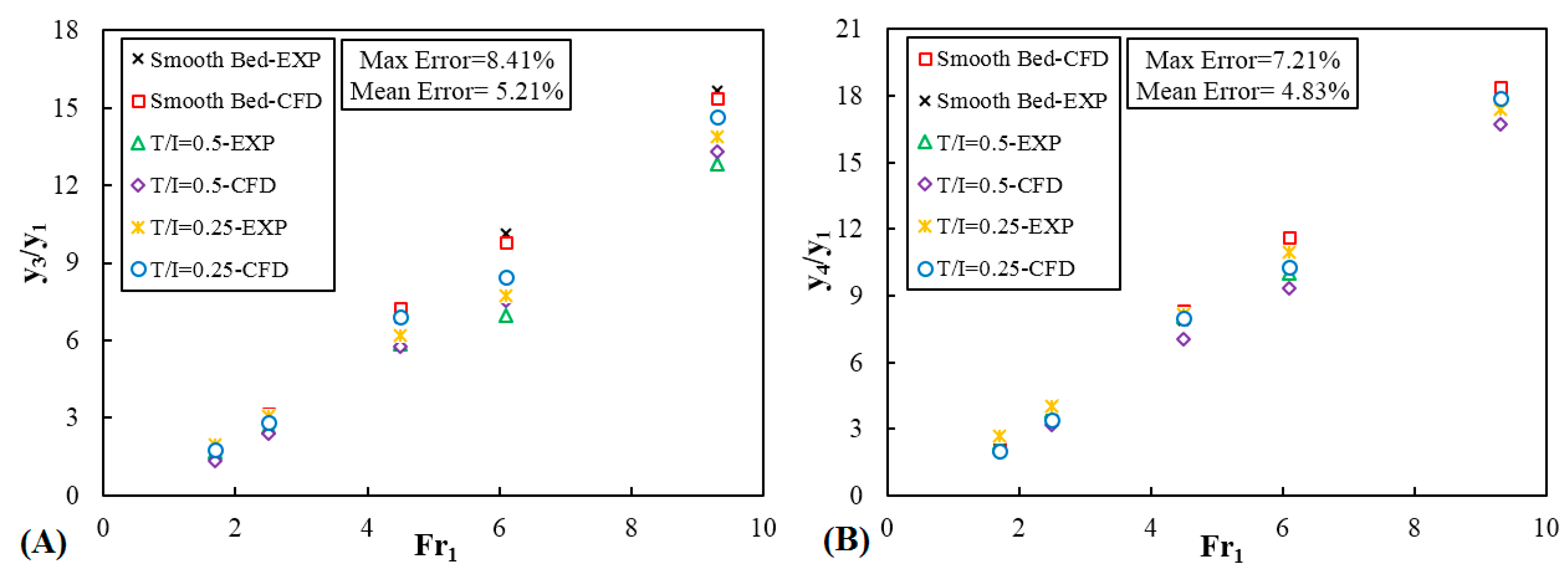
4.1. Validity of the Numerical Model Results
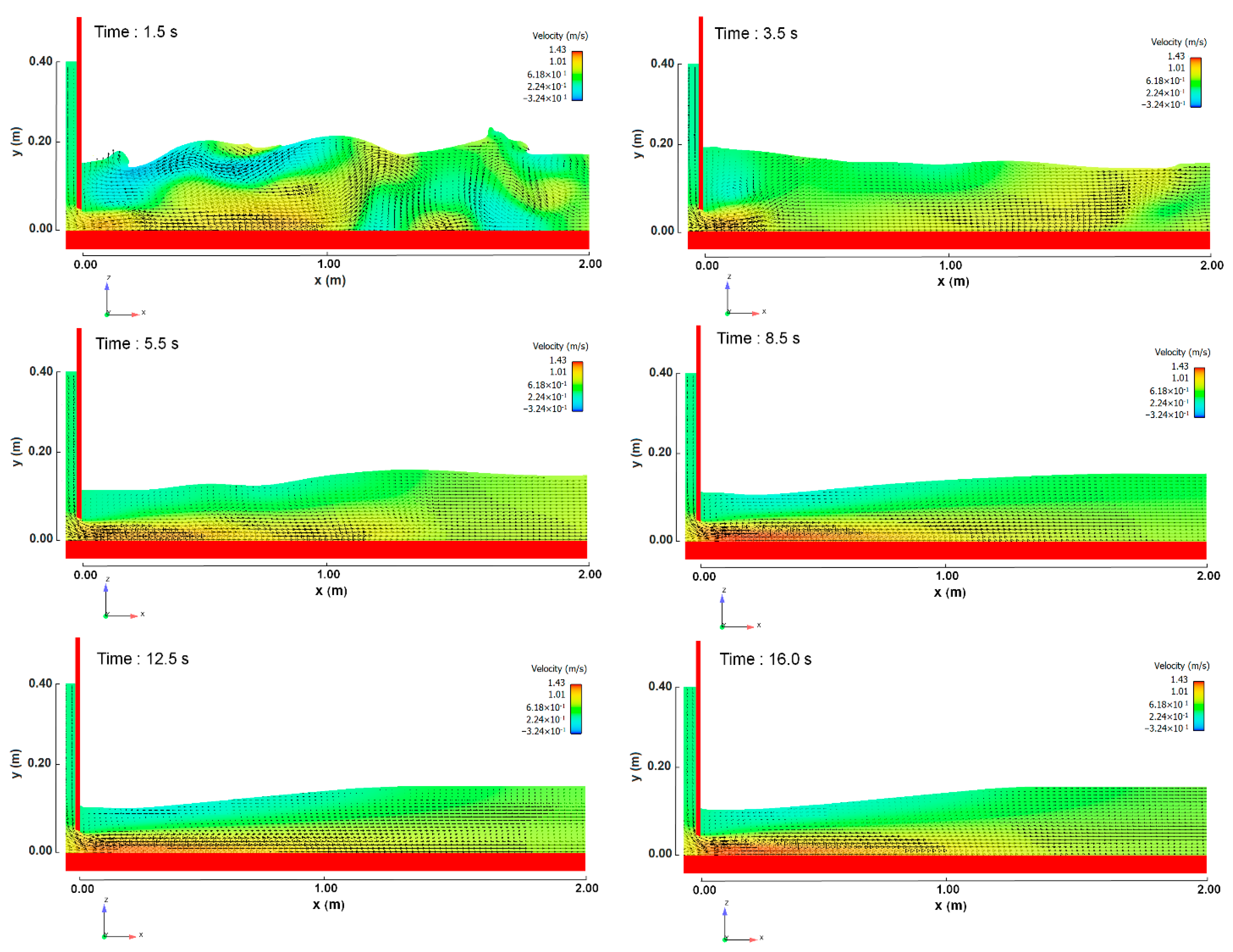
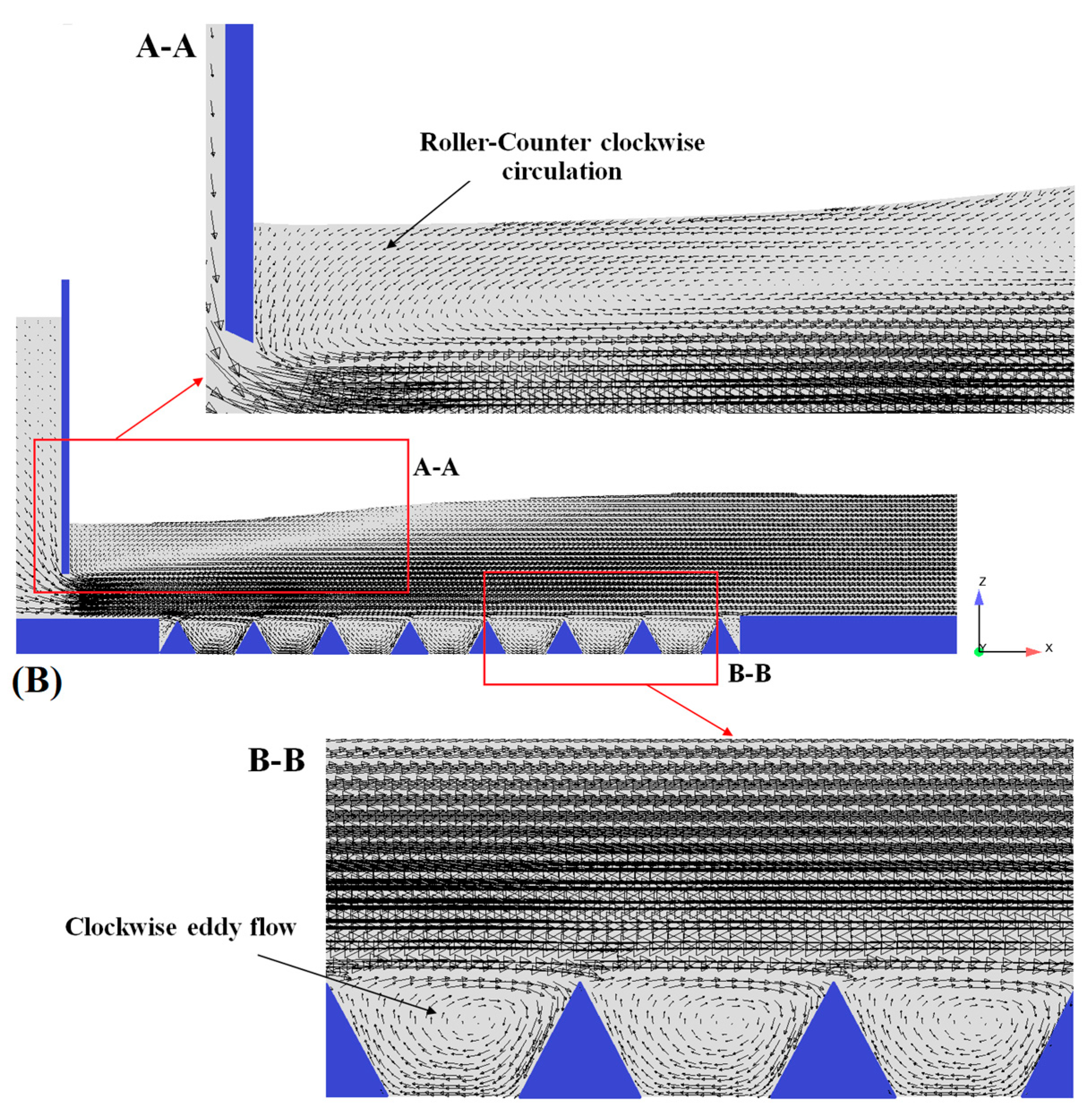
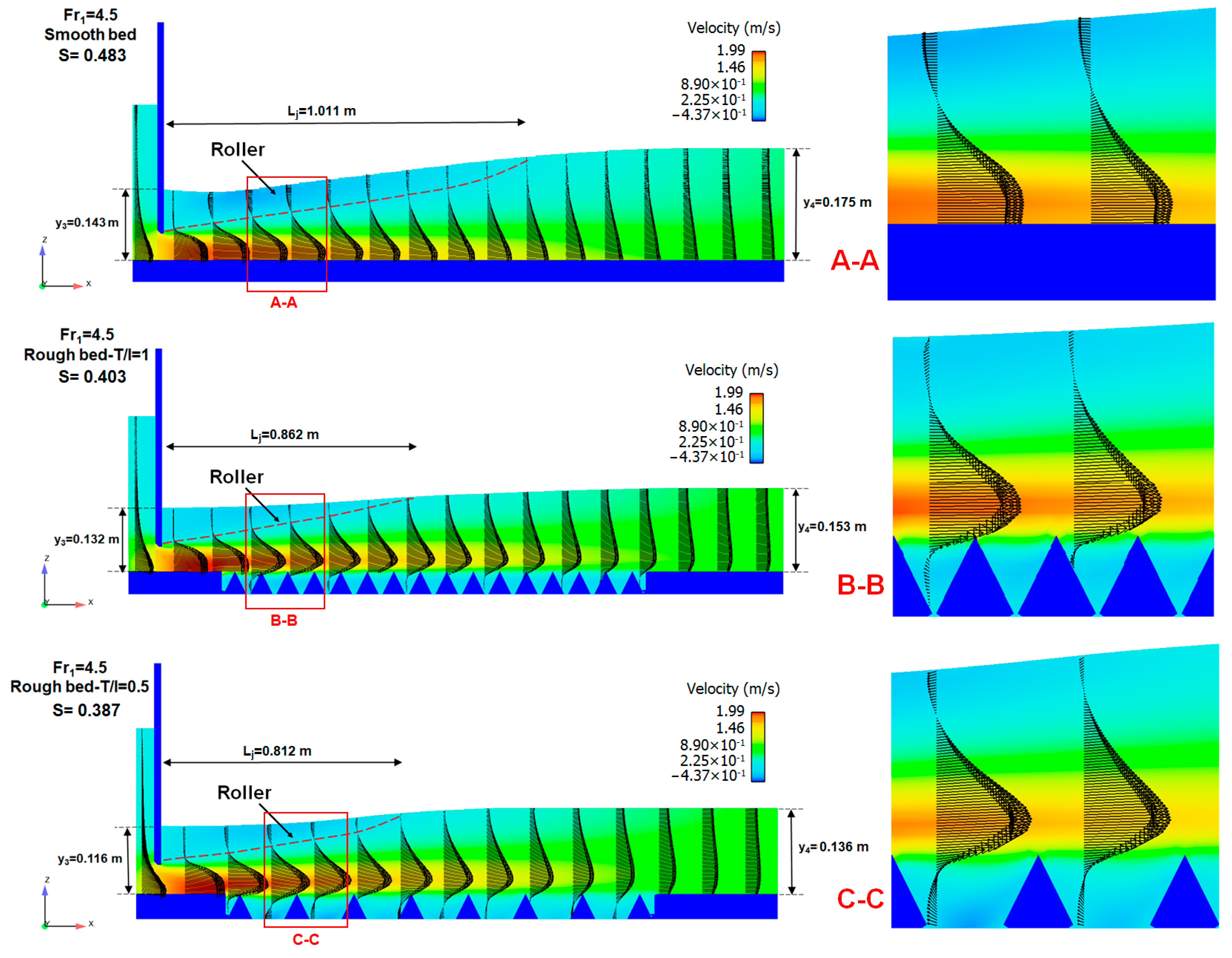
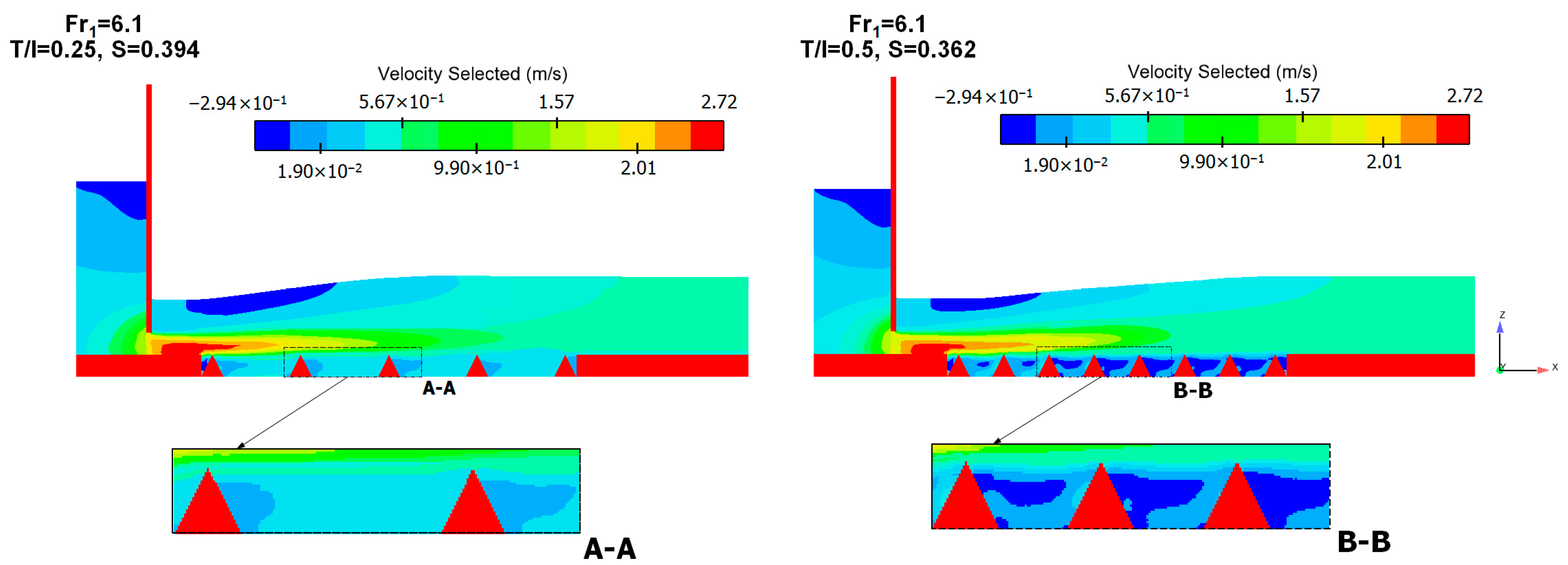
4.2. Longitudinal Profile of Streamlines
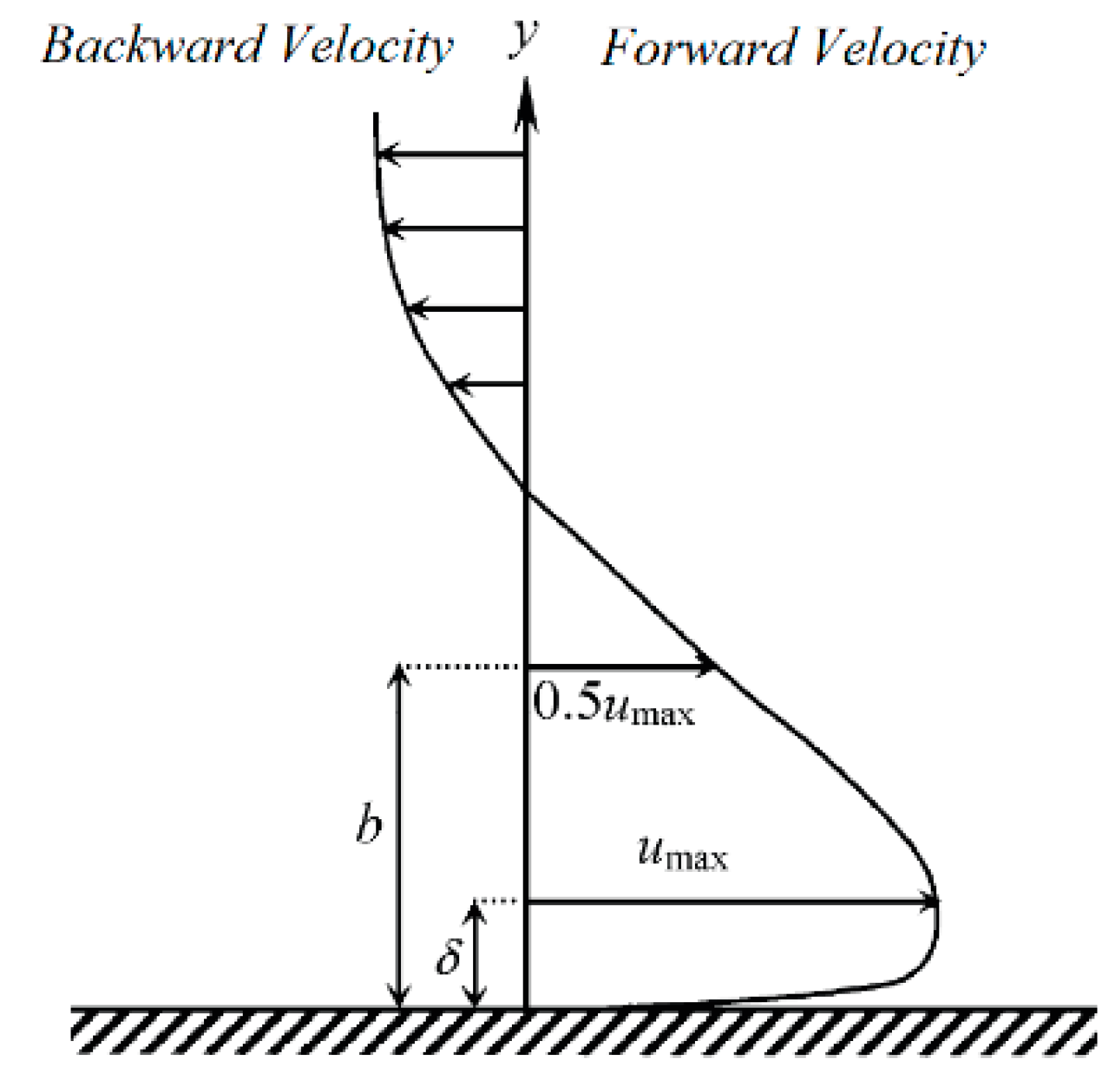
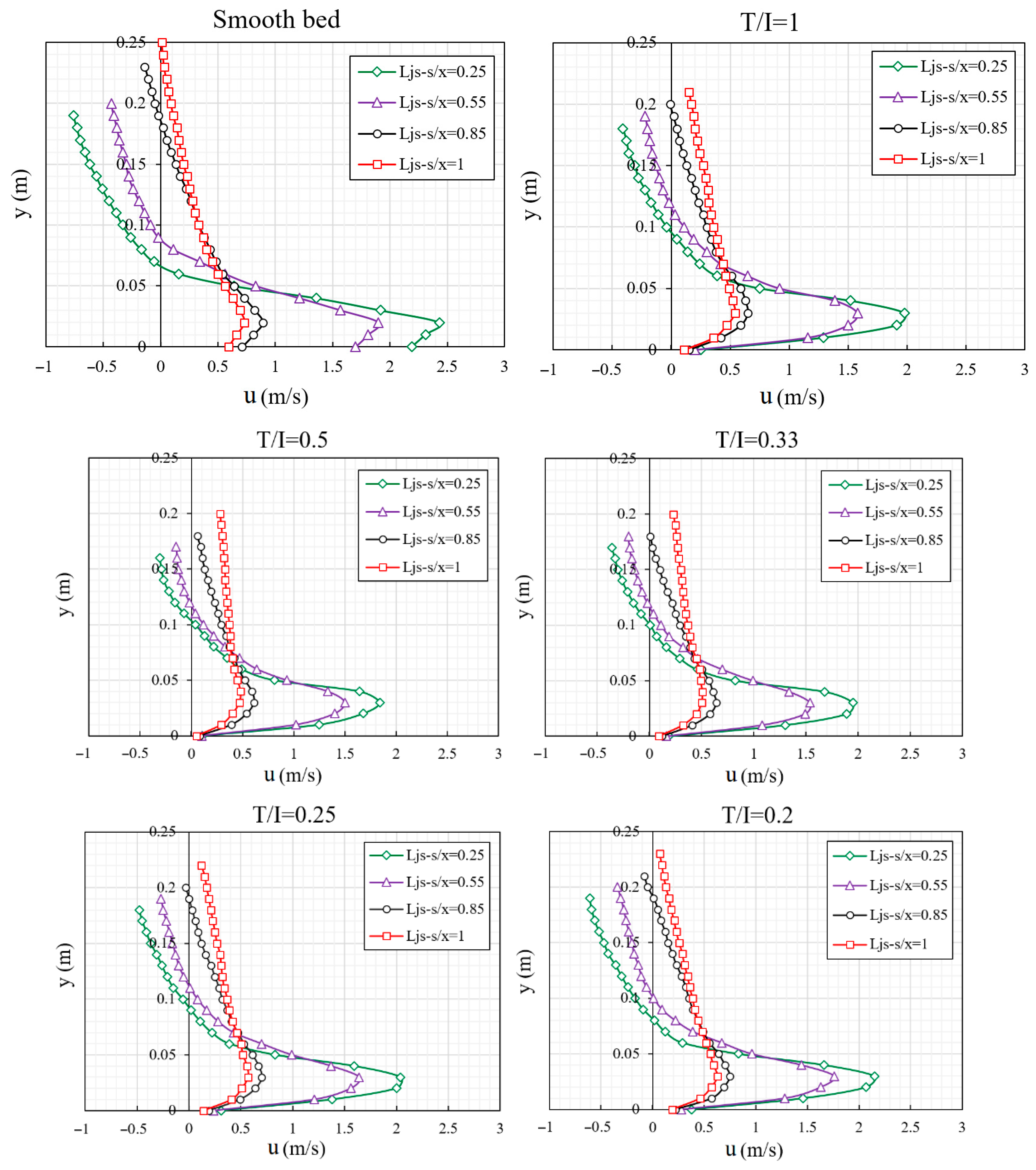
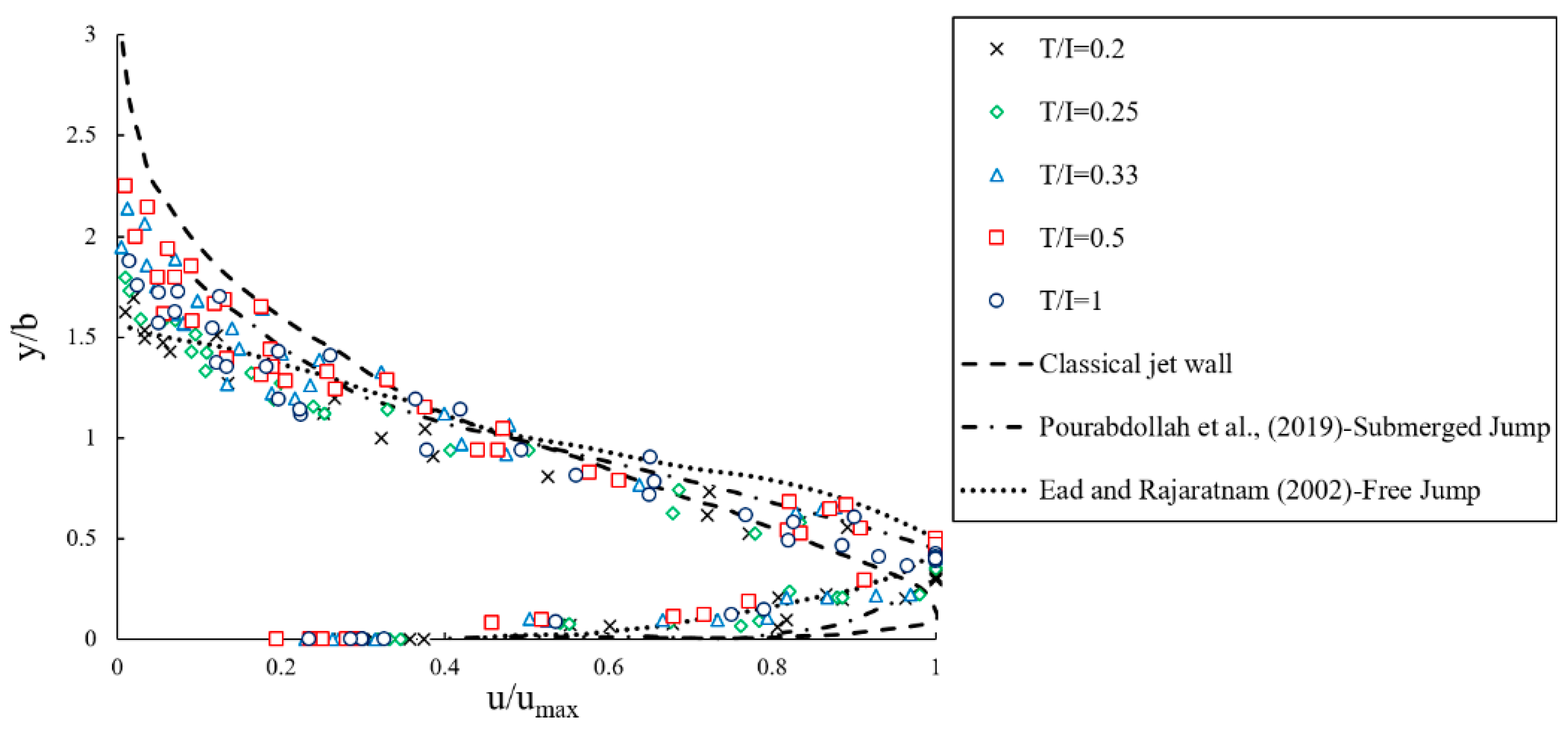
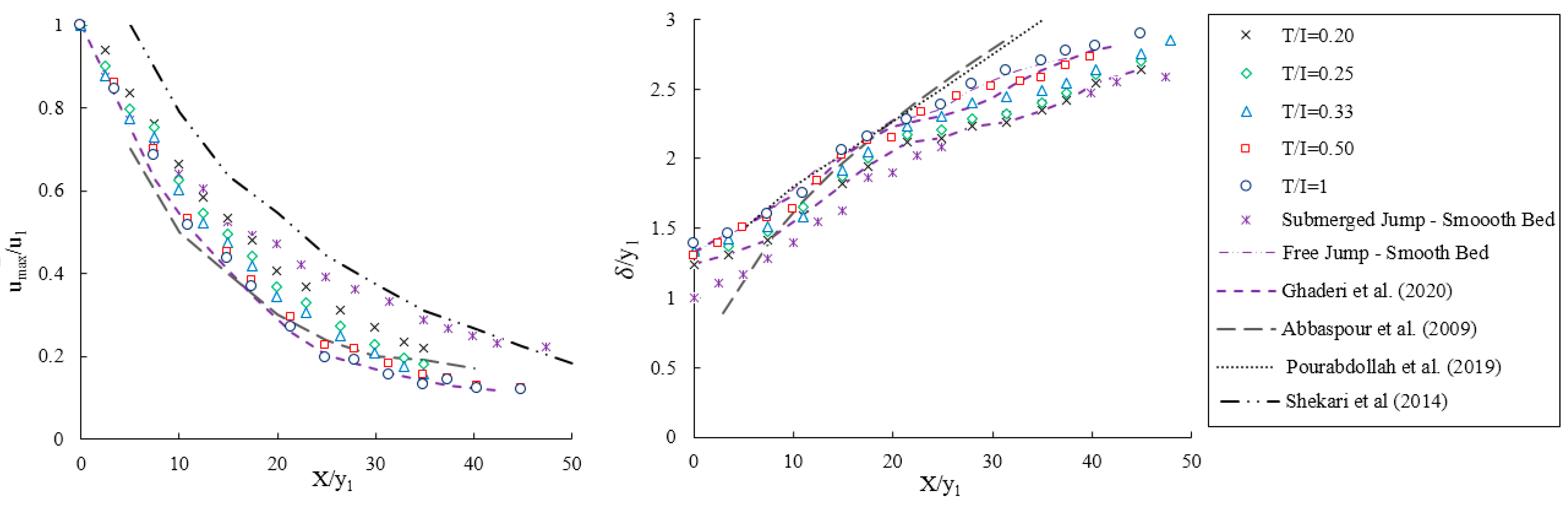
4.3. Velocity Profiles
4.4. Bed Shear Stress
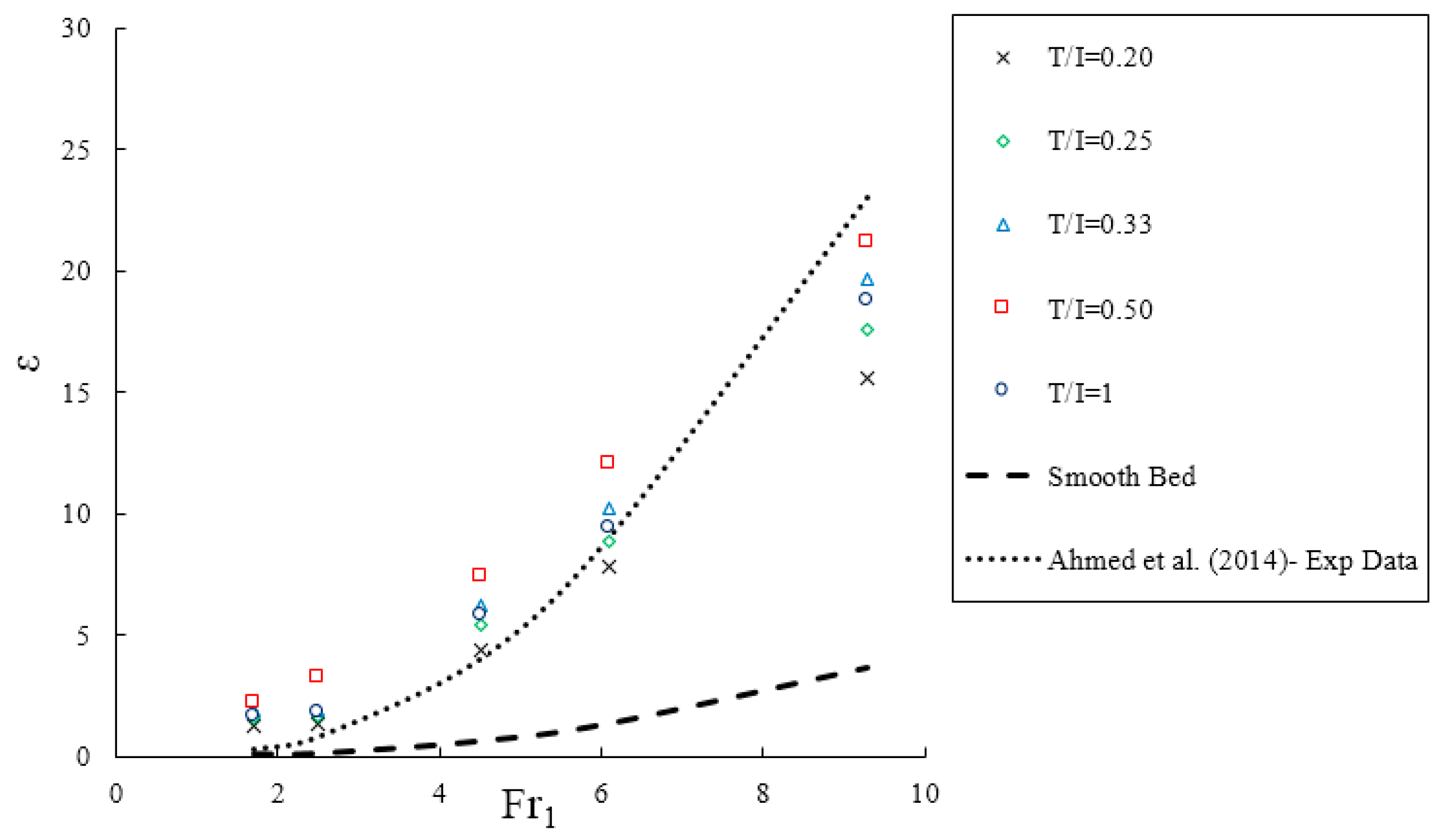
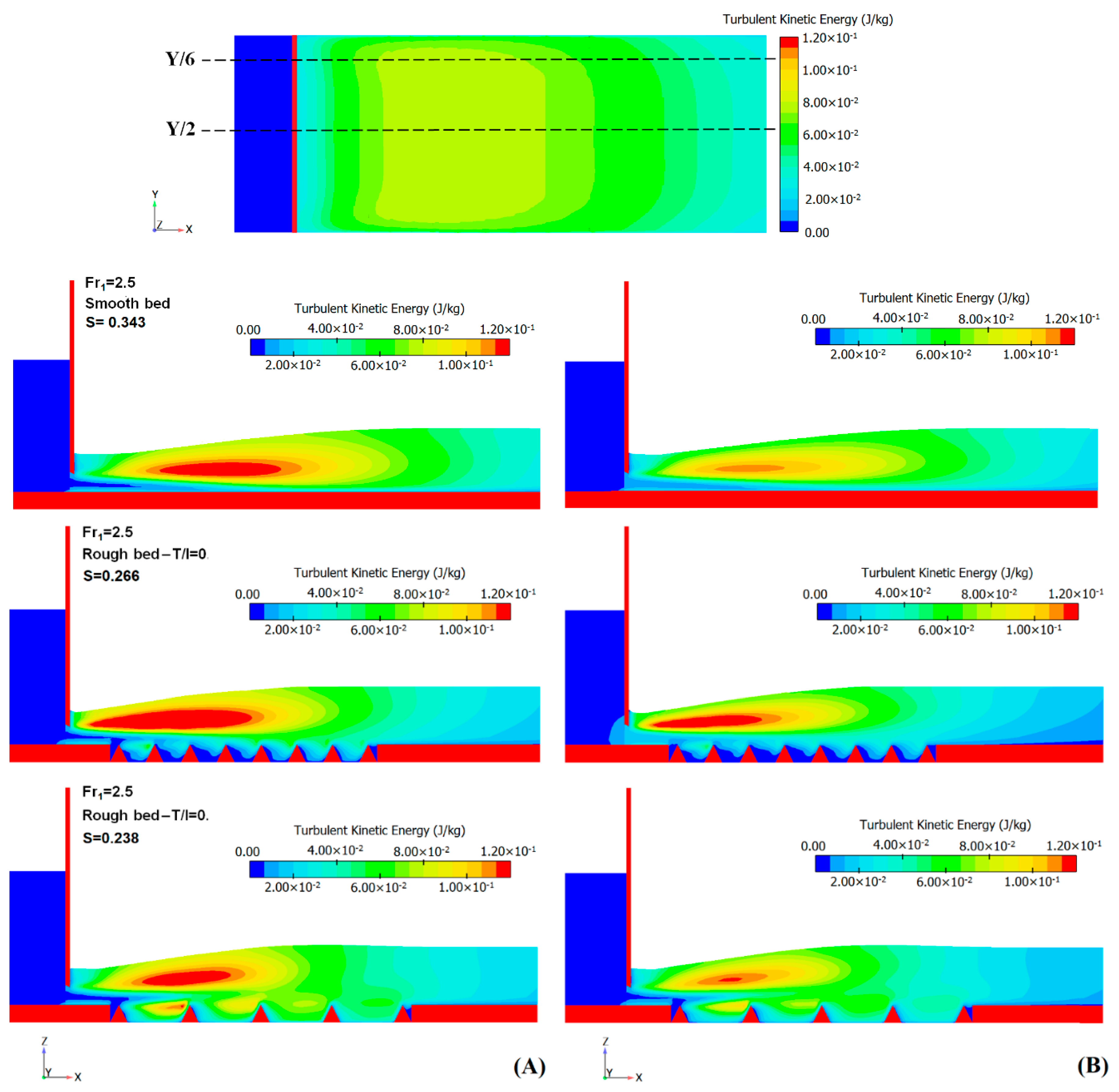
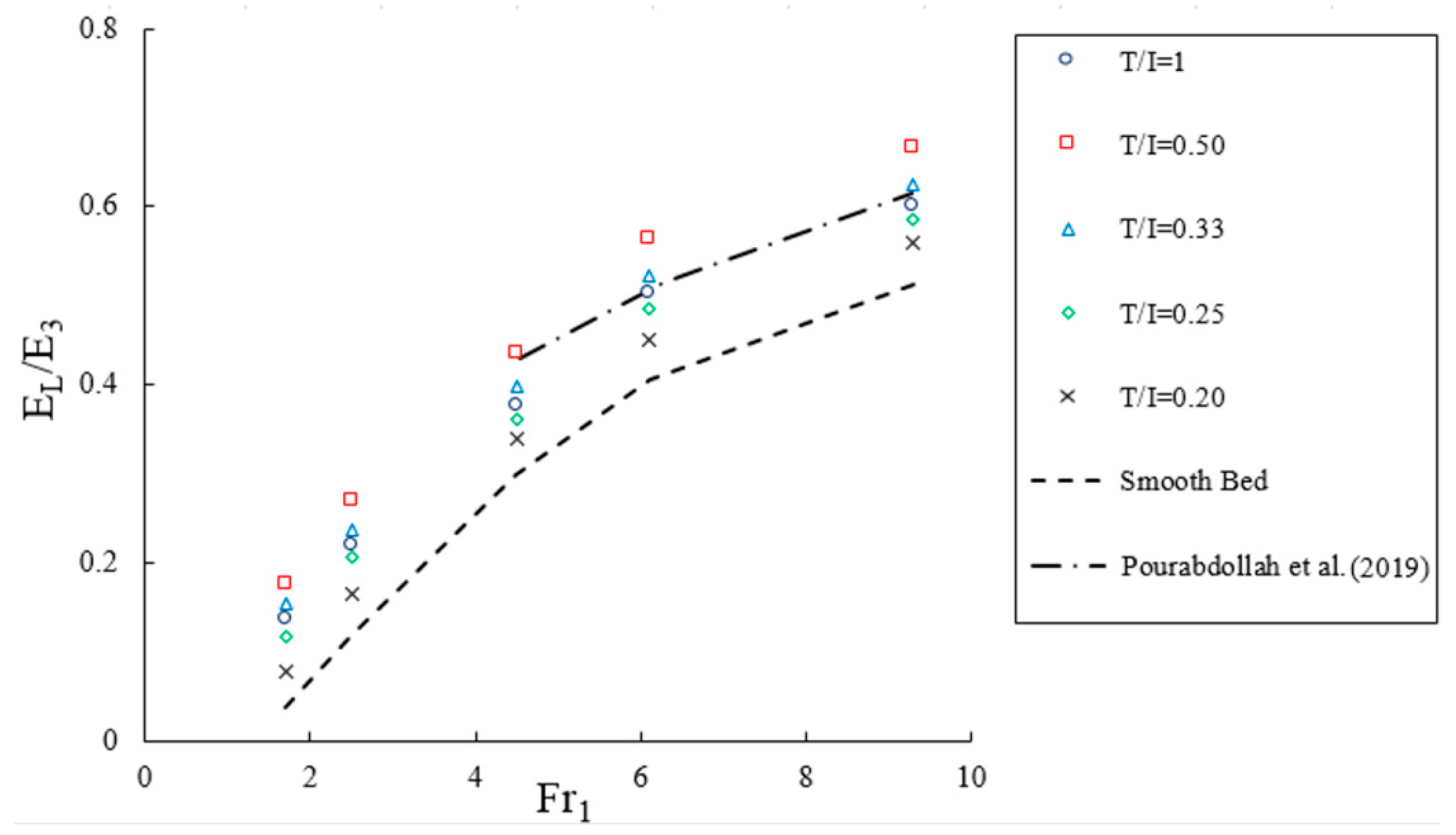
4.5. Turbulent Kinetic Energy (TKE) and Energy Loss
5. Conclusions
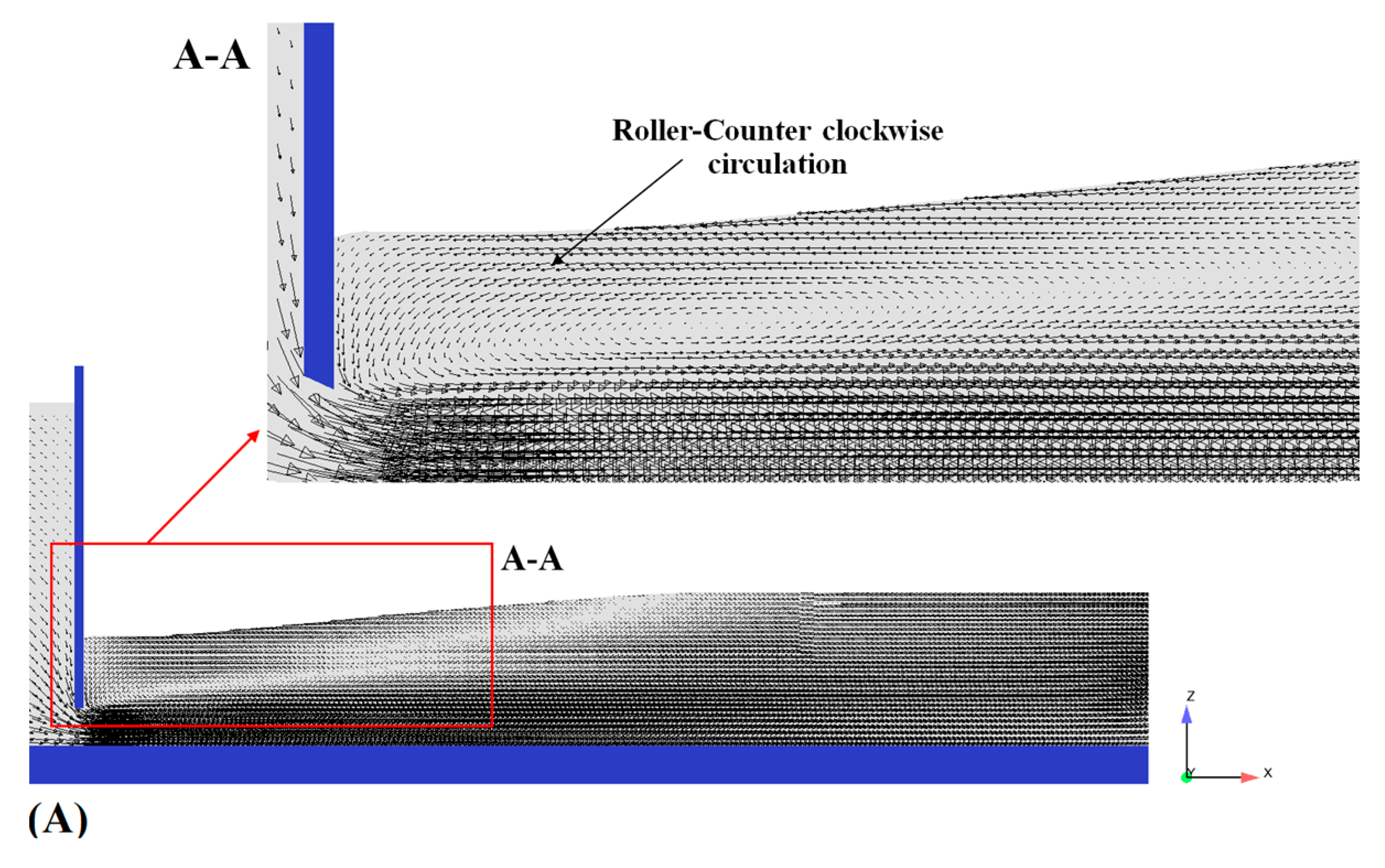
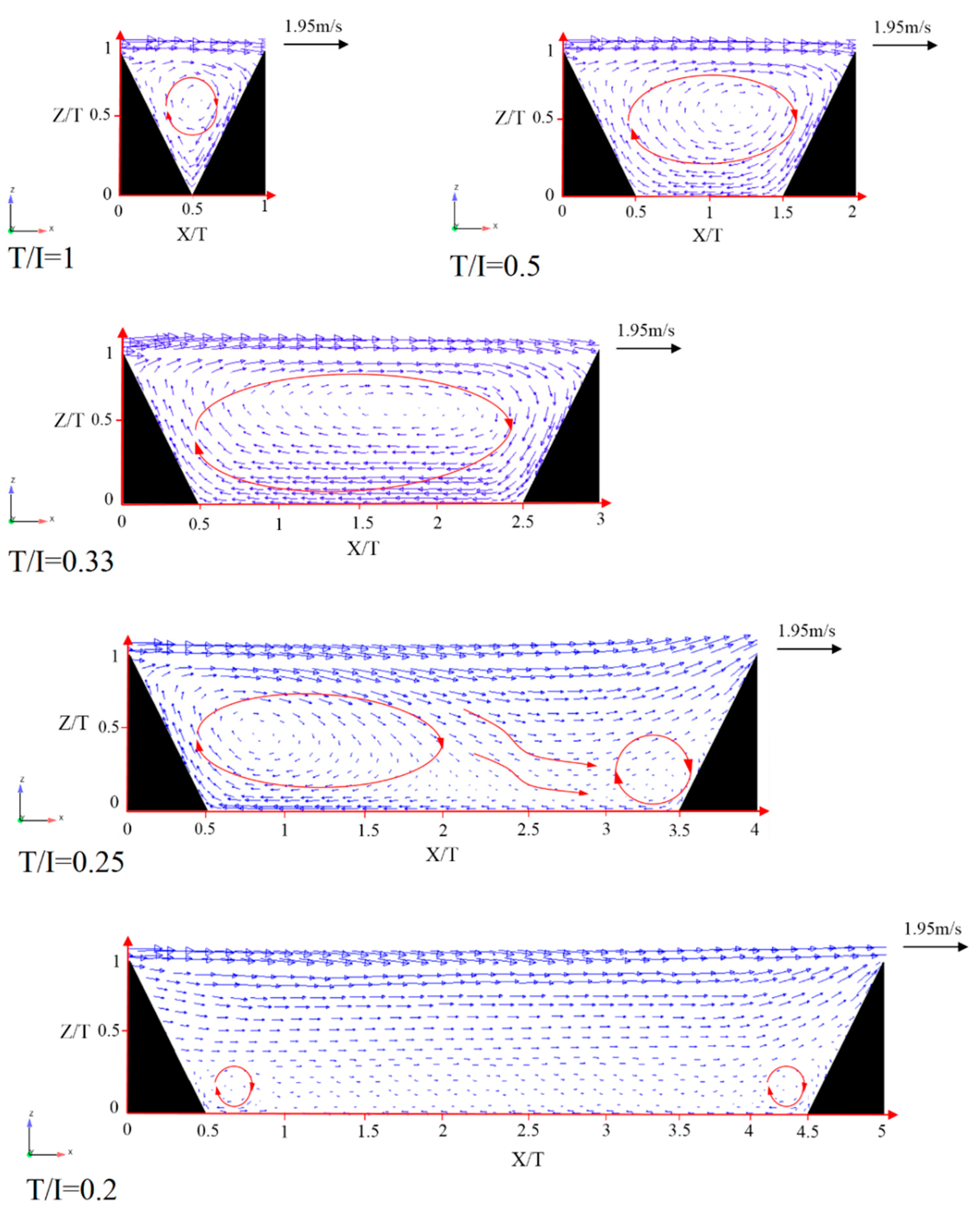
- The flow patterns in the triangular macroroughnesses in the developed and developing regions are the same with smaller areas in comparison with the smooth bed in submerged hydraulic jump conditions. The triangular macroroughnesses lead to the formation of another clockwise eddy flow in the cavity region between the macroroughnesses.
- For distances equal to T/I = 1, 0.5 and 0.33, the velocity vector distribution displays a clockwise eddy in the cavity region, where the magnitude of velocity is much smaller than the mean flow velocity. Increasing the distance between triangular macroroughnesses (T/I = 0.25 and 0.2), two eddies of different sizes are formed in the cavity region.
- When the distance between the triangular macroroughnesses is long enough, the velocity distribution has recovered by the time that the flow arrives at the next roughness. However, in the short distance, the flow arrives at the next roughness without adequate recovery of the velocity distribution. Hence, with decreasing distance between macroroughnesses, the rate of increase in the frictional coefficient decreases.
- In the triangular macroroughnesses, the maximum velocity at a specified section in the submerged jump leads to higher values than the free jump. In addition, for both types of bed (smooth and rough) in the submerged jump, the maximum velocity distance from the bed is decreased due to increasing depth and eddy flow. In the submerged jump, the boundary layer thickness is less than the free jump.
- The turbulence region on the smooth bed is created with the distance from the gate and occurs near free surface roller area, whereas on the macroroughnesses, the turbulence begins near a gate with greater intensity and limited sweep region that is the result of a counterclockwise circulating in free surface roller and clockwise eddy flow in the space between the macroroughnesses.
- The bed shear stress coefficient and energy loss of the submerged jump on the triangular macroroughnesses is larger than that found on the smooth bed that increased with the increase in inlet Froude numbers. The highest and lowest bed shear stress coefficient and energy loss occur in T/I = 0.50 and 0.20 with the increasing distance of roughness elements compared to a smooth bed.
- The reduction in the length of the jump and the submerged and tailwater depths given by the presence of triangular macroroughnesses with near-roughness elements can be used in the design of stilling basins with a resulting decrease in their size, i.e., length and height.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill University of Rhode Island: Montreal, QC, Canada, 1991. [Google Scholar]
- Launder, B.E.; Rodi, W. The turbulent wall jet. Prog. Aerosp. Sci. 1979, 19, 81–128. [Google Scholar] [CrossRef]
- McCorquodale, J.A. Hydraulic jumps and internal flows. In Encyclopedia of Fluid Mechanics; Cheremisinoff, N.P., Ed.; Golf Publishing: Houston, TX, USA, 1986; pp. 120–173. [Google Scholar]
- Federico, I.; Marrone, S.; Colagrossi, A.; Aristodemo, F.; Antuono, M. Simulating 2D open-channel flows through an SPH model. Eur. J. Mech. B Fluids 2012, 34, 35–46. [Google Scholar] [CrossRef]
- Khan, S.A. An analytical analysis of hydraulic jump in triangular channel: A proposed model. J. Inst. Eng. India Ser. A 2013, 94, 83–87. [Google Scholar] [CrossRef]
- Mortazavi, M.; Le Chenadec, V.; Moin, P.; Mani, A. Direct numerical simulation of a turbulent hydraulic jump: Turbulence statistics and air entrainment. J. Fluid Mech. 2016, 797, 60–94. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghahramanzadeh, A.; Ghaderi, A.; Joudi, A.R.; Abraham, J. Investigation of the effect of edge shape on characteristics of flow under vertical gates. J. Am. Water Works Assoc. 2016, 108, 425–432. [Google Scholar] [CrossRef]
- Azimi, H.; Shabanlou, S.; Kardar, S. Characteristics of hydraulic jump in U-shaped channels. Arab. J. Sci. Eng. 2017, 42, 3751–3760. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH numerical investigation of characteristics of hydraulic jumps. Environ. Fluid Mech. 2018, 18, 849–870. [Google Scholar] [CrossRef]
- Ead, S.A.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Tokyay, N.D. Effect of channel bed corrugations on hydraulic jumps. In Proceedings of the World Water and Environmental Resources Congress 2005, Anchorage, AK, USA, 15–19 May 2005; pp. 1–9. [Google Scholar]
- Abbaspour, A.; Dalir, A.H.; Farsadizadeh, D.; Sadraddini, A.A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Shafai-Bejestan, M.S.; Neisi, K. A new roughened bed hydraulic jump stilling basin. Asian J. Appl. Sci. 2009, 2, 436–445. [Google Scholar] [CrossRef]
- Izadjoo, F.; Shafai-Bejestan, M. Corrugated bed hydraulic jump stilling basin. J. Appl. Sci. 2007, 7, 1164–1169. [Google Scholar] [CrossRef]
- Nikmehr, S.; Aminpour, Y. Numerical Simulation of Hydraulic Jump over Rough Beds. Period. Polytech. Civil Eng. 2017, 64, 396–407. [Google Scholar] [CrossRef]
- Flow Science Inc. FLOW-3D V 11.2 User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Ghahramanzadeh, A. Characteristics of free and submerged hydraulic jumps over different macroroughnesses. J. Hydroinform. 2020, 22, 1554–1572. [Google Scholar] [CrossRef]
- Elsebaie, I.H.; Shabayek, S. Formation of hydraulic jumps on corrugated beds. Int. J. Civil Environ. Eng. IJCEE–IJENS 2010, 10, 37–47. [Google Scholar]
- Samadi-Boroujeni, H.; Ghazali, M.; Gorbani, B.; Nafchi, R.F. Effect of triangular corrugated beds on the hydraulic jump characteristics. Can. J. Civil Eng. 2013, 40, 841–847. [Google Scholar] [CrossRef]
- Ahmed, H.M.A.; El Gendy, M.; Mirdan, A.M.H.; Ali, A.A.M.; Haleem, F.S.F.A. Effect of corrugated beds on characteristics of submerged hydraulic jump. Ain Shams Eng. J. 2014, 5, 1033–1042. [Google Scholar] [CrossRef]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical simulation of hydraulic jumps. Part 2: Recent results and future outlook. Water 2019, 11, 28. [Google Scholar] [CrossRef]
- Gumus, V.; Simsek, O.; Soydan, N.G.; Akoz, M.S.; Kirkgoz, M.S. Numerical modeling of submerged hydraulic jump from a sluice gate. J. Irrig. Drain. Eng. 2016, 142, 04015037. [Google Scholar] [CrossRef]
- Jesudhas, V.; Roussinova, V.; Balachandar, R.; Barron, R. Submerged hydraulic jump study using DES. J. Hydraul. Eng. 2017, 143, 04016091. [Google Scholar] [CrossRef]
- Rajaratnam, N. The hydraulic jump as a wall jet. J. Hydraul. Div. 1965, 91, 107–132. [Google Scholar] [CrossRef]
- Hager, W.H. Energy Dissipaters and Hydraulic Jump; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1992; pp. 185–224. [Google Scholar]
- Long, D.; Steffler, P.M.; Rajaratnam, N. LDA study of flow structure in submerged Hydraulic jumps. J. Hydraul. Res. 1990, 28, 437–460. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Pourshahbaz, H.; Abbasi, S.; Pandey, M.; Pu, J.H.; Taghvaei, P.; Tofangdar, N. Morphology and hydrodynamics numerical simulation around groynes. ISH J. Hydraul. Eng. 2020, 1–9. [Google Scholar] [CrossRef]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of flow, erosion, and sedimentation pattern around varied groynes under different hydraulic and geometric conditions: A numerical study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Zhenwei, Z.; Haixia, L. Experimental investigation on the anisotropic tensorial eddy viscosity model for turbulence flow. Int. J. Heat Technol. 2016, 34, 186–190. [Google Scholar]
- Carvalho, R.; Lemos Ramo, C. Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 2008, 46, 739–752. [Google Scholar] [CrossRef]
- Bayon, A.; Valero, D.; García-Bartual, R.; López-Jiménez, P.A. Performance assessment of Open FOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A.; Akhtari, A.; Di Francesco, S. On the Effect of Block Roughness in Ogee Spillways with Flip Buckets. Fluids 2020, 5, 182. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S. CFD simulation of local scouring around airfoil-shaped bridge piers with and without collar. Sādhanā 2019, 44, 216. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Dasineh, M.; Di Francesco, S. Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs. Water 2020, 12, 1992. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of trapezoidal labyrinth shaped stepped spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef] [PubMed]
- Biscarini, C.; Di Francesco, S.; Ridolfi, E.; Manciola, P. On the simulation of floods in a narrow bending valley: The malpasset dam break case study. Water 2016, 8, 545. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Abbasi, S.; Abraham, J. Numerical analysis of the hydraulic characteristics of modified labyrinth weirs. Int. J. Energy Water Resour. 2020, 4, 425–436. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62. [Google Scholar] [CrossRef]
- Abbasi, S.; Fatemi, S.; Ghaderi, A.; Di Francesco, S. The Effect of Geometric Parameters of the Antivortex on a Triangular Labyrinth Side Weir. Water 2021, 13, 14. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 0780011–0780013. [Google Scholar]
- Khan, M.I.; Simons, R.R.; Grass, A.J. Influence of cavity flow regimes on turbulence diffusion coefficient. J. Vis. 2006, 9, 57–68. [Google Scholar] [CrossRef]
- Javanappa, S.K.; Narasimhamurthy, V.D. DNS of plane Couette flow with surface roughness. Int. J. Adv. Eng. Sci. Appl. Math. 2020, 1–13. [Google Scholar] [CrossRef]
- Nasrabadi, M.; Omid, M.H.; Farhoudi, J. Submerged hydraulic jump with sediment-laden flow. Int. J. Sediment Res. 2012, 27, 100–111. [Google Scholar] [CrossRef]
- Pourabdollah, N.; Heidarpour, M.; Abedi Koupai, J. Characteristics of free and submerged hydraulic jumps in different stilling basins. In Water Management; Thomas Telford Ltd.: London, UK, 2019; pp. 1–11. [Google Scholar]
- Rajaratnam, N. Turbulent Jets; Elsevier Science: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Aristodemo, F.; Marrone, S.; Federico, I. SPH modeling of plane jets into water bodies through an inflow/outflow algorithm. Ocean Eng. 2015, 105, 160–175. [Google Scholar] [CrossRef]
- Shekari, Y.; Javan, M.; Eghbalzadeh, A. Three-dimensional numerical study of submerged hydraulic jumps. Arab. J. Sci. Eng. 2014, 39, 6969–6981. [Google Scholar] [CrossRef]
- Khan, A.A.; Steffler, P.M. Physically based hydraulic jump model for depth-averaged computations. J. Hydraul. Eng. 1996, 122, 540–548. [Google Scholar] [CrossRef]
- De Dios, M.; Bombardelli, F.A.; García, C.M.; Liscia, S.O.; Lopardo, R.A.; Parravicini, J.A. Experimental characterization of three-dimensional flow vortical structures in submerged hydraulic jumps. J. Hydro-Environ. Res. 2017, 15, 1–12. [Google Scholar] [CrossRef]
| Reference | Shape Bed-Channel Type- Jump Type | Channel Dimension (m) | Roughness (mm) | Fr1 | Investigated Flow Properties |
|---|---|---|---|---|---|
| Ead and Rajaratnam [10] |
| CL1 = 7.60 CW2 = 0.44 CH3 = 0.60 |
| 4–10 |
|
| Tokyay et al. [11] |
| CL = 10.50 CW = 0.253 CH = 0.432 |
| 5–12 |
|
| Izadjoo and Shafai-Bejestan [14] |
| CL = 1.2, 9 CW = 0.25, 0.50 CH = 0.40 | Baffle with trapezoidal cross section (RH: 13 and 26) | 6–12 |
|
| Abbaspour et al. [12] |
| CL = 10 CW = 0.25 CH = 0.50 |
| 3.80–8.60 |
|
| Shafai-Bejestan and Neisi [13] |
| CL = 7.50 CW = 0.35 CH = 0.50 | Lozenge bed | 4.50–12 |
|
| Elsebaie and Shabayek [18] |
| CL = 9 CW = 0.295 CH = 0.32 |
| 50 |
|
| Samadi-Boroujeni et al. [19] |
| CL = 12 CW = 0.40 CH = 0.40 |
| 6.10–13.10 |
|
| Ahmed et al. [20] |
| CL = 24.50 CW = 0.75 CH = 0.70 |
| 1.68–9.29 |
|
| Nikmehr and Aminpour [15] |
| CL = 12 CW = 0.25 CH = 0.50 |
| 5.01–13.70 |
|
| Ghaderi et al. [17] |
| CL = 4.50 CW = 0.75 CH = 0.70 |
| 1.70–9.30 |
|
| Present study | Rectangular channel Smooth and rough beds Submerged jump | CL = 4.50 CW = 0.75 CH = 0.70 |
| 1.70–9.30 |
|
| Bed Type | Q (l/s) | I (cm) | T (cm) | d (cm) | y1 (cm) | y4 (cm) | Fr1= u1/(gy1)0.5 | S | Re1= (u1y1)/υ |
|---|---|---|---|---|---|---|---|---|---|
| Smooth | 30, 45 | - | - | 5 | 1.62–3.83 | 9.64–32.10 | 1.7–9.3 | 0.26–0.50 | 39,884–59,825 |
| Triangular macroroughnesses | 30, 45 | 4, 8, 12, 16, 20 | 4 | 5 | 1.62–3.84 | 6.82–30.08 | 1.7–9.3 | 0.21–0.44 | 39,884–59,825 |
| Models | Bed Type | Q (l/s) | d (cm) | y1 (cm) | u1 (m/s) | Fr1 |
|---|---|---|---|---|---|---|
| Numerical and Physical | Smooth | 45 | 5 | 1.62–3.83 | 1.04–3.70 | 1.7–9.3 |
| T/I = 0.5 | 45 | 5 | 1.61–3.83 | 1.05–3.71 | 1.7–9.3 | |
| T/I = 0.25 | 45 | 5 | 1.60–3.84 | 1.04–3.71 | 1.7–9.3 |
| Mesh | Nested Block Cell Size (cm) | Containing Block Cell Size (cm) |
|---|---|---|
| 1 | 0.55 | 1.10 |
| 2 | 0.65 | 1.30 |
| 3 | 0.85 | 1.70 |
| Parameters | Amounts |
|---|---|
| fs1 (-) | 7.15 |
| fs2 (-) | 6.88 |
| fs3 (-) | 6.19 |
| K (-) | 5.61 |
| E32 (%) | 10.02 |
| E21 (%) | 3.77 |
| GCI21 (%) | 3.03 |
| GCI32 (%) | 3.57 |
| GCI32/rp GCI21 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Aricò, C. Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water 2021, 13, 674. https://doi.org/10.3390/w13050674
Ghaderi A, Dasineh M, Aristodemo F, Aricò C. Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water. 2021; 13(5):674. https://doi.org/10.3390/w13050674
Chicago/Turabian StyleGhaderi, Amir, Mehdi Dasineh, Francesco Aristodemo, and Costanza Aricò. 2021. "Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses" Water 13, no. 5: 674. https://doi.org/10.3390/w13050674
APA StyleGhaderi, A., Dasineh, M., Aristodemo, F., & Aricò, C. (2021). Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water, 13(5), 674. https://doi.org/10.3390/w13050674









