Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations
Abstract
1. Introduction
2. Methodology
2.1. 2D Shallow Water Equations
2.2. 3D Navier Stokes Equations
3. Result and Discussion
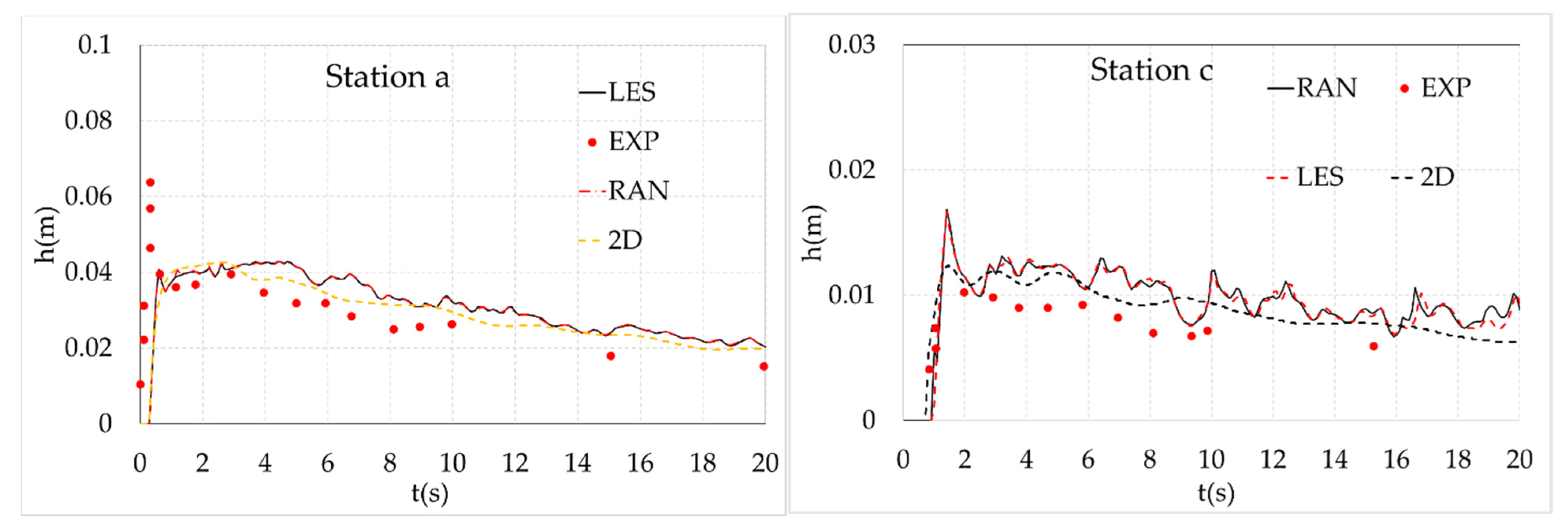
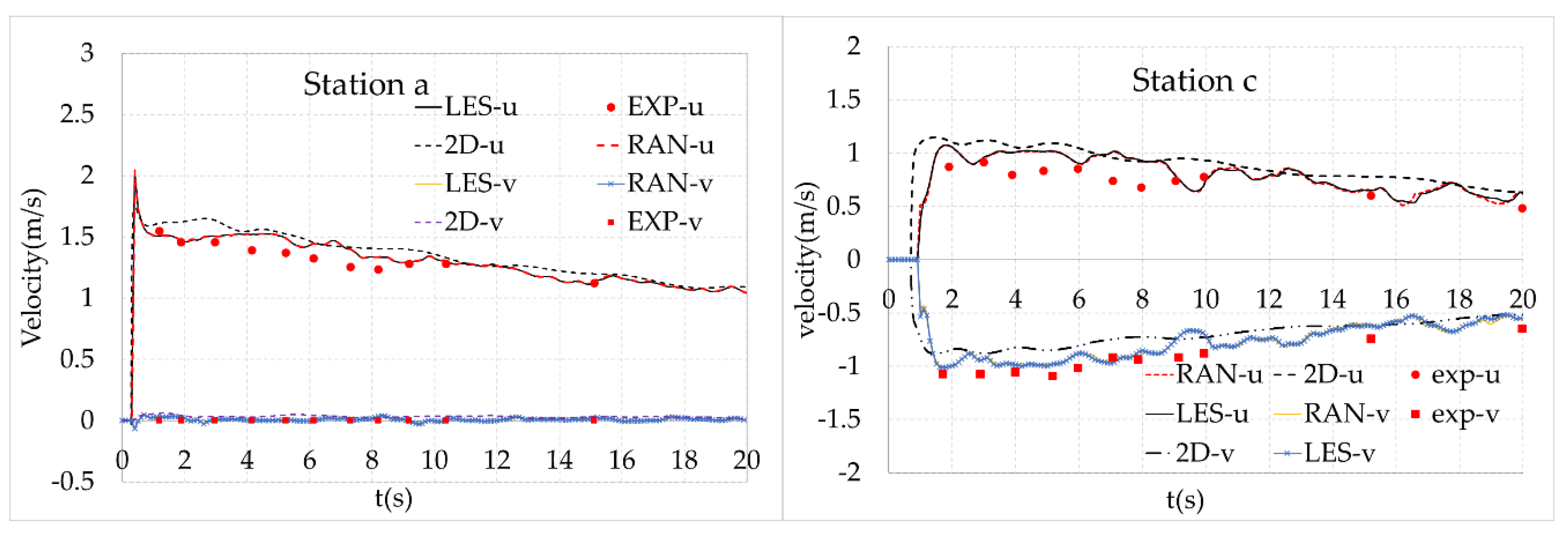
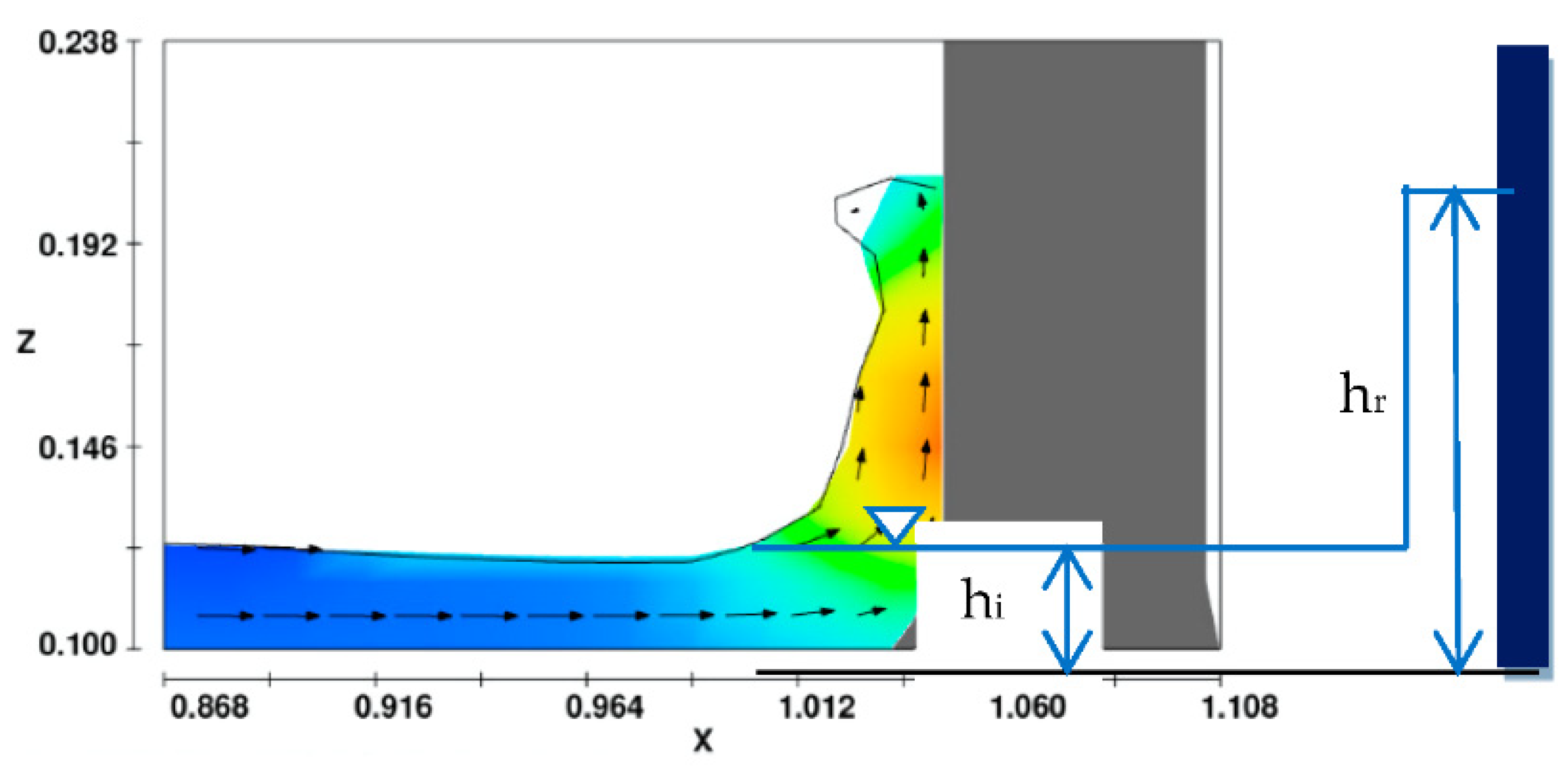
3.1. Dam-Break Wave on an Obstruction
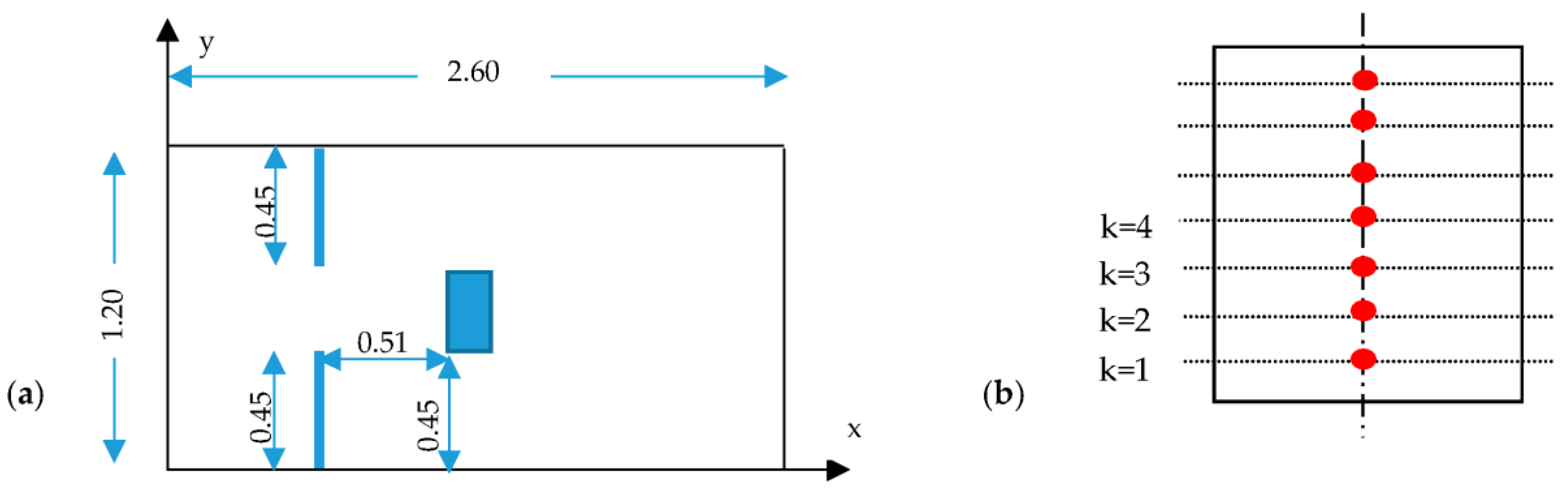
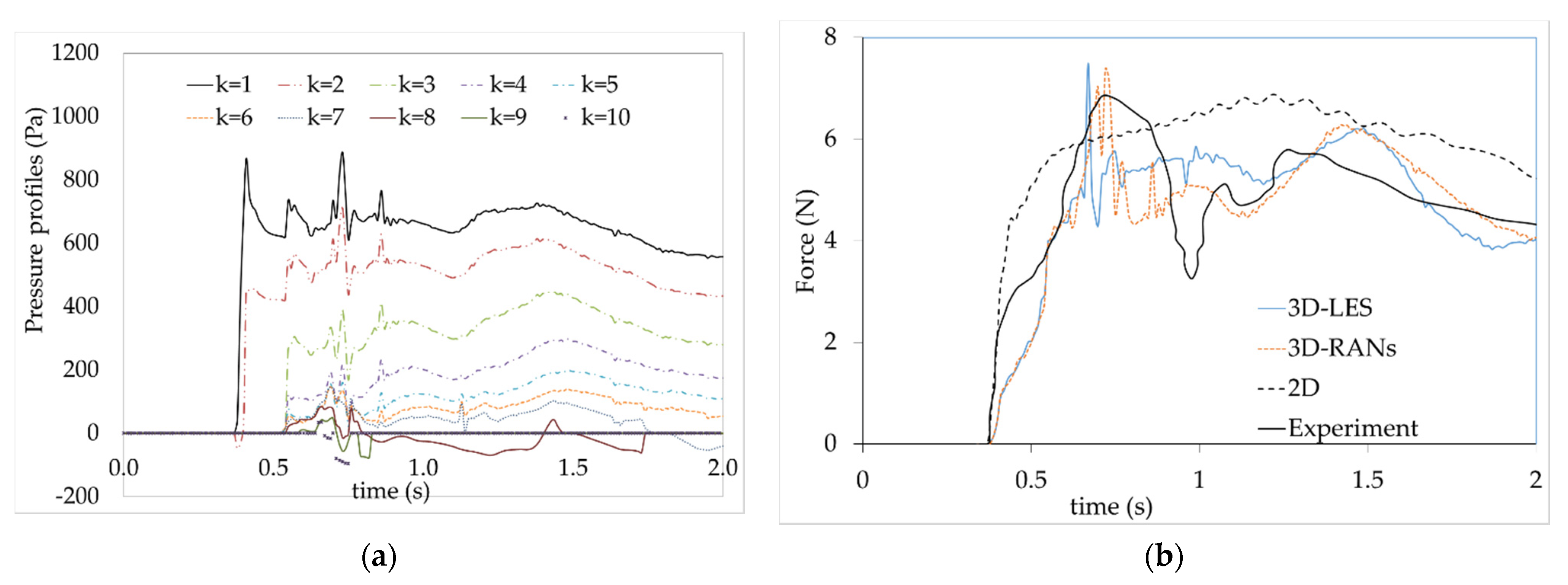
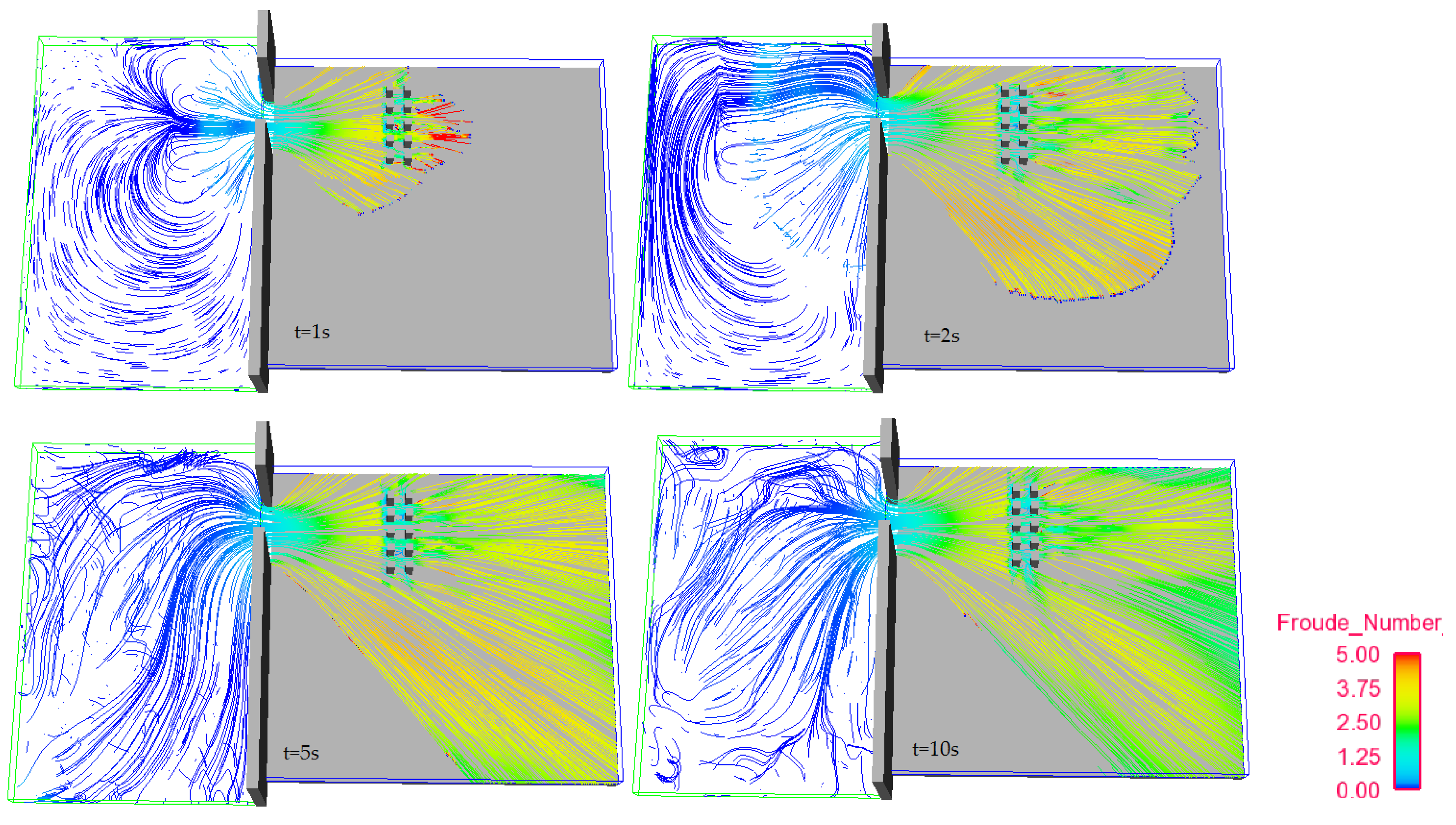
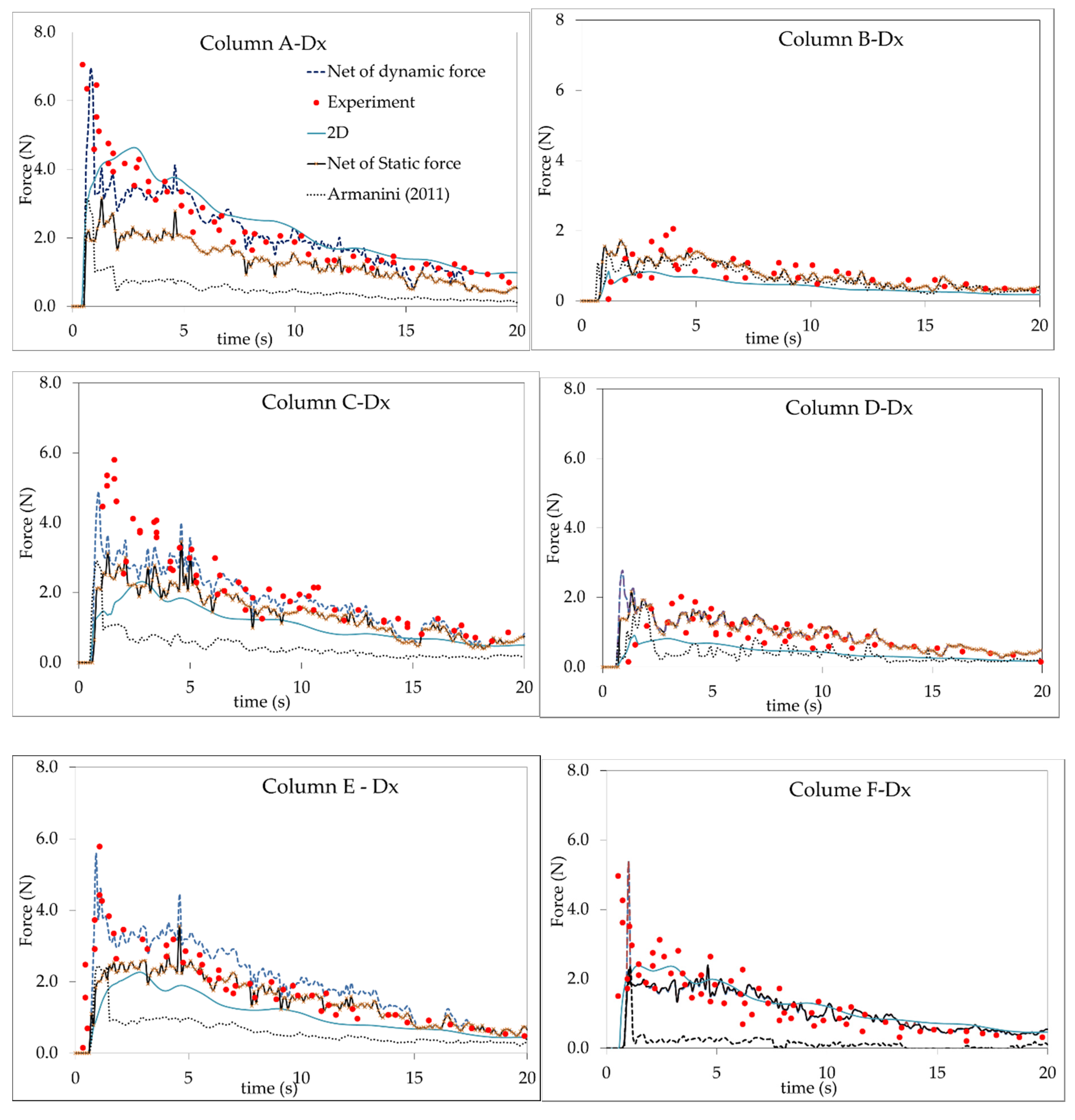
3.2. Force Due to Dam-Break Wave on a Group of Structures
- a
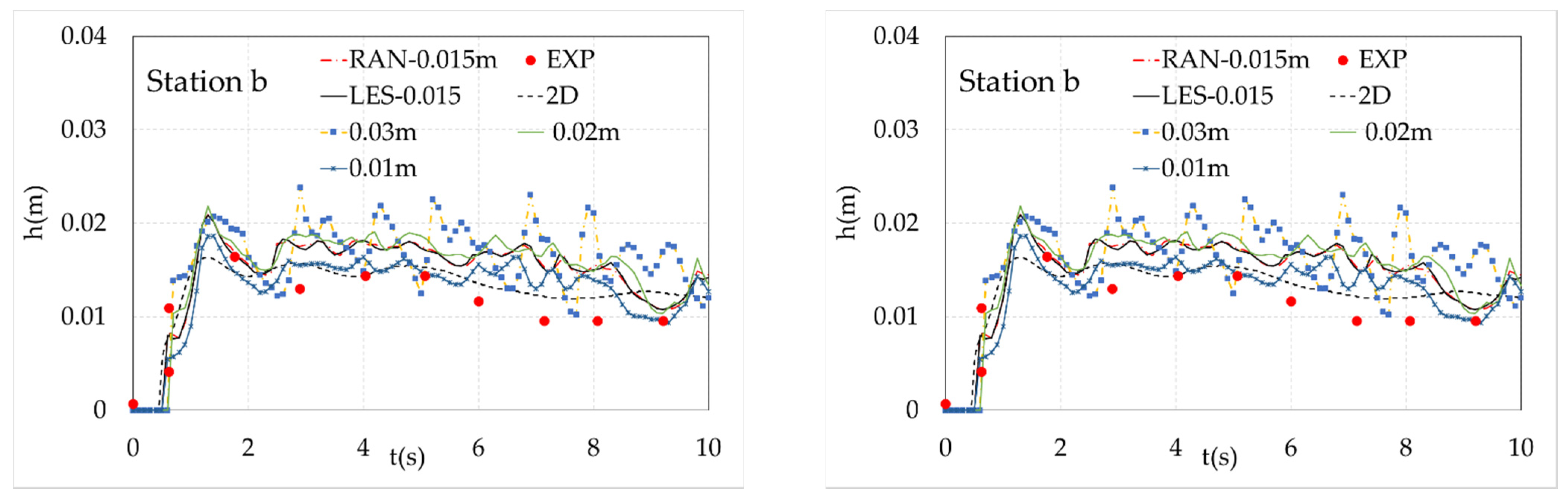
- Mesh sensitivity analysis
- b
- Forces acting on groups of building
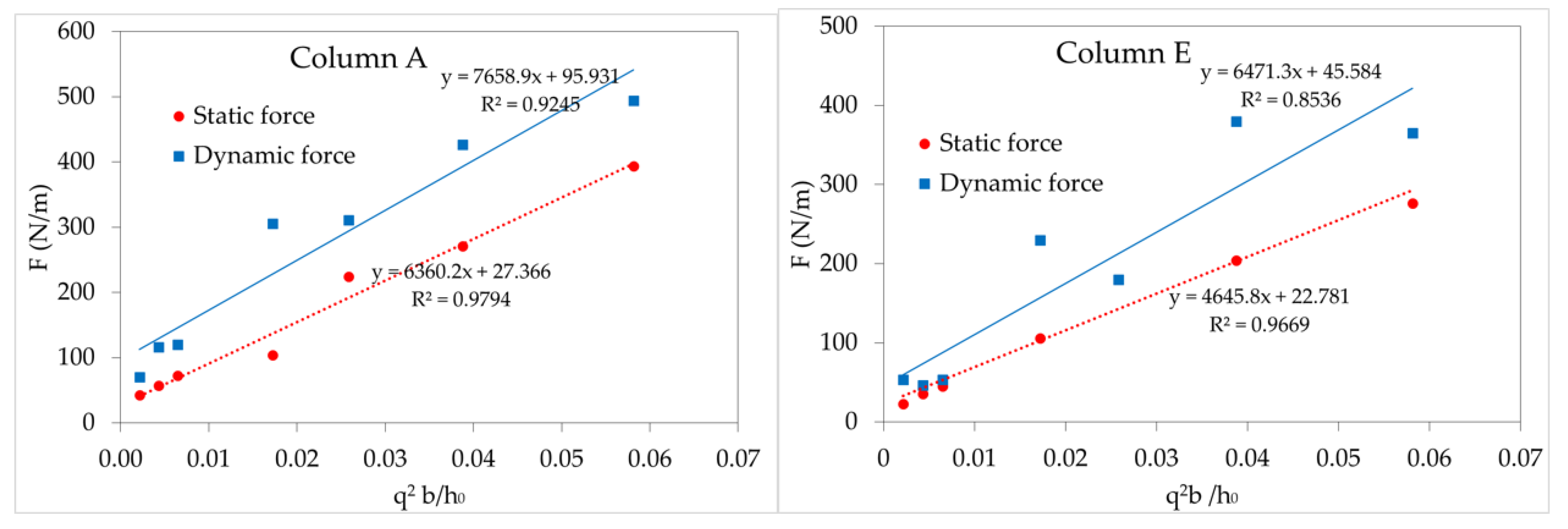
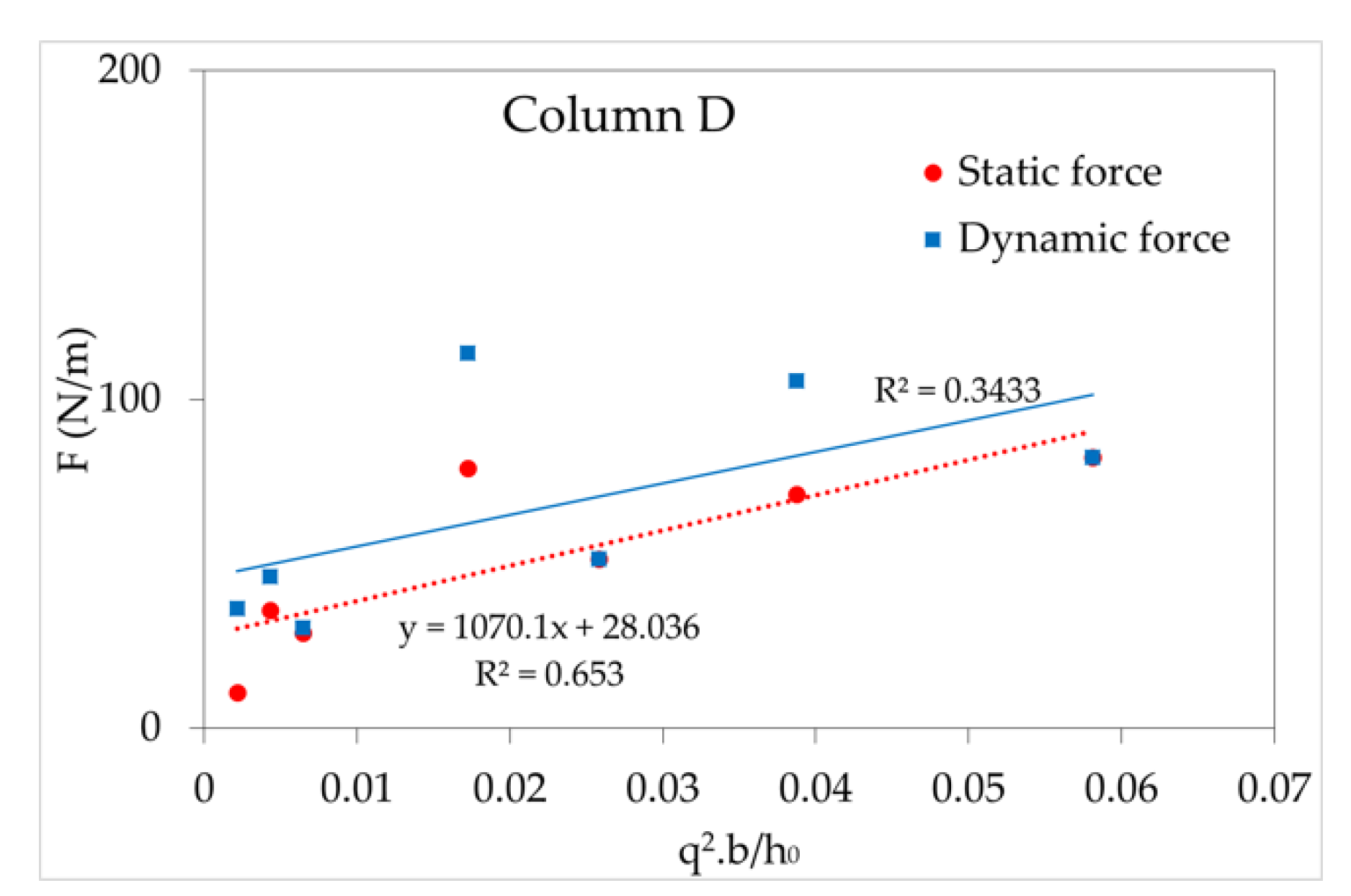
3.3. Effect of Dam-Break Width and Initial Water Level on Static Force and Dynamic Force Against Structures
4. Conclusions
- (1)
- To formulate water depth or velocity profiles, both 2D and 3D numerical solutions are quite similar. The proposed 2D numerical model is suitable for predicting hydraulic characteristics involving water depth and a velocity component as well as the maximum value of the static force. However, the 3D hydrodynamic model with the LES and RANs turbulent modules can well capture two peaks of impact load while the 2D shallow flow model presents only one. In general, the 3D result is closer to the experimental one.
- (2)
- Both the static and dynamic forces against several buildings were computed by Flow 3D with the LES module. The role of velocity-induced force and pressure force on a building varies with location. Near the damsite, the velocity-induced force is more prevalent while away from main direction of dam-break wave or in the second array the pressure force is the more important. The impact of velocity-induced force is quantified by parameter α, which is carried out as a function of the Froude number and water depth of the incident wave. The linear regression relation between q2b/h0 and the peak intensity of the static force and dynamic force is worked out with reasonable R-square quantities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Testa, G.; Zuccala, D.; Alcrudo, F.; Mulet, J.; Frazao, S.S. Flash flood flow experiment in a simplifed urban district. J. Hydraul. Res. 2007, 45, 37–44. [Google Scholar] [CrossRef]
- Soares-Frazao, S.; Zech, Y. Dam-break flow through an idealized city. J. Hydraul. Res. 2008, 46, 648–665. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Zech, Y. Experimental study of dam-break flow against an isolated obstacle. J. Hydraul. Res. 2007, 45, 27–36. [Google Scholar] [CrossRef]
- Soares-Frazão, S. Experiments of dam-break wave over a triangular bottom sill. J. Hydraul. Res. 2007, 45, 19–26. [Google Scholar] [CrossRef]
- di Cristo, C.; Evangelista, S.; Greco, M.; Iervolino, M.; Leopardi, A.; Vacca, A. Dam-break waves over an erodible embankment: Experiments and simulations. J. Hydraul. Res. 2018, 56, 196–210. [Google Scholar] [CrossRef]
- Evangelista, S. Experiments and numerical simulations of dike erosion due to a wave impact. Water 2015, 7, 5831–5848. [Google Scholar] [CrossRef]
- Li, Y.L.; Yu, C.H. Research on dam break flow induced front wave impacting a vertical wall based on the CLSVOF and level set methods. Ocean Eng. 2019, 178, 442–462. [Google Scholar] [CrossRef]
- Özgen, I.; Zhao, J.; Liang, D.; Hinkelmann, R. Urban flood modeling using shallow water equations with depth-dependent anisotropic porosity. J. Hydrol. 2016, 541, 1165–1184. [Google Scholar] [CrossRef]
- Mignot, E.; Li, X.; Dewals, B. Experimental modelling of urban flooding: A review. J. Hydrol. 2019, 568, 334–342. [Google Scholar] [CrossRef]
- Aureli, F.; Dazzi, A.; Maranzoni, A.; Mignosa, P.; Vacondio, R. Experimental and numerical evaluation of the force due to the impact of a dam break wave on a structure. Adv. Water Resour. 2015, 76, 29–42. [Google Scholar] [CrossRef]
- Milanesi, L.; Pilotti, M.; Belleri, A.; Marini, A.; Fuchs, S. Vulnerability to flash floods: A simplified structural model for masonry buldings. Water Resour. Res. 2018, 54, 7177–7197. [Google Scholar] [CrossRef]
- Shige-eda, M.; Akiyama, J. Numerical and experimental study on two dimensional flood flows with and without structures. J. Hydraul. Eng. 2003, 129, 817–821. [Google Scholar] [CrossRef]
- Cagatay, H.O.; Kocaman, S. Dam break flows during initial stage using SWE and RANs approaches. J. Hydraul. Res. 2010, 48, 603–611. [Google Scholar] [CrossRef]
- Yang, S.; Yang, W.; Qin, S.; Li, Q.; Yang, B. Numerical study on characteristics of dam break wave. Ocean Eng. 2018, 159, 358–371. [Google Scholar] [CrossRef]
- Robb., D.M.; Vasquez., J.A. Numerical simulation of dam break flows using depth averaged hydrodynamic and three dimensional CFD models. In Proceedings of the 22nd Canadian Hydrotechnical Conference, Ottawa, ON, Canada, 28–30 April 2015. [Google Scholar]
- Kocaman, S.; Evangelista, S.; Viccione, G.; Guzel, H. Experimental and Numerical analysis of 3D dam break waves in an enclosed domain with a single oriented obstacles. Environ. Sci. Proc. 2020, 2, 35. [Google Scholar] [CrossRef]
- Issakhov, A.; Zhandaulet, Y.; Nogaeva, A. Numerical simulation of dambreak flow for various forms of the obstacle by VOF method. Int. J. Multiph. Flow 2018, 109, 191–206. [Google Scholar] [CrossRef]
- Mokarani, C.; Abadie, S. Conditions for peak pressure stability in VOF simulations of dam break flow impact. J. Fluids Struct. 2016, 62, 86–103. [Google Scholar] [CrossRef]
- Liu, L.; Sun, J.; Lin, B.; Lu, L. Building performance in dam break flow—an experimental sudy. Urban Water J. 2018, 15, 251–258. [Google Scholar] [CrossRef]
- Armanini, A.; Larcher, M.; Odorizzi, M. Dynamic impact of a debris flow front against a vertical wall. In Proceedings of the 5th international conference on debris-flow hazards mitigation: Mechanics, prediction and assessment, Padua, Italy, 14–17 June 2011. [Google Scholar] [CrossRef]
- Hubbard, M.E.; Garcia Navarro, P. Flux difference splitting and the balancing of source terms and flux gradients. J. Comput. Phys. 2000, 165, 89–125. [Google Scholar] [CrossRef]
- Roe, P.L. A basis for upwind differencing of the two-dimensional unsteady Euler equations. In Numerical Methods in Fluids Dynamics II; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Bradford, S.F.; Sander, B. Finite volume model for shallow water flooding of arbitrary topography. J. Hydraul. Eng. (ASCE) 2002, 128, 289–298. [Google Scholar] [CrossRef]
- Brufau, P.; Garica-Navarro, P. Two dimensional dam break flow simulation. Int. J. Numer. Meth. Fluids 2000, 33, 35–57. [Google Scholar] [CrossRef]
- Hien, L.T.T. 2D Numerical Modeling of Dam-Break Flows with Application to Case Studies in Vietnam. Ph.D. Thesis, Brescia University, Brescia, Italy, 2014. [Google Scholar]
- Hien, L.T.T.; Tomirotti, M. Numerical modeling of dam break flows over complex topography. Case studies in Vietnam. In Proceedings of the 19th IAHR-APD Congress 2014, Hanoi, Vietnam, 21–24 September 2014; ISBN 978-604-82-1383-1. [Google Scholar]
- Flow-3D, Version 12.0; User Mannual; Flow Science Inc.: Santa Fe, NM, USA, 2020.
- Guney, M.S.; Tayfur, G.; Bombar, G.; Elci, S. Distorted physical model to study sudden partial dam break flow in an urban area. J. Hydraul. Eng. 2014, 140, 05014006. [Google Scholar] [CrossRef]
- Shige-eda, M.; Akiyama, J. Discussion and Closure to “Numerical and experimental study on two dimensional flood flows with and without structures” by Mirei Shige-eda and Juichiro Akiyama. J. Hydraul. Eng. 2005, 131, 336–337. [Google Scholar] [CrossRef]
- Ritter, A. Die Fortpflanzung der Wasserwelle (Generation of the water wave). Z. Ver. Dtsch. Ing. 1892, 36, 947–954. [Google Scholar]

| Gauges | X | Grid Sizes and Models | ||||
|---|---|---|---|---|---|---|
| 3D Model | 2D Model | |||||
| 0.01 m | 0.015 m | 0.02 m | 0.03 m | 0.01 m | ||
| a | h | 0.445 | 0.449 | 0.449 | 0.457 | 0.441 |
| u | 0.155 | 0.201 | 0.224 | 0.251 | 0.317 | |
| v | 0.277 | 0.277 | 0.294 | 0.407 | 0.454 | |
| b | h | 0.264 | 0.345 | 0.438 | 0.619 | 0.697 |
| u | 0.126 | 0.183 | 0.133 | 0.234 | 0.221 | |
| v | 0.311 | 0.248 | 0.213 | 0.443 | 0.242 | |
| Case | Initial Water Level (h0) (m) | Damsite Width (b) (m) |
|---|---|---|
| 1 | 0.2 | 0.25 |
| 2 | 0.2 | 0.50 |
| 3 | 0.4 | 0.50 |
| 4 | 0.2 | 0.75 |
| 5 | 0.6 | 0.50 |
| 6 | 0.4 | 0.75 |
| 7 | 0.6 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hien, L.T.T.; Van Chien, N. Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations. Water 2021, 13, 344. https://doi.org/10.3390/w13030344
Hien LTT, Van Chien N. Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations. Water. 2021; 13(3):344. https://doi.org/10.3390/w13030344
Chicago/Turabian StyleHien, Le Thi Thu, and Nguyen Van Chien. 2021. "Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations" Water 13, no. 3: 344. https://doi.org/10.3390/w13030344
APA StyleHien, L. T. T., & Van Chien, N. (2021). Investigate Impact Force of Dam-Break Flow against Structures by Both 2D and 3D Numerical Simulations. Water, 13(3), 344. https://doi.org/10.3390/w13030344






