Conceptual Model Modification and the Millennium Drought of Southeastern Australia
Abstract
:1. Introduction
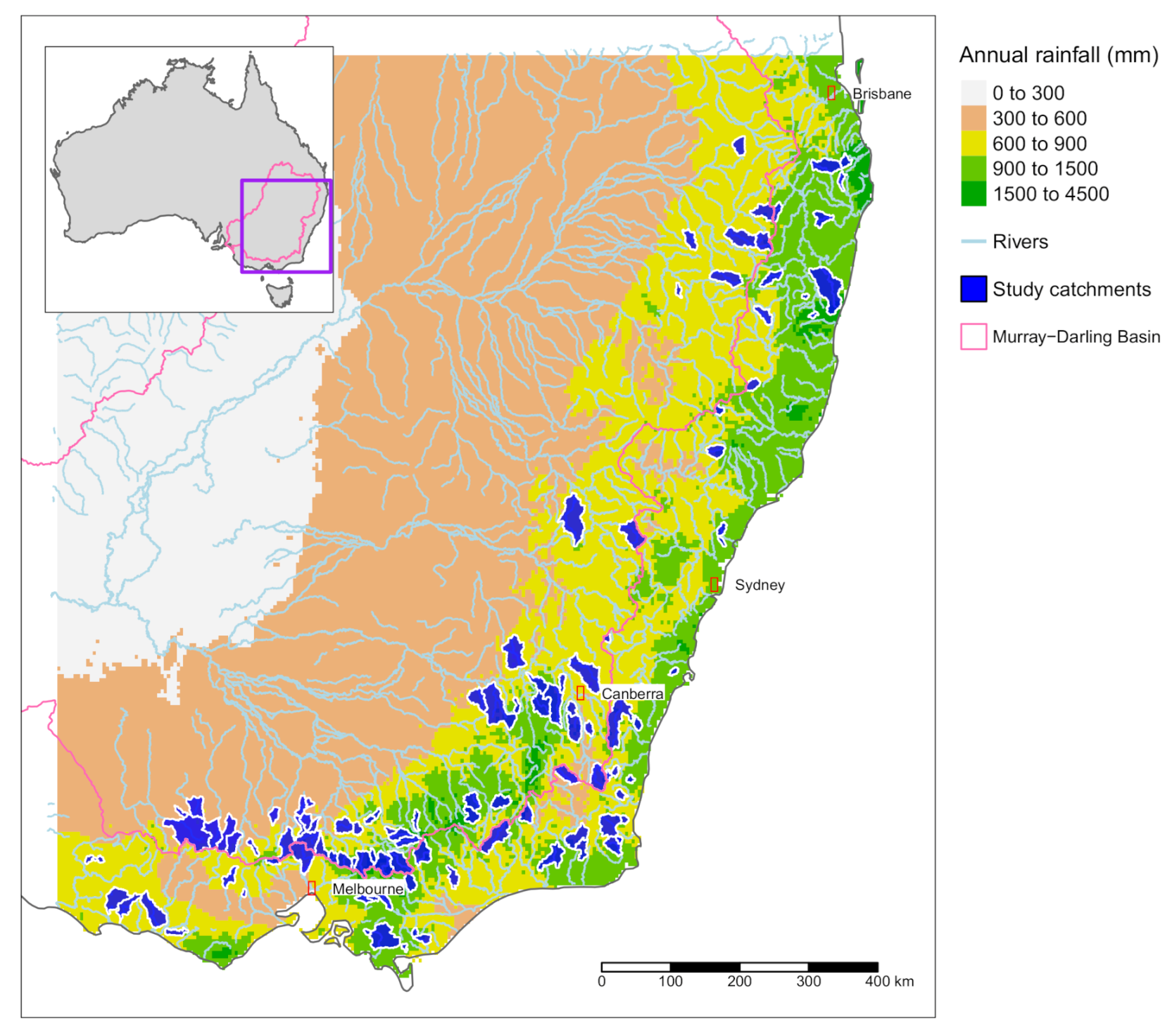
2. Site Information
3. Method
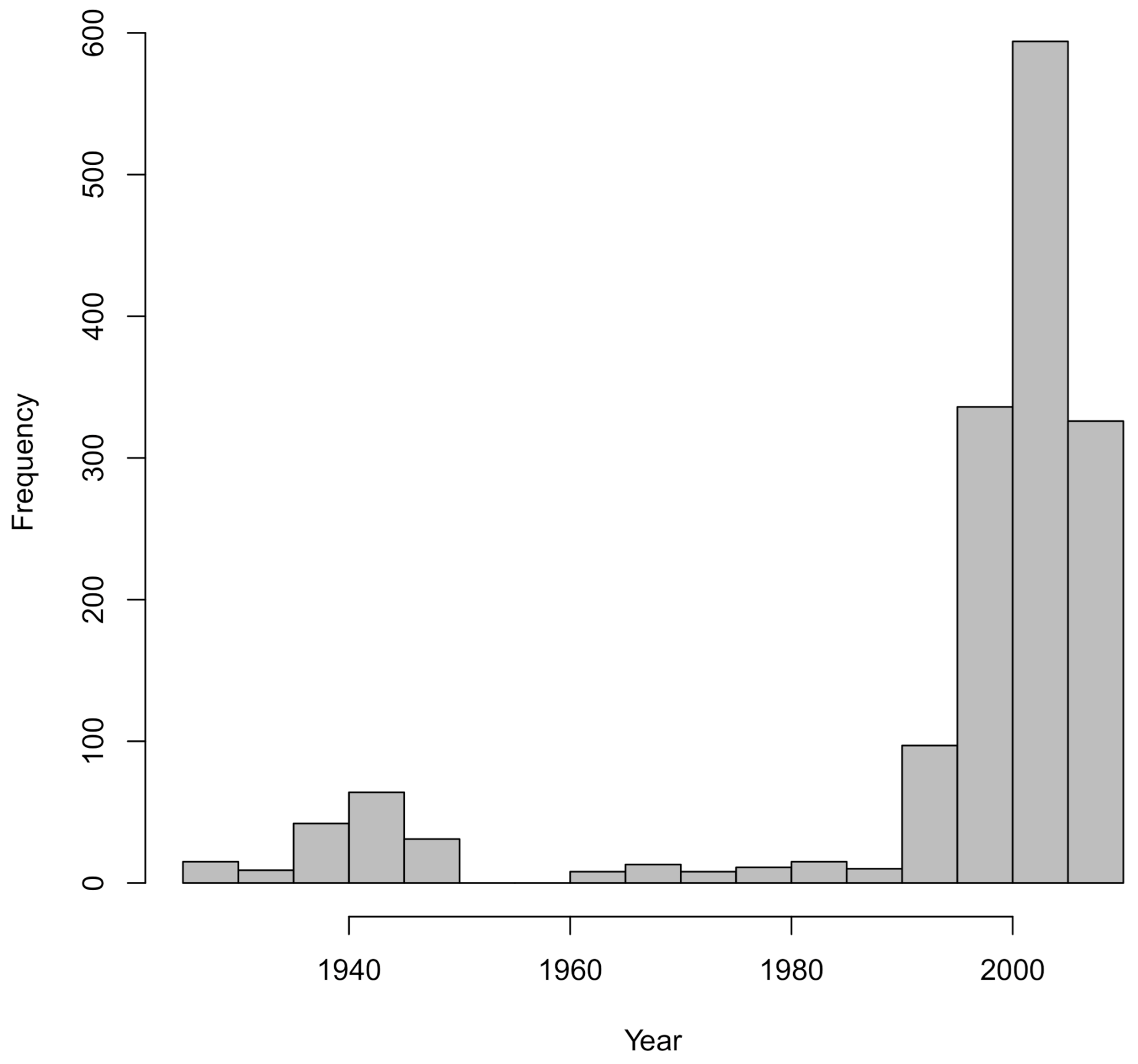
3.1. Drought Classification
- there was a year with a positive anomaly >15% of the mean, in which case the end year is set to the year prior to that year;
- if the last two years have slightly positive anomalies (but each <15% of the mean), in which case the end year is set to the first year of positive anomaly
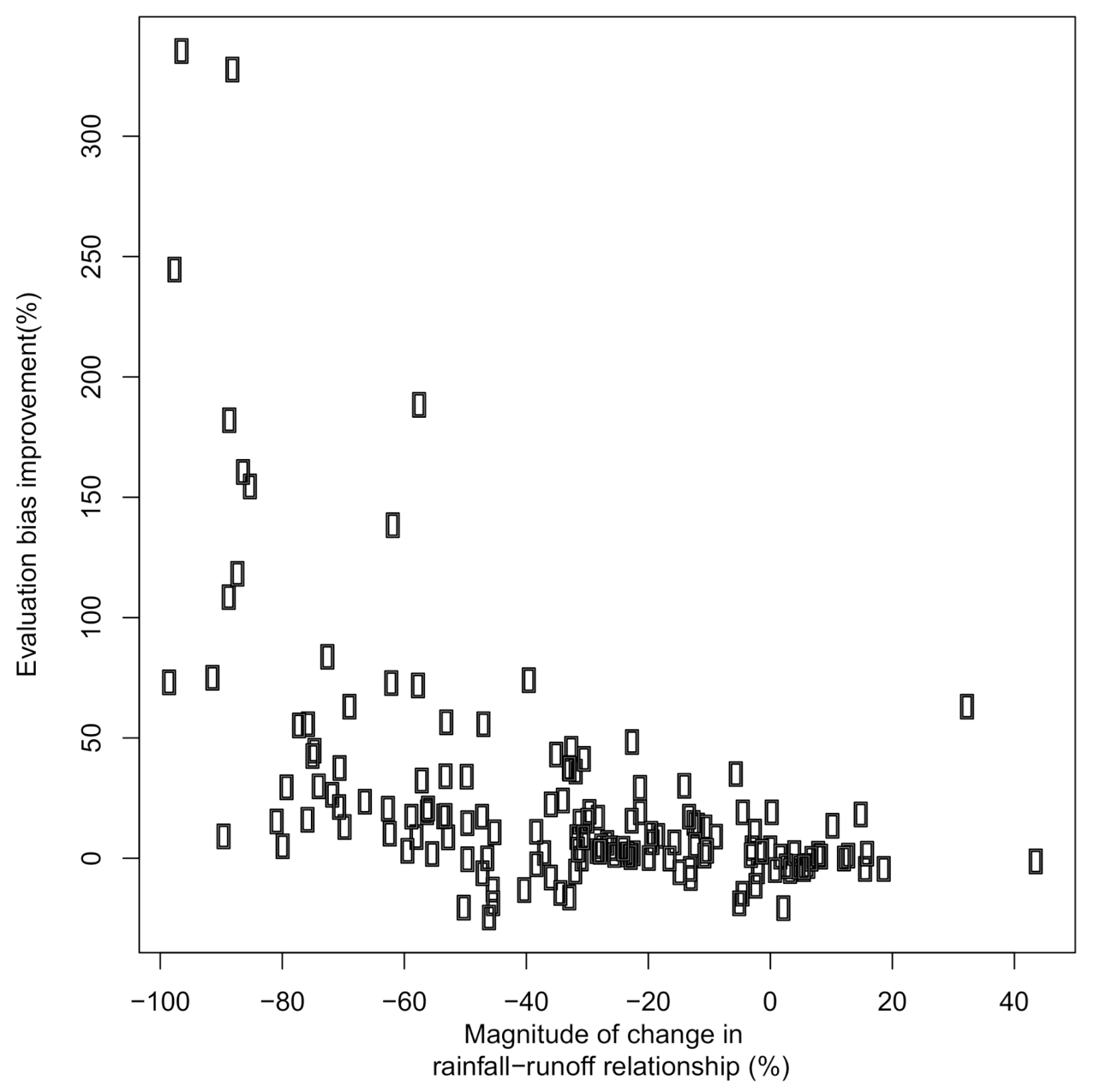
3.2. Magnitude of Change in Rainfall–Runoff Relationship Due to Drought
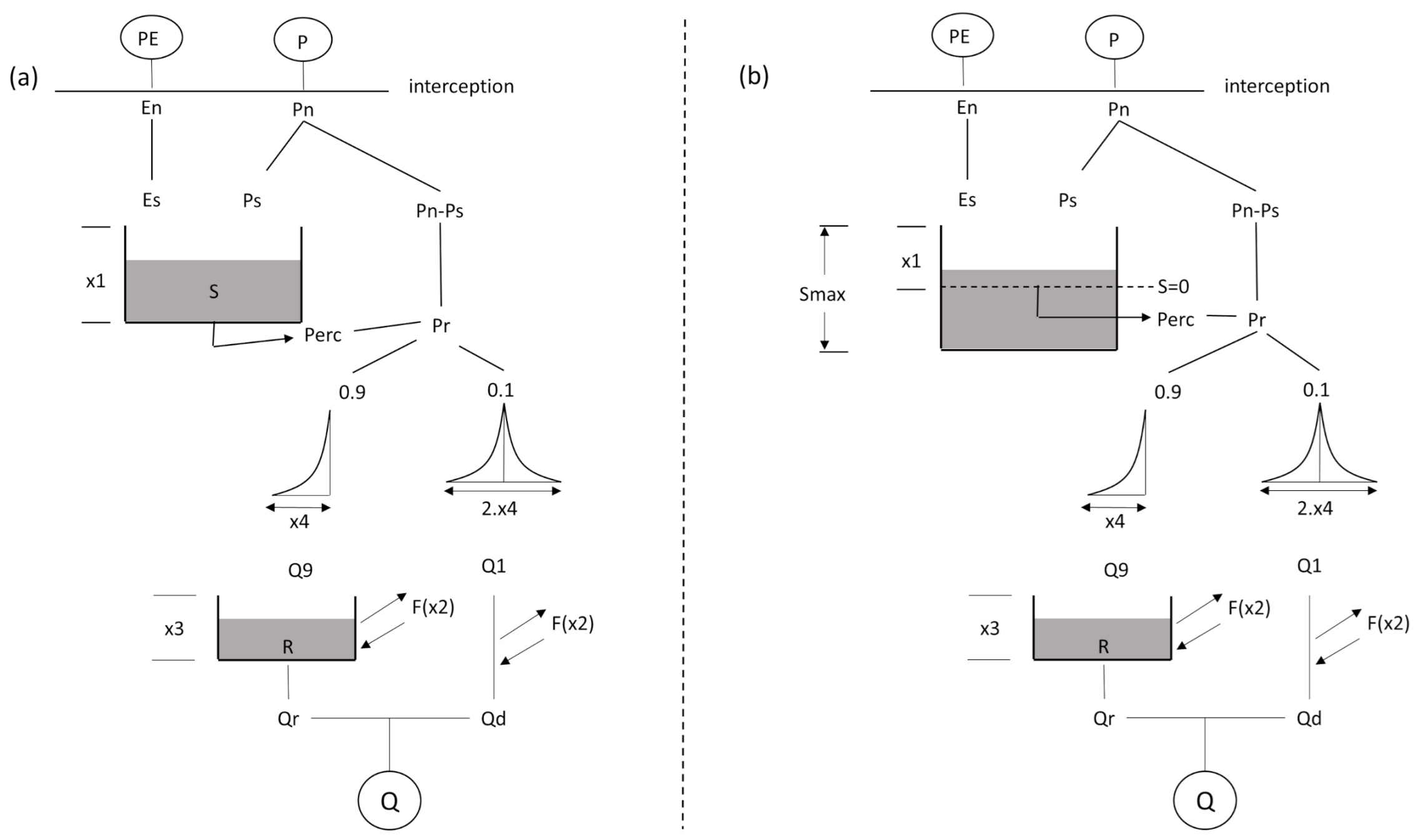
3.3. Model Framework
3.4. Model Calibration
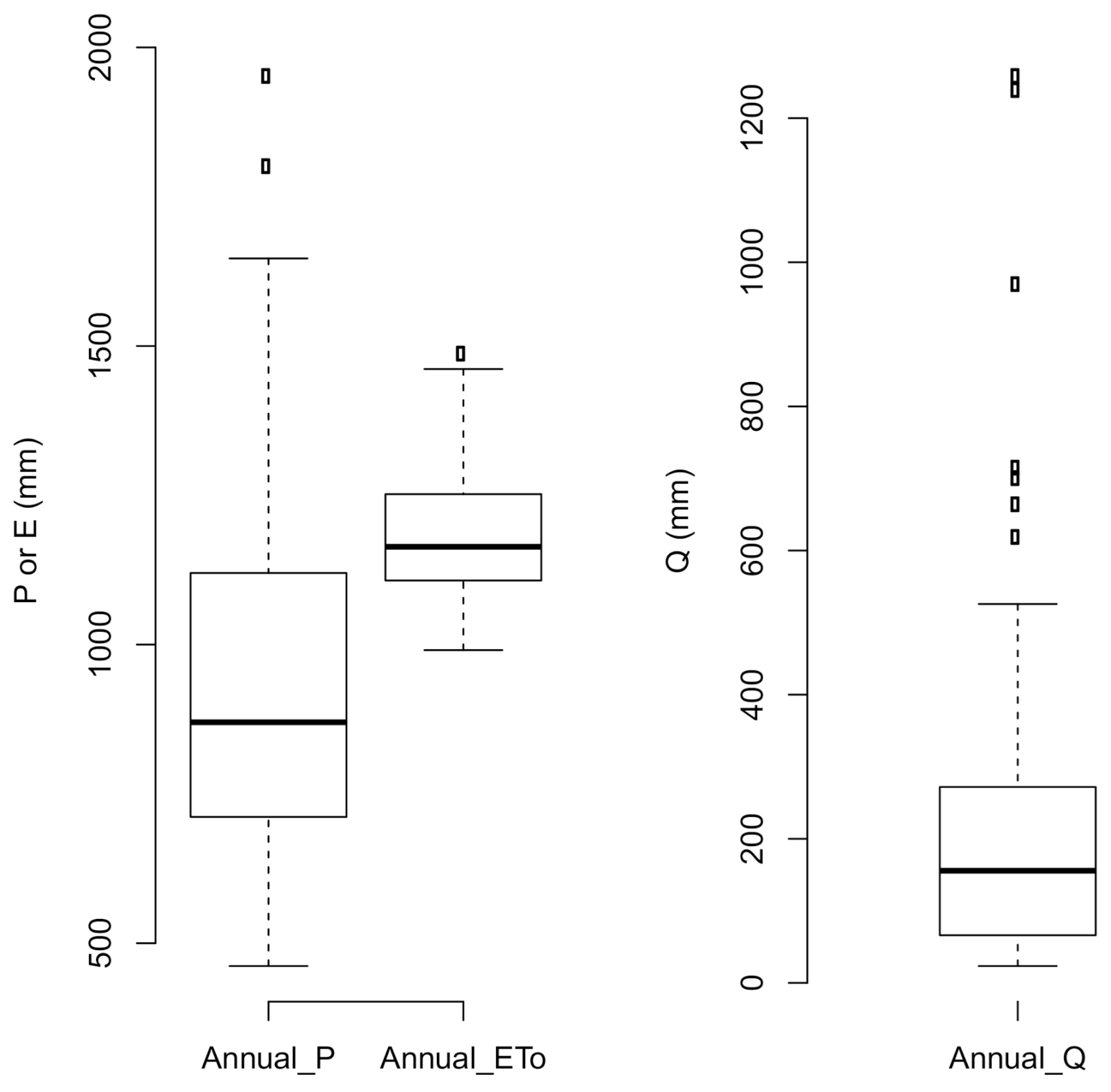
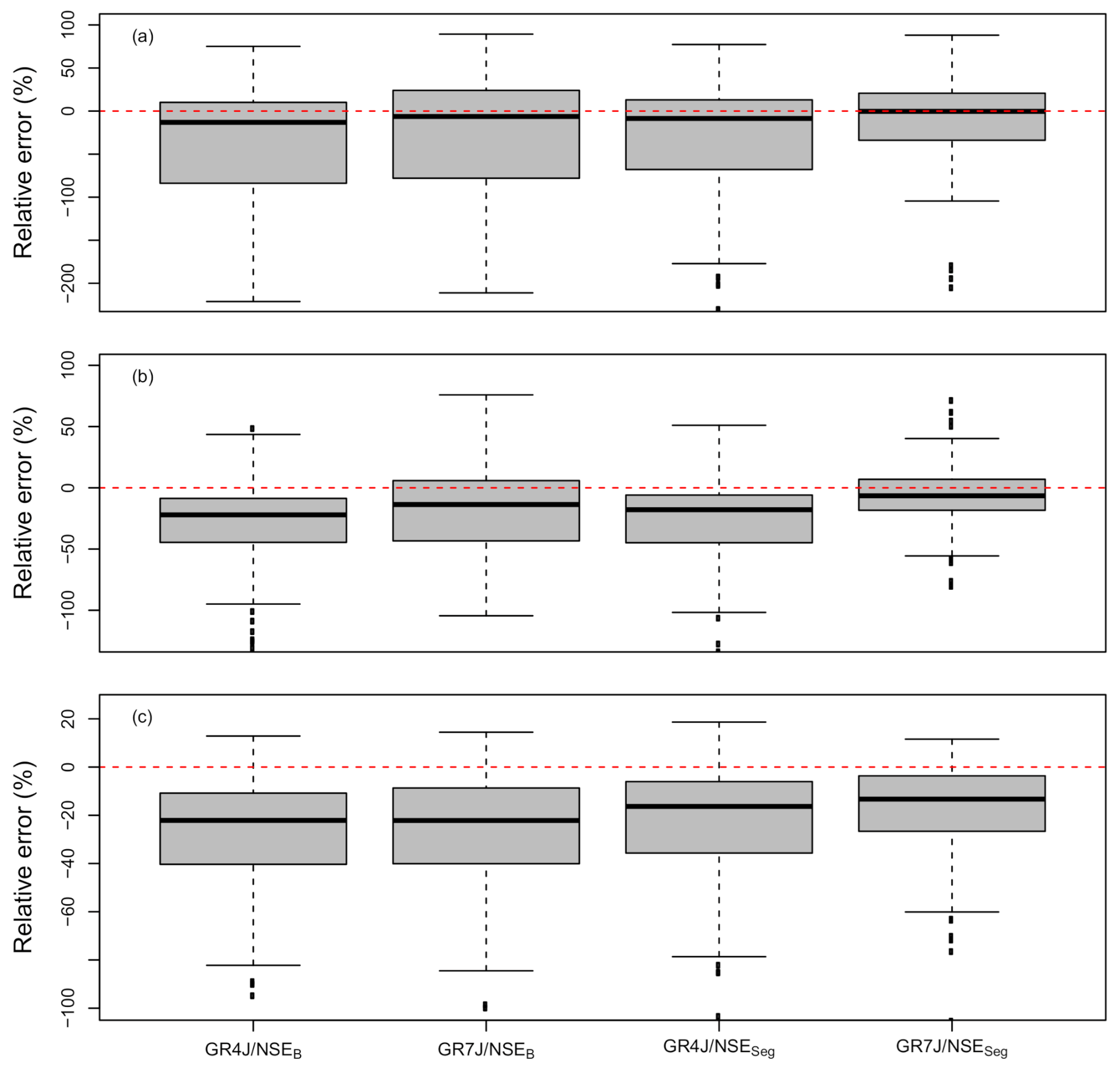
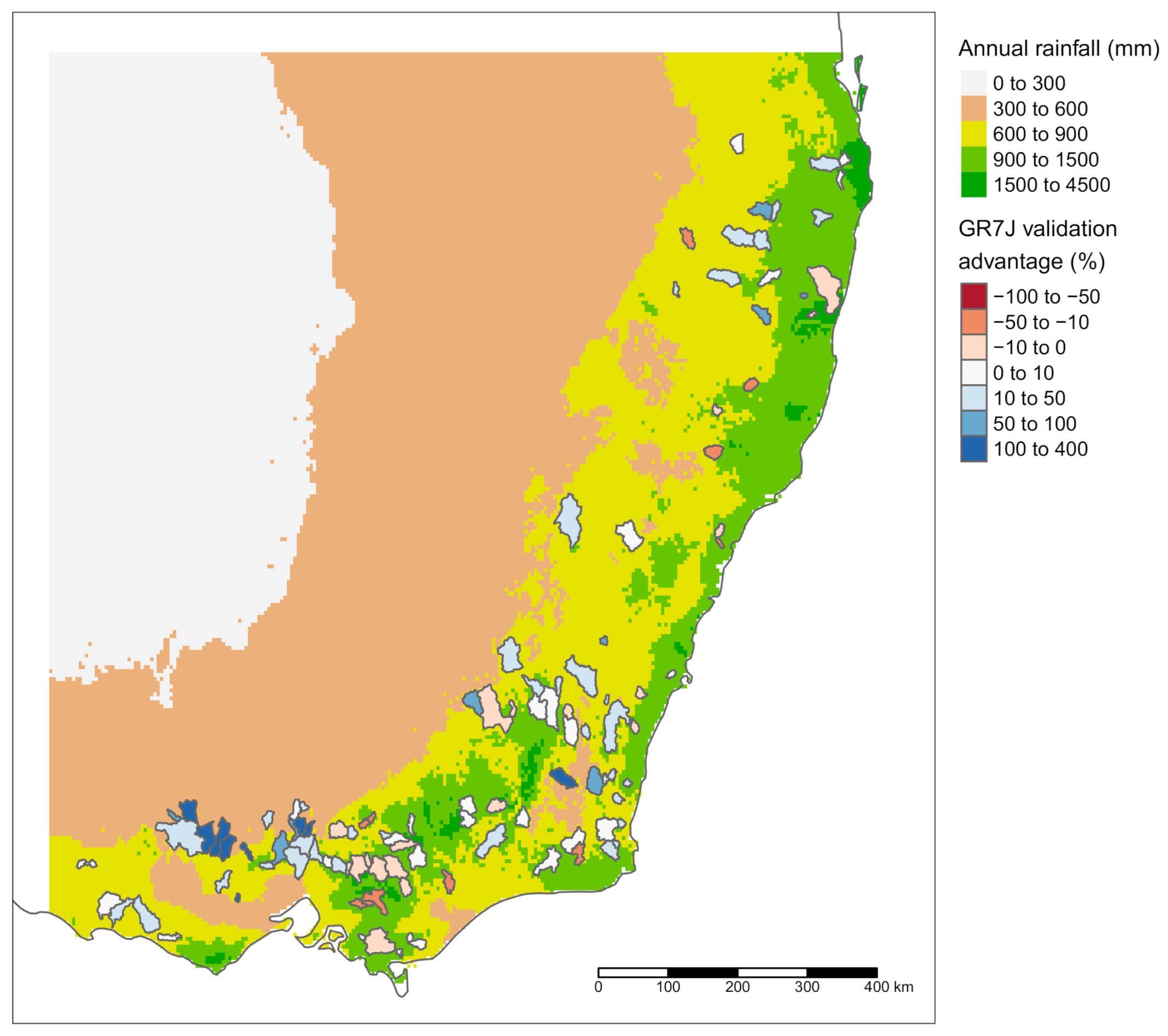
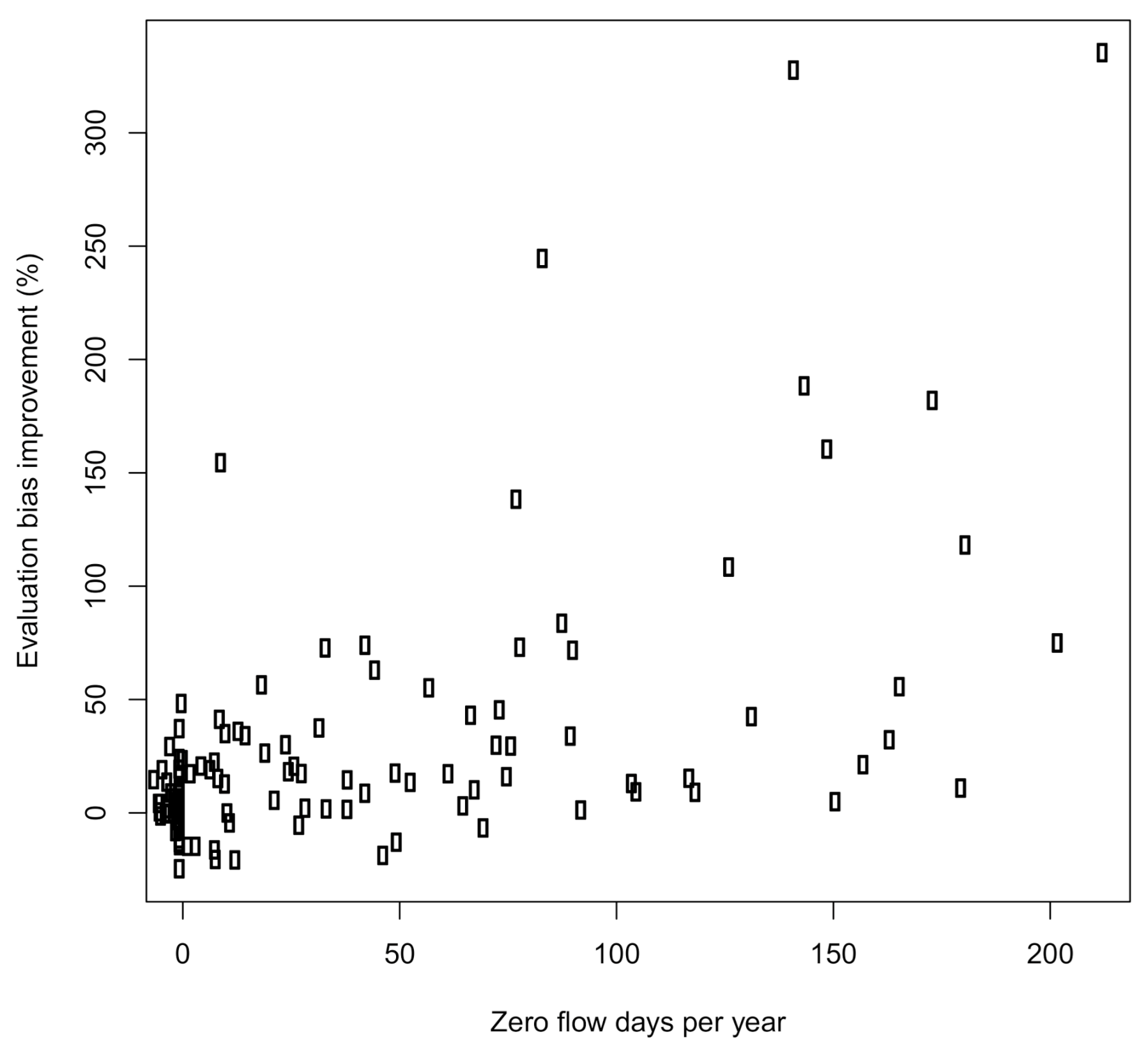
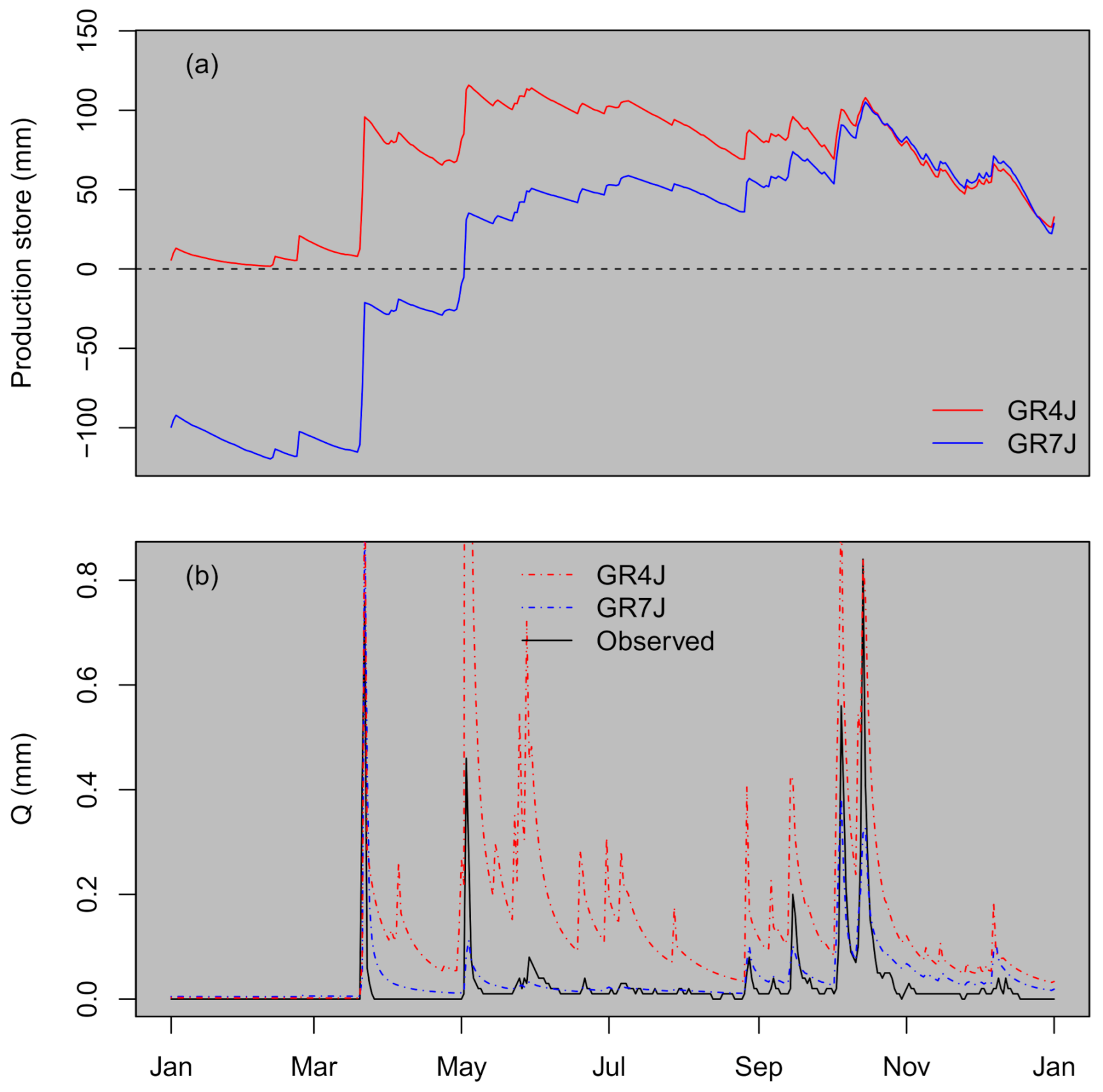
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.; Kundzewicz, Z.W.; Lettenmaier, P.; Stouffer, R.J. Climate change-stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Petrone, K.C.; Hughes, J.D.; Neil, T.G.V.; Silberstein, R.P. Streamflow decline in southwestern Australia, 1950–2008. Geophys. Res. Lett. 2010, 37, L11401. [Google Scholar] [CrossRef]
- Saft, M.; Western, A.W.; Zhang, L.; Peel, M.C.; Potter, N.J. The influence of multiyear drought on the annual rainfall-runoff relationship: An Australian perspective. Water Resour. Res. 2015, 51, 2444–2463. [Google Scholar] [CrossRef]
- Grigg, A.H.; Hughes, J.D. Nonstationarity driven by multidecadal change in catchment groundwater storage. A test of modifications to a common rainfall–run-off model. Hydrol. Process. 2018, 32, 3675–3688. [Google Scholar] [CrossRef]
- Tian, W.; Liu, X.; Liu, C.; Bai, P. Investigation and simulations of changes in the relationship of precipitation-runoff in drought years. J. Hydrol. 2018, 565, 95–105. [Google Scholar] [CrossRef]
- Grigg, A.H.; Kinal, J. On the contribution of groundwater to streamflow in laterite catchments of the Darling Range, south-western Australia. Hydrol. Process. 2020, 34, 5070–5084. [Google Scholar] [CrossRef]
- Betts, R.A.; Boucher, O.; Collins, M.; Cox, P.M.; Fallon, P.D.; Gedney, N.; Hemming, D.L.; Huntingford, C.; Jones, C.D.; Sexton, D.M.H.; et al. Projected increase in continental runoff due to plant response to increasing carbon dioxide. Nature 2007, 448, 1037–1041. [Google Scholar] [CrossRef]
- Hughes, J.D.; Petrone, K.C.; Silberstein, R.P. Drought, groundwater storage and streamflow decline in southwestern Australia. Geophys. Res. Lett. 2012, 39, L03408. [Google Scholar] [CrossRef]
- Kinal, J.; Stoneman, G. Disconnection of groundwater from surface water causes a fundamental change in hydrology in a forested catchment in south-western Australia. J. Hydrol. 2012, 472–473, 14–24. [Google Scholar] [CrossRef]
- Petheram, C.; Potter, N.J.; Vaze, J.; Chiew, F.H.S.; Zhang, L. Towards better understanding of changes in rainfall–runoff relationships during the recent drought in southeastern Australia. In MODSIM, Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; MSSANZ: Perth, Australia, 2011. [Google Scholar]
- Potter, N.J.; Petheram, C.; Zhang, L. Sensitivity of streamflow to rainfall and temperature in south-eastern Australia during the Millennium drought. In MODSIM, Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; MSSANZ: Perth, Australia, 2011. [Google Scholar]
- Tian, W.; Bai, P.; Wang, K.; Liang, K.; Liu, C. Simulating the change of precipitation-runoff relationship during drought years in the eastern monsoon region of China. Sci. Total Environ. 2020, 723, 138172. [Google Scholar] [CrossRef]
- Chawla, I.; Mujumdar, P.P. Partioning uncertainty in streamflow projections under nonstationary model conditions. Adv. Water Resour. 2018, 112, 266–282. [Google Scholar] [CrossRef]
- Avanzi, F.; Rungee, J.; Maurer, T.; Bales, R.; Ma, Q.; Glaser, S.; Conklin, M. Evapotranspiration feedbacks shift annual precipitation-runoff relationships during multi-year droughts in a Mediterranean mixed rain-snow climate. Hydrol. Earth Syst. Sci. Discuss. 2019. [Google Scholar] [CrossRef] [Green Version]
- Gal, L.; Grippa, M.; Hiernaux, P.; Pons, L.; Kergoat, L. The paradoxical evolution of runoff in the pastoral Sahel: Analysis of the hydrological changes over the Agoufou watershed (Mali) using the KINEROS-2 model. Hydrol. Earth Syst. Sci. 2017, 21, 4591–4613. [Google Scholar] [CrossRef] [Green Version]
- Vaze, J.; Post, D.A.; Chiew, F.H.S.; Perraud, J.M.; Viney, N.R.; Teng, J. Climate non-stationarity - Validity of calibrated rainfall-runoff models for use in climate change studies. J. Hydrol. 2010, 394, 447–457. [Google Scholar] [CrossRef]
- Potter, N.J.; Zhang, L.; Petheram, C.; Chiew, F.H.S. Hydrological non-stationarity in southeastern Australia. In Proceedings of the Climate and Land Surface Changes in Hydrology, IAHS-IASPSO-IASPEI Assembly, Gothenburg, Sweeden, 22–26 July 2013; IAHS: Wallingford, UK, 2013; Volume 359. [Google Scholar]
- Silberstein, R.P.; Aryal, S.K.; Braccia, M.; Durrant, J. Rainfall—runoff model performance suggests a change in flow regime and possible lack of catchment resilience. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, South Australia, 1–6 December 2013. [Google Scholar]
- Westra, S.; Theyer, M.; Leonard, M.; Kavetski, D.; Lambert, M. A strategy for diagnosing and interpreting hydrological model nonstationarity. Water Resour. Res. 2014, 50, 5090–5113. [Google Scholar] [CrossRef] [Green Version]
- Hughes, J.D.; Silberstein, R.; Grigg, A.H. Extending rainfall-runoff models for use in environments with long–term catchment storage and forest cover changes. In Proceedings of the 20th International Congress on Modelling and Simulation; Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; Society of Australia and New Zealand: Adelaide, Australia, 2013. [Google Scholar]
- Perrin, C.; Michael, C.; Andreassian, V. Improvement of a parsimonious model for streamflow simulations. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Silberstein, R.P.; Adhitya, A.; Dabrowski, C. Changes in Flood Flows, Saturated Area and Salinity Associated with Forest Clearing for Agriculture; Technical Report 03/1; Co-Operative Centre for Catchment Hydrology: Canberra, Australia, 2003. [Google Scholar]
- Bari, M.A.; Smettem, K.R.J. Development of a salt and water balance model for a large partially cleared catchment. Australas. J. Water Resour. 2003, 7, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Deb, P.; Kiem, A.S.; Willgoose, G. A linked surface water-groundwater modelling approach to more realistically simulate rainfall-runoff non-stationarity in semi-arid regions. J. Hydrol. 2019, 575, 273–291. [Google Scholar] [CrossRef]
- Hughes, J.D.; Vaze, J. Non-stationarity driven by long-term change in catchment storage: Possibilities and implications. Hydrol. Sci. J. 2015, 371, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Klemes, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Duan, Q.D. Global optimization for watershed model calibration. In Calibration of Watershed Models; Duan, Q.D., Gupta, V.K., Sorooshian, S., Rousseau, A.N., Turcotte, R., Eds.; American Geophysical Union: Washington, DC, USA, 1996; pp. 89–104. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-a discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Aitken, A.P. Assessing systematic errors in rainfall-runof models. J. Hydrol. 1973, 20, 121–136. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Brutsaert, W. Long–term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44, W02409. [Google Scholar] [CrossRef]
- Turner, J.V.; Waite, T.D.; Bradd, J.M. The conjunctive use of isotopic techniques to elucidate solute concentration and flow processes in dryland salinised catchments. In International Hydrology and Water Resources Symposium. Challenges for Sustainable Development; The Institution of Engineers, Australia: Perth, Australia, 1991; pp. 118–125. [Google Scholar]
- Hughes, J.D.; Khan, S.; Crosbie, R.S.; Helliwell, S.; Michalk, D.L. Runoff and solute mobilisation processes in a semiarid headwater catchment. Water Resour. Res. 2007, 43, W09402. [Google Scholar] [CrossRef]
- Hughes, J.D.; Crosbie, R.S.; van de Ven, R.J. Salt mobilisation processes from a salinised catchment featuring a perennial stream. J. Hydrol. 2008, 362, 308–319. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Potter, N.J.; Petheram, C.; Zhang, L.; Teng, J.; Post, D.A. Observed hydrologic non-stationarity in far south-eastern Australia: Implications for modelling and prediction. Stoch. Environ. Res. Risk Assess. 2014, 28, 3–15. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Beven, K. Rainfall-Runoff Modelling. The Primer, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2012. [Google Scholar]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L. Improved Rainfall-Runoff Calibration for Drying Climate: Choice of Objective Function. Water Resour. Res. 2018, 54, 3392–3408. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.S.H.; Hughes, J.D.; Chen, J.; Dutta, D.; Vaze, J. Determining probability distributions of parameter performances for time-series model calibrations: A river system trial. J. Hydrol. 2015, 530, 361–371. [Google Scholar] [CrossRef]
- Lane, S.N. Assessment of rainfall-runoff models based upon wavelet analysis. Hydrol. Process. 2007, 21, 586–607. [Google Scholar] [CrossRef]
- Schaefli, B. Hydrological model performance and parameter estimation in the wavelet-domain. Hydrol. Earth Syst. Sci. 2009, 13, 1921–1936. [Google Scholar] [CrossRef] [Green Version]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Siebert, J.; McDonnell, J.J. On the dialog between experimentalist and modeler in catchment hydrology: Use of soft data for multicriteria model calibration. Water Resour. Res. 2002, 38, 1241. [Google Scholar] [CrossRef]
| Period | Goodness of Fit | GR4J | GR7J | ||
|---|---|---|---|---|---|
| NSEB | NSESeg | NSEB | NSESeg | ||
| Calibration | NSE | 0.71 | 0.70 | 0.76 | 0.72 |
| Absolute bias(%) | 0.1 | 5.6 | 0.0 | 4.4 | |
| Evaluation | NSE | 0.64 | 0.62 | 0.66 | 0.59 |
| Absolute bias(%) | 59.3 | 47.9 | 50.0 | 33.0 | |
| GR4J | GR7J | |||
|---|---|---|---|---|
| NSEB | NSESeg | NSEB | NSESeg | |
| NSE | NA | 0.507 | 0.596 | 0.340 |
| Absolute bias(%) | NA | 0.110 | 0.883 | 0.004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hughes, J.; Potter, N.; Zhang, L.; Bridgart, R. Conceptual Model Modification and the Millennium Drought of Southeastern Australia. Water 2021, 13, 669. https://doi.org/10.3390/w13050669
Hughes J, Potter N, Zhang L, Bridgart R. Conceptual Model Modification and the Millennium Drought of Southeastern Australia. Water. 2021; 13(5):669. https://doi.org/10.3390/w13050669
Chicago/Turabian StyleHughes, Justin, Nick Potter, Lu Zhang, and Robert Bridgart. 2021. "Conceptual Model Modification and the Millennium Drought of Southeastern Australia" Water 13, no. 5: 669. https://doi.org/10.3390/w13050669






