Modeling the Effect of Different Forest Types on Water Balance in the Three Gorges Reservoir Area in China, with CoupModel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Field Data
2.2.1. Meteorological Variables
2.2.2. Measurement of Soil Moisture Content
2.2.3. Throughfall and Stemflow Measurement
2.2.4. Vegetation Properties
2.2.5. Collection of Soil Samples and Laboratory Analyses
2.2.6. Surface Runoff
2.3. Model Description
2.4. Model Settings and Parameterizations
2.5. Statistical Analyses
3. Results and Discussion
3.1. Model Evaluation
3.1.1. Soil Moisture Dynamics
3.1.2. Validation of Modeled Results
3.1.3. Model Prediction
3.2. Simulated Water Balance Components
3.2.1. Precipitation
3.2.2. Canopy Interception
3.2.3. Plant Transpiration
3.2.4. Soil Evaporation
3.2.5. Deep Percolation
3.2.6. Water Balance
3.3. Effect of Afforestation on Water Balance
3.3.1. Changes in Water Balance after Afforestation
3.3.2. Effect of Tree Species
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, J.G.; Huang, J.H.; Han, X.G.; Gao, X.M.; He, F.L.; Jiang, M.X.; Jiang, Z.G.; Primack, R.B.; Shen, Z.H. The Three Gorges Dam: An ecological perspective. Front. Ecol. Environ. 2004, 2, 241–248. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Lou, Z.P. The environmental changes and mitigation actions in the Three Gorges Reservoir region, China. Environ. Sci. Policy 2011, 14, 1132–1138. [Google Scholar] [CrossRef]
- Xiao, W.F.; Lei, P.J. Spatial distribution, disturbance and restoration of forests in the Three Gorges Reservoir region. Resour. Environ. Yangtze Basin 2004, 13, 138–144. [Google Scholar]
- Cheng, J.H.; Zhang, H.J.; Wang, W.; Zhang, Y.Y.; Chen, Y.Z. Changes in Preferential Flow Path Distribution and Its Affecting Factors in Southwest China. Soil Sci. 2011, 176, 652–660. [Google Scholar] [CrossRef]
- Lu, W.X.; Zhang, H.J.; Cheng, J.H.; Wang, H.Y.; Li, J.Q.; Wang, W. Effect of a hedgerow agroforestry system on soil proper-ties of sloping cultivated lands in the Three-Gorges area in China. J. Food Agric. Environ. 2012, 10, 1368–1375. [Google Scholar]
- Eckhardt, K.; Breuer, L.; Frede, H.-G. Parameter uncertainty and the significance of simulated land use change effects. J. Hydrol. 2003, 273, 164–176. [Google Scholar] [CrossRef]
- Granier, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Agric. For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
- Chen, H.S.; Shao, M.A.; Li, Y.Y. The characteristics of soil water cycle and water balance on steep grassland under natural and simulated rainfall conditions in the Loess Plateau of China. J. Hydrol. 2008, 360, 242–251. [Google Scholar] [CrossRef]
- Leauthaud, C.; Kergoat, L.; Hiernaux, P.; Grippa, M.; Musila, W.; Duvail, S.; Albergel, J. Modelling the growth of floodplain grasslands to explore the impact of changing hydrological conditions on vegetation productivity. Ecol. Model. 2018, 387, 220–237. [Google Scholar] [CrossRef]
- Rosenqvis, L.; Hansen, K.; Vesterdal, L.; van der Salm, C. Water balance in afforestation chronosequences of common oak and Norway spruce on former arable land in Denmark and southern Sweden. Agric. For. Meteorol. 2010, 150, 196–207. [Google Scholar] [CrossRef]
- Pathak, D.; Whitehead, P.G.; Futter, M.N.; Sinha, R. Water quality assessment and catchment-scale nutrient flux modeling in the Ramganga River Basin in north India: An application of INCA model. Sci. Total. Environ. 2018, 631, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wei, S.P.; Horton, R.; Shao, M.A. Effects of vegetation and slope aspect on water budget in the hill and gully region of the Loess Plateau of China. Catena 2011, 87, 90–100. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.P.; Shao, H.B.; Wu, Y.J.; Wang, Q.J. Simulated water balance of forest and farmland in the hill and gully region of the Loess Plateau in China. Plant Biosyst. 2012, 146, 226–243. [Google Scholar] [CrossRef]
- Doerr, S.H.; Ritsema, C.J.; Dekker, L.W.; Scott, D.F.; Carter, D. Water repellence of soils: New insights and emerging research needs. Hydrol. Process. 2007, 21, 2223–2228. [Google Scholar] [CrossRef]
- Farley, K.A.; Jobbágy, E.G.; Jackson, R.B. Effects of afforestation on water yield: A global synthesis with implications for poli-cy. Glob. Chang. Biol. 2005, 11, 1565–1576. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, G.Y.; Zhang, Z.Q.; Wei, X.H.; McNulty, S.G.; Vose, J.M. Potential water yield reduction due to forestation across China. J. Hydrol. 2006, 328, 548–558. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.D. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Hatten, J.A.; Segura, C.; Bladon, K.D.; Hale, V.C.; Ice, G.G.; Stednick, J.D. Effects of contemporary forest harvesting on sus-pended sediment in the Oregon Coast Range: Alsea Watershed Study Revisited. For. Ecol. Manag. 2018, 408, 238–248. [Google Scholar] [CrossRef]
- Van der Salm, C.; Denier van der Gon, H.; Wieggers, R.; Bleeker, A.; Van den Toorm, A. The effect of afforestation on water recharge and nitrogen leaching in the Netherlands. For. Ecol. Manag. 2006, 221, 170–182. [Google Scholar] [CrossRef]
- Hansen, K.; Rosenqvist, L.; Vesterdal, L.; Gundersen, P. Nitrate leaching from three afforestation chronosequences on former arable land in Denmark. Glob. Chang. Biol. 2007, 13, 1250–1264. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Morris, J.D.; Yan, J.H.; Yu, Z.Y.; Peng, S.L. Hydrological impacts of reaforestation with eucalyptus and indige-nous species: A case study in southern China. For. Ecol. Manag. 2002, 167, 209–222. [Google Scholar] [CrossRef]
- Zhao, N.N.; Liu, Y.; Cai, J.B.; Yu, F.L.; Li, C.Z. Research on soil evaporation of summer maize by field measurement and model simulation. Trans. Chin. Soc. Agric. Eng. 2012, 28, 66–73. [Google Scholar]
- Zhang, S.; Lövdahl, L.; Grip, H.; Jansson, P.-E.; Tong, Y. Modelling the effects of mulching and fallow cropping on water balance in the Chinese Loess Plateau. Soil Tillage Res. 2007, 93, 283–298. [Google Scholar] [CrossRef]
- Jansson, P.E.; Karlberg, L. Coupled Heat and Mass Transfer Model for Soil-Plant-Atmosphere Systems; Royal Institute of Technology, Dept. of Civil and Enviromental Engineering: Stockholm, Sweden, 2004; Volume 251, pp. 211–218. [Google Scholar]
- Jansson, P.-E. CoupModel: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1337–1346. [Google Scholar] [CrossRef]
- Ladekarl, U.L.; Rasmussen, K.R.; Christensen, S.; Jensen, K.H.; Hansen, B. Groundwater recharge and evapotranspiration for two natural ecosystems covered with oak and heather. J. Hydrol. 2005, 300, 76–99. [Google Scholar] [CrossRef]
- Christiansen, J.R.; Elberling, B.; Jansson, P.E. Modelling water balance and nitrate leaching in temperate Norway spruce and beech forests located on the same soil type with the CoupModel. For. Ecol. Manag. 2006, 237, 545–556. [Google Scholar] [CrossRef] [Green Version]
- Schmidt-Walter, P.; Lamersdorf, N.P. Biomass Production with Willow and Poplar Short Rotation Coppices on Sensitive Areas—the Impact on Nitrate Leaching and Groundwater Recharge in a Drinking Water Catchment near Hanover, Germany. BioEnergy Res. 2012, 5, 546–562. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.H.; Jansson, P.-E.; Zhang, X.Y. Modelling temperature, moisture and surface heat balance in bare soil under seasonal frost conditions in China. Eur. J. Soil Sci. 2011, 62, 780–796. [Google Scholar] [CrossRef]
- Zhou, J.; Kinzelbach, W.; Cheng, G.D.; Zhang, W.; He, X.B.; Ye, B.S. Monitoring and modeling the influence of snow pack and organic soil on a permafrost active layer, Qinghai–Tibetan Plateau of China. Cold Reg. Sci. Technol. 2013, 90, 38–52. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of the Porous Media. Hydrology Paper No.3. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1964. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L.; Kavanau, R.B.J.L. The State and Movement of Water in Living Organisms. Symposium of the Society for Ex-perimental Biology. by G. E. Fogg. Q. Rev. Biol. 1967, 42, 87–88. [Google Scholar]
- Manzi, A.O.; Planto, S. Implentation of the ISBA parametrization scheme for land surface processes in a GCM-an annual cycle experiment. J. Hydrol. 1994, 155, 37–46. [Google Scholar] [CrossRef]
- Gustafsson, D.; Lewan, E.; Jansson, P.-E. Modeling Water and Heat Balance of the Boreal Landscape—Comparison of Forest and Arable Land in Scandinavia. J. Appl. Meteorol. 2004, 43, 1750–1767. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of Evapotranspiration and Soil Moisture Content Across Different Scales of Observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [Green Version]
- He, C.Q.; Xue, J.H.; Wu, Y.B.; Zhang, L.Y. Application of a revised Gash analytical model to simulate subalpine Quercus aq-uifolioides forest canopy interception in the upper reaches of Minjiang River. Acta Ecol. Sin. 2010, 30, 1125–1132. [Google Scholar]
- Xue, J.H.; Hao, Q.L.; Wu, Y.B.; Liu, X.L. Relationship among canopy interception, throughfall and precipitation in three types of subalpine forest communities. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2008, 32, 9–13. [Google Scholar]
- Dai, J.F.; Chen, J.Z.; Cui, Y.L.; He, Y.Q.; Ma, J.G. Impact of forest and grass ecosystems on the water budget of the catchments. Adv. Water Sci. 2006, 17, 435–443. [Google Scholar]
- Sun, X.Y.; Wang, G.X.; Li, W.; Liu, G.S.; Lin, Y. Measurements and modelling of canopy interception in the Gongga Mountain subalpine succession forest. Adv. Water Sci. 2011, 22, 23–29. [Google Scholar]
- Liu, H.M.; Tao, S.H.; Chen, Y.Q.; Zhou, H.B.; Wang, J.G. Simulation study on the effects of vegetation on basin water balance. Meteorol. Environ. Res. 2010, 1, 62–68. [Google Scholar]
- Zhu, B.; Zhou, M.H.; Kuang, F.H.; Wang, T. Measurement and simulation of nitrogen leaching loss in hillslope cropland of purple soil. Chin. J. Eco-Agric. 2013, 21, 102–109. [Google Scholar]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
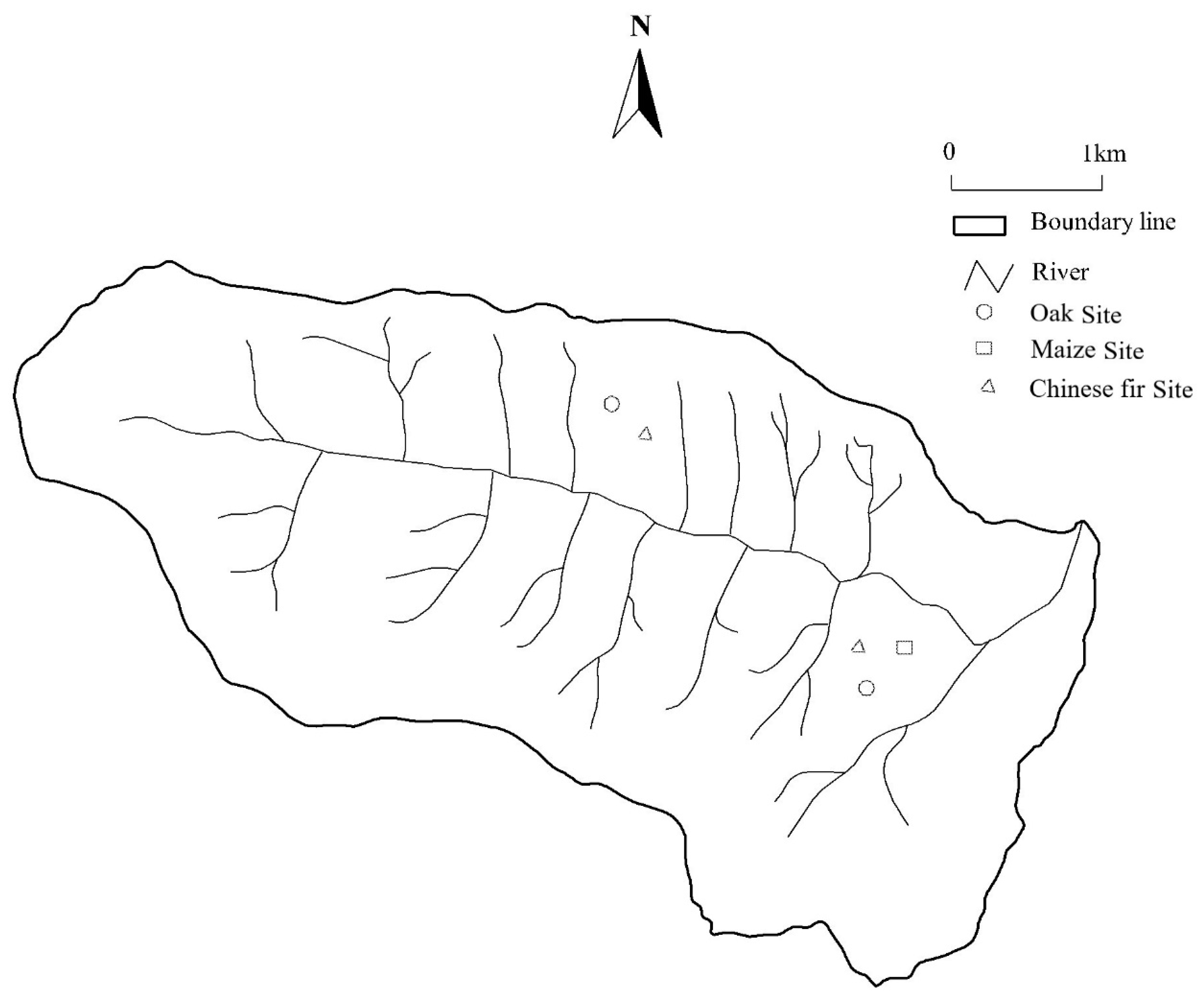
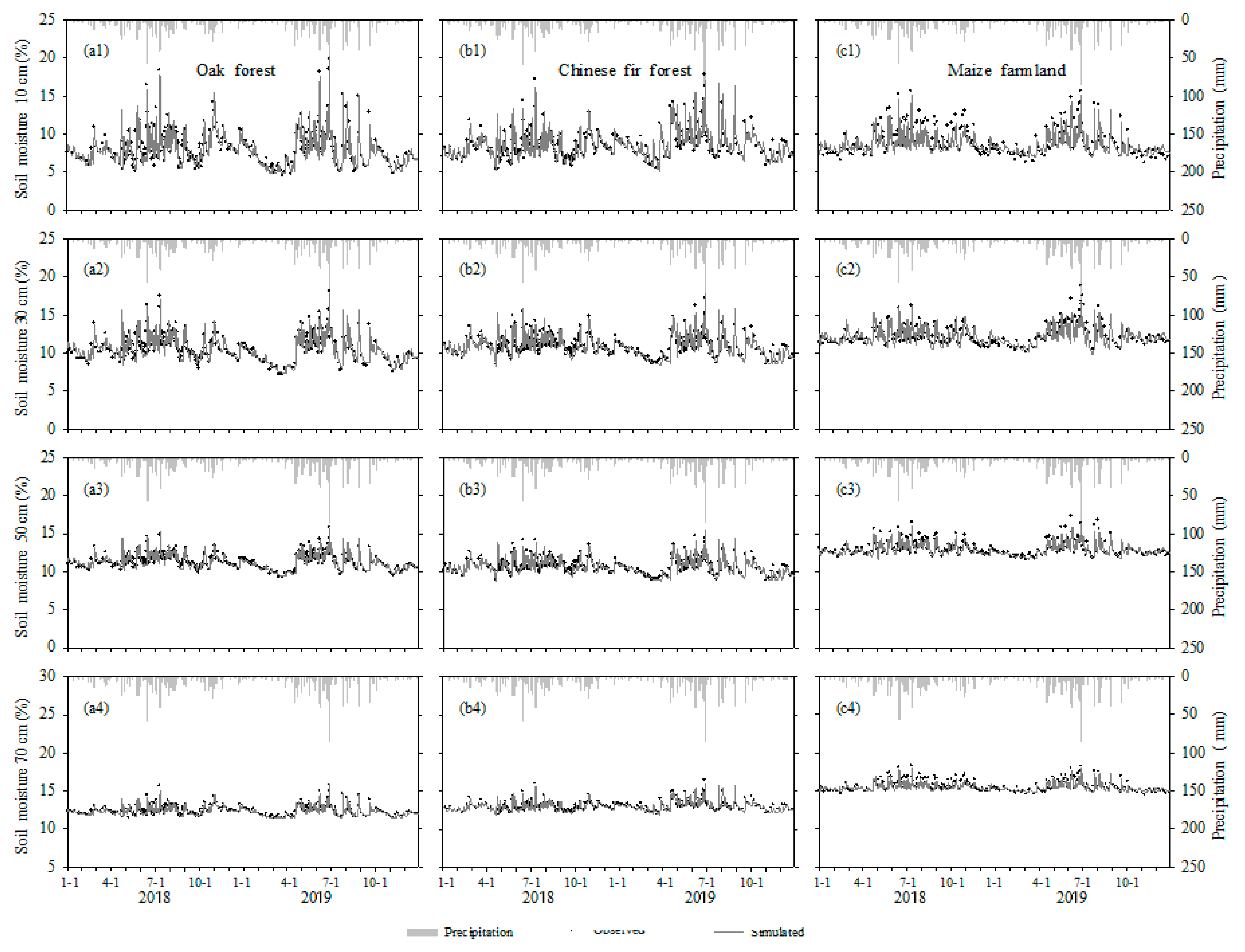
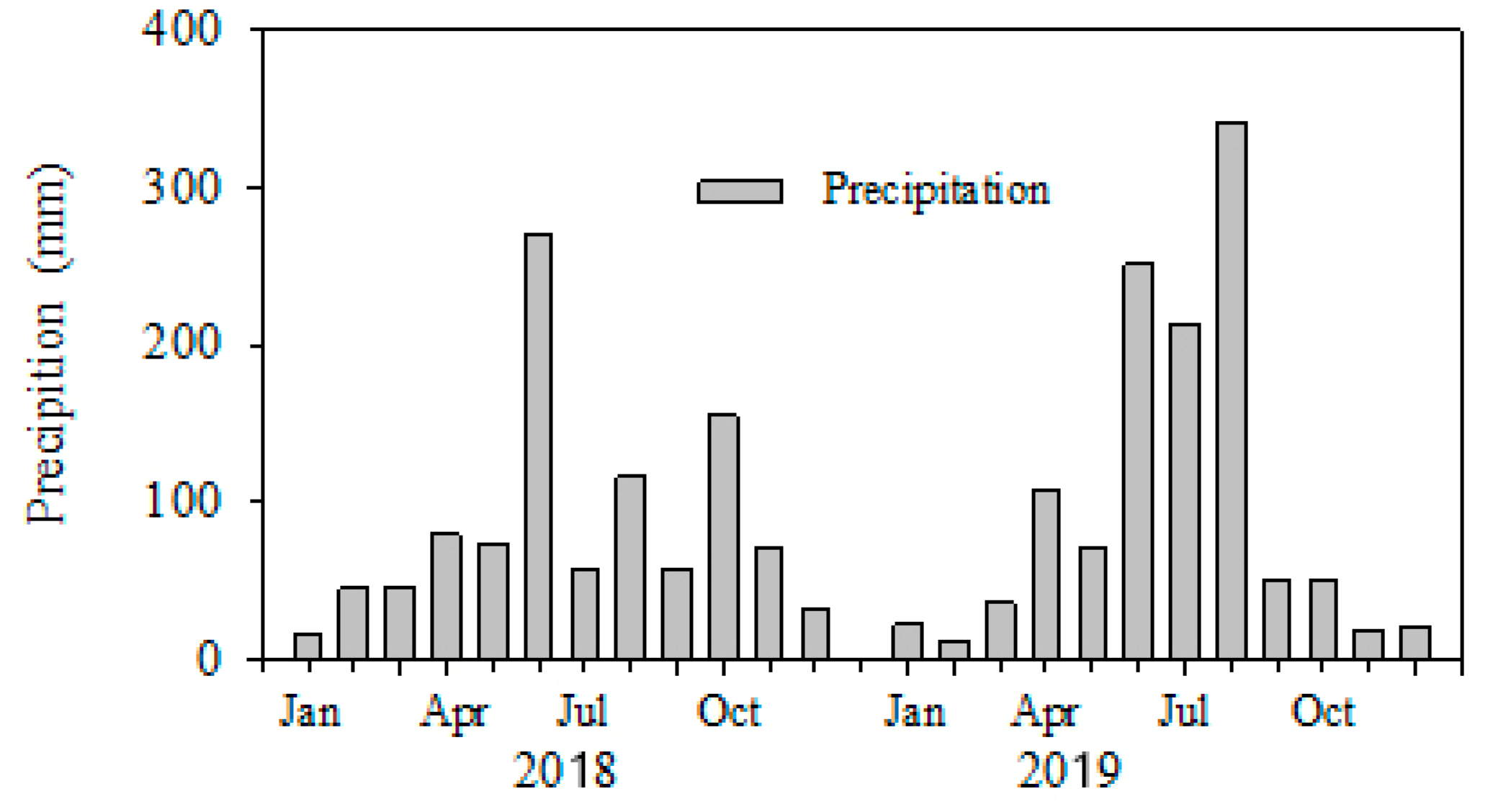
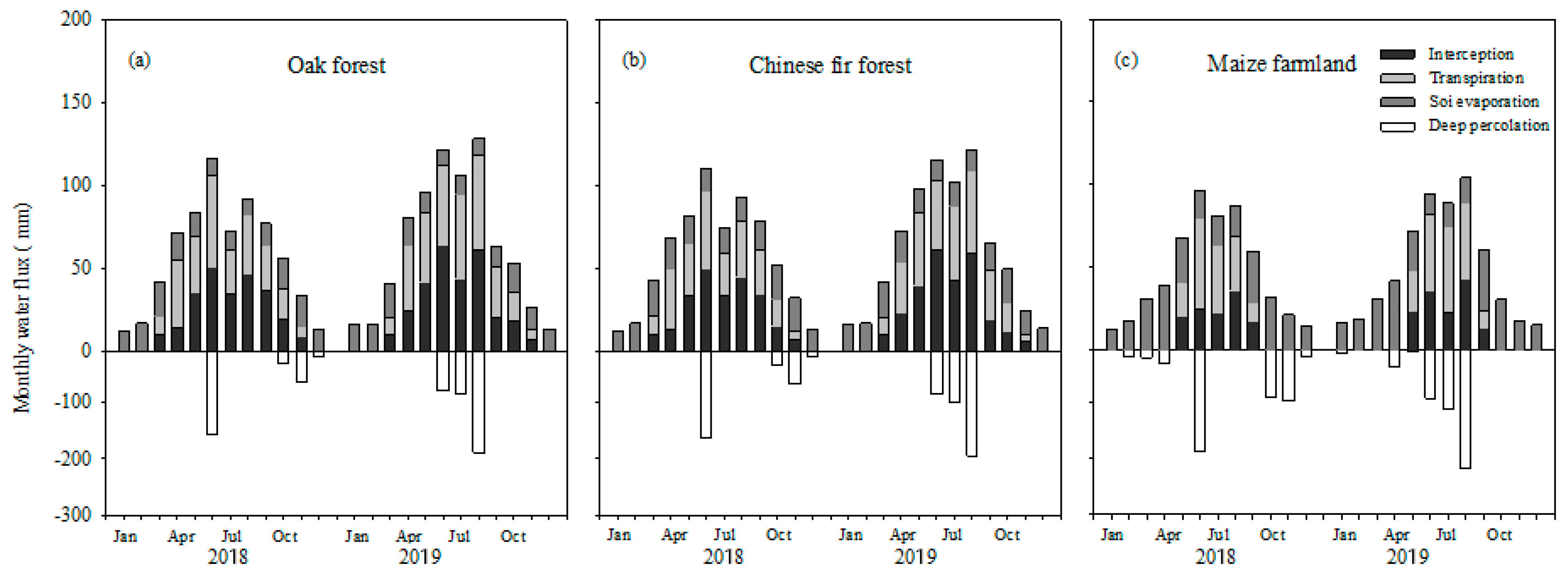
| Vegetation Type | Elevation | Gradient | Aspect | Age of Trees | Canopy Height | Tree DBH 1 | Density | Coverage | Main Vegetation |
|---|---|---|---|---|---|---|---|---|---|
| /m | /(°) | - | - | /m | /cm | /(Plant·ha−1) | /% | - | |
| Oak | 1167 | 5 | SW | 20 | 12.0 | 14 | 1000 | 90 | Lithocarpus glaber, Schima superba gardn champ, Hicriopteris chinensis, Pteridium aquilinum |
| Chinese fir | 1178 | 6 | SW | 20 | 14.0 | 10.2 | 1000 | 75 | Cunninghamia lanceolata, Pinus massoniana Lespedeza bicolor, Aster ageratoides |
| Maize | 1165 | 3 | SW | - | 1.2 | - | - | 85 | Zea mays |
| System | Parameter | Meaning | Symbol | Unit | Oak | Fir | Maize | Source |
|---|---|---|---|---|---|---|---|---|
| Climate | Alt met station | Altitude of meteorological station | elevmet | m | 1165 | 1165 | 1165 | Measurement |
| Alt sim position | Altitude of simulated site | elevsin | m | 1167 | 1178 | 1165 | Measurement | |
| Slope E–W | Slope in west–east direction | px | m·m−1 | 0.59 | 0.63 | 0.67 | Measurement | |
| Slope N–S | Slope in north–south direction | py | m·m−1 | −0.117 | −0.08 | −0.11 | Measurement | |
| Temp air mean | Mean value of analytical air temperature function | Tamean | °C | 19 | 19 | 19 | Measurement | |
| Plant properties | Max LAI | Maximum leaf area index | A1 | m2·m−2 | 4.5 | 4.0 | 4.0 | Measurement |
| Canopy height | Maximum canopy height | Hp | m | 12.0 | 14.0 | 1.5 | Measurement | |
| Root depth | Maximum root depth | zetr | m | 1.2 | 1.3 | 0.5 | Measurement | |
| Radiation properties | Latitude | Latitude of experimental site | elatit | ° | 28.51 | 28.51 | 28.51 | Measurement |
| Albedo wet | Wet soil albedo | awet | % | 15 | 15 | 15 | [23] | |
| Albedo dry | Dry soil albedo | adry | % | 25 | 25 | 25 | [24] | |
| Plant albedo | Plant albedo | aveg | % | 15 | 15 | 15 | [12] | |
| Light extinction coefficient | Light extinction coefficient | krn | - | 0.5 | 0.5 | 0.5 | [23] | |
| Soil thermal properties | ThScaleLog | Scaling coefficient for thermal conductivity of each soil layer | xhf | 0.4 | 0.4 | 0.4 | [23] | |
| Organic layer thick | Thickness of humus layer | Δzhumus | m | 0.08 | 0.05 | 0 | Measurement | |
| Soil water flows | Dvap tortuosity | Correction because of non-perfect condition for diffusion | dvap | - | 0.66 | 0.66 | 0.66 | [12,23] |
| Interception | Water capacity base | Interception storage capacity independent of LAI | Simax | mm | 2.3 | 2.3 | 0.5 | Calibrated, [35] |
| Water capacity per LAI | Interception water storage capacity per LAI unit | iLAI | mm·m−2 | 0.25 | 0.25 | 0.15 | [28,35] | |
| Potential transpiration | Cond VPD | Vapor pressure deficit corresponding to 50% reduction of stoma conductance | gvpd | Pa | 450 | 450 | 200 | Calibrated |
| Cond MAX | Maximum conductance of fully open stomata | gmax | m·s−1 | 0.005 | 0.005 | 0.02 | Calibrated, [36] | |
| Water uptake | Flexibility degree | Flexibility coefficient | fumov | - | 0.9 | 0.6 | 0.6 | [12] |
| Crit threshold dry | Critical pressure head for potential water uptake reduction | ψc | cm water | 1500 | 1000 | 1000 | Calibrated | |
| Demand RelCoef | Power coefficient | p1 | 1/d | 0.6 | 0.3 | 0.3 | Calibrated | |
| Root frac exp tail | Root fraction that remains below given root depth when exponential decrease is assumed from soil surface | rfrac | - | 0.1 | 0.05 | 0.02 | Calibrated | |
| Soil evaporation | PsiRs-1p | Governs relationship between actual surface resistance of soil surface and soil water tension of uppermost layer and surface gradient of soil moisture | rψ | - | 150 | 150 | 100 | Calibrated |
| Ra increase with LAI | Increase of aerodynamic resistance below canopy | ralai | s·m−1 | 60 | 60 | 50 | Calibrated |
| Oak Forest | Chinese Fir Forest | Maize Farmland | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Horizon/cm | R2 | ME/% | RMSE/% | AverageObs. /% | n Obs. | R2 | ME/% | RMSE/% | AverageObs. /% | n Obs. | R2 | ME/% | RMSE/% | AverageObs. /% | n Obs. |
| Soil moisture | 0–10 | 0.83 | 0.39 | 1.81 | 7.79 | 320 | 0.8 | 1.52 | 2.11 | 8.06 | 320 | 0.73 | 0.49 | 0.46 | 8.47 | 229 |
| 10–20 | 0.88 | 0.3 | 2.19 | 13.71 | 320 | 0.86 | 0.86 | 1.89 | 16.21 | 320 | 0.74 | 0.52 | 3.84 | 20.07 | 229 | |
| 20–30 | 0.84 | 0.39 | 1.41 | 10.59 | 320 | 0.85 | 0.83 | 1.48 | 13.62 | 320 | 0.85 | −0.83 | 1.41 | 15.98 | 229 | |
| 30–40 | 0.86 | −0.16 | 1.4 | 9.25 | 320 | 0.81 | −0.35 | 1.24 | 9.38 | 320 | 0.79 | −0.20 | 0.68 | 15.50 | 229 | |
| 40–50 | 0.89 | 0.42 | 1.11 | 9.49 | 320 | 0.86 | 0.41 | 0.81 | 9.02 | 320 | 0.8 | 0.95 | 0.58 | 16.17 | 229 | |
| 50–60 | 0.91 | −0.28 | 0.61 | 10.18 | 320 | 0.78 | 0.18 | 0.99 | 7.87 | 320 | 0.78 | −0.13 | 1.33 | 18.22 | 229 | |
| 60–70 | 0.86 | −0.02 | 1.38 | 10.86 | 320 | 0.83 | 0.26 | 1.22 | 12.26 | 320 | 0.87 | −0.12 | 1.89 | 15.29 | 229 | |
| 70–80 | 0.91 | −0.05 | 3.39 | 12.51 | 320 | 0.83 | −0.1 | 2.28 | 13.03 | 320 | 0.86 | −0.09 | 2.71 | 15.71 | 229 | |
| Throughfall | - | 0.62 | 2.37 mm | 4.51 mm | - | 34 | 0.69 | 1.92 mm | 4.2 mm | - | 34 | - | - | - | - | - |
| Year | Plot | Precipitation | Actual Evapotranspiration | Interception | Transpiration | Soil Evaporation | Deep Percolation | Change of Soil Water Storage |
|---|---|---|---|---|---|---|---|---|
| (P) /mm | (ET) /mm (% P) | (I) /mm (% P) | (Et) /mm (% P) | (Es) /mm (% P) | (D) /mm (% P) | ΔS /mm (% P) | ||
| 2018 | Oak forest | 1020 | 684 (67) | 261 (26) | 240 (24) | 183 (18) | 358 (35) | −22 (−2) |
| Chinese fir forest | 1020 | 670 (66) | 243 (24) | 219 (21) | 208 (20) | 368 (36) | −17 (−2) | |
| Farmland | 1020 | 581 (57) | 121 (12) | 170 (17) | 290 (28) | 408 (40) | 31 (3) | |
| 2019 | Oak forest | 1194 | 756 (63) | 293 (25) | 297 (25) | 167 (14) | 426 (36) | 12 (1) |
| Chinese fir forest | 1194 | 731 (61) | 274 (23) | 269 (23) | 189 (16) | 441 (37) | 22 (2) | |
| Farmland | 1194 | 621 (52) | 134 (11) | 213 (18) | 274 (23) | 495 (41) | 78 (7) | |
| Average (2018–2019) | Oak forest | 1107 | 720 (65) | 277 (26) | 268 (25) | 175 (16) | 392 (36) | −5 (−1) |
| Chinese fir forest | 1107 | 700 (63) | 258 (24) | 244 (22) | 198 (18) | 404 (37) | 3 (0) | |
| Farmland | 1107 | 601 (55) | 128 (12) | 192 (18) | 282 (26) | 451 (41) | 55 (5) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Hou, F.; Cheng, J.; Zhang, Y. Modeling the Effect of Different Forest Types on Water Balance in the Three Gorges Reservoir Area in China, with CoupModel. Water 2021, 13, 654. https://doi.org/10.3390/w13050654
Yang Z, Hou F, Cheng J, Zhang Y. Modeling the Effect of Different Forest Types on Water Balance in the Three Gorges Reservoir Area in China, with CoupModel. Water. 2021; 13(5):654. https://doi.org/10.3390/w13050654
Chicago/Turabian StyleYang, Zhi, Fang Hou, Jinhua Cheng, and Youyan Zhang. 2021. "Modeling the Effect of Different Forest Types on Water Balance in the Three Gorges Reservoir Area in China, with CoupModel" Water 13, no. 5: 654. https://doi.org/10.3390/w13050654





