Evaluating Traditional Empirical Models and BPNN Models in Monitoring the Concentrations of Chlorophyll-A and Total Suspended Particulate of Eutrophic and Turbid Waters
Abstract
1. Introduction
2. Data and Methods
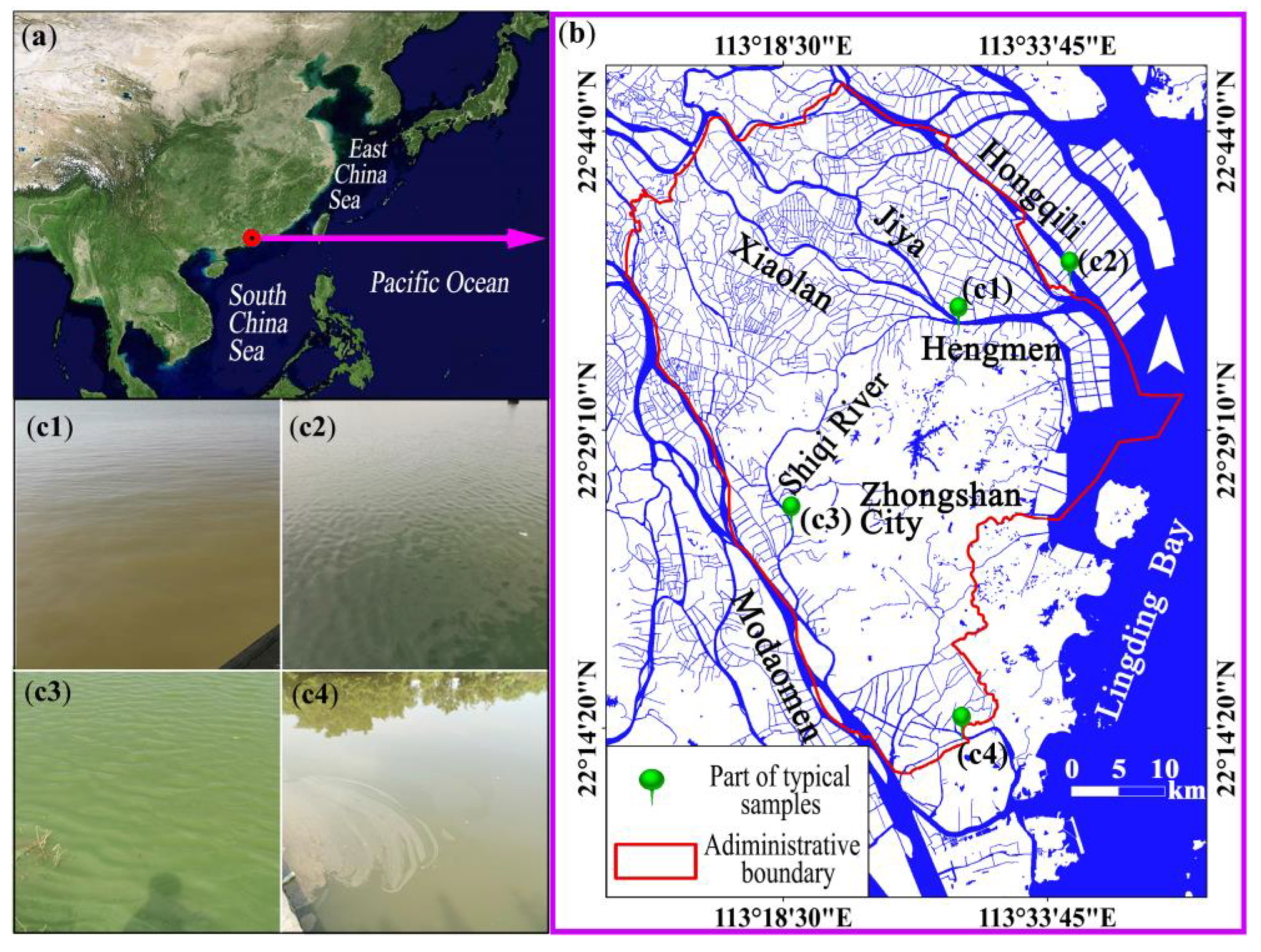
2.1. Study Area
2.2. Data Acquisition and Preprocessing
2.2.1. Data Acquisition
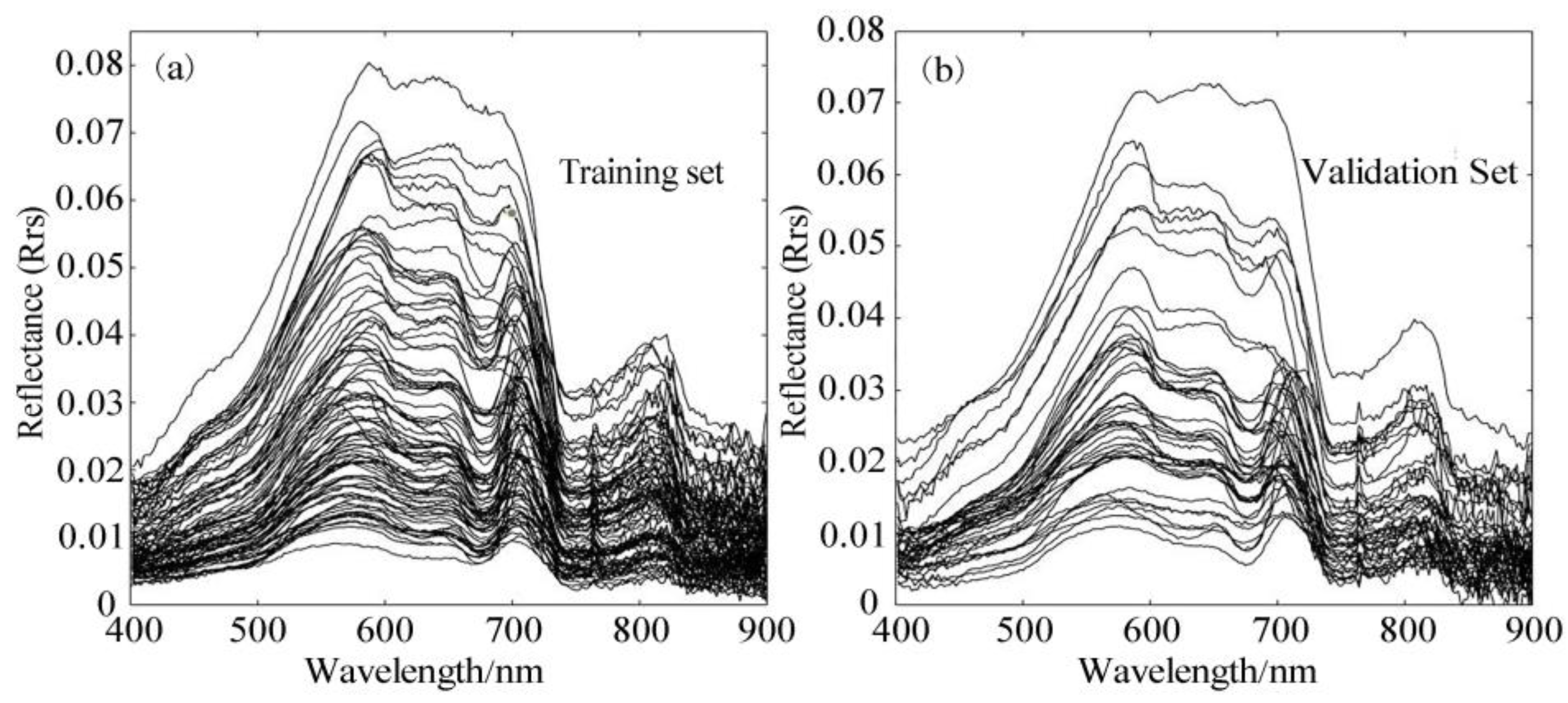
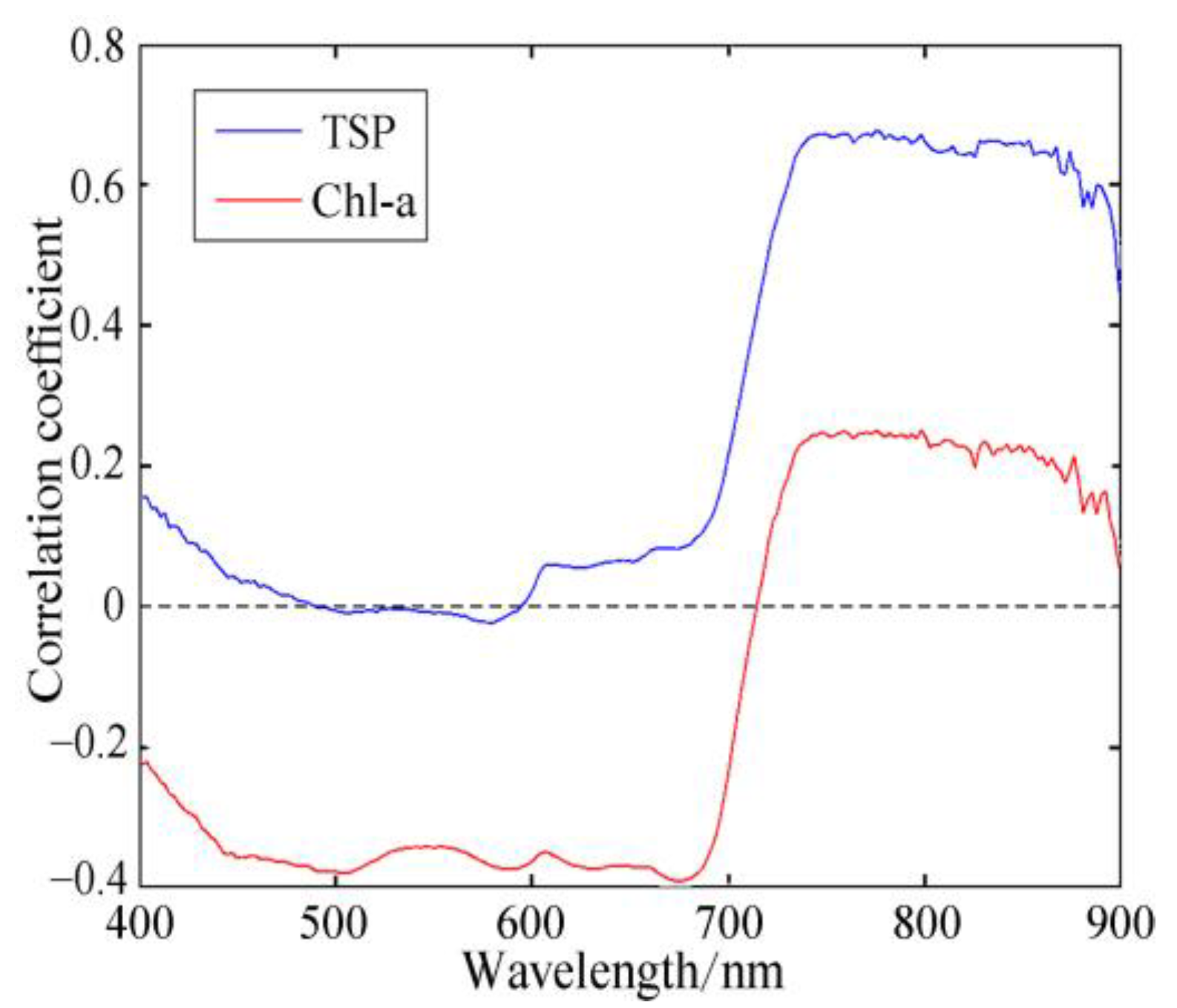
2.2.2. Data Preprocessing
2.3. Method
2.3.1. Retrieval Model of Chl-a
2.3.2. Retrieval Model of TSP
2.4. Model Training and Accuracy Verification
3. Results and Analysis
3.1. Retrieval Results of the Chl-a Concentration
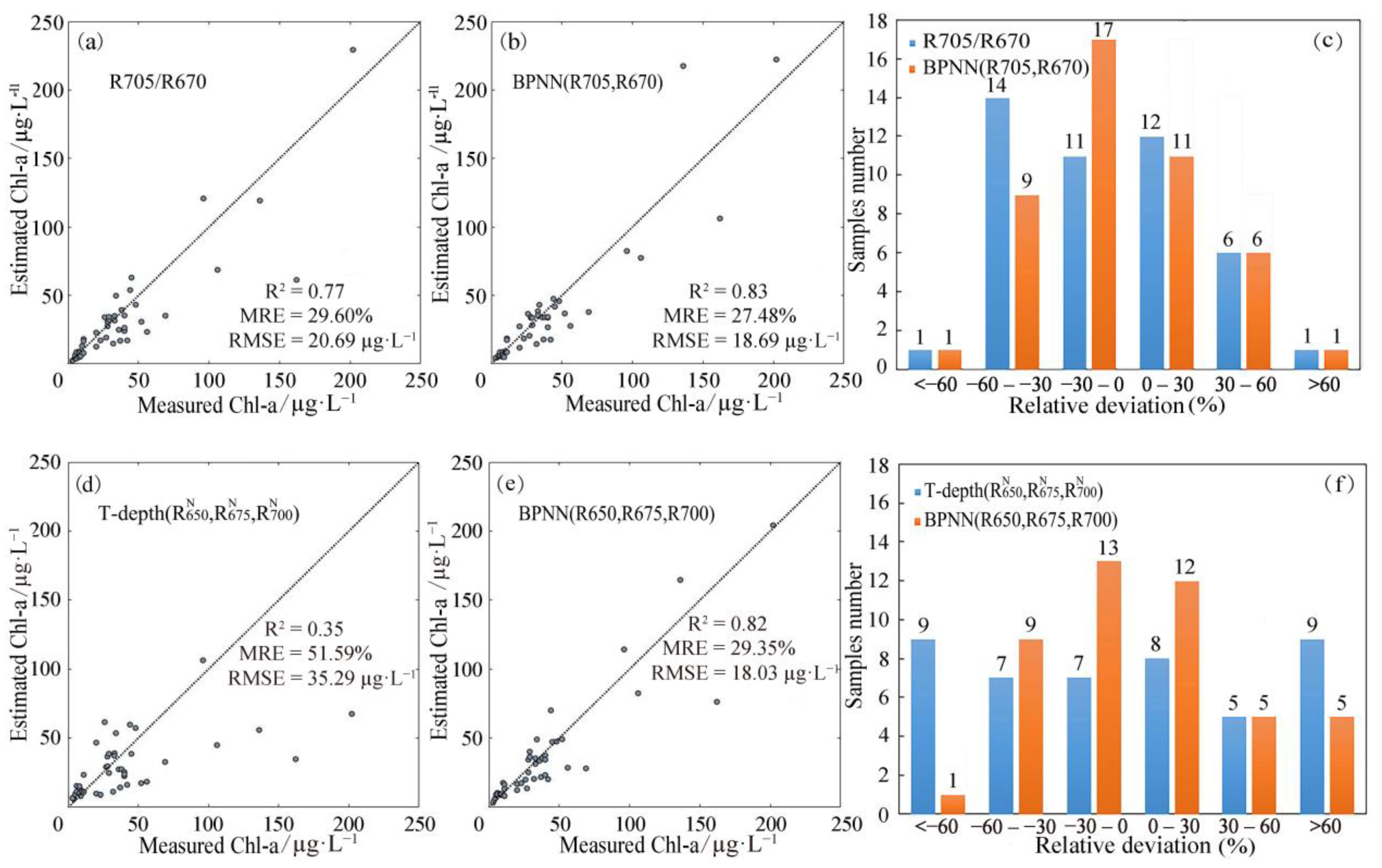
3.1.1. Two-Band Ratio Models
3.1.2. T-Depth Models
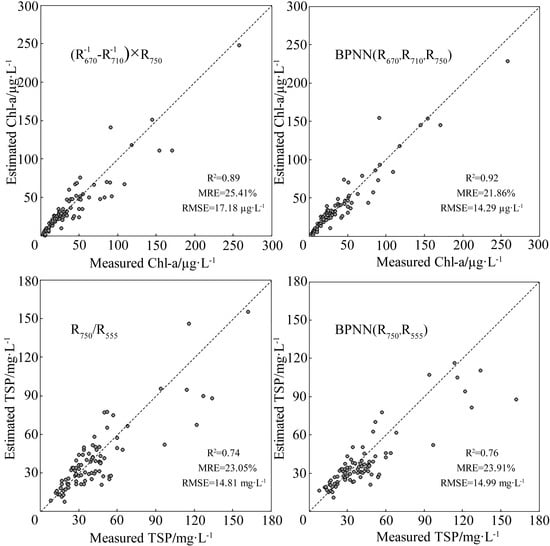
3.1.3. Three-Band Models
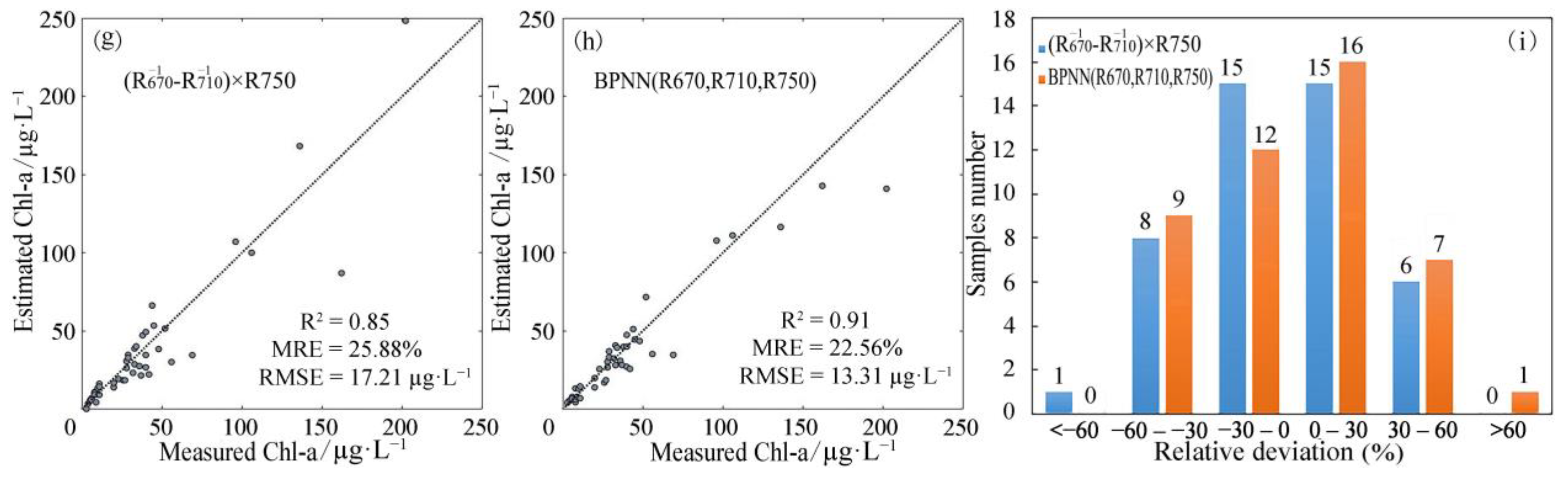
3.1.4. Model Validation
3.2. Retrieval Results of TSP Concentration
3.2.1. Two-Band Ratio Models
3.2.2. Three-Band Models
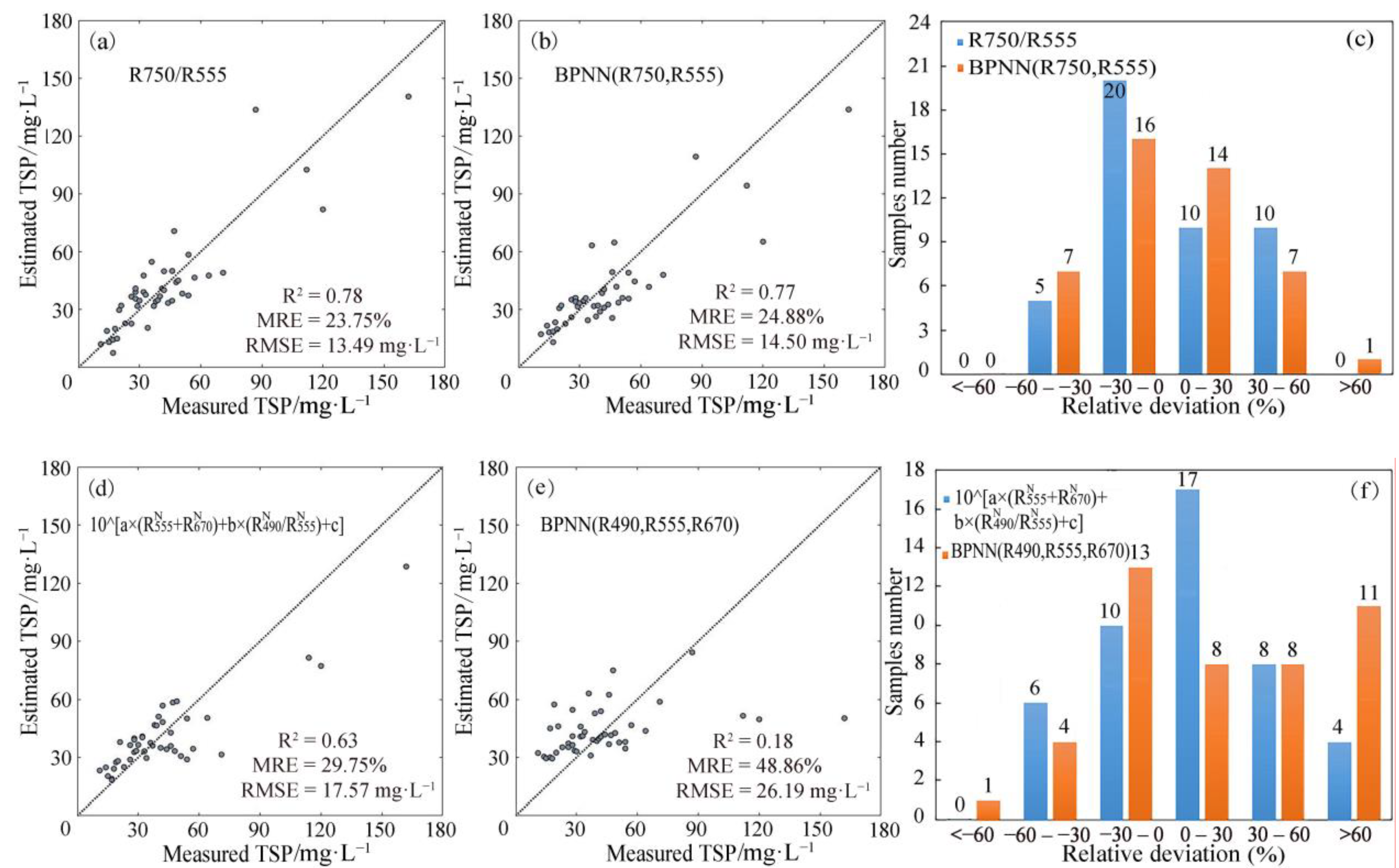
3.2.3. Model Validation
4. Discussion
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xing, Q.G.; Lou, M.J.; Chen, C.Q.; Shi, P. Using in situ and satellite hyperspectral data to estimate the surface suspended sediments concentrations in the Pearl River Estuary. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 731–738. [Google Scholar] [CrossRef]
- Liu, F.F.; Tang, S.L. Evaluation of red-peak algorithms for chlorophyll measurement in the Pearl River Estuary. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8928–8936. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.L.; Tian, L.Q.; Huang, J.; Feng, L. Improved capabilities of the Chinese high-resolution remote sensing satellite GF-1 for monitoring suspended particulate matter (SPM) in inland waters: Radiometric and spatial considerations. ISPRS-J. Photogramm. Remote Sens. 2015, 106, 145–156. [Google Scholar] [CrossRef]
- Wang, X.; Gong, Z.N.; Pu, R.L. Estimation of chlorophyll a content in inland turbidity waters using WorldView-2 imagery: A case study of the Guanting Reservoir, Beijing, China. Environ. Monit. Assess. 2018, 190, 620. [Google Scholar] [CrossRef]
- Tang, S.L.; Larouche, P.; Niemi, A.; Michel, C. Regional algorithms for remote-sensing estimates of total suspended matter in the Beaufort Sea. Int. J. Remote Sens. 2013, 34, 6562–6576. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of Chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Zhang, M.W.; Tang, J.W.; Dong, Q.; Song, Q.T.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Li, J.S.; Gao, M.; Feng, L.; Zhao, H.L.; Shen, Q.; Zhang, F.F.; Wang, S.L.; Zhang, B. Estimation of chlorophyll-a concentration in a highly turbid eutrophic lake using a classification-based MODIS land-band algorithm. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 3769–3783. [Google Scholar] [CrossRef]
- Zhang, F.F.; Li, J.S.; Shen, Q.; Zhang, B.; Wu, C.Q.; Wu, Y.F.; Wang, G.L.; Wang, S.L.; Lu, Z.Y. Algorithms and schemes for chlorophyll a estimation by remote sensing and optical classification for turbid lake Taihu, China. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 350–364. [Google Scholar] [CrossRef]
- Guo, H.W.; Huang, J.H.; Chen, B.W.; Guo, X.L.; Singh, V.P. A machine learning-based strategy for estimating non-optically active water quality parameters using Sentinel-2 imagery. Int. J. Remote Sens. 2020, 42, 1841–1866. [Google Scholar] [CrossRef]
- Kuan, H.F.; Li, J.; Zhang, X.J.; Zhang, J.P.; Cui, H.; Sun, Q. Remote estimation of water quality parameters of medium- and small-sized inland rivers using Sentinel-2 imagery. Water 2020, 12, 3124. [Google Scholar]
- Saberioon, M.; Brom, J.; Nedbal, V.; Soucek, P.; Cisar, P. Chlorophyll-a and total suspended solids retrieval and mapping using Sentinel-2A and machine learning for inland waters. Ecol. Indic. 2020, 113, 106236. [Google Scholar] [CrossRef]
- Nazeer, M.; Bilal, M.; Alsahli, M.M.; Shahzad, M.I.; Waqas, A. Evaluation of empirical and machine learning algorithms for estimation of coastal water quality parameters. ISPRS. Int. J. Geo-Inf. 2017, 6, 360. [Google Scholar] [CrossRef]
- Ioannou, I.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Deriving ocean color products using neural networks. Remote Sens. Environ. 2011, 134, 78–91. [Google Scholar] [CrossRef]
- Kim, T.H.; Kim, Y.W.; Shin, H.; Go, B.G.; Cha, Y.K. Assessing land-cover effects on stream water quality in metropolitan areas using the water quality index. Water 2020, 12, 3294. [Google Scholar] [CrossRef]
- Cai, J.N.; Liu, H.L.; Jiang, B.; He, T.H.; Chen, W.J.; Feng, Z.W.; Li, Z.L.; Xing, Q.G. Using hyperspectral imagery and GA-PLS algorithm to estimate chemical oxygen demand concentration of waters is river network. J. Irrig. Drain. 2020, 39, 126–131. [Google Scholar]
- Wang, J.L.; Fu, Z.S.; Qiao, H.X.; Liu, F.X. Assessment of eutrophication and water quality in the estuarine area of Lake Wuli, Lake Taihu, China. Sci. Total Environ. 2019, 650, 1392–1402. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y.; Ren, J.; Bao, Y.; Shi, H.Y.; Lei, Y.P.; He, Z.G.; Tang, Z.M. A preliminary study on the morphodynamic evolution of the ‘gate’ of the Pearl River Delta, China. Acta Geogr. Sin. 2006, 5, 537–548. [Google Scholar]
- Tang, J.W.; Tian, G.L.; Wang, X.Y.; Wang, X.M.; Song, Q.J. The methods of water spectra measurement and analysis I: Above-water method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Le, C.; Hu, C.; Cannizzaro, J.; English, D.; Muller-Karger, F.; Lee, Z. Evaluation of chlorophyll-a remote sensing algorithms for an optically complex estuary. Remote Sens. Environ. 2013, 129, 75–89. [Google Scholar] [CrossRef]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Xing, Q.G.; Yu, D.F.; Lou, M.J.; Lv, Y.C.; Li, S.P.; Han, Q.Y. Using in-situ reflectance to monitor the chlorophyll concentration in the surface layer of tidal flat. Spectrosc. Spectr. Anal. 2013, 33, 2188–2191. [Google Scholar]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Shen, C.Y.; Chen, C.Q.; Zhan, H.G. Inverse of chlorophyll concentration in Zhujiang River estuary using artificial neural network. J. Trop. Oceanogr. 2005, 24, 38–43. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters. Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.Q.; Wai, O.W.H.; Chen, X.L.; Li, W.B.; Li, J.; Li, W.K.; Zhang, H.D. Retrieval of total suspended matter concentration from Gaofen-1 Wide Field Imager (WFI) multispectral imagery with the assistance of Terra MODIS in turbid water–case in Deep Bay. Int. J. Remote Sens. 2016, 37, 3400–3413. [Google Scholar] [CrossRef]
- Li, J.; Tian, L.Q.; Song, Q.J.; Huang, J.; Li, W.K.; Wei, A.N. A near-infrared band-based algorithm for suspended sediment estimation for turbid waters using the experimental Tiangong 2 moderate resolution wide-wavelength imager. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 774–787. [Google Scholar] [CrossRef]
- Tassan, S. Local algorithms using SeaWiFS data for the retrieval of phytoplankton, pigments, suspended sediment, and yellow substance in coastal waters. Appl. Opt. 1994, 33, 2369–2378. [Google Scholar] [CrossRef]
- Siswanto, E.; Tang, J.W.; Yamaguchi, H.; Ahn, Y.H.; Ishizaka, J.; Yoo, S.; Kim, S.W.; Kiyomoto, Y.; Yamada, K.; Chiang, C.; et al. Empirical ocean-color algorithms to retrieve chlorophyll-a, total suspended matter, and colored dissolved organic matter absorption coefficient in the Yellow and East Chinese Seas. J. Oceanogr. 2011, 67, 627–650. [Google Scholar] [CrossRef]
- Han, B.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Bryère, P.; Ouillon, S.; Dessailly, D.; Xing, Q.G.; Zhu, J.H. Development of a semi-analytical algorithm for the retrieval of suspended particulate matter from remote sensing over clear to very turbid waters. Remote Sens. 2016, 8, 211. [Google Scholar] [CrossRef]
- Chen, S.S.; Fang, L.G.; Li, H.L.; Chen, W.Q.; Huang, W.R. Evaluation of a three-band model for estimating chlorophyll-a concentration in tidal reaches of the Pearl River Estuary, China. ISPRS-J. Photogramm. Remote Sens. 2011, 66, 356–364. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt. 2005, 44, 412–422. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Feng, S.; Ma, R.H.; Liu, M.L. Spatial variation and estimation of optically active substances in Taihu lake in Autumn of 2004. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 967–972. [Google Scholar]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ. 2010, 114, 2070–2087. [Google Scholar] [CrossRef]
- Wang, M.Z.; Zhang, Y.L.; Shi, K.; Gao, Y.; Liu, G.; Jiang, H. Characteristics of optical absorption coefficients and their differences in typical seasons in lake Qiandaohu. Environ. Sci. 2014, 35, 2528–2538. [Google Scholar]
- Wang, F.; Zhou, B.; Liu, X.M.; Zhou, G.D.; Zhao, K.L. Remote-sensing inversion model of surface water suspended sediment concentration based on in situ measured spectrum in Hangzhou Bay, China. Environ. Earth Sci. 2012, 67, 1669–1677. [Google Scholar] [CrossRef]

| Model | Equation | Band |
|---|---|---|
| Two-band | = 705 nm = 670 nm | |
| T-depth | = 650 nm, = 675 nm = 700 nm | |
| Three-band | = 670 nm, = 710 nm = 750 nm |
| Model | Equation | Band |
|---|---|---|
| Two-band | = 670 nm or 750 nm or 850 nm, = 555 nm | |
| Three-band | = 490 nm, = 555 nm = 670 nm |
| Parameter | Dataset | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|---|
| Chl-a (µg·L−1) | Training set | 3 | 258 | 38.53 | 40.92 |
| Validation set | 3 | 202 | 39.80 | 41.30 | |
| TSP (mg·L−1) | Training set | 8 | 162 | 42.39 | 28.54 |
| Validation set | 11 | 162 | 42.84 | 28.83 |
| Input | Regression Model | Equation | R2 | RMSE (µg·L−1) | MRE (%) |
|---|---|---|---|---|---|
| Logarithmic | Y = 156.19ln(x) + 2.03 | 0.62 | 29.90 | 89.44 | |
| Linear | Y = 111.43x − 106.7 | 0.70 | 26.93 | 63.06 | |
| R705/R670 | Exponential | 0.73 | 71.99 | 43.93 | |
| Power | 0.81 | 34.40 | 34.13 | ||
| Quadratic polynomial | 0.81 | 21.52 | 27.93 | ||
| R670, R705 | BPNN | -- | 0.86 | 18.18 | 28.26 |
| Input | Equation | R2 | RMSE (µg·L−1) | MRE (%) |
|---|---|---|---|---|
| T-depth () | 0.39 | 45.01 | 60.59 | |
| T-depth () | 0.61 | 39.36 | 44.72 | |
| R650, R675, R700 | BPNN | 0.83 | 20.40 | 28.01 |
| Input | Equation | R2 | RMSE (µg·L−1) | MRE (%) |
|---|---|---|---|---|
| Y = 158.07x + 15 | 0.89 | 17.18 | 25.41 | |
| R670, R710, R750 | BPNN | 0.92 | 14.29 | 21.86 |
| Input | Equation | R2 | RMSE (mg·L−1) | MRE (%) |
|---|---|---|---|---|
| R670/R555 | Y = 42.14x + 7.16 | 0.07 | 27.54 | 58.44 |
| R750/R555 | Y = 101.9x − 1.44 | 0.74 | 14.81 | 23.05 |
| R850/R555 | Y = 116.43x | 0.67 | 17.09 | 28.10 |
| R555, R670 | BPNN | 0.12 | 28.43 | 45.48 |
| R555, R750 | BPNN | 0.76 | 14.99 | 23.91 |
| R555, R850 | BPNN | 0.68 | 16.33 | 27.89 |
| Input | Equation | R2 | RMSE (mg·L−1) | MRE (%) |
|---|---|---|---|---|
| 0.01 | 29.19 | 48.10 | ||
| 0.42 | 21.89 | 32.60 | ||
| R490, R555, R670 | BPNN | 0.25 | 24.09 | 49.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Liu, H.; Xing, Q.; Cai, J.; Zheng, X.; Li, L.; Liu, S.; Zheng, Z.; Xu, H.; Meng, L. Evaluating Traditional Empirical Models and BPNN Models in Monitoring the Concentrations of Chlorophyll-A and Total Suspended Particulate of Eutrophic and Turbid Waters. Water 2021, 13, 650. https://doi.org/10.3390/w13050650
Jiang B, Liu H, Xing Q, Cai J, Zheng X, Li L, Liu S, Zheng Z, Xu H, Meng L. Evaluating Traditional Empirical Models and BPNN Models in Monitoring the Concentrations of Chlorophyll-A and Total Suspended Particulate of Eutrophic and Turbid Waters. Water. 2021; 13(5):650. https://doi.org/10.3390/w13050650
Chicago/Turabian StyleJiang, Bo, Hailong Liu, Qianguo Xing, Jiannan Cai, Xiangyang Zheng, Lin Li, Sisi Liu, Zhiming Zheng, Huiyan Xu, and Ling Meng. 2021. "Evaluating Traditional Empirical Models and BPNN Models in Monitoring the Concentrations of Chlorophyll-A and Total Suspended Particulate of Eutrophic and Turbid Waters" Water 13, no. 5: 650. https://doi.org/10.3390/w13050650
APA StyleJiang, B., Liu, H., Xing, Q., Cai, J., Zheng, X., Li, L., Liu, S., Zheng, Z., Xu, H., & Meng, L. (2021). Evaluating Traditional Empirical Models and BPNN Models in Monitoring the Concentrations of Chlorophyll-A and Total Suspended Particulate of Eutrophic and Turbid Waters. Water, 13(5), 650. https://doi.org/10.3390/w13050650