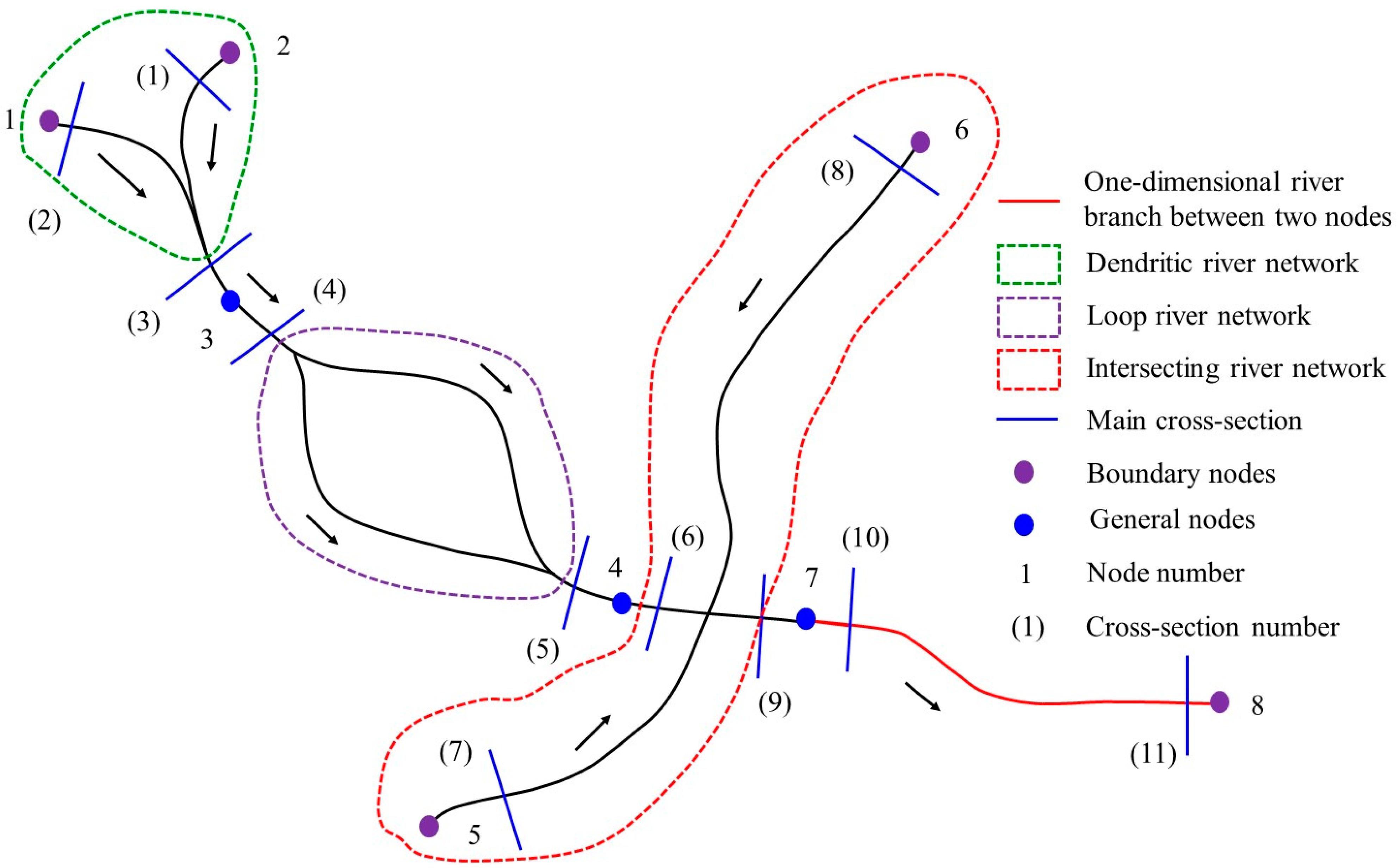
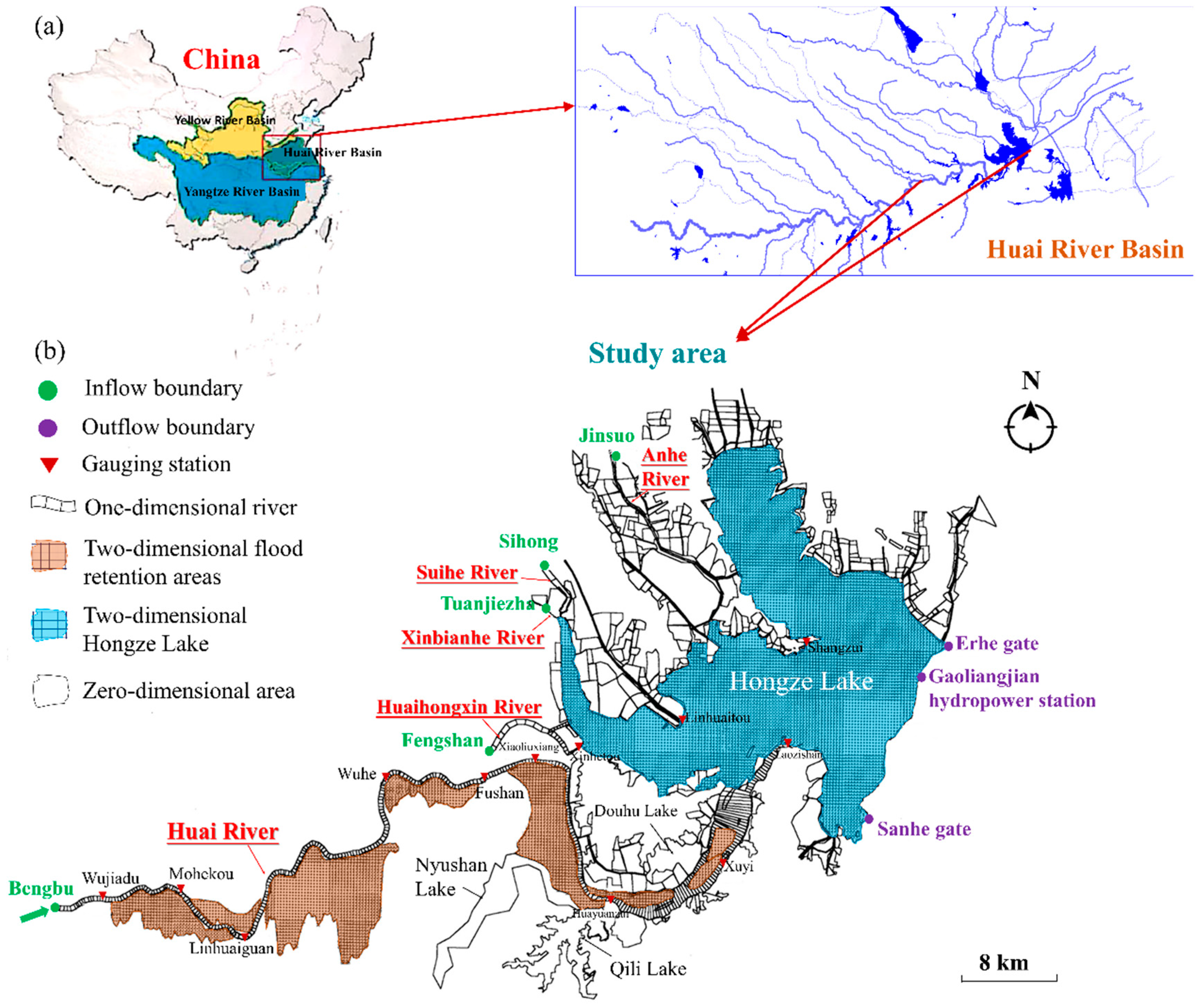
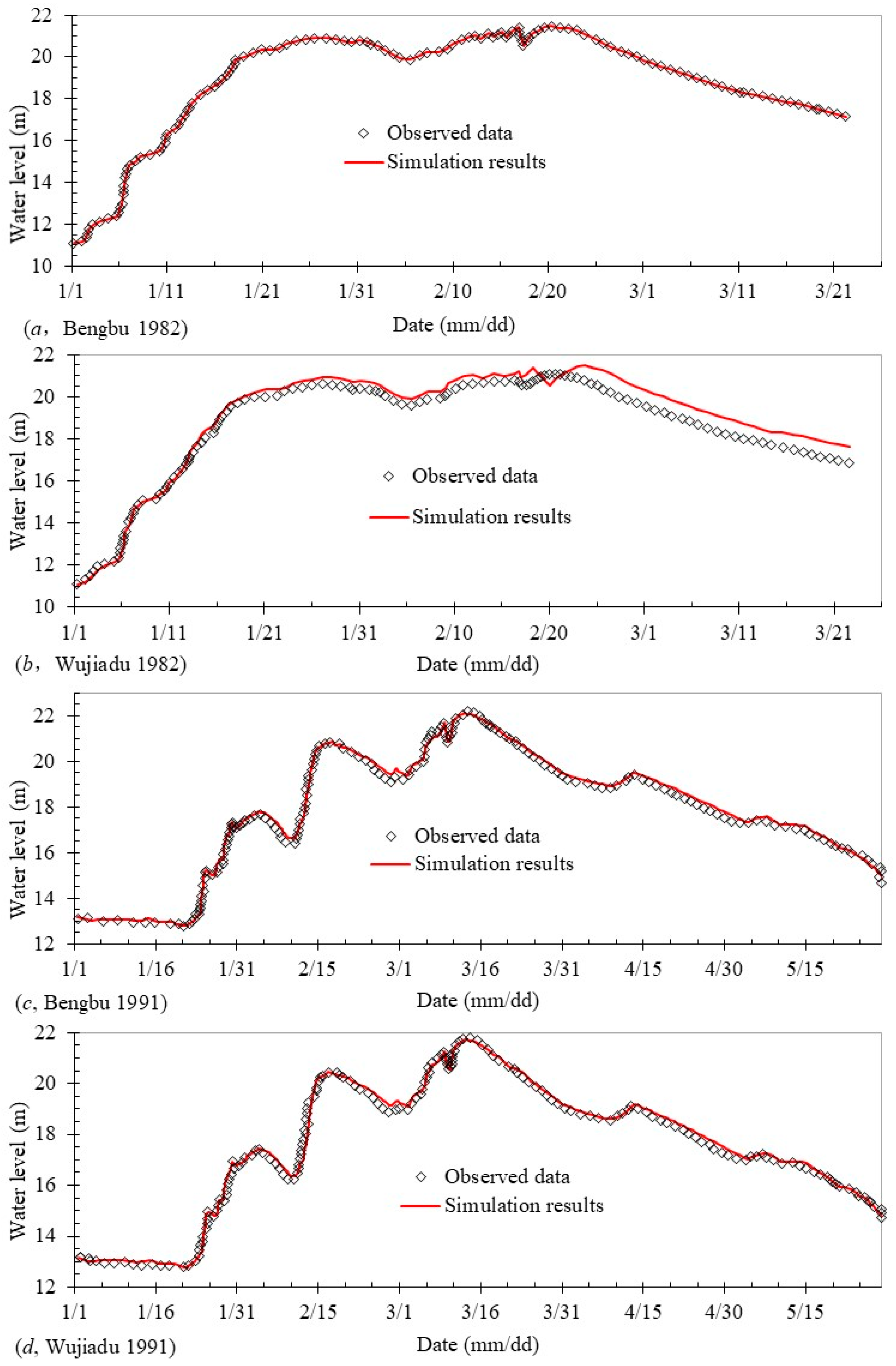
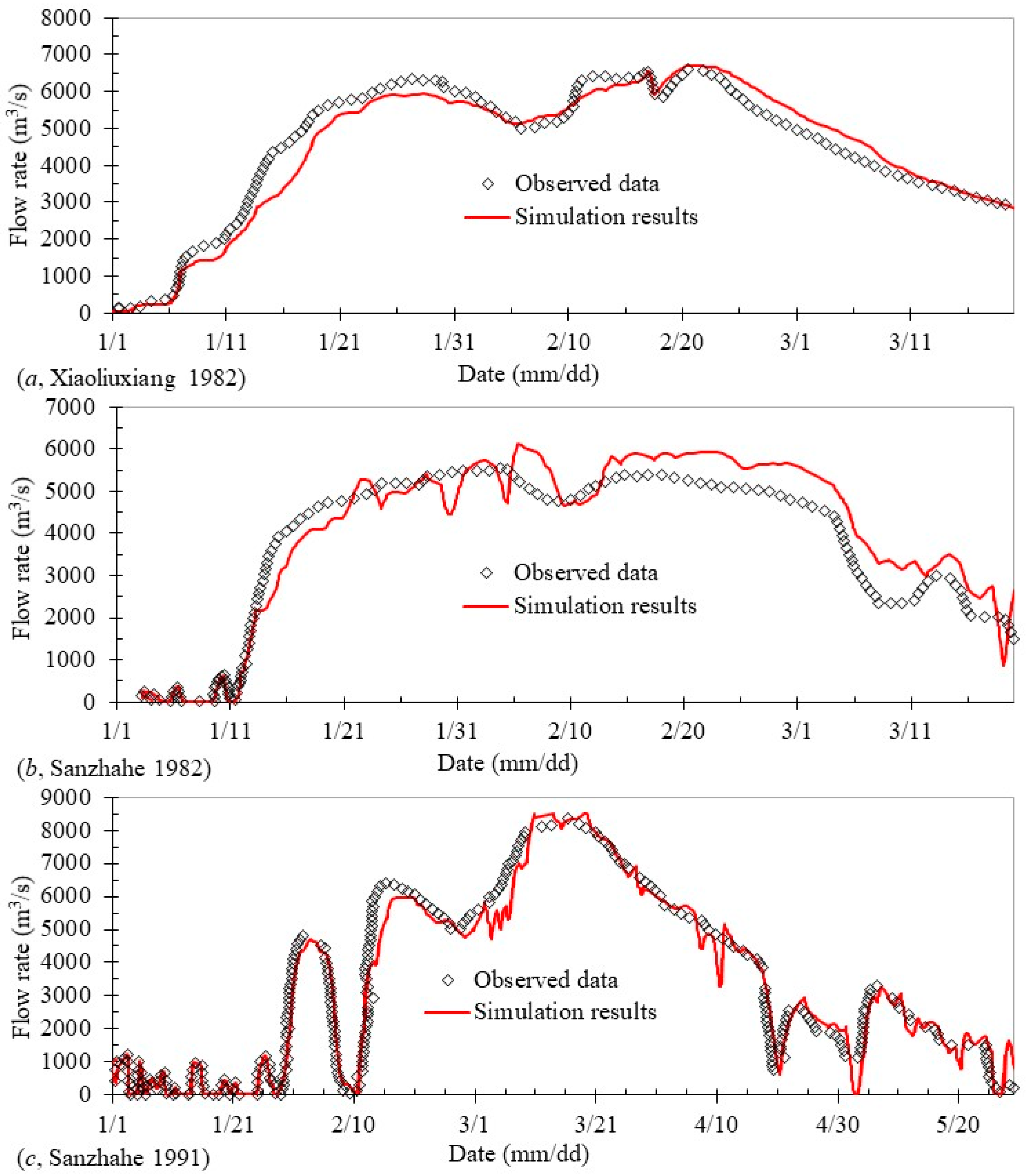
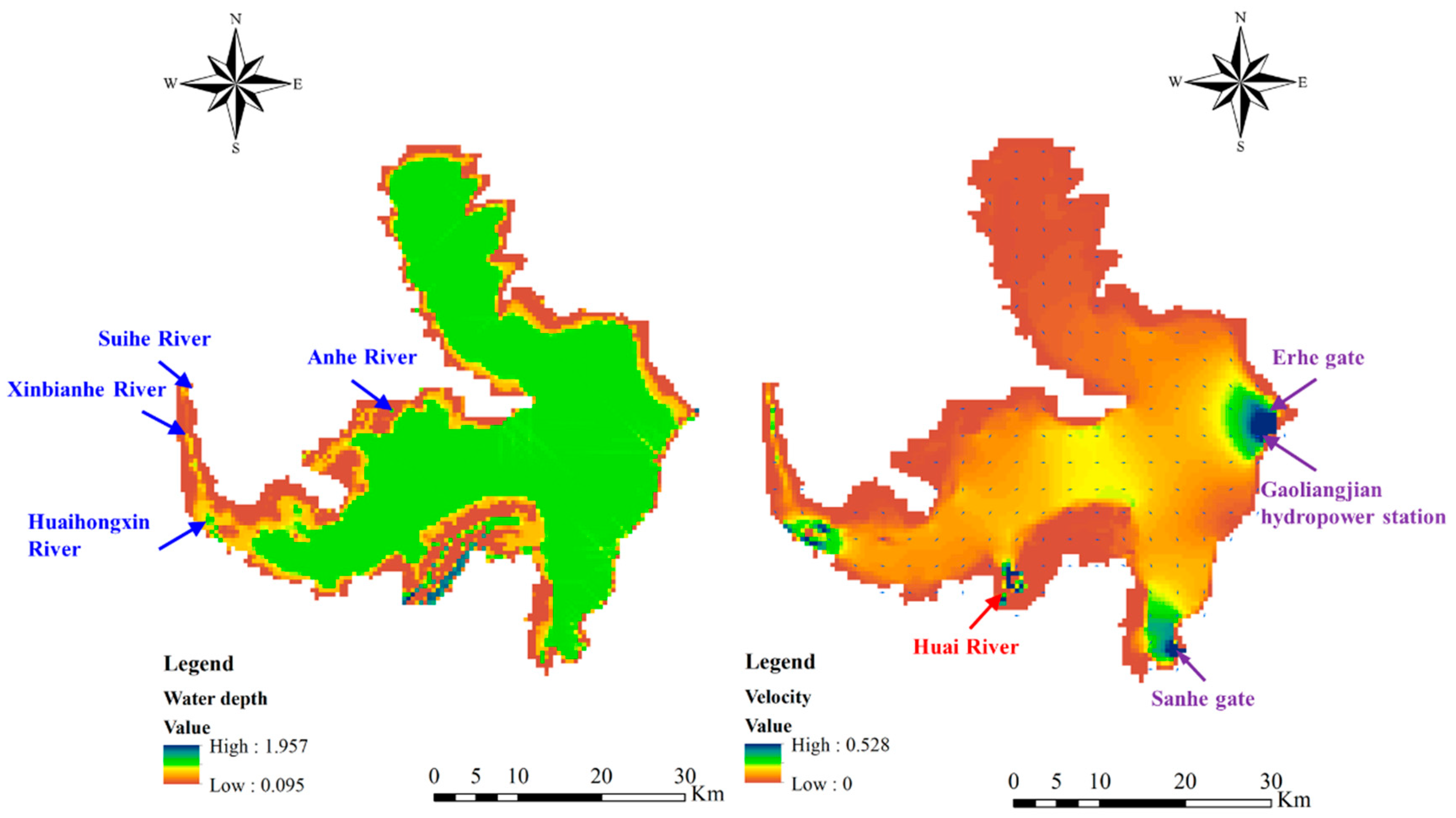
The runoff generated on the underlying surface was assigned differently to the river network in the hill area and plain area based on the digital elevation model. For the river network in the hill area, the runoff generated on the underlying surface was concentrated at the outlet of the sub-watershed and assigned to be upstream of the river. In the plain area, the land-use types for underlying surfaces included water, rain-fed land, construction land, and paddy field. The runoff generation process of different land-use types was calculated separately and lumped together for the sub-watershed based on the percentages of different land-use areas. As introduced in the second paper in the series, the fastest runoff concentration path (FRCP) with D8 procedure was promoted and adopted to deal with depressed pits on surface DEM and runoff path generation. In the D8 procedure, the runoff concentration path for a point was computed as the direction to the neighbor (based on 8-connectivity) which had minimum elevation and which was lower than the central point. The runoff on the underlying surface under grid processing was assigned to the nearest river cross-section individually rather than concentrated to the sub-watershed outlet or the upstream entrance. In the plain area, the runoff on each grid that was assigned to the corresponding river’s cross-section could be determined based on the DEM with the FRCP method. In the FRCP method, it was assumed that the runoff would be concentrated along the path with the shortest time between the outlet and upstream cells in the underlying surface. The detailed information about FRCP can be found in the second paper in this series.
2.1.2. One-Dimensional River Flow Simulation
In this case, the hydrodynamic method was used to determine the water surface elevation and flow distribution along cross-sections for river networks in plain areas. One-dimensional Saint‒Venant equations were used to describe the flow in the rivers:
where
q is the lateral inflow (m
2/s) from the surrounding surfaces;
Q is the flow rate of the cross-section (m
3/s);
A is the flow area (m
2);
B is the flow width (m);
z is the water depth (m);
Vx is the velocity of lateral flow along the main river, which was zero in this study;
K is the conveyance coefficient, which indicates the actual river convey capacity;
is the momentum correction coefficient, which describes the velocity distribution along the cross-section. The momentum correction coefficient can be calculated with
when the friction slopes are the same for the main channel and overbank area;
m is the number of the main-channel and overbank-area regions;
and
are the flow area and conveyance of the
jth flow region;
A and
K are the sum of
Aj and
Kj, respectively.
when the flow is limited in the main channel.
To discretize Equation (1) with a four-point linear implicit difference method for the
ith and (
i + 1)th cross-section of the river will yield Equation (2):
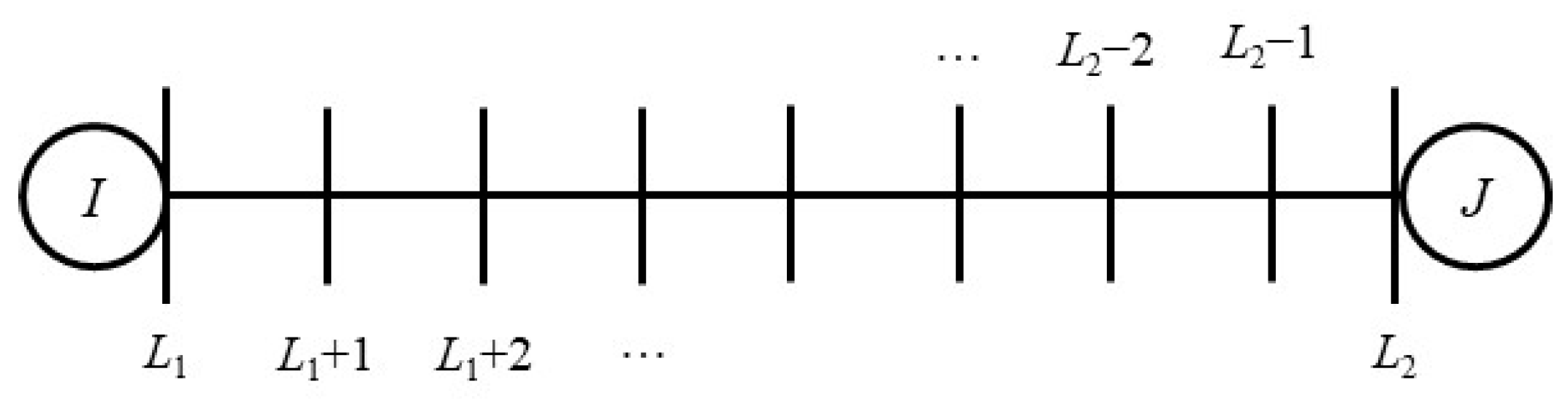
Figure 2 shows the discretization of a one-dimensional river branch between the starting and ending cross-sections. Equation (2) was discretized as shown in Equation (3) and solved by the chasing method. The relationship between the flow rate and water depth at the starting and ending cross-section could be derived by the chasing method. Therefore, the flowrate could be expressed as the linear relationship between the water depth at the starting and ending cross-sections.
where
and
are the flow rate and water depth, respectively, at the starting cross-section;
and
are the flow rate and water depth, respectively, at the ending cross-section. From the ending cross-section to the starting cross-section, the flow rate at every cross-section could be expressed as a linear relationship between the water depth at the current cross-section and the ending cross-section as shown as Equation (4):
where
i =
L2 − 1,
L2 − 2,
L2 − 3, …,
L1.
Similarly, from the starting cross-section to the ending cross-section, the flow rate at every cross-section could be expressed as the linear relationship between the water depth at the current cross-section and the starting cross-section as shown in Equation (5):
where
i =
L1 + 1,
L1 + 2,
L1 + 3, …,
L2.
Once the water depth at the starting and ending cross-sections was given (boundary condition), Equations (4) and (5) could be solved for the
ith cross-section between the starting and ending cross-sections:
The water depth at the
ith cross-section could be determined by solving Equation (6), yielding to:
The flow rate at the ith cross-section could be determined by substituting into Equation (6).
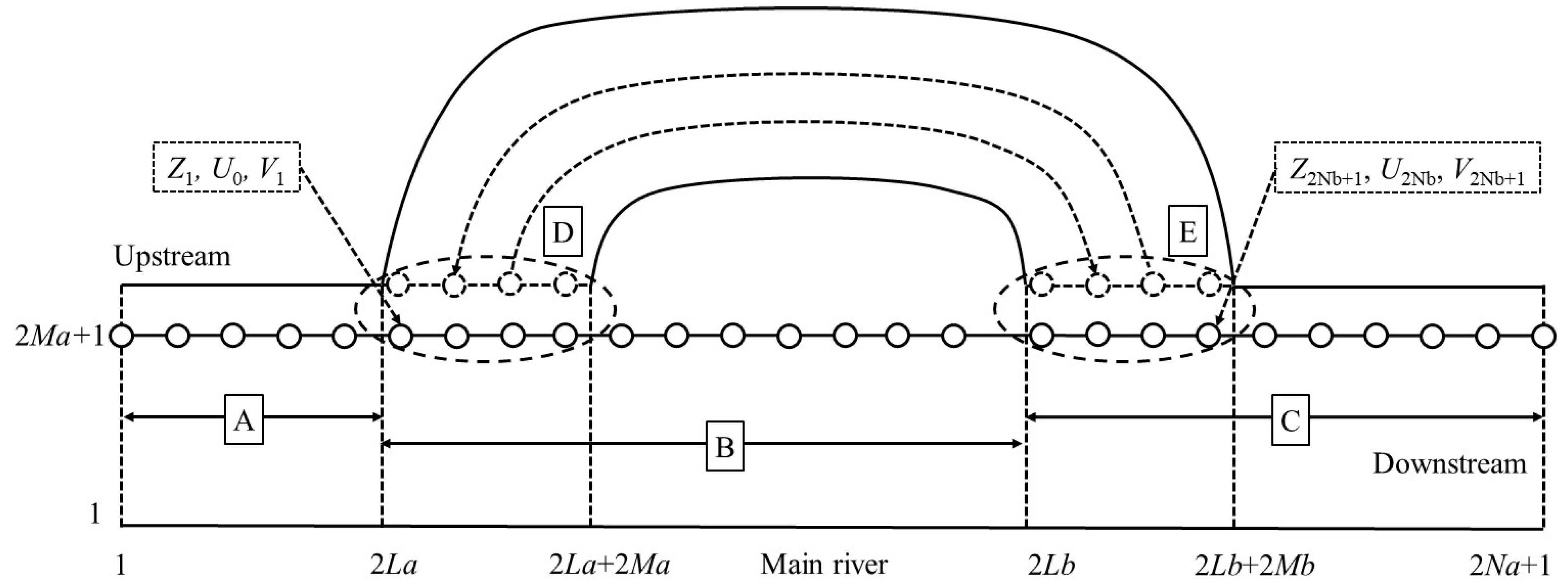
The intersection of two rivers was regarded as a computational node and treated via two different methods: (1) a node with a large surface area whose ponding volume could be calculated based on the surface area and ponding depth; (2) a node with a small surface area whose ponding volume could be neglected when the water depth changed in the node. The water depth in the node and the first cross-section were assumed to be the same, and the mass balance equation (Equation (8)) was used to calculate the water depth at the node:
where
is the ponding surface area in different water depths and
is the inflow and outflow of the node.
In one-dimensional river flow simulations, computing the water depth at the node is the key step for the river network flow simulation. The flow rate and water depth could be determined after the water depth at the node was calculated. The water depth at the node was also a key parameter to couple with the runoff generation module. A mass balance matrix could be constructed for all nodes in the river network and solved with the boundary node’s input value.
2.1.3. Two-Dimensional River Flow Simulation
The key step to couple one-dimensional and two-dimensional river network simulations is to find the water surface elevation at the node, which connects the one-dimensional model to a two-dimensional model. Different from the one-dimensional model, the computational nodes in a two-dimensional river network simulation were mainly selected from the smooth and steady section of the river branch. In the one-dimensional river network simulation, the nodes were primarily selected at the connection points of different river branches. Equation (9) is the governing equation that describes two-dimensional nonconservative flow motion in river networks:
where
,
, and
are time,
x- and
y-coordinates, respectively;
and
are the water depth and water surface elevation in the cell, respectively;
and
are the velocity in the
x- and
y-direction, respectively;
and
are the Manning’s coefficient and Coriolis coefficient, respectively;
and
are the dispersion coefficient in the
x- and
y-direction, respectively; and
is the source and sink term in the continuity equation that includes rainfall contribution, inflow, and outflow.
The boundary-fitted orthogonal coordinate transformation method was used to simulate complex boundaries and set the cell sizes when gridding the simulation river networks. The curvilinear grid system, with the computational boundary being coincident with the real river network boundary, was numerically obtained by solving the Poisson equation. Grids in the boundary-fitted coordinate system were made up of two groups of lines,
constant and
constant, respectively. Each point
in the physical domain corresponded with
in the boundary-fitted coordinate system. The boundary in the physical domain coincided with the isoline of
or
. Although the physical domain may be irregularly shaped, the transformed computational domain was foursquare. To simulate the irregular physical boundaries by the boundary-fitted coordinate transformation method, it was necessary to transform the basic differential equations and boundary conditions from
space to a boundary-fitted coordinate system in
space. In the DF-RMS, the grids were created by solving the Poisson equation, which means the transformations meet the Poisson equation (Equation (10)):
where
P and
Q are control functions that control the cell size and distribution.
With boundary-fitted orthogonal coordinate transformation, Equation (9) was transformed to Equation (11) in the
space:
where
and
;
and
are the velocities in the
- and
-directions:
;
;
and
are the length and width of the cell;
and
;
is the cell area;
,
and
are the Manning’s coefficient and Coriolis coefficient, respectively; and
and
are the dispersion coefficient in the
and
-directions, respectively.
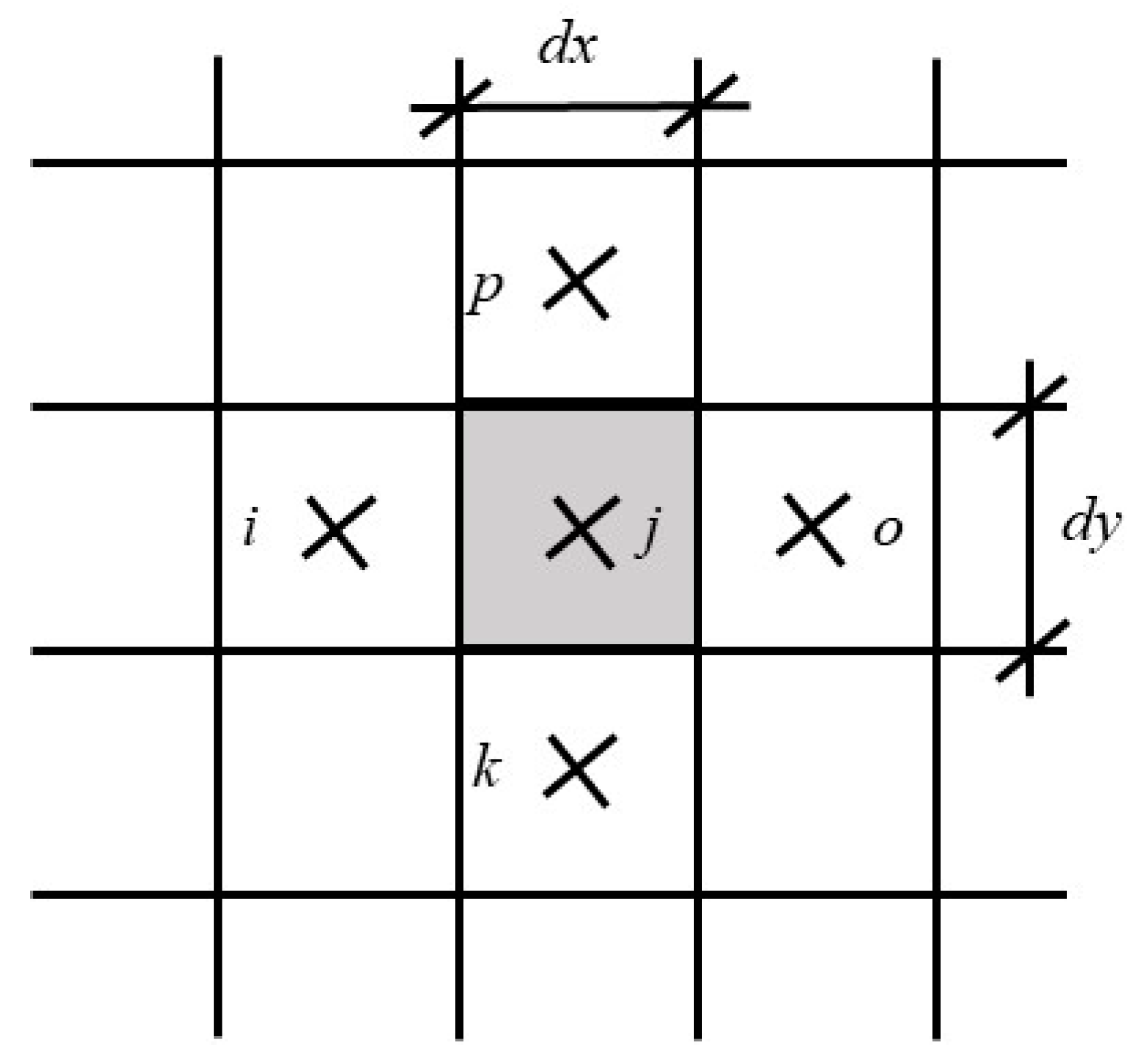
Figure 3 shows the boundary-fitted transformation and discretization of the physical river simulation domain (
Figure 3a) and the transformed numerical simulation domain (
Figure 3b). For convenience, the variables
z,
u, and
v are hereafter used to stand for water depth at the cell center, flow velocity in the
-direction, and flow velocity in the
-direction in the
and
space. The variables of water depth and flow velocity are numbered together in the computation code. The total variable number in the simulation domain for water depth, flow velocity in the
-direction, and flow velocity in the
-direction is
,
, and
, respectively. For convenience, three matrices were developed for variables
z,
u, and
v, which are listed in the following text. The variables with superscript “0” (
) and “1” (
) mean the parameter’s value of the current time step (
) and next time step (
), respectively.
Two boundary conditions of riverbank could be selected in the model: (1) wall condition, which means v = 0 and at the boundary; (2) inflow or outflow, which means v = inflow or outflow velocity and at the boundary. The water depth of upstream and downstream are given as boundary conditions in the simulation.
- (1)
The discretization of continuity Equation (Equation (11))
To discretize the continuity equation (Equation (11)) at node
for
will yield:
For the nonlinear term,
and
, which yield:
In this case, the nonlinear term will be discretized as:
and
where
is the water surface elevation of the node (
),
;
is the water depth of node (
) and equal to the water surface elevation minus cell bottom elevation;
is the water surface elevation of the node (
),
.
Finally, the continuity equation was discretized as in the following formation:
In Equation (14):
.
The matrix was built-up with the following format:
where the dimensions of matrices
,
,
,
, and
are
; the dimensions of the matrix
are
; and the dimension of the matrix
is
.
- (2)
The discretization of momentum Equation (Equation (12))
To discretize the momentum equation in the
-direction (Equation (12)) at node
will yield:
To discretize the terms
and
with the upwind scheme will yield:
The term
was discretized as follows:
The term
was discretized as follows:
The term
was discretized as follows:
Substituting all discretized terms into Equation (12) and building-up the linear matrix for the node
yields:
Similarly, we can discretize the momentum equation in the
-direction (Equation (21)) at node
and build-up the linear matrix in the following format:
where the dimensions of matrices
,
,
,
, and
are
; the dimensions of matrices
and
are
; the dimensions of matrices
,
, and
are
; the dimensions of matrices
,
, and
are
; and the dimensions of matrices
and
are
and
, respectively.
- (3)
Solving the continuity and momentum matrix with boundary condition
The , , and variables could be solved by combining Equations (15)–(17) and the known boundary variables with the chasing method.
For the upstream boundary condition, we have
and
to plot into Equation (16), which is in the following format:
We can rearrange the equation to develop the relationship between these unknown variables:
We plotted two upstream boundary condition variables and Equation (18) into Equation (17) to find
:
We plotted upstream boundary condition
, substituting Equations (18) and (19) into Equation (15) to find
:
We substituted Equations (18)–(20) into Equation (16) to find
:
For
,
was determined by the following equation:
where the dimensions of matrices
,
,
, and
are
; the dimensions of matrices
and
are
; the dimensions of matrices
and
are
; the dimensions of matrix
are
; the dimension of matrices
and
is
; and the dimension of the matrix
is
.
The downstream boundary conditions are also given as and . It was assumed that , so we can substitute these known variables into Equation (21) to find the variables , , , …, for the current time step. Three properties were found in the matrix buildup and chasing method procedure: (1) most of the matrix was composed of three diagonal matrices (, , , , , , , , , , , , , , , , , , and ) and some other diagonal matrices, which reduces the computational load and cost to a considerable extent; (2) the ratio of river width to river length is tiny for most of the river network (), which means the matrix operation was not very complex; (3) this method was mostly focused on the matrix operation, which is similar to the implicit method, and the computational time step could be huge with a Courant number ~100 and different to the explicit method.