Jacobian Free Methods for Coupling Transport with Chemistry in Heterogenous Porous Media
Abstract
:1. Introduction
- Mineral species:
- We extend the capabilities of the equilibrium chemical solver to handle mineral precipitation and dissolution;
- 2D geometries:
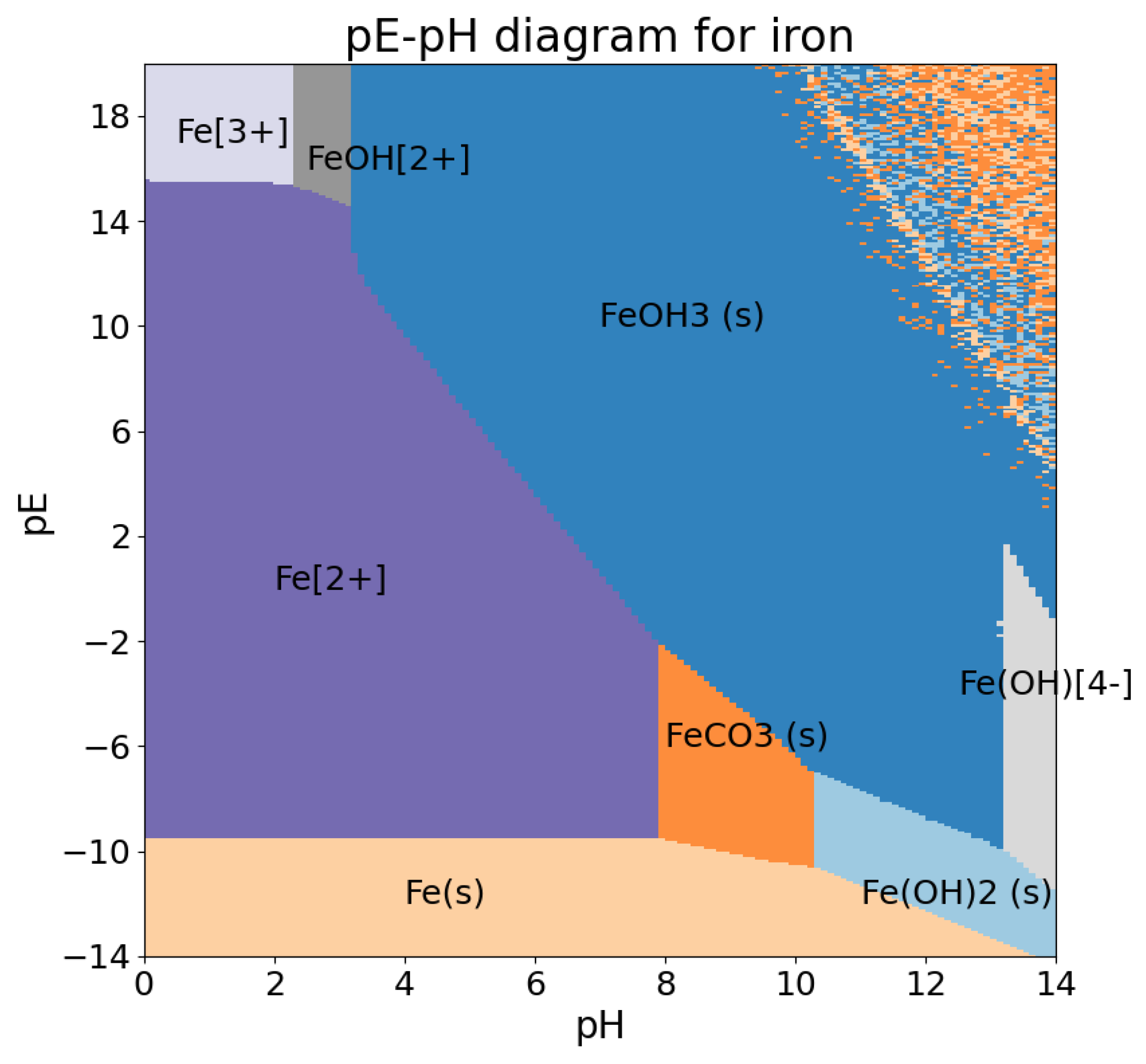
- The potential pH diagram for iron is used to validate the interior point Newton method;
- A 2D variant of the ion exchange system used in Example 11 of the PhreeqC documentation [37]. This test case involves 8 chemical species undergoing 3 ion-exchange reactions, in a simple 2D geometry.
- The so-called SHPCO2 benchmark that involves 11 chemical species, distributed among 3 phases, and undergoing 4 reactions. One species is a mineral, and one is a gas.
2. Physical Model and Mathematical Formulation
2.1. The Model
- R1
- H+ + OH− ⇄ H2O
- R2
- CO32− + H+ ⇄ HCO3−
- R3
- X2Ca + 2 Na+ ⇄ 2XNa + Ca2+
- R4
- Ca2+ + CO32− ⇄ CaCO3(s).
- Dirichlet boundary:
- on ,
- Neumann boundary:
- on , where n is the outgoing normal to along .
2.2. Elimination of the Reaction and Coupled Problem
3. The Coupled Problem
3.1. Reduction of the Coupled Problem
3.2. Semi-Discrete System in Time
- Fixed point
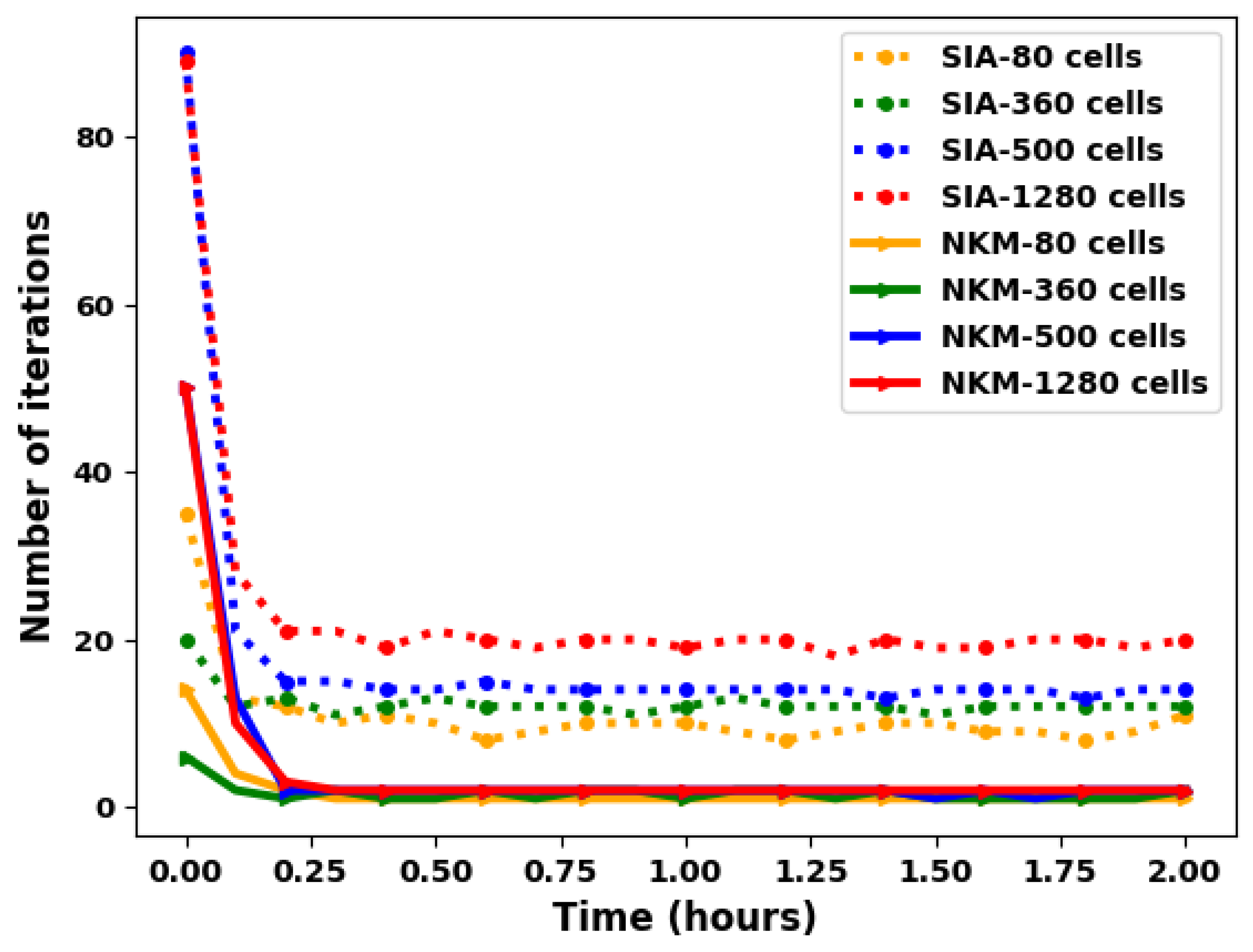
- A fixed point iteration for solving (16) is known in the reactive transport literature as the Sequential Iterative Approach (SIA, see [4,43,44,45] among many references).At each time step n, one iterates between transport and chemistry. More precisely, for each iteration k, one computesThe iterations are stopped when the relative progress indicatorbecomes small enough.One can easily show that this is equivalent with the more standard description of SIA involving three unknowns and .
- Newton–Krylov
- As was shown in previous work by the authors [22,23], the coupled system (15) can also be solved by a Newton–Krylov method, leading to a more efficient algorithm.Recall that at each step of the “pure” form of Newton’s method for solving , one should compute the Jacobian matrix , solve the linear systemusually by Gaussian elimination, and then set . In practice, one should use some form of globalization procedure in order to ensure convergence from an arbitrary starting point. If a line search is used, the last step should be replaced by , where is determined by the line search procedure [46].In our context, however, solving the linearized system (18) exactly, or even computing the J matrix, is not possible as both and are implicitly defined functions. It was shown in our previous work (see [22,23]) that this difficulty could be circumvented by resorting to the Newton–Krylov method (see [24,25,46], to which our work is closely related). The Newton–Krylov method is a variant of Newton’s method where the linear system (18) is solved by an iterative method (of Krylov type), for instance GMRES [47]. The advantage of this choice is that the Jacobian matrix J is no longer required. Instead one needs a procedure to compute the product for any given vector v.
4. Numerical Methods for Transport Furthermore, Chemistry
4.1. Solution of the Chemical Equilibrium Problem by an Interior Point Method
- Computing the Newton step
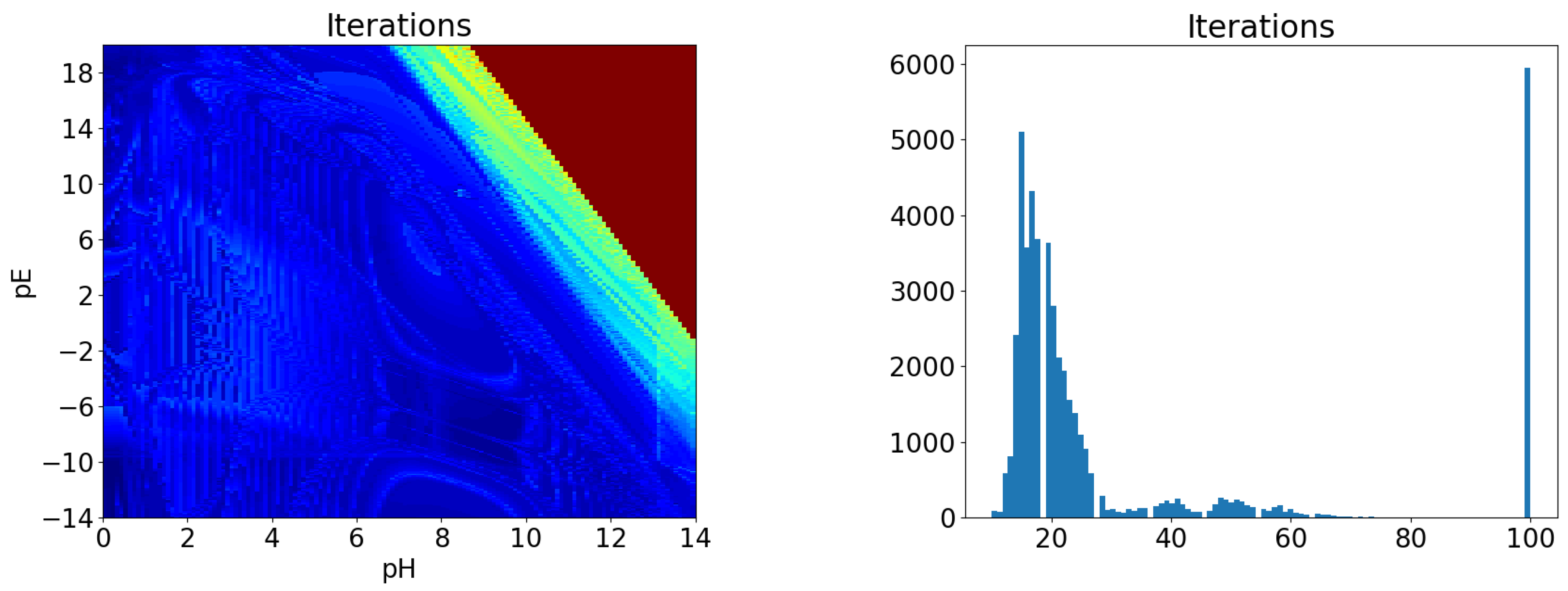
- Each Newton iteration requires the solution of a linear systemwhere the Jacobian of system (22) is given by:where , and I is an identity matrix of the appropriate size. These systems can become severely ill-conditioned (see [49]) so that Gaussian elimination may give inaccurate solutions. We monitor the condition number of the Jacobian and if it is larger than , so that the solution may have no correct digit, we perform a singular value decomposition and compute a least squares solution.
- Damping
- After the Newton step has been computed, we apply two steps of damping: the first one reduces the step to ensure that the iterates for p and z remain positive, and the second one is a line search that makes sure the size of the residual is reduced along the Newton direction.
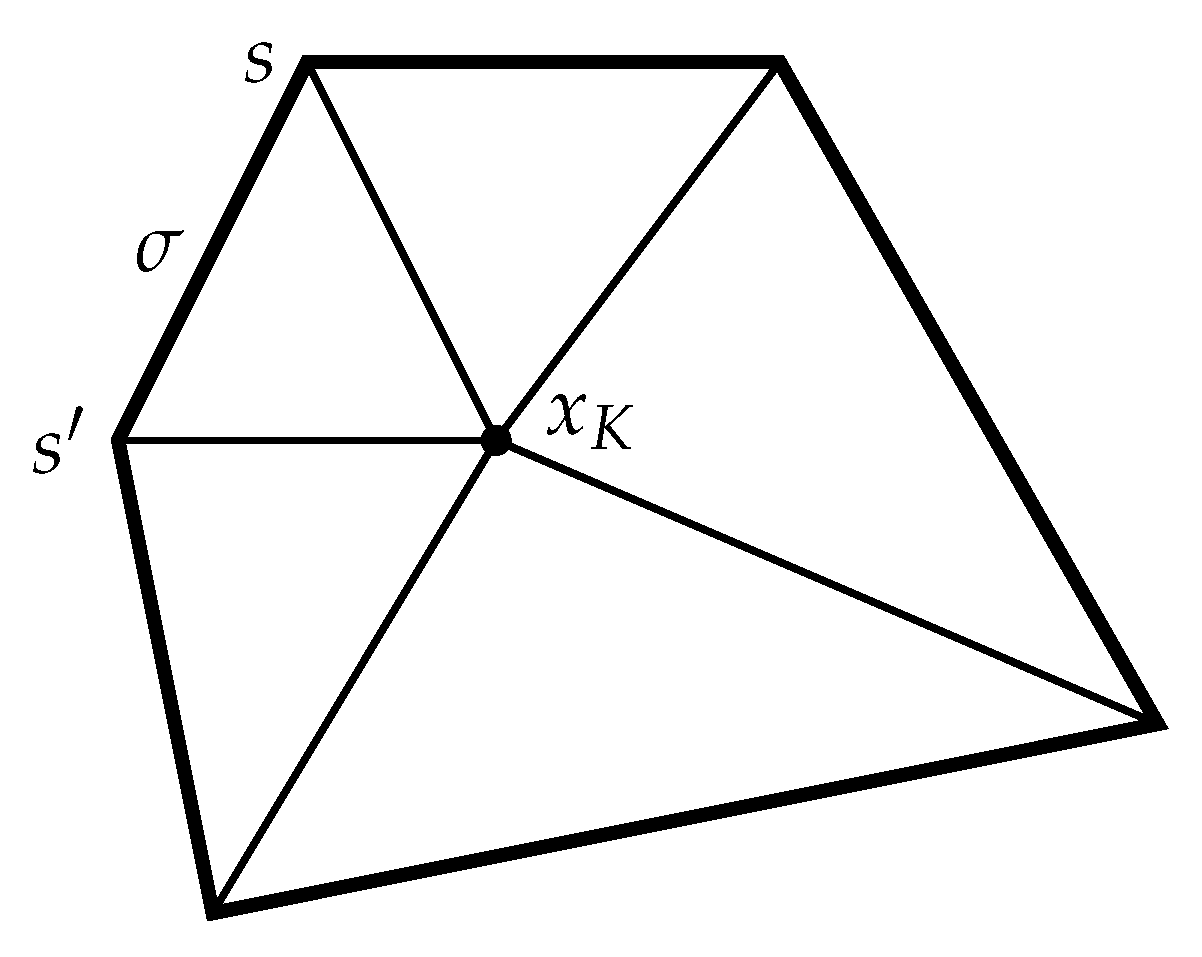
4.2. The VAG Scheme
4.3. The Discrete Coupled Problem
- the column vector of concentrations of all chemical species at the DOF j.
- the row vector of concentrations of species i at all DOFs.
- One step of a transport problem for each chemical species;
- One chemical equilibrium problem for each vertex and each cell.
5. Numerical Results
5.1. Validation Example for the Interior Point Method: The Iron Precipitation Diagram
5.2. 2D Test Case: Example 11 of PhreeQC
5.2.1. Description of the Test Case
| Ca | Na | Cl | K | X | ||
|---|---|---|---|---|---|---|
| CaX2 | 1 | 0 | 0 | 0 | 2 | 3.4576 |
| NaX | 0 | 1 | 0 | 0 | 1 | 0 |
| KX | 0 | 0 | 0 | 1 | 1 | 0.7 |
| Total | TCa | TNa | TCl | TK | W |
- 1D configuration:
- The injection is made on the entire left boundary of the domain, which leads to a solution that depends only on x. This allows for a quick check of the method;
- 2D configuration:
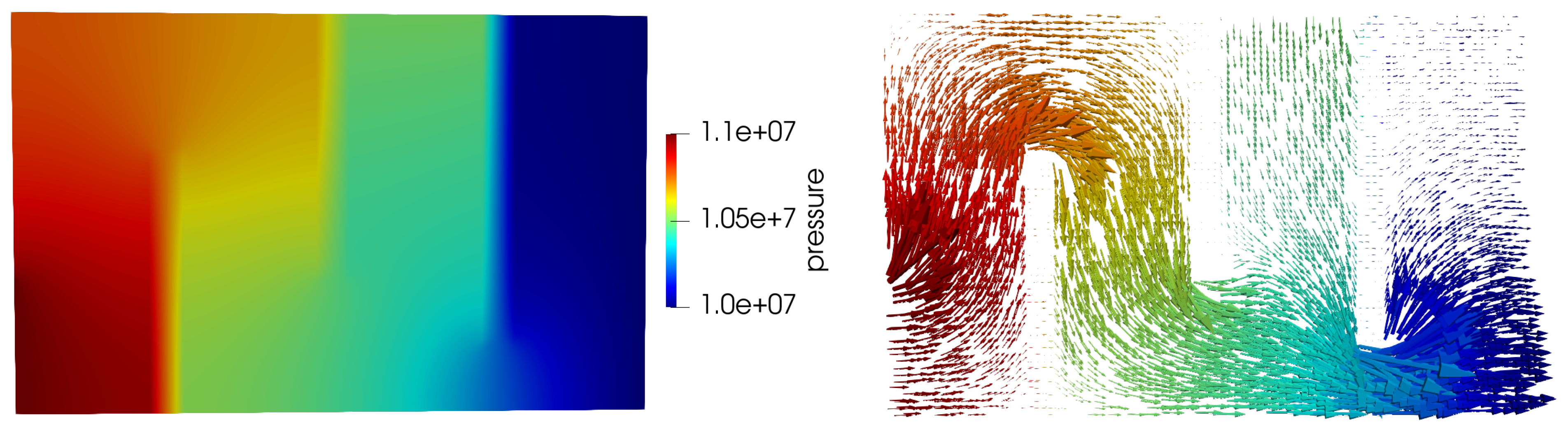
- The injection is made only on a part of the left boundary of the domain, which gives rise to a genuinely two-dimensional solution.
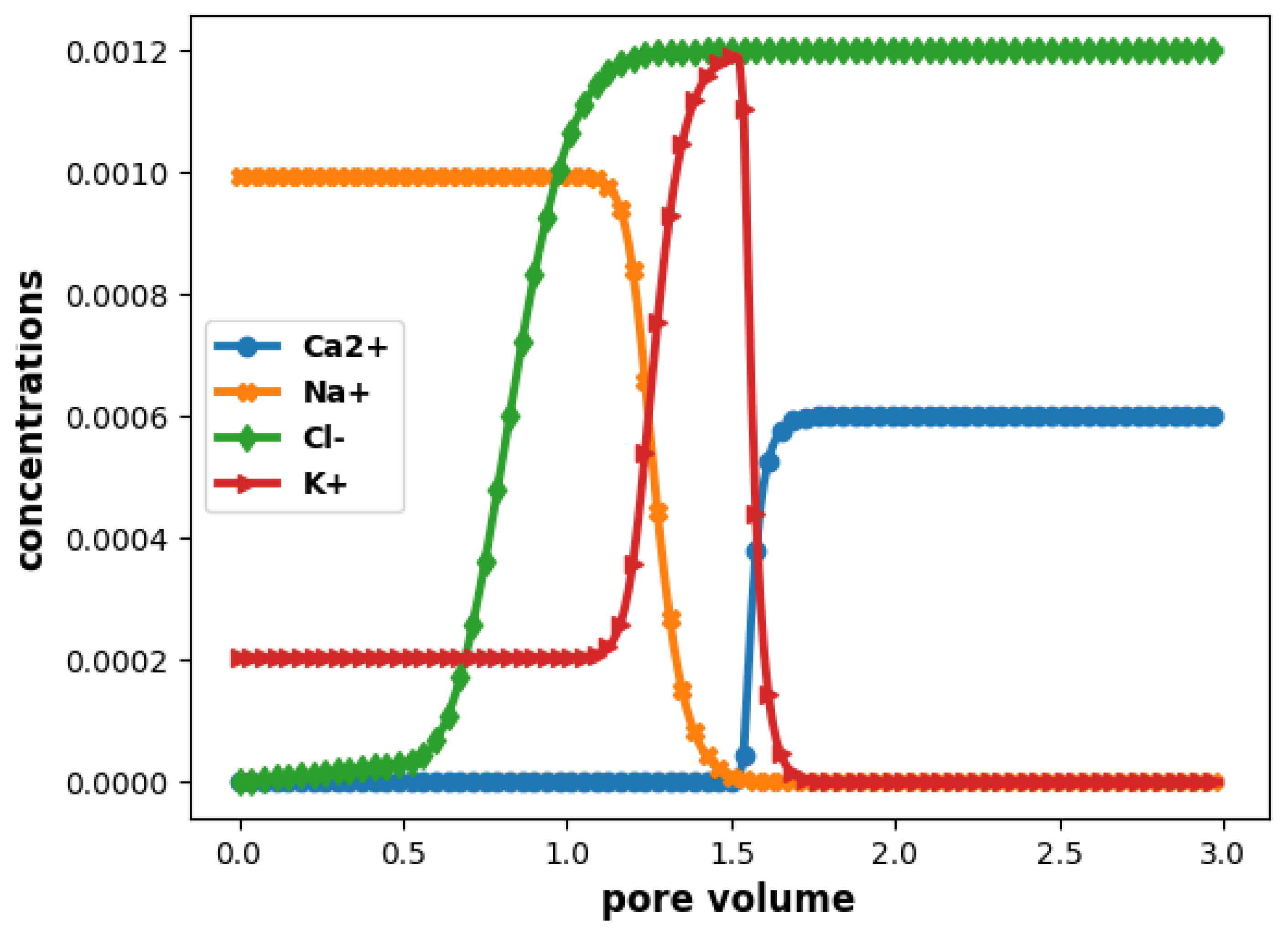
5.2.2. Numerical Results
1D Configuration
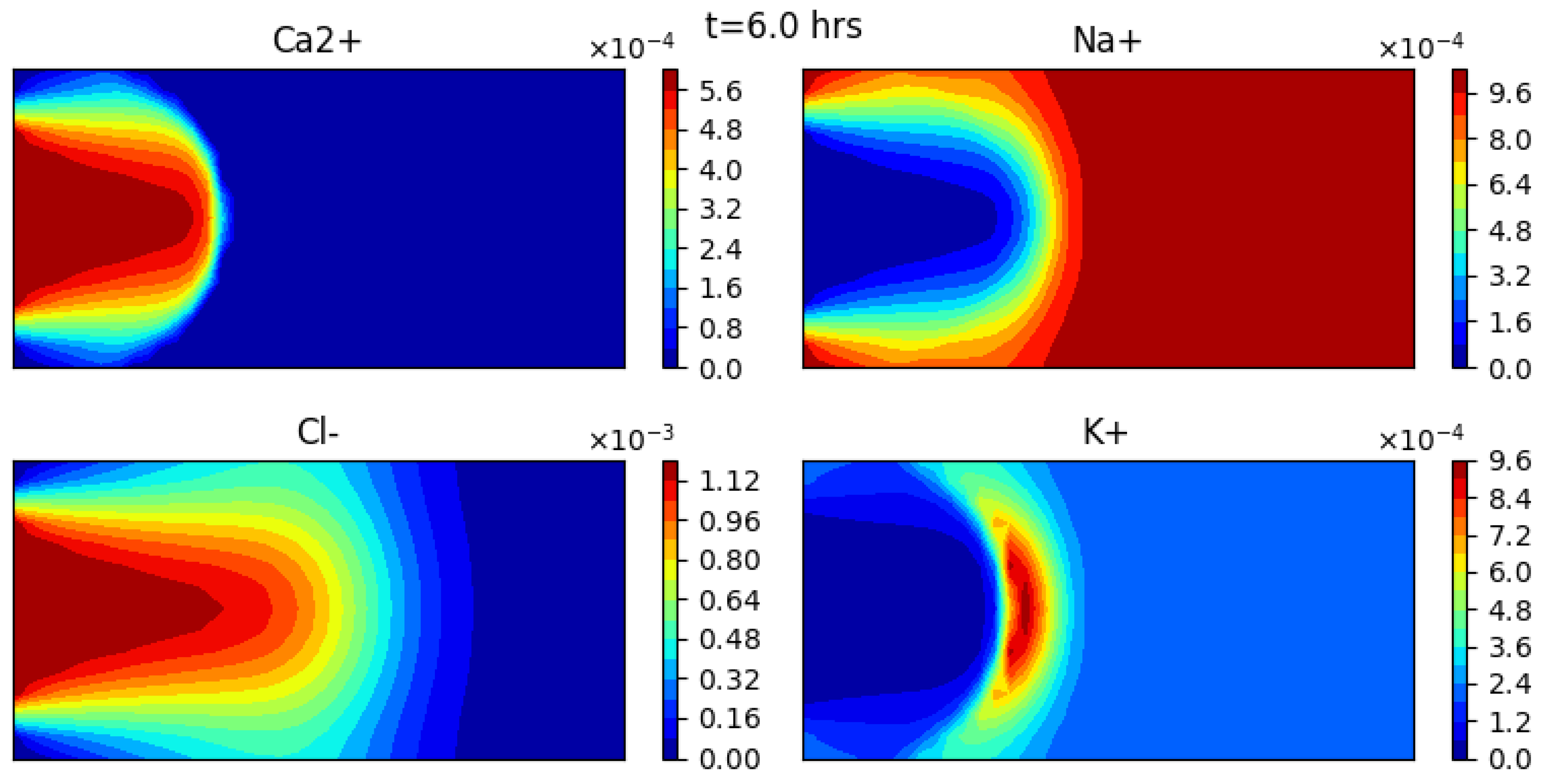
2D Configuration
5.2.3. Performance of the Elimination Method
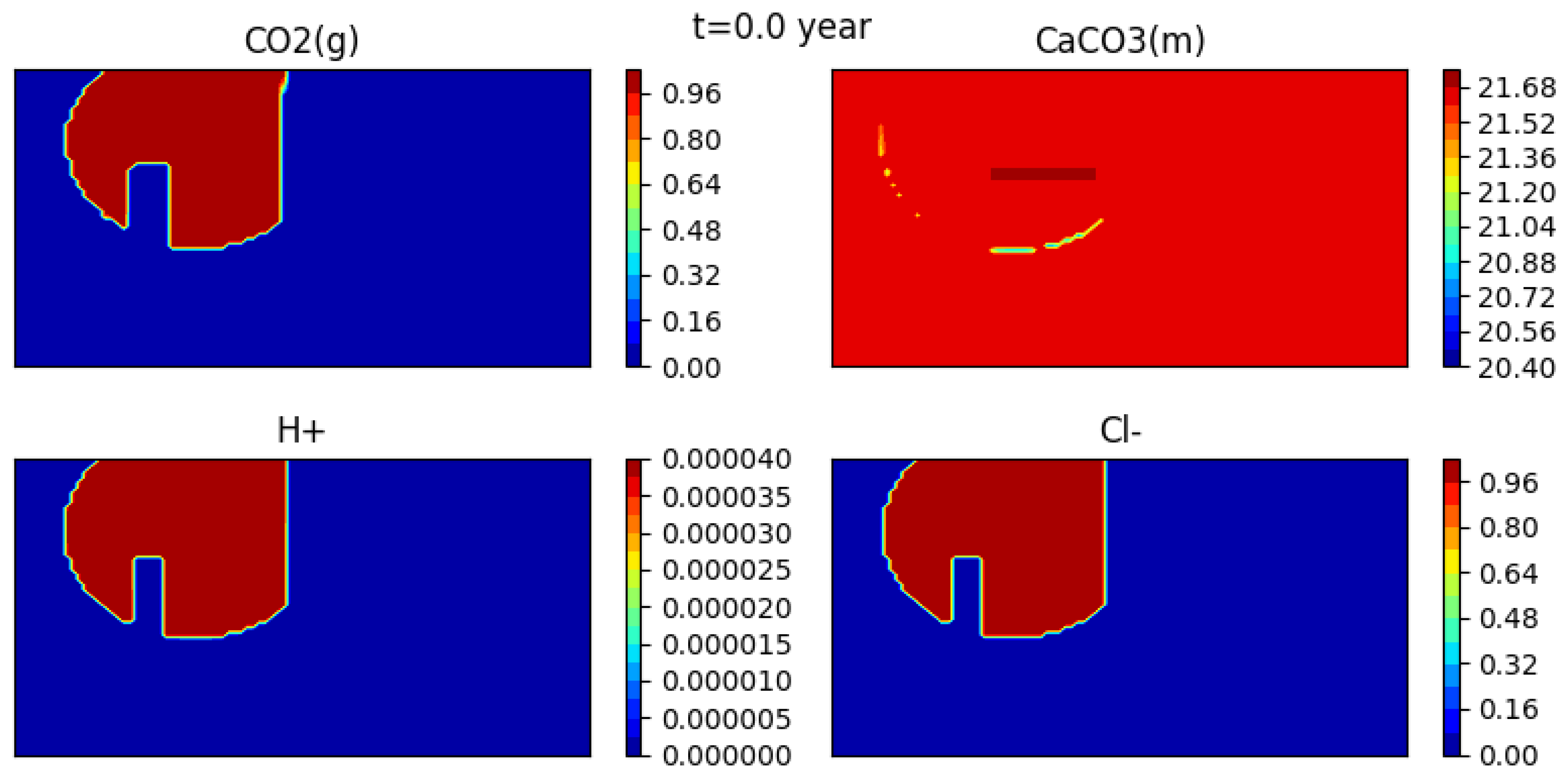
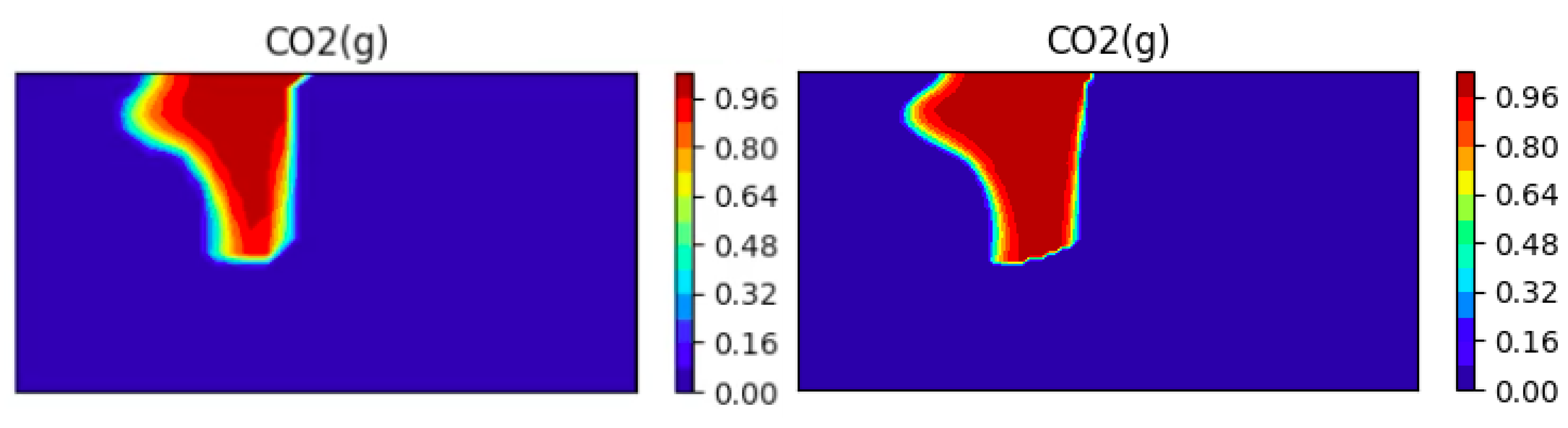
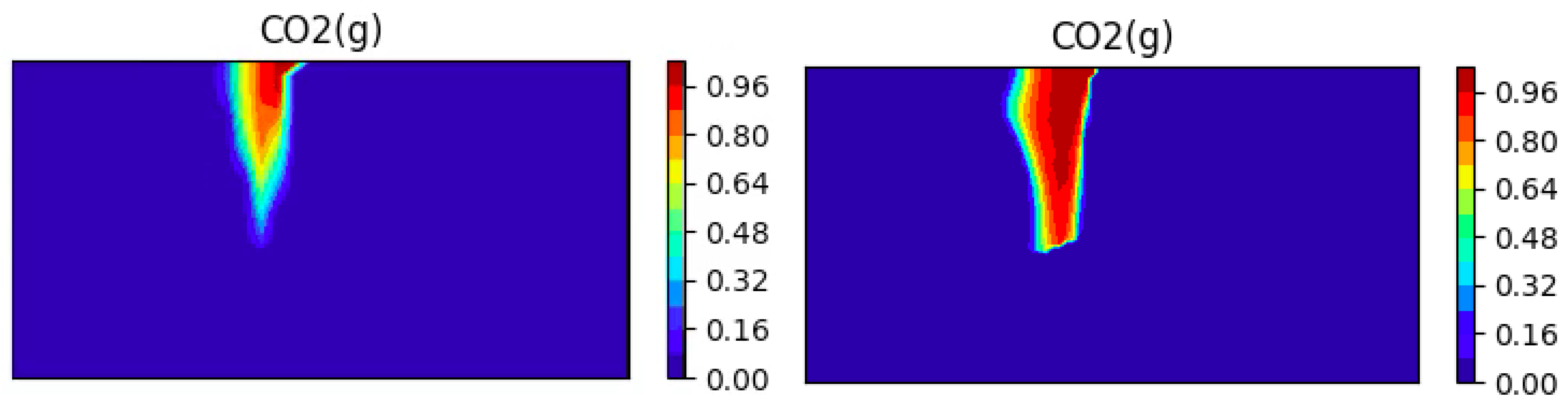
5.3. SHPCO2 Benchmark
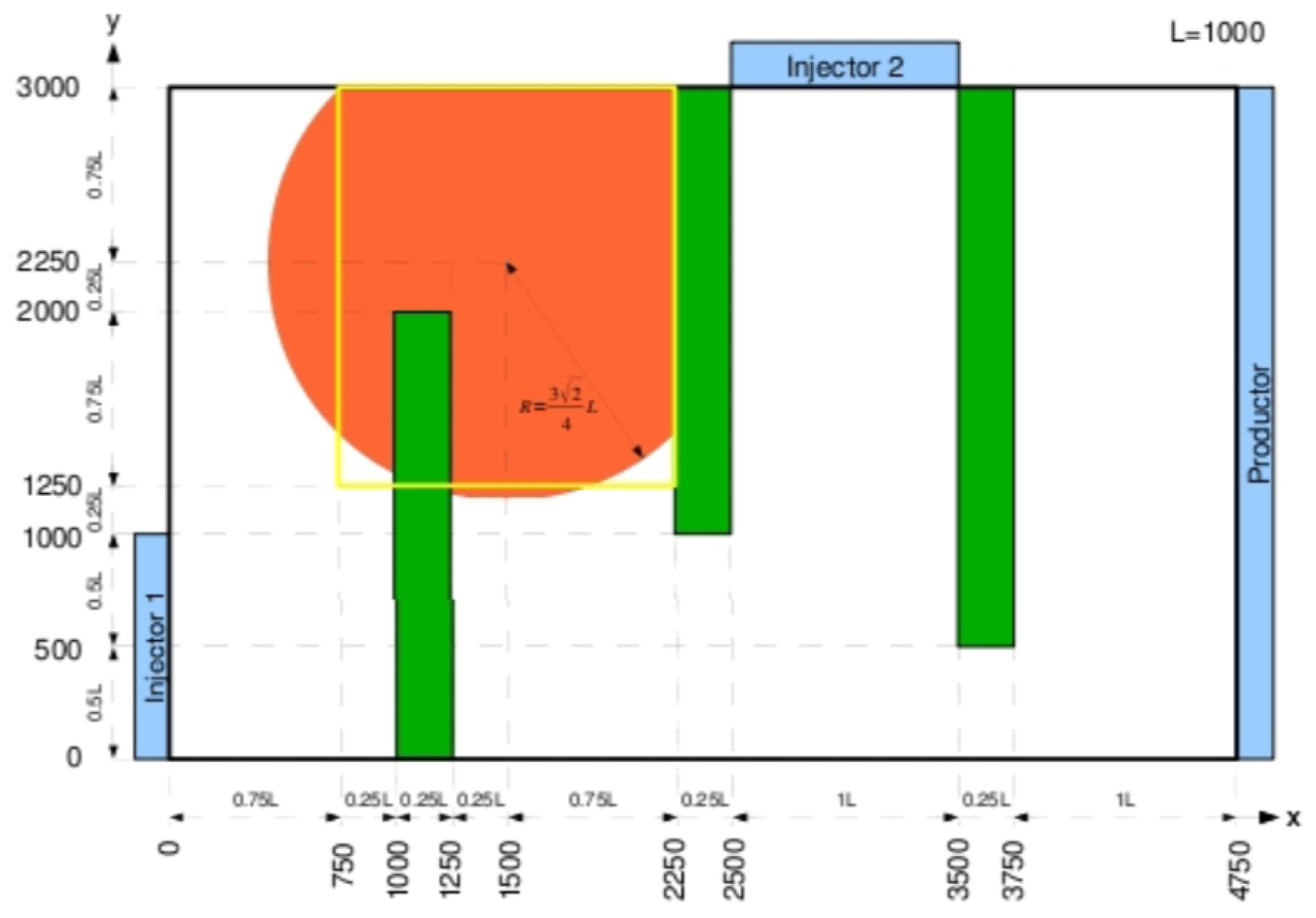
5.3.1. Description of the Test Case
Geometry and Physical Data
Chemical System
- Five liquid primary components: water (H2O), hydrogen ion (H+), carbon dioxide dissolved in water (CO2(l)), calcium ion (Ca2+), chlorine (Cl−);
- Two secondary liquid components: hydroxide ion (OH−), hydrogen carbonate (HCO3−);
- One fixed precipitated component: calcite (CaCO3);
- One gas component: gaseous carbon dioxide (CO2(g)).
- Two aqueous equilibrium reactions:
- Two precipitation–dissolution reactions (taken here to be at equilibrium):
Initial State
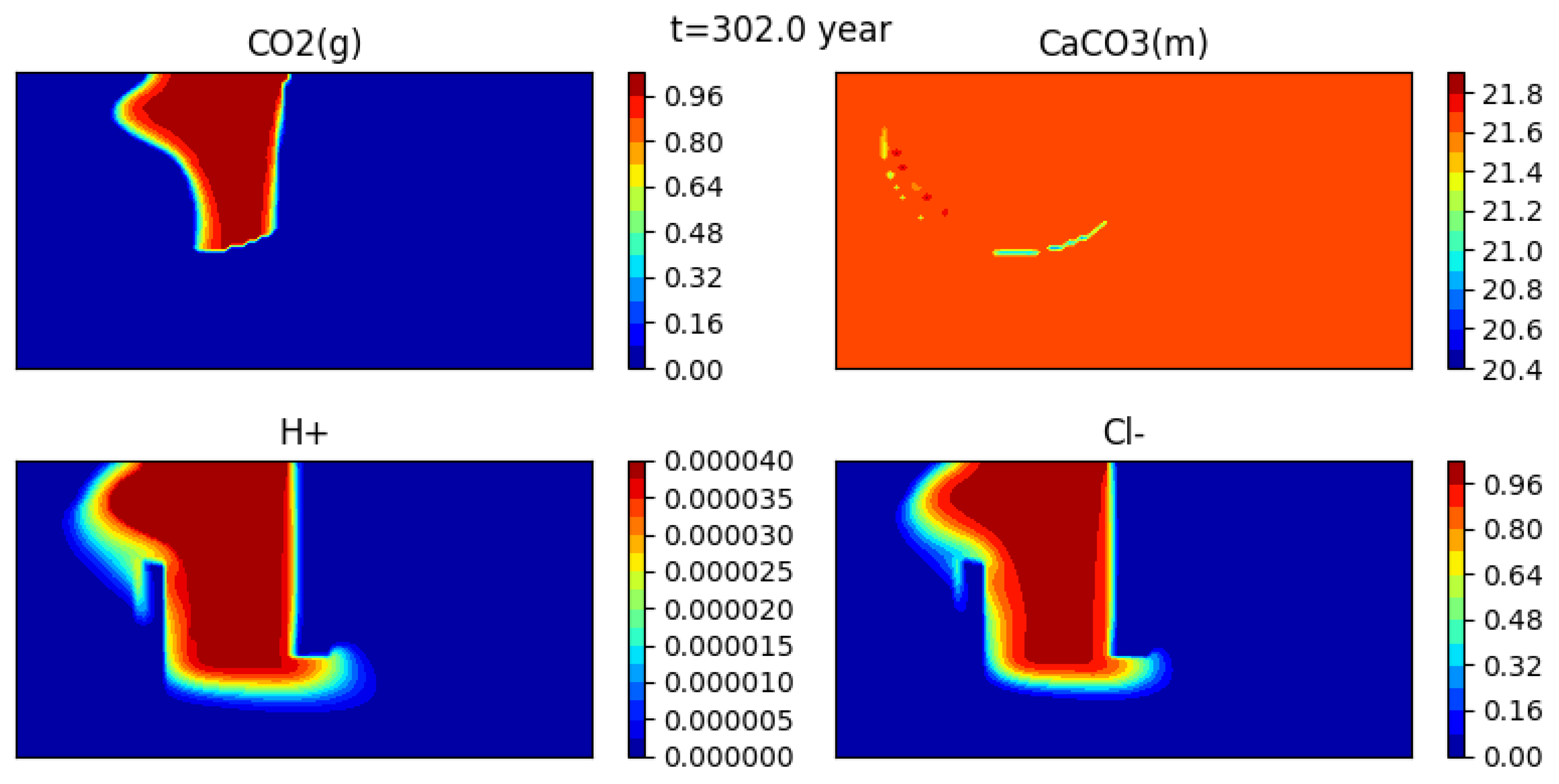
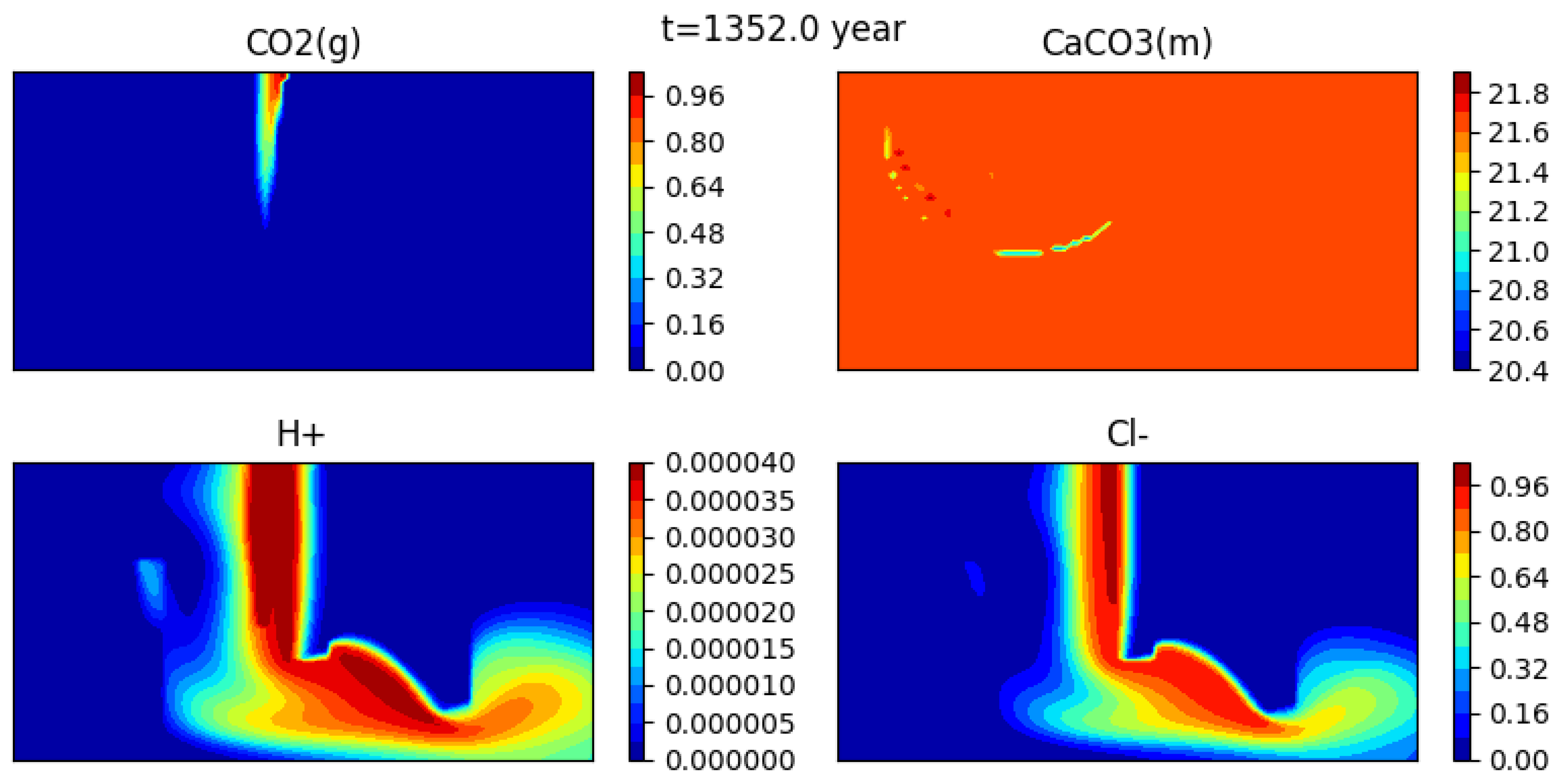
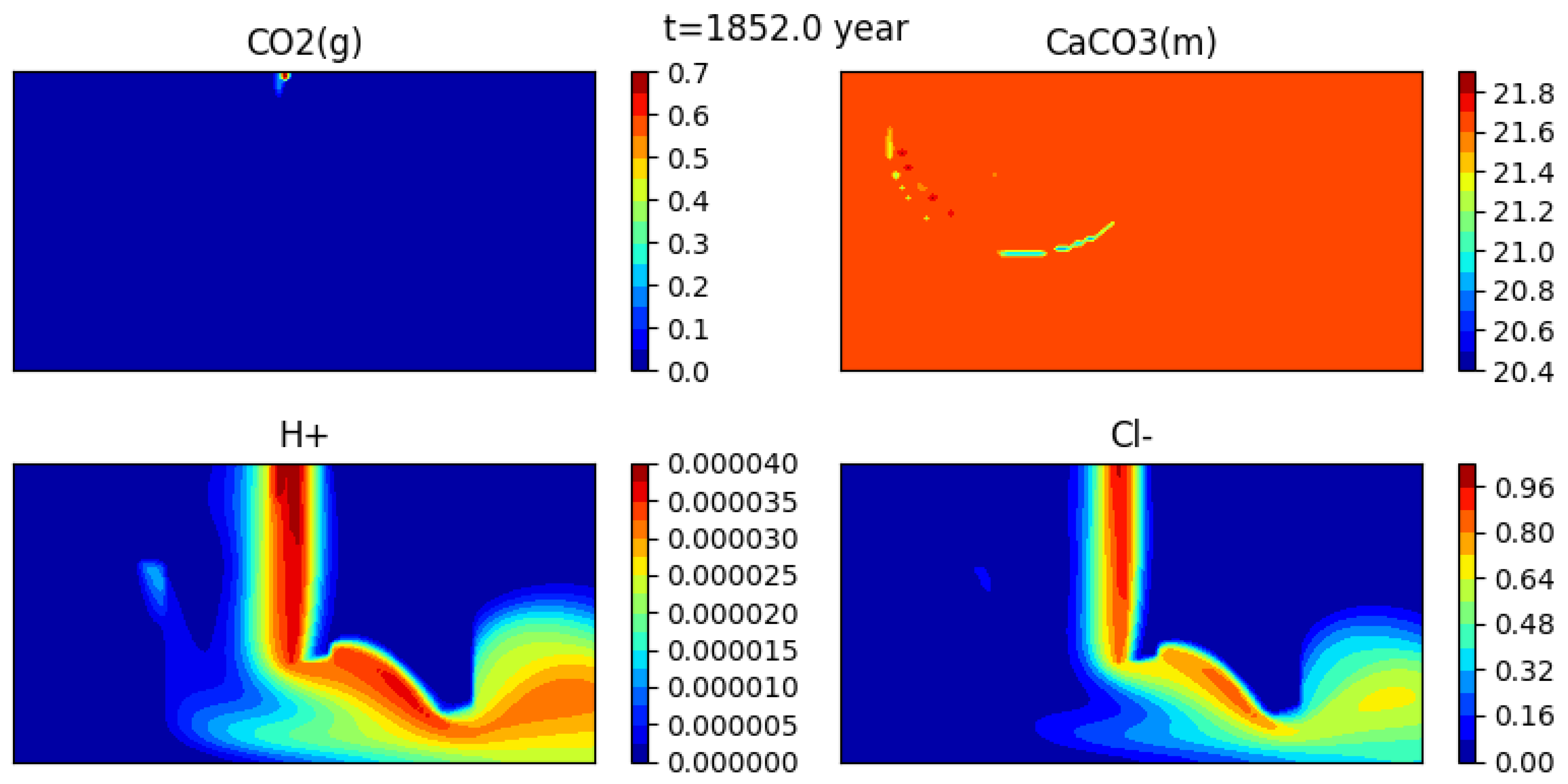
5.3.2. Numerical Results
Evolution of Concentrations
Comparison of the Dissolution CO2(g) on Two Different Meshes
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Yeh, G.; Parker, J. (Eds.) Groundwater Reactive Transport Models; Bentham Publishers: Sharjah, United Arab Emirates, 2012. [Google Scholar]
- Steefel, C.I.; Appelo, C.A.J.; Arora, B.; Jacques, D.; Kalbacher, T.; Kolditz, O.; Lagneau, V.; Lichtner, P.C.; Mayer, K.U.; Meeussen, J.C.L.; et al. Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 2015, 19, 445–478. [Google Scholar] [CrossRef] [Green Version]
- Steefel, C.; DePaolo, D.; Lichtner, P. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Yeh, G.T.; Tripathi, V.S. A critical evaluation of recent developments in hydrogeochemical transport models of reactive multichemical components. Water Resour. Res. 1989, 25, 93–108. [Google Scholar] [CrossRef]
- Carrayrou, J.; Mosé, R.; Behra, P. Operator-splitting procedures for reactive transport and comparison of mass balance errors. J. Contam. Hydrol. 2004, 68, 239–268. [Google Scholar] [CrossRef]
- Lagneau, V.; van der Lee, J. HYTEC results of the MoMas reactive transport benchmark. Comput. Geosci. 2010, 14, 435–449. [Google Scholar] [CrossRef] [Green Version]
- Mayer, K.U.; Frind, E.O.; Blowes, D.W. Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resour. Res. 2002, 38, 1174. [Google Scholar] [CrossRef]
- Samper, J.; Xu, T.; Yang, C. A sequential partly iterative approach for multicomponent reactive transport with CORE2D. Comput. Geosci. 2008, 13, 301–316. [Google Scholar] [CrossRef] [Green Version]
- Yeh, G.T.; Tripathi, V.S. A Model for Simulating Transport of Reactive Multispecies Components: Model Development and Demonstration. Water Resour. Res. 1991, 27, 3075–3094. [Google Scholar] [CrossRef]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T.B. MIN3P-HPC: A High-Performance Unstructured Grid Code for Subsurface Flow and Reactive Transport Simulation. Math. Geosci. 2020. [Google Scholar] [CrossRef]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT—A simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: Applications to geothermal injectivity and CO2 geological sequestration. Comput. Geosci. 2006, 32, 145–165. [Google Scholar] [CrossRef]
- Yapparova, A.; Gabellone, T.; Whitaker, F.; Kulik, D.A.; Matthäi, S.K. Reactive Transport Modelling of Dolomitisation Using the New CSMP++GEM Coupled Code: Governing Equations, Solution Method and Benchmarking Results. Transp. Porous Med. 2017, 117, 385–413. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Durlofsky, L.J.; Tchelepi, H.A. A fully-coupled flow-reactive-transport formulation based on element conservation, with application to CO2 storage simulations. Adv. Water Resour. 2012, 42, 47–61. [Google Scholar] [CrossRef]
- Ahusborde, E.; El Ossmani, M.; Moulay, M.I. A fully implicit finite volume scheme for single phase flow with reactive transport in porous media. Math. Comput. Simul. 2019, 164, 3–23. [Google Scholar] [CrossRef]
- Hoffmann, J.; Kräutle, S.; Knabner, P. A parallel global-implicit 2-D solver for reactive transport problems in porous media based on a reduction scheme and its application to the MoMaS benchmark problem. Comput. Geosci. 2009, 14, 421–433. [Google Scholar] [CrossRef]
- Kräutle, S.; Knabner, P. A new numerical reduction scheme for fully coupled multicomponent transport-reaction problems in porous media. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Kräutle, S.; Knabner, P. A reduction scheme for coupled multicomponent transport-reaction problems in porous media: Generalization to problems with heterogeneous equilibrium reactions. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- de Dieuleveult, C.; Erhel, J.; Kern, M. A global strategy for solving reactive transport equations. J. Comput. Phys. 2009, 228, 6395–6410. [Google Scholar] [CrossRef]
- De Dieuleveult, C.; Erhel, J. A global approach to reactive transport: Application to the MoMas benchmark. Comput. Geosci. 2010, 14, 451–464. [Google Scholar] [CrossRef] [Green Version]
- Erhel, J.; Sabit, S. Analysis of a Global Reactive Transport Model and Results for the MoMaS Benchmark. Math. Comput. Simul. 2017, 137, 286–298. [Google Scholar] [CrossRef] [Green Version]
- Erhel, J.; Sabit, S.; de Dieuleveult, C. Solving Partial Differential Algebraic Equations and Reactive Transport Models. In Developments in Parallel, Distributed, Grid and Cloud Computing for Engineering; Topping, B.H.V., Ivànyi, P., Eds.; Computational Science, Engineering and Technology Series; Saxe Coburg Publications: London, UK, 2013; pp. 151–169. [Google Scholar]
- Amir, L.; Kern, M. A global method for coupling transport with chemistry in heterogeneous porous media. Comput. Geosci. 2010, 14, 465–481. [Google Scholar] [CrossRef] [Green Version]
- Amir, L.; Kern, M. Preconditioning a Coupled Model for Reactive Transport in Porous Media. Int. J. Numer. Anal. Model. 2019, 16, 18–48. [Google Scholar]
- Knoll, D.A.; Keyes, D.E. Jacobian-free Newton-Krylov methods: A survey of approaches and applications. J. Comput. Phys. 2004, 193, 357–397. [Google Scholar] [CrossRef] [Green Version]
- Hammond, G.E.; Valocchi, A.; Lichtner, P. Application of Jacobian-free Newton–Krylov with physics-based preconditioning to biogeochemical transport. Adv. Water Resour. 2005, 28, 359–376. [Google Scholar] [CrossRef]
- Carr, E.; Turner, I.; Perré, P. A variable-stepsize Jacobian-free exponential integrator for simulating transport in heterogeneous porous media: Application to wood drying. J. Comput. Phys. 2013, 233, 66–82. [Google Scholar] [CrossRef]
- Guo, L.; Huang, H.; Gaston, D.R.; Permann, C.J.; Andrs, D.; Redden, G.D.; Lu, C.; Fox, D.T.; Fujita, Y. A parallel, fully coupled, fully implicit solution to reactive transport in porous media using the preconditioned Jacobian-Free Newton-Krylov Method. Adv. Water Resour. 2013, 53, 101–108. [Google Scholar] [CrossRef]
- Kräutle, S. The semismooth Newton method for multicomponent reactive transport with minerals. Adv. Water Resour. 2011, 34, 137–151. [Google Scholar] [CrossRef]
- Buchholzer, H.; Kanzow, C.; Knabner, P.; Kräutle, S. The semismooth Newton method for the solution of reactive transport problems including mineral precipitation-dissolution reactions. Comput. Optim. Appl. 2011, 50, 193–221. [Google Scholar] [CrossRef] [Green Version]
- Kräutle, S. Existence of global solutions of multicomponent reactive transport problems with mass action kinetics in porous media. J. Appl. Anal. Comput. 2011, 1, 497–515. [Google Scholar]
- El-Bakry, A.S.; Tapia, R.A.; Tsuchiya, T.; Zhang, Y. On the formulation and theory of the Newton interior-point method for nonlinear programming. J. Optim. Theory Appl. 1996, 89, 507–541. [Google Scholar] [CrossRef]
- Leal, A.M.M.; Kulik, D.A.; Smith, W.R.; Saar, M.O. An overview of computational methods for chemical equilibrium and kinetic calculations for geochemical and reactive transport modeling. Pure Appl. Chem. 2017, 89, 597–643. [Google Scholar] [CrossRef]
- Saaf, F.E. A Study of Reactive Transport Phenomena in Porous Media. Ph.D. Thesis, Rice University, Houston, TX, USA, 1997. [Google Scholar]
- Arbogast, T.; Bryant, S.; Dawson, C.; Saaf, F.; Wang, C.; Wheeler, M. Computational methods for multiphase flow and reactive transport problems arising in subsurface contaminant remediation. J. Comput. Appl. Math. 1996, 74, 19–32. [Google Scholar] [CrossRef] [Green Version]
- Lopez, S.; Masson, R.; Beaude, L.; Birgle, N.; Brenner, K.; Kern, M.; Smaï, F.; Xing, F. Geothermal Modeling in Complex Geological Systems with the ComPASS Code. In Stanford Geothermal Workshop 2018—43rd Workshop on Geothermal Reservoir Engineering; Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Eymard, R.; Guichard, C.; Herbin, R. Small-stencil 3D schemes for diffusive flows in porous media. ESAIM Math. Model. Numer. Anal. 2012, 46, 265–290. [Google Scholar] [CrossRef] [Green Version]
- Parkhurst, D.L.; Appelo, C. User’s Guide to PHREEQC (Version 2)—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; Technical Report 99-4259; USGS: Reston, VA, USA, 1999. [Google Scholar]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Rubin, J. Transport of reacting Solutes in Porous Media: Relation Between Mathematical Nature of Problem Formulation and Chemical Nature of reactions. Water Resour. Res. 1983, 19, 1231–1252. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, A.H.D. Modeling Groundwater Flow and Contaminant Transport; Theory and Applications of Transport in Porous Media; Springer: Berlin/Heidelberg, Germany, 2010; Volume 23. [Google Scholar]
- Saaltink, M.; Ayora, C.; Carrera, J. A Mathematical Formulation for Reactive Transport that Eliminates Mineral Concentrations. Water Resour. Res. 1998, 34, 1649–1656. [Google Scholar] [CrossRef]
- Fahs, M.; Carrayrou, J.; Younes, A.; Ackerer, P. On the efficiency of the direct substitution approach for reactive transport problems in porous media. Water Air Soil Pollut. 2008, 193, 299–308. [Google Scholar] [CrossRef]
- Saaltink, M.; Carrera, J.; Ayora, C. On the behavior of approaches to simulate reactive transport. J. Contam. Hydrol. 2001, 48, 213–235. [Google Scholar] [CrossRef]
- Kanney, J.F.; Miller, C.T.; Kelley, C.T. Convergence of Iterative Split Operator Approaches for Approximating Nonlinear Reactive Transport Problems. Adv. Water Resour. 2003, 26, 247–261. [Google Scholar] [CrossRef] [Green Version]
- Saaltink, M.; Carrera, J.; Ayora, C. A Comparison of Two Approaches for Reactive Transport Modelling. J. Geochem. Explor. 2000, 69–70, 97–101. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Linear and Nonlinear Equations; With Separately Available Software, Frontiers in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1995; Volume 16, pp. 154–165. [Google Scholar]
- Saad, Y.; Schultz, M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, J.; Kräutle, S.; Knabner, P. A general reduction scheme for reactive transport in porous media. Comput. Geosci. 2012, 16, 1081–1099. [Google Scholar] [CrossRef]
- Marinoni, M.; Carrayrou, J.; Lucas, Y.; Ackerer, P. Thermodynamic Equilibrium Solutions Through a Modified Newton Raphson Method. AIChE J. 2016, 63, 1246–1262. [Google Scholar] [CrossRef]
- Wolery, T.; Jarek, R.L. Software User’s Manual; EQ3/6, Version 8.0; Sandia National Laboratories: Albuquerque, Bernalillo, 2003. [Google Scholar]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Series in Operations Research; Springer: New York, NY, USA, 2003; Volume I, pp. 34, 624, I69. [Google Scholar]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Series in Operations Research; Springer: New York, NY, USA, 2003; Volume II, pp. 1–34, 625–1234, II1–II57. [Google Scholar]
- Bethke, C.M. Geochemical and Biogeochemical Reaction Modeling, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Carrayrou, J. Looking for some reference solutions for the reactive transport benchmark of MoMaS with SPECY. Comput. Geosci. 2010. [Google Scholar] [CrossRef]
- Leal, A.M.; Blunt, M.J.; LaForce, T.C. Efficient chemical equilibrium calculations for geochemical speciation and reactive transport modelling. Geochim. Cosmochim. Acta 2014, 131, 301–322. [Google Scholar] [CrossRef] [Green Version]
- Eymard, R.; Guichard, C.; Herbin, R.; Masson, R. Vertex centred discretization of two-phase Darcy flows on general meshes. In Congrès National de Mathématiques Appliquées et Industrielles; ESAIM Proc.; EDP Sciences: Les Ulis, France, 2011; Volume 35, pp. 59–78. [Google Scholar] [CrossRef]
- Eymard, R.; Guichard, C.; Herbin, R.; Masson, R. Vertex-centred discretization of multiphase compositional Darcy flows on general meshes. Comput. Geosci. 2012, 16, 987–1005. [Google Scholar] [CrossRef] [Green Version]
- Dalissier, E.; Guichard, C.; Havé, P.; Masson, R.; Yang, C. ComPASS: A tool for distributed parallel finite volume discretizations on general unstructured polyhedral meshes. In CEMRACS 2012; ESAIM Proc.; EDP Sciences: Les Ulis, France, 2013; Volume 43, pp. 147–163. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Brookins, D.G. Eh-pH Diagrams for Geochemistry; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Carrayrou, J. Modélisation du Transport de Solutes Réactifs en Milieu Poreux Saturé. Thèse de Doctorat, Université Louis Pasteur, Strasbourg, France, 2001. [Google Scholar]
- Ogata, A.; Banks, R.B. A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media; Technical Report Prof. Pap., 411-A; USGS: Reston, VA, USA, 1961. [Google Scholar]
- Feike, L.; Dane, J.H. Analytical solution of the one dimensional advection equation equation and two- or tree-dimentional dispersion equation. Water Ressources Res. 1990, 26, 1475–1482. [Google Scholar]
- Haeberlein, F. Time Space Domain Decomposition Methods for Reactive Transport—Application to CO2 Geological Storage. Thèse de Doctorat, Université Paris 13, Paris, France, 2011. [Google Scholar]
- Ahusborde, E.; El Ossmani, E. A sequential approach for numerical simulation of two-phase multicomponent flow with reactive transport in porous media. Math. Comput. Simul. 2017, 137, 71–89. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Darcy Velocity (/) | |
| Diffusion coeff (/) | |
| Domain dimensions () | 0.1 × 0.015 |
| Mesh size () | 0.002 × 0.0015 |
| Time duration (day) | 1 |
| Comp. | ||
|---|---|---|
| Ca2+ | 0 | |
| Cl− | 0 | |
| K+ | 0 | |
| Na+ | 0 |
| Constants | Bulk | Barriers |
|---|---|---|
| Permeability K | ||
| Diffusion coefficient D | ||
| Porosity | 0.2 | 0.2 |
| HO | H | CO(l) | Ca | Cl | ||
|---|---|---|---|---|---|---|
| OH− | 1 | 0 | 0 | 0 | ||
| HCO3− | 1 | 1 | 0 | 0 | ||
| CO2(g) | 0 | 0 | 1 | 0 | 0 | |
| CaCO3 | 1 | 1 | 1 | 0 | ||
| Total |
| Components | [mol/L] | [mol/L] |
|---|---|---|
| H2O | ||
| H+ | ||
| CO2(l) | ||
| Ca2+ | ||
| Cl− | 0 | 1 |
| Start Time (Year) | End Time (Year) | Timestep (Year) |
|---|---|---|
| 0 | 2 | 0.1 |
| 2 | 20 | 1 |
| 20 | 400 | 10 |
| 400 | 1210 | 50 |
| 1210 | 1900 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amir, L.; Kern, M. Jacobian Free Methods for Coupling Transport with Chemistry in Heterogenous Porous Media. Water 2021, 13, 370. https://doi.org/10.3390/w13030370
Amir L, Kern M. Jacobian Free Methods for Coupling Transport with Chemistry in Heterogenous Porous Media. Water. 2021; 13(3):370. https://doi.org/10.3390/w13030370
Chicago/Turabian StyleAmir, Laila, and Michel Kern. 2021. "Jacobian Free Methods for Coupling Transport with Chemistry in Heterogenous Porous Media" Water 13, no. 3: 370. https://doi.org/10.3390/w13030370






