Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems
Abstract
1. Introduction
2. Fundamentals and Methods
2.1. Energy Intensity Framework
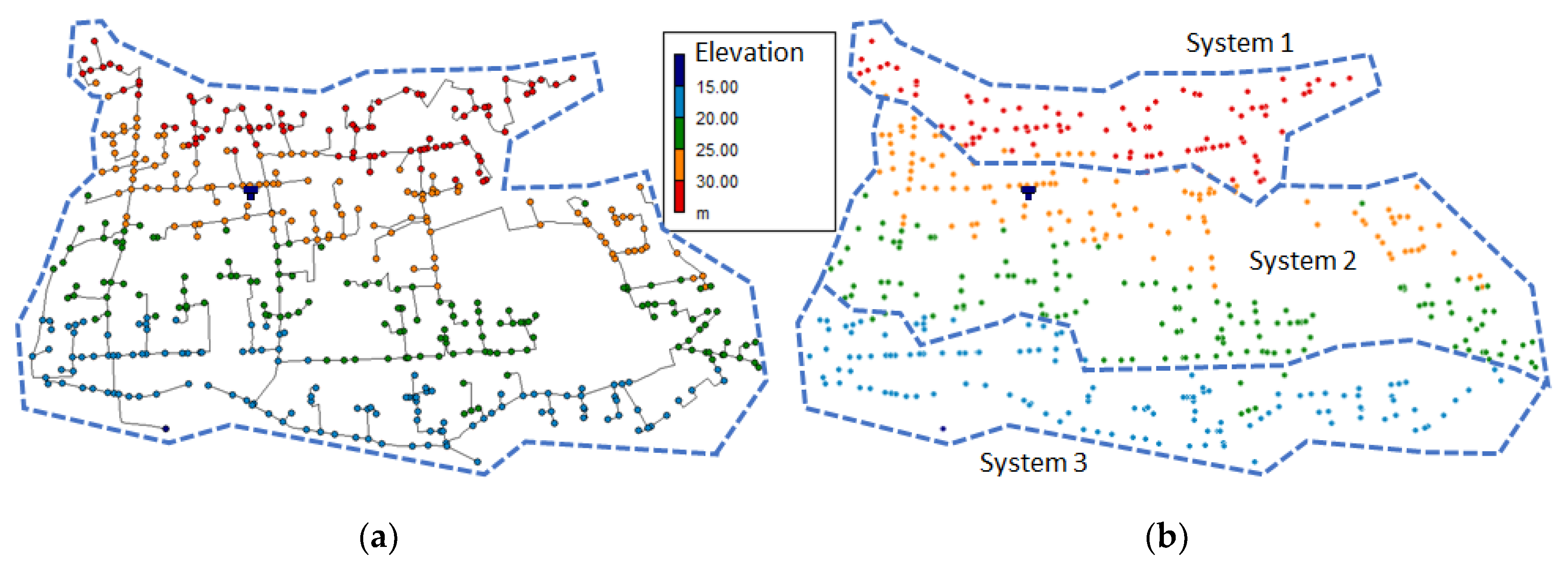
- Figure 1, shows a real pressurized network for the irrigation of agricultural plots (Cap de Terme, Spain). Each plot is represented as a node in the model. All nodes are included in the system and supplied from a pumping station (Figure 1a). Following an optimization study, it was determined that it was more energetically efficient to divide the irrigation area in three sectors based on node elevation [36]. As a result, three independent pumping stations were set up, resulting in three fully decoupled individual systems (Figure 1b).
2.2. Factors Influencing a System’s Energy Needs
- Topography, summarized in three elevation figures: the elevation of the network’s lowest node (which sets the reference level), the elevation of the most energy-demanding node (as explained later, in a few cases it is not the same as the highest node), and the source’s elevation;
- The distances traveled by water;
- The natural energy supplied to the system;Factors linked to service conditions;
- The pressure values at the supply sources (usually zero) and at the delivery nodes (dependent on use), where any excess of pressure over the required value leads to energy loss; and
- The water volume injected to the system Vt, the spatial distribution of water delivered to users (with the corresponding elevations), and the total metered volume Vr;
- Pumping efficiency;
- Leakage; and
- Friction losses.
- Analytically estimated values (top-down): estimated energy intensity (Iee), including all the supplied energy (natural and pumped), or the estimated pump energy intensity (Iee,p), only considering mechanical or shaft energy; and
- Real values (bottom-up), calculated from real operating data: real energy intensity (Ier), including all supplied energy (Es), and the real pump energy intensity (Ier,p), which only accounts for shaft energy (Ep).
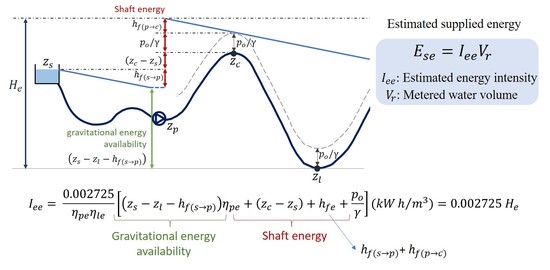
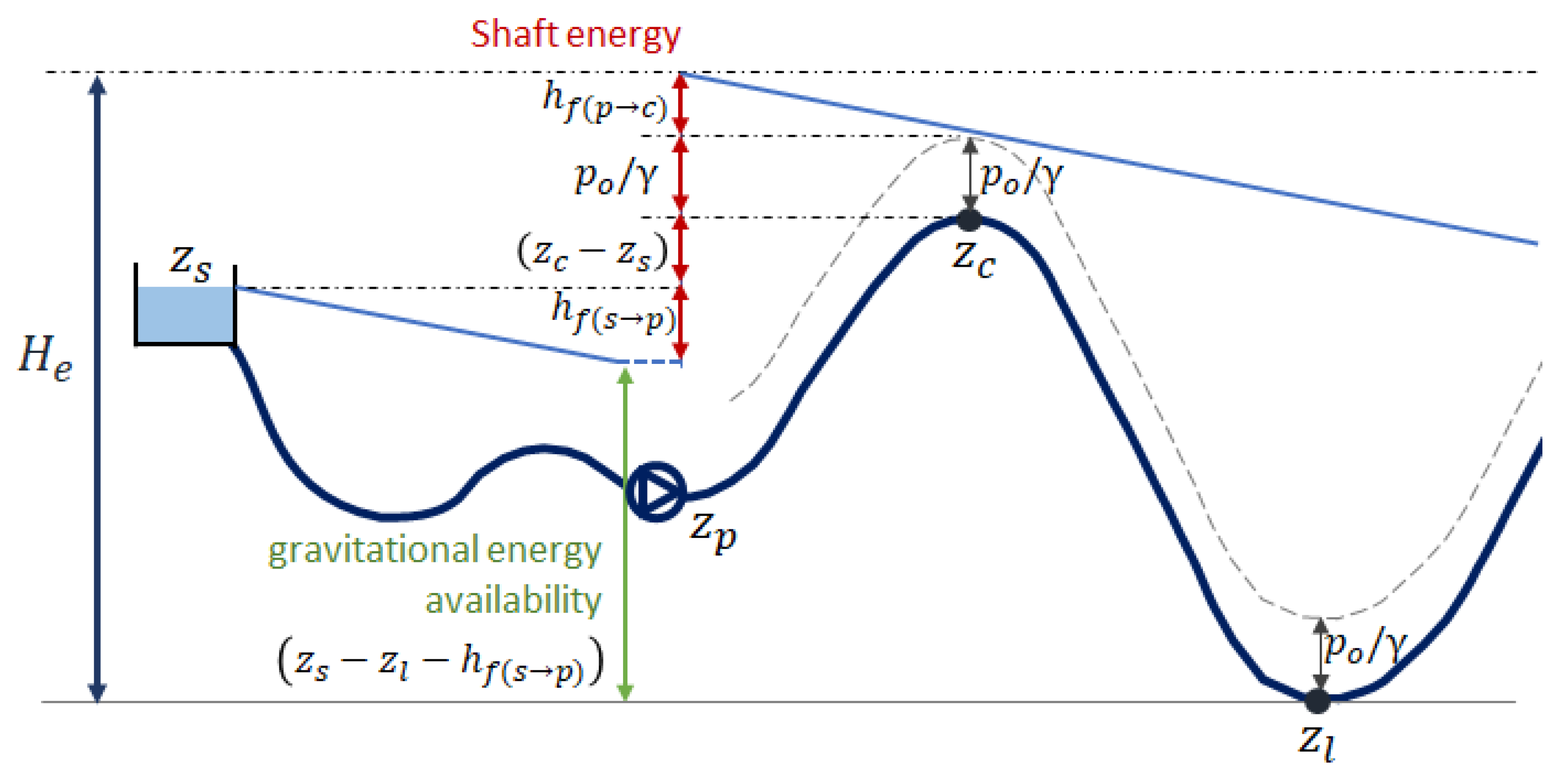
2.3. Deterministic Model for the Prediction of the Energy Demand of a System
- 0.002725, a unit conversion factor (pressure, expressed in m, to kWh/m3);
- zs, elevation of the supply source;
- zl, lowest elevation node;
- zc, elevation of the node with the highest energy demand, also known as the critical node (it should be noted that zc is not necessarily the same as the highest node, zh, as friction losses also play a role and difference in elevation could be compensated by additional distance from the source);
- hfe, friction losses from the source to the critical node = ;
- friction losses from the source to the pumping station;
- friction losses from the pumping station to the critical node;
- po, service pressure; and
- γ: specific weight for water (9810 N/m3).
2.4. Generalization of the Model to Other Systems
- The difference in elevation between the source and the critical node is lower than the friction losses plus the service pressure:where is the friction losses between the source and the critical node. In this case, additional pumping energy is needed to satisfy the energy demand of the gravitational system. This situation is similar to the previous one analyzed, modeled by Equation (1).
- The difference in elevation between the source and the critical node is equal to or greater than the friction losses plus the service pressure:
3. Application of the Model to a Real Case. Results and Discussion
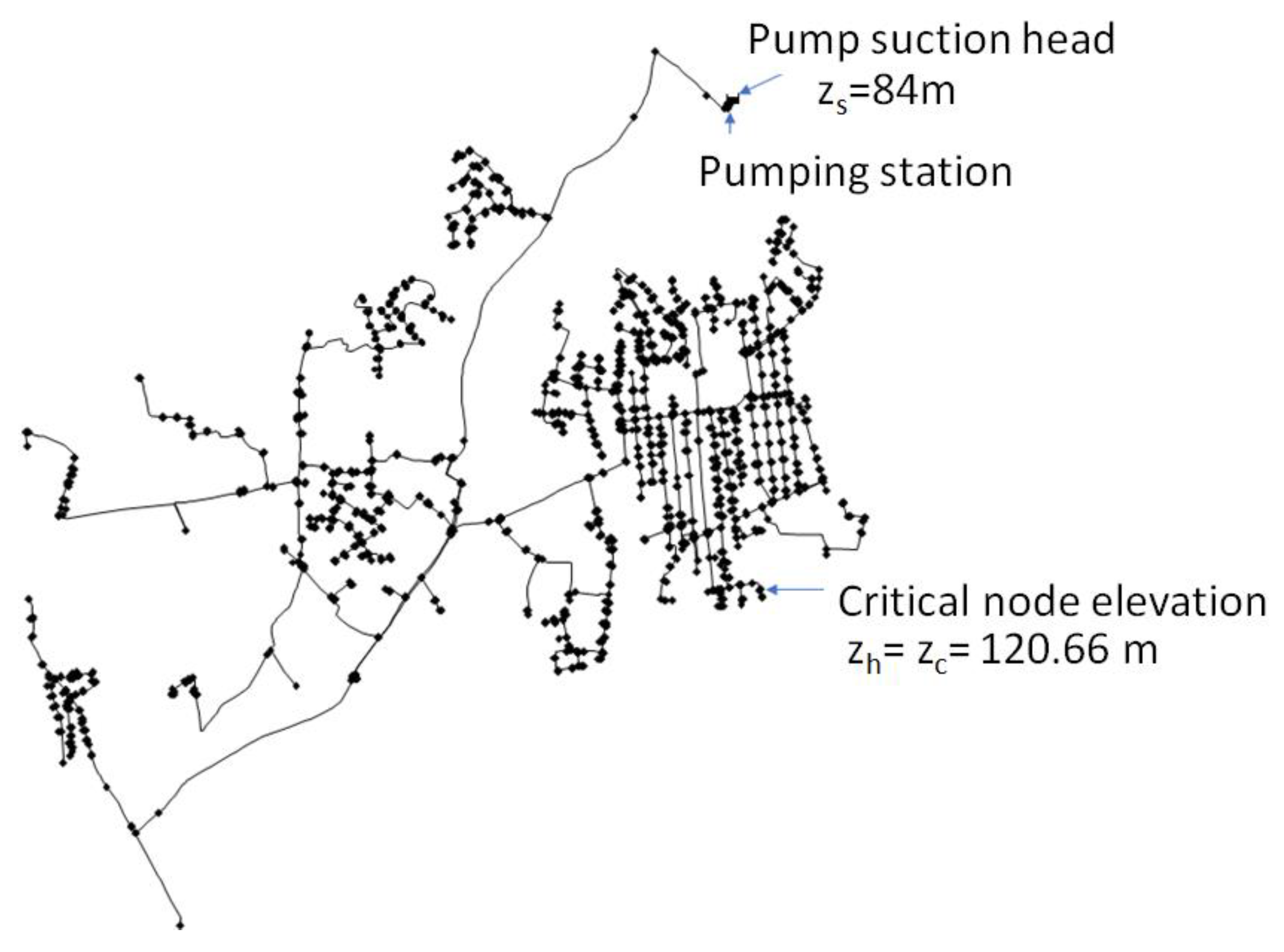
- Length = 45.1 km;
- Critical node elevation (in this case, it coincides with the highest node) zc = 120.66 m;
- Pump suction head zs = 84.00 m;
- Elevation of the lowest node zl = 35.64 m;
- Distance between the source and the critical node = 4.5 km;
- Minimum service pressure po/γ = 20 m; and
- m (pumping station next to tank).
- Input water volume Vt = 15,386 m3/month;
- Metered water volume Vr= 8994 m3/month;
- Real water efficiency (includes real and apparent losses) ηlr = 0.58;
- Energy consumed by the pumping station = 3902.25 kWh/ month;
- Average pumping efficiency, ηpr = 0.70; and
- Friction losses were estimated at 1.4 m/km [45], resulting in an estimated friction hfe of 6.3 m.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Symbols | Meaning of Symbols |
| C1 | Energy origin context indicator (kW h) |
| Es | Supplied (or injected) energy (kW h) |
| Ese | Estimated supplied energy (kW h) |
| En | Natural or gravitational energy (kW h) |
| Ep | Shaft (pumping) energy (kW h) |
| Epe | Estimated shaft energy (kW h) |
| Et | Topographic energy (kW h) |
| Hc | Piezometric head of the critical node (m) |
| He | Estimated maximum piezometric head of the system (m) |
| Hi | Piezometric head of a generic node i (m) |
| Hs | Piezometric head of source (m) |
| Hs,i | Piezometric head of source i (m) |
| Elevation of the highest source of supply | |
| hfe | Friction losses from the source to the critical node (m) |
| Friction losses between the source and the generic node i (m) | |
| Friction losses between the source and the critical node (m) | |
| Friction losses between the highest source and the generic node i (m) | |
| Ie | Energy intensity (kW h m−3) |
| Iee | Estimated energy intensity (kW h m−3) |
| Iee,p | Estimated pump energy intensity (kW h m−3) |
| Ier | Real energy intensity (m km−1) |
| Ier,p | Real pump energy intensity (m km−1) |
| k | Number of supply sources in the system |
| po | Service pressure (N m−2) |
| Vr | Metered water volume (m3) |
| Vt | Total input water volume (m3) |
| Vi | Input volume from source i (m3) |
| VT | Total supplied volume (m3) |
| Weighted average elevation of the system (m) | |
| zc | Elevation of the node with the highest energy demand (m) |
| zh | Elevation of the highest node (m) |
| zi | Elevation of a generic node i (m) |
| zs | Elevation of the supply source (m) |
| zs,max | Elevation of the source with a higher piezometric head (m) |
| zl | Elevation of the lowest node (m) |
| Weighted average elevation of the supply sources (m) | |
| γ | Specific weight of water (N m−3) |
| ηle | Estimated water efficiency |
| ηpe | Estimated pumping efficiency |
| Average estimated pumping efficiency | |
| θt | Topographic energy context indicator |
References
- Stahel, W.R. Circular economy. Nature 2016, 531, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Carlson, S.W.; Walburger, A. Energy Index Development for Benchmarking Water and Wastewater Utilities; AWWA Research Foundation: Denver, CO, USA, 2007. [Google Scholar]
- Plappally, A.K.; Lienhard, J.H. Energy requirements for water production, treatment, end use, reclamation, and disposal. Renew. Sustain. Energy Rev. 2012, 16, 4818–4848. [Google Scholar] [CrossRef]
- Wakeel, M.; Chen, B.; Hayat, T.; Alsaedi, A.; Ahmad, A. Energy consumption for water use cycles in different countries: A review. Appl. Energy 2016, 178, 868–885. [Google Scholar] [CrossRef]
- Klein, G.; Krebs, M.; Hall, V.; O’Brien, T.; Blevins, B. California’s Water–Energy Relationship. Final Staff Report; California Energy Commission: Sacramento, CA, USA, 2015.
- Sowby, R.B. New Techniques to Analyze Energy Use and Inform Sustainable Planning, Design, and Operation of Public Water Systems. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA, 2018. [Google Scholar]
- Vilanova, M.R.N.; Balestieri, J.A.P. Energy and hydraulic efficiency in conventional water supply systems. Renew. Sustain. Energy Rev. 2014, 30, 701–714. [Google Scholar] [CrossRef]
- Sowby, R.B.; Burian, S.J.; Chini, C.M.; Stillwell, A.S. Data Challenges and Solutions in Energy-for-Water: Experience from Two Recent Studies. J. Awwa 2019, 112, 28–33. [Google Scholar] [CrossRef]
- Liu, F.; Ouedraogo, A.; Manghee, S.; Danilenko, A. A Primer on Energy Efficiency for Municipal Water and Wastewater Utilities; Technical Report 001/12; The International Bank for Reconstruction and Development: Washington, DC, USA, 2012. [Google Scholar]
- Lee, M.; Kellerb, A.A.; Chianga, P.C.; Denc, W.; Wangd, H.; Houa, C.H.; Wue, J.; Wange, X.; Yane, J. Water-energy nexus for urban water systems: A comparative review on energy intensity and environmental impacts in relation to global water risks. Appl. Energy 2017, 205, 589–601. [Google Scholar] [CrossRef]
- Sanders, K.T.; Webber, M.E. Evaluating the energy consumed for water use in the United States. Environ. Res. Lett. 2012, 7, 1–11. [Google Scholar] [CrossRef]
- Hardy, L.; Garrido, A.; Juana, L. Evaluation of Spain’s Water-Energy Nexus. Int. J. Water Resour. Dev. 2012, 28, 151–170. [Google Scholar] [CrossRef]
- California Public Utilities Commission. Water/Energy Cost-Effectiveness Analysis; Navigant Consulting, Inc.: San Francisco, CA, USA, 2015.
- Ferrer, J.; Aguado, D.; Barat, R.; Serralta, J.; Lapuente, E. Huella Energética en el ciclo Integral del Agua en la Comunidad de Madrid; Fundación Canal: Madrid, Spain, 2017. [Google Scholar]
- Arzbaecher, C.; Parmenter, K.; Ehrhard, R.; Murphy, J. Electricity Use and Management in the Municipal Water Supply and Wastewater Industries; Electric Power Research Institute: Palo Alto, CA, USA, 2013. [Google Scholar]
- Voltz, T.; Grischek, T. Energy management in the water sector. Comparative case study of Germany and the United States. Water-Energy Nexus 2018, 1, 2–16. [Google Scholar] [CrossRef]
- Chini, C.M.; Stillwell, A.S. Where Are All the Data? The Case for a Comprehensive Water and Wastewater Utility Database. J. Water Resour. Plan. Manag. 2017, 143, 01816005. [Google Scholar] [CrossRef]
- GAO (United States Government Accountability Office). Amount of Energy Needed to Supply, Use, and Treat Water Is Location-Specific and Can Be Reduced by Certain Technologies and Approaches; US Government Accountability Office: Washington, DC, USA, 2011.
- Sowby, R.B.; Burian, S. Survey of Energy Requirements for Public Water Supply in the United States. J. Awwa 2017, 109, 320–330. [Google Scholar] [CrossRef]
- WW (Water in the West). Water and Energy Nexus: A Literature Review; Stanford University: Stanford, CA, USA, 2013. [Google Scholar]
- Pelli, T.; Hitz, H.U. Energy indicators and savings in water supply. J. Am. Water Work. Assoc. 2000, 92, 55–62. [Google Scholar] [CrossRef]
- Duarte, P.; Alegre, H.; Covas, D. PI for assessing effectiveness of energy management processes in water supply systems. In Proceedings of the PI09 Conference. Benchmarking Water Services, The Way Forward, Amsterdam, The Netherlands, 12–13 March 2009. [Google Scholar]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera, E., Jr. Energy audit of water networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Bolognesi, A.; Bragalli, C.; Lenzi, C.; Artina, S. Energy efficiency optimization in water distribution systems. Procedia Eng. 2014, 70, 181–190. [Google Scholar] [CrossRef]
- Snider, B.; Filion, Y. A streamlined energy efficiency performance indicator for water distribution systems: A case study. Can. J. Civ. Eng. 2018, 46, 61–66. [Google Scholar] [CrossRef]
- Bylka, J.; Mroz, T. A Review of Energy Assessment Methodology for Water Supply Systems. Energies 2019, 12, 4599. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Sala-Garrido, R. Evaluation of energy performance of drinking water treatment plants: Use of energy intensity and energy efficiency metrics. Appl. Energy 2018, 229, 1095–1102. [Google Scholar] [CrossRef]
- Cooley, H.; Wilkinson, R. Implications of Future Water Supply Sources for Energy Demands; Water Reuse Research Foundation: Alexandria, VA, USA, 2012. [Google Scholar]
- Gerbens-Leenes, P.W. Energy for freshwater supply, use and disposal in the Netherlands: A case study of Dutch households. Int. J. Water Resour. Dev. 2016, 32, 398–411. [Google Scholar] [CrossRef]
- Cabrera, E.; Estrela, T.; Lora, J. Desalination in Spain. Past, present and future. Ing. Agua 2019, 23, 199–214. [Google Scholar] [CrossRef]
- Longo, S.; Mirko d’Antoni, B.; Bongards, M.; Chaparro, A.; Cronrath, A.; Fatone, F.; Lema, J.M.; Mauricio-Iglesias, M.; Soares, A.; Hospido, A. Monitoring and diagnosis of energy consumption in wastewater treatment plants. A state of the art and proposals for improvement. Appl. Energy 2016, 179, 1251–1268. [Google Scholar] [CrossRef]
- Niu, K.; Wu, J.; Qi, L.; Niu, Q. Energy intensity of wastewater treatment plants and influencing factors in China. Sci. Total Environ. 2019, 670, 961–970. [Google Scholar] [CrossRef] [PubMed]
- Griffiths-Sattenspiel, B.; Wilson, W. The Carbon Footprint of Water; River Network: Portland, OR, USA, 2009. [Google Scholar]
- Siddiqi, A.; Fletcher, S. Energy Intensity of Water End-Uses. Curr. Sustain. Renew. Energy Rep. 2015, 2, 25–31. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 1979; ISBN 10:0070696675. [Google Scholar]
- Cabrera, E.; Gómez, E.; Soriano, J.; del Teso, R. Towards eco-layouts in water distribution systems. J. Water Resour. Plan. Manag. 2019, 145, 04018088. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: User’s Manual; U.S. EPA: Cincinnati, OH, USA, 2000.
- Giustolisi, O.; Berardi, L.; Laucelli, D.; Savic, D.; Walski, T.; Brunone, B. Battle of Background Leakage Assessment for Water Networks (BBLAWN) at WDSA Conference 2014. Procedia Eng. 2014, 89, 4–12. [Google Scholar] [CrossRef]
- Cabrera, E.; del Teso, R.; Gómez, E.; Estruch-Juan, E.; Soriano, J. Quick energy assessment of irrigation water transport systems. Biosyst. Eng. 2019, 188, 96–105. [Google Scholar] [CrossRef]
- Sanjuan-Delmás, D.; Petit-Boix, A.; Gasol, C.M.; Farreny, R.; Villalba, G.; Suárez-Ojeda, M.E.; Gabarrell, X.; Josa, A.; Rieradevall, J. Environmental assessment of drinking water transport and distribution network use phase for small to medium-sized municipalities in Spain. J. Clean. Prod. 2015, 87, 573–582. [Google Scholar] [CrossRef]
- Lam, K.L.; Kenway, S.J.; Lant, P.A. Energy use for water provision in cities. J. Clean. Prod. 2017, 143, 699–709. [Google Scholar] [CrossRef]
- Madani, K.; Khatami, S. Water for Energy: Inconsistent Assessment Standards and Inability to Judge Properly. Curr. Sustain. Renew. Energy Rep. 2015, 2, 10–16. [Google Scholar] [CrossRef]
- Cabrera, E.; Gómez, E.; Cabrera, E.; Soriano, J.; Espert, V. Energy assessment of pressurized water systems. J. Water Resour. Plan. Manag. 2015, 141, 04014095. [Google Scholar] [CrossRef]
- Gómez, E.; Cabrera, E.; Soriano, J.; Balaguer, M. On the weaknesses and limitations of EPANET as regards energy. Water Sci. Technol. Water Supply 2015, 16, 369–377. [Google Scholar] [CrossRef]
- Cabrera, E.; Gómez, E.; Cabrera, E., Jr.; Soriano, J. Calculating the economic level of friction in pressurized water systems. Water 2018, 9, 763. [Google Scholar] [CrossRef]
- ERSAR. Guia de Avaliação da Qualidade dos Serviços se Águas E Resíduos Prestados aos Utilizadores. 3.ª Geração do Sistema de Avaliação; ERSAR: Lisboa, Portugal, 2019.
- Fontanella, S.; Fecarotta, E.; Molino, B.; Cozzolino, L.; Della Morte, R. A performance Prediction Model for Pumps as Turbines (PATs). Water 2020, 12, 1175. [Google Scholar] [CrossRef]
- del Teso, R.; Gómez, E.; Estruch, M.E.; Cabrera, E.; Estruch-Juan, E. Topographic Energy Management in Water Distribution Systems. Water Resour. Manag. 2019, 33, 4385–4400. [Google Scholar] [CrossRef]
- Papa, F.; Rita Cavaleiro de Ferreira, R.; Radul, D. Pumps: Energy Efficiency & Performance Indicators. In Proceedings of the Efficient 2015-PI 2015 Joint Specialist IWA International Conference, Cincinnati, OH, USA, 20–24 April 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrera, E.; del Teso, R.; Gómez, E.; Cabrera, E., Jr.; Estruch-Juan, E. Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems. Water 2021, 13, 345. https://doi.org/10.3390/w13030345
Cabrera E, del Teso R, Gómez E, Cabrera E Jr., Estruch-Juan E. Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems. Water. 2021; 13(3):345. https://doi.org/10.3390/w13030345
Chicago/Turabian StyleCabrera, Enrique, Roberto del Teso, Elena Gómez, Enrique Cabrera, Jr., and Elvira Estruch-Juan. 2021. "Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems" Water 13, no. 3: 345. https://doi.org/10.3390/w13030345
APA StyleCabrera, E., del Teso, R., Gómez, E., Cabrera, E., Jr., & Estruch-Juan, E. (2021). Deterministic Model to Estimate the Energy Requirements of Pressurized Water Transport Systems. Water, 13(3), 345. https://doi.org/10.3390/w13030345