Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control
Abstract
:1. Introduction
2. Methods and Materials
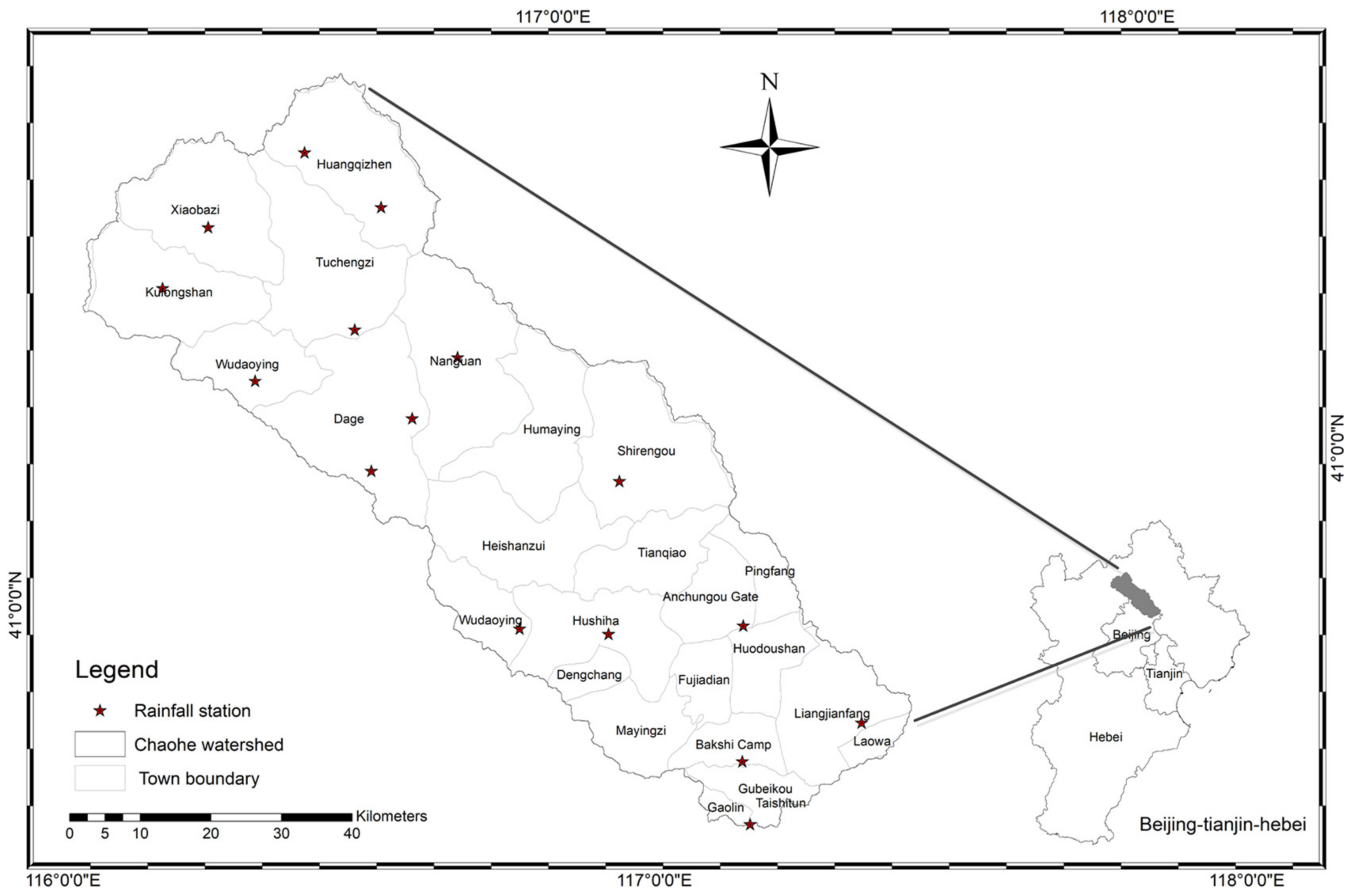
2.1. Study Area
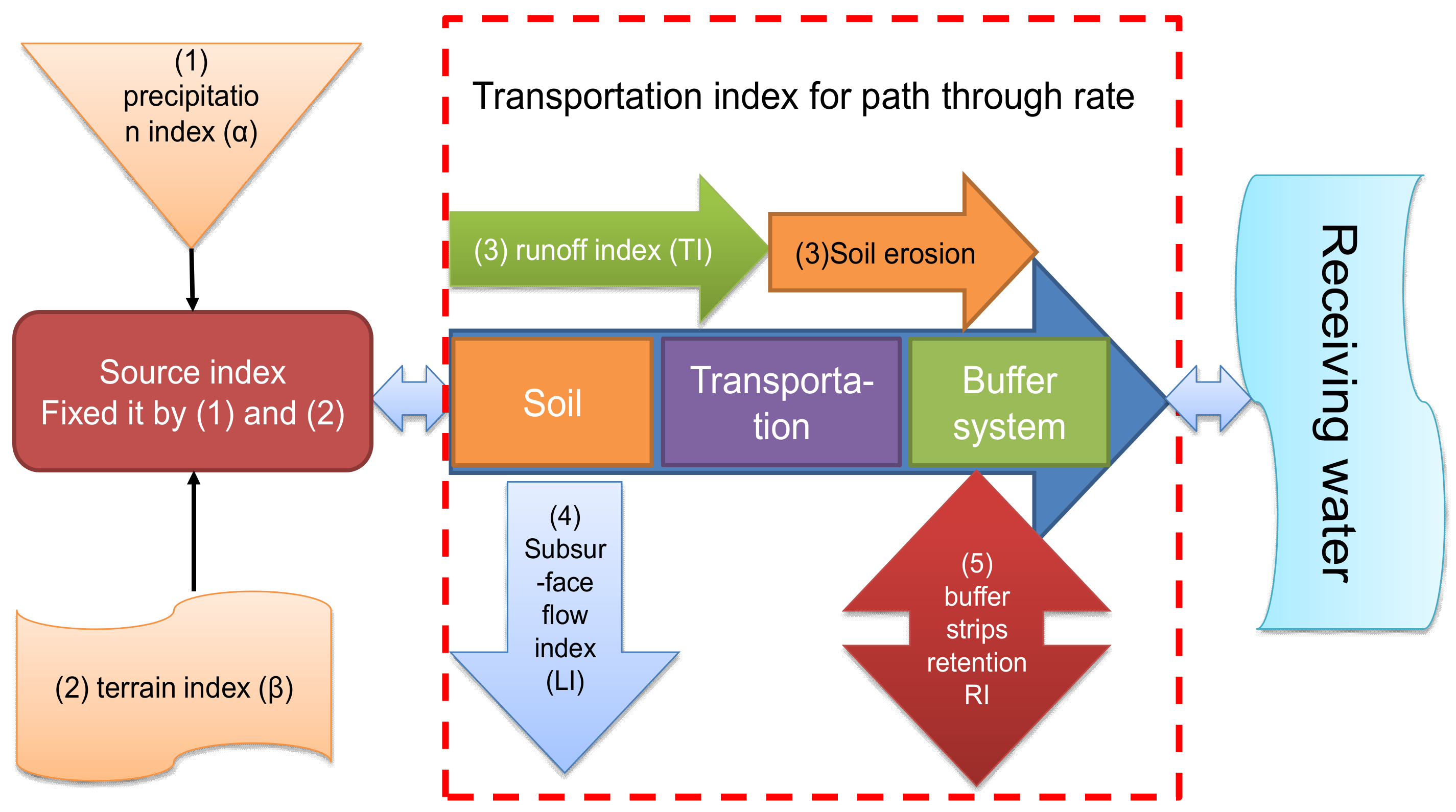
2.2. Construction of the PTRFFM
2.2.1. Conceptualization of Five Major Parameters
2.2.2. Data Standardization of the PTRFFM
2.3. Data Source
2.4. Estimation of the Agricultural NPS Pollutant Loads
3. Results and Discussion
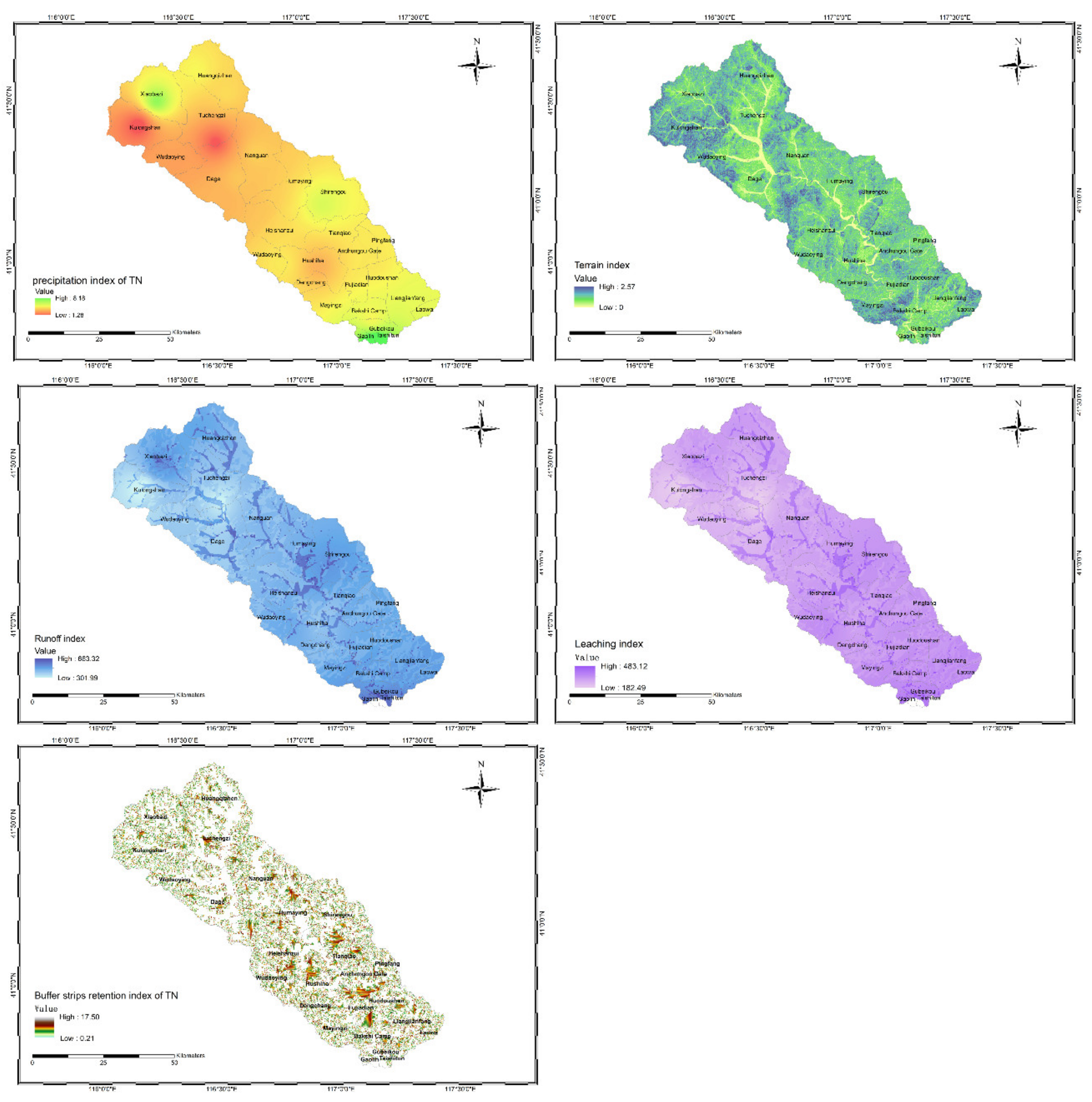
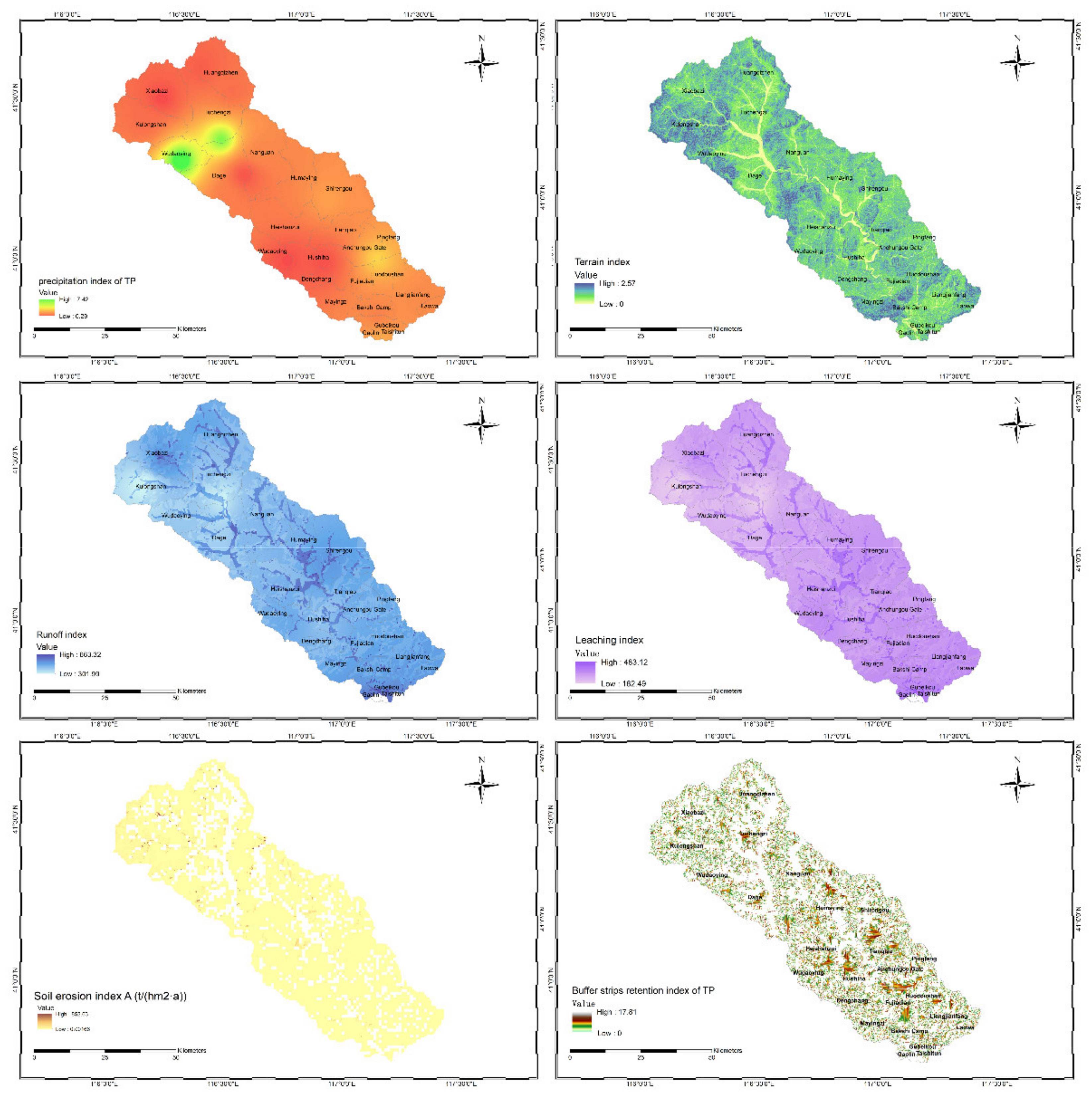
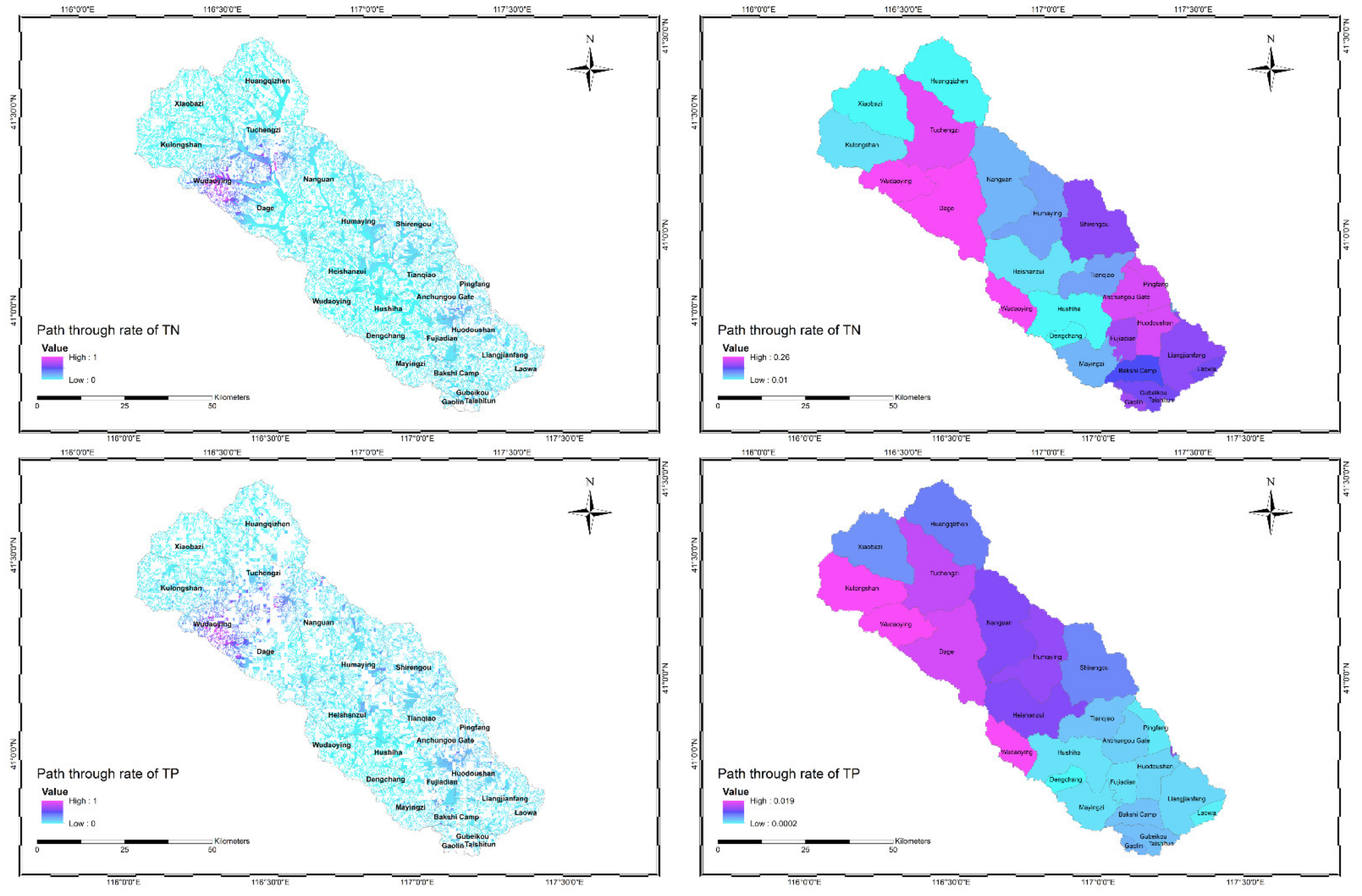
3.1. Major Parameters of the Spatial Distribution from the PTRFFM
3.2. Spatial Distribution Characteristics of the Path-through Rate
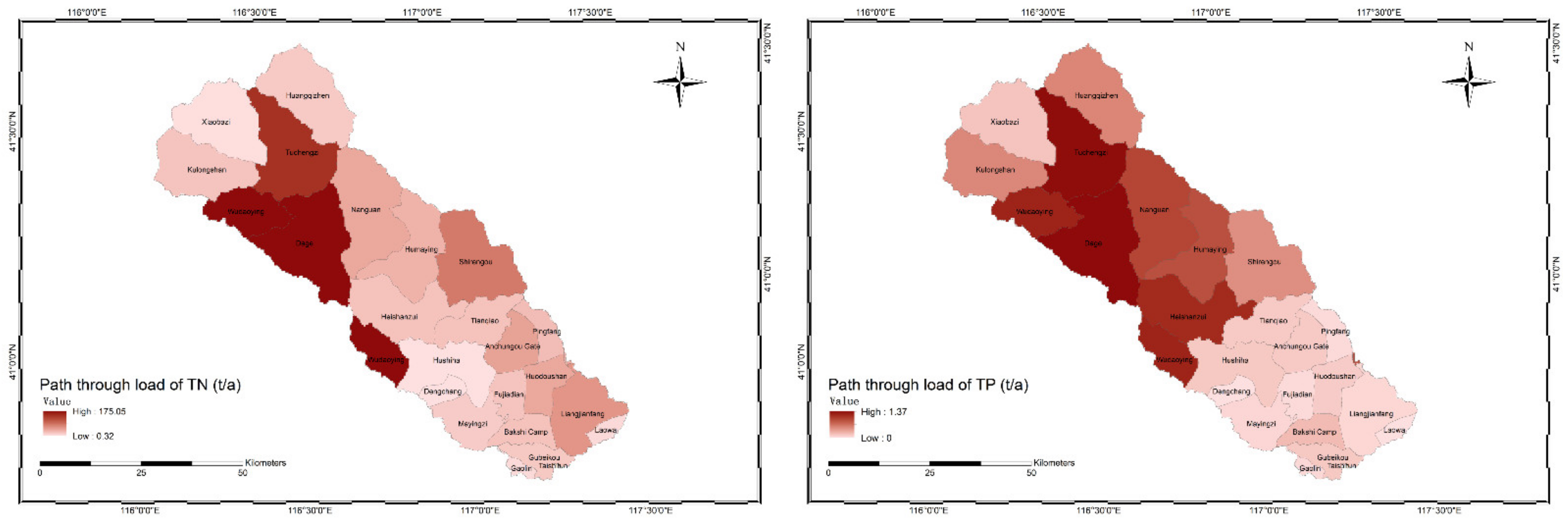
3.3. NPS Pollution Load and Source Analysis
3.4. Validation of the Results from the PTRFFM
3.5. Identification of the Critical Source Area of NPS Pollution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MEE. Bulletin of the Second National Census of Pollution Sources; MEE: Beijing, China, 2020.
- Adu, J.T.; Kumarasamy, M.V. Assessing Non-Point Source Pollution Models: A Review. Pol. J. Environ. Stud. 2018, 27, 1913–1922. [Google Scholar] [CrossRef]
- Zou, L.; Liu, Y.; Wang, Y.; Hu, X. Assessment and analysis of agricultural non-point source pollution loads in China: 1978–2017. J. Environ. Manag. 2020, 263, 110400. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Liao, Q.; Hong, Q.; Gong, Y. An overview of research on agricultural non-point source pollution modelling in China. Sep. Purif. Technol. 2012, 84, 104–111. [Google Scholar] [CrossRef]
- Kaushal, S.S.; Groffman, P.M.; Band, L.E.; Elliott, E.M.; Shields, C.A.; Kendall, C. Tracking Nonpoint Source Nitrogen Pollution in Human-Impacted Watersheds. Environ. Sci. Technol. 2011, 45, 8225–8232. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L.; Shen, Z. Dynamic export coefficient model for evaluating the effects of environmental changes on non-point source pollution. Sci. Total Environ. 2020, 747, 141164. [Google Scholar] [CrossRef]
- Srinivas, R.; Singh, A.P.; Dhadse, K.; Garg, C. An evidence based integrated watershed modelling system to assess the impact of non-point source pollu-tion in the riverine ecosystem. J. Clean. Prod. 2020, 246, 118963. [Google Scholar] [CrossRef]
- Wu, S.; Yin, P.; Wang, M.; Zhou, L.; Geng, R. A new watershed eco-zoning scheme for evaluate agricultural nonpoint source pollution at national scale. J. Clean. Prod. 2020, 273, 123033. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of Watershed-Scale Water Quality and Nonpoint Source Pollution Models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Daniels, M.; Sharpley, A.; Harmel, R.; Anderson, K. The utilization of edge-of-field monitoring of agricultural runoff in addressing nonpoint source pollution. J. Soil Water Conserv. 2018, 73, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Sun, Z.; Zheng, S.; Yu, J.; Liang, X. An integrated approach to identify critical source areas of agricultural nonpoint-source pollution at the wa-tershed scale. J. Environ. Qual. 2018, 47, 922–929. [Google Scholar] [CrossRef]
- Johnes, P. Evaluation and management of the impact of land use change on the nitrogen and phosphorus load delivered to surface waters: The export coefficient modelling approach. J. Hydrol. 1996, 183, 323–349. [Google Scholar] [CrossRef]
- Xueman, Y.; Wenxi, L.; Yongkai, A.; Weihong, D. Assessment of parameter uncertainty for non-point source pollution mechanism modeling: A Bayesi-an-based approach. Environ. Pollut. 2020, 263, 114570. [Google Scholar] [CrossRef]
- Ding, X.; Shen, Z.; Hong, Q.; Yang, Z.; Wu, X.; Liu, R. Development and test of the Export Coefficient Model in the Upper Reach of the Yangtze River. J. Hydrol. 2010, 383, 233–244. [Google Scholar] [CrossRef]
- Aschmann, S.G.; Anderson, D.P.; Croft, R.J.; Cassell, E.A. Using a watershed nutrient dynamics model, WEND, to address watershed-scale nutrient management challenges. J. Soil Water Conserv. 1999, 54, 630–635. [Google Scholar]
- Buchanan, B.P.; Archibald, J.A.; Easton, Z.M.; Shaw, S.B.; Schneider, R.L.; Walter, M.T. A phosphorus index that combines critical source areas and transport pathways using a travel time approach. J. Hydrol. 2013, 486, 123–135. [Google Scholar] [CrossRef]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forest-ed watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Van Es, H.; Czymmek, K.; Ketterings, Q. Management effects on nitrogen leaching and guidelines for a nitrogen leaching index in New York. J. Soil Water Conserv. 2002, 57, 499–504. [Google Scholar]
- Kiese, R.; Heinzeller, C.; Werner, C.; Wochele, S.; Grote, R.; Butterbach-Bahl, K. Quantification of nitrate leaching from German forest ecosystems by use of a process oriented biogeochemical model. Environ. Pollut. 2011, 159, 3204–3214. [Google Scholar] [CrossRef]
- Endreny, T.A.; Wood, E.F. Watershed Weighting of Export Coefficients to Map Critical Phosphorous Loading Areas. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 165–181. [Google Scholar] [CrossRef]
- Kruk, E. Use of Chosen Methods for Determination of the USLE Soil Erodibility Factor on the Example of Loess Slope. J. Ecol. Eng. 2021, 22, 151–161. [Google Scholar] [CrossRef]
- Geng, R. Optimizing Best Management Practices Using a Multi-Objective Optimization Tool to Improve Water Quality Goals under Different Spatial Scales; Capital Normal University: Beijing, China, 2015. [Google Scholar]
- Yang, D.H. Analysis on aquatic environment of Anhui Province in Xinanjiang River watershed. Water Resour. Prot. 2006, 5, 77–80. [Google Scholar]
- Deng, O.-P.; Sun, S.-Y.; Lü, J. [Nitrogen non-point source pollution identification based on ArcSWAT in Changle River]. Huan Jing Ke Xue Huanjing Kexue 2013, 34, 1284–1290. [Google Scholar]
- Ma, D.; Shi, H.; Feng, A. Estimation of agricultural non-point source pollution based on watershed unit: A case study of Laizhou Bay. Acta Ecol. Sin. 2014, 34, 173–181. [Google Scholar]
- Kim, H.; Surdyk, N.; Møller, I.; Graversgaard, M.; Blicher-Mathiesen, G.; Henriot, A.; Dalgaard, T.; Hansen, B. Lag Time as an Indicator of the Link between Agricultural Pressure and Drinking Water Quality State. Water 2020, 12, 2385. [Google Scholar] [CrossRef]
| Type | Scale | Resolution | Description | Source |
|---|---|---|---|---|
| DEM | 1:1,000,000 | 30 × 30 m | Elevation, overland and channel slopes and lengths | National Geomatics Center of China |
| Land use | 1:50,000 | 30 × 30 m | Land use classifications | Institute of Geographical and Natural Resources Research, Chinese |
| Livestock | _ | Village | Breeding number of cow, pig, sheep, and poultry | National pollution source census |
| Soil type | 1:1,000,000 | 30 × 30 m | Soil type classifications | Institute of Soil Science, Chinese Academy of Sciences |
| Administrative division | 1:1,000,000 | 1 × 1 km | Towns and municipalities of the study area | National Geomatics Center of China |
| Vegetation coverage | 1 × 1 km | |||
| Precipitation | 2001–2014 | Daily step | 16 stations in the study area | China Meteorological Administration |
| Hydrological data | 2001–2014 | Monthly step | Calibration and validation of the five-factor model | China Meteorological Administration |
| Water quality data | 2001–2014 | Monthly step | Calibration and validation of the five-factor model | Miyun Reservoir Management Office Xiahui Hydrological Station |
| Social economics | 24 towns | Township level | Population, livestock rearing, fertilizer application | Field investigation; Statistics year-book |
| Export coefficient | Different sources | Losses of various nutrient sources | Statistical data and field monitoring |
| Pollution Source | TN | TP | |
|---|---|---|---|
| Land use (kg·ha−1·a−1) | Farm land | 2.97 | 0.041 |
| Forest | 0.24 | 0.0071 | |
| Grassland | 1.57 | 0.013 | |
| Unused land | 5.00 | 0.008 | |
| Residential land | 2.00 | 0.003 | |
| Rural living (kg·ca−1·a−1) | rural resident | 2.83 | 0.89 |
| Livestock | Big livestock | 7.36 | 0.31 |
| Pig | 0.41 | 0.15 | |
| Sheep | 1.4 | 0.045 | |
| Poultry | 0.071 | 0.004 |
| Pollution Source | Total NPS Pollution Load of 2014 | ||||||
|---|---|---|---|---|---|---|---|
| TN (t/a) | Percent | Total | TP (t/a) | Percent | Total | ||
| Rural living | 1118.2 | 15.0 | 15.0 | 351.65 | 65.00 | 65.00 | |
| Livestock | Big stock | 1404.9 | 18.7 | 37.4 | 59.17 | 10.94 | 28.95 |
| Pig | 70.0 | 0.9 | 25.61 | 4.73 | |||
| Sheep | 152.7 | 2.0 | 4.91 | 0.09 | |||
| Poultry | 1187.7 | 15.8 | 66.91 | 12.37 | |||
| Land use | Farmland | 2258.9 | 30.1 | 47.6 | 22 | 4.07 | 6.05 |
| Forest | 412.8 | 5.5 | 3.1 | 0.57 | |||
| Grassland | 878.1 | 11.7 | 6.4 | 1.18 | |||
| Unused land | 43.3 | 0.6 | 0.7 | 0.13 | |||
| Residential land | 23.4 | 0.03 | 0.5 | 0.09 | |||
| Total | 7505.0 | 100% | 100% | 540.95 | 100% | 100% | |
| NPS Pollutants | Simulated | Re % | |
|---|---|---|---|
| TN | 705.11 | 570.86 | 19.62 |
| TP | 2.54 | 3.16 | 24.45 |
| Watershed | Study Area | Scale | Method | Reference | ||
|---|---|---|---|---|---|---|
| Haihe Basin | Chaohe River watershed | Mesoscale | PTRFFM | 0.17–0.26 | 0.012–0.019 | This study |
| Haihe Basin | Haihe Basin | Large scale | ECM | 0.20 | 0.10 | Zhou et al., 2004 |
| Yangtze River Basin | Xinanjiang River Basin | Large scale | Investigation and monitoring | 0.20 | 0.21 | Yang et al., 2006 |
| Songhua River Basin | Harbin Section of Songhua River | Middle scale | Pollutant load estimation method | 0.10 | _ | Fu et al., 2010 |
| Yangtze River Basin | Changle River Basin | Middle scale | SWAT | 0.17 (Atmospheric deposition) | _ | Deng et al., 2012 |
| 0.12 (Rural living) | _ | |||||
| 0.03 (Livestock) | _ | |||||
| 0.15 (nitrogen fertilizer) | _ | |||||
| Yellow River Basin | Laizhou Bay | Large scale | Pollutant load estimation method | 0.1 (Farmland) | 0.1 (Farmland) | Ma et al., 2012 |
| 0.25 (Rural living) | 0.25 (Rural living) | |||||
| 0.07 (Livestock) | 0.07 (Livestock) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Geng, R. Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control. Water 2021, 13, 3156. https://doi.org/10.3390/w13223156
Zhou L, Geng R. Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control. Water. 2021; 13(22):3156. https://doi.org/10.3390/w13223156
Chicago/Turabian StyleZhou, Lili, and Runzhe Geng. 2021. "Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control" Water 13, no. 22: 3156. https://doi.org/10.3390/w13223156
APA StyleZhou, L., & Geng, R. (2021). Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control. Water, 13(22), 3156. https://doi.org/10.3390/w13223156






