Probability of Non-Exceedance of Arsenic Concentration in Groundwater Estimated Using Stochastic Multicomponent Reactive Transport Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Background
2.2. Model Setup
- A 3-D flow model embedding a heterogeneous distribution of lithological materials was setup to simulate groundwater flow in the WAA.
- The flow model was used for the advective and dispersive transport of a multidimensional MRTM model. This model inherited the geochemical reactions proposed by DL2020 to describe As mobility in the WAA.
- Within a Monte-Carlo framework, indicator-based geostatistical modeling was used to build spatially correlated random realizations of GICs. Such GICs were employed to run independent MRTM simulations.
- The ensemble of results was then collected and examined to estimate the PNE and useful statistics that allow gaining insight into the expected variation of As and related key variables in the WAA.
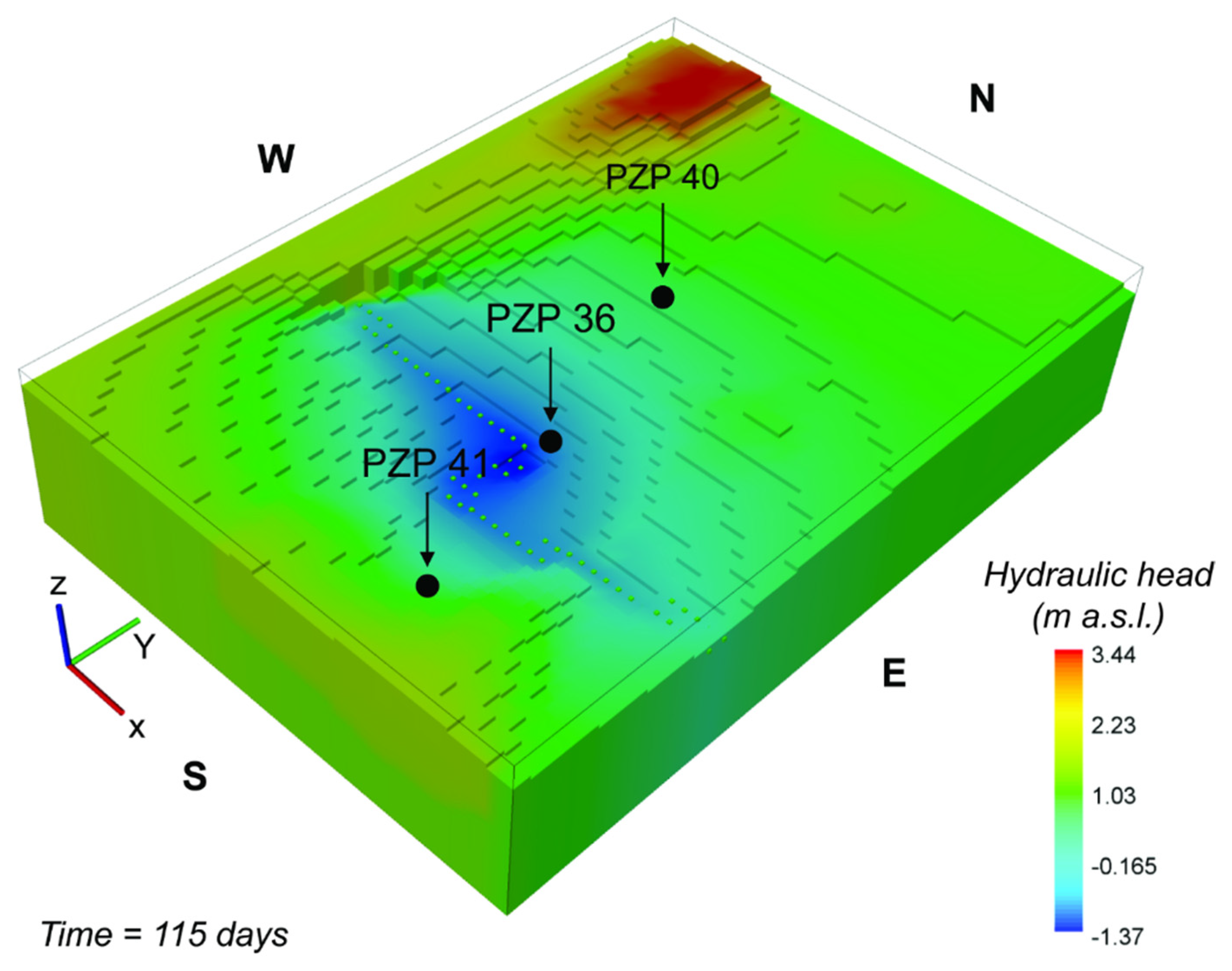
2.2.1. Flow Model
2.2.2. Deterministic Transport Model
2.2.3. Stochastic Transport Model
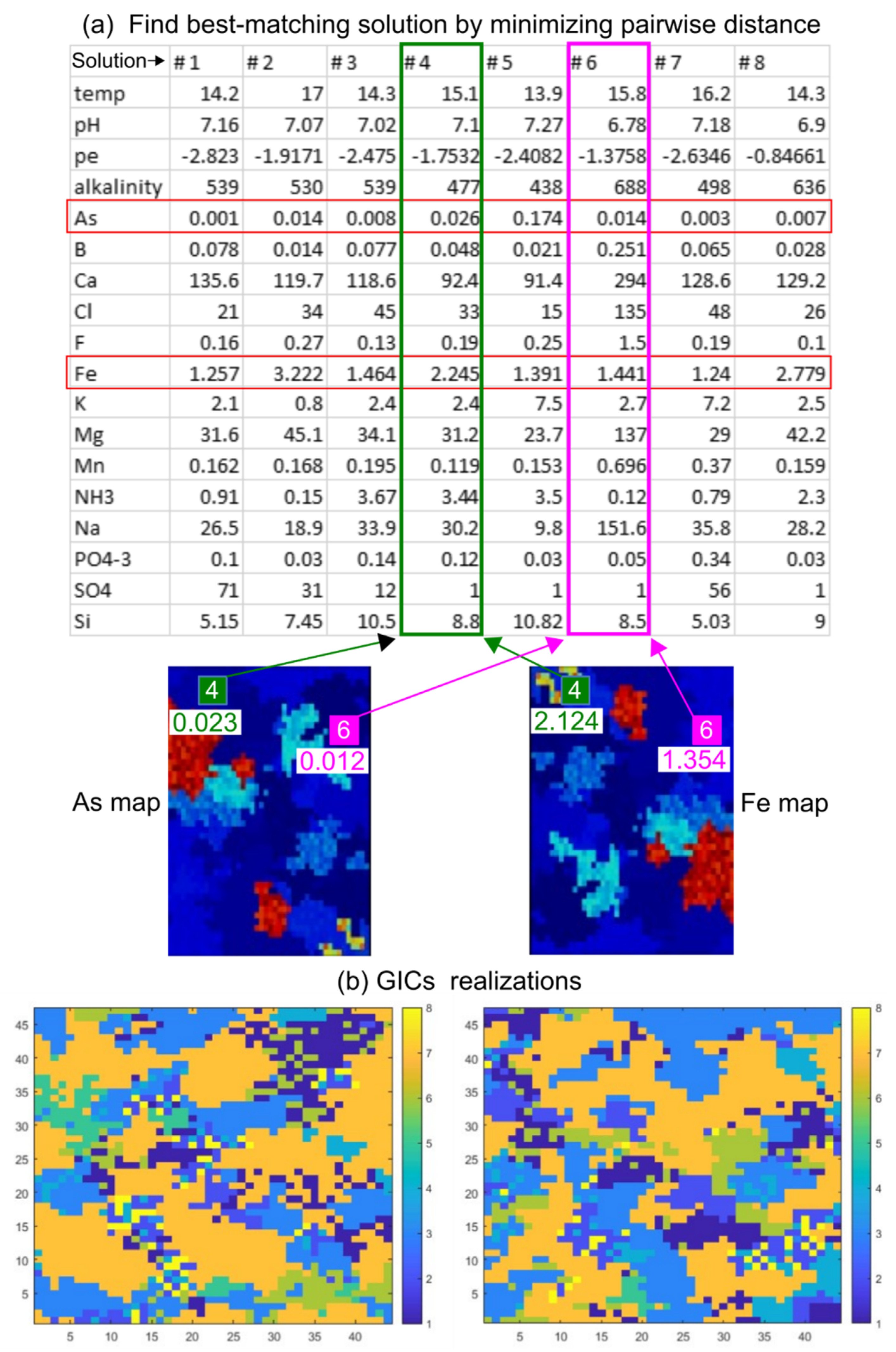
- The spatial structure (i.e., the variogram) of As was initially computed from the 34 boreholes sampled in 2009. The As variogram was used to generate Nmc = 100 sequential indicator simulations (SISs) [43,44] of As. The simulations were created on a 2D grid having the same size as the PHAST models (43 × 46 cells).
- These simulations (or “realizations”) were conditioned to the 2017 measurements of As and obtained from the eight sampled piezometers. Examples of maps generated using the SIS algorithm are shown in the Supplementary Information SI-4.
- The procedure at steps 1 and 2 was repeated for Fe, to obtain Nmc = 100 Fe realizations.
- We treated the eight hydrogeochemical surveys performed in 2017 as eight PHREEQC “solutions”. We then created Nmc = 100 empty grids of the same size of the stochastic realizations (43 × 46 cells) and populated them with a unique solution in each grid cell. Such solution was chosen by minimizing, for each cell of each j-th pair of As and Fe realizations (), the pairwise Euclidean distance between the simulated As and Fe concentrations and the observed concentrations from the 8 PHREEQC solutions.
- A “full depth” analysis, where the statistics of As concentrations and other variables were calculated considering the entire model extension in the vertical direction.
- A “shallow depth” analysis, where the same statistics were calculated for the top half of the model (i.e., up to 6 m), as a representative value for partially-penetrating pumping wells.
3. Results
3.1. Flow and Deterministic Transport Model
3.2. Stochastic Transport Model
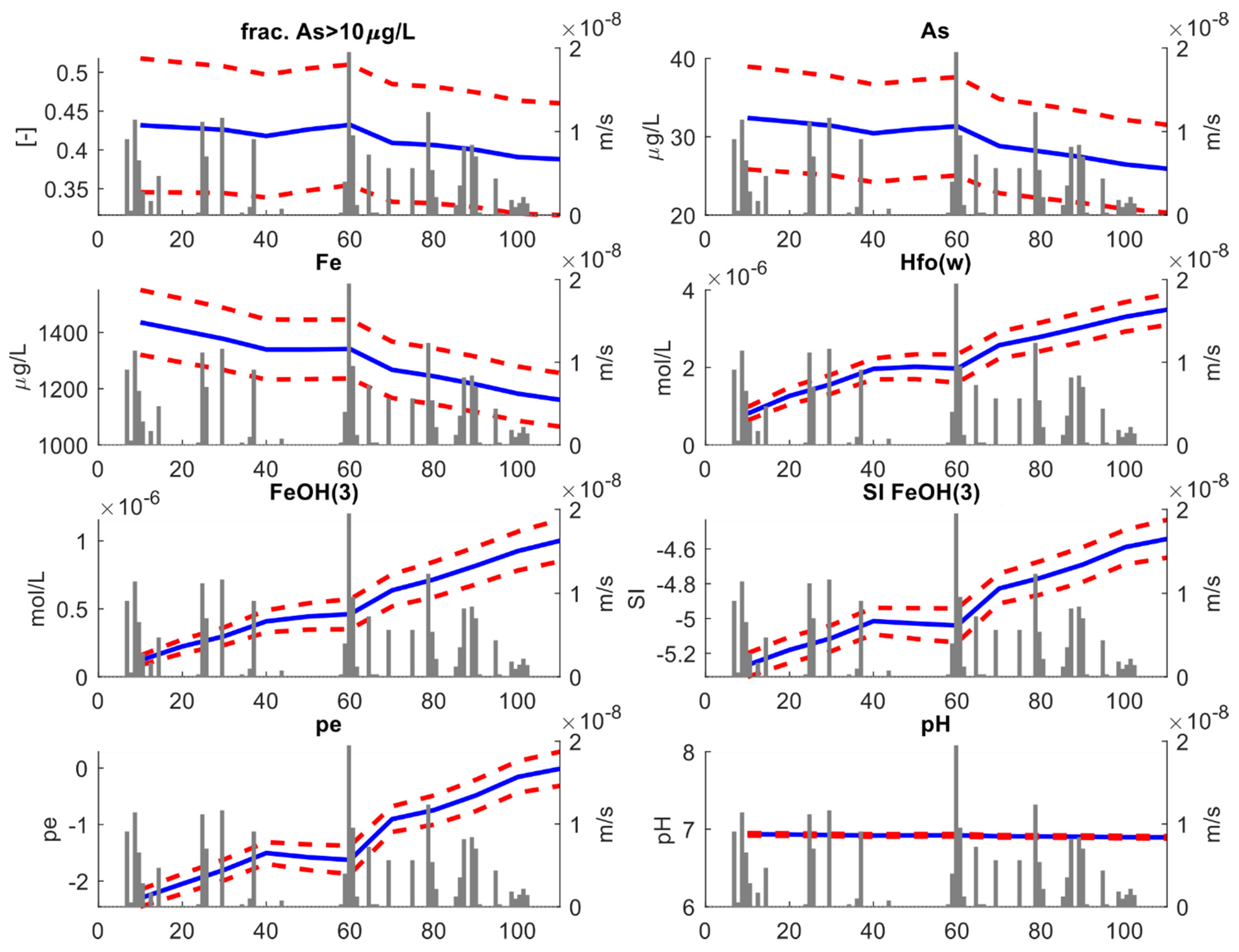
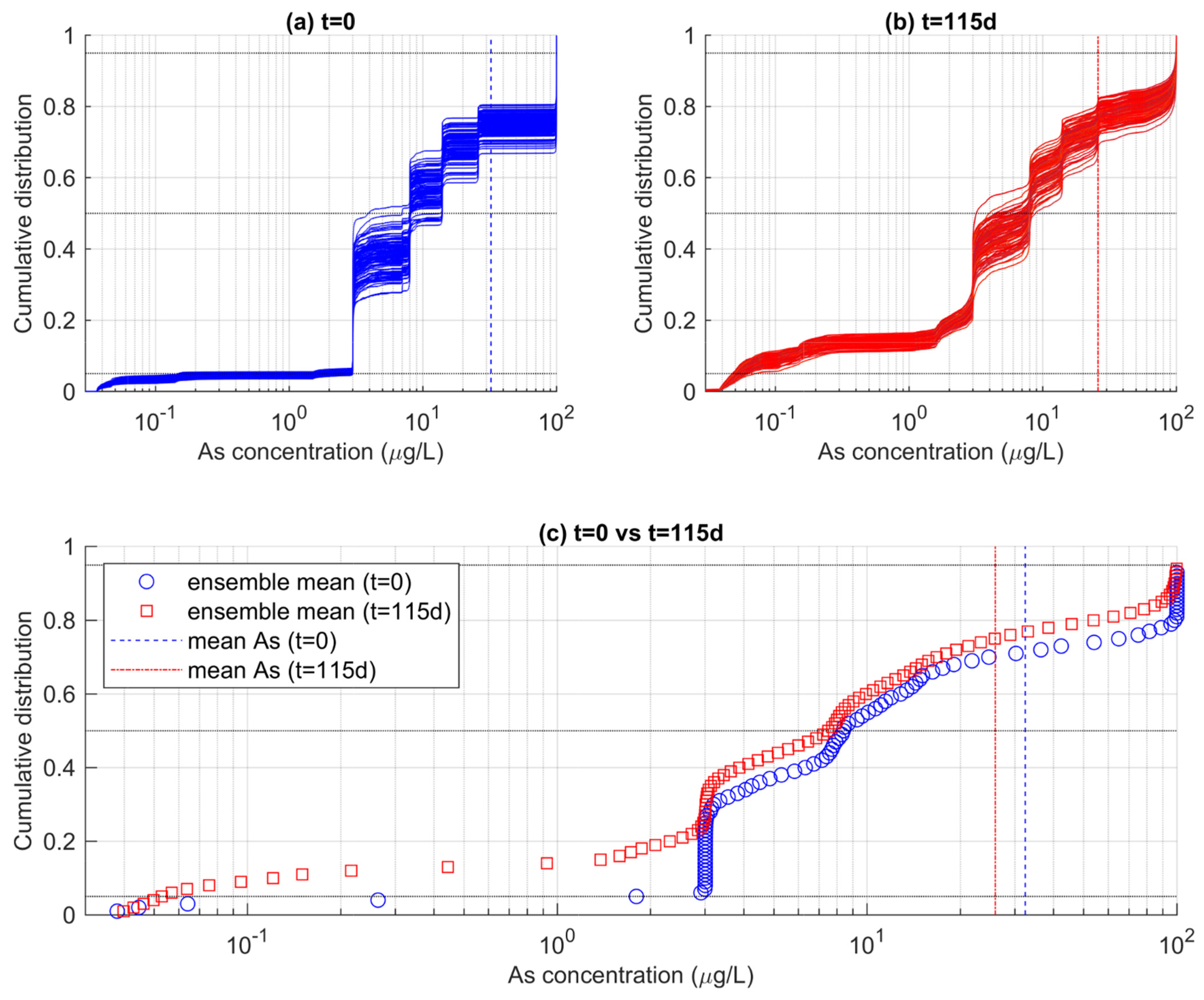
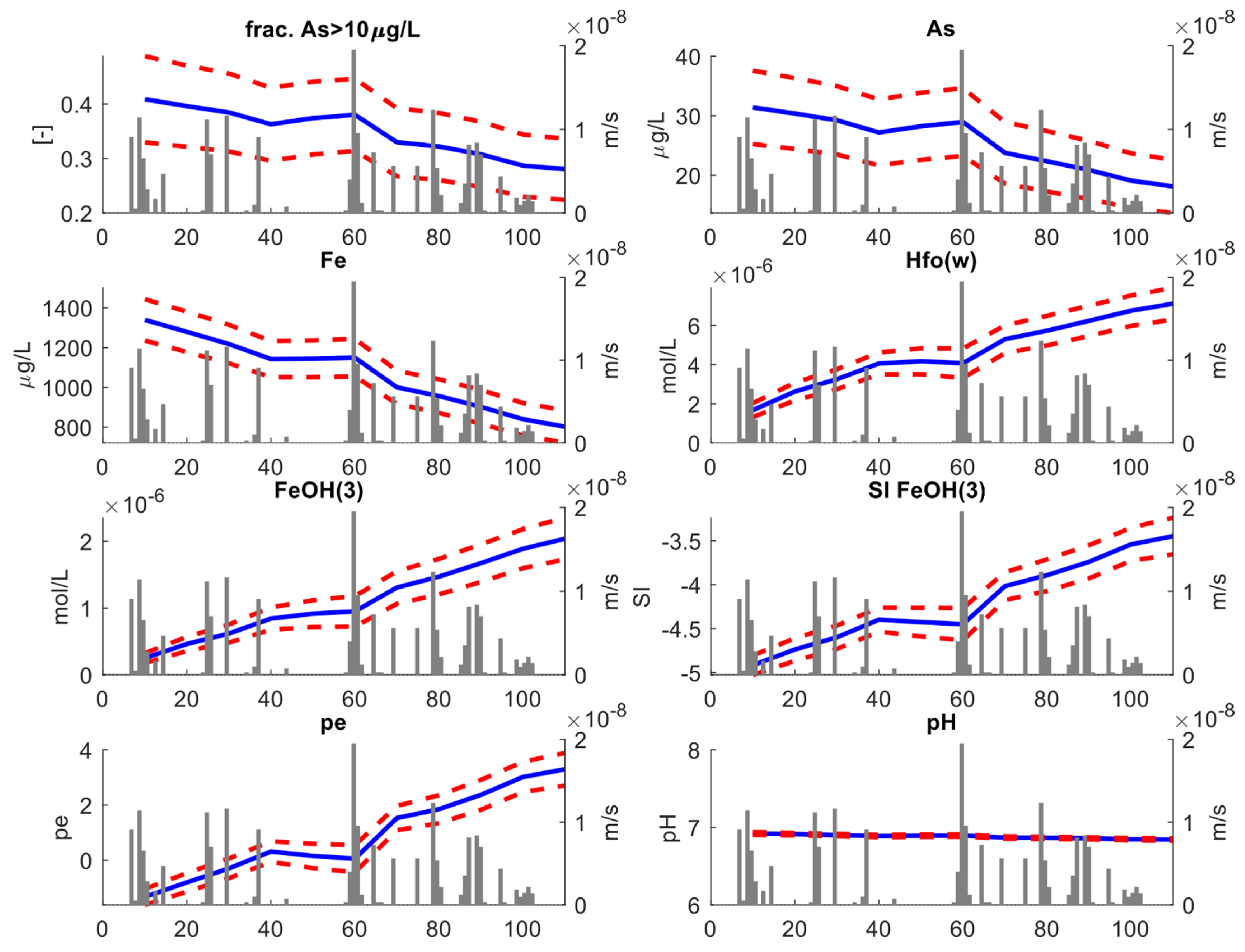
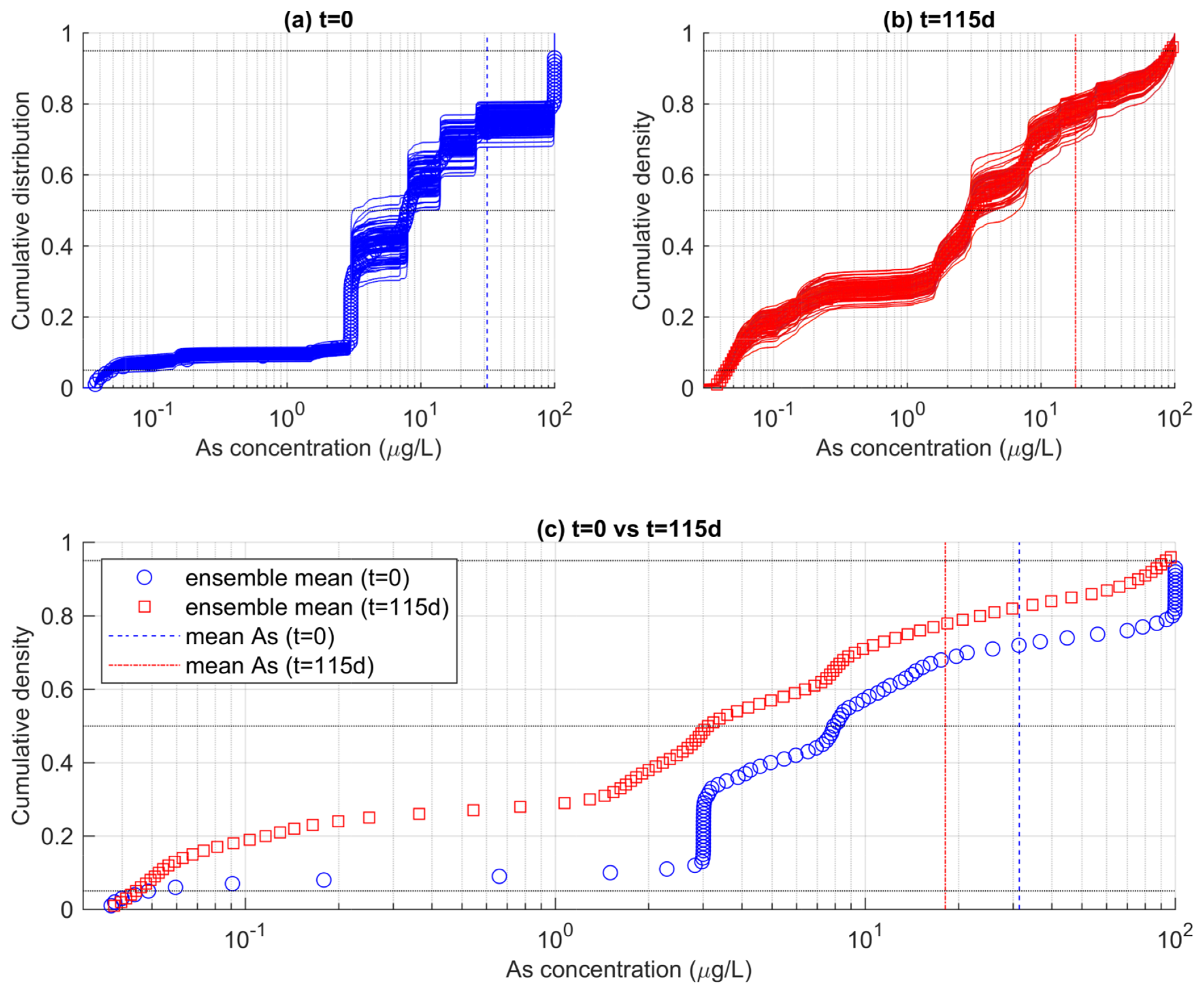
3.2.1. Whole Aquifer Depth
3.2.2. Shallower Aquifer Portion
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smedley, P.L.; Kinniburgh, D.G. Arsenic in Groundwater and the Environment. In Essentials in Medical Geology; Springer: Dordrecht, The Netherlands, 2013; pp. 279–310. [Google Scholar]
- Mueller, B. Results of the First Improvement Step Regarding Removal Efficiency of Kanchan Arsenic Filters in the Lowlands of Nepal—A Case Study. Water 2021, 13, 1765. [Google Scholar] [CrossRef]
- Podgorski, J.; Berg, M. Global Threat of Arsenic in Groundwater. Science 2020, 368, 845–850. [Google Scholar] [CrossRef] [PubMed]
- UNICEF Arsenic Primer: Guidance on the Investigation & Mitigation of Arsenic Contamination. UNICEF Water, Sanitation and Hygiene Section and WHO Water; Sanitation and Hygiene and Health Unit, United Nations Children’s Fund (UNICEF): New York, NY, USA, 2018.
- Fendorf, S.; Michael, H.A.; van Geen, A. Spatial and Temporal Variations of Groundwater Arsenic in South and Southeast Asia. Science 2010, 328, 1123–1127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, A.H.; Lingas, E.O.; Rahman, M. Contamination of Drinking-Water by Arsenic in Bangladesh: A Public Health Emergency. Bull. World Health Organ. 2000, 11, 1093–1103. [Google Scholar]
- Polya, D.; Charlet, L. Environmental Science: Rising Arsenic Risk? Nat. Geosci. 2009, 2, 383–384. [Google Scholar] [CrossRef]
- Gao, Z.P.; Jia, Y.F.; Guo, H.M.; Zhang, D.; Zhao, B. Quantifying Geochemical Processes of Arsenic Mobility in Groundwater From an Inland Basin Using a Reactive Transport Model. Water Resour. Res. 2020, 56, e2019WR025492. [Google Scholar] [CrossRef]
- Jakobsen, R.; Kazmierczak, J.; Sø, H.U.; Postma, D. Spatial Variability of Groundwater Arsenic Concentration as Controlled by Hydrogeology; Conceptual Analysis Using 2-D Reactive Transport Modeling. Water Resour. Res. 2018, 54, 10–254. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution; A.A. Balkema Publishers: London, UK, 2005. [Google Scholar]
- Battistel, M.; Stolze, L.; Muniruzzaman, M.; Rolle, M. Arsenic Release and Transport during Oxidative Dissolution of Spatially-Distributed Sulfide Minerals. J. Hazard. Mater. 2021, 409, 124651. [Google Scholar] [CrossRef]
- Postma, D.; Larsen, F.; Minh Hue, N.T.; Duc, M.T.; Viet, P.H.; Nhan, P.Q.; Jessen, S. Arsenic in Groundwater of the Red River Floodplain, Vietnam: Controlling Geochemical Processes and Reactive Transport Modeling. Geochim. Cosmochim. Acta 2007, 71, 5054–5071. [Google Scholar] [CrossRef]
- Rathi, B.; Neidhardt, H.; Berg, M.; Siade, A.; Prommer, H. Processes Governing Arsenic Retardation on Pleistocene Sediments: Adsorption Experiments and Model-Based Analysis. Water Resour. Res. 2017, 53, 4344–4360. [Google Scholar] [CrossRef]
- Sracek, O.; Bhattacharya, P.; Jacks, G.; Gustafsson, J.-P.; von Brömssen, M. Behavior of Arsenic and Geochemical Modeling of Arsenic Enrichment in Aqueous Environments. Appl. Geochem. 2004, 19, 169–180. [Google Scholar] [CrossRef]
- Ross, J.L.; Ozbek, M.M.; Pinder, G.F. Aleatoric and Epistemic Uncertainty in Groundwater Flow and Transport Simulation: UNCERTAINTY IN GROUNDWATER SIMULATION. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Michael, H.A.; Khan, M.R. Impacts of Physical and Chemical Aquifer Heterogeneity on Basin-Scale Solute Transport: Vulnerability of Deep Groundwater to Arsenic Contamination in Bangladesh. Adv. Water Resour. 2016, 98, 147–158. [Google Scholar] [CrossRef] [Green Version]
- Duan, Y.; Li, R.; Gan, Y.; Yu, K.; Tong, J.; Zeng, G.; Ke, D.; Wu, W.; Liu, C. Impact of Physico-Chemical Heterogeneity on Arsenic Sorption and Reactive Transport under Water Extraction. Environ. Sci. Technol. 2020, 54, 14974–14983. [Google Scholar] [CrossRef]
- Rubin, Y. Applied Stochastic Hydrogeology; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Tartakovsky, D.M. Assessment and Management of Risk in Subsurface Hydrology: A Review and Perspective. Adv. Water Resour. 2013, 51, 247–260. [Google Scholar] [CrossRef]
- Sanchez-Vila, X.; Fernàndez-Garcia, D. Debates—Stochastic Subsurface Hydrology from Theory to Practice: Why Stochastic Modeling Has Not yet Permeated into Practitioners? Water Resour. Res. 2016, 52, 9246–9258. [Google Scholar] [CrossRef] [Green Version]
- Pedretti, D.; Mayer, K.U.; Beckie, R.D. Controls of Uncertainty in Acid Rock Drainage Predictions from Waste Rock Piles Examined through Monte-Carlo Multicomponent Reactive Transport. Stoch Environ. Res. Risk Assess. 2020, 34, 219–233. [Google Scholar] [CrossRef]
- Ayotte, J.D.; Nolan, B.T.; Nuckols, J.R.; Cantor, K.P.; Robinson, G.R.; Baris, D.; Hayes, L.; Karagas, M.; Bress, W.; Silverman, D.T.; et al. Modeling the Probability of Arsenic in Groundwater in New England as a Tool for Exposure Assessment. Environ. Sci. Technol. 2006, 40, 3578–3585. [Google Scholar] [CrossRef] [PubMed]
- Dalla Libera, N.; Fabbri, P.; Mason, L.; Piccinini, L.; Pola, M. Geostatistics as a Tool to Improve the Natural Background Level Definition: An Application in Groundwater. Sci. Total Environ. 2017, 598, 330–340. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; Song, J.; Li, S.; Tick, G.R.; Wei, W.; Zhu, J.; Zheng, C.; Zhang, Y. Quantifying Transport of Arsenic in Both Natural Soils and Relatively Homogeneous Porous Media Using Stochastic Models. Soil Sci. Soc. Am. J. 2018, 82, 1057–1070. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Dalla Libera, N.; Fabbri, P.; Mason, L.; Piccinini, L.; Pola, M. A Local Natural Background Level Concept to Improve the Natural Background Level: A Case Study on the Drainage Basin of the Venetian Lagoon in Northeastern Italy. Environ. Earth Sci. 2018, 77, 487. [Google Scholar] [CrossRef]
- Carraro, A.; Fabbri, P.; Giaretta, A.; Peruzzo, L.; Tateo, F.; Tellini, F. Effects of Redox Conditions on the Control of Arsenic Mobility in Shallow Alluvial Aquifers on the Venetian Plain (Italy). Sci. Total Environ. 2015, 532, 581–594. [Google Scholar] [CrossRef] [PubMed]
- Carraro, A.; Fabbri, P.; Giaretta, A.; Peruzzo, L.; Tateo, F.; Tellini, F. Arsenic Anomalies in Shallow Venetian Plain (Northeast Italy) Groundwater. Environ. Earth Sci. 2013, 70, 3067–3084. [Google Scholar] [CrossRef]
- Dalla Libera, N.; Pedretti, D.; Tateo, F.; Mason, L.; Piccinini, L.; Fabbri, P. Conceptual Model of Arsenic Mobility in the Shallow Alluvial Aquifers near Venice (Italy) Elucidated through Machine Learning and Geochemical Modeling. Water Resour. Res. 2020, 56, e2019WR026234. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program. For Speciation, Batch-Reaction, One-Dimensional Transport., and Inverse Geochemical Calculations; U.S. Geological Survey: Denver, CO, USA, 2013; p. 493.
- Parkhurst, D.L.; Kipp, K.L.; Engesgaard, P.; Charlton, S.R. PHAST—A Program for Simulating Ground-Water Flow, Solute Transport, and Multicomponent Geochemical Reactions; U.S. Geological Survey: Denver, CO, USA, 2004; p. 154.
- Charlton, S.R.; Parkhurst, D.L. Phast4Windows: A 3D Graphical User Interface for the Reactive-Transport Simulator PHAST. Groundwater 2013, 51, 623–628. [Google Scholar] [CrossRef]
- Kipp, J.L., Jr. Guide to the Revised Heat and Solute Transport. Simulator: HST3D—Version 2; U.S. Geological Survey (USGS) Water-Resources Investigation Report 97-4157; USGS: Denver, CO, USA, 1997.
- Fabbri, P.; Gaetan, C.; Sartore, L.; Dalla Libera, N. Subsoil Reconstruction in Geostatistics beyond Kriging: A Case Study in Veneto (NE Italy). Hydrology 2020, 7, 15. [Google Scholar] [CrossRef] [Green Version]
- Sartore, L. SpMC: Modelling Spatial Random Fields with Continuous Lag Markov Chains. R J. 2013, 5, 13. [Google Scholar] [CrossRef] [Green Version]
- Sartore, L.; Fabbri, P.; Gaetan, C. SpMC: An R-Package for 3D Lithological Reconstructions Based on Spatial Markov Chains. Comput. Geosci. 2016, 94, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Carle, S.F.; Fogg, G.E. Transition Probability-Based Indicator Geostatistics. Math. Geol. 1996, 28, 453–476. [Google Scholar] [CrossRef]
- Ball, J.W.; Nordstrom, D.K. WATEQ4F—User’s Manual with Revised Thermodynamic Data Base and Test. Cases for Calculating Speciation of Major, Trace and Redox Elements in Natural Waters; Open-File Report; U.S. Geological Survey: Menlo Park, CA, USA, 1991.
- Dzombak, D.A.; Morel, F.M. Surface Complexation Modeling: Hydrous Ferric Oxide; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A Critical Review of Data on Field-Scale Dispersion in Aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Environmental Applications; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Beretta, G.P.; Terrenghi, J. Groundwater Flow in the Venice Lagoon and Remediation of the Porto Marghera Industrial Area (Italy). Hydrogeol. J. 2017, 25, 847–861. [Google Scholar] [CrossRef]
- Journel, A.G. Fundamentals of Geostatistics in Five Lessons; Short Course In Geology; American Geophysical Union: Washington, DC, USA, 1989; Volume 8. [Google Scholar]
- Deutsch, C.; Journel, A. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1998; 340p. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS. A User’s Guide; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Georgopoulos, P.G.; Wang, S.-W.; Yang, Y.-C.; Xue, J.; Zartarian, V.G.; Mccurdy, T.; Özkaynak, H. Biologically Based Modeling of Multimedia, Multipathway, Multiroute Population Exposures to Arsenic. J. Expo. Sci. Environ. Epidemiol. 2008, 18, 462–476. [Google Scholar] [CrossRef]
- Serre, M.L.; Kolovos, A.; Christakos, G.; Modis, K. An Application of the Holistochastic Human Exposure Methodology to Naturally Occurring Arsenic in Bangladesh Drinking Water. Risk Anal. 2003, 23, 515–528. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, R.; Ramos, J.A.; Armienta, A. Groundwater Arsenic Variations: The Role of Local Geology and Rainfall. Appl. Geochem. 2004, 19, 245–250. [Google Scholar] [CrossRef]
- Duan, Y.; Gan, Y.; Wang, Y.; Deng, Y.; Guo, X.; Dong, C. Temporal Variation of Groundwater Level and Arsenic Concentration at Jianghan Plain, Central China. J. Geochem. Explor. 2015, 149, 106–119. [Google Scholar] [CrossRef]

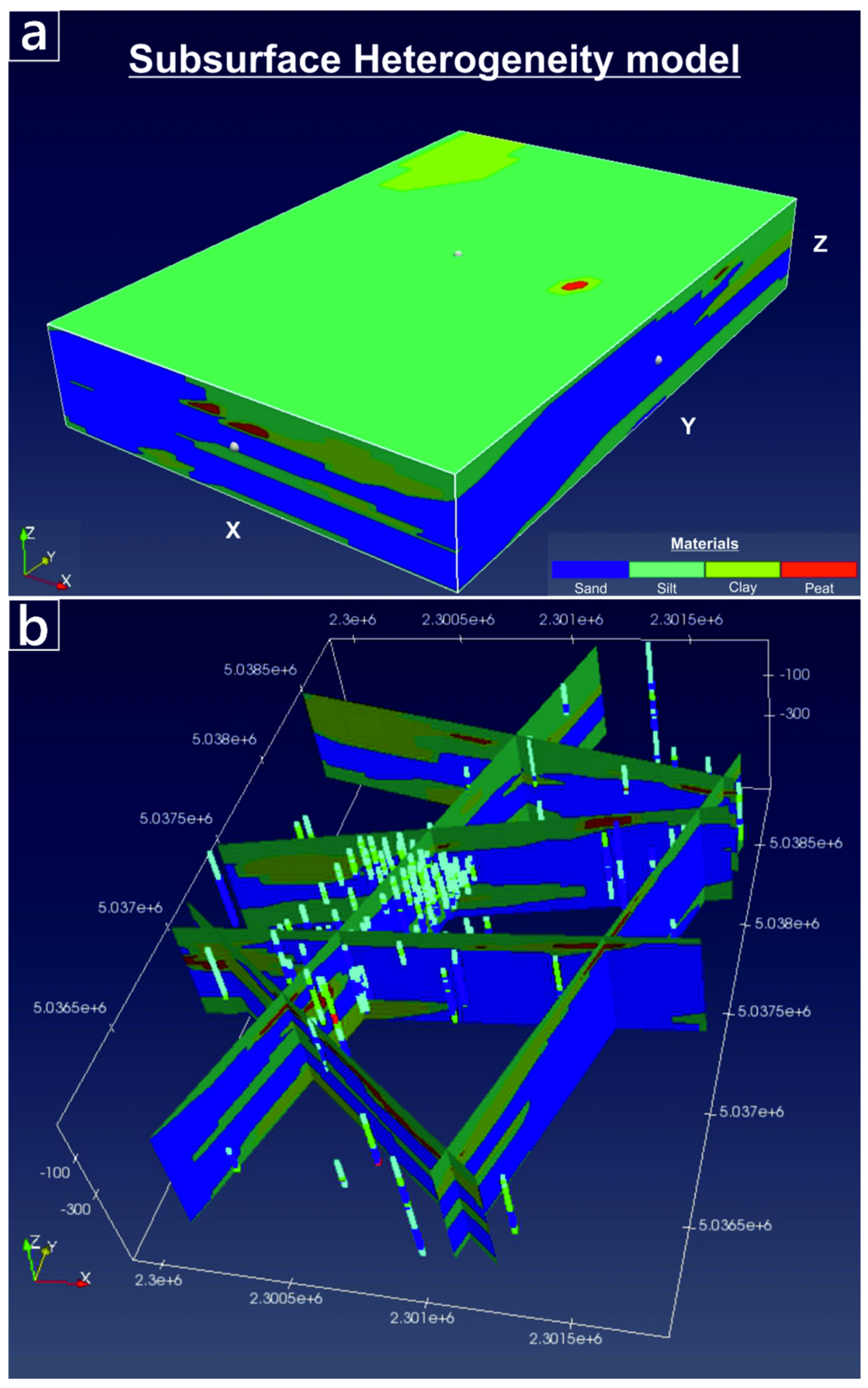

| Material | K (ms−1) | Ss (m−1) | Sy (-) |
|---|---|---|---|
| Sand | 1.25 × 10−4 | 1.00 × 10−7 | 2.00 × 10−1 |
| Silt | 5.00 × 10−6 | 1.00 × 10−4 | 1.00 × 10−2 |
| Clay | 1.00 × 10−8 | 5.00 × 10−4 | 5.00 × 10−3 |
| Peat | 1.00 × 10−8 | 5.00 × 10−4 | 5.00 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalla Libera, N.; Pedretti, D.; Casiraghi, G.; Markó, Á.; Piccinini, L.; Fabbri, P. Probability of Non-Exceedance of Arsenic Concentration in Groundwater Estimated Using Stochastic Multicomponent Reactive Transport Modeling. Water 2021, 13, 3086. https://doi.org/10.3390/w13213086
Dalla Libera N, Pedretti D, Casiraghi G, Markó Á, Piccinini L, Fabbri P. Probability of Non-Exceedance of Arsenic Concentration in Groundwater Estimated Using Stochastic Multicomponent Reactive Transport Modeling. Water. 2021; 13(21):3086. https://doi.org/10.3390/w13213086
Chicago/Turabian StyleDalla Libera, Nico, Daniele Pedretti, Giulia Casiraghi, Ábel Markó, Leonardo Piccinini, and Paolo Fabbri. 2021. "Probability of Non-Exceedance of Arsenic Concentration in Groundwater Estimated Using Stochastic Multicomponent Reactive Transport Modeling" Water 13, no. 21: 3086. https://doi.org/10.3390/w13213086
APA StyleDalla Libera, N., Pedretti, D., Casiraghi, G., Markó, Á., Piccinini, L., & Fabbri, P. (2021). Probability of Non-Exceedance of Arsenic Concentration in Groundwater Estimated Using Stochastic Multicomponent Reactive Transport Modeling. Water, 13(21), 3086. https://doi.org/10.3390/w13213086









