Wave Impact Loads on Vertical Seawalls: Effects of the Geometrical Properties of Recurve Retrofitting
Abstract
:1. Introduction
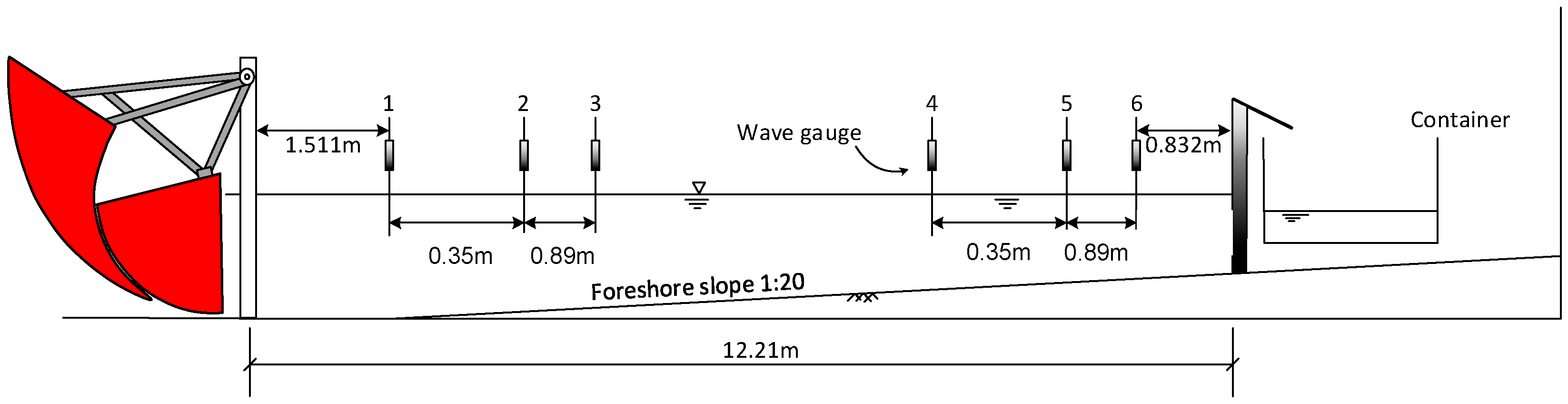
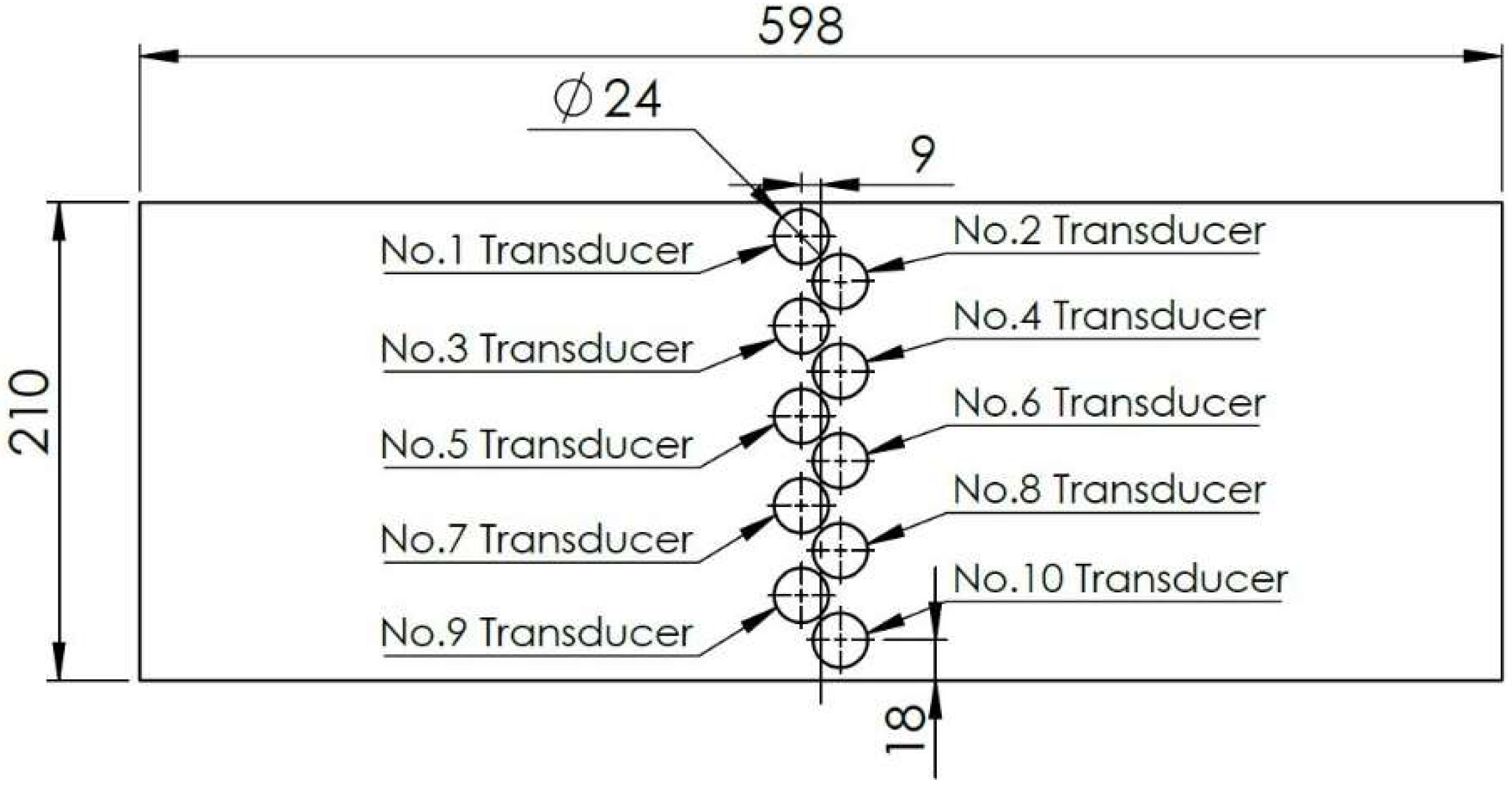
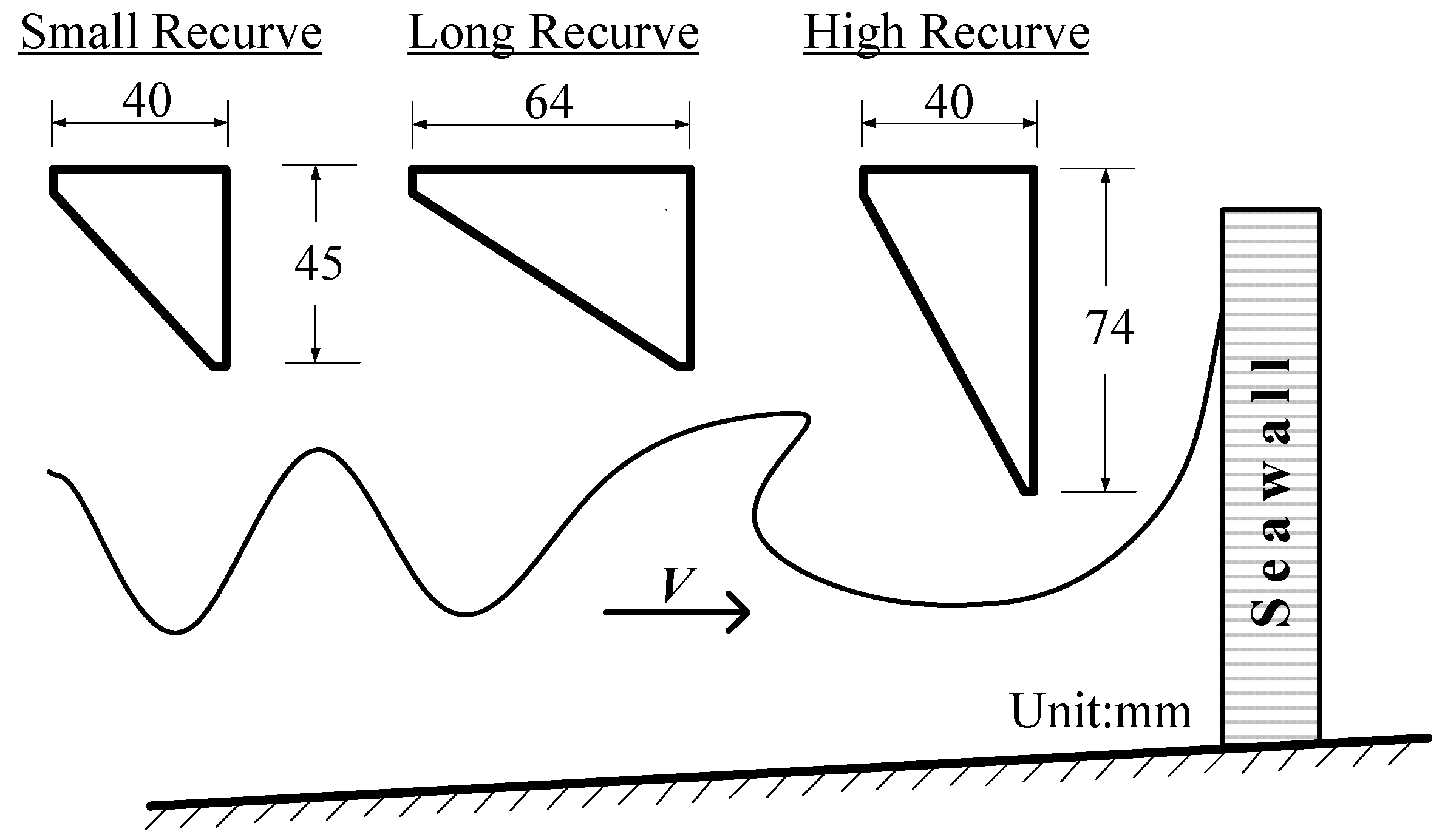
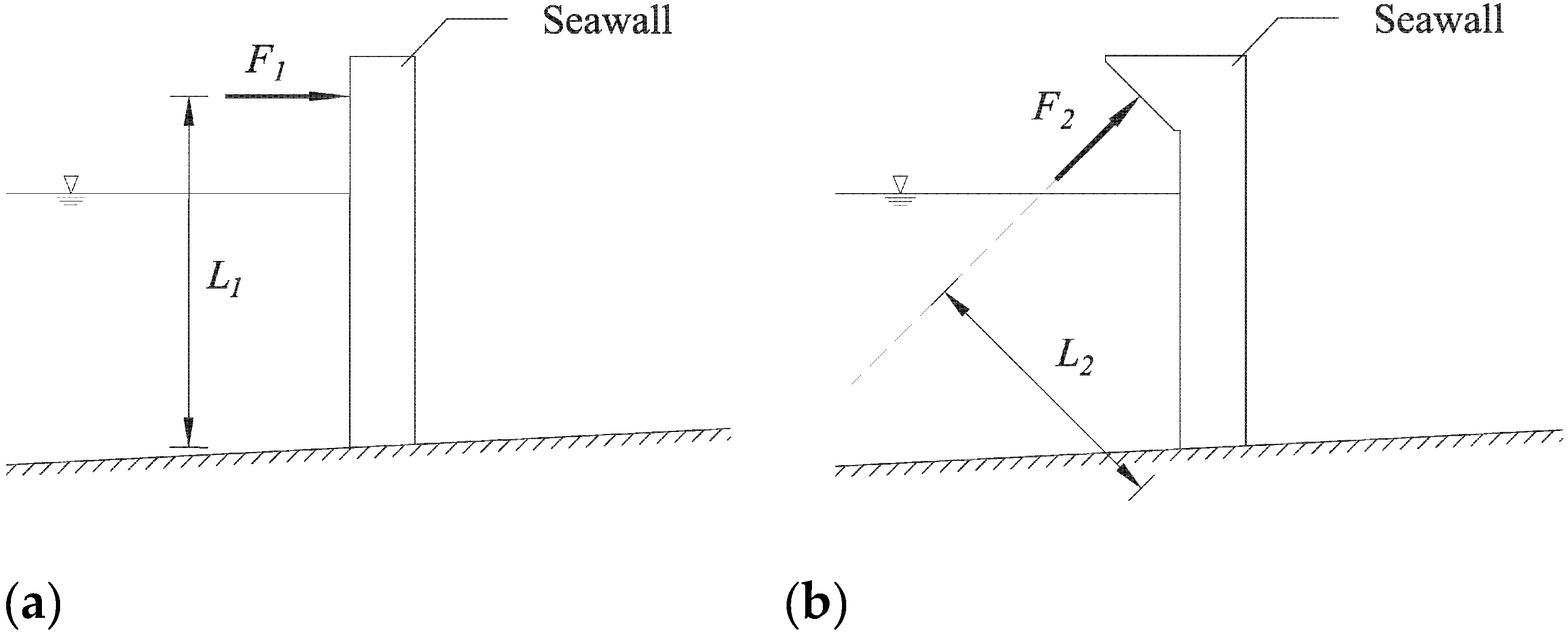
2. Materials and Methods
3. Results and Discussion
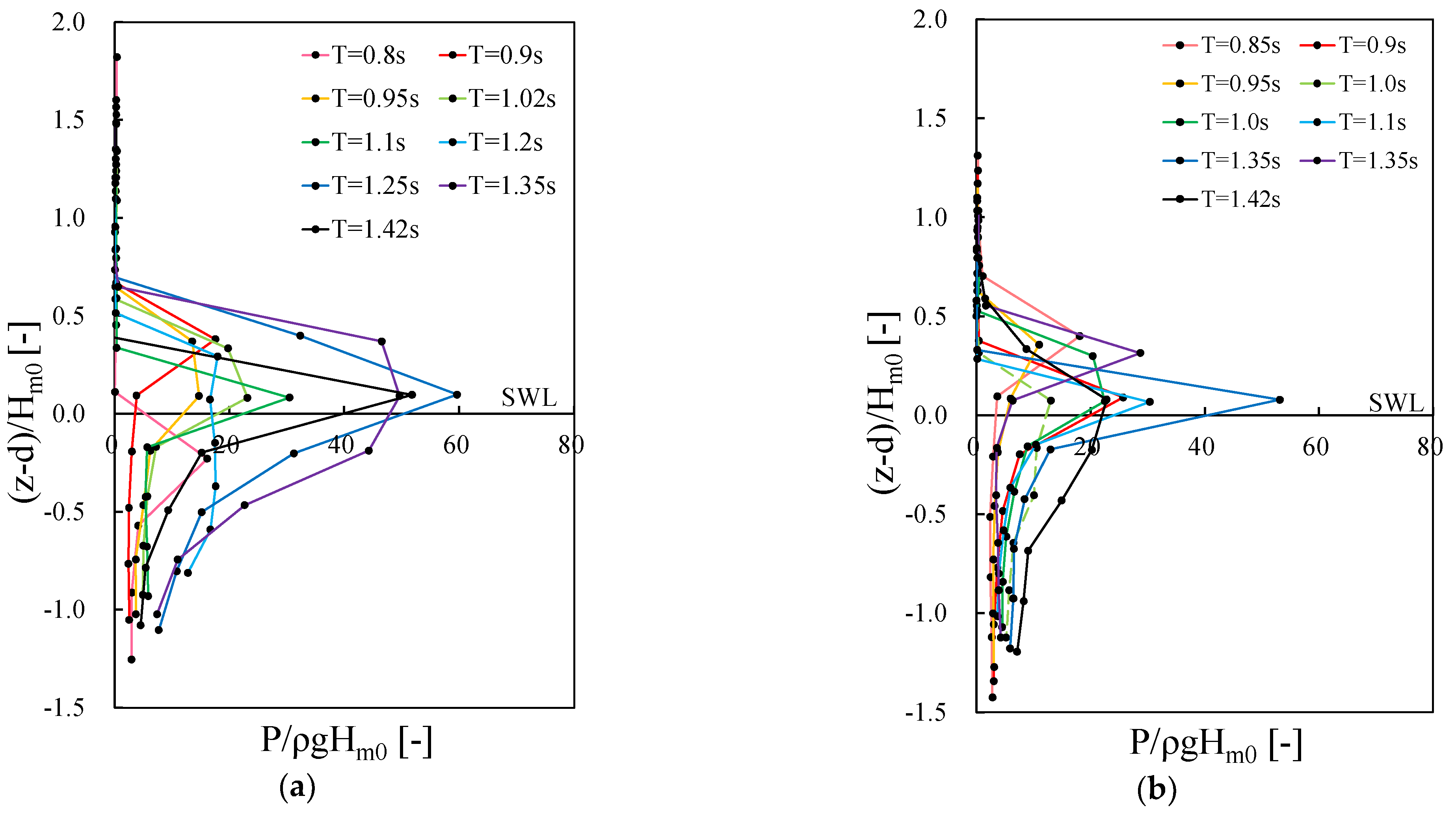
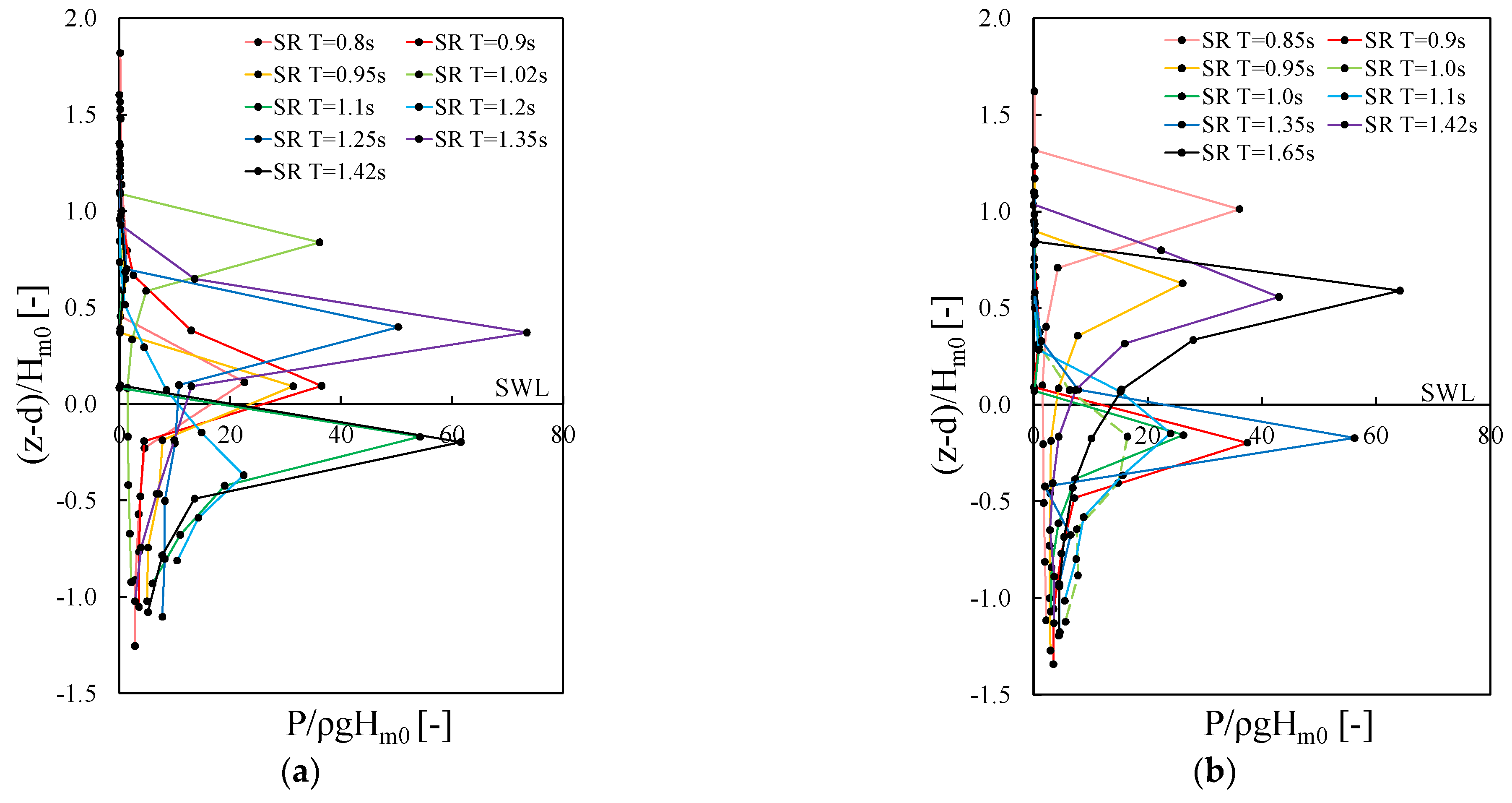
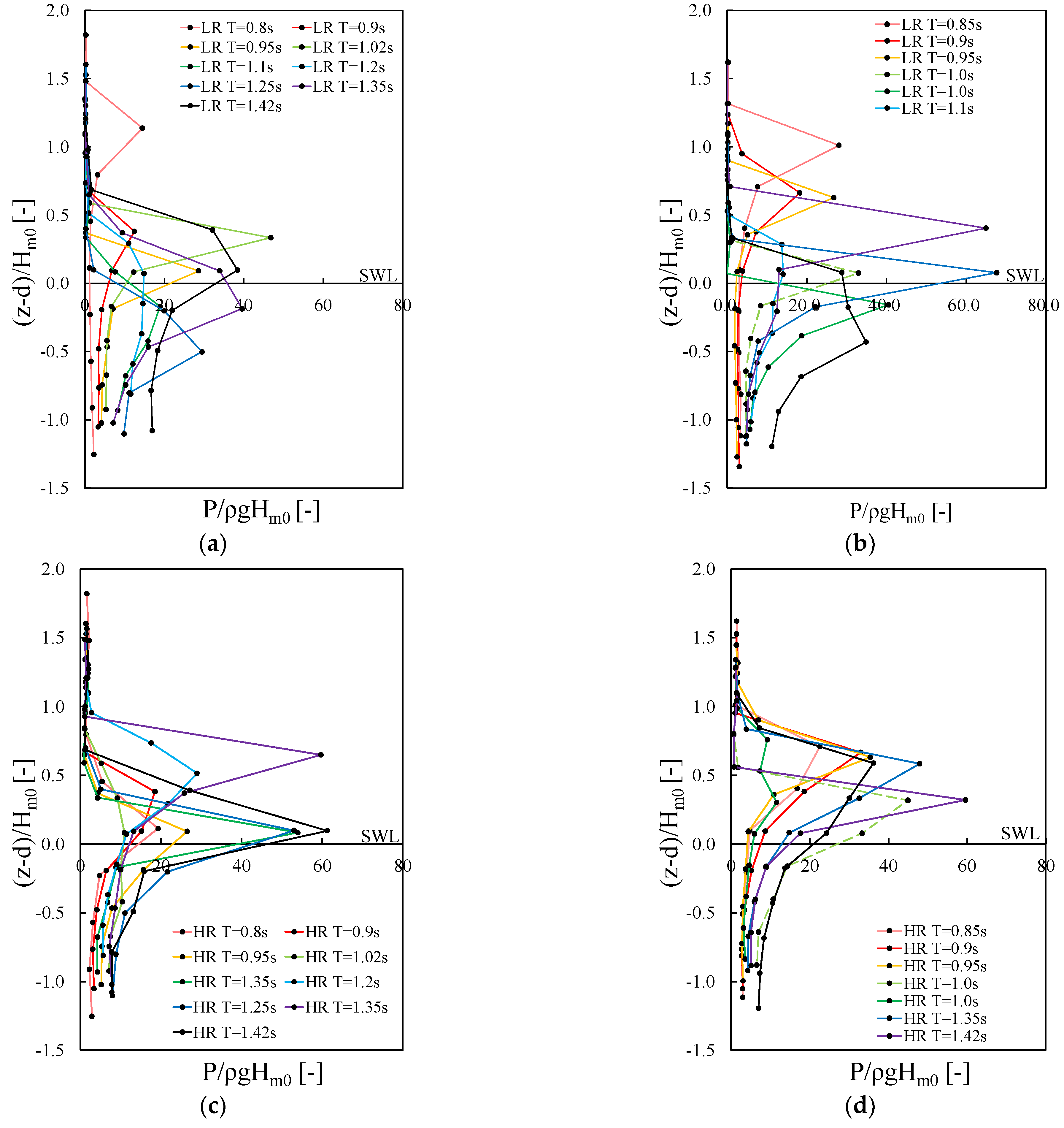
3.1. Pressure Distribution up the Wall
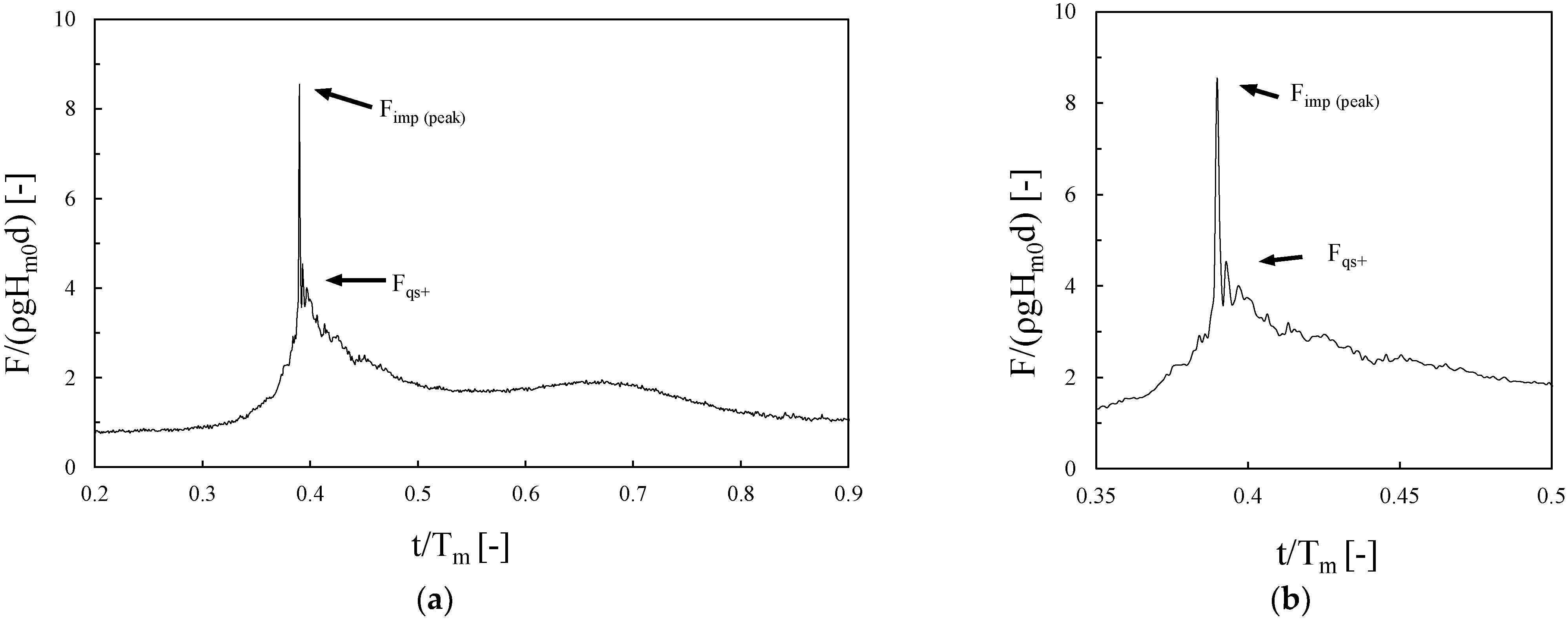
3.2. Impact and Quasi-Static Force
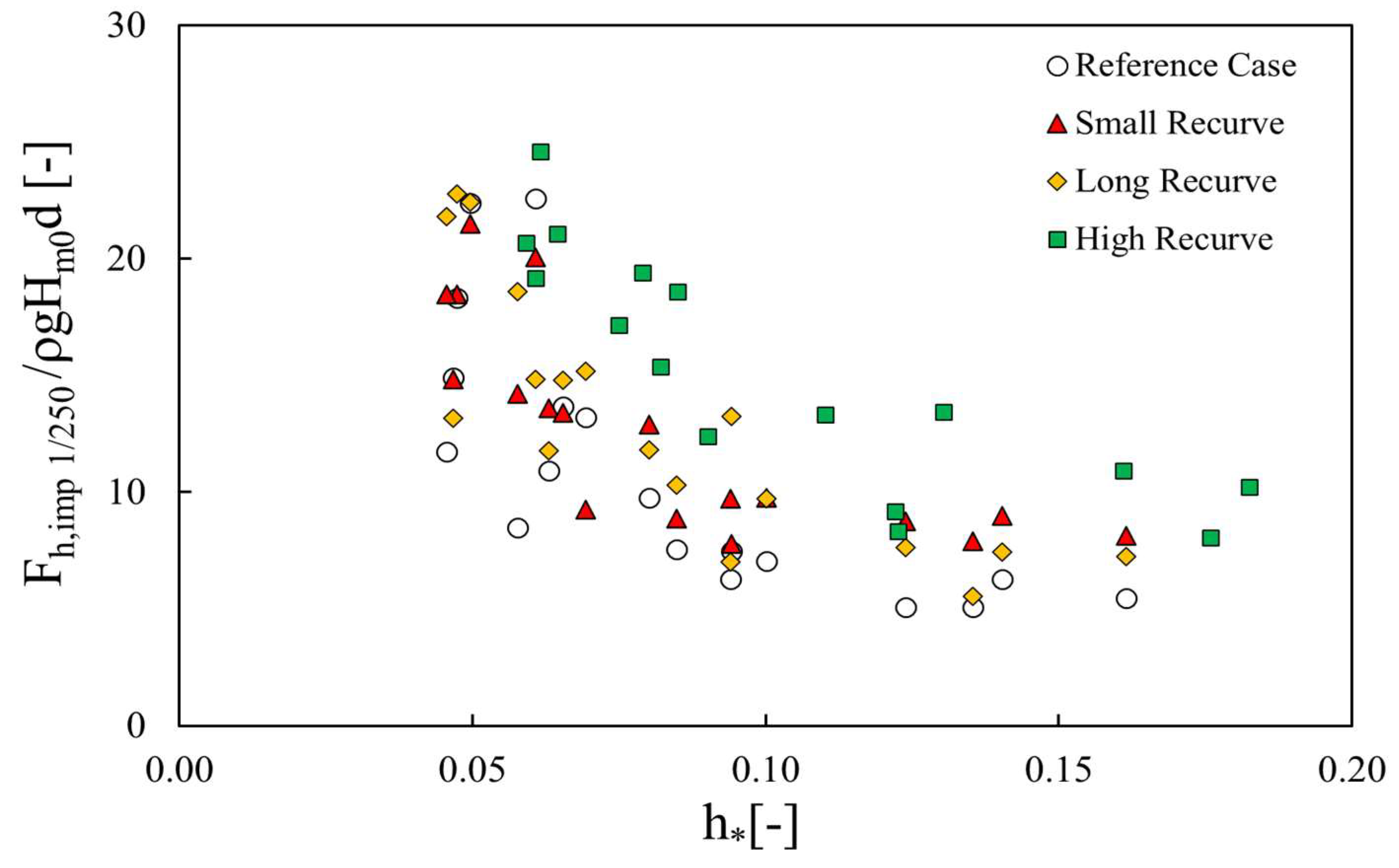
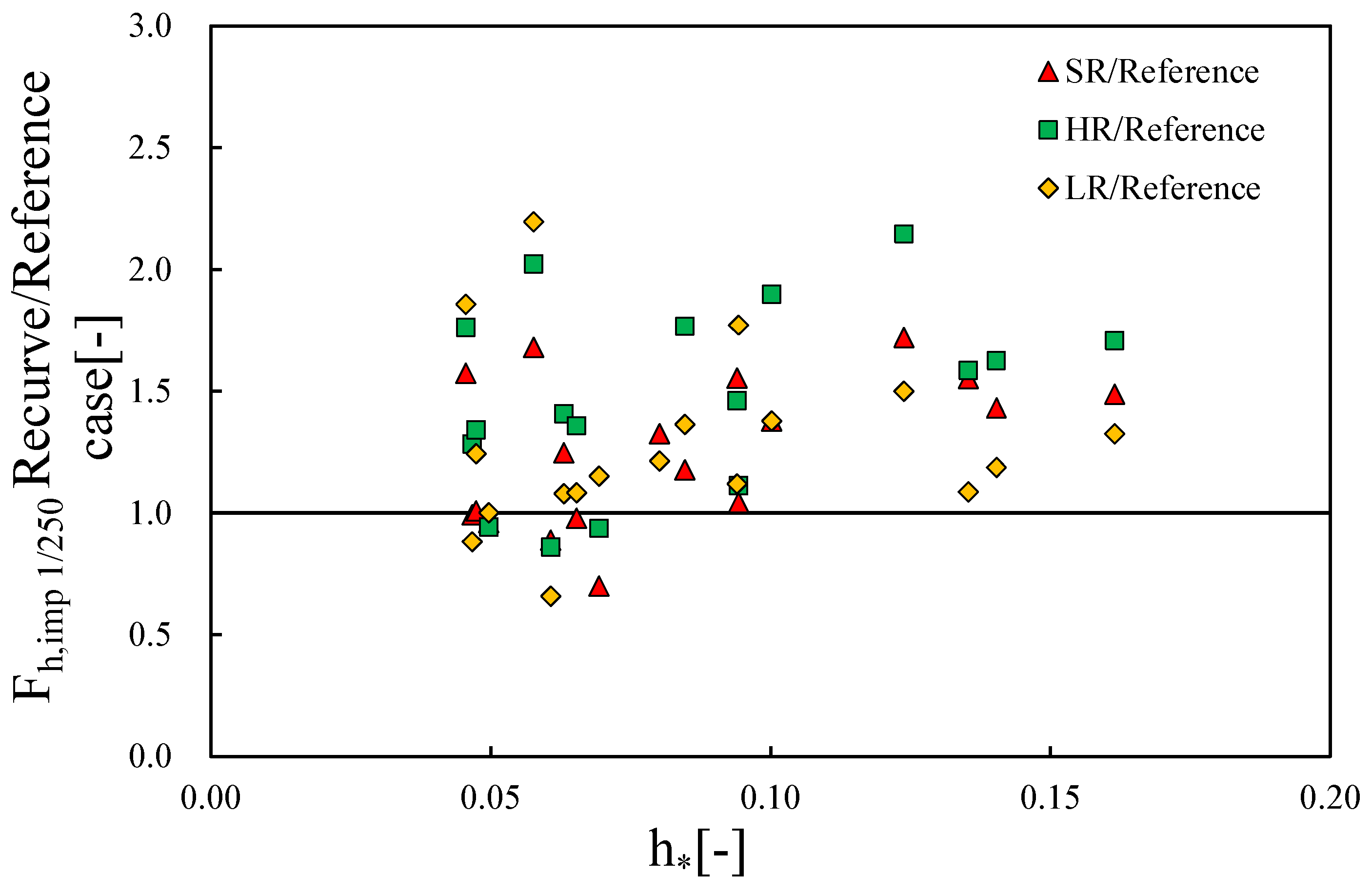
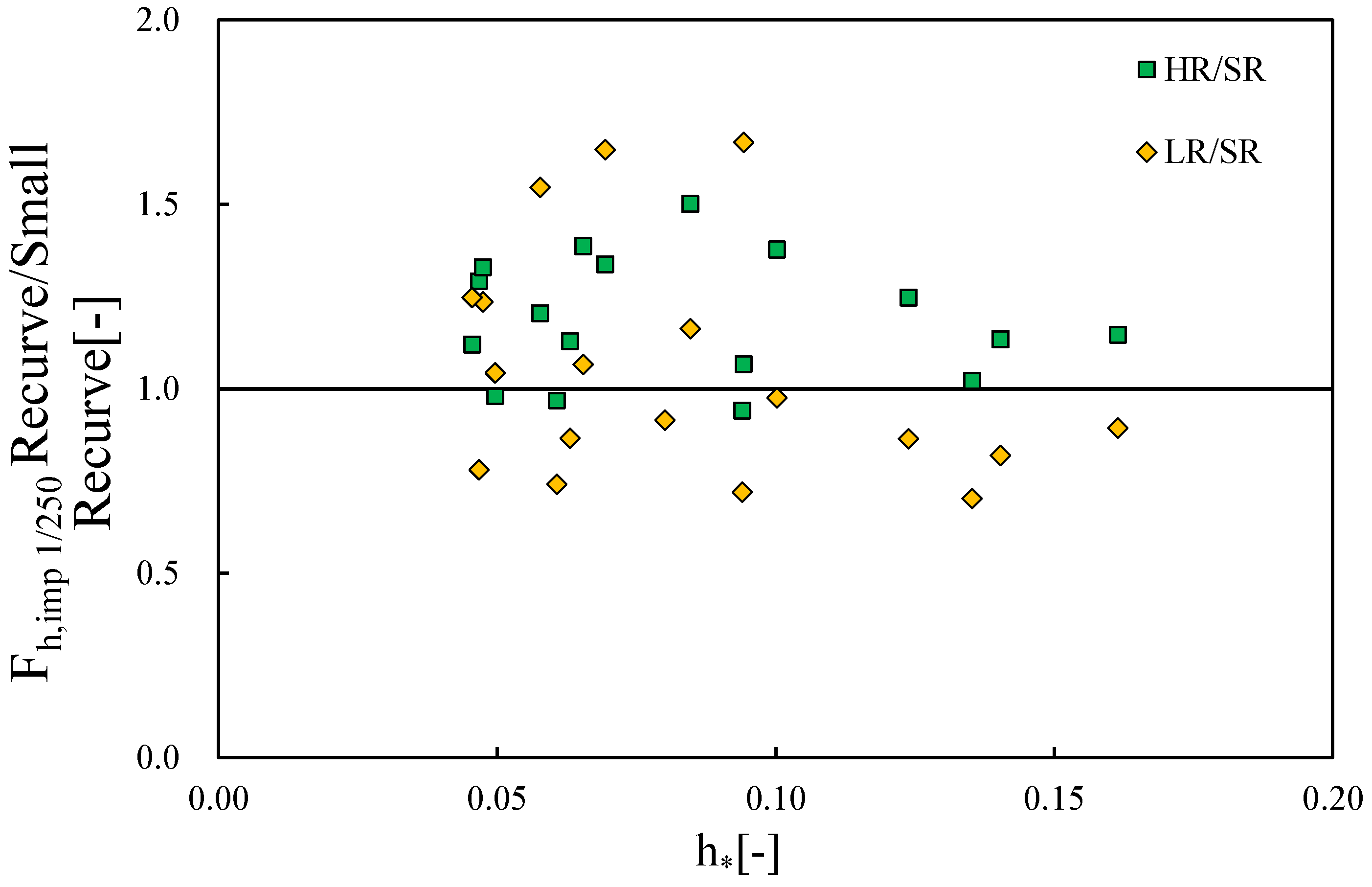
3.3. Wave Impact Force
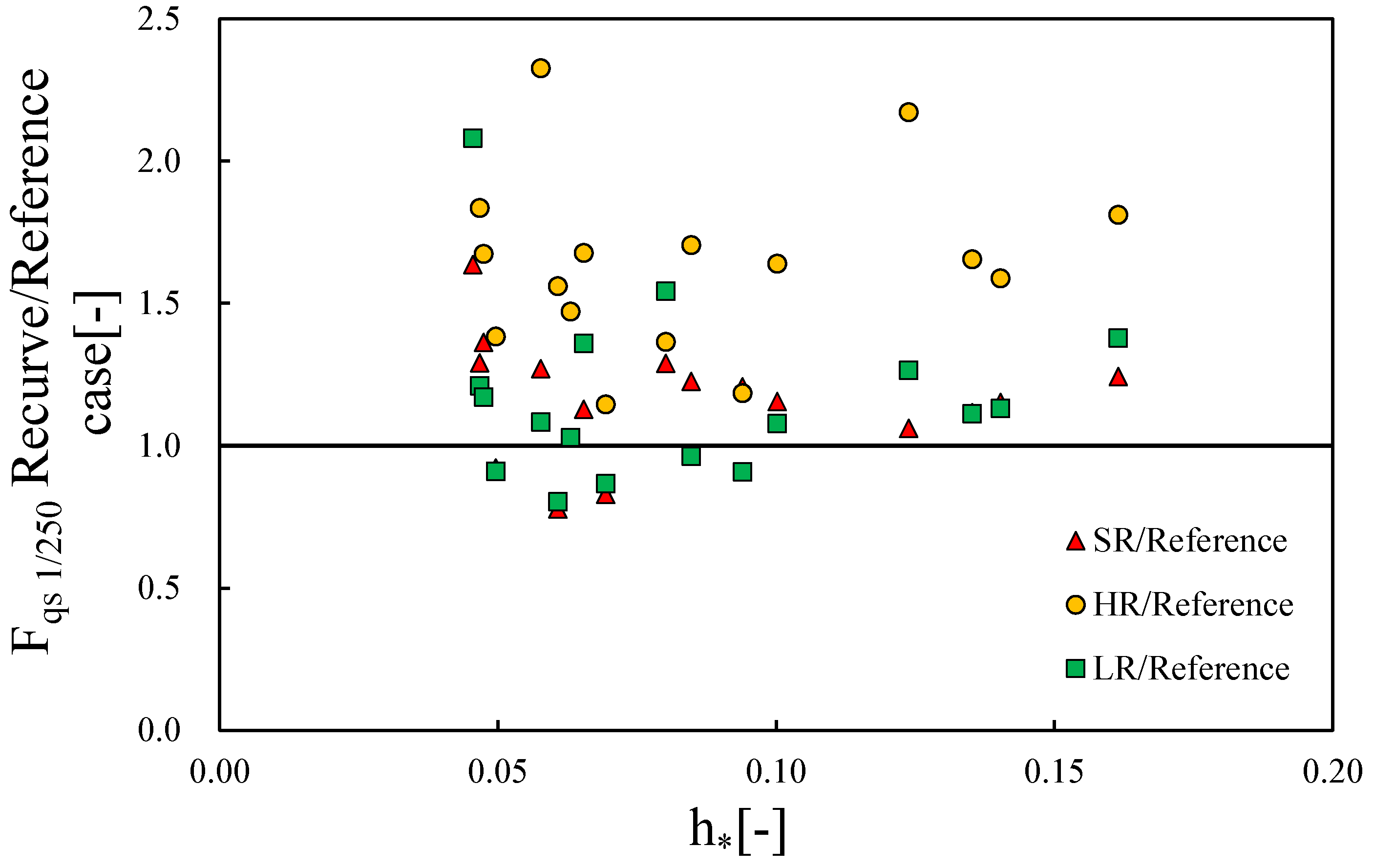
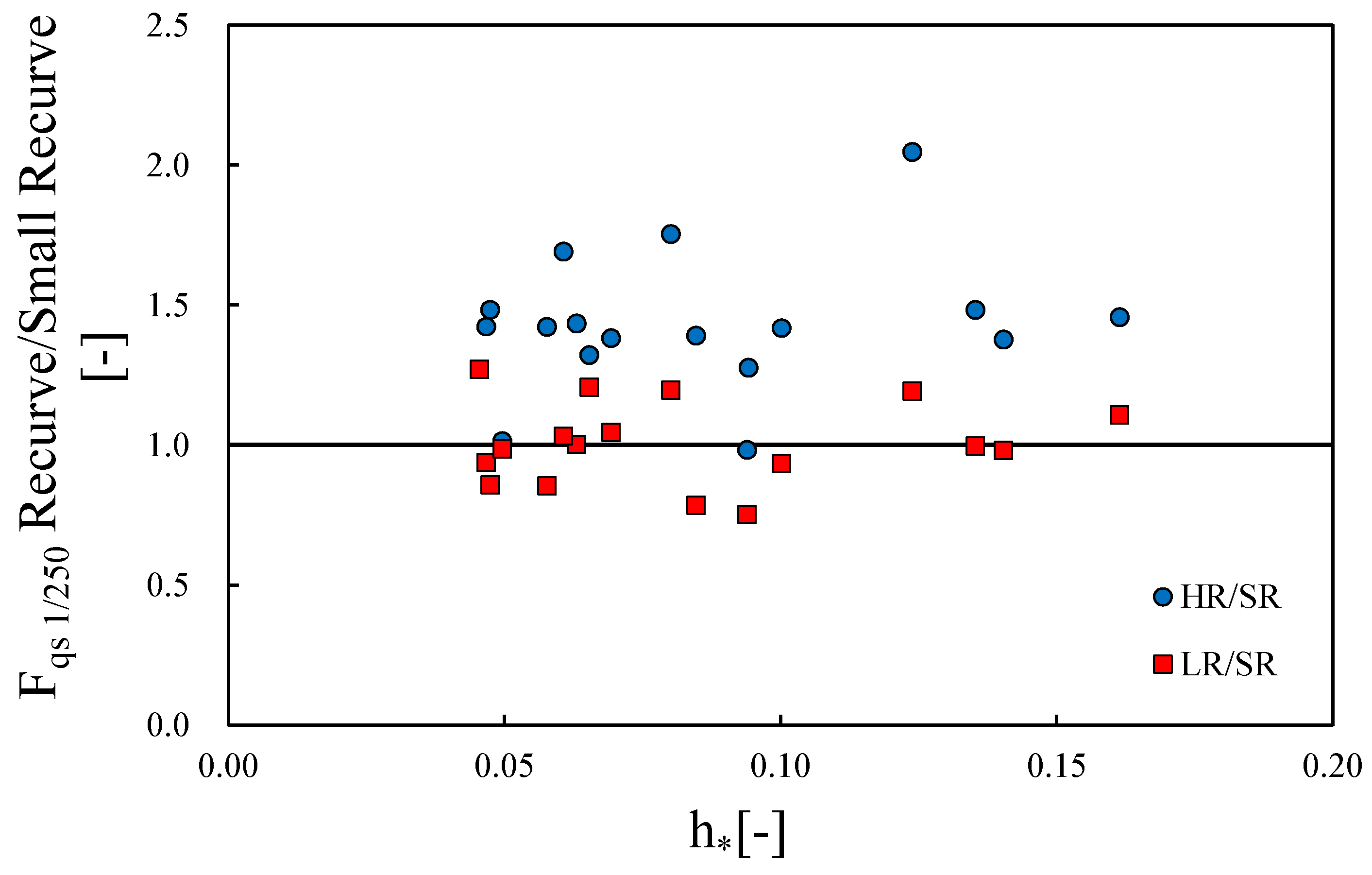
3.4. Wave Quasi-Static Force
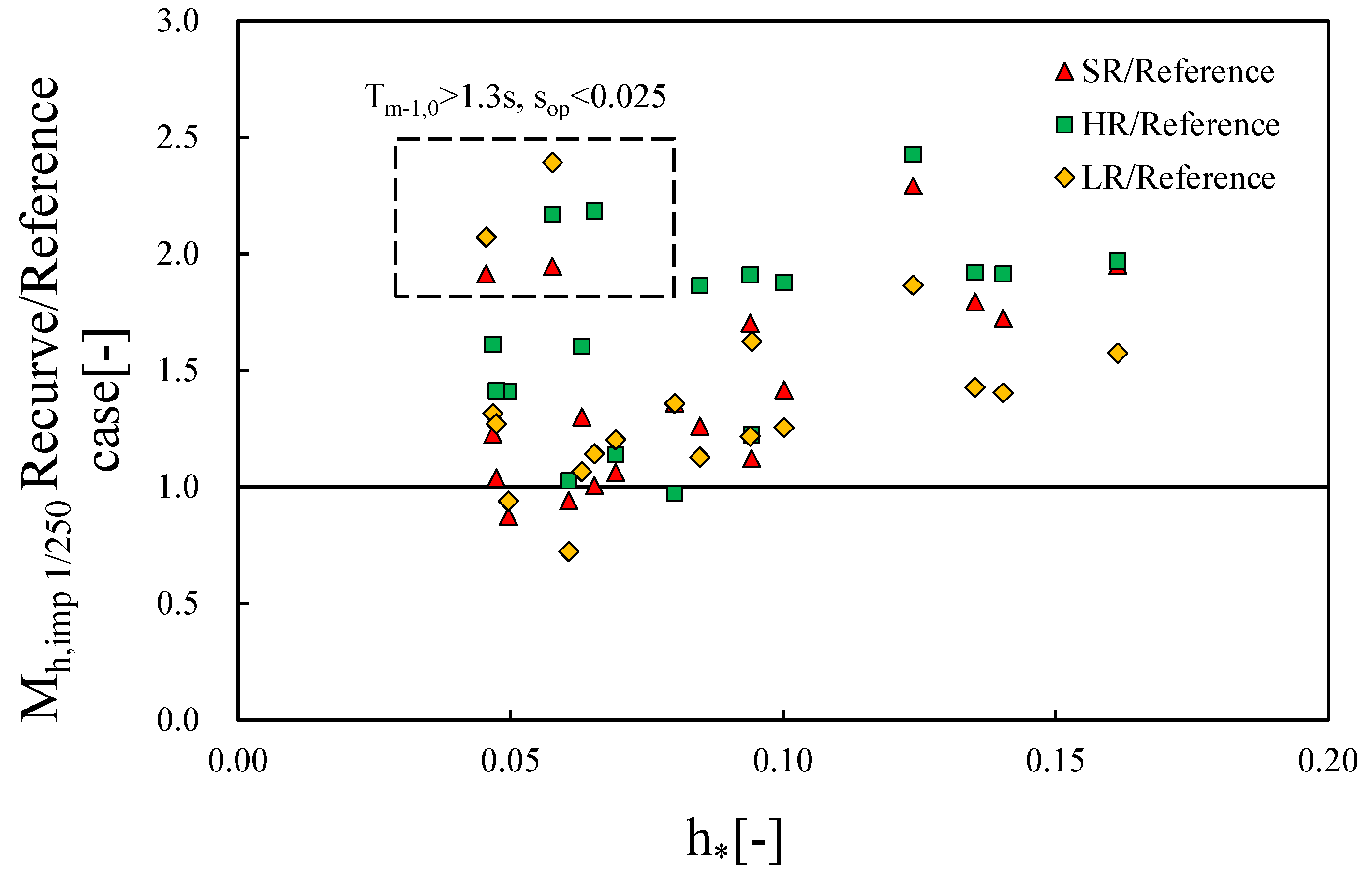
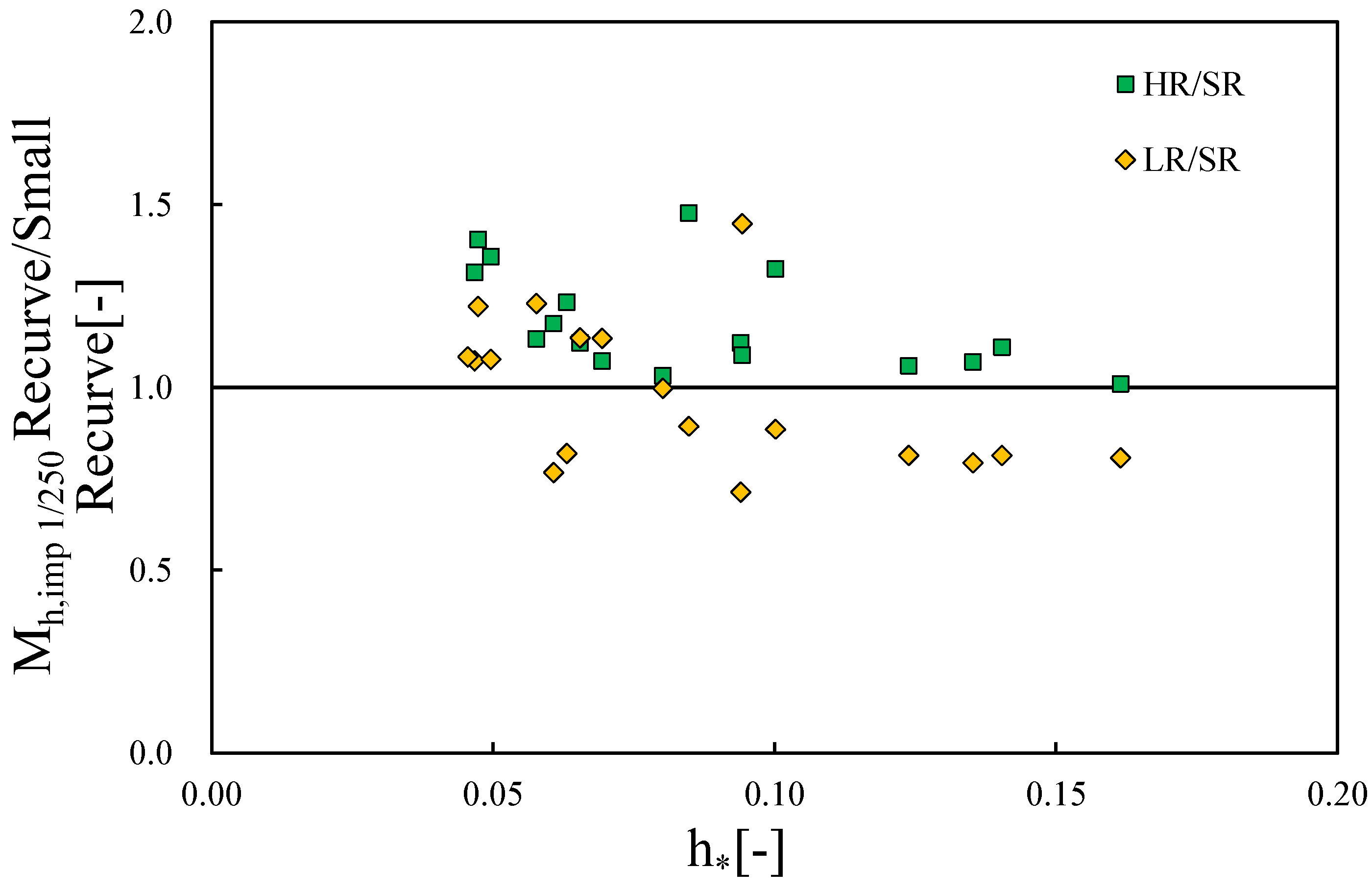
3.5. Overturning Moment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Global Warming of 1.5 °C: An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways. In The Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2018. [Google Scholar]
- Abolfathi, S.; Yeganeh-Bakhtiary, A.; Hamze-Ziabari, S.M.; Borzooei, S. Wave runup prediction using M5′ model tree algorithm. Ocean. Eng. 2016, 112, 76–81. [Google Scholar] [CrossRef]
- Abolfathi, S.; Dong, S.; Borzooei, S.; Yeganeh-Bakhtiari, A.; Pearson, J.M. Application of smoothed particle hydrodynamics in evaluating the performance of coastal retrofit structures. Coast. Eng. Proc. 2018, 1, 109. [Google Scholar] [CrossRef] [Green Version]
- Fitri, A.; Hashim, R.; Abolfathi, S.; Maulud, K.N.A. Dynamics of sediment transport and erosion-deposition patterns in the locality of a detached low-crested breakwater on a cohesive coast. Water 2019, 11, 1721. [Google Scholar] [CrossRef] [Green Version]
- Yeganeh-Bakhtiary, A.; Houshangi, H.; Hajivalie, F.; Abolfathi, S. A numerical study on hydrodynamics of standing waves in front of caisson breakwaters with WCSPH model. Coast. Eng. J. 2017, 59, 1750005-1–1750005-31. [Google Scholar] [CrossRef] [Green Version]
- Yeganeh-Bakhtiary, A.; Houshangi, H.; Abolfathi, S. Lagrangian two-phase flow modeling of scour in front of vertical breakwater. Coast. Eng. J. 2020, 62, 252–266. [Google Scholar] [CrossRef]
- O’Sullivan, J.J.; Salauddin, M.; Abolfathi, S.; Pearson, J.M. Effectiveness of eco-retrofits in reducing wave overtopping on seawalls. Coast. Eng. Proc. 2020, 36, 13. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Pearson, J.M. Extreme wave overtopping at ecologically modified sea defences. In Proceedings of the EGU General Assembly, Online, 4–8 May 2020. EGU2020-6162. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Dong, S.; Pearson, J.M. Distribution of individual wave overtopping volumes on a sloping structure with a permeable foreshore. Coast. Eng. Proc. 2020, 36, 54. [Google Scholar] [CrossRef]
- Dong, S.; Abolfathi, S.; Salauddin, M.; Pearson, J.M. Spatial distribution of wave-by-wave overtopping behind vertical seawall with recurve retrofitting. Ocean Eng. 2021, 238, 109674. [Google Scholar] [CrossRef]
- Salauddin, M.; Pearson, J.M. Laboratory investigation of overtopping at a sloping structure with permeable shingle foreshore. Ocean Eng. 2020, 197, 106866. [Google Scholar] [CrossRef]
- Allsop, N.W.H.; Vicinanza, D.; McKenna, J. Report SR 443; HR Wallingford: Wallingford, UK, 1996. [Google Scholar]
- Allsop, N.W.H.; Mckenna, J.E.; Vicinanza, D.; Wittaker, T.T.J. New design methods for wave impact loading on vertical Breakwaters and seawalls. In Proceedings of the 25th ICCE, Rome, Italy, 16–22 June 2017; pp. 2508–2521. [Google Scholar]
- Pearson, J.; Bruce, T.; Allsop, W.; Kortenhaus, A.; Van der Meer, J.W. Effectiveness of recurve walls in reducing wave overtopping on seawalls and breakwaters. Coast. Eng. 2004, 4, 4404–4416. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Salauddin, M.; Abolfathi, S.; Tan, Z.H.; Pearson, J.M. The Influence of Geometrical Shape Changes on Wave Overtopping: A Laboratory and SPH Numerical Study, in Coasts, Marine Structures and Breakwaters 2017: Realising the Potential; ICE Publishing: London, UK, 2018; pp. 1217–1226. [Google Scholar] [CrossRef]
- Dong, S.; Abolfathi, S.; Salauddin, M.; Tan, Z.H.; Pearson, J.M. Enhancing climate resilience of vertical seawall with retrofitting-A physical modelling study. Appl. Ocean. Res. 2020, 103, 102331. [Google Scholar] [CrossRef]
- Dong, S.; Abolfathi, S.; Salauddin, M.; Pearson, J.M. Spatial distribution of wave-by-wave overtopping at vertical seawalls. Coast. Eng. Proc. 2020, 36, 17. [Google Scholar] [CrossRef]
- Kortenhaus, A.; Pearson, J.; Bruce, T.; Allsop, N.; Van der Meer, J.W. Influence of parapets and recurves on wave overtopping and wave loading of complex vertical walls. Coast. Struct. 2003, 369–381. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Pearson, J.M. Eco-Engineering of Seawalls—An Opportunity for Enhanced Climate Resilience from Increased Topographic Complexity. Front. Mar. Sci. 2021, 8, 674630. [Google Scholar] [CrossRef]
- Oh, S.; Jang, S.; Lee, J. Wave Overtopping and Loading for the Recurved Parapets on the Crest of Rubble Mound Breakwater. In Proceedings of the Coasts, Marine Structures and Breakwaters, Liverpool, UK, 5–7 September 2017. [Google Scholar] [CrossRef]
- Van Doorslaer, K.; De Rouck, J.; Trouw, K.; van der Meer, J.W.; Schimmels, S. Wave forces on storm walls, small and large scale experiments. In Proceedings of the COPEDEC VIII, Chennai, India, 20–24 February 2012. [Google Scholar]
- Castellino, M.; Lara, J.L.; Romano, A.; Losada, I.J.; De Girolamo, P. Wave loading for recurved parapet walls in non-breaking wave conditions: Analysis of the induced impulsive forces. Coast. Eng. Proc. 2018, 1, 34. [Google Scholar] [CrossRef] [Green Version]
- Castellino, M.; Sammarco, P.; Romano, A.; Martinelli, L.; Ruol, P.; Franco, L.; De Girolamo, P. Large impulsive forces on recurved parapets under non-breaking waves:A numerical study. Coast. Eng. 2018, 136, 1–15. [Google Scholar] [CrossRef]
- Martinelli, L.; Ruol, P.; Volpato, M.; Favaretto, C.; Castellino, M.; De Girolamo, P.; Sammarco, P. Experimental investigation on non-breaking wave forces and overtopping at the recurved parapets of vertical breakwaters. Coast. Eng. 2018, 141, 52–67. [Google Scholar] [CrossRef]
- Swart, E. Effect of the Overhang Length of a Recurve Seawall in Reducing Wave Overtopping; Stellenbosch University: Stellenbosch, South Africa, 2016. [Google Scholar]
- Bullock, G.; Obhrai, C.; Peregrine, D.; Bredmose, H. Violent breaking wave impacts. Part 1: Results from large-scale regular wave tests on vertical and sloping walls. Coast. Eng. 2007, 54, 602–617. [Google Scholar] [CrossRef]
- Cuomo, G.; Allsop, N.W.H.; Bruce, T.; Pearson, J.M. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 4. [Google Scholar] [CrossRef] [Green Version]
- Stagonas, D.; Lara, J.L.; Losada, I.J.; Higuera, P.; Jaime, F.F.; Muller, G. Large scale measurements of wave loads and mapping of impact pressure distribution at the underside of wave recurves. In Proceedings of the HYDRALAB IV Joint User Meeting, Lisbon, Portugal, 2–4 July 2014. [Google Scholar]
- Kisacik, D.; Troch, P.; Van Bogaert, P. Experimental study of violent wave impact on a vertical structure with an overhanging horizontal cantilever slab. Ocean. Eng. 2012, 49, 1–15. [Google Scholar] [CrossRef]
- Kisacik, D.; Troch, P.; Van Bogaert, P. Description of loading conditions due to violent wave impacts on a vertical structure with an overhanging horizontal cantilever slab. Coast. Eng. 2012, 60, 201–226. [Google Scholar] [CrossRef]
- Abolfathi, S.; Pearson, J.M. Solute dispersion in the nearshore due to oblique waves. Coast. Eng. Proc. 2014, 34, 49. [Google Scholar] [CrossRef] [Green Version]
- Abolfathi, S.; Pearson, J.M. Application of smoothed particle hydrodynamics (SPH) in nearshore mixing: A comparison to laboratory data. Coast. Eng. Proc. 2017, 1, 16. [Google Scholar] [CrossRef]
- Ravindar, R.; Sriram, V.; Schimmels, S.; Stagonas, D. Characterization of breaking wave impact on vertical wall with recurve. ISH J. Hydraul. Eng. 2017, 25, 153–161. [Google Scholar] [CrossRef]
- Stagonas, D.; Ravindar, R.; Sriram, V.; Schimmels, S. Experimental Evidence of the Influence of Recurves on Wave Loads at Vertical Seawalls. Water 2020, 12, 889. [Google Scholar] [CrossRef] [Green Version]
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. Coast. Eng. 1980, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.M.; Bruce, T.; Allsop, N.W.H. Prediction of wave overtopping at steep seawalls—Variabilities and uncertainties. In Proceedings of the Fourth International Symposium on Ocean Wave Measurement and Analysis, San Francisco, CA, USA, 2–6 September 2001; pp. 1797–1808. [Google Scholar]
- Salauddin, M.; Pearson, J.M. A laboratory study on wave overtopping at vertical seawalls with a shingle foreshore. Coast. Eng. Proc. 2018, 1, 56. [Google Scholar] [CrossRef] [Green Version]
- Salauddin, M.; Pearson, J.M. Wave overtopping and toe scouring at a plain vertical seawall with shingle foreshore: A Physical model study. Ocean Eng. 2019, 171, 286–299. [Google Scholar] [CrossRef] [Green Version]
- Salauddin, M.; Pearson, J.M. Experimental Study on Toe Scouring at Sloping Walls with Gravel Foreshores. J. Mar. Sci. Eng. 2019, 7, 198. [Google Scholar] [CrossRef] [Green Version]
- Salauddin, M.; Peng, Z.; Pearson, J. The effects of wave impacts on toe scouring and overtopping concurrently for permeable shingle foreshores. In Proceedings of the EGU General Assembly, Online, 19–30 April 2021. EGU21-548. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: London, UK, 2000. [Google Scholar]
- Hull, P.; Müller, G. An investigation of breaker heights, shapes and pressures. Ocean Eng. 2002, 29, 59–79. [Google Scholar] [CrossRef]
- Peregrine, D. Water-wave impact on walls. Annu. Rev. Fluid Mech. 2003, 35, 23–43. [Google Scholar] [CrossRef]
- Bullock, G.N.; Crawford, A.R.; Hewson, P.J.; Walkden, M.J.A.; Bird, P.A.D. The influence of air and scale on wave impact pressures. Coast. Eng. 2001, 42, 291–312. [Google Scholar] [CrossRef]
- Wood, D.J.; Peregrine, D.H.; Bruce, T. Wave impact on a wall using pressure-impulse theory I: Trapped air. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 182–190. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures, 2nd ed.; 2018; Available online: http://www.overtopping-manual.com (accessed on 10 December 2020).

| hs [m] | Hm0 [m] | Tp [s] | Lp [m] | sop [−] | Rc [m] | Rc/Hm0 [−] |
|---|---|---|---|---|---|---|
| 0.07 | 0.05 | 0.79 | 0.98 | 0.054 | 0.14 | 2.67 |
| 0.07 | 0.06 | 0.88 | 1.20 | 0.054 | 0.14 | 2.17 |
| 0.07 | 0.07 | 0.94 | 1.38 | 0.050 | 0.14 | 2.01 |
| 0.09 | 0.06 | 0.79 | 0.98 | 0.059 | 0.12 | 2.08 |
| 0.09 | 0.07 | 0.88 | 1.20 | 0.057 | 0.12 | 1.75 |
| 0.09 | 0.07 | 0.94 | 1.38 | 0.051 | 0.12 | 1.70 |
| 0.09 | 0.08 | 1.03 | 1.66 | 0.047 | 0.12 | 1.53 |
| 0.09 | 0.08 | 1.10 | 1.90 | 0.041 | 0.12 | 1.54 |
| 0.09 | 0.09 | 1.21 | 2.28 | 0.039 | 0.12 | 1.35 |
| 0.09 | 0.07 | 1.26 | 2.46 | 0.027 | 0.12 | 1.83 |
| 0.09 | 0.07 | 1.36 | 2.90 | 0.024 | 0.12 | 1.70 |
| 0.09 | 0.07 | 1.46 | 3.31 | 0.020 | 0.12 | 1.79 |
| 0.09 | 0.07 | 1.73 | 4.67 | 0.014 | 0.12 | 1.82 |
| 0.11 | 0.06 | 0.88 | 1.20 | 0.054 | 0.10 | 1.54 |
| 0.11 | 0.07 | 0.88 | 1.20 | 0.057 | 0.10 | 1.45 |
| 0.11 | 0.07 | 0.94 | 1.38 | 0.052 | 0.10 | 1.38 |
| 0.11 | 0.08 | 0.99 | 1.51 | 0.054 | 0.10 | 1.22 |
| 0.11 | 0.08 | 0.94 | 1.38 | 0.057 | 0.10 | 1.26 |
| 0.11 | 0.08 | 1.36 | 2.90 | 0.027 | 0.10 | 1.27 |
| 0.11 | 0.08 | 1.46 | 3.31 | 0.025 | 0.10 | 1.22 |
| 0.11 | 0.08 | 1.73 | 4.67 | 0.017 | 0.10 | 1.29 |
| 0.12 | 0.08 | 1.00 | 1.56 | 0.051 | 0.09 | 1.13 |
| 0.11 | 0.09 | 0.99 | 1.51 | 0.057 | 0.10 | 1.16 |
| 0.11 | 0.09 | 1.10 | 1.90 | 0.048 | 0.10 | 1.10 |
| 0.11 | 0.09 | 1.12 | 1.97 | 0.048 | 0.10 | 1.05 |
| 0.12 | 0.10 | 1.10 | 1.90 | 0.051 | 0.09 | 0.93 |
| 0.12 | 0.11 | 1.31 | 2.66 | 0.040 | 0.09 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Salauddin, M.; Abolfathi, S.; Pearson, J. Wave Impact Loads on Vertical Seawalls: Effects of the Geometrical Properties of Recurve Retrofitting. Water 2021, 13, 2849. https://doi.org/10.3390/w13202849
Dong S, Salauddin M, Abolfathi S, Pearson J. Wave Impact Loads on Vertical Seawalls: Effects of the Geometrical Properties of Recurve Retrofitting. Water. 2021; 13(20):2849. https://doi.org/10.3390/w13202849
Chicago/Turabian StyleDong, Shudi, Md Salauddin, Soroush Abolfathi, and Jonathan Pearson. 2021. "Wave Impact Loads on Vertical Seawalls: Effects of the Geometrical Properties of Recurve Retrofitting" Water 13, no. 20: 2849. https://doi.org/10.3390/w13202849
APA StyleDong, S., Salauddin, M., Abolfathi, S., & Pearson, J. (2021). Wave Impact Loads on Vertical Seawalls: Effects of the Geometrical Properties of Recurve Retrofitting. Water, 13(20), 2849. https://doi.org/10.3390/w13202849








