A Simplified Model for Predicting the Effectiveness of Bioswale’s Control on Stormwater Runoff from Roadways
Abstract
:1. Introduction
2. Systematic Approach to Develop a Simplified Mathematical Model
- A field-scale bioswale testing facility was designed and constructed.
- A Personal Computer Storm Water Management Model (PCSWMM) numerical model based on the physical conditions of this field-scale bioswale was developed. PCSWMM is derived from SWMM. Although software tools have the same hydraulic and hydrologic analysis capability, PCSWMM offers enhanced graphic user interfaces that are much improved from USEPA SWMM 5. PCSWMM was chosen for this research work.
- The PCSWMM model was validated using the experimental data from testing the field-scale bioswale [23]
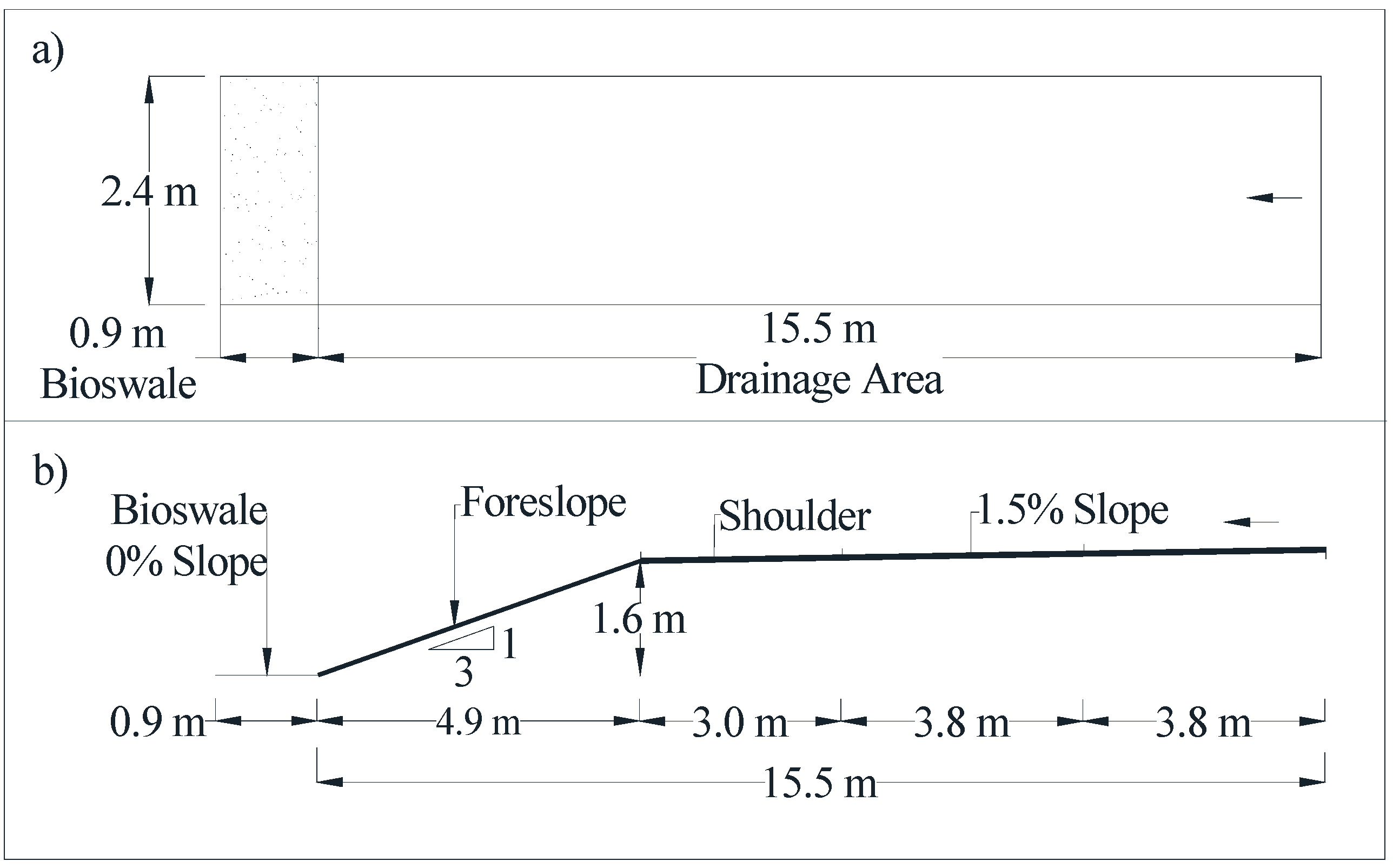
- An idealized (conceptual) catchment model that represents typical highway geometries and characteristics was developed for PCSWMM modeling and simulations.
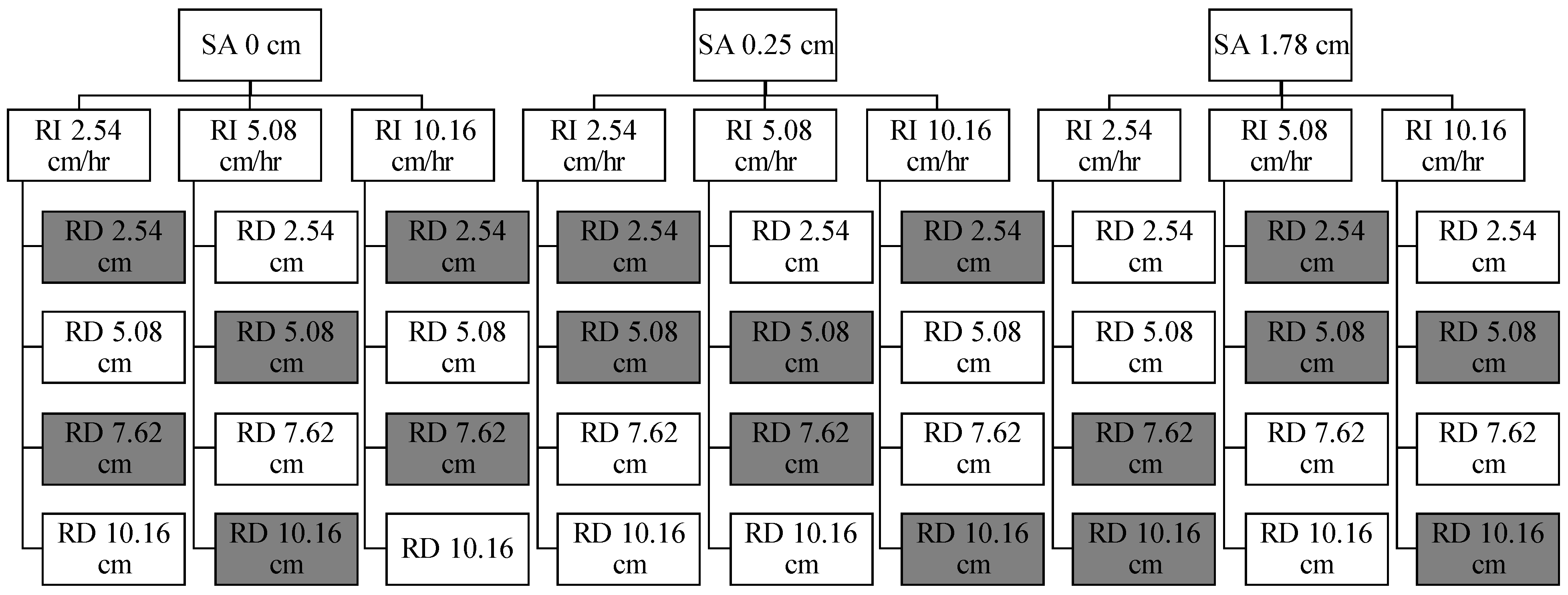
- A matrix of simulated conditions of the studied factors (i.e., AR, RD, RI, SA) was developed.
- Results from half of PCSWMM’s simulated scenarios were used to develop a simplified mathematical model for predicting the bioswale’s control of stormwater runoff.
- The newly developed mathematical model was used to predict the bioswale’s control of stormwater runoff, which was compared to results from the second half of the PCSWMM-simulated scenarios.
- The applications of the newly developed mathematical model were discussed.Each of the above tasks and components are discussed in detail in the following sections.
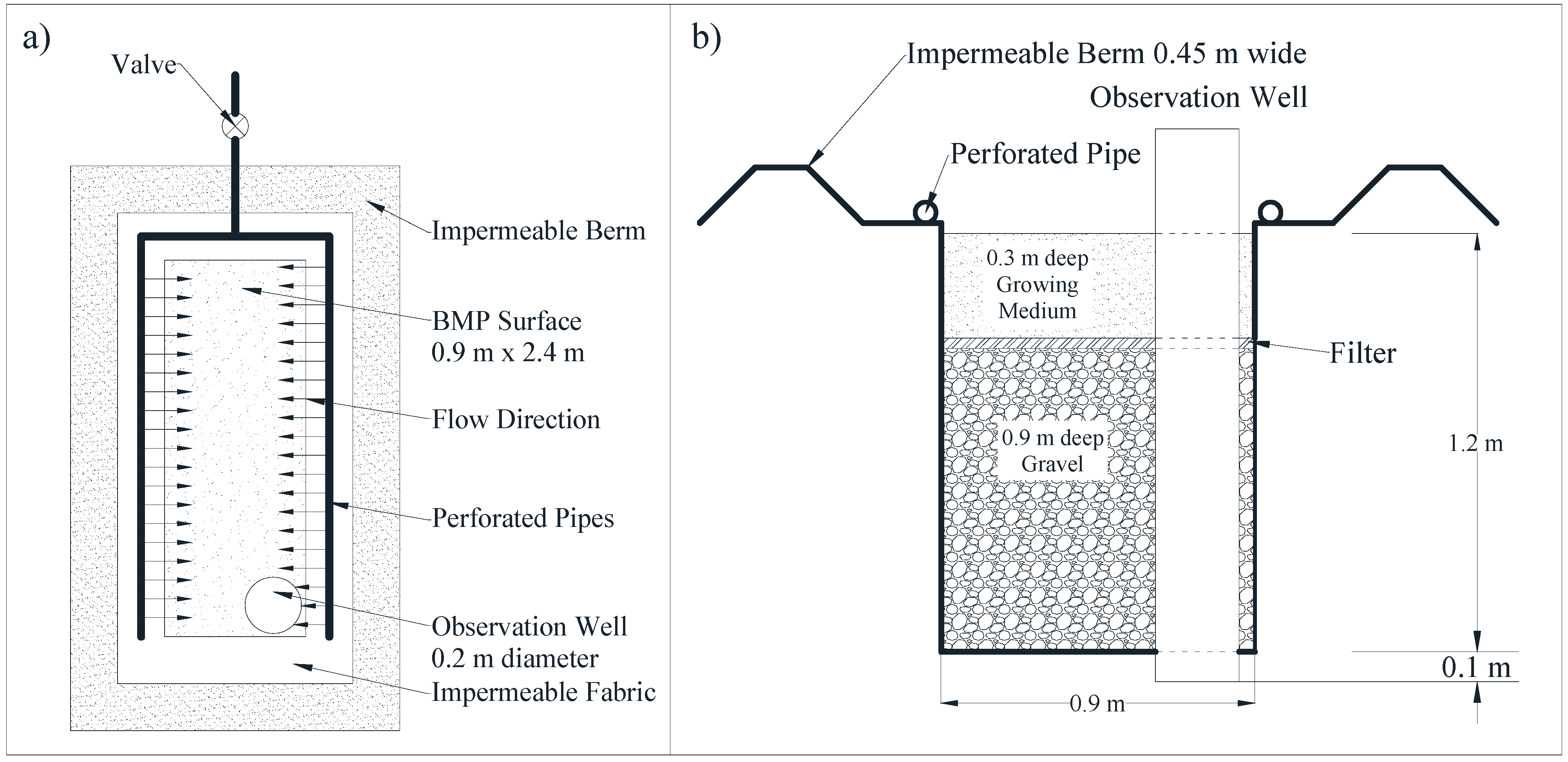
3. Field-Scale Bioswale Testing Facility
Operation of the Testing Facility
4. Modeled Conditions of AR, RD, RI, and SA
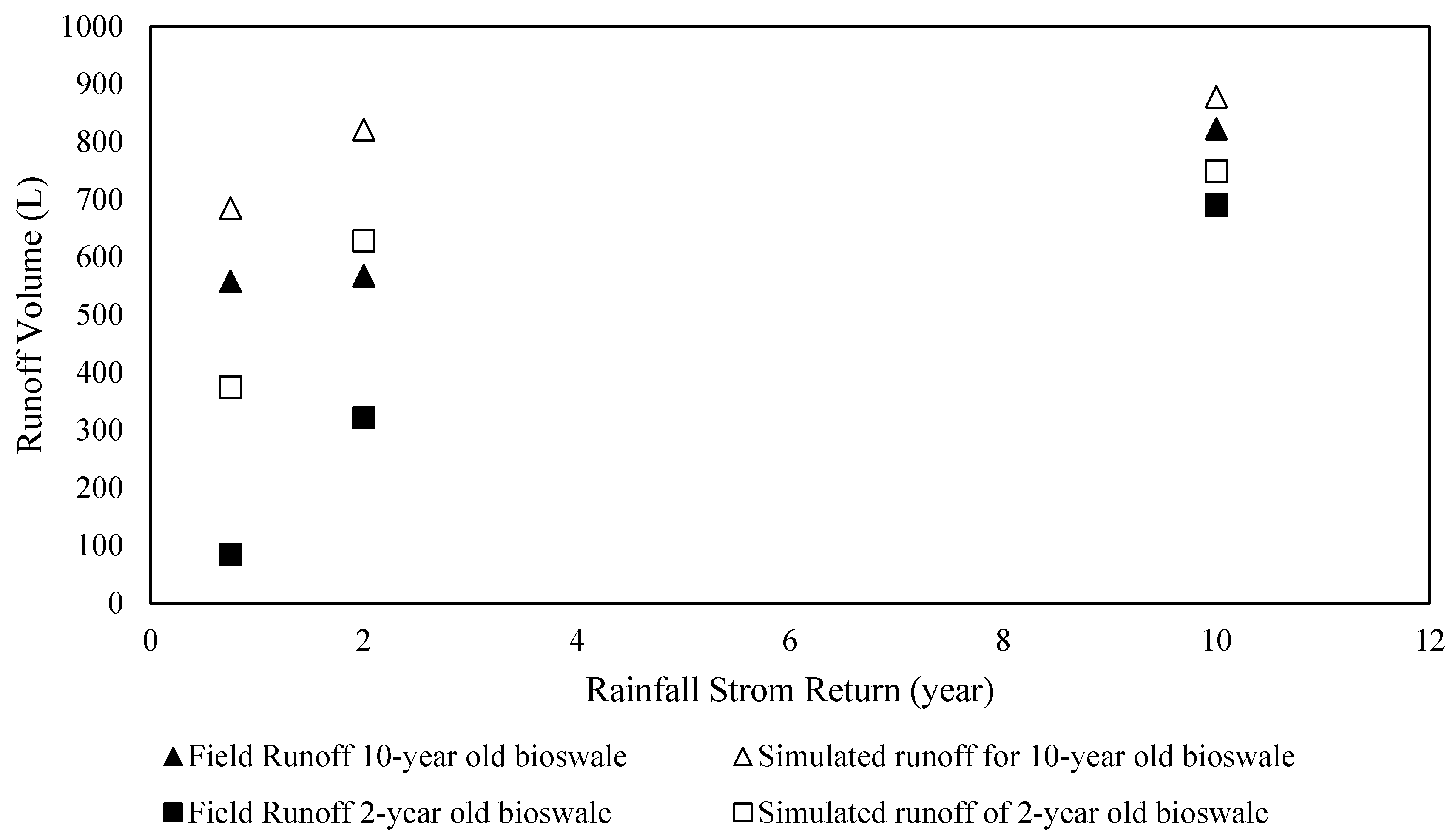
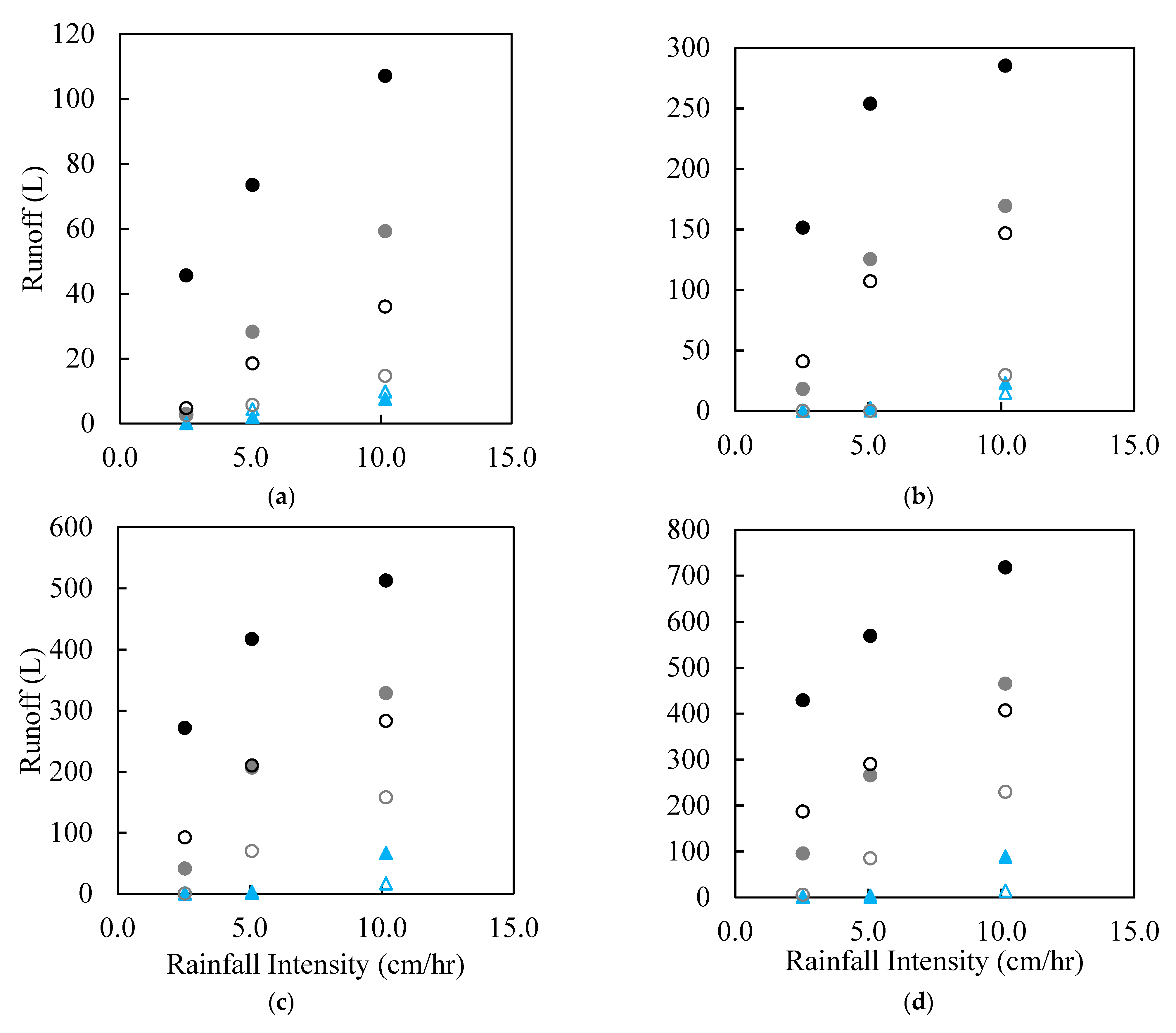
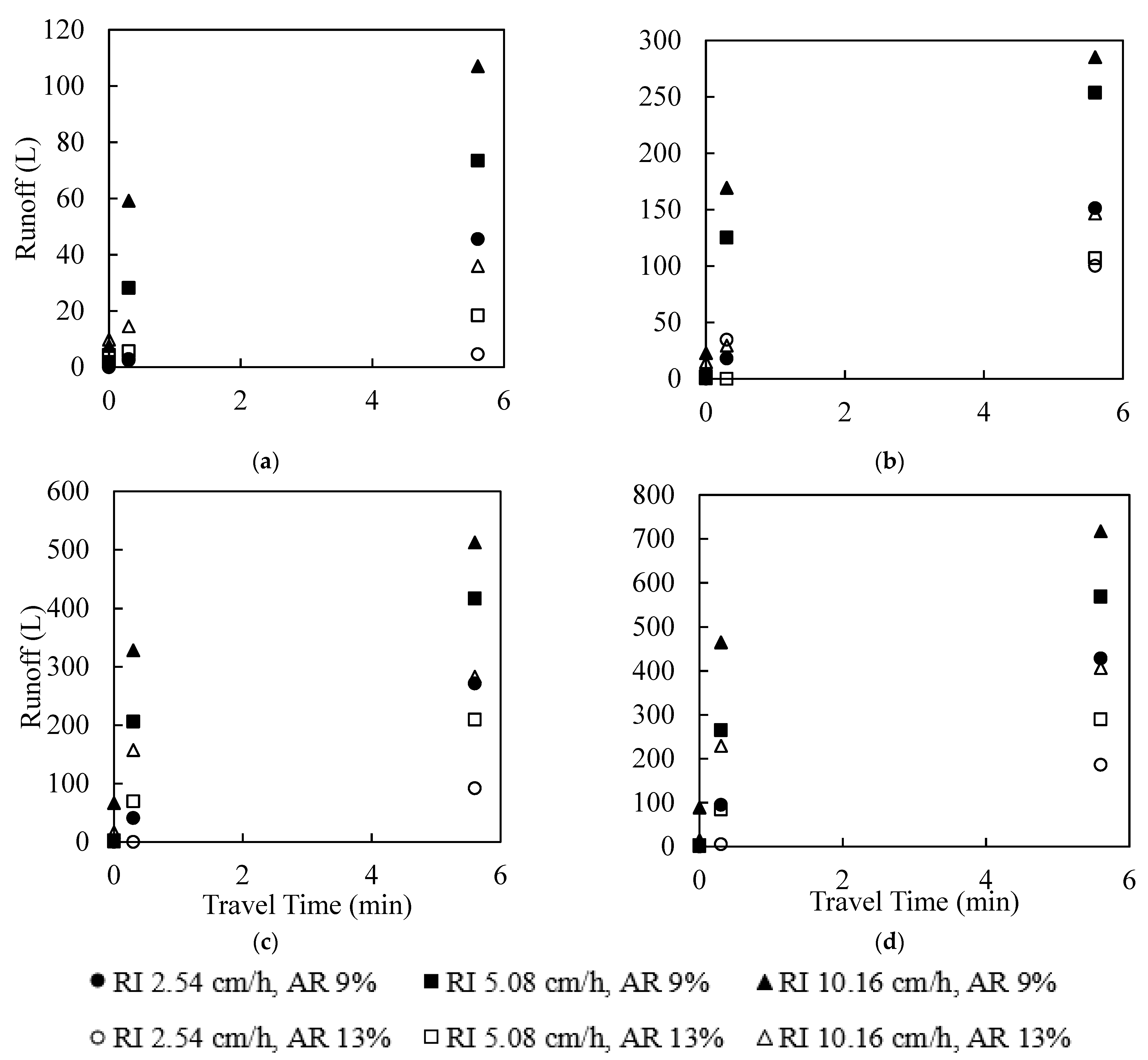
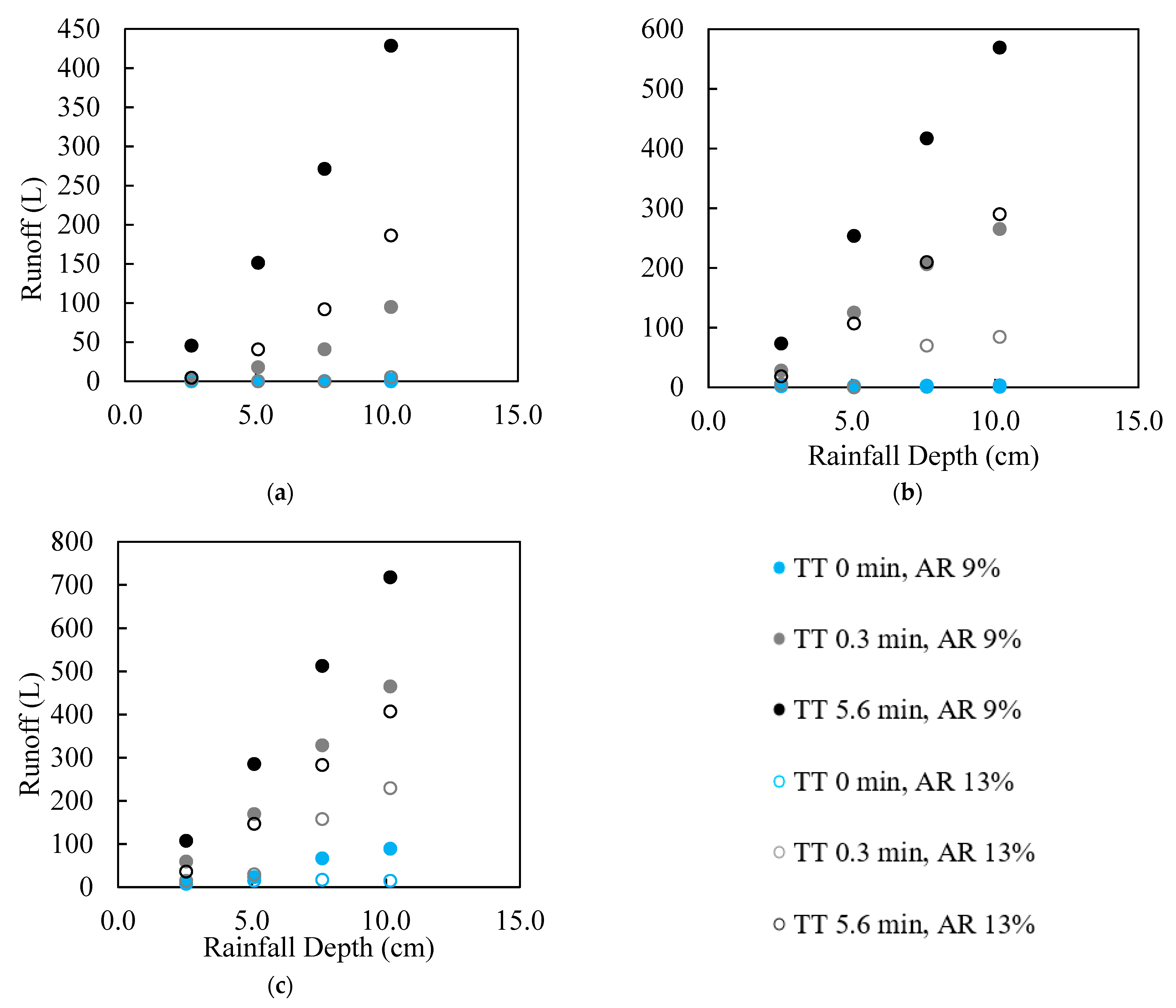
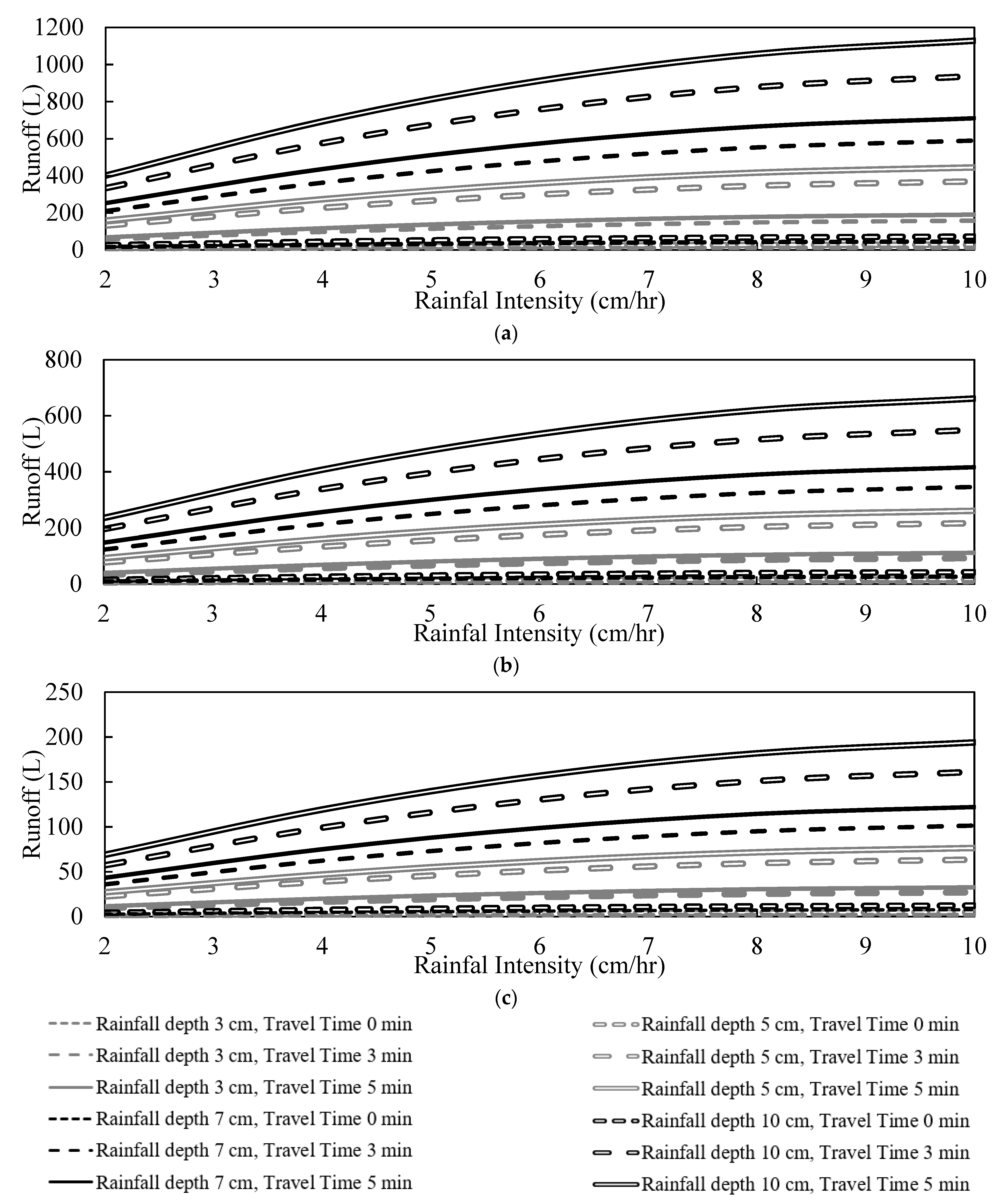
5. Simulation Results of Runoffs from the Idealized Catchment Area
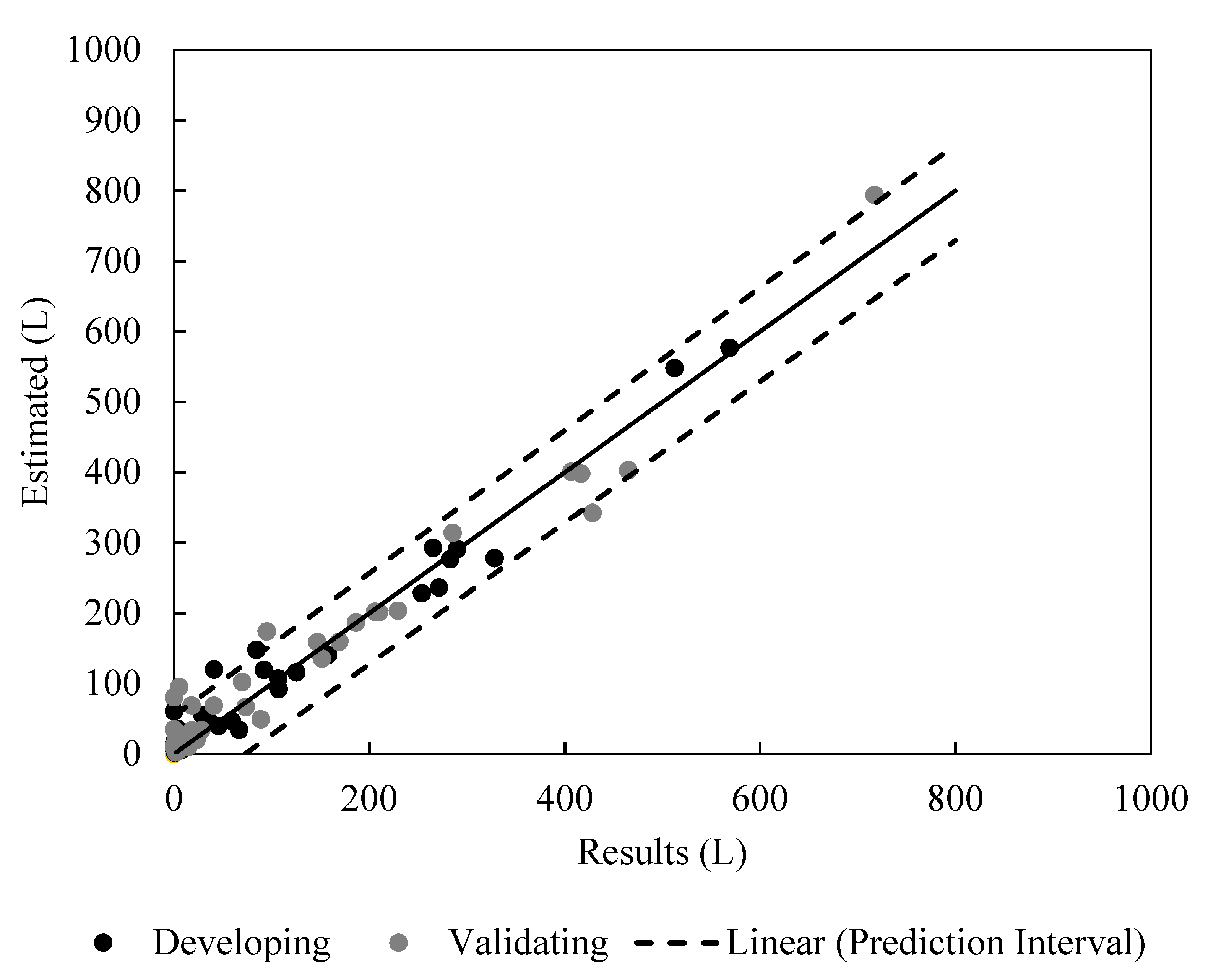
6. Developing a Simplified Mathematical Model for Runoff Prediction
7. Engineering Application of the New Mathematical Model
8. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- AASHTO. A Policy All Design Standards Interstate System; Standing Committee on Highways AASHTO Highway Subcommittee on Design Technical Committee on Geometric Design: Washington, DC, USA, 2005. [Google Scholar]
- Ackerman, D.; Stein, E.D. Evaluating the Effectiveness of Best Management Practices Using Dynamic Modeling. J. Environ. Eng. 2008, 134, 628–639. [Google Scholar] [CrossRef]
- Akhavan Bloorchian, A. Effect of Major Factors on Bioswale Performance and Hydrologic Processes for the Control of Stormwater Runoff from Highways. Ph.D. Thesis, Southern Illinois University, Carbondale, IL, USA, 2018. [Google Scholar]
- Beyerlein, D. Low Impact Development Computations—WWHM. In World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability; ASCE: Restone, VA, USA, 2011; pp. 558–576. [Google Scholar]
- Caltrans. BMP Retrofit Pilot Program Final Report; CTSW-RT 01-050; California Department of Transportation: Sacramento, CA, USA, 2004.
- Chen, W. Monitoring and Modeling of the Hydrologic Performance of the Carroll Street Right-of-Way Bioswale. Master’s Thesis, Department of Civil, Architectural, and Environmental Engineering, Drexel University, Philadelphia, PA, USA, 2014. [Google Scholar]
- Clary, J.; Leisenring, M.; Quigley, M.; Jones, J.; Strecker, E. International Stormwater Best Management Practices (BMP) Database, Narrative Overview of BMP Database Study Characteristics; Wright Water Engineers, Inc. Geosyntec Consultant: Water Environment Research Foundation: Alexaandra, VA, USA, 2012. [Google Scholar]
- Geosyntec. Post-Construction BMP Technical Guidance Manual; Storm Water BMP Guidance Manual: Santa Barbara, CA, USA, 2008.
- Geosyntec and Wright Water Inc. International Stormwater Best Management Practices (BMP) Database Individual BMP Summaries: Chesapeake Bay and Related Areas; The Water Research Doundation: Alexandra, VA, USA, 2012. [Google Scholar]
- Harwood, D.W.; Hutton, J.M.; Fees, C.; Bauer, K.M.; Glen, A.; Ouren, H. Evaluation of the 13 Controlling Criteria for Geometric Design; NCHRP 783 (No. Project 17-53); The National Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- Huber, W.C. Use of EPA SWMM5 for Generation of BMP Effluent EMC Distribution. In Proceedings of the Second BMP Technology Symposium, EWRI World Water and Environmental Resources Congress, Omaha, Nebraska, 21–25 May 2006. [Google Scholar]
- Heaney, J.P.; Sample, D.; Wright, L.; Fan, C. Costs of Urban Stormwater Control; US Environmental Protection Agency, Office of Research and Development, National Risk Management Research Laboratory: Cincinnati, OH, USA, 2002.
- Illinois Department of Transportation (IDOT). Drainage Manual; Illinois Department of Transporation: Springfield, IL, USA, 2011.
- Illinois Environmental Protection Agency (IEPA, 2013). Stormwater Performance Standards Recommendations; Post-Development Stormwater Runoff Standards (PDSWRS); Workgroup and Association of Illinois Soil and Water Conservation Districts (AISWCD): Springfield, IL, USA, 2013.
- James, W.; Rossman, L.E.; James, W.R. User’s Guide to SWMM 5, 13th ed.; CHI Press Publication: Guelph, ON, Canada, 2010. [Google Scholar]
- Li, H. Green infrastructure for Highway Stormwater Management: Field Investigation for Future Design, Maintenance, and Management Needs. J. Infrastruct. Syst. 2015, 21, 05015001. [Google Scholar] [CrossRef]
- Li, J.; Orland, R.; Hogenbirk, T. Environmental Road and Lot Drainage Designs: Alternatives to Curb-Gutter-Sewer System. Can. J. Civ. Eng. 1998, 25, 26–39. [Google Scholar] [CrossRef]
- NCHRP. Evaluation of Best Management Practices for Highway Runoff Control; Report 565; Transportation Research Board: Washington, DC, USA, 2006. [Google Scholar]
- NCHRP. Guidelines for Evaluating and Selecting Modifications to Existing Roadway Drainage Infrastructure to Improve Water Quality in Ultra-Urban Areas; Report 728; Transportation Research Board: Washington, DC, USA, 2012. [Google Scholar]
- NCHRP. Long-Term Performance and Life-Cycle Costs of Stormwater Best Management Practices; Report 792; Transportation Research Board: Washington, DC, USA, 2014. [Google Scholar]
- Natural Resources Conservation Service (NRCS). Technical Guide, Section I, Erosion Prediction; NRCS: Champaign, IL, USA, 1997. Available online: https://efotg.sc.egov.usda.gov/references/public/IL/ArchivedRUSLE.pdf (accessed on 13 December 2017).
- Osouli, A.; Bloorchian, A.A.; Grinter, M.; Alborzi, A.; Marlow, S.L.; Ahiablame, L.; Zhou, J. Performance and Cost Perspective in Selecting BMPs for Linear Projects. Water 2017, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Osouli, A.; Bloorchian, A.A.; Nassiri, S.; Marlow, S.L. Effect of Sediment Accumulation on Best Management Practice (BMP) Stormwater Runoff Volume Reduction Performance for Roadways. Water 2017, 9, 980. [Google Scholar] [CrossRef] [Green Version]
- Osouli, A.; Grinter, M.; Zhou, J.; Ahiablame, L.; Stark, T. Effective Post-Construction Best Management Practices (BMPs) to Infiltrate and Retain Stormwater Run-Off; Report No. FHWA-ICT-17-011; Illinois Center for Transportation/Illinois Department of Transportation: Rantoul, IL, USA, 2017. [Google Scholar]
- Pellant, M.; Shaver, P.; Pyke, D.A.; Herrick, J.E. Interpreting Indicators of Rangeland Health, Version 4. Technical Reference 1734-6; BLM/WO/ST-00/001+1734/REV05; U.S. Department of the Interior, Bureau of Land Management, National Science and Technology Center: Denver, CO, USA, 2005; p. 122.
- Poresky, A.; Bracken, C.; Strecker, E.; Clary, J. International Stormwater Best Management Practices (BMP) Database, Technical Summary: Volume Reduction; Geosyntec Consultants & Wright Water Engineers, Inc. Water Environment Research Foundation: Alexaandra, VA, USA, 2011. [Google Scholar]
- Roess, R.P.; Prasses, E.S.; McShane, W.R. Traffic Engineering, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2011; ISBN 978-0136135739. [Google Scholar]
- Stevens, M.R. Assessment of Water Quality, Road Runoff, and Bulk Atmospheric Deposition, Guanella Pass Area, Clear Creek and Park Counties, Colorado, Water Years 1995–97; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2001.
- Strecker, E.; Poresky, A.; Roseen, R.; Soule, J.; Gummadi, V.; Dwivedi, R.; Littleton, C.O. Volume Reduction of Highway Runoff in Urban Areas: National Cooperative Highway Research Program (NCHRP) Report 802; Transportation Research Board (TRB): Washington, DC, USA, 2015. [Google Scholar]
- Sun, Y.W.; Li, Q.Y.; Liu, L.; Xu, C.D.; Liu, Z.P. Hydrological simulation approaches for BMPs and LID practices in highly urbanized area and development of hydrological performance indicator system. Water Sci. Eng. 2014, 7, 143–154. [Google Scholar]
- Urban Drainage and Flood Control District (UDFCD). Urban Strom Drainage-Criteria Manual—Volume 1: Management, Hydrology, and Hydraulics; Urban Drainage and Flood Control District: Denver, CO, USA, 2008.
- Xiao, Q.; McPherson, G.E. Testing a Bioswale to Treat and Reduce Parking Lot Runoff; University of California, Davis and USDA Forest Service: Washington, DC, USA, 2009. [Google Scholar]


| Material | Infiltration Rate (cm/min) | Specific Gravity | Void Ratio | Bulk Density (kg/m3) | LL (%) | PL (%) | Soil Description |
|---|---|---|---|---|---|---|---|
| Natural Soil | 0.5 | 2.65 | 0.56 | 1723 | 30 | 20 | Sandy Lean Clay |
| Growing Medium | - | - | 0.45 | - | 0 | 0 | Highly Organic |
| Aggregate | - | 2.63 | 0.42 | - | 0 | 0 | Crushed Gravel |
| Rainfalls | Volume (L) | Duration (Min) | Intensity (cm/h) |
|---|---|---|---|
| 10-year-return | 945 | 10 | 15.24 |
| 2-year-return | 945 | 20 | 7.62 |
| 9-month-return | 945 | 45 | 3.39 |
| 36 Scenarios for Developing the Model | ||||
|---|---|---|---|---|
| AR | RD | RI | TT | Runoff |
| (%) | (cm) | (cm/h) | (min) | (L) |
| 9 | 2.54 | 2.54 | 0 | 2.05 |
| 9 | 2.54 | 10.16 | 0 | 7.57 |
| 9 | 5.08 | 5.08 | 0 | 12.43 |
| 9 | 7.62 | 2.54 | 0 | 14.42 |
| 9 | 7.62 | 10.16 | 0 | 36.66 |
| 9 | 10.16 | 5.08 | 0 | 31.42 |
| 9 | 2.54 | 2.54 | 0.3 | 12.88 |
| 9 | 2.54 | 10.16 | 0.3 | 59.20 |
| 9 | 5.08 | 5.08 | 0.3 | 125.30 |
| 9 | 7.62 | 2.54 | 0.3 | 40.98 |
| 9 | 7.62 | 10.16 | 0.3 | 328.40 |
| 9 | 10.16 | 5.08 | 0.3 | 265.30 |
| 9 | 2.54 | 2.54 | 5.6 | 45.56 |
| 9 | 2.54 | 10.16 | 5.6 | 107.05 |
| 9 | 5.08 | 5.08 | 5.6 | 253.70 |
| 9 | 7.62 | 2.54 | 5.6 | 271.39 |
| 9 | 7.62 | 10.16 | 5.6 | 512.61 |
| 9 | 10.16 | 5.08 | 5.6 | 568.95 |
| 13 | 2.54 | 2.54 | 0 | 1.38 |
| 13 | 2.54 | 10.16 | 0 | 2.84 |
| 13 | 5.08 | 4.572 | 0 | 5.40 |
| 13 | 7.62 | 2.54 | 0 | 1.24 |
| 13 | 7.62 | 10.16 | 0 | 16.78 |
| 13 | 10.16 | 5.08 | 0 | 9.96 |
| 13 | 2.54 | 2.54 | 0.3 | 0.00 |
| 13 | 2.54 | 10.16 | 0.3 | 14.57 |
| 13 | 5.08 | 4.572 | 0.3 | 29.48 |
| 13 | 7.62 | 2.54 | 0.3 | 32.74 |
| 13 | 7.62 | 10.16 | 0.3 | 157.53 |
| 13 | 10.16 | 5.08 | 0.3 | 84.50 |
| 13 | 2.54 | 2.54 | 5.6 | 4.63 |
| 13 | 2.54 | 10.16 | 5.6 | 35.96 |
| 13 | 5.08 | 4.572 | 5.6 | 107.00 |
| 13 | 7.62 | 2.54 | 5.6 | 92.05 |
| 13 | 7.62 | 10.16 | 5.6 | 282.95 |
| 13 | 10.16 | 5.08 | 5.6 | 289.92 |
| 9 | 2.54 | 5.08 | 0 | 1.89 |
| 9 | 5.08 | 2.54 | 0 | 8.20 |
| 9 | 5.08 | 10.16 | 0 | 22.93 |
| 9 | 7.62 | 5.08 | 0 | 22.84 |
| 9 | 10.16 | 2.54 | 0 | 12.35 |
| 9 | 10.16 | 10.16 | 0 | 48.89 |
| 9 | 2.54 | 5.08 | 0.3 | 28.20 |
| 9 | 5.08 | 2.54 | 0.3 | 18.10 |
| 9 | 5.08 | 10.16 | 0.3 | 169.35 |
| 9 | 7.62 | 5.08 | 0.3 | 206.26 |
| 9 | 10.16 | 2.54 | 0.3 | 95.05 |
| 9 | 10.16 | 10.16 | 0.3 | 464.91 |
| 9 | 2.54 | 5.08 | 5.6 | 73.44 |
| 9 | 5.08 | 2.54 | 5.6 | 151.38 |
| 9 | 5.08 | 10.16 | 5.6 | 285.20 |
| 9 | 7.62 | 5.08 | 5.6 | 417.03 |
| 9 | 10.16 | 2.54 | 5.6 | 428.55 |
| 9 | 10.16 | 10.16 | 5.6 | 717.30 |
| 13 | 2.54 | 5.08 | 0 | 1.39 |
| 13 | 5.08 | 2.54 | 0 | 3.22 |
| 13 | 5.08 | 10.16 | 0 | 14.78 |
| 13 | 7.62 | 5.08 | 0 | 0.87 |
| 13 | 10.16 | 2.794 | 0 | 5.06 |
| 13 | 10.16 | 10.16 | 0 | 14.52 |
| 13 | 2.54 | 5.08 | 0.3 | 5.68 |
| 13 | 5.08 | 2.54 | 0.3 | 0.00 |
| 13 | 5.08 | 10.16 | 0.3 | 21.03 |
| 13 | 7.62 | 5.08 | 0.3 | 69.78 |
| 13 | 10.16 | 2.794 | 0.3 | 85.31 |
| 13 | 10.16 | 10.16 | 0.3 | 229.24 |
| 13 | 2.54 | 5.08 | 5.6 | 18.43 |
| 13 | 5.08 | 2.54 | 5.6 | 40.85 |
| 13 | 5.08 | 10.16 | 5.6 | 146.61 |
| 13 | 7.62 | 5.08 | 5.6 | 209.80 |
| 13 | 10.16 | 2.794 | 5.6 | 186.35 |
| 13 | 10.16 | 10.16 | 5.6 | 406.76 |
| Area Ratio (AR) | Traveling Time (TT) | Rainfall Depth (RD) | Rainfall Intensity (RI) |
|---|---|---|---|
| (%) | (Min) | (cm) | (cm/h) |
| Up to 17 | Up to time of concentration | Greater than 1.45 | Up to 21.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Bloorchian, A.A.; Nassiri, S.; Osouli, A. A Simplified Model for Predicting the Effectiveness of Bioswale’s Control on Stormwater Runoff from Roadways. Water 2021, 13, 2798. https://doi.org/10.3390/w13202798
Zhou J, Bloorchian AA, Nassiri S, Osouli A. A Simplified Model for Predicting the Effectiveness of Bioswale’s Control on Stormwater Runoff from Roadways. Water. 2021; 13(20):2798. https://doi.org/10.3390/w13202798
Chicago/Turabian StyleZhou, Jianpeng, Azadeh Akhavan Bloorchian, Sina Nassiri, and Abdolreza Osouli. 2021. "A Simplified Model for Predicting the Effectiveness of Bioswale’s Control on Stormwater Runoff from Roadways" Water 13, no. 20: 2798. https://doi.org/10.3390/w13202798
APA StyleZhou, J., Bloorchian, A. A., Nassiri, S., & Osouli, A. (2021). A Simplified Model for Predicting the Effectiveness of Bioswale’s Control on Stormwater Runoff from Roadways. Water, 13(20), 2798. https://doi.org/10.3390/w13202798





