Spatial and Temporal Characteristics of Precipitation and Potential Influencing Factors in the Loess Plateau before and after the Implementation of the Grain for Green Project
Abstract
1. Introduction
2. Study Area and Data Collection
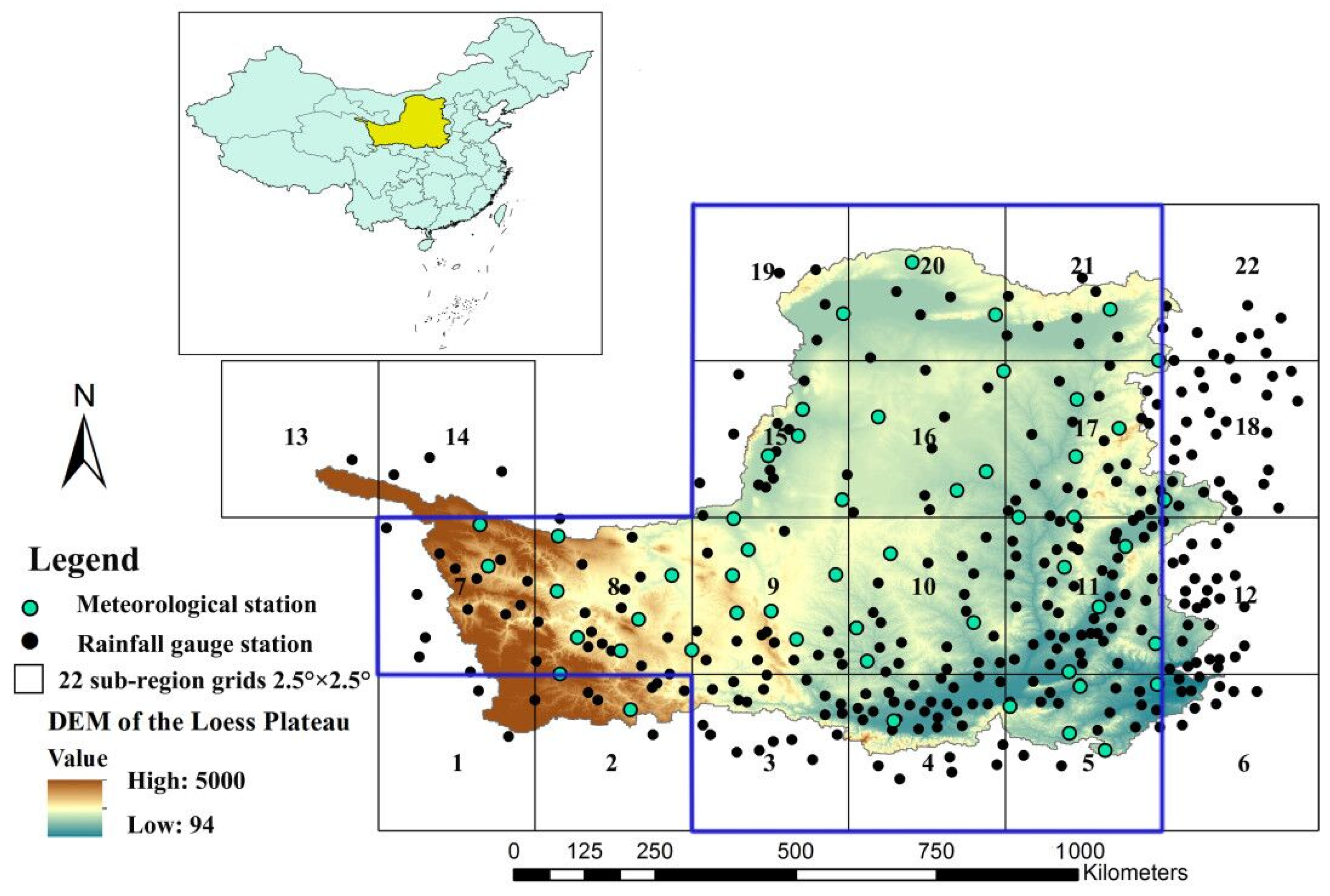
2.1. Study Area
2.2. Data
3. Methodologies
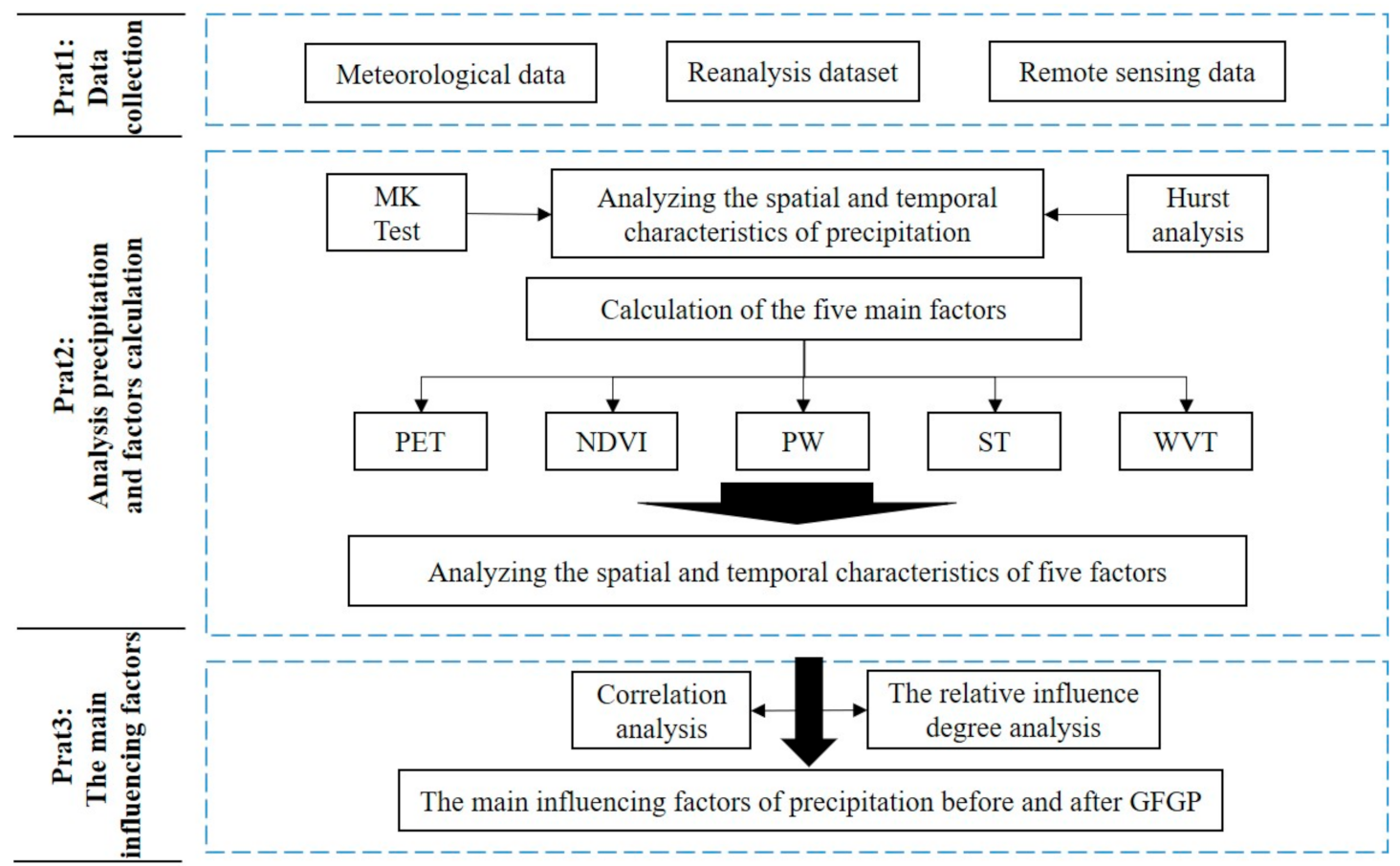
3.1. Technical Framework
3.2. Trend Analysis
3.2.1. Mann–Kendall Trend Test with Trend-Free Pre-Whitening
3.2.2. Hurst Exponent and Rescaled Range (R/S) Analysis
3.3. Calculation of the Five Main Factors
3.3.1. Potential Evapotranspiration (PET)
3.3.2. Normalized Difference Vegetation Index (NDVI)
3.3.3. Precipitable Water (PW)
3.3.4. Surface Temperature (ST)
3.3.5. Water Vapor Transport
3.4. Principal Component Regression Analysis
4. Results
4.1. The Spatial-Temporal Characteristic of Precipitation Changes in the Loess Plateau
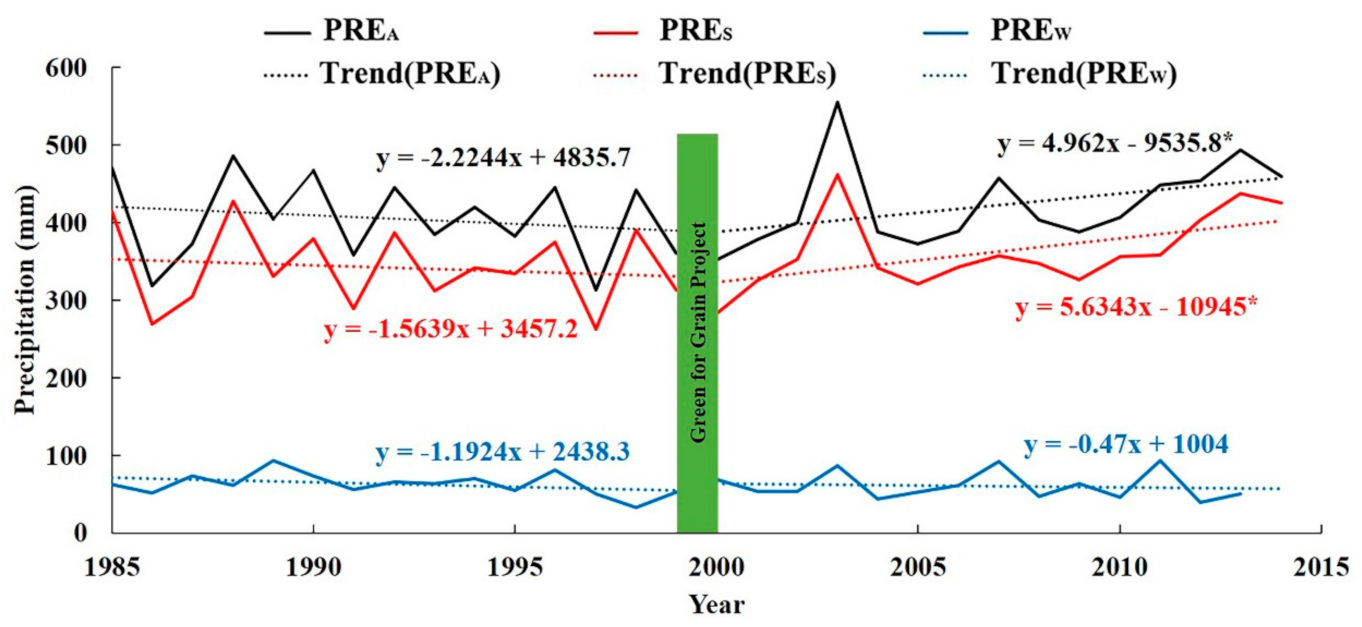
4.1.1. The Temporal Variability of Precipitation
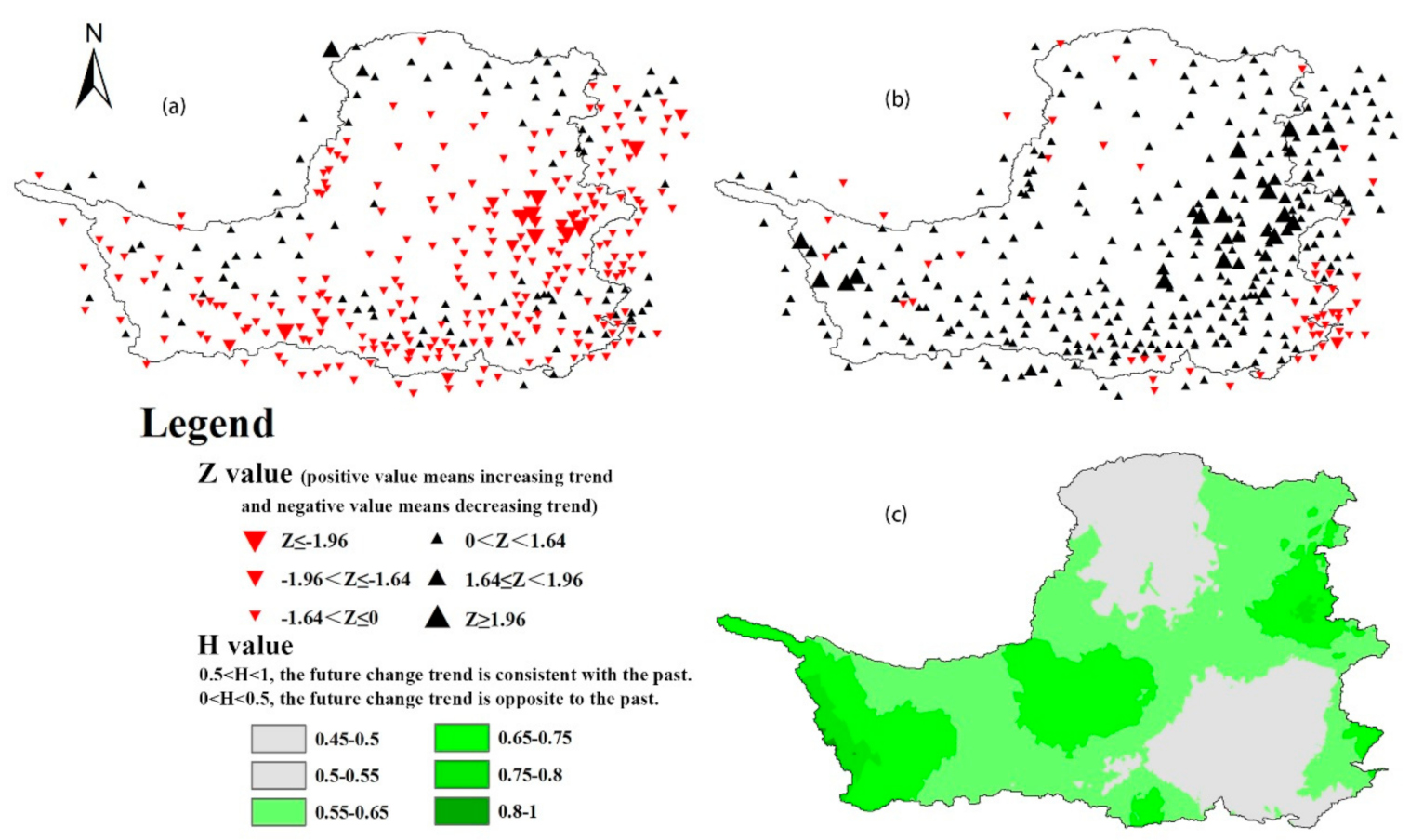
4.1.2. Changes and the Continuity of Station-Scale Precipitation in the Loess Plateau before and after GFGP
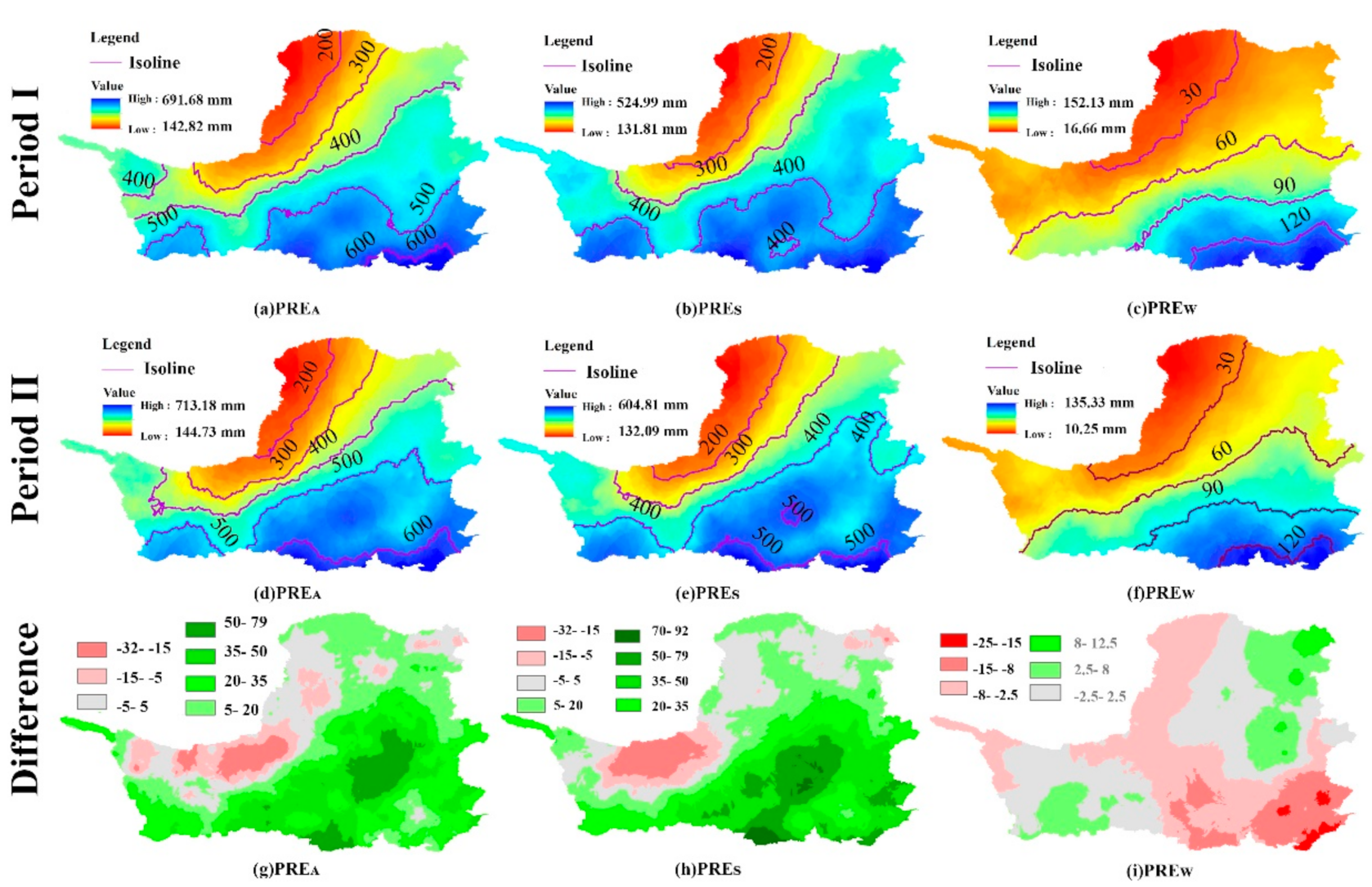
4.1.3. The Spatial Variability of Precipitation
4.2. The Spatial-Temporal Characteristic of the Main Influencing Factors
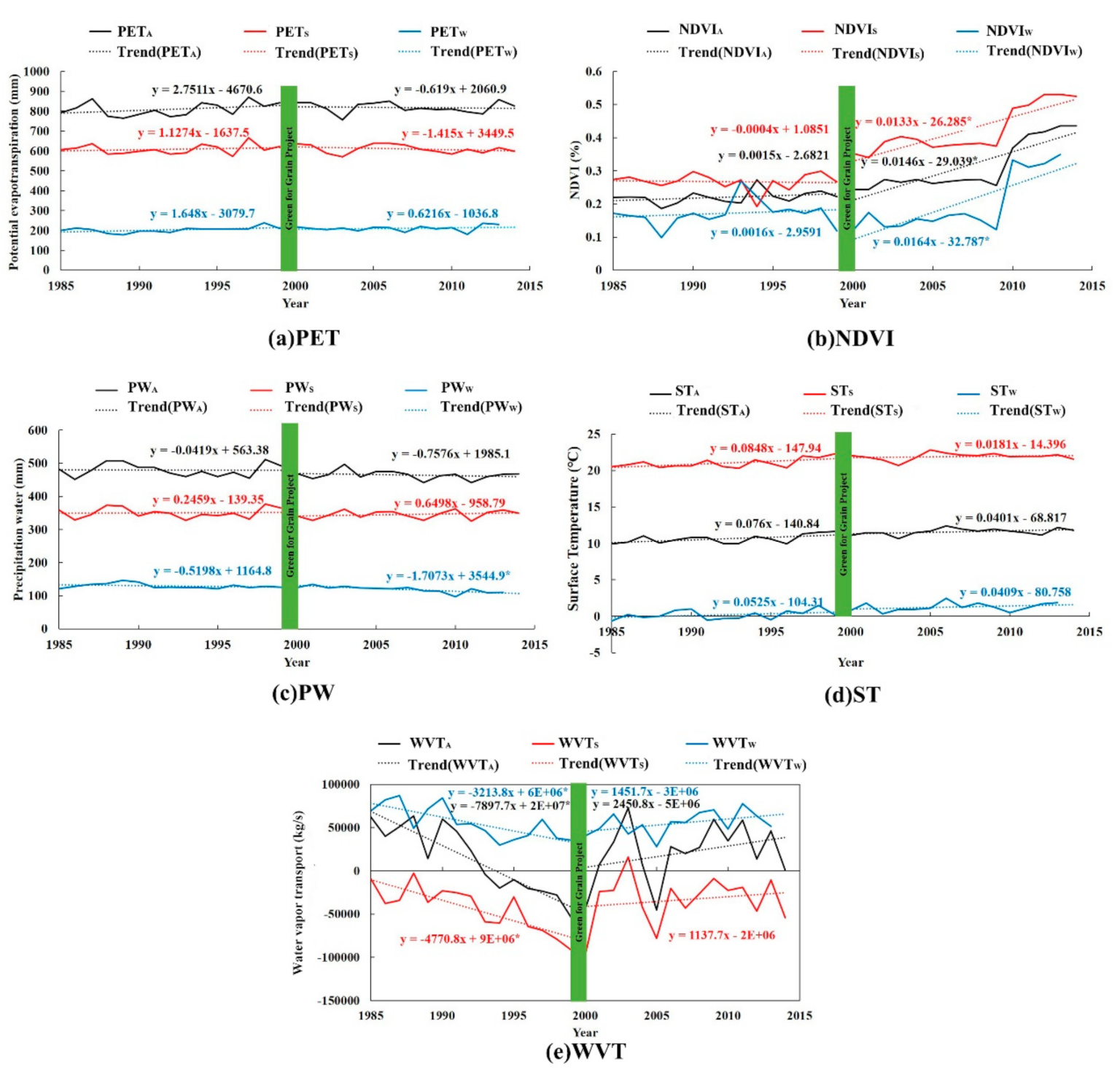
4.2.1. The Annual and Seasonal Variation in the Main Factors
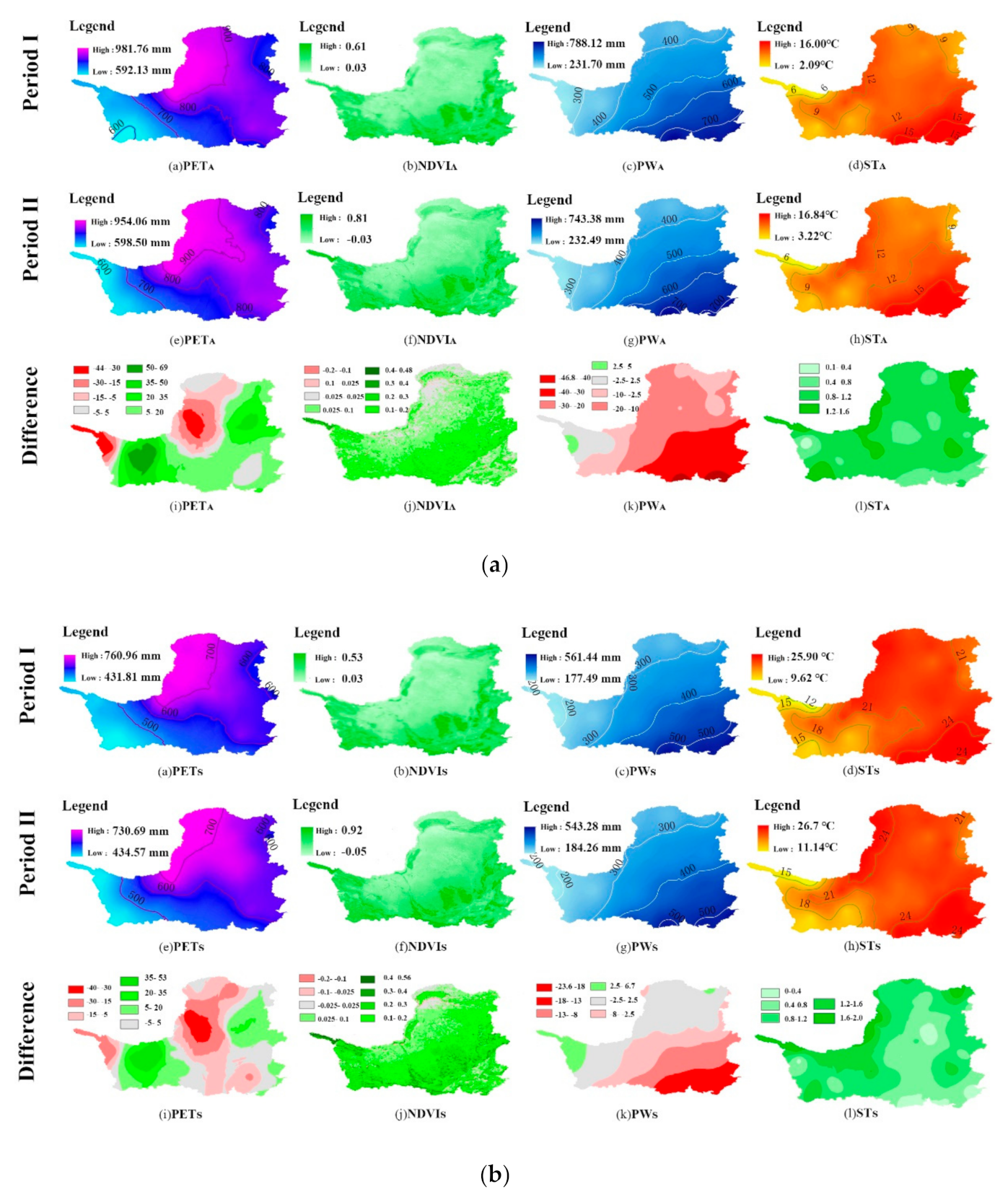
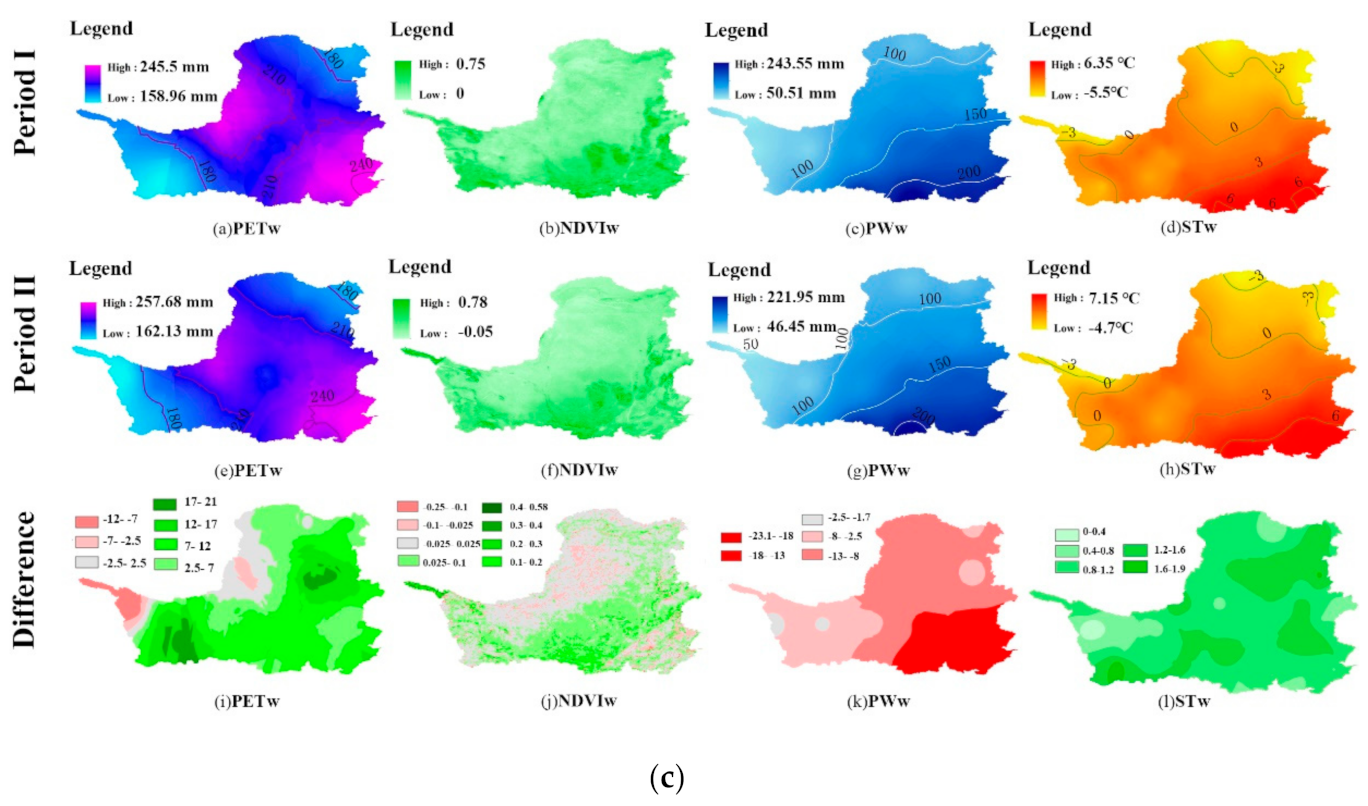
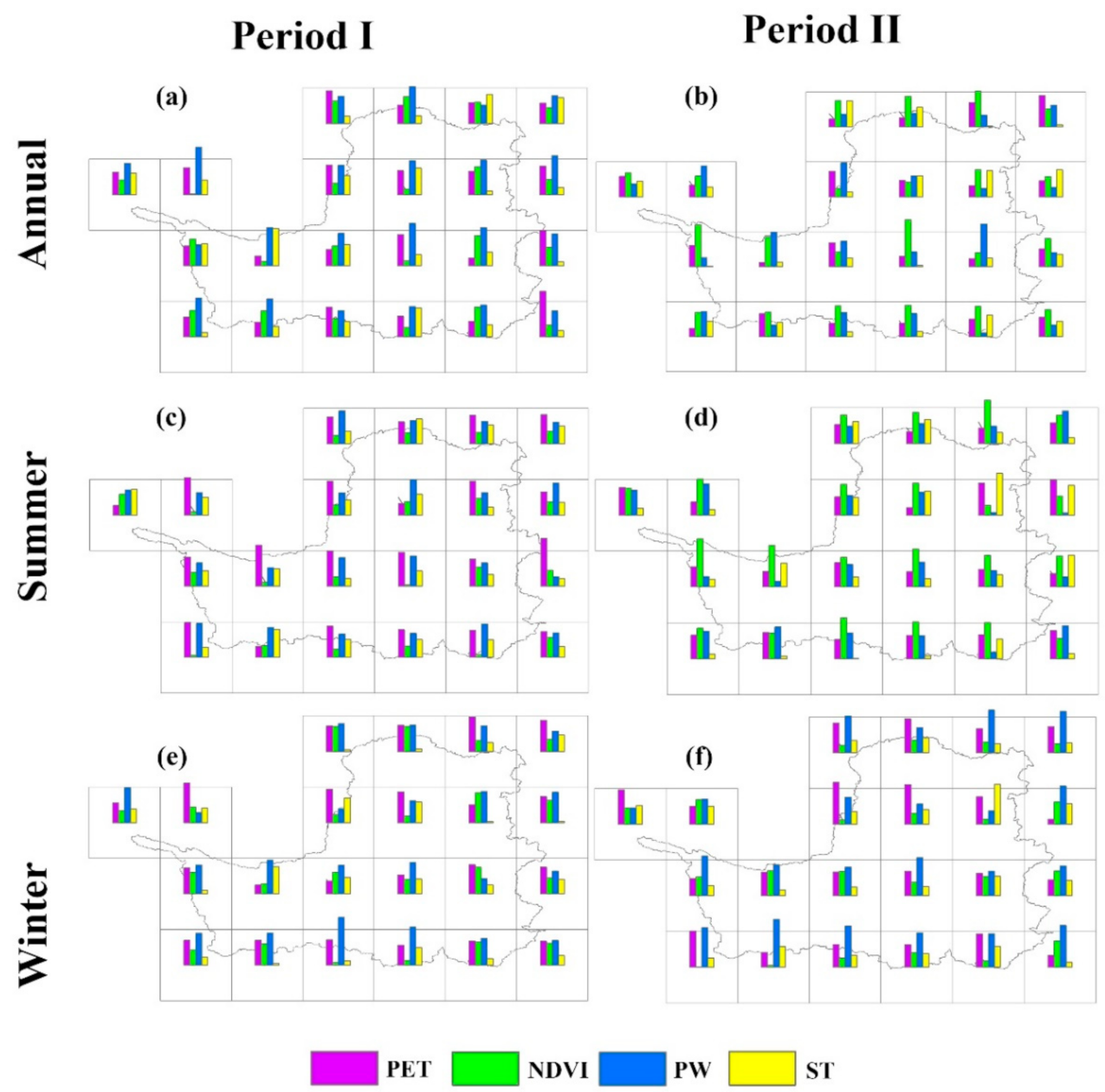
4.2.2. The Spatial Variability of the Main Factors
4.3. Identification of the Main Influencing Factors of Precipitation Change
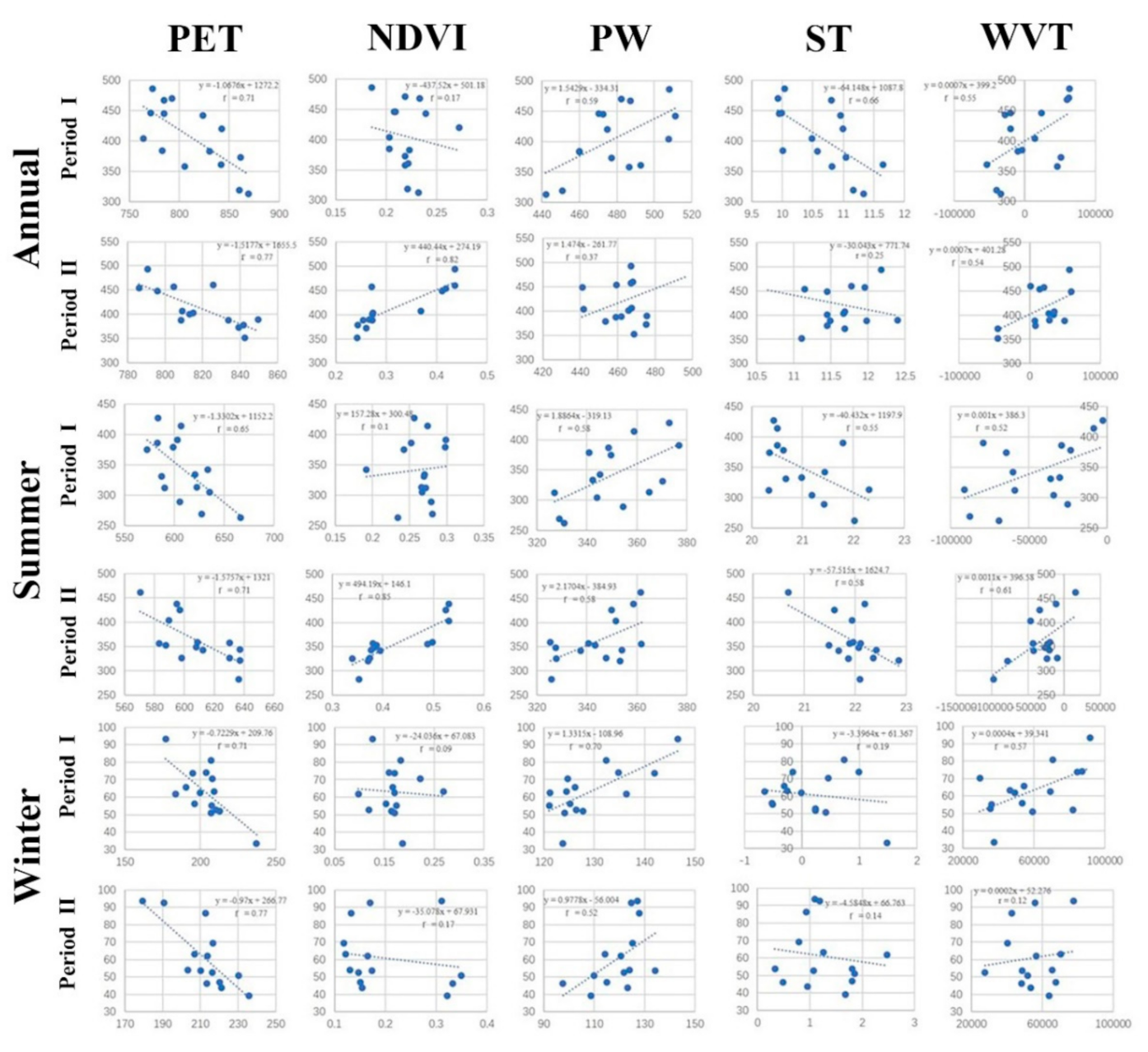
4.3.1. Correlation Analysis
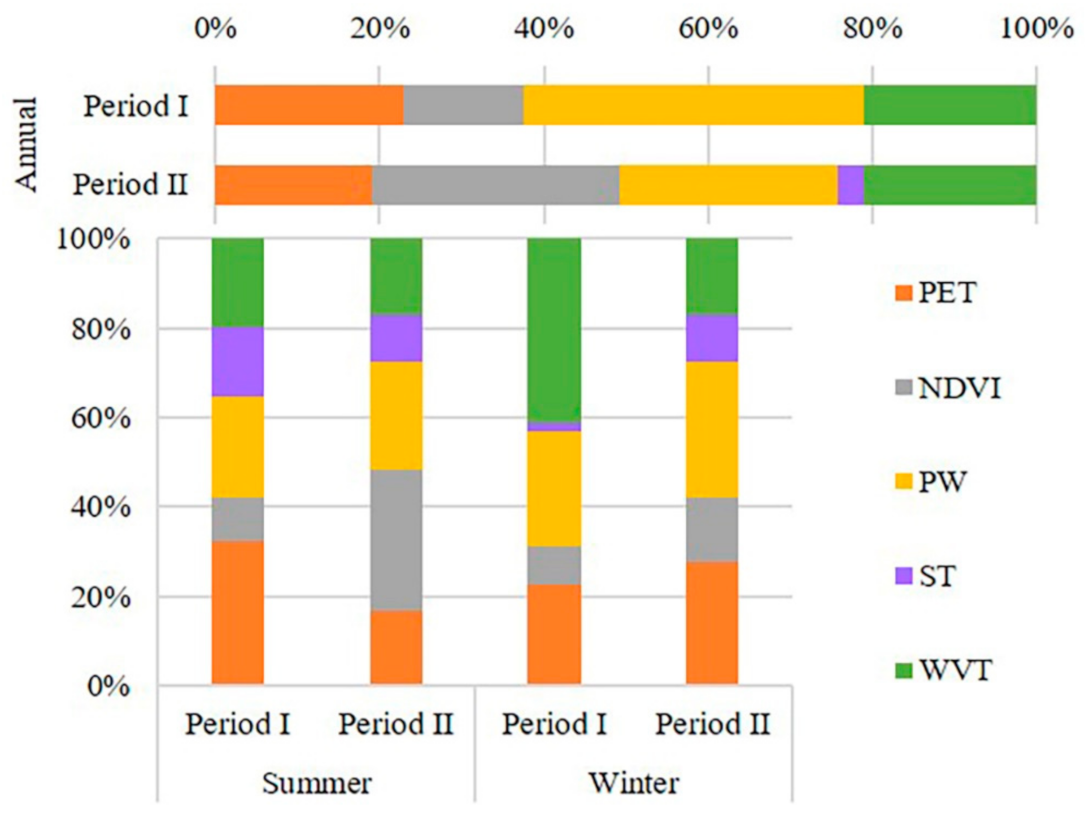
4.3.2. The Relative Influence Degree of the Five Factors to Precipitation Change
5. Discussion
5.1. Identification of Main Factors in Sub-Regions
5.2. The Comparison between Our Findings and Those of the Previous Studies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Peng, S.; Li, Z. Detecting and attributing vegetation changes on China’s Loess Plateau. Agr. Forest Meteorol. 2017, 247, 260–270. [Google Scholar] [CrossRef]
- Gao, X.; Sun, M.; Zhao, Q.; Wu, P.; Zhao, X.; Pan, W.; Wang, Y. Actual ET modelling based on the Budyko framework and the sustainability of vegetation water use in the loess plateau. Sci. Total Environ. 2017, 579, 1550–1559. [Google Scholar] [CrossRef] [PubMed]
- Liang, K.; Liu, C.; Liu, X.; Song, X. Impacts of climate variability and human activity on streamflow decrease in a sediment concentrated region in the Middle Yellow River. Stoch. Environ. Res. Risk A 2013, 27, 1741–1749. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lu, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lu, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Yang, X.; Sun, W.; Li, P.; Mu, X.; Gao, P.; Zhao, G. Reduced sediment transport in the Chinese Loess Plateau due to climate change and human activities. Sci. Total Environ. 2018, 642, 591–600. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Liu, G.; Shangguan, Z. Land-use conversion and changing soil carbon stocks in China’s ‘Grain-for-Green’ Program: A synthesis. Glob. Chang. Biol. 2014, 20, 3544–3556. [Google Scholar] [CrossRef]
- Yan, L. Characteristics of temperature and precipitation on the Loess Plateau from1961 to 2014. J. Earth Environ. 2015, 6, 276–282. (In Chinese) [Google Scholar] [CrossRef]
- Li, G.; Sun, S.; Han, J.; Yan, J.; Liu, W.; Wei, Y.; Lu, N.; Sun, Y. Impacts of Chinese Grain for Green program and climate change on vegetation in the Loess Plateau during 1982–2015. Sci. Total Environ. 2019, 660, 177–187. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, Q.; Jiao, M.; Wu, P.; Gao, X.; Ma, M.; Hong, Y. The Temporal-Spatial Characteristics of Drought in the Loess Plateau Using the Remote-Sensed TRMM Precipitation Data from 1998 to 2014. Remote Sens. 2018, 10, 838. [Google Scholar] [CrossRef]
- Wang, Q.; Fan, X.; Qin, Z.; Wang, Q. Change trends of temperature and precipitation in the Loess Plateau Region of China, 1961–2010. Glob. Planet Chang. 2012, 138–147. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Hossain, I.; Perera, B.J. Effect of climate change and variability on extreme rainfall intensity–frequency–duration relationships: A case study of Melbourne. Hydrol. Earth Syst. Sci. 2014, 18, 4065–4076. [Google Scholar] [CrossRef]
- Onyutha, C.; Willems, P. Influence of spatial and temporal scales on statistical analyses of rainfall variability in the River Nile basin. Dynam. Atmos. Oceans 2017, 77, 26–42. [Google Scholar] [CrossRef]
- Cheng, N.; He, H.; Lu, Y.; Jing, Z. Spatial-temporal Dynamic Characteristics of Precipitation in the Loess Plateau, China for Recent 52 Years. J. Shandong Agric. Univ. (Natural Science Edition) 2016, 47, 388–392. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, Y.; He, Y.; Chen, X. Spatiotemporal pattern of precipitation concentration and its possible causes in the Pearl River basin, China. J. Clean Prod. 2017, 161, 1020–1031. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, S. Sensitivity Analysis of the Response of Precipitation to Climate Change over China Loess Plateau. J. Glaciol. Geocryol. 2008, 30, 43–51. (In Chinese) [Google Scholar]
- Choudhury, G.; Tyagi, B.; Singh, J.; Sarangi, C.; Tripathi, S.N. Aerosol-orography-precipitation–A critical assessment. Atmos Environ. 2019, 214, 1–19. [Google Scholar] [CrossRef]
- Pan, B.; Yao, Z.; Wang, M.; Pan, H.; Bu, L.; Kumar, K.R.; Gao, H.; Huang, X. Evaluation and utilization of CloudSat and CALIPSO data to analyze the impact of dust aerosol on the microphysical properties of cirrus over the Tibetan Plateau. Adv. Space Res. 2019, 63, 2–15. [Google Scholar] [CrossRef]
- Martens, H.; Martens, M. Modified Jack-knife estimation of parameter uncertainty in bilinear modelling by partial least squares regression (PLSR). Food Qual. Prefer. 2000, 11, 5–16. [Google Scholar] [CrossRef]
- Fang, S.; Jia, R.; Tu, W.; Sun, Z. Assessing Factors Driving the Change of Irrigation Water-Use Efficiency in China Based on Geographical Features. Water 2017, 9, 759. [Google Scholar] [CrossRef]
- Chen, M.; Luo, Y.; Shen, Y.; Han, Z.; Cui, Y. Driving force analysis of irrigation water consumption using principal component regression analysis. Agr. Water Manage. 2020, 234, 106089. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). Clean Prod. 2020. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, X.; Fang, N.; Shi, Z. Large-scale afforestation significantly increases permanent surface water in China’s vegetation restoration regions. Agr. Forest Meteorol. 2020, 290, 108001. [Google Scholar] [CrossRef]
- Chen, L.; Wei, W.; Fu, B.; Lu, Y. Soil and water conservation on the Loess Plateau in China: Review and perspective. Prog. Phys. Geog. 2007, 31, 389–403. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.; Liu, W.; Jiang, D. Spatially downscaling GCMs outputs to project changes in extreme precipitation and temperature events on the Loess Plateau of China during the 21st Century. Global Planet. Chang. 2012, 82, 65–73. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Guclu, Y.S. Improved visualization for trend analysis by comparing with classical Mann-Kendall test and ITA. J. Hydrol. 2020, 584, 124674. [Google Scholar] [CrossRef]
- Kendziorski, C.M.; Bassingthwaighte, J.B.; Tonellato, P.J. Evaluating maximum likelihood estimation methods to determine the Hurst coefficient. Physica A 1999, 273, 439–451. [Google Scholar] [CrossRef]
- Tong, S.; Lai, Q.; Zhang, J.; Bao, Y.; Lusi, A.; Ma, Q.; Li, X.; Zhang, F. Spatiotemporal drought variability on the Mongolian Plateau from 1980–2014 based on the SPEI-PM, intensity analysis and Hurst exponent. Sci. Total Environ. 2017, 15, 1557–1565. [Google Scholar] [CrossRef]
- Xie, S.; Mo, X.; Hu, S.; Liu, S. Contributions of climate change, elevated atmospheric CO2 and human activities to ET and GPP trends in the Three-North Region of China. Agr. Forest Meteorol. 2020, 295, 108183. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Li, J.; Hua, T. Identifying the effect of climate change on desertification in northern China via trend analysis of potential evapotranspiration and precipitation. Ecol. Indic. 2020, 112, 106141. [Google Scholar] [CrossRef]
- Jin, K.; Wang, F.; Li, P. Responses of Vegetation Cover to Environmental Change in Large Cities of China. Sustainability 2018, 10, 270. [Google Scholar] [CrossRef]
- Wang, H.; He, J. Temporal and Spatial Evolution Features of Precipitable Water in China during a Recent 65-Year Period (1951–2015). Adv. Meteorol. 2017, 1–11. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Gao, S. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, P.; Zhao, X.; Wang, Y.; Gao, X. Changes in vegetation condition in areas with different gradients (1980–2010) on the Loess Plateau, China. Environ. Earth Sci. 2013, 68, 2427–2438. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, J.; Dai, A. Evaluation of atmospheric precipitable water from reanalysis products using homogenized radiosonde observations over China. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Li, L.; Zha, Y.; Wang, R. Relationship of surface urban heat island with air temperature and precipitation in global large cities. Ecol. Indic. 2020, 117, 106683. [Google Scholar] [CrossRef]
- Huang, D.; Yan, P.; Xiao, X.; Zhu, J.; Tang, X.; Huang, A.; Cheng, J. The tri-pole relation among daily mean temperature, atmospheric moisture and precipitation intensity over China. Glob. Planet Chang. 2019, 179, 1–9. [Google Scholar] [CrossRef]
- Jin, K.; Wang, F.; Zong, Q.; Qin, P.; Liu, C. Impact of variations in vegetation on surface air temperature change over the Chinese Loess Plateau. Sci. Total Environ. 2020. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y.; Zhao, Y.; Guan, X.; Mao, W.; Yang, L. Climatic and associated atmospheric water cycle changes over the Xinjiang, China. J. Hydrol. 2020, 585, 124823. [Google Scholar] [CrossRef]
- Liu, R. The Calculation and Analysis of Atmospheric Precipitable Water and Water Vapor Transportation and Net Income in Xinjiang. Master’s Thesis, Xinjiang Normal University, Xinjiang, China, 2009. (In Chinese). [Google Scholar]
- Wu, Y.; Shen, Y.; Li, B.L. Possible physical mechanism of water vapor transport over Tarim River Basin. Ecol. Complex. 2012, 9, 63–70. [Google Scholar] [CrossRef]
- Shi, Y. A Study on the Spatial-Temporal Distributions of Areal Precipitation and Water Vapor over Xinjiang. Ph.D. Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2009. (In Chinese). [Google Scholar]
- Pandžic, K.; Trninic, D. Principal component analysis of a river basin discharge and precipitation anomaly fields associated with the global circulation. J. Hydrol. 1992, 132, 343–360. [Google Scholar] [CrossRef]
- Nagel, J.B.; Rieckermann, J.; Sudret, B. Principal component analysis and sparse polynomial chaos expansions for global sensitivity analysis and model calibration: Application to urban drainage simulation. Reliab. Eng. Syst. Safe 2020, 195, 106737. [Google Scholar] [CrossRef]
- Voukantsis, D.; Karatzas, K.; Kukkonen, J.; Räsänen, T.; Karppinen, A.; Kolehmainen, M. Intercomparison of air quality data using principal component analysis, and forecasting of PM 10 and PM 2.5 concentrations using artificial neural networks, in Thessaloniki and Helsinki. Sci. Total Environ. 2011, 409, 1266–1276. [Google Scholar] [CrossRef] [PubMed]
- Arjo, D. Statistical Models: Theory and Practice. Technometrics 2009, 48, 315. [Google Scholar] [CrossRef]
- Wang, X.; Wang, B.; Xu, X.; Liu, T.; Duan, Y.; Zhao, Y. Spatial and temporal variations in surface soil moisture and vegetation cover in the Loess Plateau from 2000 to 2015. Ecol. Indic. 2018, 95, 320–330. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, J.; Guan, X.; Chen, B.; Zhang, L. Long-term trends of precipitable water and precipitation over the Tibetan Plateau derived from satellite and surface measurements. J. Quant. Spectrosc. Radiat. Transf. 2013, 122, 64–71. [Google Scholar] [CrossRef]
- Sun, W.; Song, X.; Mu, X.; Gao, P.; Wang, F.; Zhao, G. Spatiotemporal vegetation cover variations associated with climate change and ecological restoration in the Loess Plateau. Agr. Forest Meteorol. 2015, 2015, 87–99. [Google Scholar] [CrossRef]
- Xin, Z.; Xu, J.; Zheng, W. Spatiotemporal variations of vegetation cover on the Chinese Loess Plateau (1981–2006): Impacts of climate changes and human activities. Sci. China Ser. D 2008, 51, 67–78. [Google Scholar] [CrossRef]
- Tang, X.; Miao, C.; Xi, Y.; Duan, Q.; Lei, X.; Li, H. Analysis of precipitation characteristics on the loess plateau between 1965 and 2014, based on high-density gauge observations. Atmos. Res. 2018, 213, 264–274. [Google Scholar] [CrossRef]
| Station | Name | Lon | Lat | Station | Name | Lon | Lat |
|---|---|---|---|---|---|---|---|
| 52,765 | Menyuan | 101.62 | 37.38 | 53,740 | Hengshan | 109.23 | 37.93 |
| 52,787 | Wushaoling | 102.87 | 37.20 | 53,754 | Suide | 110.22 | 37.50 |
| 52,866 | Xining | 101.77 | 36.62 | 53,764 | Lishi | 111.10 | 37.50 |
| 52,876 | Minhe | 102.85 | 36.32 | 53,772 | Taiyuan | 112.55 | 37.78 |
| 52,895 | Jingyuan | 104.68 | 36.57 | 53,806 | Haiyuan | 105.65 | 36.57 |
| 52,983 | Yuzhong | 104.15 | 35.87 | 53,810 | Tongxin | 105.90 | 36.98 |
| 52,984 | Linxia | 103.18 | 35.58 | 53,817 | Guyuan | 106.27 | 36.00 |
| 52,986 | Lintao | 103.87 | 35.37 | 53,821 | Huanxian | 107.30 | 36.58 |
| 52,996 | Huajialing | 105.00 | 35.38 | 53,853 | Xixian | 110.95 | 36.70 |
| 53,336 | Wulatehouqi | 108.52 | 41.57 | 53,863 | Jiexiu | 111.92 | 37.03 |
| 53,446 | Baotou | 109.85 | 40.67 | 53,868 | Linfen | 111.50 | 36.07 |
| 53,463 | Huhehaote | 111.68 | 40.82 | 53,903 | Xiji | 105.72 | 35.97 |
| 53,478 | Youyu | 112.45 | 40.00 | 53,915 | Pingliang | 106.67 | 35.55 |
| 53,513 | Linhe | 107.42 | 40.75 | 53,923 | Xifengzhen | 107.63 | 35.73 |
| 53,519 | Huinong | 106.77 | 39.22 | 53,929 | Changwu | 107.80 | 35.20 |
| 53,529 | Etuokeqi | 107.98 | 39.10 | 53,942 | Luochuan | 109.50 | 35.82 |
| 53,543 | Hedong | 109.98 | 39.83 | 53,959 | Yuncheng | 111.02 | 35.03 |
| 53,564 | Hequ | 111.15 | 39.38 | 53,975 | Yangcheng | 112.40 | 35.48 |
| 53,614 | Yinchuan | 106.22 | 38.48 | 56,080 | Hezuo | 102.90 | 35.00 |
| 53,615 | Taole | 106.70 | 38.80 | 56,093 | Minxian | 104.02 | 34.43 |
| 53,646 | Yulin | 109.70 | 38.23 | 57,034 | Wugong | 108.22 | 34.25 |
| 53,663 | Wuzhai | 111.82 | 38.92 | 57,046 | Huashan | 110.08 | 34.48 |
| 53,664 | Xingxian | 111.13 | 38.47 | 57,051 | Sanmenxia | 111.20 | 34.80 |
| 53,705 | Zhongning | 105.67 | 37.48 | 57,067 | Lushi | 111.03 | 34.05 |
| 53,723 | Yanchi | 107.40 | 37.78 | 57,071 | Mengjin | 112.43 | 34.83 |
| 53,738 | Wuqi | 108.18 | 36.83 | 57,077 | Luanchuan | 111.60 | 33.78 |
| Scale | Cumulative Contribution Rate/% | Number of Principal Components | Adjusted-R2 | Sig. | |
|---|---|---|---|---|---|
| Annual | Period I | 98 | 4 | 0.50 | 0.026 |
| Period II | 98 | 4 | 0.45 | 0.038 | |
| Summer | Period I | 98 | 4 | 0.67 | 0.004 |
| Period II | 96 | 4 | 0.67 | 0.003 | |
| Winter | Period I | 96 | 4 | 0.58 | 0.011 |
| Period II | 96 | 4 | 0.39 | 0.048 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Sun, M.; Gao, X.; Zhao, X.; Zhao, Y. Spatial and Temporal Characteristics of Precipitation and Potential Influencing Factors in the Loess Plateau before and after the Implementation of the Grain for Green Project. Water 2021, 13, 234. https://doi.org/10.3390/w13020234
Wang J, Sun M, Gao X, Zhao X, Zhao Y. Spatial and Temporal Characteristics of Precipitation and Potential Influencing Factors in the Loess Plateau before and after the Implementation of the Grain for Green Project. Water. 2021; 13(2):234. https://doi.org/10.3390/w13020234
Chicago/Turabian StyleWang, Jichao, Miao Sun, Xuerui Gao, Xining Zhao, and Yong Zhao. 2021. "Spatial and Temporal Characteristics of Precipitation and Potential Influencing Factors in the Loess Plateau before and after the Implementation of the Grain for Green Project" Water 13, no. 2: 234. https://doi.org/10.3390/w13020234
APA StyleWang, J., Sun, M., Gao, X., Zhao, X., & Zhao, Y. (2021). Spatial and Temporal Characteristics of Precipitation and Potential Influencing Factors in the Loess Plateau before and after the Implementation of the Grain for Green Project. Water, 13(2), 234. https://doi.org/10.3390/w13020234







