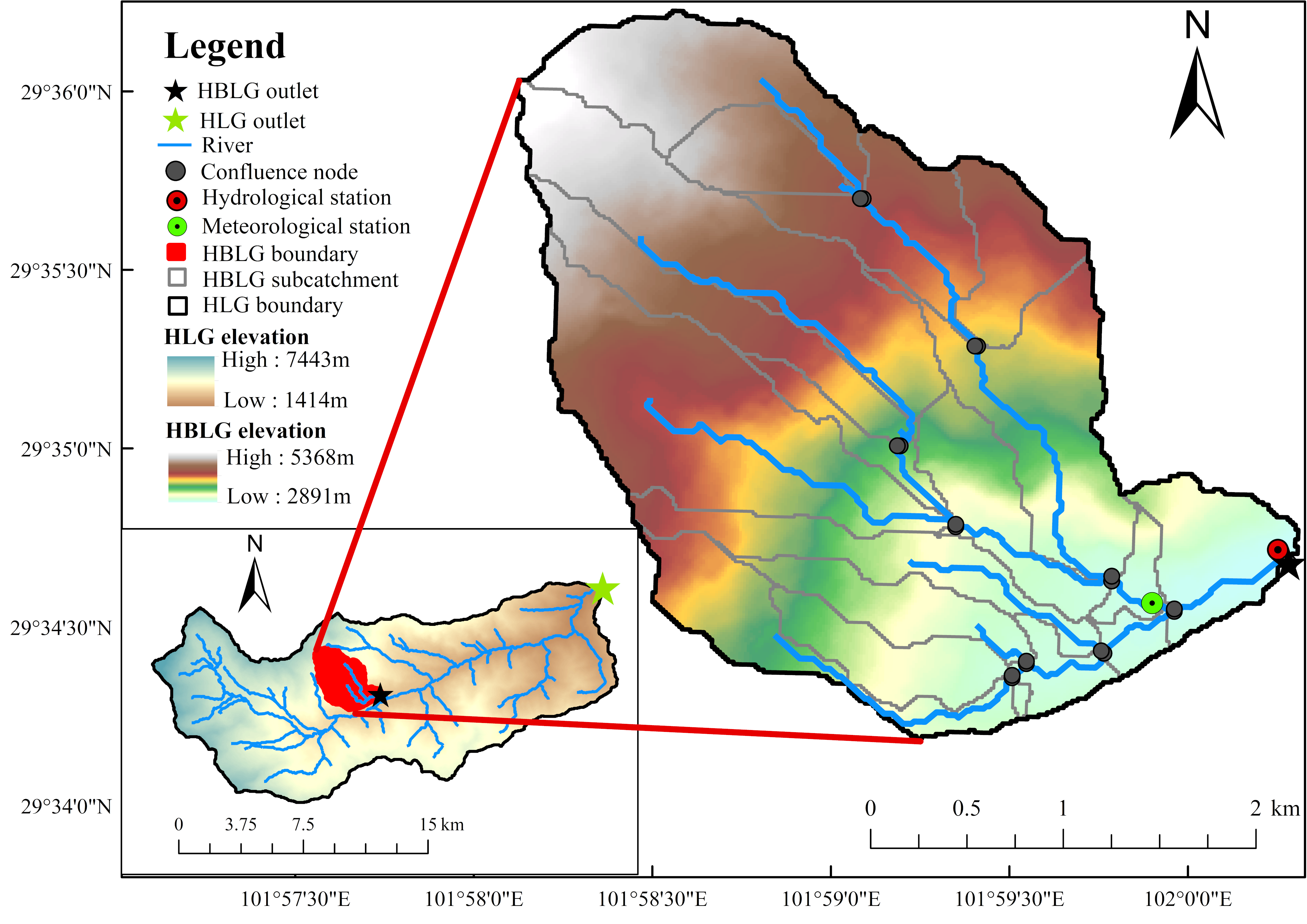
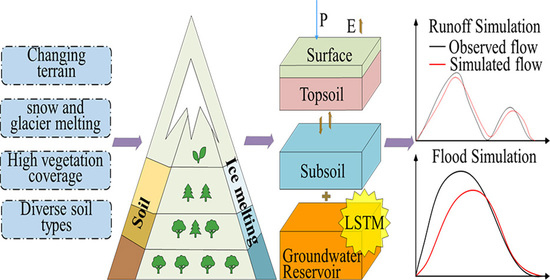
The SVSMRG-SBS model includes plane, vertical, and interval mixing. Plane mixing refers to the division of different eco-geomorphic units into different HRUs in consideration of uneven underlying surfaces, which correspond to different runoff formation mechanisms. There are four major HRU types: (1) rapid responding units (RRUs), which respond rapidly to rainfall and usually generate major infiltration-excess runoff, such as bedrock, fractured areas with bare soil, and subsidence areas; (2) disconnected rapid responding units (DRRUs), which are similar to RRUs, but lack hydraulic connection with the surrounding areas, wherein its discharge contributes less to the outlets; (3) delay responding units (DRUs), which refer to the relatively slow response speed to rainfall, and are usually grassland and woodland, wherein runoff formations are multiple components and their combinations, for instance, infiltration-excess runoff, saturation-excess runoff, and interflow; and (4) small contribution units (SCUs), which have a small contribution to runoff generation, and are usually cultivated lands. Runoff components are mainly saturation-excess runoff and interflow. These HRUs are subdivided into three types: fast, medium, and slow. Vertical mixing refers to the hydrological process in which the generation mechanisms of infiltration-excess runoff and saturation-excess runoff may be mixed in consideration of the dynamic balance of soil water. In addition, interval mixing refers to the formation of infiltration-excess runoff and saturation-excess runoff in the varying processes of instantaneous infiltration rate and infiltration capacity, soil water content, and water storage capacity. The summary of SVSMRG-SBS model characteristics is listed in
Table 3.
2.3.1. Runoff Generation Modules
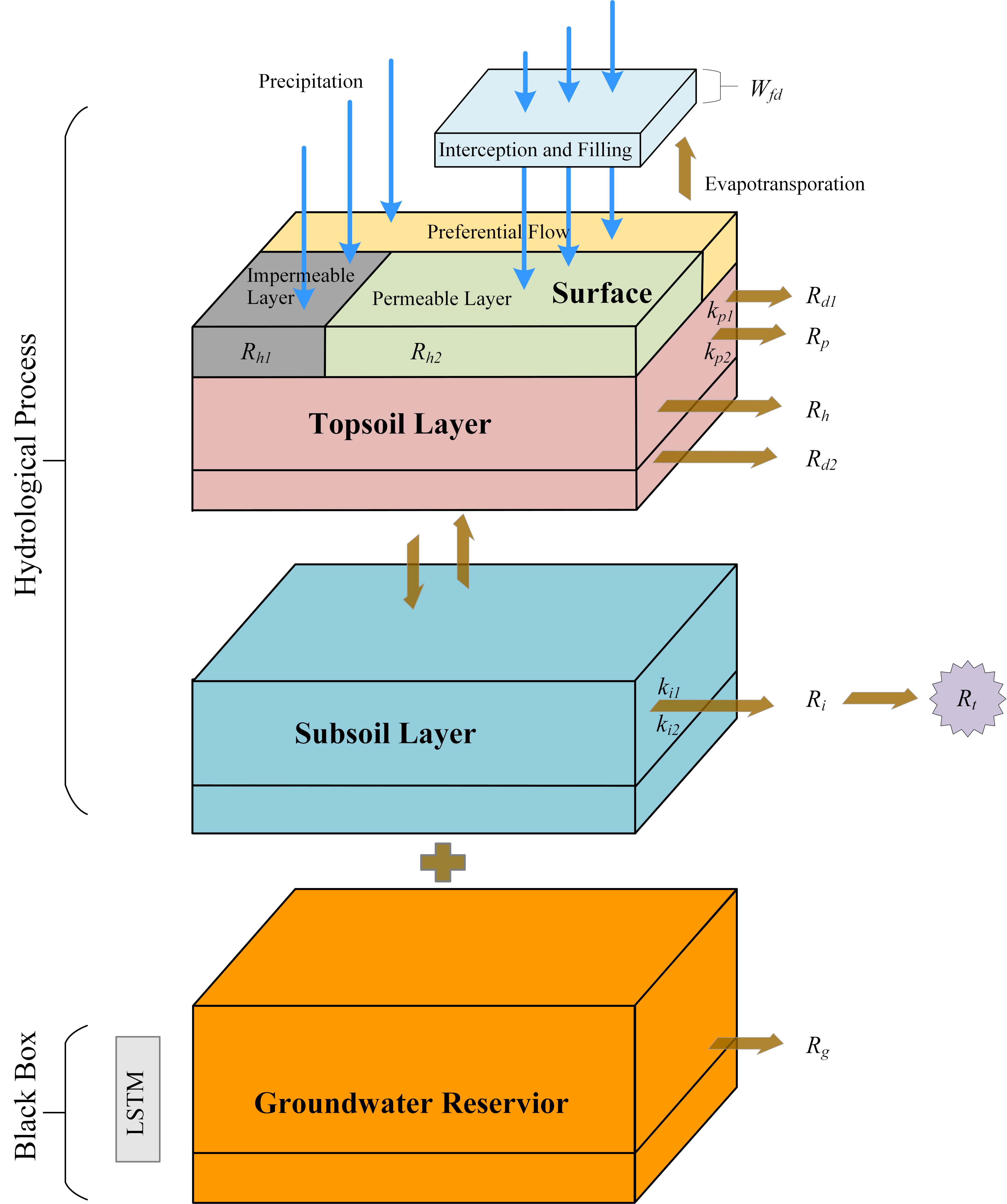
Herein, the runoff generation modules include surface flow and baseflow, where surface flow considers the unevenness of precipitation and underlying surface, and baseflow is simulated using the black box model–LSTM.
- (1)
Surface flow;
- (a)
interception and filling.
Regarding interception:
In the intercept process, precipitation is divided into interception and net rain. Interception is related to the vegetation coverage density and intercept capacity, and is divided into summer and winter interception.
Summer interception is calculated as follows:
where
is the effective intercept capacity (mm∙m
2),
is the intercept capacity of the main vegetation types in summer (mm),
is the intercept capacity of the vegetation coverage density (mm),
is the area of the
HRU (m
2),
is the intercept rainfall (mm),
is the precipitation (mm),
is the vegetation coverage density in summer (-), and
is the net rainfall after interception (mm).
Meanwhile, winter interception is calculated as follows:
where
is the intercept capacity of the main vegetation types in winter (mm),
is the vegetation coverage density in winter, while the other parameters are the same as that in Equations (1)–(3).
Regarding filling:
The filling calculation is as follows:
where
is the net rainfall (mm),
is the percentage of the basin area of depression (%), and
is the average water storage capacity of the depression (mm).
- (b)
Infiltration
The model simulates the spatiotemporal transformation process of the infiltration-excess runoff and saturation-excess runoff in the HRUs in the vertical direction. Different conceptual reservoirs are used to simulate topsoil and subsoil layers, of which the topsoil is generalized into impermeable and permeable areas, and the permeable areas are separated into preferential and non-preferential flow areas. The infiltration-excess runoff formation in topsoil is simulated by the non-linear infiltration calculation method of the unsaturated zone. Meanwhile, the preferential flow areas of topsoil and subsoil are calculated based on the saturation-excess runoff formation mechanism. The preferential flow areas represent the area of proportional distribution of the infiltration-excess runoff and saturation-excess runoff areas in the HRUs. The underground reservoir is replaced by the LSTM to determine the baseflow, as detailed in
Section 2.3.1–(2).
Regarding infiltration-excess runoff:
The infiltration-excess runoff formation is composed of the total net rain that falls on both pervious and impervious areas.
The net rain falling on impervious area generates surface runoff
immediately as:
where
is the percentage of impervious area (%).
For the net rainfall on pervious areas, if the rain intensity is stronger than the infiltration capacity, it will generate the infiltration-excess runoff
as follows:
where
is the infiltration capacity (mm).
Thus, the total infiltration-excess runoff
is:
Regarding saturation-excess runoff:
The relationships between the water content of the topsoil and subsoil with soil depth and time are as follows:
where
is the maximum water content of the topsoil (mm),
is the topsoil depth (mm),
is the saturated soil water content rate,
is the maximum water content of the preferential flow aquifer (mm),
is the percentage of preferential flow area,
is the maximum soil water content (mm),
is the whole soil depth (mm),
is the field capacity of the topsoil (mm),
is the field capacity rate,
is the field capacity of preferential flow aquifer (mm),
is the field capacity (mm),
is the initial water content of topsoil (mm),
is the initial soil water content rate,
is the initial soil water content of the preferential flow aquifer (mm),
is the initial soil water content (mm).
After the infiltration-excess runoff formation process, the actual infiltration amount of the topsoil is:
The infiltration amount of the preferential flow area of the topsoil
is:
Thus, the soil water content of the preferential flow aquifer
is:
The first saturation-excess runoff
of the preferential flow aquifer is calculated as follows:
The topsoil water content
is:
Water content of the soil
is calculated as follows:
The subsoil water content
is calculated as follows:
The second saturation-excess runoff
is:
The total saturation-excess runoff is:
Regarding preferential flow:
Preferential flow
generated in the preferential flow area of the topsoil is:
where
is the linear outflow coefficient of the preferential aquifer, and
is the non-linear outflow coefficient of preferential.
Regarding interflow:
Interflow
generated by the subsoil layer is:
where
is the linear outflow coefficient of interflow, which includes the linear outflow coefficient of slow interflow
and the linear outflow coefficient of fast interflow
, and
is the non-linear outflow coefficient of interflow, which includes the non-linear outflow coefficient of slow interflow
and non-linear outflow coefficient of fast interflow
.
Regarding baseflow:
The outflow of the groundwater reservoir is baseflow
, which is simulated by the LSTM, as detailed in
Section 2.3.1–(2).
- (2)
Baseflow
The long short-term memory (LSTM) is a variant of the recurrent neural network (RNN), which is designed to avoid gradient vanishing and exploding during the process of NN training [
34]. On the basis of the RNN structure, a memory block is added to the LSTM to store the information of long-term dependencies. Accordingly, the LSTM model is an effective model used for time-series and sequential data applications. Because time series forecasting has obvious characteristics of periodicity and time delay, the LSTM has been successfully applied in various forecasts, such as water table depth forecasting [
35], runoff forecasting [
36], and streamflow forecasting [
37].
The baseflow consists of trained baseflow and predicted baseflow. Since there is no measured baseflow data, the trained baseflow is calculated via the digital filtering method called Boughton–Chapman (F4) [
38] with observed or flood data series to obtain predicted baseflow in this paper.
2.3.2. Flow Routing Modules
- (1)
Overland flow routing
Overland flow routing adopts a kinematic wave for description [
39]. The inflow of overland is from both pervious and impervious areas. The former adopts the total amount of saturation-excess runoff and infiltration-excess runoff as the inflow, while the latter adopts net rainfall. The partial differential equation of each slope runoff field described by the kinematic wave is as follows:
where
is the surface water depth (m),
is the surface discharge per unit width (m
2/s),
is the time (s),
is the distance to the downstream of the runoff field (m).
The relationship between
and
is as follows:
where
and
m are functions representing the characteristics of the slope runoff field. See the values given by [
39].
- (2)
Channel flow routing
Channel flow comes from the upstream unit inflow confluence and the lateral inflow per unit channel length, described by the kinematic wave [
40]. The partial differential equation is as follows:
The following is the assumed relationship between river cross-sectional flow
and river cross-sectional area
:
where
is the cross-sectional area (m
2),
is the cross-sectional flow (m
3/s),
is the lateral inflow per unit length of channel (m
2/s),
is the time (s),
is the distance to the downstream (m), and
and
are the kinematic wave parameters (see [
39] for details).
For overland flow, as initial and boundary conditions a discharge and flow depth equal to zero is assumed. In addition, for channel flow, the initial discharge value is set as 0.028 m3/s.