Abstract
Substantial uncertainty is inherent in reservoir inflow forecasting, which exerts a potential negative impact on reservoir risk. However, the risk propagation from the inflow forecast uncertainty (IFU) to reservoir operations remains elusive. Thus, a new integrated assessment framework was developed in this study to characterize the risk coupling with flood and electricity curtailment risks that propagate from the IFU to the reservoir operations. First, to incorporate the IFU, an improved Gaussian mixture distribution (IGMD) and Markov chain Monte Carlo (MCMC) algorithm were constructed to model the measured forecast errors and generate ensemble inflow forecasts, respectively. Next, to assess the reservoir risk, the flood risk induced by the IFU overestimation and the electricity curtailment risk related to the IFU underestimation were identified according to the reservoir operation rules. The sub-daily inflow forecast at the Jinping First Stage Hydropower Plant Reservoir of Yalong River, China (Jinping I Reservoir) was selected. The results indicated that the IGMD-based MCMC was capable of deriving robust ensemble forecasts. Furthermore, there was no flood risk (risk rate was zero) induced by the IFU when taking designed reservoir floods with a ≥10-year return period as the benchmark. In contrast, the electricity curtailment risk rate significantly increased up to 41% when considering the IFU. These findings suggested that compared with the flood prevention pressure, the IFU would more likely result in severe electricity curtailment risk at the Jinping I Reservoir.
1. Introduction
The process of reservoir inflow forecasting plays a critical role in short-term reservoir optimal operations and directly influences the reservoir-adjusted flood prevention and water resources management effectiveness, as well as the hydropower generation efficiency [1,2]. Normally, the short-term, especially sub-daily, forecasting of reservoir inflows is carried out in practice at a certain time with multiple lead times. The current forecasted inflows with sub-daily lead times contain a large uncertainty, which constrains the capacity of reservoir optimal operations and leads to multiple risk events, owing to the strong randomness of the forecast error and the high real-time demand [3]. As a risk factor, the inflow forecast uncertainty (IFU) is closely related to the reservoir operation effects on flood prevention and the power generation capacity, and thus results in a risk when operation failure occurs. Thus, how to quantify the risk that propagates from the IFU to the reservoir operations is a huge challenge concerning the complex response process.
The reservoir operation risks can be roughly categorized into two types, namely, the occurrence of hazard events and various natural and/or socioeconomic losses [4,5,6]. For the first type, flood damage and inundation risks are the primary hazard events [7] when the reservoir operation is failing. Food damage risk is frequently short-term and caused by flooding from external waters, while the inundation risk is caused by flooding from internal waters during reservoir operations. As for the second type, a water shortage related to water supply and ecological water utilization and a reduction in power generation capacity of a hydropower plant often appear. Although these losses will not result in an extremely critical hazard, they can induce large losses in the long run. Among various risks, both flood and electricity curtailment risks are the most concerning regarding reservoir inflow-related risks.
In practice, a certain inflow forecast series is normally provided to the engineers to operate reservoirs. The engineers frequently analyze the forecast quality by modeling forecast errors. To analyze the reservoir inflow forecast errors, the forecast errors of the inflow discharge is obtained as the difference between the forecasted inflow discharge and the corresponding observations. Current studies primarily focus on quantifying the stochastic characteristics of inflow forecast errors using parametric and non-parametric estimation [8,9] and maximum entropy approaches [10] to approximate the theoretical distribution of the forecast errors [11,12]. These approaches were applied mainly based on a single probabilistic distribution [13,14], which cannot quantify the theoretical distribution that captures all the characteristics of the inflow discharge due to the varying tail features, although satisfactory results may be possible under some conditions. Thus, it is necessary to profile the forecasting errors using multiple distributions to depict various characteristics of the forecasted inflow errors with strong randomness.
Finite mixture distributions, especially the Gaussian mixture distribution (GMD), have been widely applied to modeling the daily or sub-daily discharge forecast errors in previous studies due to their ability to fit the complex forecast errors [15,16]. For example, Ji et al. [17] established the stochastic GMD model to fit the sub-daily forecast error series of reservoir inflows. However, two important problems were unsolved in these studies. The first one is the identification of the mixture number in the Gaussian function. If the mixture number is too small, the fitness precision may be hindered, whereas the model may be too complex to run if the mixture number is too large. The other problem is related to the initialization of the model parameters used. The parameters of GMD, including the weighting coefficient of Gaussian components and others, need to be initialized first before they are numerically optimized using optimal algorithms. Different initialization schemes lead to very different iteration results and exert a significant influence on the goodness-of-fit. However, the number of Gaussian components and the initialization of parameters were frequently decided arbitrarily in previous studies, which lacks a scientific trade-off decision. Based on the theoretical distribution model of the forecasted inflow, ensemble forecasts can be generated with various sampling techniques to represent the forecast uncertainty. The Markov chain Monte Carlo (MCMC) algorithm provides a flexible tool for generating ensemble inflow forecasts based on the raw deterministic forecasts [18,19]. In similar investigations, the IFU can be derived using the synthetic ensemble forecast [20]. Although the ensemble reservoir inflow forecast was explored in quite a few previous investigations [21], the IFU has rarely been linked to the risk propagation of reservoir flood prevention and power generation operations to quantify the risk.
Overall, from an uncertainty point of view, it is difficult to generate a robust ensemble inflow forecast via modeling the inflow forecast error with a single Gaussian distribution (SGD), due to the heterogeneity of inflow forecast errors that is related to unregulated temporal dynamics. Accordingly, we introduced the improved GMD (named IGMD) to depict the forecast errors for reservoir inflow, which is suitable for the heterogeneous structures of errors that result from multiple hydro-meteorological conditions and runoff generation processes over a lengthy period, as emphasized in previous studies [22,23]; we also introduced the GMD model, which is different from the IGMD in the means of Gaussian component and the initial parameter identification. The other problem concerns how to quantify the reservoir operation risk that propagates from the IFU. In this study, the operation risk driven by the ensemble inflow forecast was estimated for the flood risk achieved by the reservoir design flood rules and for the electricity curtailment risk via stochastic dynamic programming.
This study aimed at analyzing the response of the reservoir operation risk related to the flood hazard and the electricity curtailment loss to the IFU. The specific objectives of the present study were to (1) construct the IGMD model in order to model the error in the reservoir inflow forecast and generate an ensemble forecast series with multiple lead times via an MCMC algorithm, and (2) quantify and assess the risk, which was coupled with the flood risk and electricity curtailment losses, that was induced by the IFU. To verify the performance of the integrated framework for assessing the risk propagating from the IFU to reservoir operations, the First Stage of the Jinping Cascade Hydropower Plant Reservoirs located at Yalong River was exploited as the study area to investigate the short-term inflow forecast.
Following this introduction, the method of modeling the inflow forecast error and risk quantification is described in Section 2. Next, the study area and sub-daily inflow data obtained from forecasts and observation techniques are introduced in Section 3. Section 4 provides the results and discussion derived from the quantification framework of the risk propagation. Finally, the primary conclusions are given in Section 5.
2. Methods
Figure 1 illustrates the overall research schemes of the developed framework for assessing the risk propagation from the uncertainty in the reservoir inflow forecasts to the reservoir operation risks used in this study. Correspondingly, the approaches of the traditional GMD model, the improved GMD model coupling the quantification of mixture component number and the initialization of model parameters, the MCMC sampling algorithm, the flood risk identification, and the dynamic programming for quantifying electricity curtailment were introduced in Section 2.1, Section 2.2, Section 2.3, Section 2.4 and Section 2.5, respectively.
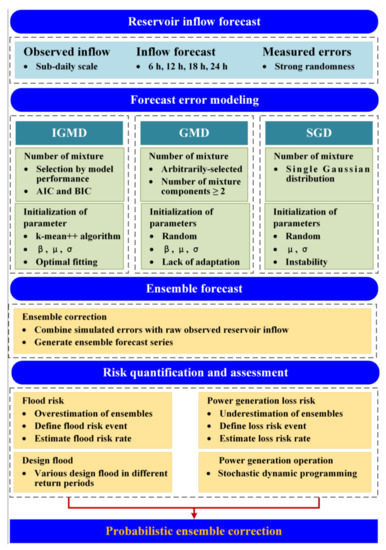
Figure 1.
Flowchart for the integrated framework proposed in this study. GMD, IGMD, and SGD denote the Gaussian mixture distribution, the improved Gaussian mixture distribution, and the single Gaussian distribution models, respectively. Note that the IGMD was the model proposed in this study and was used to quantify the inflow forecast uncertainty (IFU) and flood risk, as well as the electricity curtailment risk, while the GMD and SGD were used for comparison with the IGMD. AIC: Akaike information criterion, BIC: Bayesian information criterion.
2.1. Gaussian Mixture Distribution (GMD) Model
The streamflow data exhibited strong temporal heterogeneity from the low flow period to the flood period, showing multimodal features. Therefore, it is quite natural and intuitive to assume that the cohorts come from different Gaussian distributions. Thus, the probabilistic model of the GMD, which exhibited normally distributed subpopulations of forecast errors within an overall population, was used to depict the error variable. Mixture models, for example, the GMD, do not generally require identification of the specific subpopulation that a data point belongs to, which allows the model to search the subpopulations adaptively with a form of unsupervised learning [24,25]. The measured forecast error was considered as the errors between the past forecasted () and their verifying observed () inflow discharge. The forecast errors, denoted as , can be expressed as:
where T(i) and t(j) represent the beginning time of the forecast and the lead time, respectively; i is the index of the forecast number, i = 1, 2, …, N; j is the index of the forecast period number, j = 1, 2, …, M. The forecast errors of a specific lead time t(j) can be fitted using the Gaussian mixture model with a probability density function (PDF) expressed as follows:
where denotes the parameter set in the mixture model, and for a specific kth Gaussian model component , the parameters include the weighting coefficient , where , component mean , and component variance . To solve the mixture model, the parameter set needs to be identified. The expectation maximum (EM) algorithm is a powerful tool for optimizing the parameters and contains three steps, as follows:
(a) “E” Step: Define a latent variable that represents whether the ith sample belongs to the kth Gaussian model, k = 1, 2, …, K. Merging with Equation (2), we can derive the log-transformed likelihood function of a single sample (see Equation (3)):
Then, the parameter set is initialized by setting , a random complying with the uniform distribution, and . Based on Equation (3), the posterior probability distribution of in Bayesian theory can be written as:
(b) “M” Step: Partially derive the log-transformed likelihood function with respect to the parameters using Equation (5):
The estimated parameters can be derived by setting the partial derivative function equal to zero:
(c) Step iterations: Update the parameters by iterating the steps (1) and (2) until the difference between the two continuous estimates reaches a small enough value, for example, .
2.2. Improved Gaussian Mixture Distribution (IGMD) Model
The modification of the GMD, including the quantification of the suitable number of Gaussian mixture models via the Akaike information criterion (AIC) and Bayesian information criterion (BIC), as well as the initialization of the model parameters via the k-mean++ algorithm in the data mining, is described in Section 2.2.1 and Section 2.2.2, respectively. Then, we introduce the indices of the optimal model test that was used to diagnose the performance of the improved GMD model in Section 2.2.3. The advantages lie in the fact that the improved modeling accuracy of the IGMD for fitting the inflow forecast errors provides benefits to the inflow forecast uncertainty analysis and reservoir operation risk that was driven by the ensemble inflow forecast. Figure 1 shows the flowchart of the construction and application of the forecast error model using the IGMD for the reservoir inflow.
2.2.1. Deciding on the Optimal GMD Models Using the AIC and BIC
Both the AIC and BIC can evaluate the goodness-of-fit for a model’s performance. The difference between these two indices is that BIC is more appropriate for cases with large amounts of sample data due to the punishment term for the model parameters and taking the sample length into consideration. The mathematical functions of AIC and BIC can be formulated as Equations (7) and (8), respectively, as given below:
where K represents the number of model parameters and refers to the number of Gaussian mixture model components in this context; N and L denote the length of the sample and the likelihood function, respectively. Varying the parameters results in various AIC and BIC estimates. Lower estimate values for AIC and BIC indicate a better performance of the model fitting. Furthermore, the K value for a specific lead time corresponding to the lowest AIC and BIC is considered the optimal number of GMD model components for the subsequent modeling.
2.2.2. Initializing the Model Parameters Using the k-Mean++ Algorithm
The k-mean++ algorithm was frequently used to determine the beginning state of the cluster iteration, in which the distances between the centers of primary clusters were as large as possible. To classify the sample data of the forecast errors, the components in the Gaussian mixture model can also be considered as a cluster model. The clustering process is achieved by mapping each data point into an appropriate Gaussian component, with the detailed steps as follows (see Figure 2):
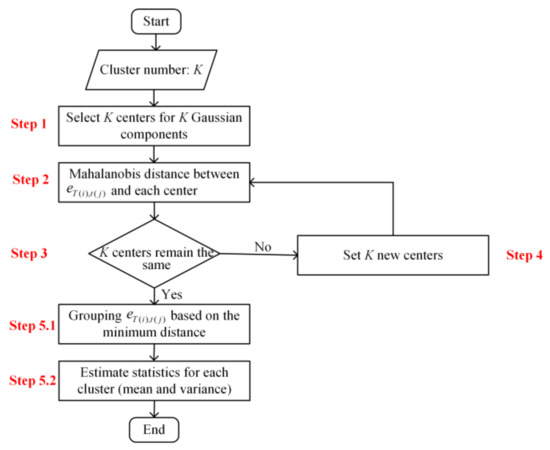
Figure 2.
Flowchart of the k-mean++ algorithm.
- (a)
- Randomly select K centers for K Gaussian components (K is set to the optimal number quantified in Section 2.2.1) for each sub-daily forecast period.
- (b)
- Estimate the Mahalanobis distance between the forecast error with a lead time of t(j) beginning at time T(i) and the nearest center of the Gaussian model cluster.
- (c)
- Calculate the probability that an error is taken as the next cluster center using the formula , according to the Roulette wheel theory.
- (d)
- Iterate steps (2) and (3) until all the cluster centers remain the same.
- (e)
- Group each error into a specific cluster, where the distance of the error to the center is minimum among K clusters, and derive the cluster mean and variance for each cluster ().
The , , and identified above are the initialized parameters. The optimized values for them can then be obtained using an iterative EM algorithm, as demonstrated in Section 2.1. Furthermore, the forecast error distribution of a single sub-daily lead time in Equation (3) is then identified using these parameters.
2.2.3. Indices of the Optimal Model Test
The Kolmogorov–Smirnov (K–S) test was introduced into this study to identify the goodness-of-fit of the constructed Gaussian distribution. The K–S test is a non-parametric approach, which can diagnose whether a population complies with a theoretical distribution. Compared with the test, the K–S test can make full use of the sample data, allowing for continuous and quantitative data. The index of the K–S test statistic DN can be written in the following format:
where HN() and H() denote the empirical and theoretical distribution functions, respectively. The significance level of the K–S test was set to 0.01. A smaller DN value indicates a better goodness-of-fit. When the HN represents the probability density distribution of the GMD in this study, then it can be expressed as:
where Nq denotes the number of samples that are subject to , , while N is the sample size.
Furthermore, to quantitatively evaluate the discrepancy between the empirical and theoretical distribution functions, the root of the mean square error (RMSE) and mean error in the percentage (MAPE) were calculated using the expressions below [24]. Lower RMSE and MAPE values indicate better performance.
2.3. Metropolis–Hastings MCMC Algorithm Based on the IGMD
The realization of high-quality sampling in statistics with complex computations is heavily dependent on Markov chain Monte Carlo (MCMC) methods. The Metropolis–Hastings (MH) algorithm, which allows for scalable parallelization of existing MCMC methods, was introduced to randomly sample from the distribution of the modeling of the inflow forecast error described by Equation (2). A finite-state Markov chain on multiple proposals was defined in a way that ensures asymptotic convergence to the IGMD distribution. The detailed algorithm steps can be obtained from the general introductions in previous studies [26,27]. The aim of the MH algorithm in this context is to generate multiple forecasts using a stochastic process of sampling of the modeled forecast errors. The ensemble forecast series were derived for each of the forecasted inflows of four sub-daily lead times, while each MH routine was implemented with 10,000 simulations to provide a stable convergence.
The IFU in this study was represented using the ensemble forecast series that contained varying errors. In order to quantify the IFU based on the IGMD modeling and MH resampling, each sampled error was extracted from the raw inflow forecast and observations using Equation (13); this process can be regarded as a “correction” of the raw inflow forecast:
where is the simulated forecast error derived from the IGMD model, the absolute value of is normally small, and denotes the corrected forecasted inflow.
The 95% confidence interval of the retrospective ensemble-corrected inflow forecasts, focusing on band assessment, can graphically depict the effect of the ensemble correction on the raw inflow forecast. In addition, the containing ratio (CR) index was used to quantitatively count the percentage of the observed inflow that was located within the band of the 95% confidence interval [28,29]. High-quality performance of the ensemble correction was characterized by high values of CR (≤100%):
where Qo denotes the observed inflow discharge; the Qf,l and Qf,u represent the lower and upper bound values of the 95% confidence interval, respectively; the Count() function calculates the number of inflows that satisfy the boundary condition; N is the length of the data series, as mentioned above.
In order to drive the reservoir operation system, we applied a different strategy to use the sampled error to generate an ensemble forecast, in which the samples were extracted from the inflow observations:
where is the simulated forecast error derived from the IGMD model and denotes the ensemble forecast, which comprises the input space of the reservoir power generation operation that is solved using the dynamic programming algorithm introduced in Section 2.5.
2.4. Defining a Flood Risk Event Using a Design Flood
The flood risk events induced by the IFU were diagnosed via reservoir routing with the inflow ensemble forecast (generated using Equation (15)) based on design floods. Based on the ensemble forecast, the risk within the forecast lead time can be expressed as the risk rate (), which represents the rate that the ensemble forecasted flood event () exceeds the design flood () in the return period rp [30,31]:
where NMCMC denotes the number of MCMC samples, i.e., the inflow ensemble forecast number. This definition of the flood risk rate assumes that the longer the return period of the design flood, the more severe the risk is. Given a design flood in a specific return period, the more forecasted flood events with a specific lead time that exceeds the design flood, the more severe the risk is. Equation (16) was derived under the condition that the MH-based MCMC algorithm approximates the convergence state.
2.5. Dynamic Programming Used to Estimate the Electricity Curtailment
Dynamic programming is used to search for an optimal power generation capacity with high dimensionality. The objective function of this dynamic programming, i.e., the primary goal for non-convex impoundment operations, is to find the maximum total hydropower generation capacity given the specific inflow series, which belongs to the set of “water-to-electricity” optimization problems [32,33]. In addition, the constraints of a reservoir system need to satisfy the common operation conditions, for example, the water balance and water level, power generation capacity, and hydraulic relation constraints. The ensemble forecast, the raw forecast, and the observed inflow of sub-daily lead times individually force the reservoir power generation to quantify the maximum power generation capacity for each scheme. Then, the losses of electricity curtailment are evaluated as deviations of the optimal total power generation capacity, which are derived from the operation driven by the observed and forecasted inflow. The mathematical model of stochastic dynamic programming approach for the short-term optimal operation targets of the reservoir that are related to power generation includes the objective function and the constraint conditions. In this study, the objective function, aiming at the maximum generation benefit of the cascade system, can be expressed as follows:
where Ntime, qtime, and Htime denote the generated output, power flow, and hydraulic head of the reservoir during the time interval . TT is the number of time intervals. Therefore, the total generation benefit in the operation cycle has the unit of GW·h.
In addition, the main constraint conditions are related to the water balance, capacity, the upper and lower bounds of flow rate and output, and water level. For a detailed construction with stochastic dynamic programming equations and a solution with an optimization algorithm of the model, please refer to the study of Zhao et al. [11].
3. Study Area and Data
The First Stage of the Jinping Hydropower Plant Reservoir (hereafter abbreviated as JinPing I Reservoir) controls the whole cascade hydropower station reservoirs, which consist of the Jinping First Stage, Jinping Second Stage, and Guandi hydropower reservoirs. The Jinping I Reservoir was selected as the study area because large forecast errors inherent in the inflow forecast have resulted in the water level of the reservoir often fluctuating beyond the normal range since its operations began. Jinping I Reservoir is located on the eastern edge of the structural belt of the Qingzang Plateau and on the western side of a sharp bend in the Yalong River. The double-curvature arch dam of Jinping I Reservoir, with a height of 305 m, is constructed in a typical V-shaped valley [34]. The water level in the river is approximately 1630 m a.s.l., while the reservoir is able to reach a maximum water level of approximately 1880 m a.s.l. The mean inflow discharge at the dam site is about 1200 m3/s over a long-term record [34].
The inflow discharge contains the 6-hourly observed data and short-term forecasted data at 6 h, 12 h, 18 h, and 24 h of the Jinping I Reservoir collected during 1 January 2014–23 June 2017. The forecast time begins from 9:00 a.m. each day such that the lead times for the four periods are thus at 15:00 p.m. and 21:00 p.m. on the same day and at 3:00 a.m. and 9:00 a.m. on the next day. That is, each observed inflow discharge corresponds to four forecasted inflow values. For each observation, four types of forecast errors can be derived by subtracting the same observed value from the corresponding forecasted values at four sub-daily lead times. Subsequently, the four types of errors were applied when producing the GMD model used to generate probabilistic ensemble-corrected forecasts. Although finite lead times from the operation example in the real world were applied, any lead times ≤24 h (daily scale) can be forecasted and used to analyze the reservoir operation risk mentioned in this study.
4. Results and Discussion
4.1. Analysis of the IGMD Model
4.1.1. Performance of the IGMD Model
The fitting performance of the IGMD model to the measured forecast errors derived using the 6 h, 12 h, 18 h, and 24 h lead times was analyzed. To quantify the optimal number of IGMD models at each lead time, the AIC and BIC values of the IGMD models were estimated with various K numbers, beginning from 2. It can be seen from Figure 3, which shows the AIC and BIC values when K ranges from 2 to 5 for each of the four forecast periods, that both the AIC and BIC reached their minima at K = 3.
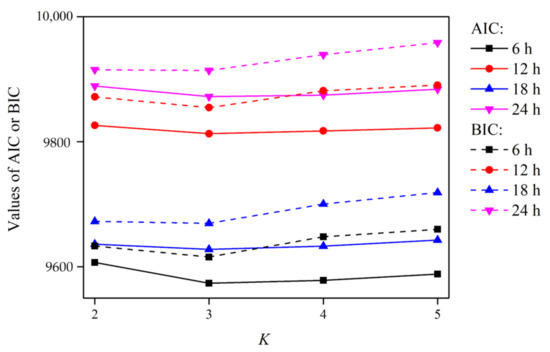
Figure 3.
AIC and BIC values of the optimal IGMD-model-fitted forecast errors of multiple lead times when the Gaussian mixture number K changed.
In addition, the performance generated from the traditional GMD model, which was configured according to a previous study with an arbitrary selection of the Gaussian component number and model parameter initialization [17], as well as the SGD, were used for comparison with the modified GMD, i.e., the IGMD, to validate its improvement. The fitting performance of the IGMD, traditional GMD, and SGD models for the inflow discharge forecast errors are graphically displayed in Figure 4, which are compared with the measured error histogram for each of the 6 h, 12 h, 18 h, and 24 h lead time schemes. The density curve of the improved model IGMD was fitted to the frequency histogram of the binned error data that was the best among the three models for each of the four lead times. The traditional GMD performed second best, following the IGMD. Compared with the traditional and the improved GMD, the SGD model significantly deviated from the shape of the sample data of the forecast discharge errors and exhibited a much lower peak. The peak of the SGD was not sharp enough to represent the error structure of the four lead times, and thus could not capture the random behavior of the errors between the observed and forecasted reservoir inflow, confirming the major finding in Li et al. [35]. Furthermore, as for the case of the SGD, the significant deterioration of the deviation that occurred at the tail ends of the distribution may have been caused by the fact that the lower histograms, which were linked to the larger absolute errors, exhibited different distributional biases during storm seasons or wet seasons with a tendency toward resulting in strong inflow forecast biases.
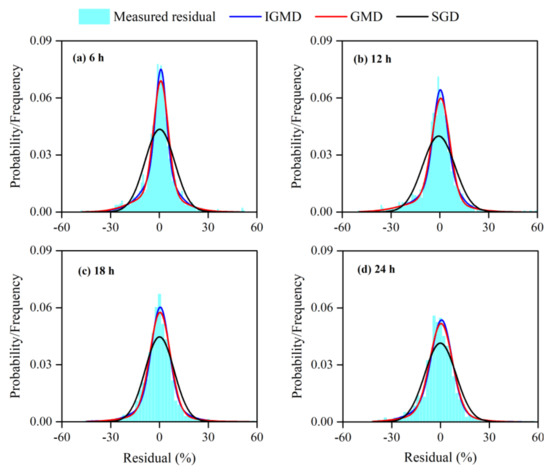
Figure 4.
Histograms of the measured forecast errors and probability density curves of the IGMD, GMD, and SGD models that were used to model the forecast errors of four sub-daily lead times.
4.1.2. Goodness-of-Fit for the IGMD
To test the robustness and randomness of the constructed mixture distribution of the inflow discharge error data, the goodness-of-fit of the IGMD was tested using historical data based on the K–S test. The index of the K–S test, DN, is summarized in Table 1, which shows that both the improved and traditional GMD distribution passed the K–S test at the significance level of 0.01, indicating the adequacy of the IGMD and GMD for modeling the forecast errors with sub-daily lead times. Furthermore, the DN value generated from the IGMD model was lower compared with the GMD and SGD models at each of the four lead times, which demonstrates the superior performance of the modified GMD model.

Table 1.
DN values for the Kolmogorov–Smirnov (K–S) test of the IGMD model at the significance level of 0.01 with the critical value of 0.044.
Furthermore, to verify the robustness of the IGMD, Figure 5 displays the Q–Q plot of the simulated vs. measured errors with the 6 h, 12 h, 18 h, and 24 h lead times. The scatters derived using the IGMD model were much closer to the perfect location of the 1:1 line compared with the GMD model for the four lead times, while the scatters generated by the SGD model significantly departed from the perfect line. This indicates that it was necessary to use a mixture distribution instead of single model; furthermore, the improved model IGMD exhibited better skill when reproducing the random errors. Table 2 shows the statistics of the mean, variance, and coefficient of variation generated from the IGMD and the GMD model vs. the measured errors. The statistics of the errors simulated using the IGMD model were generally nearer to the measured errors than those simulated using the GMD.
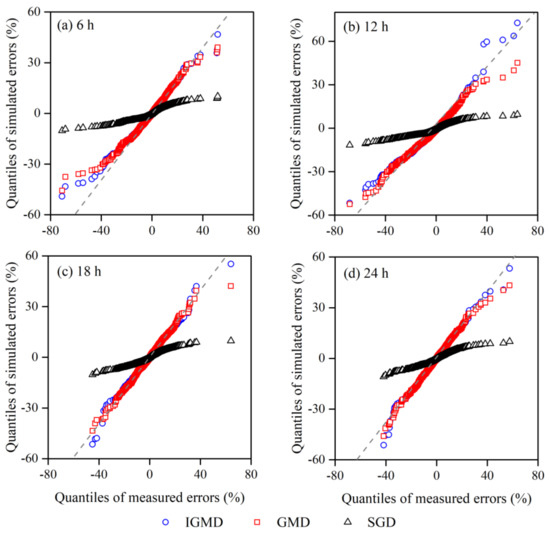
Figure 5.
Q–Q plots of the simulated and measured forecast errors generated from the IGMD, GMD, and SGD models under different sub-daily lead times. The gray short-dash line in each of the subplots represents the 1:1 line for the two coordinate axes.

Table 2.
Statistics of the sampled errors based on the IGMD and GMD models vs. the measured errors.
The posterior test can be used to quantify the difference between theoretical and empirical cumulative distributions of the sample data. The RMSE and MAPE indices were calculated to evaluate the posterior performance of the modeled error distribution, taking the empirical distribution of the measured forecast errors as a benchmark (Figure 6). The RMSE index generated using the IGMD was the lowest among the three models, followed by the GMD for each of the four lead times, while that from the SGD was much higher than the IGMD and GMD. Similar to the pattern of RMSE for the three models, the MAPE index of the IGMD had the lowest values for each of the four forecast periods. As the reference that represents the case of only using one Gaussian distribution, the SGD performed much worse than the mixture cases of IGMD and GMD when compared using the forecast error histogram, K–S test, Q–Q graphical plot, and the RMSE and MAPE indices. The inferior and limited modeling capability of SGD mainly results from the characteristics of SGD, such as only using two-parameter tuning and simple-structure modeling. Although there were no uniform trends in both the RMSE and MAPE values among the different lead times, the RMSE and MAPE values of the SGD fluctuated more dramatically than the improved GMD and traditional GMD. This also suggests that the mixture distribution exhibited stronger stability with increases in the lead time.
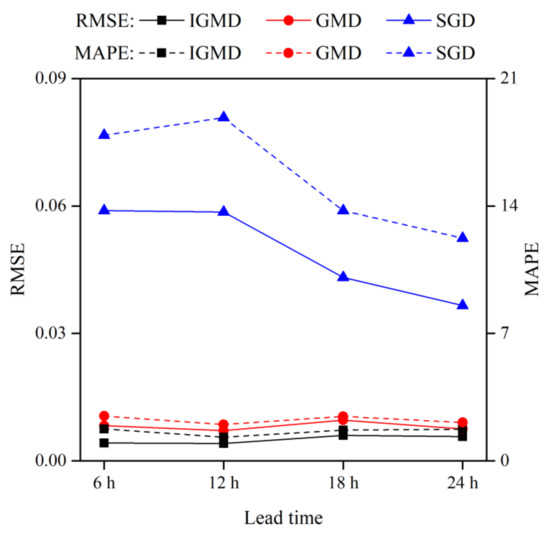
Figure 6.
The RMSE and MAPE values that were used to evaluate the discrepancies between the fitted theoretical cumulative distribution models of the IGMD, GMD, and SGD models and the empirical cumulative distribution.
To compare the differences in the fitted IGMD distribution between different lead times, four curves of the IGMD at multiple lead times are displayed together in Figure 7. The changes in the curves can be observed, which show that with the lead times becoming longer, the shapes of the curves developed from “narrow and high” into “wide and low.” Despite the modeling biases, the changes in difference curves may have resulted from the error feature of the inflow forecast at different lead times. The forecasted discharge associated with longer lead times theoretically contains more values with larger errors due to the limited forecasting skill. The increasing number of larger errors resulted in a highly dispersive histogram. Thus, the theoretical curves generated from fitting the error histogram look “wider and lower.” In general, the density curves of all three models fit the shape of the frequency of the sample error data with 6 h lead time the best while fitting the shape of the frequency histogram of the 24 h lead-time errors worst. This analysis is easy to understand and remains highly consistent with the common knowledge about the discharge forecast uncertainty in hydrology, as a longer forecast period results in a larger uncertainty [15,35]. Compared with the similar application of the IGMD in previous investigations focusing on other fields, the IGMD in this study exhibited a satisfactory performance that was consistent with those reported by Pan et al. [24] and Zhuang et al. [25]. Furthermore, the IGMD in this study, which is only available for univariate modeling, could be constructed based on multivariate modeling by combining inflow forecasting errors of various lead times [23].
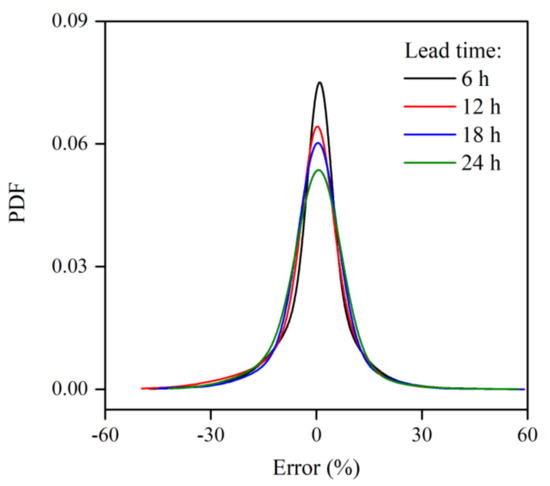
Figure 7.
Comparison of the characteristics of the probability density function (PDF) of the proposed IGMD that were fitted using the forecast errors generated using different lead times.
4.2. Uncertainty Analysis of the Reservoir Inflow Forecast
The 95% confidence interval of the daily ensemble-corrected inflow derived from IGMD, GMD, and SGD models are graphically displayed in Figure 8, Figure 9 and Figure 10. The superior performance of the IGMD correction for the inflow during the study period 1 January 2014–23 June 2017 was reflected in the band of the 95% confidence interval with more observations located inside under the circumstances of the same ensemble size as that used for the GMD and SGD (Figure 8). The CR of the 95% confidence interval for the IGMD model with each lead time (92 to 95%) was significantly higher than that for the GMD (41 to 94%) and SGD (29 to 38%) models. The outliers mainly occurred during the dry seasons (from November to the next April). In contrast, the 95% confidence interval corrected using the IGMD-dependent errors had a relatively wider band than those corrected using the GMD- and SGD-dependent errors, especially during the wet seasons (from May to October). Although the fact that the ensemble correction of the inflow forecast performed better in the IGMD model than in the GMD and SGD models was related to the higher 95% confidence interval bands, as shown in Figure 8, Figure 9 and Figure 10, the effect of the ensemble correction on the raw inflow forecast of the IGMD was considered better than the GMD and SGD. This was because the primary factor of concern in this study was the time and cost of computation associated with the ensemble correction and the resulting optimal operation of the reservoir, which are frequently considerable. The CR evaluating how many observations are covered by the 95% confidence interval bands was superior to the band width since the computation time and cost were comparable between the three models. The ensemble correction of the raw forecast provided an available tool to quantify the IFU, in which the observed inflow was made full use of. These results demonstrate that the IGMD-based MCMC is capable of generating a corrected ensemble to quantify the IFU with a 95% confidence interval and a CR index.
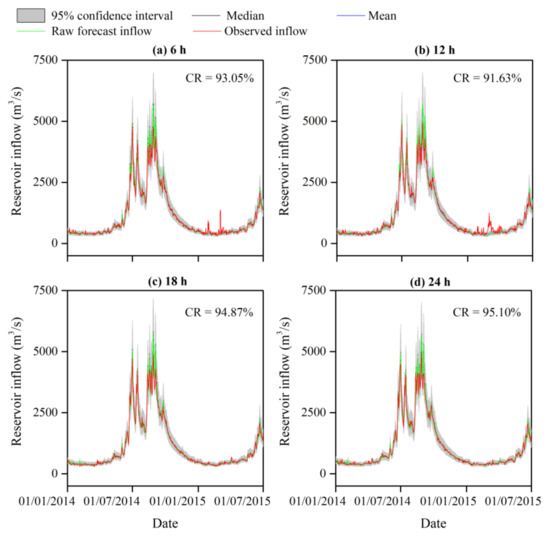
Figure 8.
The 95% confidence intervals, the median and mean values of the corrected inflow ensembles that were derived from the developed IGMD model compared with the raw forecasted and observed inflow series for the lead times of (a) 6 h, (b) 12 h, (c) 18 h, and (d) 24 h. The median line in black and the mean line in blue were largely overlaid by the lines of the raw forecasted and observed inflow. Note that only the data during 1 January 2014 to 1 July 2015 are presented to ensure the clarity of the figure; however, the CR values were derived based on the whole study period.
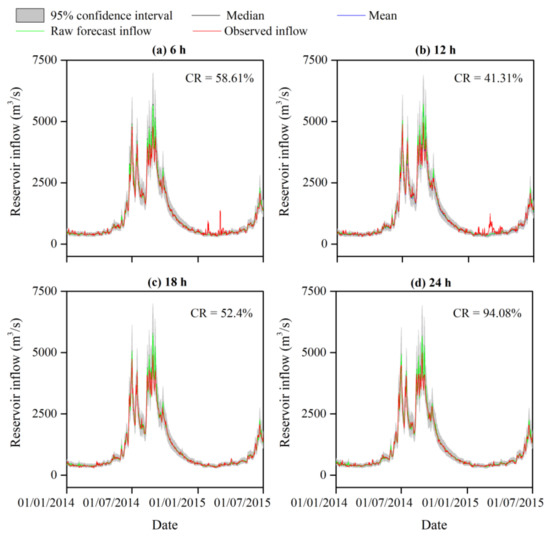
Figure 9.
Same as Figure 8 but for the traditional GMD model.
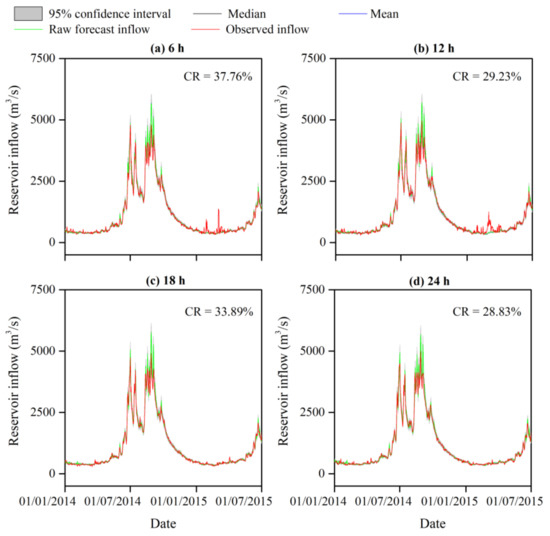
Figure 10.
Same as Figure 8 but for the SGD model.
The drastic change in the CR of the observed inflow data covered by 95% confidence interval bands of the IGMD, GMD, and SGD models suggests the different representations of these three models (Figure 8, Figure 9 and Figure 10). Indeed, the sampled errors generated from the proposed IGMD could capture the underlying characteristics of the measured forecast errors, even though those errors are from historical measurements. Overall, the updated Gaussian mixture model was able to reflect the reliable characteristics of the measured errors and to support the correction of the raw forecasts. Moreover, ensemble error correction of the inflow forecast can provide ensemble schemes of reservoir operation optimization and further improve the optimization accuracy and operation levels, as well as the increased hydropower generation benefit [30]. In addition, if the band of the 95% CI is wide enough, all of the observations could be covered (CR would reach 100%). However, the IFU considered in this study could not increase infinitely because the number of Gaussian mixture components was controlled by the AIC and BIC, and the ensemble convergence was determined by the MH-based MCMC algorithm. For the decision-making-dependent optimization (e.g., reservoir optimal operation), the ensemble-corrected inflow scenarios could guarantee relatively higher reliability due to covering more of the observed inflow compared with the input strategy of the deterministic reservoir inflow forecast (i.e., the raw inflow forecast series before generating the ensemble forecast).
4.3. Risk Assessment from the IFU to the Reservoir Operations
4.3.1. Assessment of the Flood Risk
The flood risk rates derived from the observed inflow and the raw inflow forecast of each of the four lead times were all zero for the design flood for all the return periods. For the ensemble forecast, there was still no flood risk when accounting for the risk rate using design flood with a return period of ≥2 years and ≥5 years for 6 and 12 h forecast times and 18 and 24 h forecast times, respectively. In contrast, the risk rates obtained from ensemble forecast with a return period of 2 years increased with the increase of lead times from 16 to 47%, while the ensemble inflow forecast exhibited much lower risk rates for the 5-year return period only for the 18 h (0.01) and 24 h (0.08) lead times (Table 3). Thus, taking the IFU into account would lead to flood risk rates defined using design floods with low return periods. However, the IFU could not increase infinitely, and the ensemble inflow forecast reached to a convergence state in MCMC algorithm. Compared with a previous similar study on flood risks that occurred with a 20-year return period [31], the flood risk rates resulting from the IFU were lower, suggesting that the study area of Jinping I reservoir exhibited a lower flood risk.

Table 3.
Flood risk rates of the forecasted ensemble inflows while taking the IFU into account.
4.3.2. Assessment of the Electricity Curtailment Risk
Figure 11 displays the temporal dynamic of the power generation derived from the raw inflow forecast (without IFU), ensemble inflow forecast (with IFU), and observed inflow series. In general, the power generation level forced by ensemble forecast was significantly lower than those forced by the raw inflow forecast and observations. During a flood period, although the peaks of the power generation capacity curve related to the IFU (in blue) reached similarly high levels to the curves related to the observations (in red) and raw inflow forecast (in black) sometimes, the persistence time occurring at high levels of the ensemble inflow forecast was much shorter than that of the observed and raw forecasted inflow. The reduction in power generation capacity seen with the blue curve of Figure 11 is related to a water deficit. In some periods (for example, a dry period), if the inflow reached the lower boundary of the water yield in the power generation operation rule, the underestimation of the inflow when the IFU was considered resulted in a water deficit.
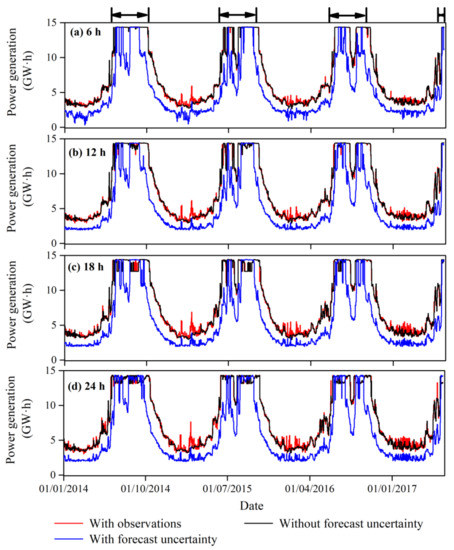
Figure 11.
Temporal series of the power generation capacity that was optimized using the raw and ensemble inflow forecast with 6 h (a), 12 h (b), 18 h (c), and 24 h (d) lead times, which were compared with those derived from observations. The time intervals covered by double-headed arrows represent flood periods.
Furthermore, Figure 12 represents the total electricity curtailment derived from the inflow with and without the consideration of the forecast uncertainty for each of the lead times. The total electricity curtailment was calculated as the deviation of the power generation capacity that was found using the inflow with/without the consideration of the IFU from the power generation that was found using the observations, which can be expressed as , where Eobs, EIFU, and Eraw denote the power generation related to the observed inflow, ensemble inflow forecast, and raw inflow forecast, respectively. The total electricity curtailment related to the ensemble inflow forecast (i.e., with the consideration of the IFU) ranged from 3015.3 to 3113.1 GW·h as a magnitude and from 29 to 33% as a percentage, which were both significantly higher than that related to the raw forecast without the consideration of the IFU (ranging from 61.53 to 124.18 GW·h and from 0.65 to 1%, respectively) during the study period. This was because, in the ensemble forecast, some members in the ensemble largely underestimated the true inflow. In addition, the electricity curtailment percentages related to both with and without the IFU were generally much lower during the entire study period than those during the flood period only. This might have resulted from the fact that large water resources were available and the reservoir stored a lot of water to generate power from during the flood period. Thus, the electricity curtailment risks in the non-flood periods were higher than in the flood periods. Nevertheless, the electricity curtailment with the IFU during the flood period was much larger than that without the IFU for each of the four lead times. Overall, the higher curtailment, with a risk rate up to 41%, might have occurred when considering the IFU, which would severely reduce the power generation capacity and lead to negative effects on the benefits for the hydropower plant.
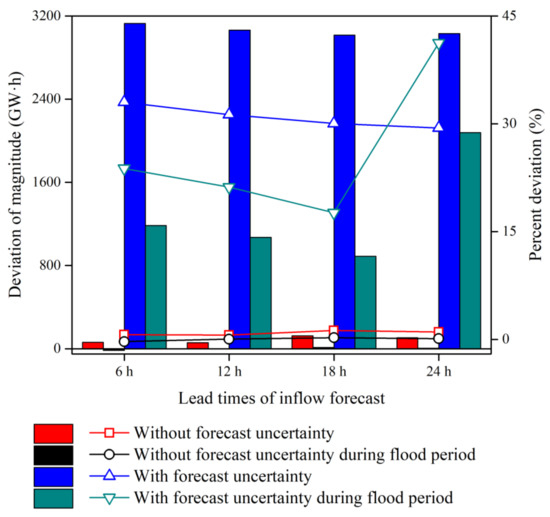
Figure 12.
Total electricity curtailment as a magnitude and a percentage of the ensemble inflow forecast (with the forecast uncertainty considered) and the raw inflow forecast (without the consideration of the forecast uncertainty) over the entire study period and flood period only.
5. Conclusions
To identify the reservoir operation risks that propagate from the IFU, we proposed an integrated statistical framework using the IGMD coupled with the MCMC sampling algorithm to obtain the ensemble inflow forecast, and then assessed the response of the flood and electricity curtailment risks to the ensemble IFU. Taking the forecasted inflow discharge of the Jinping First Stage Hydropower Plant Reservoir, Yalong River, China with four lead times (6 h, 12 h, 18 h, and 24 h) as a case study, the following key conclusions were emphasized:
- (1)
- The IGMD model substantially improved the modeling skill of the measured forecast error characteristics and the IGMD-based MCMC algorithm offers a flexible and attractive tool to obtain robust ensemble inflow forecast.
- (2)
- The IGMD-based ensemble approach displayed a high capability of reproducing the observed inflow to support the subsequent reservoir optimal operation and risk assessment, given the limited ensemble size and computational resources.
- (3)
- There existed no flood risk that was defined via the design flood with 10-year and longer return periods when considering the reservoir IFU for each of the sub-daily forecast lead times. In contrast, the electricity curtailment risk significantly increased up to 41%, especially during the non-flood periods, when taking the IFU into account.
Other aspects also warrant attention for further investigation. Multivariate Gaussian mixture distribution is worth investigating to provide the combined forecast errors over multiple lead times, as they are physically relevant. In addition, the electricity curtailment risk as well as the flood risk is expected to reduce by correcting the forecast errors in the reservoir inflow.
Author Contributions
Q.M. and Y.Z. conceived and designed the experiments; J.Z. analyzed the data; Q.M. and B.X. performed the experiments and wrote the manuscript; C.J. and T.Z. edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Postdoctoral Science Foundation (Grant No.: 2020M680487), Fundamental Research Funds for the Central Universities (Grant Nos.: 2019MS031 and 2020MS026), and the Natural Science Fund of Anhui Province (Grant No.: 2008085ME158).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to acknowledge the Yalong River Hydropower Development Company for the data support. We also thank the anonymous reviewers for their constructive comments that helped improve the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Bobée, B. Daily reservoir inflow forecasting using artificial neural networks with stopped training approach. J. Hydrol. 2000, 230, 244–257. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, R.; Li, A.; Ji, C. Runoff forecast uncertainty considered load adjustment model of cascade hydropower stations and its application. Energy 2018, 158, 693–708. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Z.; Jin, J.; Hu, H. Assessing the impacts of univariate and bivariate flood frequency approaches to flood risk accounting for reservoir operation. Water 2019, 11, 475. [Google Scholar] [CrossRef]
- Lu, Q.; Zhong, P.; Xu, B.; Zhu, F.; Ma, Y.; Wang, H.; Xu, S. Risk analysis for reservoir flood control operation considering two-dimensional uncertainties based on Bayesian network. J. Hydrol. 2020, 589, 125353. [Google Scholar]
- Winsemius, H.C.; Aerts, J.C.J.H.; Van Beek, L.P.H.; Bierkens, M.F.P.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.J.; Ligtvoet, W.; Lucas, P.L.; Van Vuuren, D.P.; et al. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381–385. [Google Scholar] [CrossRef]
- Wasimi, S.A.; Kitanidis, P.K. Real-time forecasting and daily operation of a multireservoir system during floods by linear quadratic Gaussian control. Water Resour. Res. 1983, 19, 1511–1522. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Lu, W.; Zhang, J.; Zhou, J.; Guo, S. Streamflow forecast uncertainty evolution and its effect on real-time reservoir operation. J. Hydrol. 2016, 540, 712–726. [Google Scholar] [CrossRef]
- Smith, J.A.; Day, G.N.; Kane, M.D. Nonparametric framework for long-range streamflow forecasting. J. Water Resour. Plan. Manag. 1992, 118, 82–92. [Google Scholar] [CrossRef]
- Liu, X.; Guo, S.; Li, X.; Li, Y. Flood control operation chart for Three Gorges Reservoir considering errors in inflow forecasting. Adv. Water Sci. 2011, 22, 771–779. [Google Scholar]
- Zhao, T.; Cai, X.; Yang, D. Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv. Water Resour. 2011, 34, 495–504. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Yang, D.; Wang, H. Generalized martingale model of the uncertainty evolution of streamflow forecasts. Adv. Water Resour. 2013, 57, 41–51. [Google Scholar] [CrossRef]
- Li, X.; Guo, S.; Liu, P.; Chen, G. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 2010, 391, 124–132. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Risk analysis for flood control operation of seasonal flood-limited water level incorporating inflow forecasting error. Hydrol. Sci. J. 2014, 59, 1006–1019. [Google Scholar] [CrossRef]
- Li, M.; Wang, Q.; Robertson, D.E.; Bennett, J.C. Improved error modelling for streamflow forecasting at hourly time steps by splitting hydrographs into rising and falling limbs. J. Hydrol. 2017, 555, 586–599. [Google Scholar] [CrossRef]
- Li, M.; Wang, Q.J.; Bennett, J.C.; Robertson, D.E. Error reduction and representation in stages (ERRIS) in hydrological modelling for ensemble streamflow forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 3561–3579. [Google Scholar] [CrossRef]
- Ji, C.; Liang, X.; Zhang, Y.; Liu, Y. Stochastic model of reservoir runoff forecast errors and its application. J. Hydroelectr. Eng. 2019, 38, 75–85. [Google Scholar]
- Krzysztofowicz, R. The case for probabilistic forecasting in hydrology. J. Hydrol. 2001, 249, 2–9. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Fang, H.; Lai, R.; Zhang, Y.; Huang, L.; Liu, X. A real-time probabilistic channel flood-forecasting model based on the Bayesian particle filter approach. Environ. Model. Softw. 2017, 88, 151–167. [Google Scholar] [CrossRef]
- Ma, C.; Cui, X. Rolling forecast for reservoir monthly average flows and its uncertainty. J. Hydroelectr. Eng. 2018, 37, 59–67. [Google Scholar]
- Bourdin, D.R.; Stull, R.B. Bias-corrected short-range Member-to-Member ensemble forecasts of reservoir inflow. J. Hydrol. 2013, 502, 77–88. [Google Scholar] [CrossRef]
- Gournelos, T.; Kotinas, V.; Poulos, S. Fitting a Gaussian mixture model to bivariate distributions of monthly river flows and suspended sediments. J. Hydrol. 2020, 590, 125166. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Liu, D.; Hu, T.; Xu, C.-Y. Frequency analysis of nonstationary annual maximum flood series using the time-varying two-component mixture distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Pan, L.; Li, Y.; He, K.; Li, Y.; Li, Y. Generalized linear mixed models with Gaussian mixture random effects: Inference and application. J. Multivar. Anal. 2020, 175, 104555. [Google Scholar]
- Zhuang, X.; Huang, Y.; Palaniappan, K.; Zhao, Y. Gaussian mixture density modeling, decomposition, and applications. IEEE Trans. Image Process. 1996, 5, 1293–1302. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E. Understanding the Metropolis-Hastings Algorithm. Am. Stat. 1995, 49, 327. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Wang, Y.; Gao, X.; Yu, C. Bayesian forecasting and uncertainty quantifying of stream flows using Metropolis–Hastings Markov Chain Monte Carlo algorithm. J. Hydrol. 2017, 549, 476–483. [Google Scholar]
- Ma, Q.; Xiong, L.; Liu, D.; Xu, C.-Y.; Guo, S. Evaluating the temporal dynamics of uncertainty contribution from satellite precipitation input in rainfall-runoff modeling using the variance decomposition method. Remote Sens. 2018, 10, 1876. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation/Indices pour évaluer les bornes de prévision de modèles hydrologiques et mise en œuvre pour une estimation d’incertitude par vraisemblance généralisée. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar]
- Li, B.; Liang, Z.; Zhang, J.; Chen, X.; Jiang, X.; Wang, J.; Hu, Y. Risk analysis of reservoir flood routing calculation based on inflow forecast uncertainty. Water 2016, 8, 486. [Google Scholar] [CrossRef]
- Liu, Z.; Lyu, J.; Jia, Z.; Wang, L.-X.; Xu, B. Risks analysis and response of forecast-based operation for Ankang Reservoir flood control. Water 2019, 11, 1134. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.; Cai, X.; Zhou, Y.; Wang, X. Improved dynamic programming for parallel reservoir system operation optimization. Adv. Water Resour. 2019, 131, 103373. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Chen, K.; Deng, L.; Liao, Z.; Xiong, F.; Yin, J. Optimal impoundment operation for cascade reservoirs coupling parallel dynamic programming with importance sampling and successive approximation. Adv. Water Resour. 2019, 131, 103375. [Google Scholar] [CrossRef]
- Wu, S.; Shen, M.; Wang, J. Jinping hydropower project: Main technical issues on engineering geology and rock mechanics. Bull. Eng. Geol. Environ. 2010, 69, 325–332. [Google Scholar]
- Li, M.; Wang, Q.J.; Bennett, J.C.; Robertson, D.E. A strategy to overcome adverse effects of autoregressive updating of streamflow forecasts. Hydrol. Earth Syst. Sci. 2015, 19, 1. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).