Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison
Abstract
1. Introduction
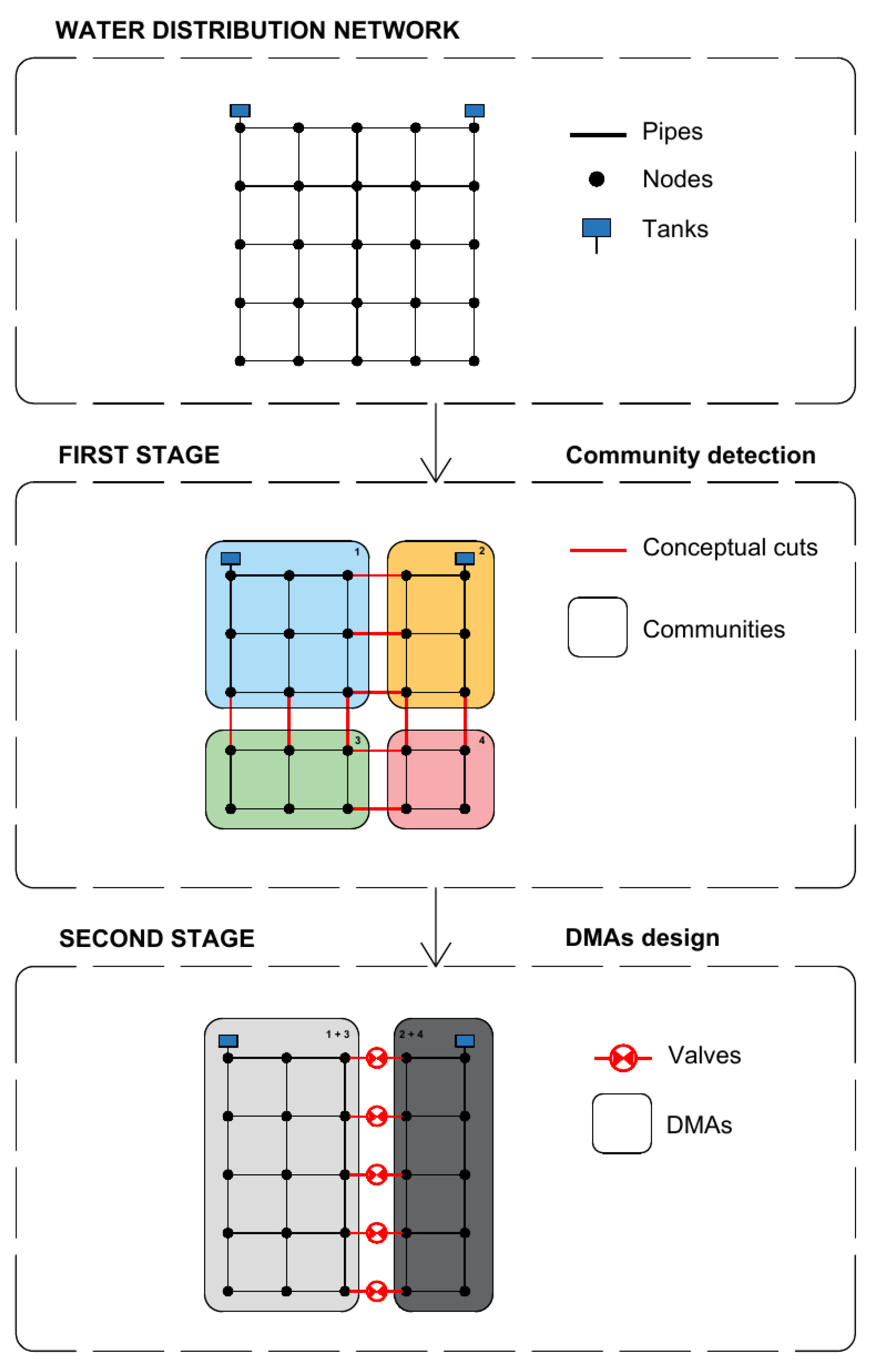
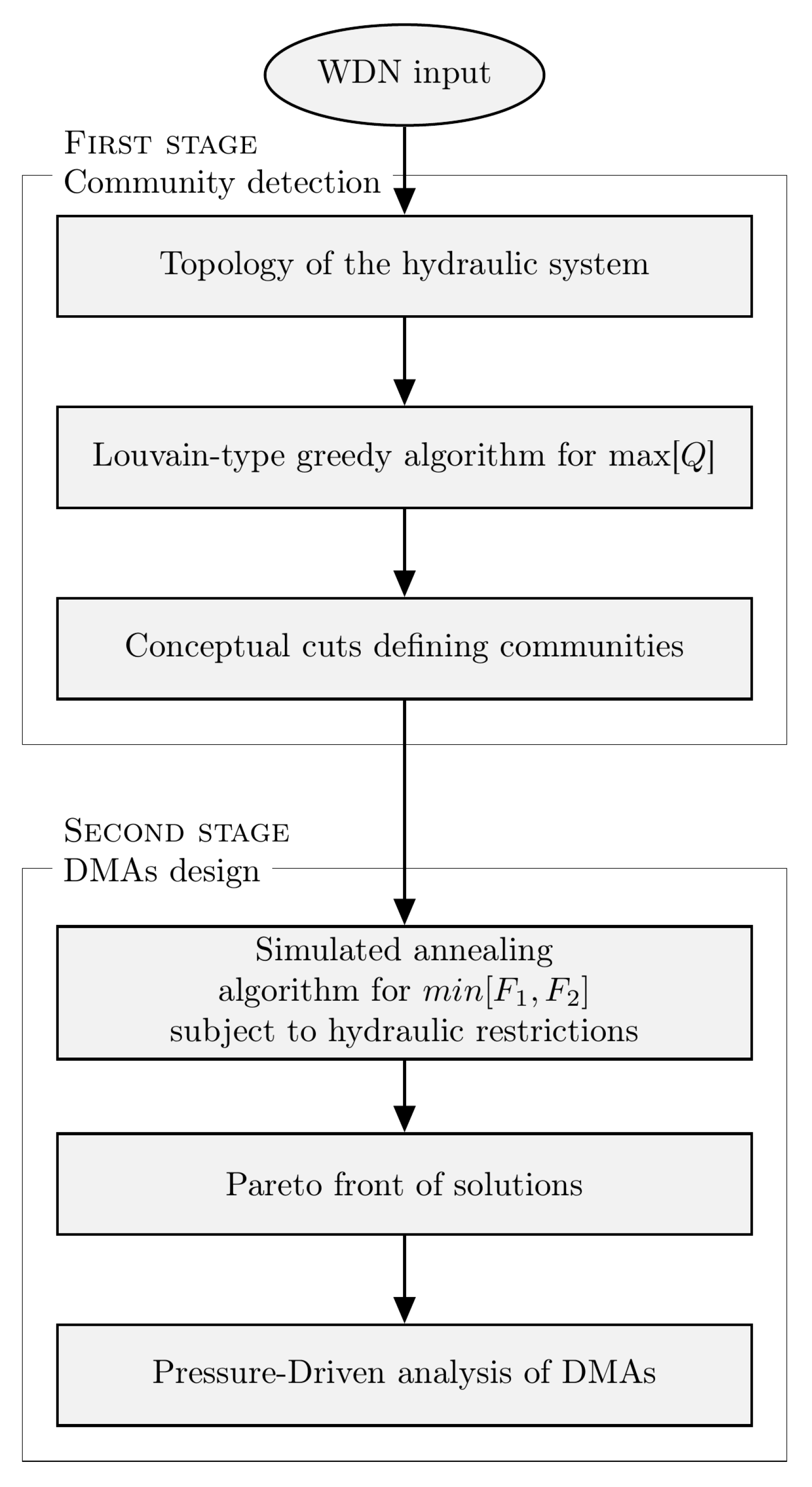
2. Methodology
2.1. First Stage: Clustering of the System
2.2. Second Stage: Physical Dividing of the System
2.3. Simulated Annealing
2.4. Case Studies
3. Results
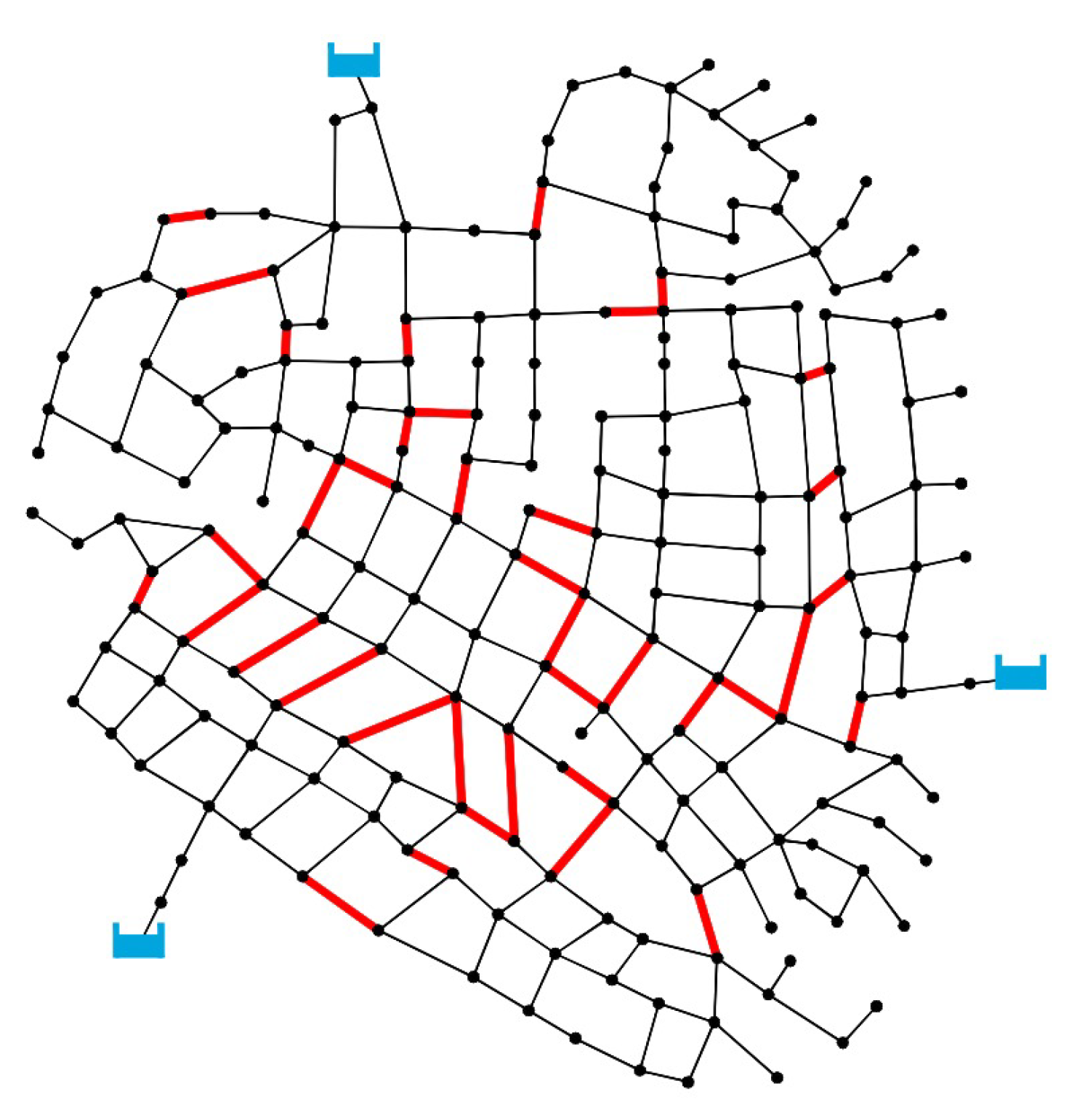
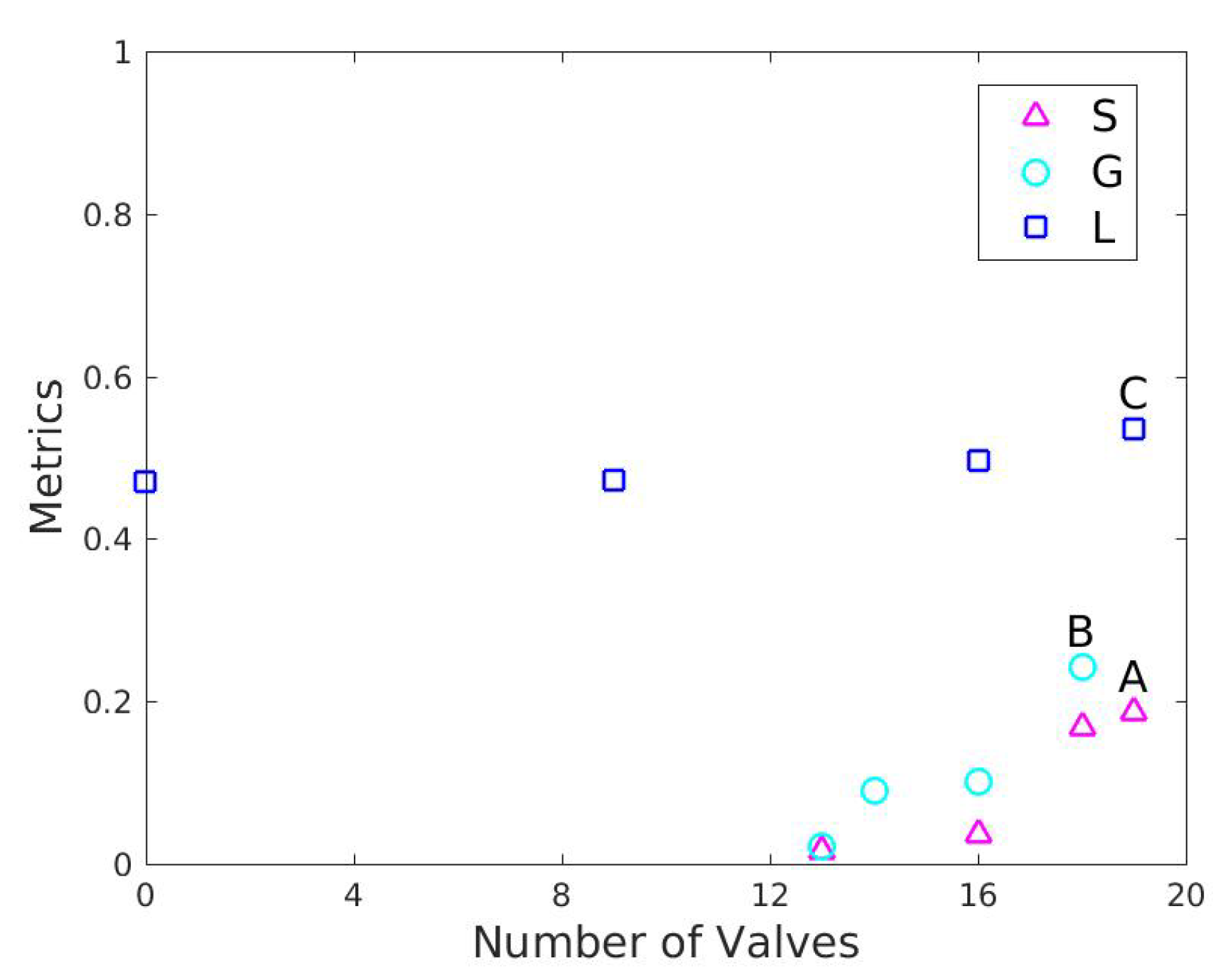
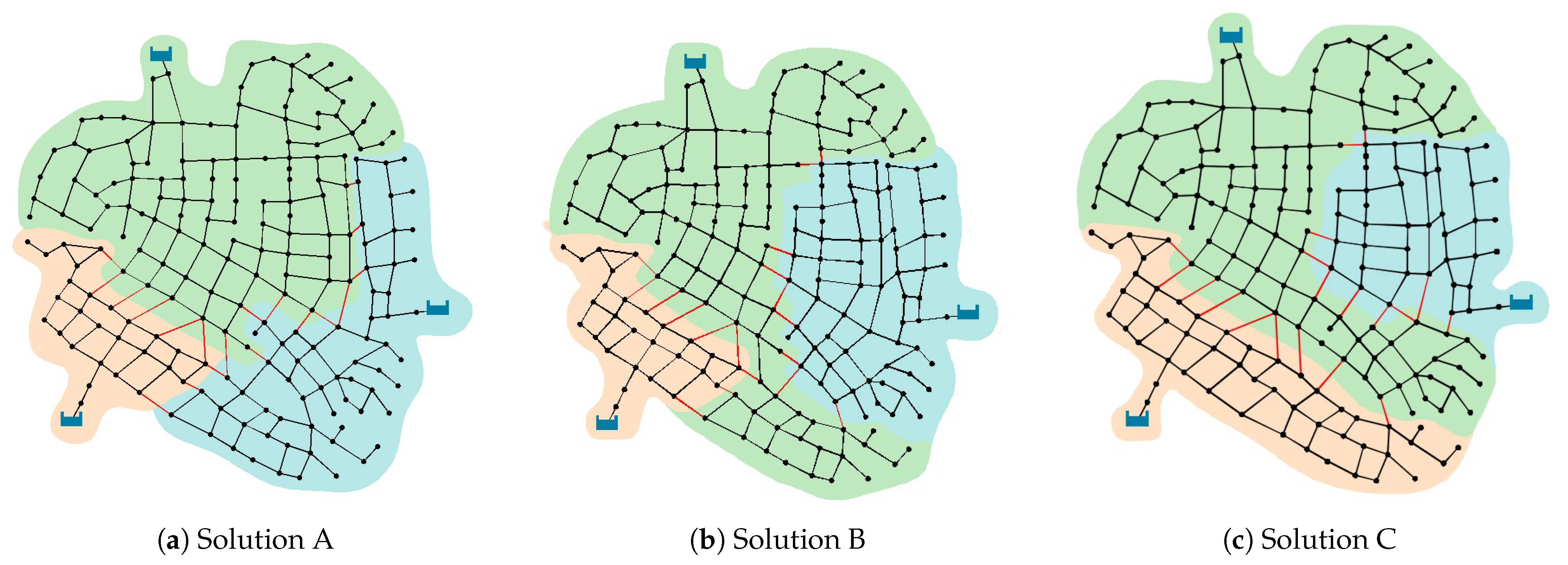
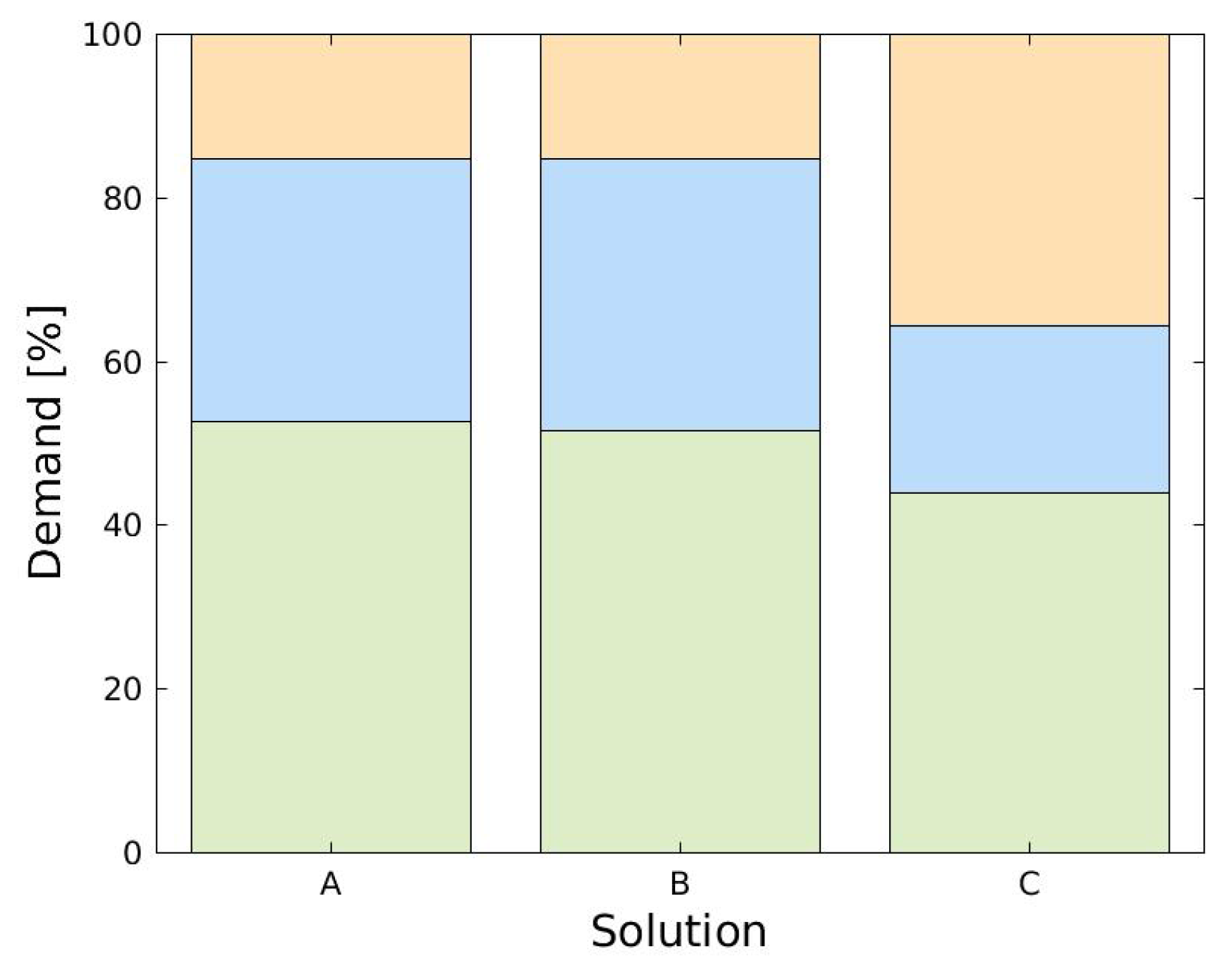
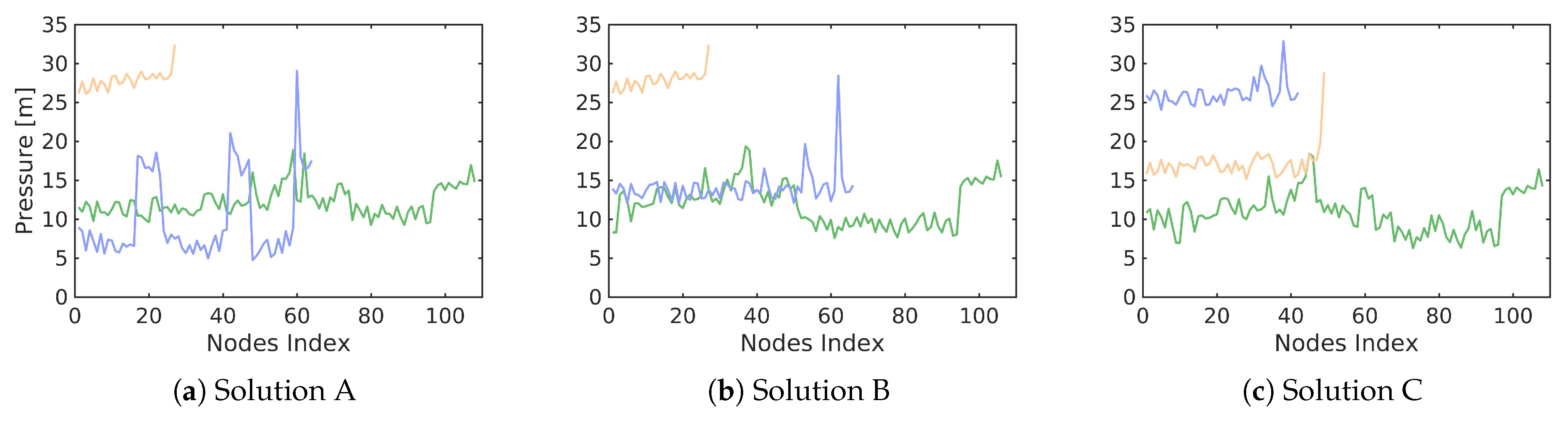
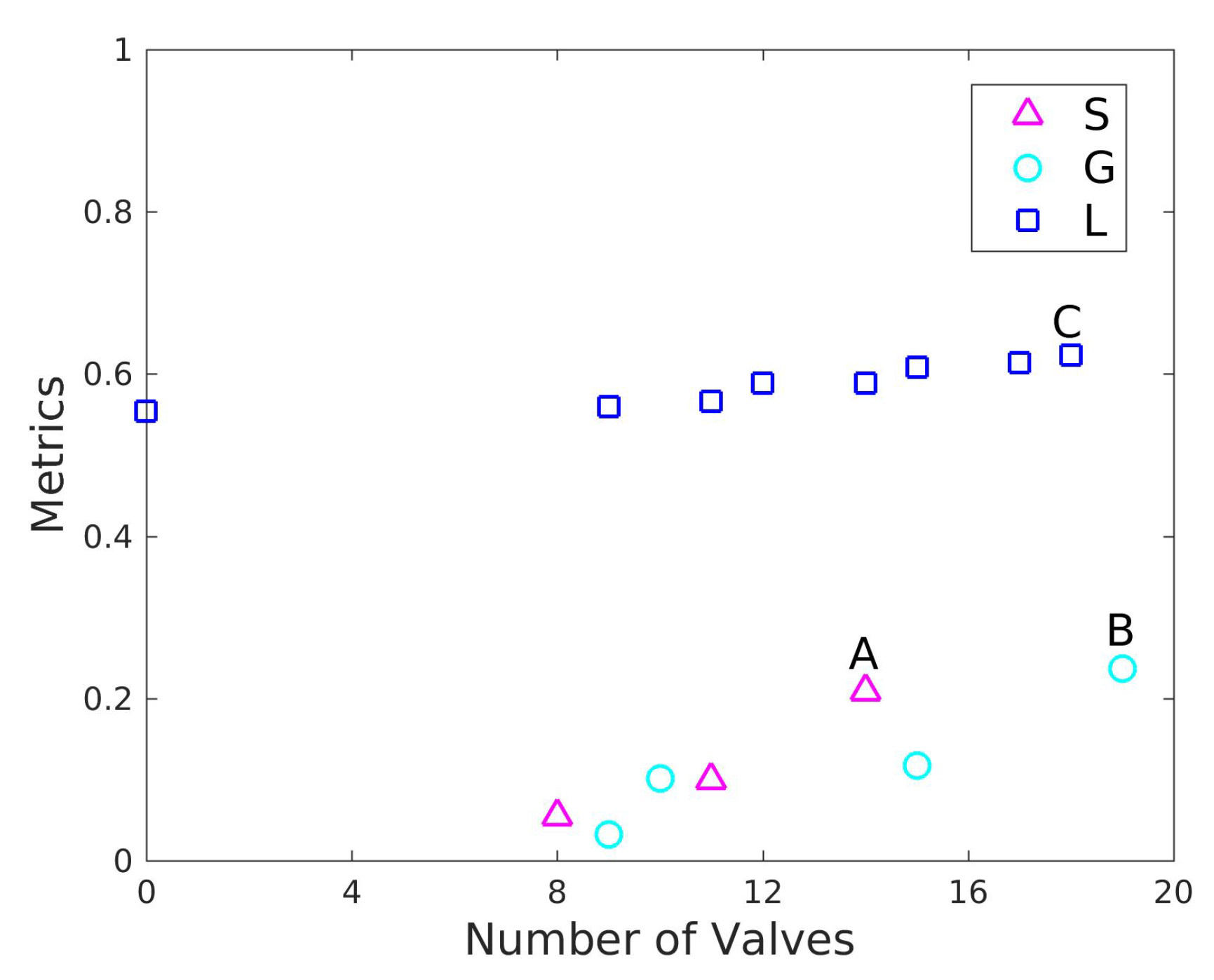
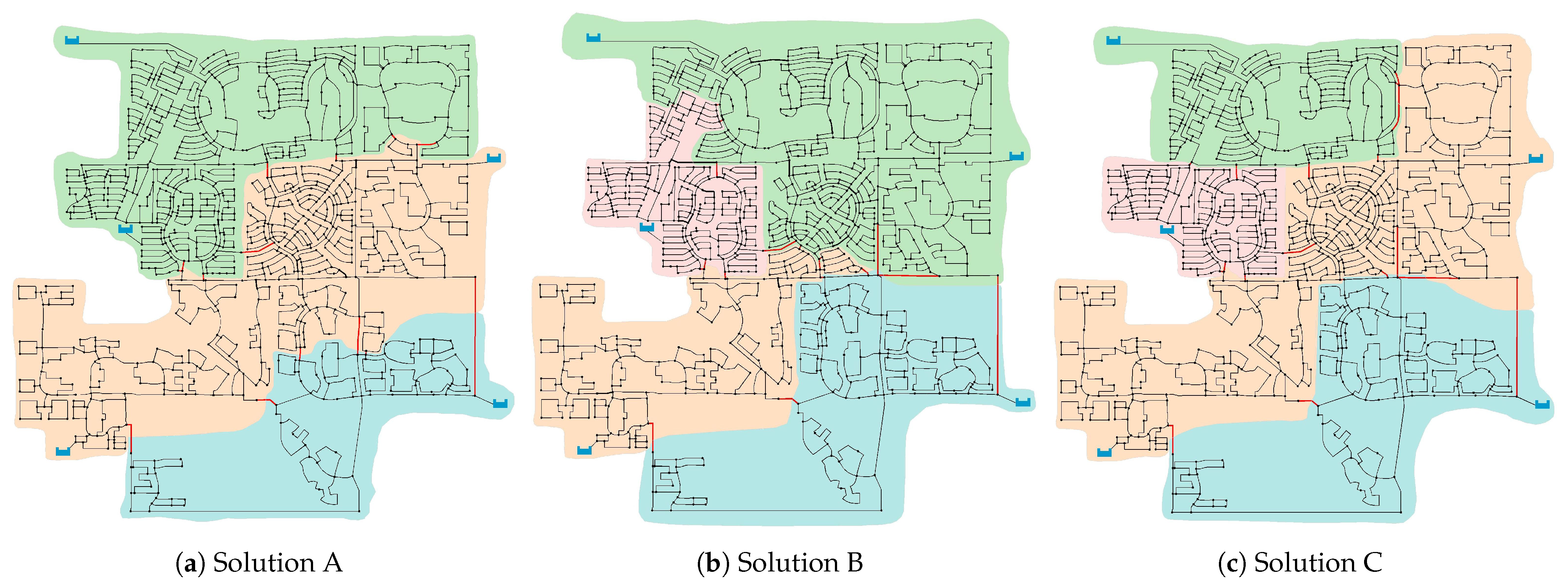
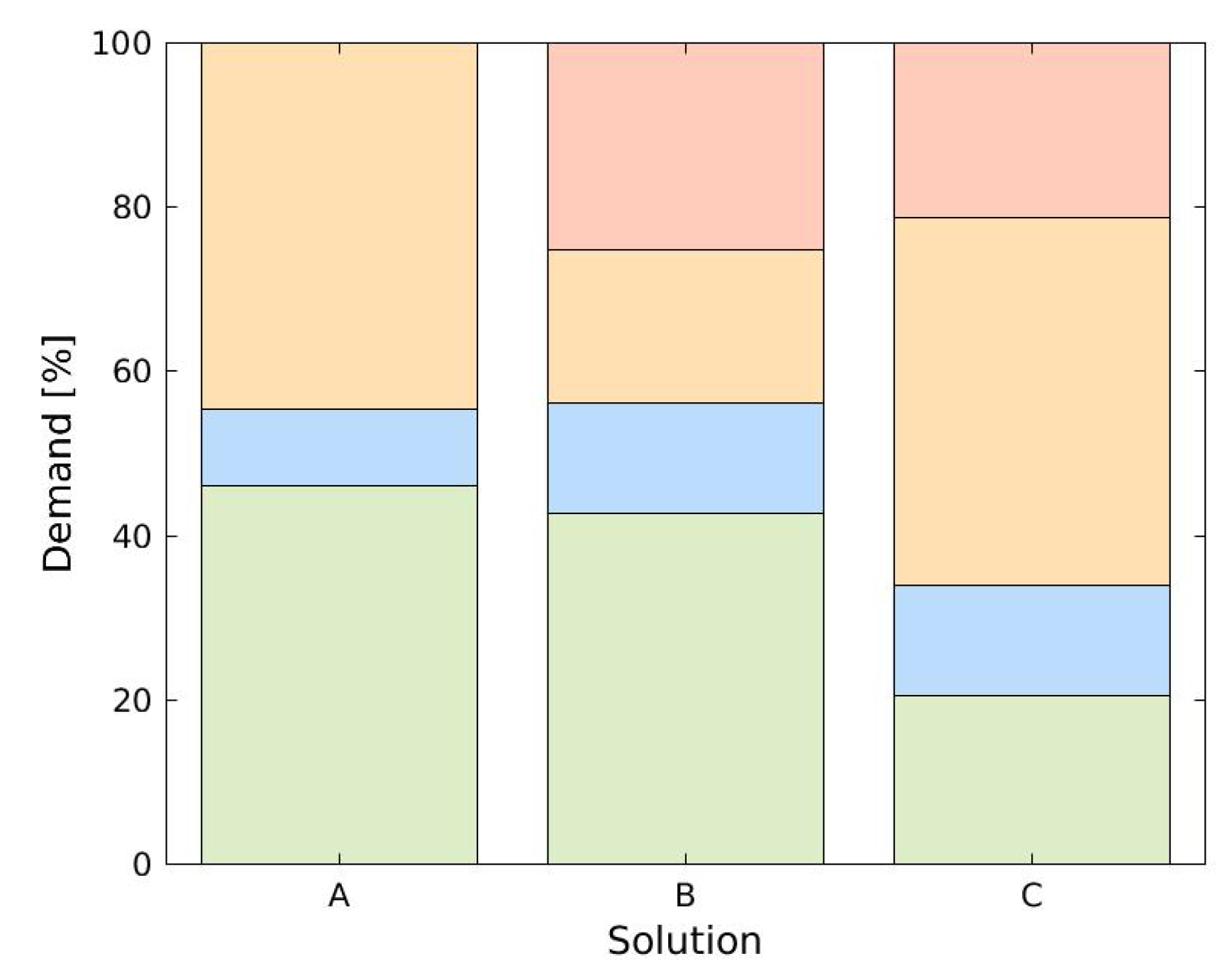
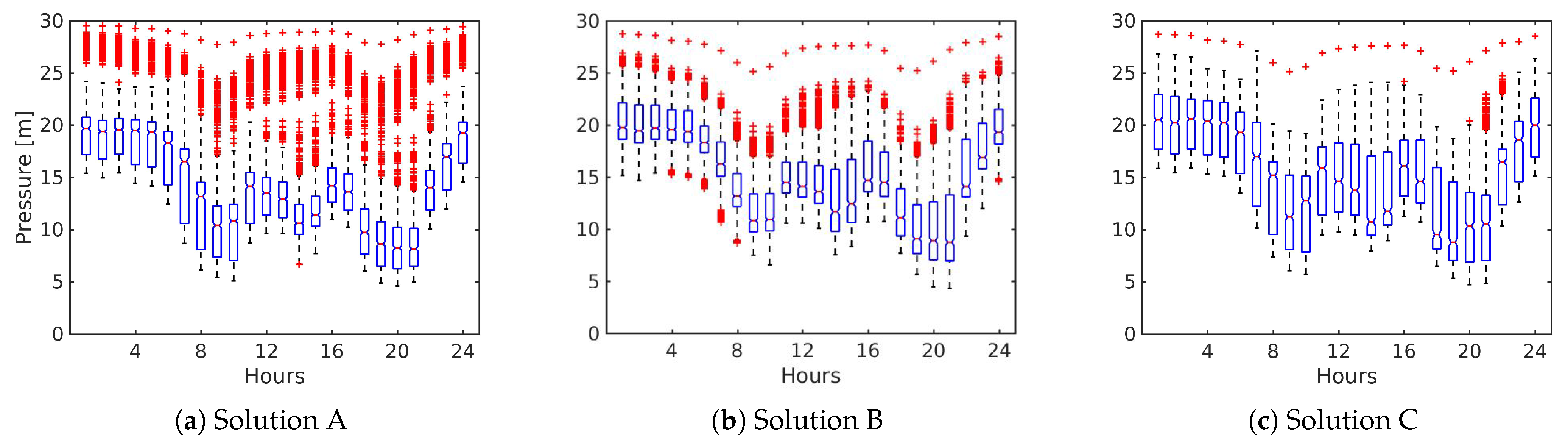
3.1. Case Study 1: Three-Reservoir Water Network (TRN)
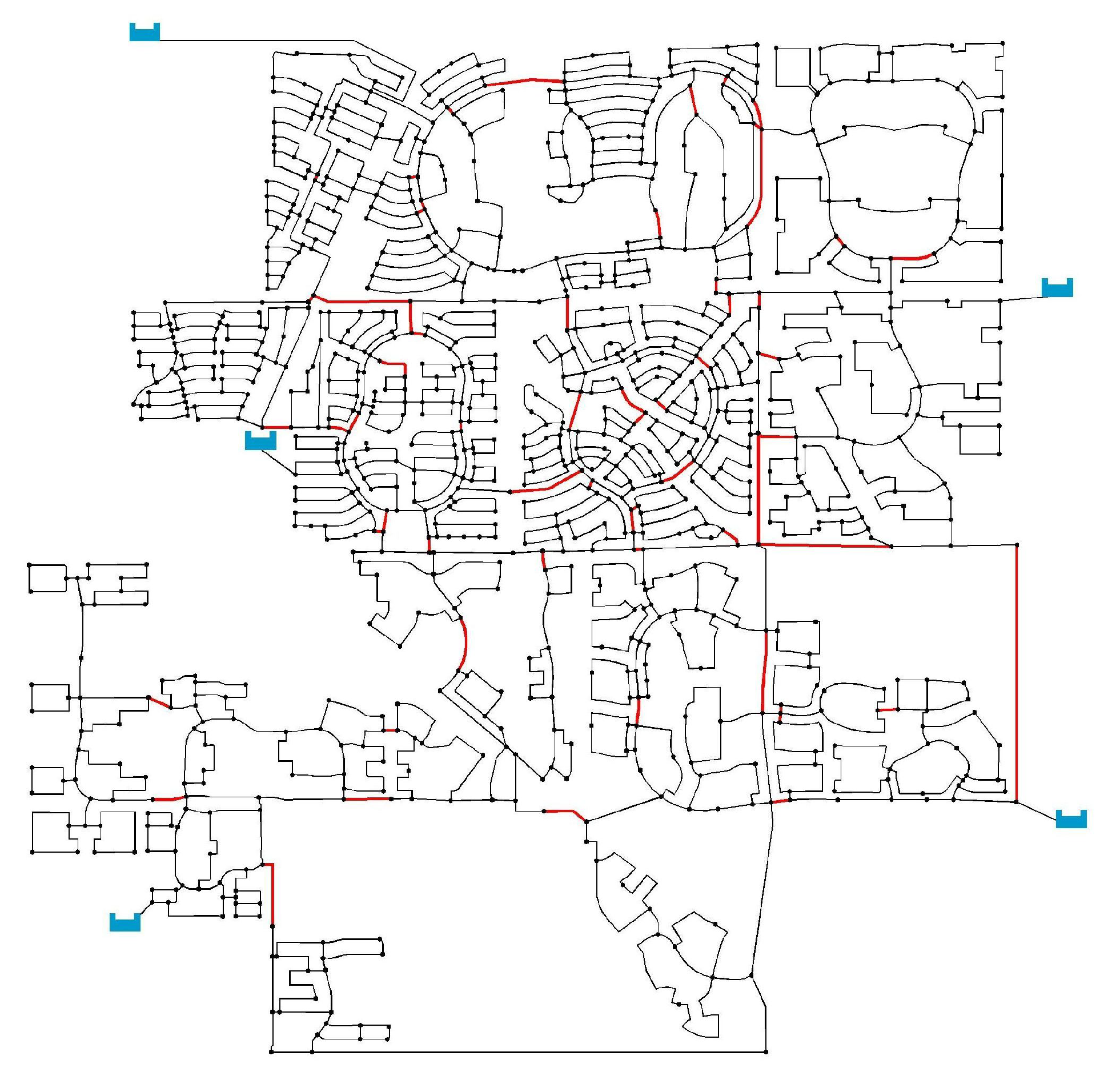
3.2. Case Study 2: Five-Reservoir Water Network (MLN)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bui, X.K.; Marlim, M.S.; Kang, D. Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review. Water 2020, 12, 1002. [Google Scholar]
- Hajebi, S.; Roshani, E.; Cardozo, N.; Barrett, S.; Clarke, A.; Clarke, S. Water distribution network sectorisation using graph theory and many-objective optimisation. J. Hydroinform. 2015, 18, 77–95. [Google Scholar] [CrossRef]
- Chatzivasili, S.; Papadimitriou, K.; Kanakoudis, V. Optimizing the Formation of DMAs in a Water Distribution Network through Advanced Modelling. Water 2019, 11, 278. [Google Scholar] [CrossRef]
- DiNardo, A.; DiNatale, M. A heuristic design methodology based on graph theory for district metering of water supply networks. Procedia Eng. 2011, 43, 193–211. [Google Scholar]
- Di-Nardo, A.; Di-Natale, M.; Santonastaso, G.F.; Venticinque, S. An automated tool for smart water network partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- DiNardo, A.; DiNatale, M.; Santonastaso, G.; Tzatchkov, V.; Yamanaka, V. Divide and conquer partitioning technoques for smart water netwoks. Procedia Eng. 2014, 89, 1176–1183. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. A heuristic procedure for the automatic creation of district metered areas in water distribution systems. Urban Water J. 2014, 11, 137–159. [Google Scholar] [CrossRef]
- Scarpa, F.; Lobba, A.; Becciu, G. Elementary DMA Design of Looped Water Distribution Networks with Multiple Sources. J. Water Resour. Plan. Manag. 2016, 142, 04016011. [Google Scholar] [CrossRef]
- Zevnik, J.; Kramar-Fijavž, M.; Kozelj, D. Generalized Normalized Cut and Spanning Trees for Water Distribution Network Partitioning. J. Water Resour. Plan. Manag. 2019, 145, 04019041. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A practical multi-objective optimization sectorization method for water distribution network. Sci. Total. Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef]
- Scibetta, M.; Boano, F.; Revelli, R.; Ridolfi, L. Community detection as a tool for district metered areas identification. Procedia Eng. 2014, 70, 1518–1523. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L. New Modularity-Based Approach to Segmentation of Water Distribution Networks. J. Hydraul. 2014, 140, 1–14. [Google Scholar] [CrossRef]
- Campbell, E.; Ayala-Cabrera, D.; Izquierdo, J.; Perez-García, R.; Tavera, M. Warer supply network sectorizarion based on social networks community detection algorithms. Procedia Eng. 2014, 89, 1208–1215. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L.; Berardi, L. General metrics for segmenting infrastructure networks. J. Hydroinform. 2015, 17, 505–517. [Google Scholar] [CrossRef]
- Castro-Gama, M.; Pan, Q.; Jonoski, A.; Solomatine, D. A graph theorical sectorization approach for energy reduction in water distribution networks. Procedia Eng. 2016, 154, 19–26. [Google Scholar] [CrossRef][Green Version]
- Laucelli, D.B.; Simone, A.; Berardi, L.; Giustolisi, O. Optimal Design of District Metering Areas. Procedia Eng. 2016, 162, 403–410. [Google Scholar] [CrossRef][Green Version]
- Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J. Automatic partitioning of water distribution networks using multiscale community detection and multiobjective optimization. J. Water Resour. Plan. Manag. 2017, 149, 04017057. [Google Scholar] [CrossRef]
- Di-Nardo, A.; Di-Natale, M.; Di-Mauro, A.; Martinez-Díaz, E.; Blazquez-García, J.; Santonastaso, G.; Tuccinardi, F. An advanced software to design automatically permanent partitioning of a water distribution network. Urban Water J. 2020, 17, 259–265. [Google Scholar] [CrossRef]
- Herrera, M.; Izquierdo, J.; Perez-García, R.; Ayala-Cabrera, D. Water Supply Clusters by Multi-Agent Based Approach. In Proceedings of the Water Distribution System Analysis 2010–WDSA2010, Tucson, AZ, USA, 12–15 September 2010; pp. 861–869. [Google Scholar]
- Liu, H.; Zhao, M.; Zhang, C.; Fu, G. Comparing Topological Partitioning Methods for District Metered Areas in the Water Distribution Network. Water 2018, 10, 368. [Google Scholar] [CrossRef]
- Perelman, L.S.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated sub-zoning of water distribution systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef]
- Di-Nardo, A.; Di-Natale, M.; Santonastaso, G.F.; Venticinque, S. Graph partitioning for automatic sectorization of a water distribution system. In Proceedings of the Computer and Control in Water Industry CCWI, Exeter, UK, 5–7 September 2011; pp. 841–846. [Google Scholar]
- Vasilic, Z.; Stanic, M.; Kapelan, Z.; Prodanovic, D.; Babic, B. Uniformity and Heuristics-Based DeNSE Method for Sectorization of Water Distribution Networks. J. Water Resour. Plan. Manag. 2020, 146, 04019079. [Google Scholar] [CrossRef]
- Shao, Y.; Yao, H.; Zhang, T.; Chu, S.; Liu, X. An Improved Genetic Algorithm for Optimal Layout of Flow Meters and Valves in Water Network Partitioning. Water 2019, 11, 1087. [Google Scholar] [CrossRef]
- Creaco, E.; Cunha, M.; Franchini, M. Using heuristic techniques to account for engineering aspects in modularity-based water distribution network partitioning algorithm. J. Water Resour. Plan. Manag. 2019, 145, 04019062. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di-Nardo, A.; Carravetta, A.; Ramos, H.M.; Adeyeye, K. Zero-net energy management for the monitoring and control of dynamically-partitioned smart water systems. J. Clean. Prod. 2020, 252, 119745. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di-Nardo, A.; Adeyeye, K. Automatic multiscale approach for water networks partitioning into dynamic district metered areas. Water Resour. Manag. 2020, 34, 835–848. [Google Scholar] [CrossRef]
- Rahmani, F.; Muhammed, K.; Behzadian, K.; Farmani, R. Optimal Operation of Water Distribution Systems Using a Graph Theory-Based Configuration of District Metered Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018042. [Google Scholar] [CrossRef]
- Saldarriaga, J.; Bohorquez, J.; Celeita, D.; Vega, L.; Paez, D.; Savic, D.; Dandy, G.; Filion, Y.; Grayman, W.; Kapelan, Z. Battle of the Water Networks District Metered Areas. J. Water Resour. Plan. Manag. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in netwoks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theor. Exper. 2008, 10, P10008. [Google Scholar] [CrossRef]
- Jeub, L.; Bazziand, M.; Jutla, I.; Mucha, P. A Generalized Louvain Method for Community Detection Implemented in MATLAB. 2011–2019. Available online: https://github.com/GenLouvain/GenLouvain (accessed on 18 November 2019).
- Reichardt, J.; Bornholdt, S. Detecting Fuzzy Community Structures in Complex Networks with a Potts Model. Phys. Rev. Lett. 2004, 93, 218701. [Google Scholar] [CrossRef] [PubMed]
- Gomes, R.; Marques, A.; Sousa, J. identification of the optimal entry points at District Metered Areas and implementation of pressure management. Urban Water J. 2012, 9, 365–384. [Google Scholar] [CrossRef]
- Castro-Gama, M.; Pan, Q.; Jonoski, A.; Chiesa, C. Model-Based Sectorization of Water Distribution Networks For Increased Energy Efficiency. In Proceedings of the HIC2014, New York, NY, USA, 17–21 August 2014. Paper 233. [Google Scholar]
- Castro-Gama, M.; Popescu, I.; Jonoski, A.; Pan, Q. Towards increased water and energy efficiencies in water distribution systems. Environ. Eng. Manag. J. 2015, 14, 1271–1278. [Google Scholar]
- Castro-Gama, M.; Lanfranchi, E.; Pan, Q.; Jonoski, A. Water distribution network model building, case study: Milano, Italy. Procedia Eng. 2015, 119, 573–582. [Google Scholar]
- Zheng, F.; Zecchin, A. An efficient decomposition and dual-stage multi-objective optimization method for water distribution systems with multiple supply sources. Environ. Model. Softw. 2014, 55, 143–155. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Revisiting Optimal Water-Distribution System Design: Issues and a Heuristic Hierarchical Approach. J. Water Resour. Plan. Manag. 2012, 138, 208–217. [Google Scholar] [CrossRef]
- Alireza, Y.; Paul, J. Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 016111. [Google Scholar] [CrossRef]
- Todini, E.; Pilati, S. A gradient algorithm for the analysis of pipe networks. In Computer Application in Water Supply, System Analysis and Simulation; John Wiley: London, UK, 1988; Volume I, pp. 1–20. [Google Scholar]
- Porter, M.A.; Onnela, J.; Mucha, P.J. Communities in Networks. Not. AMS 2009, 56, 1082–1097. [Google Scholar]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Brandes, U.; Delling, D.; Gaertler, M.; Gorke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On finding graph clusterings with maximum modularity. In Graph-Theoretic Concepts in Computer Science, WG 2007. Lecture Notes in Computer Science; Springer: Berlin, Germany, 2007; Volume 4769, pp. 121–132. [Google Scholar]
- Todini, E. Looped water distribution netowrks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.; Kapelan, Z. Pressure-Driven Demand and Leakage Simulation for Water Distribution Networks. J. Hydraul. Eng. 2008, 134, 626–635. [Google Scholar] [CrossRef]
- Wagner, J.; Shamir, U.; Marks, D. Water distributions system reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Schneider, J.J.; Kirkpatrick, S. Stochastic Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Suppapitnarm, A.; Seffen, K.; Parks, G.; Clarkson, P. Simulated annealing: An alternative approach to true multiobjective optimization. Eng. Optim. 2000, 33, 59–85. [Google Scholar] [CrossRef]
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 19 | 0.597 | 0.249 | 0.187 | 4.7 | 161 | 32.4 | 199 |
| 3 | 18 | 0.514 | 0.208 | 0.168 | 9.3 | 118 | 32.6 | 173 |
| 2 | 16 | 0.510 | 0.026 | 0.037 | 9.3 | 118 | 31.8 | 173 |
| 3 | 13 | 0.547 | 0.021 | 0.016 | 7.4 | 136 | 28.4 | 173 |
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 18 | 0.555 | 0.242 | 0.182 | 7.6 | 118 | 32.5 | 199 |
| 3 | 16 | 0.499 | 0.100 | 0.075 | 12.0 | 5 | 28.9 | 199 |
| 2 | 14 | 0.496 | 0.090 | 0.128 | 13.5 | 5 | 28.9 | 173 |
| 3 | 13 | 0.548 | 0.022 | 0.016 | 7.4 | 136 | 28.4 | 173 |
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 19 | 0.535 | 0.221 | 0.177 | 6.2 | 118 | 32.9 | 173 |
| 3 | 16 | 0.496 | 0.139 | 0.104 | 12.0 | 5 | 30.0 | 199 |
| 2 | 9 | 0.471 | 0.241 | 0.340 | 15.2 | 136 | 29.8 | 173 |
| 0 | 0 | 0.470 | - | - | 15.1 | 118 | 29.7 | 173 |
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 14 | 0.708 | 0.245 | 0.208 | 4.6 | 846 | 29.5 | 700 |
| 2 | 11 | 0.658 | 0.070 | 0.099 | 5.2 | 303 | 29.0 | 932 |
| 2 | 8 | 0.589 | 0.039 | 0.055 | 5.1 | 627 | 26.6 | 700 |
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 4 | 19 | 0.666 | 0.237 | 0.128 | 4.3 | 362 | 28.7 | 700 |
| 3 | 15 | 0.650 | 0.117 | 0.088 | 4.3 | 362 | 28.4 | 700 |
| 2 | 10 | 0.580 | 0.101 | 0.143 | 7.3 | 289 | 26.3 | 700 |
| 2 | 9 | 0.644 | 0.032 | 0.046 | 4.9 | 535 | 28.0 | 700 |
| DMAs | N° Valves | L | G | S | Node Index | Node Index | ||
|---|---|---|---|---|---|---|---|---|
| 4 | 18 | 0.685 | 0.238 | 0.137 | 4.7 | 535 | 28.7 | 700 |
| 4 | 17 | 0.615 | 0.121 | 0.078 | 6.1 | 159 | 27.7 | 700 |
| 3 | 15 | 0.609 | 0.135 | 0.106 | 6.6 | 502 | 27.7 | 700 |
| 3 | 14 | 0.591 | 0.160 | 0.121 | 6.0 | 159 | 26.8 | 700 |
| 2 | 12 | 0.589 | 0.151 | 0.214 | 6.9 | 159 | 26.8 | 700 |
| 3 | 11 | 0.566 | 0.251 | 0.215 | 6.0 | 159 | 26.2 | 700 |
| 2 | 9 | 0.560 | 0.082 | 0.116 | 9.6 | 159 | 26.2 | 700 |
| 0 | 0 | 0.555 | - | - | 10.9 | 303 | 26.2 | 700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchotti, J.D.; Denardi, M.; Castro-Gama, M.; Puccini, G.D. Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison. Water 2021, 13, 131. https://doi.org/10.3390/w13020131
Bianchotti JD, Denardi M, Castro-Gama M, Puccini GD. Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison. Water. 2021; 13(2):131. https://doi.org/10.3390/w13020131
Chicago/Turabian StyleBianchotti, Jezabel D., Melina Denardi, Mario Castro-Gama, and Gabriel D. Puccini. 2021. "Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison" Water 13, no. 2: 131. https://doi.org/10.3390/w13020131
APA StyleBianchotti, J. D., Denardi, M., Castro-Gama, M., & Puccini, G. D. (2021). Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison. Water, 13(2), 131. https://doi.org/10.3390/w13020131






