A Robust Neutrosophic Modeling and Optimization Approach for Integrated Energy-Food-Water Security Nexus Management under Uncertainty
Abstract
1. Introduction
2. Literature Review
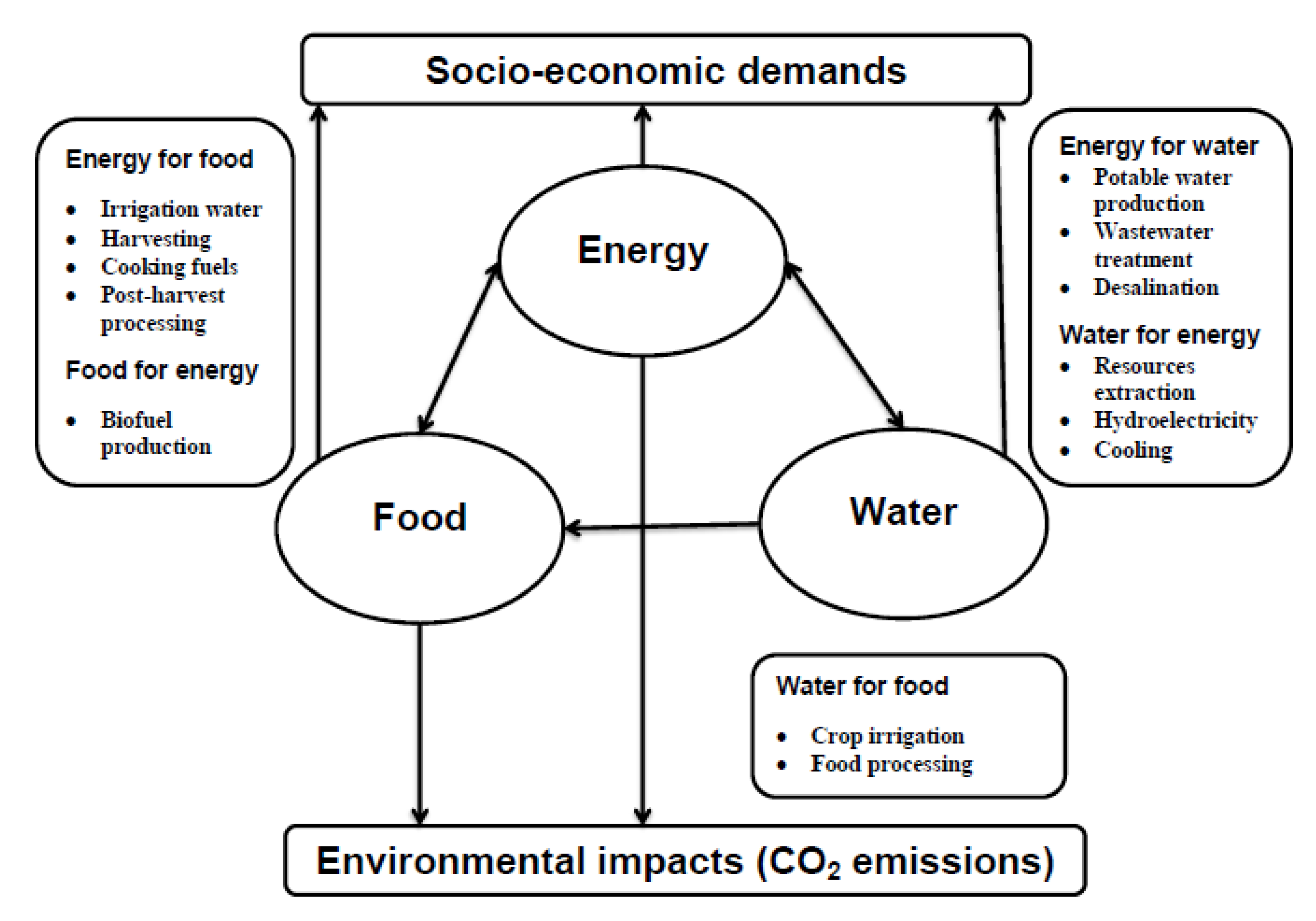
3. Development of Energy-Food-Water Security Nexus Model
3.1. Objective Functions
3.2. Constraints
3.2.1. Proposed Interative Neutrosophic Programming Approach (INPA)
4. Model Implementation
4.1. Evaluations of Solution Results
4.1.1. Optimal Objectives Values
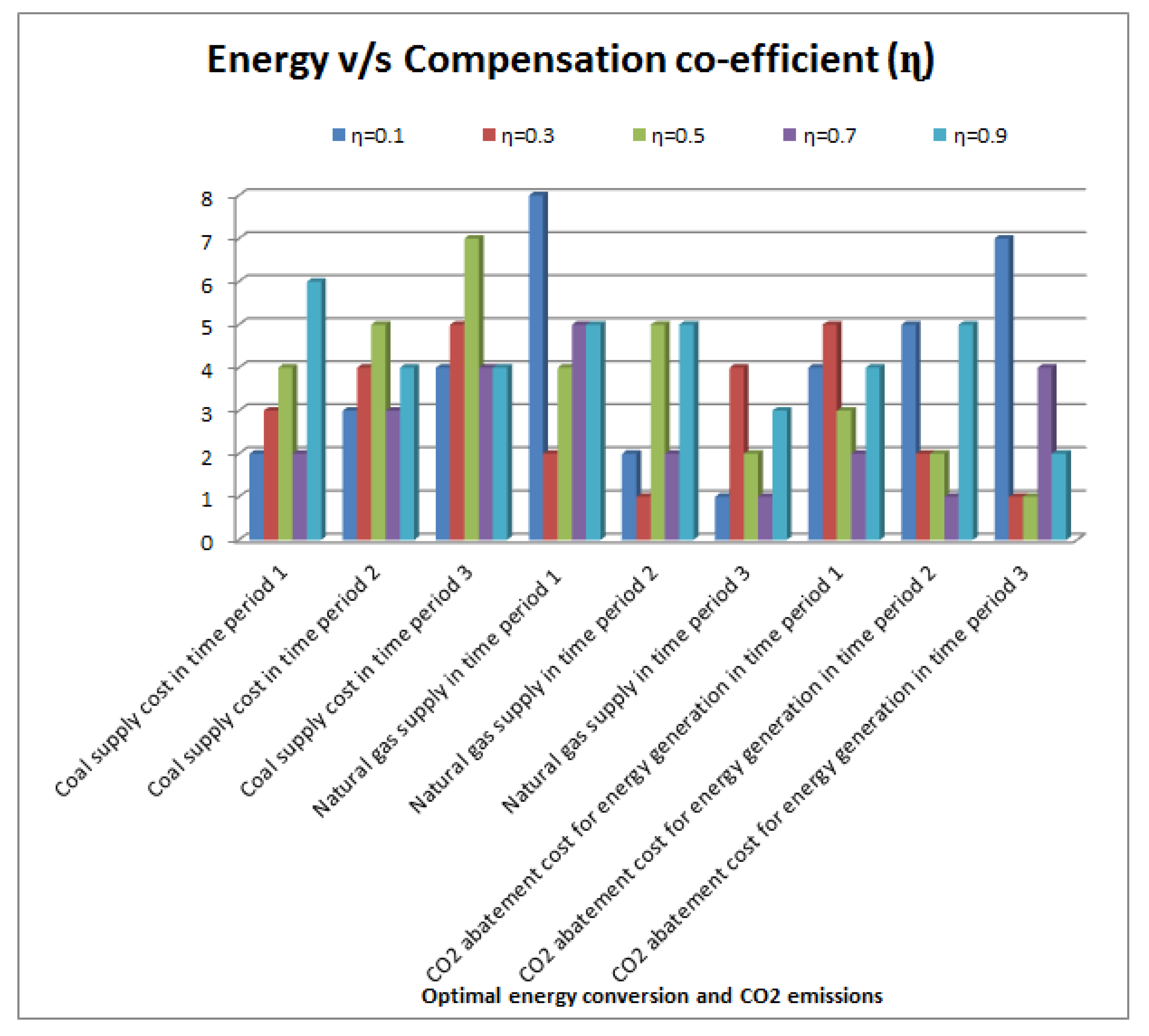
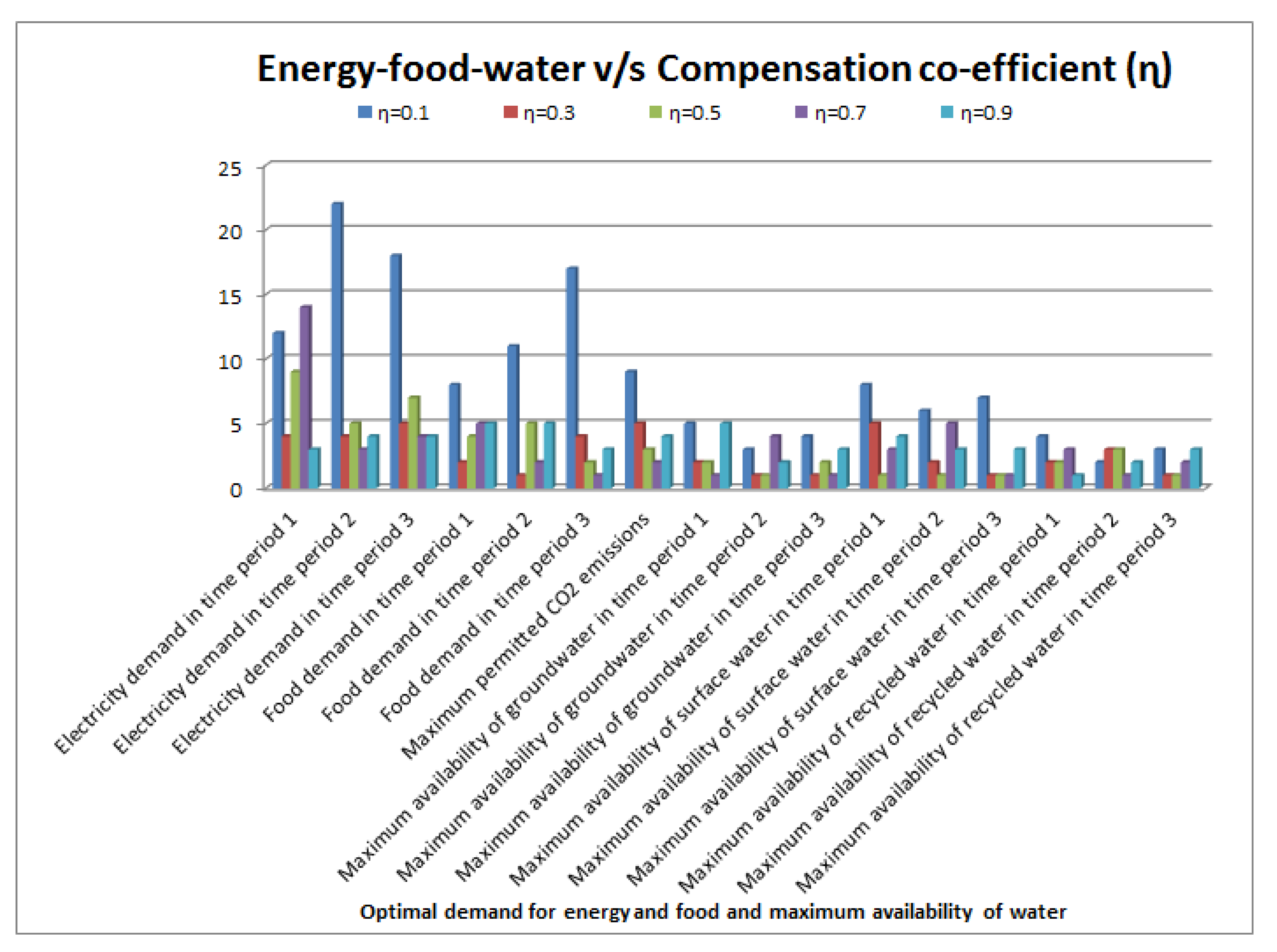
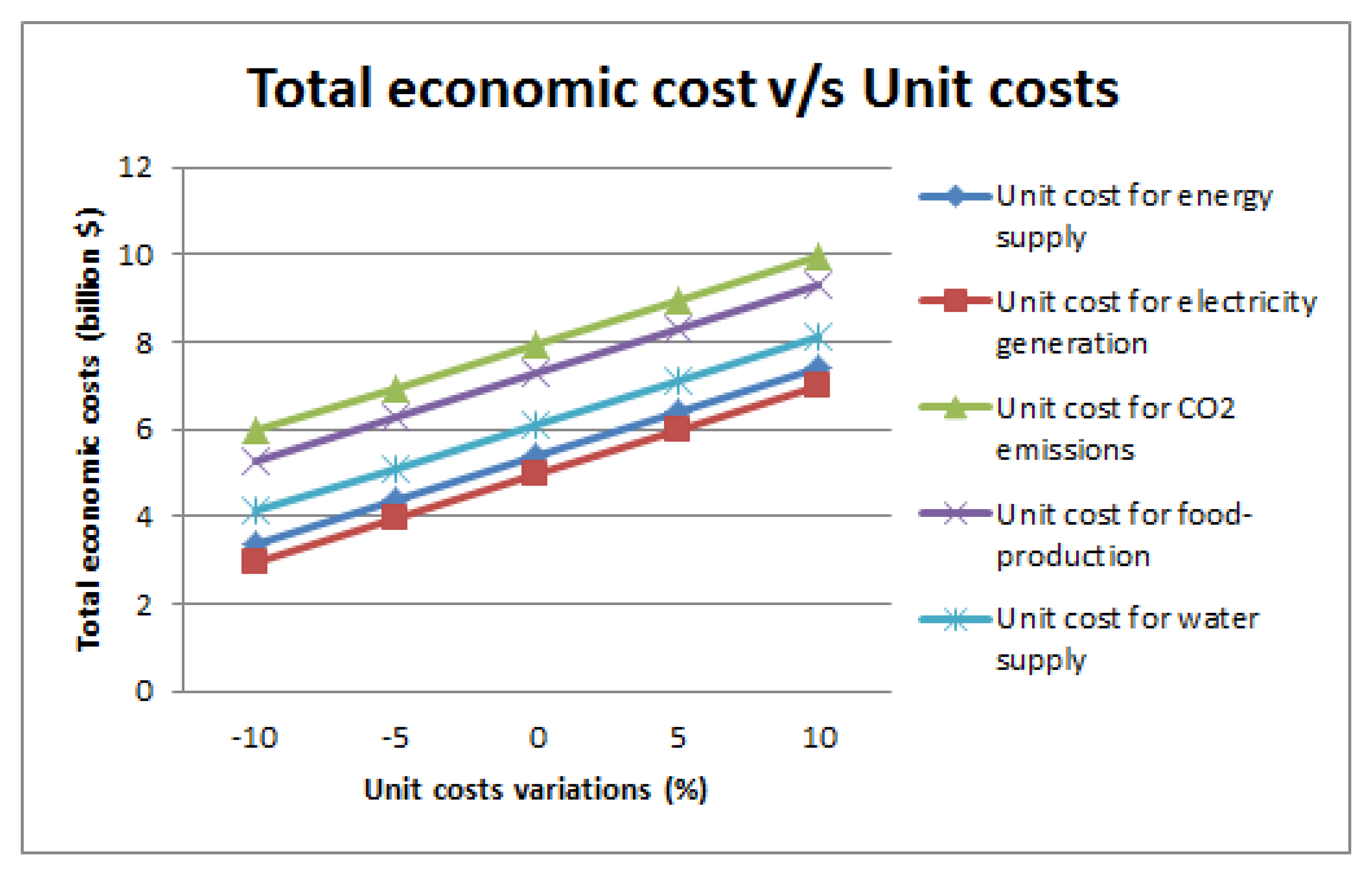
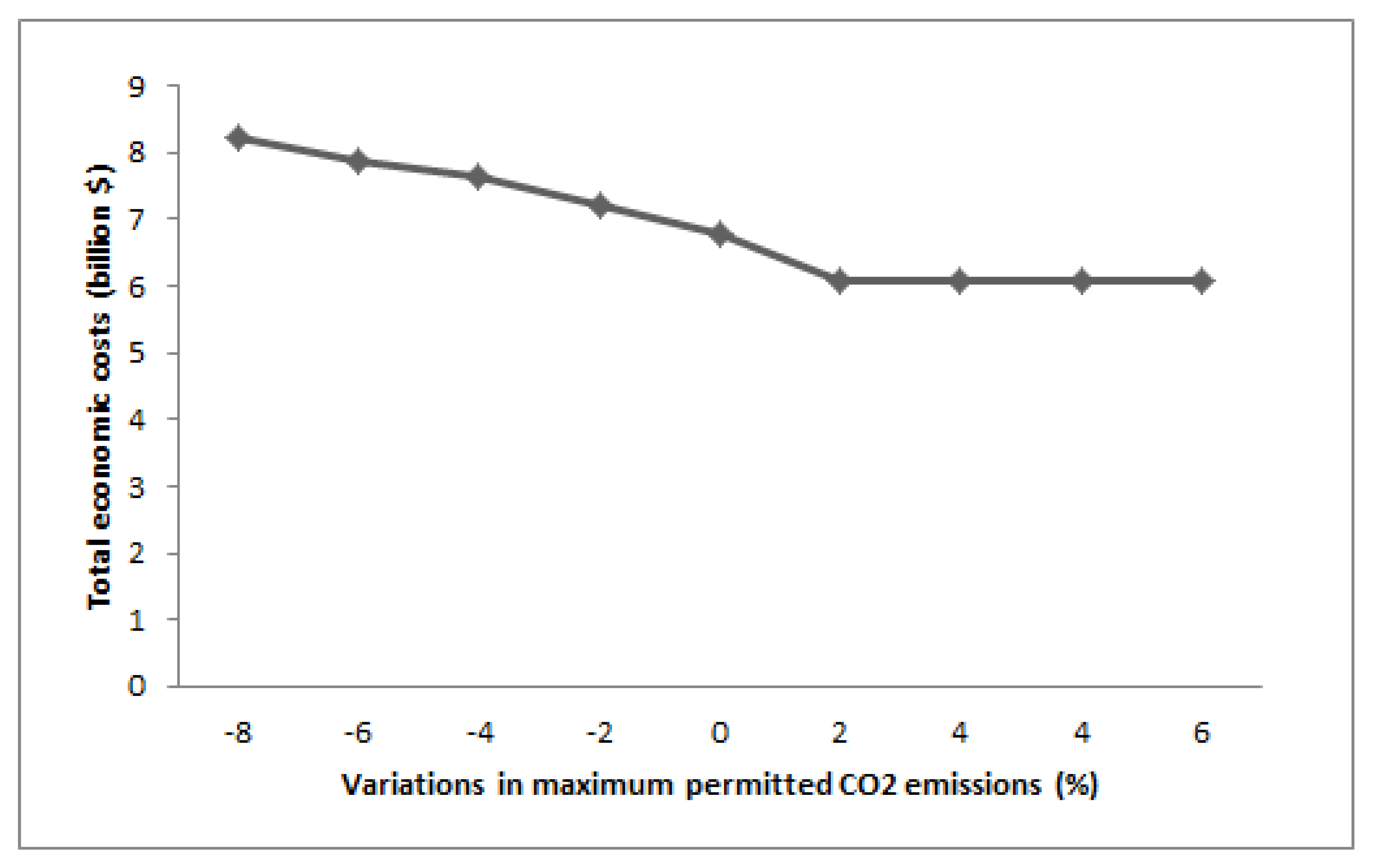
4.1.2. Sensitivity Analysis
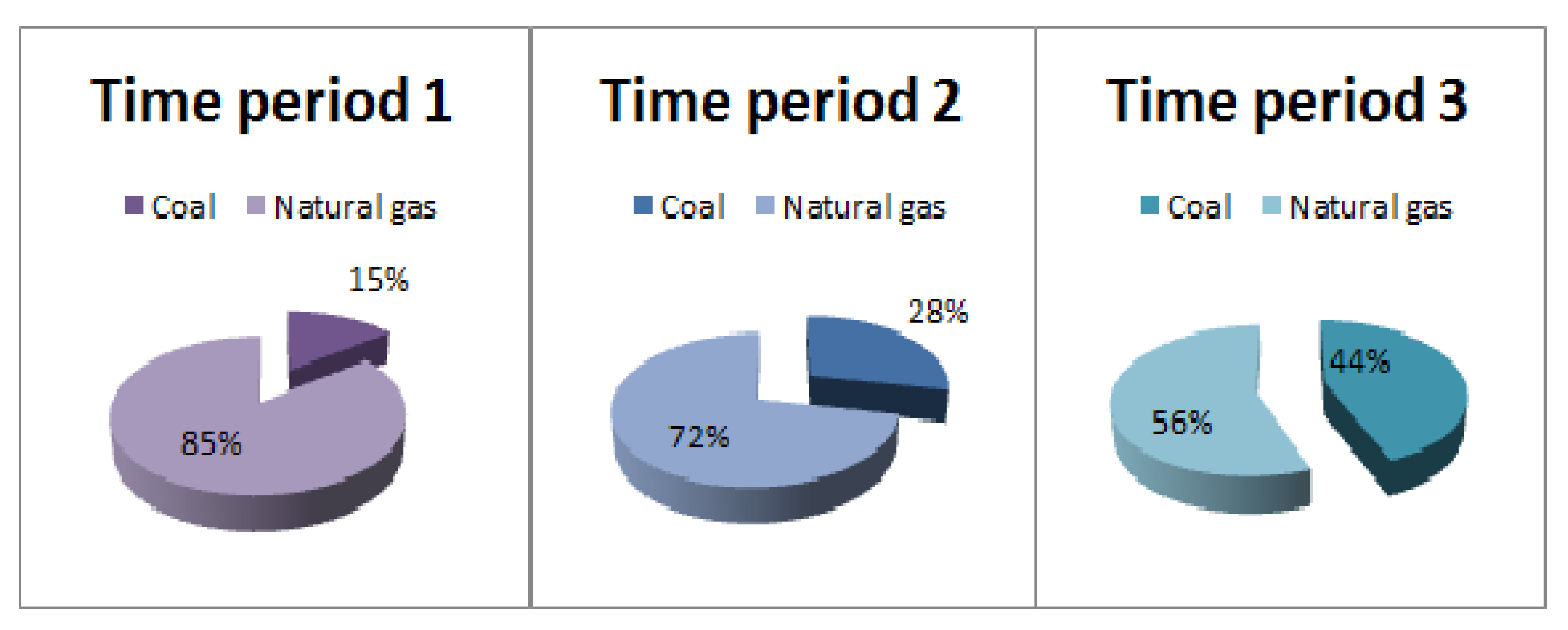
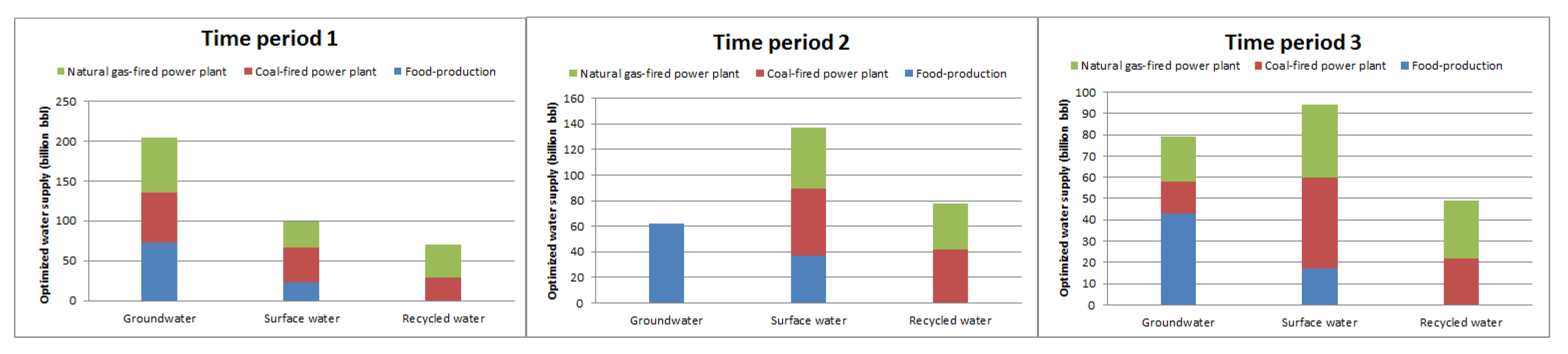
4.1.3. Discussions and Practical Implications
5. Conclusions
- The proposed EFWS model may assist the decision-makers and policy-developers in arriving at the optimal decision without violating the risk uncertainty due to hesitation. Moreover, the policy-makers may avail the sequential and most promising alternatives for the robust EFWS management network by adjusting the socio-economic demands of electricity, food, and water resources along with the ecological impacts restrictions.
- The established trade-offs among the socio-economic and environmental objectives, resource restrictions, and CO emission control would be feasible in applying the practical EFWS nexus management system.
- The analyzed effects of parameters’ values reveal that when decision-makers are more concerned about uncertainty, it will lead to the worst objectives (both economic and environmental) and vice versa.
- It is concluded that high socio-economic demands for electricity, food, and water resources will result in higher financial cost and simultaneously high CO emissions. The increment in the amount of maximum available water resources and permissible CO emission would reduce the total economic costs.
- The proposed EFWS nexus model is reliable in tackling the uncertainty and is computationally efficient in implementing large-scale energy-food-water nexus management systems.
- The need for electricity and food will also enhance the CO emissions in both the processes. The outcomes support the modeling approach and emphasize the essence of using and analyzing the proposed EFWS nexus management system.
- It can be useful for decision-makers and policy-developers to identify, quantify, and establish the trade-offs among typical inter-connections between energy, food, and water subsystems and to arrive at a decision for an integrated energy-food-water management system.
5.1. Treating Intuitionistic Fuzzy Parameters
5.2. Solution Methodology
5.2.1. Zimmermann’s Method
5.2.2. Werners’ Method
5.2.3. Selim and Ozkarahan’s Approach
5.2.4. Torabi and Hassini’s Optimization Technique
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- US Energy Information Administration. How much Carbon Dioxide Is Produced Per Kilowatthour When Generating Electricity with Fossil Fuels; US Energy Information Administration: Washington, DC, USA, 2015.
- Diehl, T.H.; Harris, M.A. Withdrawal and Consumption of Water by Thermoelectric Power Plants in the United States, 2010; USGS: Reston, VA, USA, 2014.
- FAO. The Water-Energy-Food Nexus: A New Approach in Support of Food Security and Sustainable Agriculture; FAO: Rome, Italy, 2014. [Google Scholar]
- Bazilian, M.; Rogner, H.; Howells, M.; Hermann, S.; Arent, D.; Gielen, D.; Steduto, P.; Mueller, A.; Komor, P.; Tol, R.S.; et al. Considering the energy, water and food nexus: Towards an integrated modelling approach. Energy Policy 2011, 39, 7896–7906. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. Neutrosophic Optimization Model and Computational Algorithm for Optimal Shale Gas Water Management under Uncertainty. Symmetry 2019, 11, 544. [Google Scholar] [CrossRef]
- Bieber, N.; Ker, J.H.; Wang, X.; Triantafyllidis, C.; van Dam, K.H.; Koppelaar, R.H.; Shah, N. Sustainable planning of the energy-water-food nexus using decision making tools. Energy Policy 2018, 113, 584–607. [Google Scholar] [CrossRef]
- Uen, T.S.; Chang, F.J.; Zhou, Y.; Tsai, W.P. Exploring synergistic benefits of Water-Food-Energy Nexus through multi-objective reservoir optimization schemes. Sci. Total Environ. 2018, 633, 341–351. [Google Scholar] [CrossRef] [PubMed]
- Tsolas, S.D.; Karim, M.N.; Hasan, M.F. Optimization of water-energy nexus: A network representation-based graphical approach. Appl. Energy 2018, 224, 230–250. [Google Scholar] [CrossRef]
- Namany, S.; Al-Ansari, T.; Govindan, R. Sustainable energy, water and food nexus systems: A focused review of decision-making tools for efficient resource management and governance. J. Clean. Prod. 2019, 225, 610–626. [Google Scholar] [CrossRef]
- Gao, J.; Xu, X.; Cao, G.; Ermoliev, Y.M.; Ermolieva, T.Y.; Rovenskaya, E.A. Optimizing regional food and energy production under limited water availability through integrated modeling. Sustainability 2018, 10, 1689. [Google Scholar] [CrossRef]
- Zhang, T.; Tan, Q.; Yu, X.; Zhang, S. Synergy assessment and optimization for water-energy-food nexus: Modeling and application. Renew. Sustain. Energy Rev. 2020, 134, 110059. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Li, Y. Synergies within the Water-Energy-Food Nexus to Support the Integrated Urban Resources Governance. Water 2019, 11, 2365. [Google Scholar] [CrossRef]
- Hamidov, A.; Helming, K. Sustainability Considerations in Water–Energy–Food Nexus Research in Irrigated Agriculture. Sustainability 2020, 12, 6274. [Google Scholar] [CrossRef]
- Saif, Y.; Almansoori, A.; Bilici, I.; Elkamel, A. Sustainable management and design of the energy-water-food nexus using a mathematical programming approach. Can. J. Chem. Eng. 2020. [Google Scholar] [CrossRef]
- Ji, L.; Zheng, Z.; Wu, T.; Xie, Y.; Liu, Z.; Huang, G.; Niu, D. Synergetic optimization management of crop-biomass coproduction with food-energy-water nexus under uncertainties. J. Clean. Prod. 2020, 258, 120645. [Google Scholar] [CrossRef]
- Okola, I.; Omullo, E.O.; Ochieng, D.O.; Ouma, G. A Multiobjective Optimisation Approach for Sustainable Resource Consumption and Production in Food-Energy-Water Nexus. In Proceedings of the 2019 IEEE AFRICON, Accra, Ghana, 25–27 September 2019; pp. 1–5. [Google Scholar]
- Li, M.; Fu, Q.; Singh, V.P.; Ji, Y.; Liu, D.; Zhang, C.; Li, T. An optimal modelling approach for managing agricultural water-energy-food nexus under uncertainty. Sci. Total Environ. 2019, 651, 1416–1434. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Stochastic multi-objective modeling for optimization of water-food-energy nexus of irrigated agriculture. Adv. Water Resour. 2019, 127, 209–224. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, J. Optimization of sustainable bioenergy production considering energy-food-water-land nexus and livestock manure under uncertainty. Agric. Syst. 2020, 184, 102900. [Google Scholar] [CrossRef]
- Yu, L.; Xiao, Y.; Jiang, S.; Li, Y.; Fan, Y.; Huang, G.; Lv, J.; Zuo, Q.; Wang, F. A copula-based fuzzy interval-random programming approach for planning water-energy nexus system under uncertainty. Energy 2020, 196, 117063. [Google Scholar] [CrossRef]
- Elsayed, H.; Djordjević, S.; Savić, D.A.; Tsoukalas, I.; Makropoulos, C. The Nile Water-Food-Energy Nexus under Uncertainty: Impacts of the Grand Ethiopian Renaissance Dam. J. Water Resour. Plan. Manag. 2020, 146, 04020085. [Google Scholar] [CrossRef]
- Tan, Q.; Zhang, T. Robust fractional programming approach for improving agricultural water-use efficiency under uncertainty. J. Hydrol. 2018, 564, 1110–1119. [Google Scholar] [CrossRef]
- Hurford, A. Accounting for Water-, Energy-and Food-Security Impacts in Developing Country Water Infrastructure Decision-Making under Uncertainty. Ph.D. Thesis, University College London, London, UK, 2016. [Google Scholar]
- Govindan, R.; Al-Ansari, T. Computational decision framework for enhancing resilience of the energy, water and food nexus in risky environments. Renew. Sustain. Energy Rev. 2019, 112, 653–668. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, B.; Huang, G.; Lu, Y. Multi-stage stochastic fuzzy random programming for food-water-energy nexus management under uncertainties. Resour. Conserv. Recycl. 2020, 155, 104665. [Google Scholar] [CrossRef]
- Yu, L.; Xiao, Y.; Zeng, X.; Li, Y.; Fan, Y. Planning water-energy-food nexus system management under multi-level and uncertainty. J. Clean. Prod. 2020, 251, 119658. [Google Scholar] [CrossRef]
- Hang, M.Y.L.P.; Martinez-Hernandez, E.; Leach, M.; Yang, A. Designing integrated local production systems: A study on the food-energy-water nexus. J. Clean. Prod. 2016, 135, 1065–1084. [Google Scholar] [CrossRef]
- Martinez-Hernandez, E.; Leach, M.; Yang, A. Understanding water-energy-food and ecosystem interactions using the nexus simulation tool NexSym. Appl. Energy 2017, 206, 1009–1021. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. In Philosophy; American Research Press: Rehoboth, DE, USA, 1999; pp. 1–141. [Google Scholar]
- Ahmad, F.; Adhami, A.Y. Neutrosophic programming approach to multiobjective nonlinear transportation problem with fuzzy parameters. Int. J. Manag. Sci. Eng. Manag. 2019, 14, 218–229. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. 15—Modified neutrosophic fuzzy optimization model for optimal closed-loop supply chain management under uncertainty. In Optimization Theory Based on Neutrosophic and Plithogenic Sets; Smarandache, F., Abdel-Basset, M., Eds.; Academic Press: New York, NY, USA, 2020; pp. 343–403. [Google Scholar]
- Adhami, A.Y.; Ahmad, F. Interactive Pythagorean-hesitant fuzzy computational algorithm for multiobjective transportation problem under uncertainty. Int. J. Manag. Sci. Eng. Manag. 2020, 15, 288–297. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y. Total cost measures with probabilistic cost function under varying supply and demand in transportation problem. Opsearch 2019, 56, 583–602. [Google Scholar] [CrossRef]
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. Single Valued Neutrosophic Hesitant Fuzzy Computational Algorithm for Multiobjective Nonlinear Optimization Problem. Neutrosophic Sets Syst. 2018, 22, 76–86. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-Making in a Fuzzy Environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Canning, P.N. Fuel for Food: Energy Use in the US Food System; Technical Report; United States Department of Agriculture, Economic Research Service: Washington, DC, USA, 2010.
- Hellegers, P.; Zilberman, D.; Steduto, P.; McCornick, P. Interactions between water, energy, food and environment: Evolving perspectives and policy issues. Water Policy 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Change, O.C. Intergovernmental Panel on Climate Change; WMO: Geneva, Switzerland; UNEP: Athens, Greece, 2007. [Google Scholar]
- Montagnini, F.; Ibrahim, M.; Murgueitio, E. Silvopastoral systems and climate change mitigation in Latin America. Bois. ForÊTs Des. Trop. 2013, 316, 3–16. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, G. Optimization of environmental management strategies through a dynamic stochastic possibilistic multiobjective program. J. Hazard. Mater. 2013, 246, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Huang, G.; Lin, Q.; Zhang, X.; Tan, Q.; Chen, Y. Development of a GHG-mitigation oriented inexact dynamic model for regional energy system management. Energy 2011, 36, 3388–3398. [Google Scholar] [CrossRef]
- Dolan, E. The Neos Server 4.0 Administrative Guide; Technical Report; Memorandum ANL/MCS-TM-250; Mathematics and Computer Science Division, Argonne National Laboratory: Argonne, IL, USA, 2001.
- Drud, A.S. CONOPT—A large-scale GRG code. ORSA J. Comput. 1994, 6, 207–216. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Werners, B.M. Aggregation models in mathematical programming. In Mathematical Models for Decision Support; Springer: New York, NY, USA, 1988; pp. 295–305. [Google Scholar]
- Selim, H.; Ozkarahan, I. A supply chain distribution network design model: An interactive fuzzy goal programming-based solution approach. Int. J. Adv. Manuf. Technol. 2008, 36, 401–418. [Google Scholar] [CrossRef]
- Torabi, S.A.; Hassini, E. An interactive possibilistic programming approach for multiple objective supply chain master planning. Fuzzy Sets Syst. 2008, 159, 193–214. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Heilpern, S. The expected value of a fuzzy number. Fuzzy Sets Syst. 1992, 47, 81–86. [Google Scholar] [CrossRef]

| Indices | Descriptions |
|---|---|
| e | Associated with the energy-production |
| f | Associated with the food production |
| Denotes the types of available energy supply and power conversion plant | |
| Represents the effective planning time periods such as a time horizon for energy, food and water security management | |
| w | Associated with the water-resources use |
| Decision variables | |
| Amount of available energy supply j in time period t (PJ) | |
| Amount of electricity conversion by a power plant o using energy supply j in time period t (PJ) | |
| Quantity of groundwater consumed in food production processes in time period t (bbl) | |
| Quantity of surface water consumed in food production processes in time period t (bbl) | |
| Groundwater quantity delivered to power-conversion plant j in time period t (bbl) | |
| Surface water quantity delivered to power-conversion plant j in time period t (bbl) | |
| Amount of recycled water sent to power-conversion plant j in time period t (bbl) | |
| Total quantity of food production in time period t (ton) | |
| Parameters | |
| Average cost associated with energy supply j in time period t (million $/PJ) | |
| Fixed cost associated with power conversion plant j (million $) | |
| Average operational cost incurred over electricity production by power conversion plant j in time period t (million $/PJ) | |
| Total cost related to groundwater supply for food production in time horizon t ($/bbl) | |
| Total cost related to groundwater supply for power conversion plant j in time horizon t ($/bbl) | |
| Total cost related to surface water supply for food production in time horizon t ($/bbl) | |
| Total cost related to surface water supply for power conversion plant j in time horizon t ($/bbl) | |
| Total cost related to recycled water supply for power conversion plant j in time horizon t ($/bbl) | |
| Unit cost associated with food production in time period t (million $/ton) | |
| Total cost of CO emission abatement for electricity production in time period t ($/kg) | |
| Units of CO emission per unit of electricity production by power conversion plant j in time period t (million kg/PJ) | |
| Total cost of CO emission abatement for food production in time period t ($/ton) | |
| Units of CO emission per unit of food production in time period t (million kg/ton) | |
| Unit energy carrier per unit of electricity production for transformation technique j in time period t (PJ/PJ) | |
| Total available energy supply j in time period t (PJ) | |
| Maximum unit of electricity available for food production in time period t (PJ) | |
| Maximum unit of electricity available for water collection, treatment and supply in time period t (PJ) | |
| Demand of unit energy for food production in time period t (PJ/ton) | |
| Demand of unit energy for water collection, treatment and supply in time period t (PJ) | |
| Socio-economic demand for energy (or electricity) in time period t (PJ) | |
| Socio-economic demand for food in time period t (ton) | |
| Units of water consumption per unit of food production in time period t (bbl/ton) | |
| Maximum quantity of available groundwater safe yield in time period t (bbl) | |
| Maximum quantity of available surface water in time period t (bbl) | |
| Maximum quantity of available recycled water in time period t (bbl) | |
| Maximum permissable CO emission during planning periods (million ton) | |
| Loss factor of water supply to the food sub-system | |
| Unit water demand per unit of electricity production by power conversion plant j (bbl/GWh) | |
| Loss factor of water supply to the power conversion plant j | |
| Average efficiency factor for CO emission abatement by power conversion plant j in time period t |
| Time Period (05 Years Each) | |||
|---|---|---|---|
| Average operational costs | |||
| Coal supplies (million $/PJ) | (3.0,3.2,3.4;2.8,3.2,3.6) | (3.4,3.6,3.8;3.2,3.6,4.0) | (3.8,4.0,4.2;3.6,4.2,4.4) |
| Natural gas supplies (million $/PJ) | (5.2,5.6,6.0;4.8,5.6,6.2) | (6.0,6.3,6.6;5.8,6.3,6.8) | (6.6,6.7,6.8;6.4,6.7,6.9) |
| Electricity production in | (6.0,6.5,7.0;5.8,6.5,7.2) | (6.6,6.9,7.2;6.4,6.9,7.4) | (7.1,7.4,7.7;6.8,7.4,7.9) |
| coal-fired plant (million $/PJ) | |||
| Electricity production in | (2.8,2.9,3.0;2.4,2.9,3.3) | (3.5,3.7,3.9;3.2,3.74.2) | (4.2,4.4,4.6;3.8,4.4,4.8) |
| natural gas-fired plant (million $/PJ) | |||
| Unit food production cost ($/ton) | (3.2,3.4,3.6;2.8,3.4,4.0) | (3.5,3.9,4.3;3.2,3.9,4.2) | (4.1,4.2,4.3;3.8,4.2,4.4) |
| Costs of COemissions abatement | |||
| For electricity production ($/million kg) | (14.2,14.4,14.6;14.0,14.4,14.8) | (12.1,12.3,12.5;12.0,12.3,12.6) | (13.1,13.3,13.5;13.0,13.3,13.6) |
| For food production ($/ton) | (12.2,12.5,12.8;12.1,12.5,12.9) | (11.3,11.5,11.7;11.2,11.5,11.8) | (17.2,17.4,17.6;17.1,17.4,17.7) |
| Groundwater supply costs | |||
| For electricity production ($/ bbl) | |||
| Coal-fired power plant | (15.6,15.8,16.0;15.4,15.8,16.2) | (17.2,17.4,17.6;17.1,17.4,17.7) | (14.3,14.6,14.9;14.2,14.6,15.0) |
| Natural gas-fired plant | (09.6,09.8,10.0;09.5,09.8,10.1) | (16.2,16.4,16.6;16.1,16.4,16.7) | (12.2,12.4,12.6;12.1,12.4,12.7) |
| For food production ($/ bbl) | (13.2,13.4,13.6;13.0,13.4,13.8) | (11.2,11.4,11.6;11.1,11.4,11.7) | (16.2,16.4,16.6;16.1,16.4,16.7) |
| Surface water supply costs | |||
| For electricity production ($/ bbl) | |||
| Coal-fired power plant | (5.6,5.8,6.0;5.4,5.8,6.2) | (7.2,7.4,7.6;7.1,7.4,7.7) | (4.3,4.6,4.9;4.2,4.6,5.0) |
| Natural gas-fired plant | (9.5,9.6,9.7;9.4,9.6,9.8) | (6.2,6.4,6.6;6.1,6.4,6.7) | (2.2,2.4,2.6;2.1,2.4,2.7) |
| For food production ($/ bbl) | (2.2,2.4,2.6;2.0,2.4,2.8) | (3.3,3.5,3.7;3.2,3.5,3.8) | (1.2,1.4,1.6;1.1,1.4,1.7) |
| Recycled water supply costs | |||
| For electricity production ($/ bbl) | |||
| Coal-fired power plant | (4.2,4.4,4.6;4.0,4.4,4.8) | (2.1,2.3,2.5;2.0,2.3,2.6) | (3.1,3.3,3.5;3.0,3.3,3.6) |
| Natural gas-fired plant | (3.2,3.4,3.6;3.0,3.4,3.8) | (1.2,1.4,1.6;1.1,1.4,1.7) | (6.2,6.4,6.6;6.1,6.4,6.7) |
| Time Period (05 Years Each) | |||
|---|---|---|---|
| Electricity consumption (PJ) | (1.2,1.4,1.6;1.1,1.4,1.7) | (4.2,4.4,4.6;4.1,4.4,4.7) | (4.1,4.3,4.5;4.0,4.3,4.6) |
| Food-demand (ton) | (2.1,2.3,2.5;1.9,2.3,2.7) | (3.2,3.4,3.6;3.1,3.4,3.7) | (3.2,3.4,3.6;3.0,3.4,3.8) |
| Coal availability (PJ) | (3.4,3.6,3.8;3.2,3.6,4.0) | (2.2,2.4.2.6;2.1,2.4,2.7) | (2.2,2.4,2.6;2.0,2.4,2.8) |
| Natural gas availability (PJ) | (2.2,2.4,2.6;2.1,2.4,2.7) | (1.5,1.8,1.9;1.4,1.8,2.1) | (1.5,1.7,1.9;1.4,1.7,2.0) |
| Maximum available quantity | |||
| Groundwater (billion bbl) | (1.4,1.6,1.8;1.2,1.6,2) | (1.8,2,2.2;1.8,2,2.2) | (2.6,2.8,3.0;2.5,2.8,3.1) |
| Surface water (billion bbl) | (2.2,2.4,2.6;2.1,2.4,2.7) | (1.5,1.8,1.9;1.4,1.8,2.1) | (1.5,1.7,1.9;1.4,1.7,2.0) |
| Recycled water (billion bbl) | (1.4,1.6,1.8;1.2,1.6,2) | (1.8,2,2.2;1.8,2,2.2) | (2.6,2.8,3.0;2.5,2.8,3.1) |
| Maximum CO emissions (million ton) | (13.2,13.4,13.6;13.0,13.4,13.8) | (11.2,11.4,11.6;11.1,11.4,11.7) | (16.2,16.4,16.6;16.1,16.4,16.7) |
| Time Period (05 Years Each) | |||
|---|---|---|---|
| Unit energy demand for | (1.2,1.4,1.6;1.1,1.4,1.7) | (4.2,4.4,4.6;4.1,4.4,4.7) | (4.1,4.3,4.5;4.0,4.3,4.6) |
| food production ( PJ/ton) | |||
| Unit energy demand for water | (2.1,2.3,2.5;1.9,2.3,2.7) | (3.2,3.4,3.6;3.1,3.4,3.7) | (3.2,3.4,3.6;3.0,3.4,3.8) |
| collection, treatment and supply (KWh/bbl) | |||
| Maximum available electricity | (3.4,3.6,3.8;3.2,3.6,4.0) | (2.2,2.4.2.6;2.1,2.4,2.7) | (2.2,2.4,2.6;2.0,2.4,2.8) |
| for food production (PJ) | |||
| Maximum available electricity for water | (2.5,2.7,2.9;2.4,2.7,3.0) | (1.5,1.7,1.9;1.4,1.7,2.0) | (1.5,1.7,1.9;1.4,1.7,2.0) |
| collection, treatment and supply (PJ) | |||
| Unit of energy produced per unit | |||
| of electricity conversion (PJ/PJ) | |||
| Coal-fired power plant | (3.2,3.4,3.6;3.0,3.4,3.8) | (1.2,1.4,1.6;1.1,1.4,1.7) | (6.2,6.4,6.6;6.1,6.4,6.7) |
| Natural gas-fired power plant | (2.4,2.6,2.8;2.0,2.4,3.0) | (1.3,1.5,1.7;1.1,1.5,1.9) | (0.5,0.7,0.9;0.3,0.7,1.1) |
| Objective Values | Compensation Co-Efficient () | ||||
|---|---|---|---|---|---|
| Min (billion $) | (7.17, 7.21) | (7.21, 7.25) | (7.27, 7.31) | (7.32, 7.36) | (7.34, 7.38) |
| Min (million ton) | (14.96, 15.00) | (15.00, 15.04) | (15.09, 15.13) | (15.17, 15.21) | (15.25, 15.31) |
| Overall satisfaction | 0.89 | 0.87 | 0.86 | 0.85 | 0.84 |
| Time (sec.) | 2.65 | 1.44 | 1.67 | 2.58 | 2.74 |
| Objective Values | Zimmermann [44] | Werners [45] | Selim and Ozkarahan [46] | Torabi and Hassini [47] | Proposed INPA |
|---|---|---|---|---|---|
| Total economic cost (billion $) | (9.68, 9.76) | (8.27, 8.39) | (8.03, 8.07) | (7.51, 7.59) | (7.16, 7.22) |
| emissions (million ton) | (17.32, 17.42) | (16.48, 16.56) | (16.16, 16.22) | (15.82, 15.86) | (14.96, 15.00) |
| Overall satisfaction | 0.72 | 0.77 | 0.79 | 0.81 | 0.89 |
| Time (sec.) | 1.12 | 2.34 | 1.35 | 1.95 | 2.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, F.; Ahmad, S.; Zaindin, M.; Adhami, A.Y. A Robust Neutrosophic Modeling and Optimization Approach for Integrated Energy-Food-Water Security Nexus Management under Uncertainty. Water 2021, 13, 121. https://doi.org/10.3390/w13020121
Ahmad F, Ahmad S, Zaindin M, Adhami AY. A Robust Neutrosophic Modeling and Optimization Approach for Integrated Energy-Food-Water Security Nexus Management under Uncertainty. Water. 2021; 13(2):121. https://doi.org/10.3390/w13020121
Chicago/Turabian StyleAhmad, Firoz, Shafiq Ahmad, Mazen Zaindin, and Ahmad Yusuf Adhami. 2021. "A Robust Neutrosophic Modeling and Optimization Approach for Integrated Energy-Food-Water Security Nexus Management under Uncertainty" Water 13, no. 2: 121. https://doi.org/10.3390/w13020121
APA StyleAhmad, F., Ahmad, S., Zaindin, M., & Adhami, A. Y. (2021). A Robust Neutrosophic Modeling and Optimization Approach for Integrated Energy-Food-Water Security Nexus Management under Uncertainty. Water, 13(2), 121. https://doi.org/10.3390/w13020121







