Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy
Abstract
1. Introduction
- (a)
- Empirical direct methods to estimate evapotranspiration based on the processing of remotely sensed data using semi-empirical models, such as simplified relationships using thermal infrared (TIR) remotely sensed data and meteorological models.
- (b)
- (c)
- Deterministic methods, which are based on SVAT models, estimating the different components of the energy budget (Interactions between the Soil Biosphere and Atmosphere–ISBA, Non-Hydrostatic Mesoscale atmospheric model–Meso-NH) and using remote sensing data at different levels, either as input parameters or in data assimilation procedures.
- (d)
2. Hydrogeological and Climatic Settings
3. Data and Methodologies
3.1. Cartographic Database and the Precipitation and Air Temperature Time Series
3.2. Estimation of Evapotranspiration Using Remotely Sensed Data and Classical Empirical Formulas
- ETRji—real evapotranspiration for the jth rain gauge station and the ith year (mm).
- APji—annual precipitation for the jth rain gauge station and the ith year (mm).
- ATji—annual air temperature for the jth rain gauge station and the ith year (°C).
- PETji—potential evapotranspiration for the jth rain gauge station and the ith month (mm).
- K—coefficient that depends on the monthly average of hours of insolation and a function of the latitude and month.
- Tmji—mean monthly air temperature (°C).
3.3. Groundwater Recharge Estimation
4. Results
4.1. Distributed Modelling of Precipitation and Air Temperature
4.2. Distributed Models of the Mean Annual AET
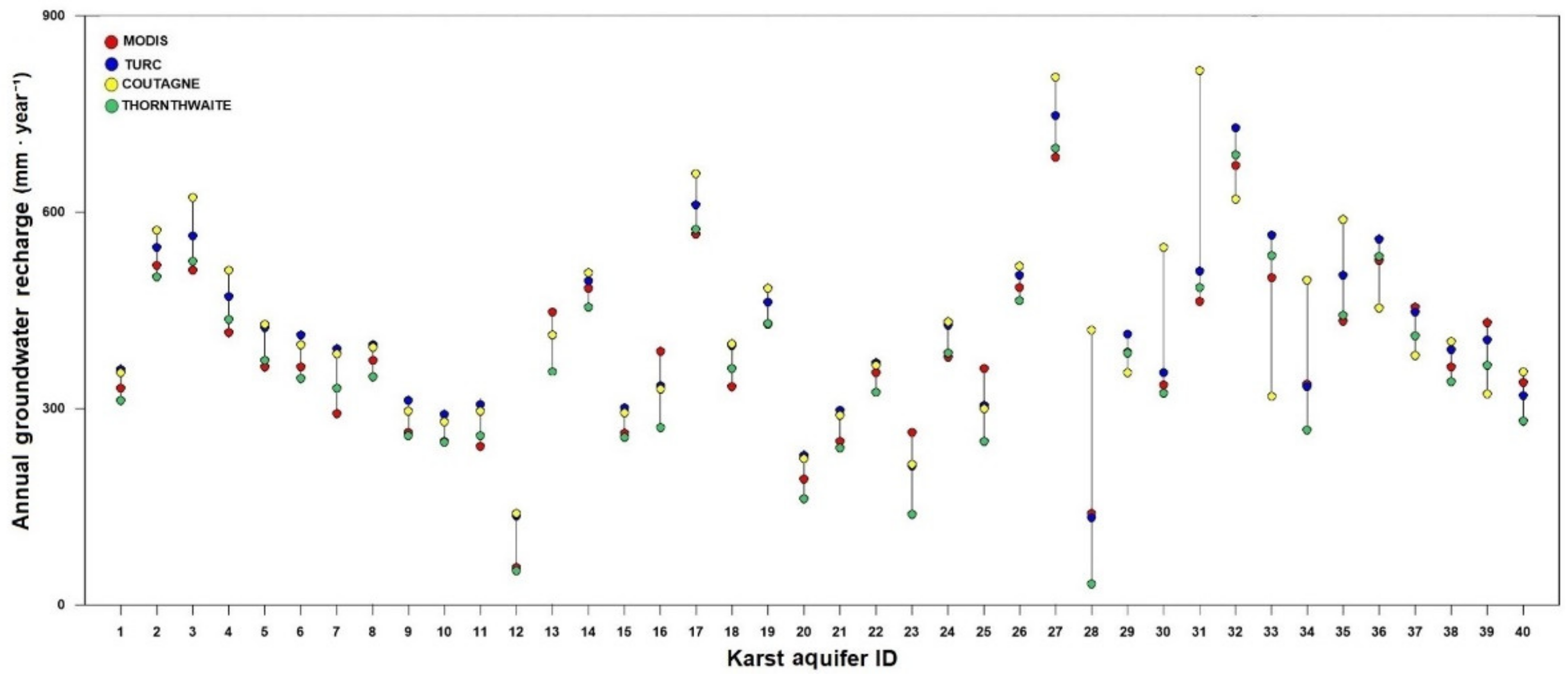
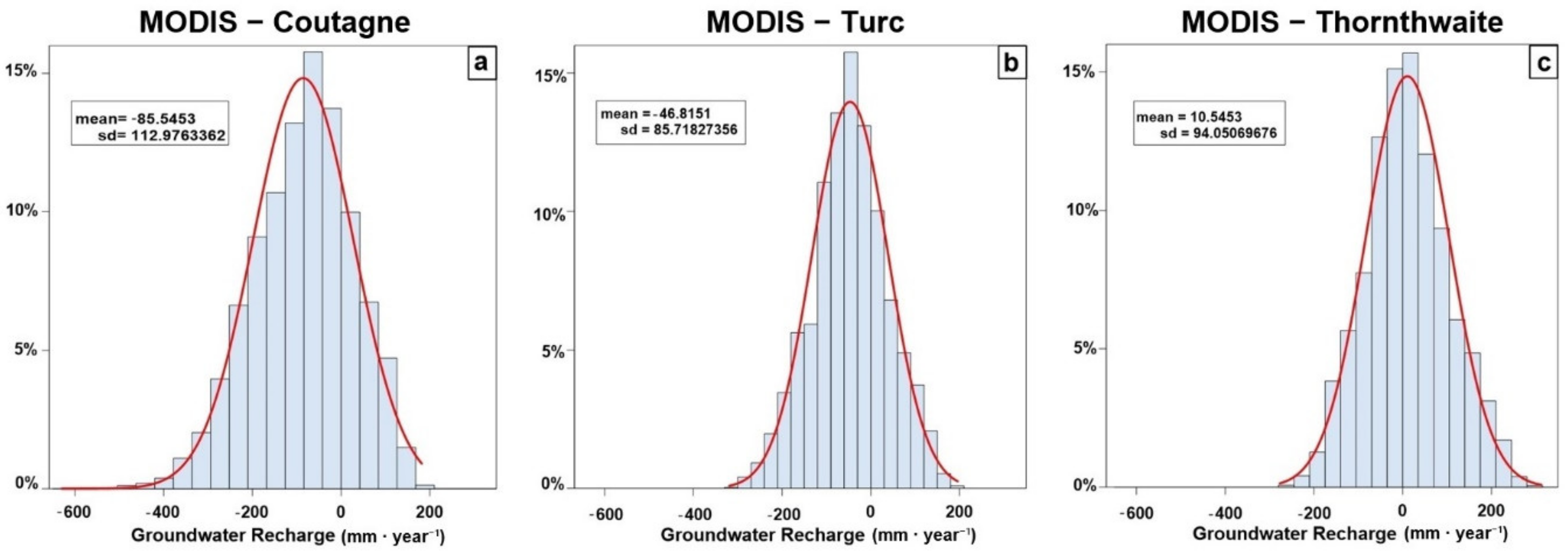
4.3. Groundwater Recharge Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldscheider, N. A holistic approach to groundwater protection and ecosystem services in karst terrains. Aquat. Mundi Am. 2012, 06046, 117–124. [Google Scholar] [CrossRef]
- Allocca, V.; Manna, F.; De Vita, P. Estimating annual groundwater recharge coefficient for karst aquifers of the southern Apennines (Italy). Hydrol. Earth Syst. Sci. 2014, 18, 803–817. [Google Scholar] [CrossRef]
- Allocca, V.; De Vita, P.; Manna, F.; Nimmo, J.R. Groundwater recharge assessment at local and episodic scale in a soil mantled perched karst aquifer in southern Italy. J. Hydrol. 2015, 529, 843–853. [Google Scholar] [CrossRef]
- Manna, F.; Nimmo, J.R.; Allocca, V.; De Vita, P. Recharge in karst aquifers: From regional to local and annual to episodic scale. Rend. Online Soc. Geol. Ital. 2015, 35, 196–199. [Google Scholar] [CrossRef]
- De Vita, P.; Allocca, V.; Manna, F.; Fabbrocino, S. Coupled decadal variability of the North Atlantic Oscillation, regional rainfall and karst spring discharges in the Campania region (southern Italy). Hydrol. Earth Syst. Sci. 2012, 16, 1389–1399. [Google Scholar] [CrossRef]
- Manna, F.; Allocca, V.; Fusco, F.; Napolitano, E.; De Vita, P. Effect of the North Atlantic Oscillation on groundwater recharge in karst aquifers of the Cilento Geopark (Italy). Rend. Online Soc. Geol. Ital. 2013, 28, 106–109. [Google Scholar]
- Jackson, T.J. Remote sensing of soil moisture: Implications for groundwater recharge. Hydrogeol. J. 2002, 10, 40–51. [Google Scholar] [CrossRef]
- Bouwer, H. Estimating and enhancing groundwater recharge. In Groundwater Recharge; Sharma, M.L., Ed.; A.A. Balkema: Rotterdam, The Netherlands, 1989; pp. 1–10. [Google Scholar]
- Walter, T.; Wilks, D.S.; Parlange, J.-Y.; Schneider, R.L. Increasing Evapotranspiration from the Conterminous United States. J. Hydrometeorol. 2004, 5, 405–408. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Kustas, W.P.; Ritchie, J.C.; Jackson, T.J.; Rango, A. Remote sensing in hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Kustas, W.P.; French, A.N.; Hatfield, J.; Jackson, T.J.; Moran, M.S.; Rango, A.; Ritchie, J.C.; Schmugge, T.J. Remote Sensing Research in Hydrometeorology. Photogramm. Eng. Remote Sens. 2003, 69, 631–646. [Google Scholar] [CrossRef]
- Overgaard, J.; Rosbjerg, D.; Butts, M.B. Land-surface modelling in hydrological perspective—A review. Biogeosciences 2006, 3, 229–241. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Jayanthi, H.; Wright, J.L. Irrigation water management using high resolution airborne remote sensing. Irrig. Drain. Syst. 2005, 19, 321–336. [Google Scholar] [CrossRef]
- Garatuza-Payan, J.; Watts, C.J. The use of remote sensing for estimating ET of irrigated wheat and cotton in NorthwestMexico. Irrig. Drain. Syst. 2005, 19, 301–320. [Google Scholar]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Drexler, Z.; Snyder, R.; Spano, D.; Kyaw Tha Pasw, U. A review of models and micrometeorological methods used to estimate wetland evapotranspiration. Hydrol. Process. 2004, 18, 2071–2101. [Google Scholar]
- Glenn, E.P.; Huete, A.R.; Nagler, P.; Hirschboeck, K.K.; Brown, P. Integrating Remote Sensing and Ground Methods to Estimate Evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Ranson, J. Terra: The EOS Flagship. 2006. Available online: http://terra.nasa.gov/ (accessed on 26 April 2006).
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Meijerink, A.M.J. Groundwater. In Remote Sensing in Hydrology and Water Management; Engman, E.T., Schultz, G.A., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2000; pp. 305–325. [Google Scholar]
- Petrella, E.; Capuano, P.; Celico, F. Unusual behaviour of epikarst in the Acqua dei Faggi carbonate aquifer (Southern Italy). Terra Nova 2007, 19, 82–88. [Google Scholar] [CrossRef]
- Manna, F.; Allocca, V.; De Vita, P.; Fusco, F.; Napolitano, E. Groundwater recharge assessment in karst aquifers of southern Apennines (Italy). Rend. Online Soc. Geol. Ital. 2013, 24, 202–204. [Google Scholar]
- Celico, F.; Naclerio, G.; Bucci, A.; Nerone, V.; Capuano, P.; Carcione, M.; Allocca, V.; Celico, P. Influence of pyroclastic soil on epikarst formation: A test study in southern Italy. Terra Nova 2010, 22, 110–115. [Google Scholar] [CrossRef]
- De Vita, P.; Nappi, M. Regional distribution of ash-fall pyroclastic deposits in Campania (southern Italy) for landslide susceptibility assessment. In Landslide Science and Practice: Spatial Analysis and Modelling; Sassa, K., Margottini, C., Canuti, P., Eds.; Springer: Berlin, Germany, 2013; pp. 103–110. ISBN 978-3-642-31310-3. [Google Scholar]
- Fusco, F.; Allocca, V.; De Vita, P. Hydro-geomorphological modelling of ash-fall pyroclastic soils for debris flow initiation and groundwater recharge in Campania (southern Italy). Catena 2017, 158, 235–249. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Napolitano, E.; Allocca, V.; Manna, F. Monitoring the soil suction regime of landslide-prone ash-fall pyroclastic deposits covering slopes in the Sarno area (Campania-southern Italy). Rend. Online Soc. Geol. Ital. 2013, 24, 146–148. [Google Scholar]
- Celico, P. Idrogeologia dei massicci carbonatici, delle piane quaternarie e delle aree vulcaniche dell’Italia centromeridionale (Marche e Lazio meridionale, Abruzzo, Molise e Campania). Quad. Cassa Mezzog. 1983, 4, 1–203. [Google Scholar]
- Petrella, E.; Celico, F. Heterogeneous aquitard properties in sedimentary successions in the Apennine chain: Case studies in southern Italy. Hydrol. Process. Int. J. 2009, 23, 3365–3371. [Google Scholar] [CrossRef]
- De Vita, P.; Allocca, V.; Celico, F.; Fabbrocino, S.; Mattia, C.; Monacelli, G.; Musilli, I.; Piscopo, V.; Scalise, A.R.; Summa, G.; et al. Hydrogeology of continental southern Italy. J. Maps 2018, 14, 230–241. [Google Scholar] [CrossRef]
- Bandini, A. Tipi Pluviometrici Dominanti Sulle Regioni Italiane. Il Servizio Idrografico Italiano 1931; Ministero dei Lavori Pubblici: Rome, Italy, 1931. [Google Scholar]
- Henderson-Sellers, A.; Robinson, P.J. Contemporary Climatology; John Wiley & Sons: New York, NY, USA, 1986; p. 439. [Google Scholar]
- Geiger, R. Klassifikation der klimate nach W. Köppen. Landolt-Börnstein–Zahlenwerte und Funktionen aus Physik Chemie Astronomie Geophysik und Technik; Springer: Berlin, Germany, 1954; Volume 3, pp. 603–607. [Google Scholar]
- Allocca, V.; Celico, F.; Celico, P.; De Vita, P.; Fabbrocino, S.; Mattia, S.; Monacelli, G.; Musilli, I.; Piscopo, V.; Scalise, A.R.; et al. Illustrative Notes of the Hydrogeological Map of Southern Italy; Istituto Poligrafico e Zecca dello Stato: Rome, Italy, 2007; p. 211. ISBN 88-448-0215-5. [Google Scholar]
- Copernicus Land Monitoring Service. Available online: http://land.copernicus.eu/ (accessed on 26 April 2006).
- Di Gennaro, A. I Sistemi di Terre della Campania. Carta 1:250.000 e Legenda; SELCA: Florence, Italy, 2000. [Google Scholar]
- Earth Data USGS. Available online: https://lpdaac.usgs.gov (accessed on 26 April 2006).
- Hudson, G.; Wackernagel, H. Mapping temperature using kriging with external drift: Theory and an example from scotland. Int. J. Clim. 1994, 14, 77–91. [Google Scholar] [CrossRef]
- Houze, R.A. Orographic effects on precipitating clouds. Rev. Geophys. 2012, 50, 1–47. [Google Scholar] [CrossRef]
- Brunsdon, C.; McClatchey, J.; Unwin, D. Spatial variations in the average rainfall-altitude relationship in Great Britain: An approach using geographically weighted regression. Int. J. Clim. 2001, 21, 455–466. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In The State and Movement of Water in Living Organisms; Fogg, G.E., Ed.; Cambridge University Press: Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Coutagne, A. Quelques considérations sur le pouvoir évaporant de l’tmosphere, le déficit d’écoulement effectif et le déficit d’écoulement maximum. La Houille Blanche 1954, 360–374. [Google Scholar] [CrossRef]
- Turc, L. Le bilan d’eau des sols: Relations entre les précipitations, l’évaporation et l’éecolument. Ann. Agron. 1954, 5, 491–595. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance. Publ. Climatol. 1955, 8, 1–104. [Google Scholar]
- Tweed, S.; Leblanc, M.; Webb, J.A.; Lubczynski, M.W. Remote sensing and GIS for mapping groundwater recharge and discharge areas in salinity prone catchments, southeastern Australia. Hydrogeol. J. 2006, 15, 75–96. [Google Scholar] [CrossRef]
- Wang, H.; Kgotlhang, L.; Kinzelbach, W. Using remote sensing data to model groundwater recharge potential in Kanye region, Botswana. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 751–756. [Google Scholar]
- Szilagyi, J.; Kovács, Á.; Jozsa, J. Remote-Sensing Based Groundwater Recharge Estimates in the Danube-Tisza Sand Plateau Region of Hungary. J. Hydrol. Hydromech. 2012, 60, 64–72. [Google Scholar] [CrossRef]
- Niraula, R.; Meixner, T.; Ajami, H.; Rodell, M.; Gochis, D.; Castro, C.L. Comparing potential recharge estimates from three Land Surface Models across the western US. J. Hydrol. 2017, 545, 410–423. [Google Scholar] [CrossRef] [PubMed]
- Lubczynskia, M.W.; Gurwinb, J. Integration of various data sources for transient groundwater modeling with spatio-temporally variable fluxes—Sardon study case, Spain. J. Hydrol. 2005, 306, 71–96. [Google Scholar] [CrossRef]
- Jasrotia, A.S.; Kumar, R.; Saraf, A.K. Delineation of groundwater recharge sites using integrated remote sensing and GIS in Jammu district, India. Int. J. Remote Sens. 2007, 28, 5019–5036. [Google Scholar] [CrossRef]
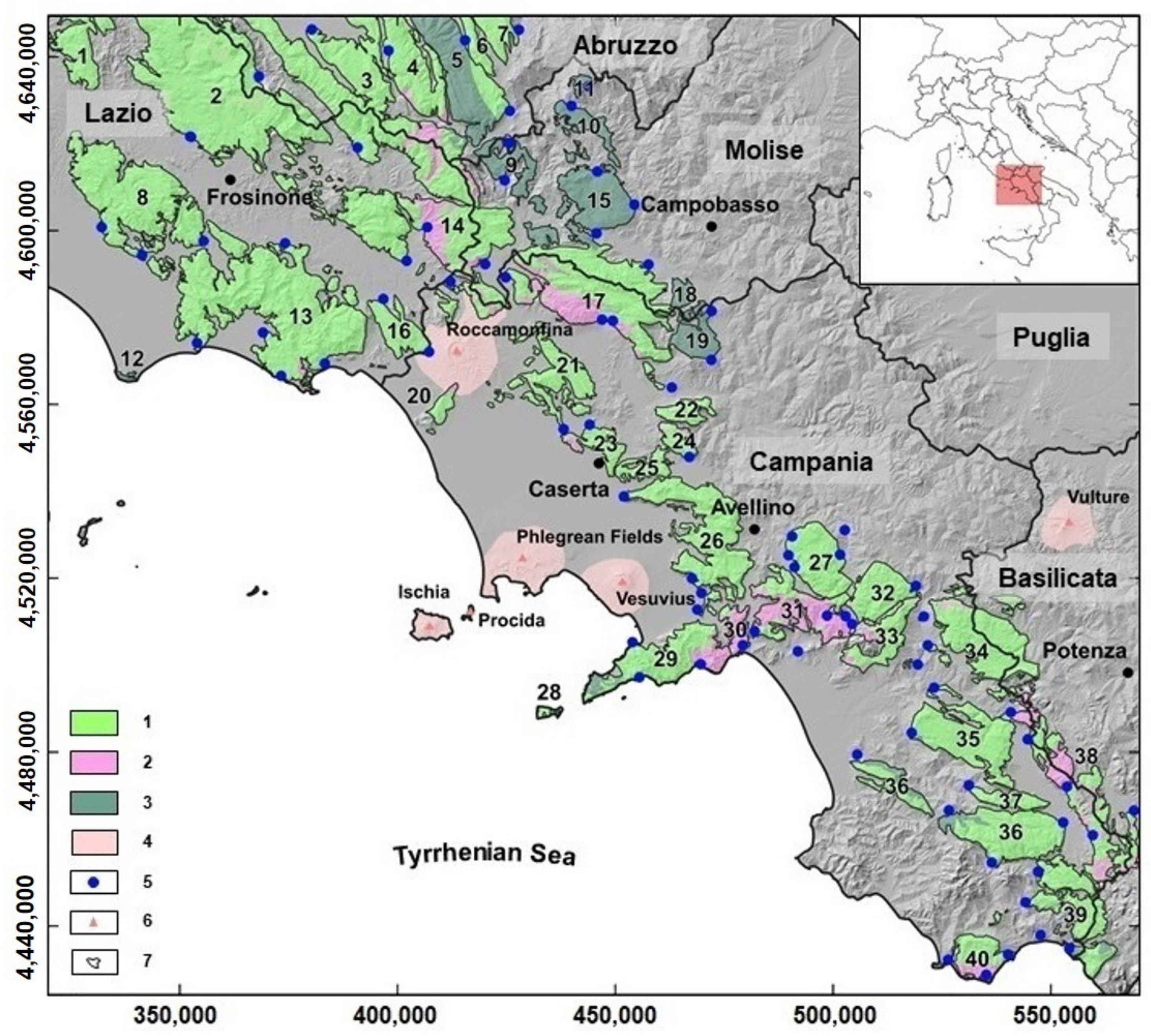
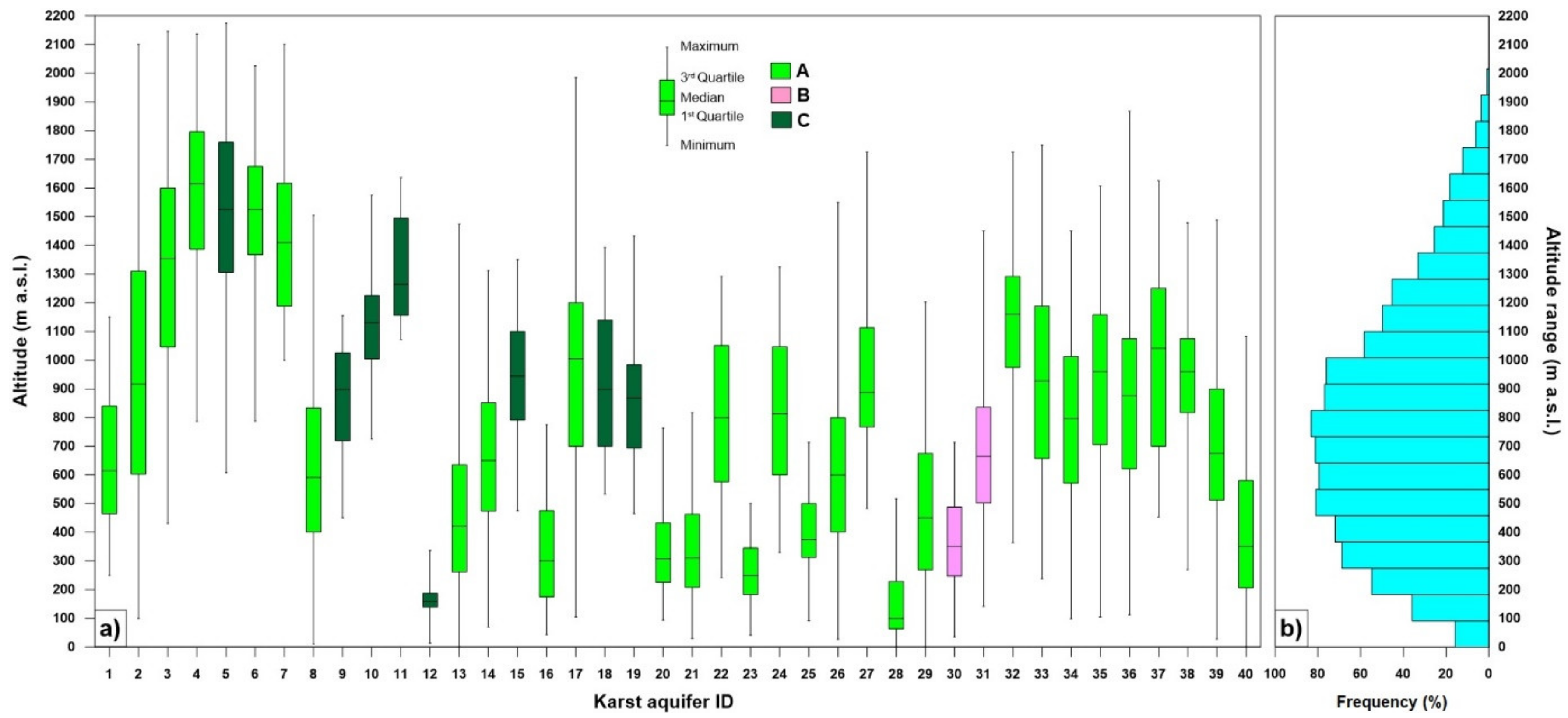
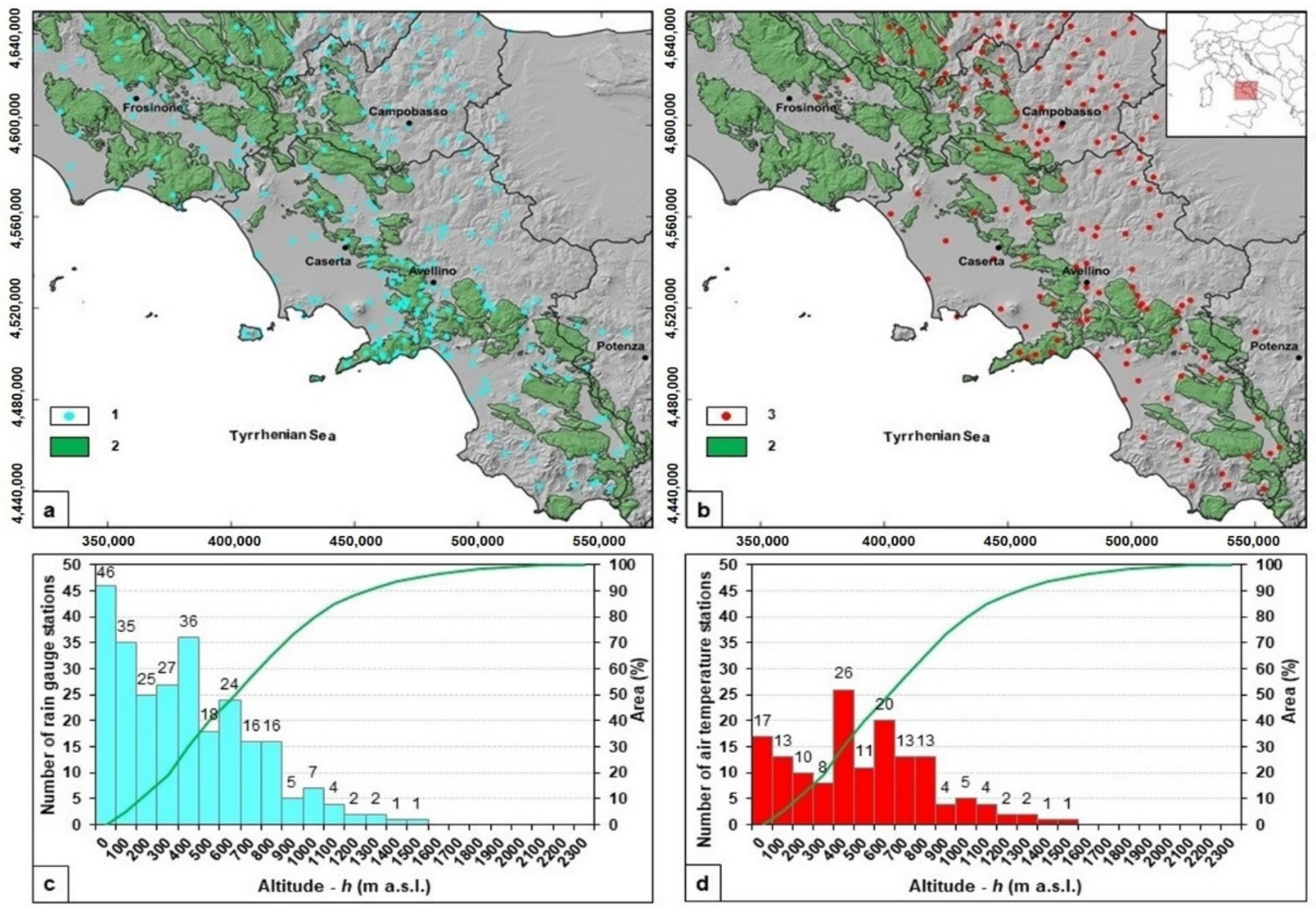
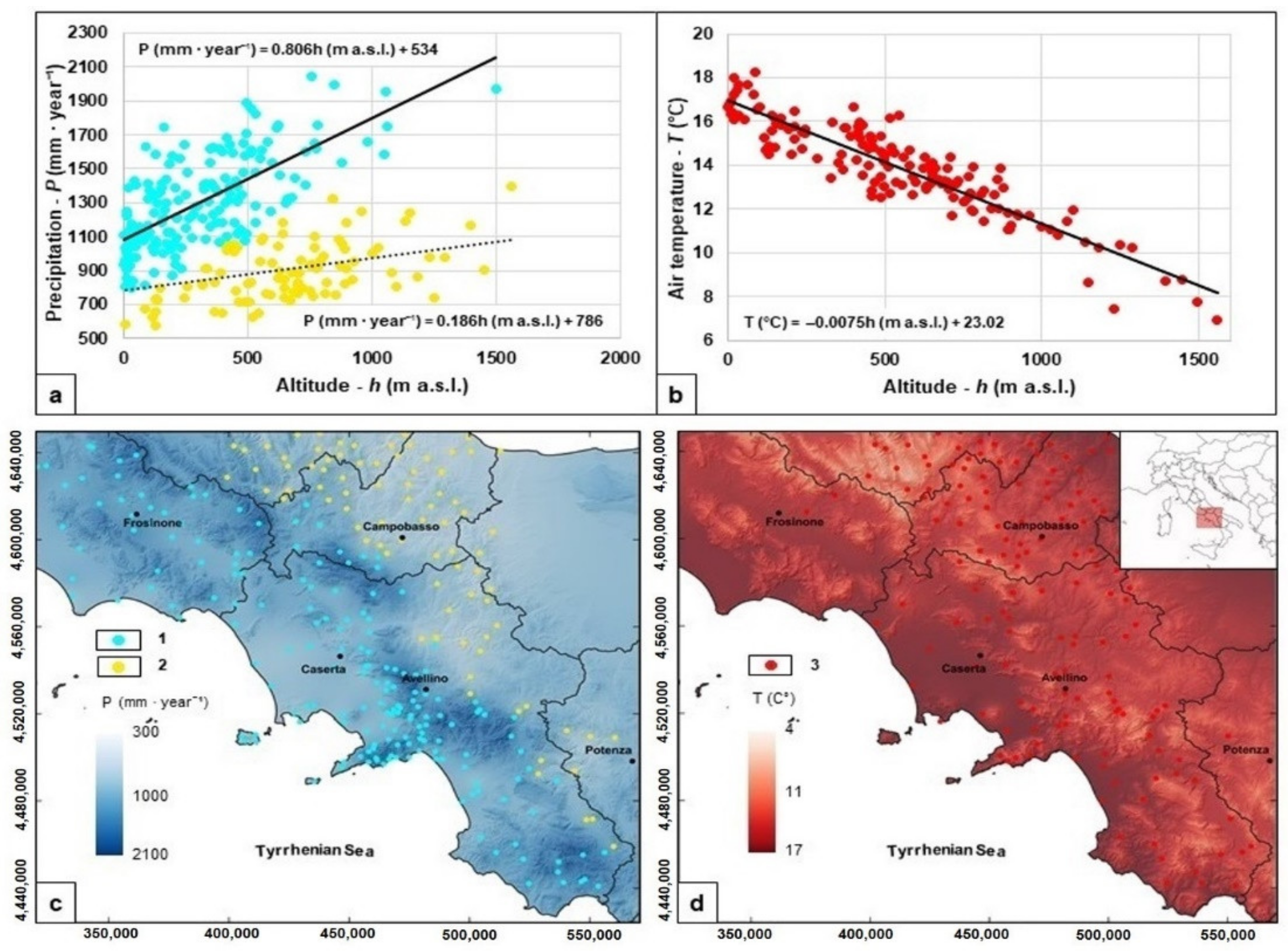
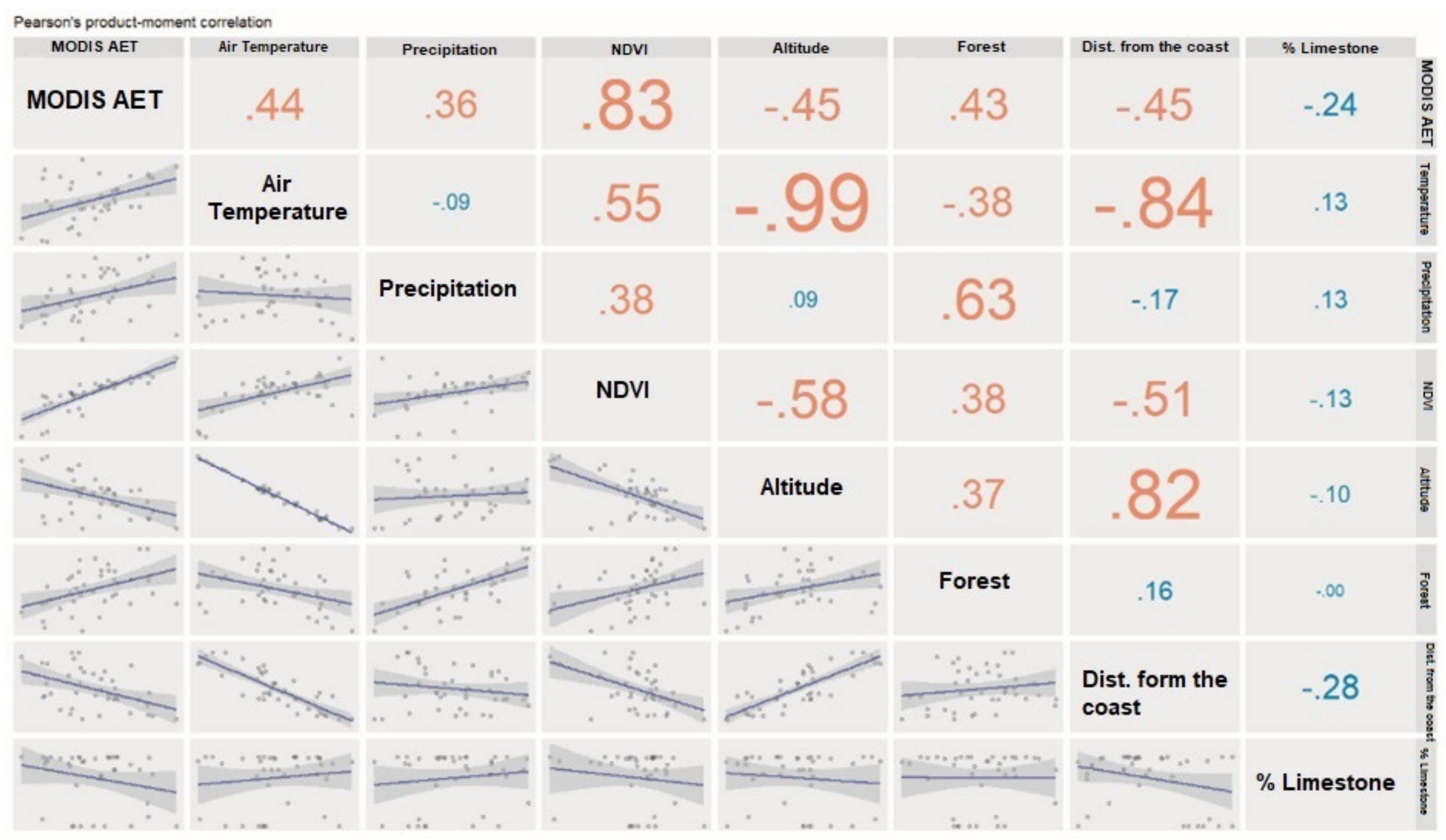
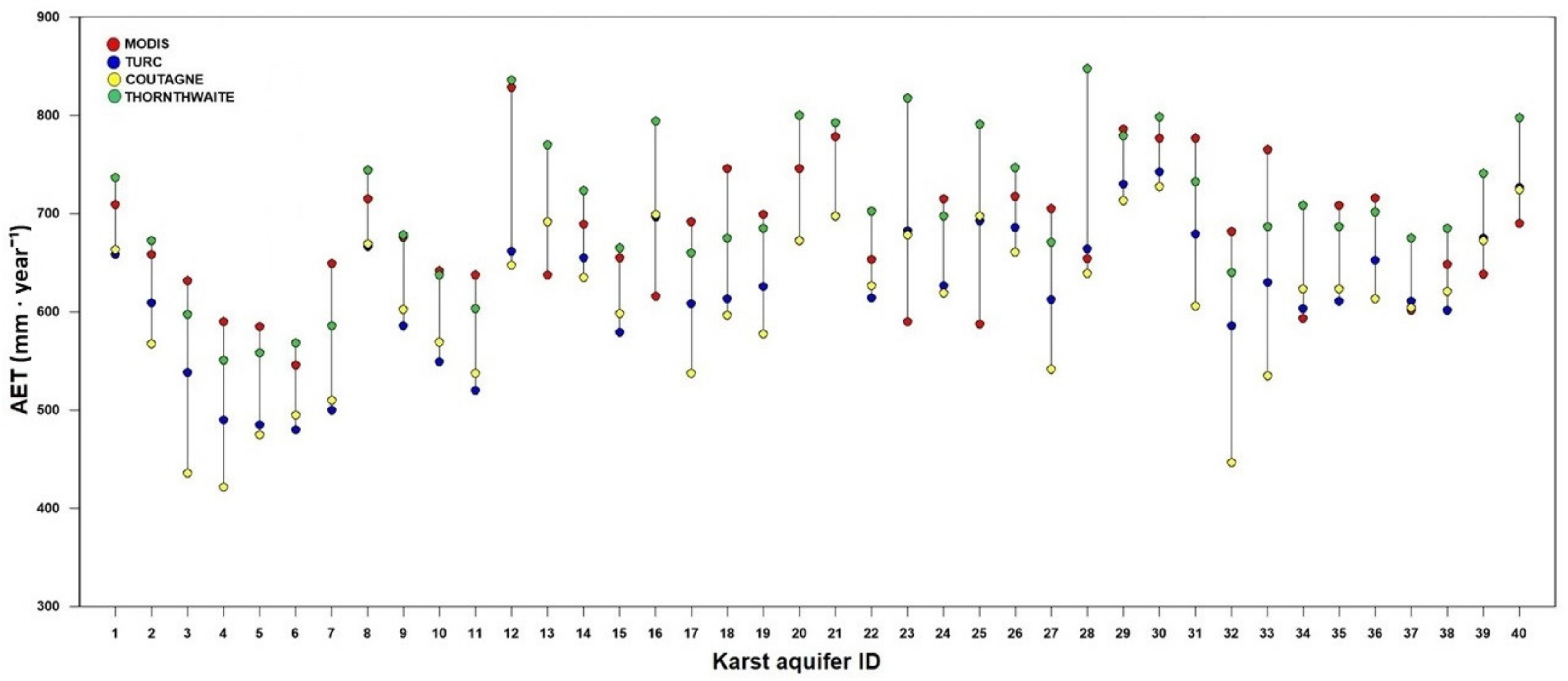
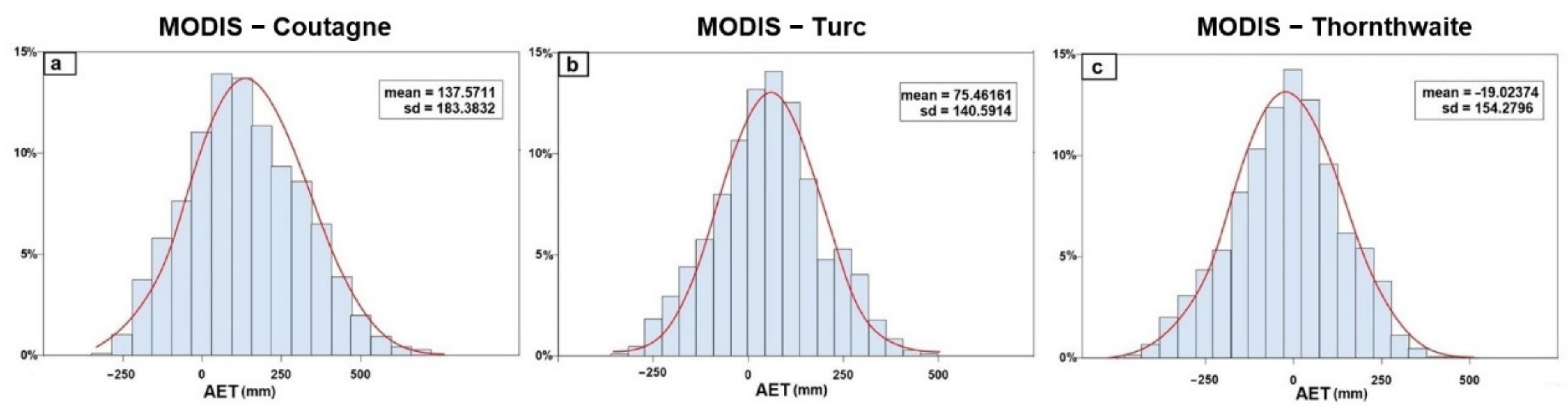
| ID | Karst Aquifer | Area (km2) | Limestone Area (%) | Summit Plateau and Endorheic Area (%) | AGRC (%) | AGRCS (%) | Average Altitude (m a.s.l.) |
|---|---|---|---|---|---|---|---|
| 1 | Cerella | 137 | 100 | 0 | 56 | 56 | 655 |
| 2 | Simbruini | 1076 | 94 | 12 | 62 | 57 | 952 |
| 3 | Cornacchia | 723 | 90 | 7 | 59 | 56 | 1324 |
| 4 | Marsicano | 204 | 94 | 5 | 58 | 56 | 1575 |
| 5 | Genzana | 277 | 10 | 34 | 66 | 49 | 1528 |
| 6 | Rotella | 40 | 100 | 40 | 77 | 62 | 1499 |
| 7 | Porrara | 64 | 100 | 25 | 69 | 59 | 1420 |
| 8 | Lepini | 483 | 100 | 2 | 57 | 57 | 617 |
| 9 | Colli Campanari | 97 | 0 | 12 | 54 | 48 | 863 |
| 10 | Capraro | 61 | 0 | 5 | 51 | 48 | 1114 |
| 11 | Campo | 16 | 0 | 13 | 55 | 48 | 1314 |
| 12 | Circeo | 7 | 0 | 0 | 48 | 48 | 163 |
| 13 | Ausoni | 826 | 99 | 15 | 64 | 58 | 607 |
| 14 | Venafro | 365 | 74 | 11 | 60 | 55 | 654 |
| 15 | Totila | 195 | 0 | 8 | 52 | 48 | 940 |
| 16 | Maio | 93 | 98 | 12 | 63 | 58 | 327 |
| 17 | Matese | 588 | 71 | 19 | 64 | 56 | 955 |
| 18 | Tre Confini | 28 | 0 | 4 | 50 | 48 | 913 |
| 19 | Moschiaturo | 85 | 0 | 7 | 51 | 48 | 865 |
| 20 | Massico | 29 | 89 | 0 | 55 | 55 | 334 |
| 21 | Maggiore | 173 | 99 | 0 | 56 | 56 | 344 |
| 22 | Camposauro | 50 | 99 | 4 | 58 | 56 | 807 |
| 23 | Tifatini | 65 | 90 | 2 | 56 | 56 | 257 |
| 24 | Taburno | 43 | 81 | 4 | 57 | 55 | 829 |
| 25 | Durazzano | 52 | 100 | 0 | 56 | 56 | 395 |
| 26 | Avella | 334 | 100 | 9 | 61 | 57 | 617 |
| 27 | Terminio | 167 | 100 | 43 | 78 | 62 | 934 |
| 28 | Capri | 9 | 93 | 0 | 56 | 56 | 152 |
| 29 | Lattari | 245 | 75 | 0 | 54 | 54 | 494 |
| 30 | Salerno | 46 | 13 | 0 | 49 | 49 | 362 |
| 31 | Accellica | 206 | 33 | 0 | 51 | 51 | 689 |
| 32 | Cervialto | 129 | 98 | 20 | 67 | 58 | 1119 |
| 33 | Polveracchio | 114 | 81 | 0 | 55 | 55 | 930 |
| 34 | Marzano | 308 | 97 | 13 | 63 | 57 | 808 |
| 35 | Alburni | 254 | 99 | 42 | 78 | 62 | 917 |
| 36 | Cervati | 318 | 81 | 13 | 62 | 56 | 862 |
| 37 | Motola | 52 | 100 | 4 | 59 | 57 | 1004 |
| 38 | Maddalena | 300 | 59 | 21 | 64 | 54 | 939 |
| 39 | Forcella | 217 | 86 | 5 | 58 | 56 | 676 |
| 40 | Bulgheria | 101 | 68 | 1 | 54 | 54 | 396 |
| ID | Karst Aquifer | Area (km2) | Coutagne (106 m3·year−¹) | Turc (106 m3·year−¹) | Thornthwaite (106 m3·year−¹) | MODIS AET (106 m3·year−¹) |
|---|---|---|---|---|---|---|
| 1 | Cerella | 137 | 51.7 | 51.3 | 42.6 | 44.3 |
| 2 | Simbruini | 1076 | 664.9 | 611.7 | 554.3 | 561.2 |
| 3 | Cornacchia | 723 | 464.5 | 410.9 | 380.7 | 366.9 |
| 4 | Marsicano | 204 | 111.5 | 96.6 | 88.6 | 84.0 |
| 5 | Genzana | 277 | 128.7 | 116.8 | 102.2 | 98.2 |
| 6 | Rotella | 40 | 17.6 | 16.6 | 13.9 | 14.6 |
| 7 | Porrara | 64 | 26.1 | 25.0 | 21.1 | 18.3 |
| 8 | Lepini | 483 | 211.1 | 206.0 | 175.2 | 180.7 |
| 9 | Colli Campanari | 97 | 30.9 | 30.8 | 25.0 | 25.4 |
| 10 | Capraro | 61 | 19.4 | 19.4 | 14.8 | 14.7 |
| 11 | Campo | 16 | 5.1 | 5.0 | 4.2 | 3.8 |
| 12 | Circeo | 7 | 1.0 | 1.0 | 0.4 | 0.5 |
| 13 | Ausoni | 826 | 374.8 | 368.1 | 302.3 | 372.4 |
| 14 | Venafro | 365 | 193.8 | 189.8 | 168.3 | 174.9 |
| 15 | Totila | 195 | 59.2 | 59.4 | 49.8 | 50.4 |
| 16 | Maio | 93 | 33.4 | 32.8 | 25.0 | 35.3 |
| 17 | Matese | 588 | 412.7 | 367.3 | 342.5 | 331.2 |
| 18 | Tre Confini | 28 | 11.5 | 11.0 | 9.9 | 8.8 |
| 19 | Moschiaturo | 85 | 41.9 | 39.9 | 36.2 | 35.8 |
| 20 | Massico | 29 | 7.1 | 7.0 | 4.5 | 5.6 |
| 21 | Maggiore | 173 | 53.9 | 52.8 | 41.8 | 42.9 |
| 22 | Camposauro | 50 | 19.8 | 19.2 | 16.1 | 17.7 |
| 23 | Tifatini | 65 | 14.8 | 14.4 | 8.6 | 17.0 |
| 24 | Taburno | 43 | 20.4 | 19.3 | 17.2 | 16.4 |
| 25 | Durazzano | 52 | 17.1 | 16.8 | 13.4 | 19.1 |
| 26 | Avella | 334 | 212.5 | 188.3 | 172.1 | 174.3 |
| 27 | Terminio | 167 | 143.3 | 127.9 | 117.7 | 114.0 |
| 28 | Capri | 9 | 1.4 | 1.3 | 0.4 | 1.2 |
| 29 | Lattari | 245 | 118.6 | 110.7 | 99.9 | 98.2 |
| 30 | Salerno | 46 | 18.8 | 17.8 | 16.1 | 16.2 |
| 31 | Accellica | 206 | 121.9 | 109.4 | 102.2 | 96.9 |
| 32 | Cervialto | 129 | 110.8 | 94.3 | 89.0 | 85.6 |
| 33 | Polveracchio | 114 | 75.9 | 65.7 | 61.5 | 56.4 |
| 34 | Marzano | 308 | 108.1 | 105.2 | 82.7 | 103.1 |
| 35 | Alburni | 254 | 139.8 | 133.2 | 113.0 | 109.1 |
| 36 | Cervati | 318 | 197.1 | 181.8 | 163.3 | 160.8 |
| 37 | Motola | 52 | 25.6 | 23.9 | 20.9 | 23.1 |
| 38 | Maddalena | 300 | 124.7 | 122.8 | 102.9 | 109.1 |
| 39 | Forcella | 217 | 97.0 | 94.4 | 80.3 | 92.4 |
| 40 | Bulgheria | 101 | 38.4 | 37.0 | 29.8 | 35.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruggieri, G.; Allocca, V.; Borfecchia, F.; Cusano, D.; Marsiglia, P.; De Vita, P. Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy. Water 2021, 13, 118. https://doi.org/10.3390/w13020118
Ruggieri G, Allocca V, Borfecchia F, Cusano D, Marsiglia P, De Vita P. Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy. Water. 2021; 13(2):118. https://doi.org/10.3390/w13020118
Chicago/Turabian StyleRuggieri, Giovanni, Vincenzo Allocca, Flavio Borfecchia, Delia Cusano, Palmira Marsiglia, and Pantaleone De Vita. 2021. "Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy" Water 13, no. 2: 118. https://doi.org/10.3390/w13020118
APA StyleRuggieri, G., Allocca, V., Borfecchia, F., Cusano, D., Marsiglia, P., & De Vita, P. (2021). Testing Evapotranspiration Estimates Based on MODIS Satellite Data in the Assessment of the Groundwater Recharge of Karst Aquifers in Southern Italy. Water, 13(2), 118. https://doi.org/10.3390/w13020118








