Flow Resistance in Open Channel Due to Vegetation at Reach Scale: A Review
Abstract
1. Introduction
2. Flow Resistance Equations
3. Descriptive and Photographic Comparison Approaches
4. Analytical Methods
4.1. Rigid Vegetation
4.1.1. Emergent Rigid Vegetation
4.1.2. Submerged Rigid Vegetation
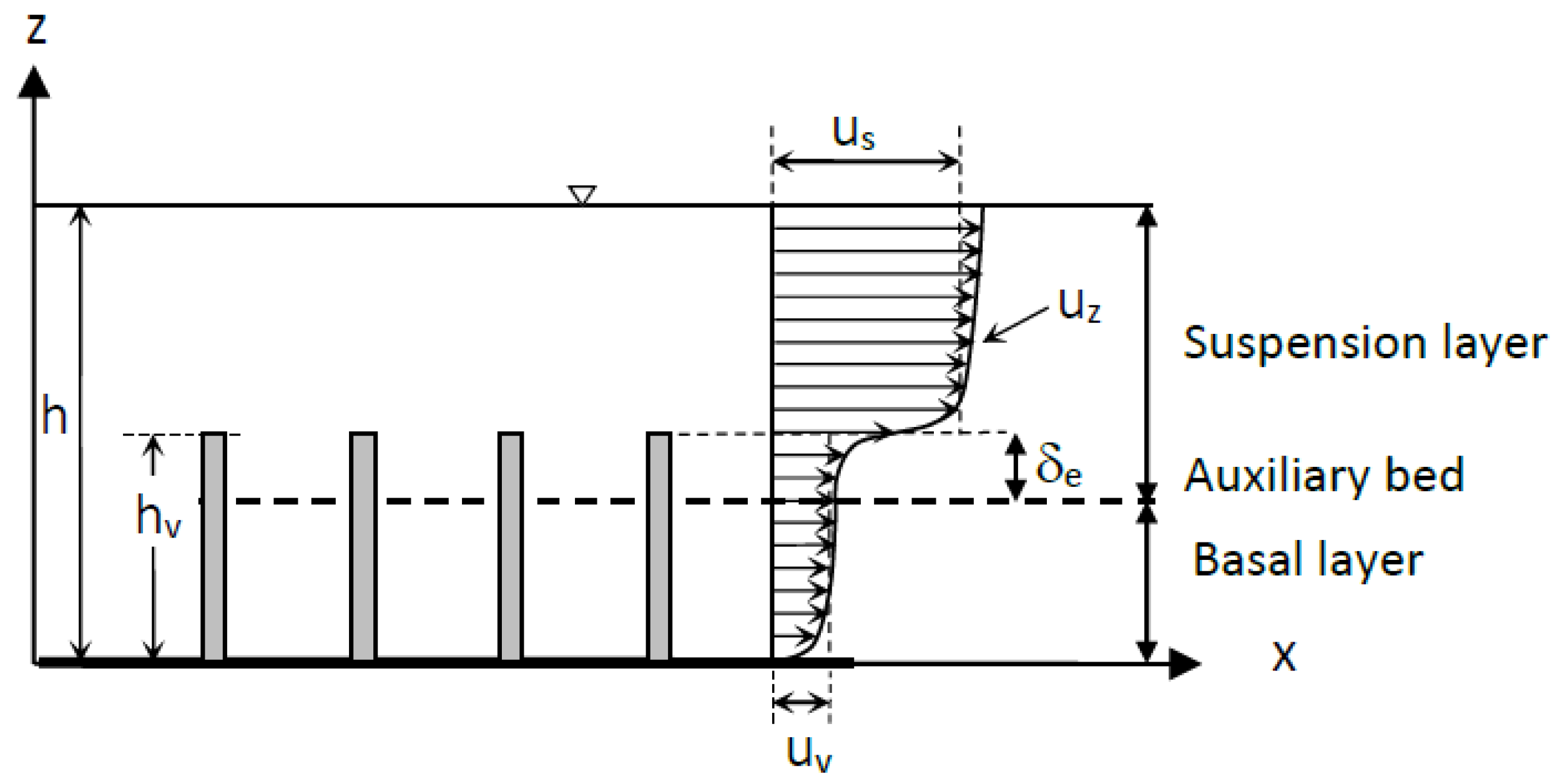
4.1.3. Submerged and Emergent Rigid Vegetation
4.2. Flexible Vegetation
4.2.1. Potentially Changing Vegetation Condition
4.2.2. Submerged Flexible Vegetation
4.2.3. Non-Submerged Flexible Vegetation
5. Numerical Methods
6. Hydraulic Roughness Assessment
7. Flow Resistance and Vegetation Management
8. Future Research and Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| A | area of water cross-section |
| a | projected plant area per unit volume |
| A0 | plant area projected onto a plan orthogonal to the flow direction when the plant is on free air |
| Ab | bed area related to a plant |
| Ac | characteristic area of plants |
| Ai | projected area of the ith plant on a plane normal to the streamwise direction |
| Ai* | net submerged frontal area of the plant in the plane normal to the flow direction |
| AL | one-sided leaf area |
| Ap | plant area projected onto a plan orthogonal to the flow direction when the plant is under the flow action |
| AS | total cross-sectional area of all of the stems of an individual plant, measured at a quarter of the non-deflected height of the plant |
| b | Vogel exponent |
| Bx | fraction of channel cross section blocked by vegetation |
| C | Chézy coefficient |
| Cb | Chézy coefficient of the bed |
| CD | drag coefficient |
| CDχ | species-specific drag coefficient |
| CDχ,F | species-specific drag coefficient of leaves |
| CDχ,S | species-specific drag coefficient of stems |
| Cf | Luhar-Nepf [11] friction coefficient |
| Ck | Chézy coefficient in the presence of emergent vegetation |
| Cr | Chézy coefficient in the presence of submerged rigid vegetation |
| Cu | coefficient in the Yang and Choi [76] model and in the Katul [87] model |
| C0, C1 | coefficient in the Kouwen model |
| D | vegetation diameter |
| E | modulus of elasticity |
| f | Darcy Weisbach friction factor |
| fc | function |
| FD | drag force |
| fv | friction factor due to vegetation |
| g | gravity acceleration |
| h | water depth or depth of the immersed part of the cylinder |
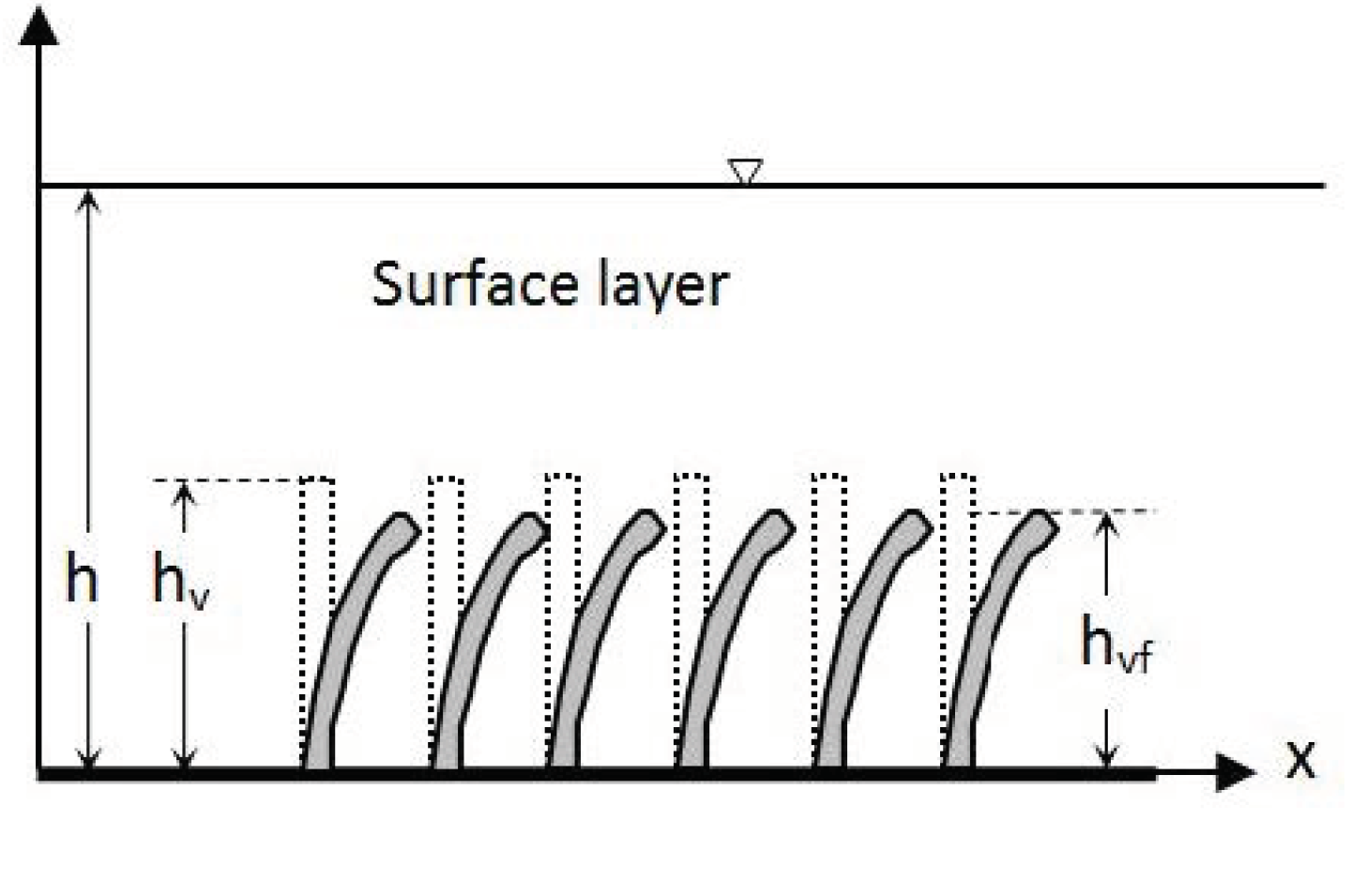
| hv | vegetation height or vegetation height in the absence of flow |
| hvf | bent vegetation height |
| representative length in Li et al. model [77] | |
| i | bed slope |
| I | second moment of the cross-sectional area of the stems |
| J | energy line slope |
| K | Gauckler-Strickler velocity coefficient |
| L | length of river reach |
| LAI | Leaf area index |
| M | number of stems per unit bed area |
| m | number of cylinders per unit bed area |
| MEI | flexural rigidity |
| n | Manning roughness coefficient |
| nb | soil Manning roughness coefficient |
| Q | discharge |
| R | hydraulic radius |
| ReD | stem Reynolds number (=VD/ν) |
| ReD* | vegetation Reynolds number calculate with the average pore velocity (=VvD/ν) |
| Rev | vegetation Reynolds number (=Vvrv/ν) |
| rv | vegetation-related hydraulic radius |
| rv* | dimensionless vegetation-related hydraulic radius |
| s | separation between individual resistance element |
| S | energy slope |
| SP | stream power |
| u | mean velocity along the vertical |
| us | mean velocity along the vertical in the surface layer in the case of submerged vegetation |
| uv | mean velocity along the vertical in the vegetated layer in the case of submerged vegetation |
| uz | local time-averaged velocity |
| shear velocity | |
| vegetal critical shear velocity | |
| V | mean flow velocity or approach velocity |
| Vv | average pore velocity |
| Vχ | lowest velocity used in determining χ in Västilä et al. [104] model |
| x | streamwise coordinate |
| z | vertical coordinate |
| α0E, α1E | coefficients in the Ergun relationship for the drag coefficient |
| αKA | characteristic eddy size coefficient in the Katul et al. [87] model |
| characteristic turbulence length scale in the Klopstra et al. model [73] | |
| β1, β2, β3 | numerical coefficients in the Carollo et al. [91] model |
| χ | vegetation parameter in Västilä et al. [104] model |
| χF | parameter in Västilä et al. [104] model relative to leaves |
| χS | parameter in Västilä et al. [104] model relative to stems |
| δe | depth of penetration of suspension layer in vegetation in Li et al. [77] model |
| γ | water specific weight |
| λ | density of vegetation |
| ν | water kinematic viscosity |
| ξ | parameter that takes into account the deformation of the plant |
| ξE | vegetation index |
| ρ | water density |
References
- Penman, H.L. Vegetation and Hydrology; Commonwealth Agricultural Bureau: Harpenden, UK, 1963; p. 124. [Google Scholar]
- Peel, M.C. Hydrology: Catchment vegetation and runoff. Prog. Phys. Geog. 2009, 33, 837–844. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Ferrari, E.; Iovino, F.; Nicolaci, A.; Veltri, A. Reforestation and land use change in a drainage basin of Southern Italy. iForest 2013, 6, 175–182. [Google Scholar] [CrossRef]
- Rowiński, P.M.; Västilä, K.; Aberle, J.; Järvelä, J.; Kalinowska, M. How vegetation can aid in coping with river management challenges: A brief review. Ecohydrol. Hydrobiol. 2018, 18, 345–354. [Google Scholar] [CrossRef]
- Wynn, T.S.; Mostaghimi, S. The effects of vegetation and soil type on streambank erosion, southwestern Virginia, USA. J. Am. Water Resour. Assoc. 2006, 42, 69–82. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Dey, S. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment. Res. 2009, 24, 236–246. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Krzeminska, D.; Kerkhof, T.; Skaalsveen, K.; Stolte, J. Effect of riparian vegetation on stream bank stability in small agricultural catchments. Catena 2019, 172, 87–96. [Google Scholar] [CrossRef]
- Julien, P.Y. River Mechanics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Green, J.C. Comparison of blockage factors in modelling the resistance of channels containing submerged macrophytes. River Res. Appl. 2005, 21, 671–686. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherfurd, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Environ. Modell. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Rutherfurd, I.D.; Anderson, B.; Ladson, A. Managing the effects of riparian vegetation on flooding. In Principles for Riparian Lands Management; Lovett, S., Price, P., Eds.; Land and Water Australia: Canberra, Australia, 2007; p. 190. [Google Scholar]
- Dawson, F.H.; Charlton, F.G. Bibliography on the Hydraulic Resistance or Roughness of Vegetated Watercourses; Occasional Publication No. 25; Freshwater Biological Association: Ambleside, UK, 1998; p. 25. ISBN 0308-6739. [Google Scholar]
- Curran, J.C.; Hession, W.C. Vegetative impacts on hydraulics and sediment processes across the fluvial system. J. Hydrol. 2013, 505, 364–376. [Google Scholar] [CrossRef]
- Hession, W.C.; Curran, J.C. The impact of vegetation on roughness in fluvial systems. In Treatise on Geomorphology; Shroder, J.F., Butler, D.R., Hupp, C.R., Eds.; Ecogeomorphology; Academic Press: San Diego, CA, USA, 2013; Volume 12, pp. 75–93. [Google Scholar]
- Marjoribanks, T.I.; Hardy, R.J.; Lane, S.N. The hydraulic description of vegetated river channels: The weaknesses of existing formulations and emerging alternatives. WIREs Water 2014, 1, 549–560. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, S.; Wang, P.; Hou, J. Interactions between vegetation, water flow and sediment transport: A review. J. Hydrodyn. 2015, 27, 24–37. [Google Scholar] [CrossRef]
- Maji, S.; Hanmaiahgari, P.R.; Balachandar, R.; Pu, J.H.; Ricardo, A.M.; Ferreira, R.M. A Review on hydrodynamics of free surface flows in emergent vegetated channels. Water 2020, 12, 1218. [Google Scholar] [CrossRef]
- Yen, B.C. Open channel flow resistance. J. Hydraul. Eng. 2002, 128, 20–39. [Google Scholar] [CrossRef]
- Yang, J.Q.; Kerger, F.; Nepf, H.M. Estimation of the bed shear stress in vegetated and bare channels with smooth bed. Water Resour. Res. 2015, 51, 3647–3663. [Google Scholar] [CrossRef]
- Liu, D.; Valyrakis, M.; Williams, R. Flow hydrodynamics across open channel flows with riparian zones: Implications for riverbank stability. Water 2017, 9, 720. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 045102. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. A modified log-law of flow velocity distribution in partly obstructed open channels. Environ. Fluid Mech. 2016, 16, 453–479. [Google Scholar] [CrossRef]
- Yang, J.Q.; Chung, H.; Nepf, H.M. The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 2016, 43, 11261–11268. [Google Scholar] [CrossRef]
- Tang, C.; Lei, J.; Nepf, H.M. Impact of vegetation-generated turbulence on the critical, near-bed, wave-velocity for sediment resuspension. Water Resour. Res. 2019, 55, 5904–5917. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Characterizing natural riparian vegetation for modeling of flow and suspended sediment transport. J. Soils Sediments 2018, 18, 3114–3130. [Google Scholar] [CrossRef]
- Box, W.; Västilä, K.; Järvelä, J. The interplay between flow field, suspended sediment concentration, and net deposition in a channel with flexible bank vegetation. Water 2019, 11, 2250. [Google Scholar] [CrossRef]
- Yang, J.Q.; Nepf, H.M. Impact of vegetation on bed load transport rate and bedform characteristics. Water Resour. Res. 2019, 55, 6109–6124. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V. Bed-load through emergent vegetation. Adv. Water Resour. 2019, 129, 250–259. [Google Scholar] [CrossRef]
- Li, J.F.; Tfwala, S.S.; Chen, S.C. Effects of vegetation density and arrangement on sediment budget in a sediment-laden flow. Water 2018, 10, 1412. [Google Scholar] [CrossRef]
- Sukhodolova, T.; Sukhodolov, A. Vegetated mixing layer around a finite-size patch of submerged plants: 1. Theory and field experiments. Water Resour. Res. 2012, 48, W10533. [Google Scholar] [CrossRef]
- Sukhodolov, A.N.; Sukhodolova, T.A. Vegetated mixing layer around a finite-size patch of submerged plants: 2. Turbulence and coherent structures. Water Resour. Res. 2012, 48, W12506. [Google Scholar] [CrossRef]
- Yilmazer, D.; Ozan, A.Y.; Cihan, K. Flow characteristics in the wake region of a finite-length vegetation patch in a partly vegetated channel. Water 2018, 10, 459. [Google Scholar] [CrossRef]
- Li, W.; Wang, D.; Jiao, J.; Yang, K. Effects of vegetation patch density on flow velocity characteristics in an open channel. J. Hydrodyn. 2018. [Google Scholar] [CrossRef]
- Cheng, N.S.; Hui, C.L.; Wang, X.; Tan, S.K. Laboratory study of porosity effect on drag induced by circular vegetative patch. J. Eng. Mech. 2019, 145. [Google Scholar] [CrossRef]
- Kitsikoudis, V.; Yagci, O.; Kirca, V.S.O. Experimental analysis of flow and turbulence in the wake of neighboring emergent vegetation patches with different densities. Environ. Fluid Mech. 2020, 1417–1439. [Google Scholar] [CrossRef]
- Yan, C.; Shan, Y.; Sun, W.; Liu, C.; Liu, X. Modeling the longitudinal profiles of streamwise velocity in an open channel with a model patch of vegetation. Environ. Fluid Mech. 2020, 1441–1462. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Analytical model for predicting the longitudinal profiles of velocities in a channel with a model vegetation patch. J. Hydrol. 2019, 576, 561–574. [Google Scholar] [CrossRef]
- Mossa, M.; De Serio, F. Rethinking the process of detrainment: Jets in obstructed natural flows. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Mossa, M.; Ben Meftah, M.; De Serio, F.; Nepf, H.M. How vegetation in flows modifies the turbulent mixing and spreading of jets. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- De Serio, F.; Ben Meftah, M.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017, 120, 98–113. [Google Scholar] [CrossRef]
- Termini, D. Turbulent mixing and dispersion mechanisms over flexible and dense vegetation. Acta Geophys. 2019, 67, 961–970. [Google Scholar] [CrossRef]
- Zhang, J.; Huai, W.X.; Shi, H.R.; Wang, W.J. Estimation of the longitudinal dispersion coefficient using a two-zone model in a channel partially covered with artificial emergent vegetation. Environ. Fluid Mech. 2020. [Google Scholar] [CrossRef]
- Yamasaki, T.N.; de Lima, P.H.; Silva, D.F.; Cristiane, G.D.A.; Janzen, J.G.; Johannes, G.; Nepf, H.M. From patch to channel scale: The evolution of emergent vegetation in a channel. Adv. Water Res. 2019, 129, 131–145. [Google Scholar] [CrossRef]
- Mulahasan, S.; Stoesser, T. Flow resistance of in-line vegetation in open channel flow. Int. J. River Basin Manag. 2017, 15, 329–334. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill Book Co.: New York, NY, USA, 1959; p. 680. [Google Scholar]
- Rouse, H. Fluid Mechanics for Hydraulic Engineers; McGraw-Hill Book Co.: New York, NY, USA, 1938; p. 422. [Google Scholar]
- Cowan, W.L. Estimating hydraulic roughness coefficients. J. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Barnes, H.H., Jr. Roughness Characteristics of Natural Channels; U.S. Geological Survey Water-Supply Paper; Paper 1849; United States Government Printing Office: Washington, DC, USA, 1967; p. 213.
- Phillips, J.V.; Ingersoll, J.V. 1998a—Verification of Roughness Coefficients for Selected Natural and Constructed Stream Channels in Arizona; Professional Paper 1584; U.S. Geological Survey: Denver, CO, USA, 1998; p. 77.
- Coon, W.F. Estimation of Roughness Coefficients for Natural Stream Channels with Vegetated Banks; U.S. Geological Survey Water-Supply Paper; Paper 2441; United States Government Printing Office: Denver, CO, USA, 1998; p. 133.
- Land & Water Australia. An Australian Handbook of Stream Roughness Coefficients; Australian Government: Canberra, Australia, 2009; p. 29.
- Arcement, G.J., Jr.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; U.S. Geological Survey Water-Supply Paper; Paper 2339; United States Government Printing Office: Denver, CO, USA, 1989; p. 38.
- Petryk, S.; Bosmajian, G. Analysis of flow through vegetation. J. Hydraul. Div. 1975, 101, 871–884. [Google Scholar]
- Li, R.M.; Shen, H.W. Effect of tall vegetations on flow and sediment. J. Hydraul. Div. 1973, 99, 793–814. [Google Scholar]
- Nepf, H.M. Drag, turbulence and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, F04015. [Google Scholar] [CrossRef]
- Petryk, S. Drag on Cylinders in Open Channel Flow. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1969. [Google Scholar]
- Stone, M.C.; Shen, H.T. Hydraulic resistance of flow in channel with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, V.; Rodríguez Uthurburu, J.; Keijzer, M.; Uittenbogaard, R.E.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Mizuhara, K.; Ashida, S. Effect of density of trees on drag exerted on trees in river channels. J. For. Res. 2000, 5, 271–279. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Lauria, A.; Alfonsi, G.; Calomino, F. Investigation of flow resistance exerted by rigid emergent vegetation in open channel. Acta Geophys. 2019, 67, 971–986. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Cheng, N.S.; Nguyen, H.T. Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flow. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Wang, H.; Tang, H.W.; Yuan, S.Y.; Lv, S.Q.; Zhao, X.Y. An experimental study of the incipient bed shear stress partition in mobile bed channels filled with emergent rigid vegetation. Sci. China Technol. Sci. 2014, 57, 1165–1174. [Google Scholar] [CrossRef]
- Sonnenwald, F.; Stovin, V.; Guymer, I. Estimating drag coefficient for arrays of rigid cylinders representing emergent vegetation. J. Hydraul. Res. 2018. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Tinoco, R.O.; Cowen, E.A. The direct and indirect measurement of boundary stress and drag on individual and complex array of elements. Exp. Fluids 2013, 54, 1–16. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Klopstra, D.; Barneveld, H.J.; van Noortwijk, J.; van Velzen, E. Analytical model for hydraulic roughness of submerged vegetation. In Proceedings of the 27th IAHR Congress, San Francisco, CA, USA, 10–15 August 1997; pp. 775–780. [Google Scholar]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41, W07006. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.; Hulscher, S. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43, W06413. [Google Scholar] [CrossRef]
- Yang, W.; Choi, S. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48, 466–475. [Google Scholar] [CrossRef]
- Li, S.; Shi, H.; Xiong, Z.; Huai, W.; Cheng, N. New formulation for the effective relative roughness height of open channel flows with submerged vegetation. Adv. Water Resour. 2015, 86, 46–57. [Google Scholar] [CrossRef]
- Augustijn, D.C.M.; Galema, A.A.; Huthoff, F. Evaluation of flow formulas for submerged vegetation. In Proceedings of the EUROMECH Colloquium 523 Ecohydraulics: Linkages Between Hydraulics, Morphodynamics and Ecological Processes in University Blaise Pascal Clermont-Ferrand, Organiser Maison des Sciences de l’Homme (MSH), 4 rue Ledru, Clermont-Ferrand, France, 15–17 June 2011. [Google Scholar]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth Surf. Process. Landform 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Morri, M.; Soualmia, A.; Belleudy, P. Mean velocity modeling of open chnnel flow with submerged rigid vegetation. Int. J. Mech. Mechatron. Eng. 2015, 9, 302–307. [Google Scholar]
- Pasquino, V.; Gualtieri, P. Flow resistance of submerged rigid vegetation: Focus and validation on two layer approach. In Proceedings of the 37th IAHR World Congress, Kuala Lampur, Malaysia, 13–18 August 2017; pp. 2502–2510. [Google Scholar]
- Romdhane, H.; Soualmia, A.; Cassan, L.; Dartus, D. Flow over flexible vegetated bed: Evaluation of analytical models. J. Appl. Fluid Mech. 2019, 12, 351–359. [Google Scholar] [CrossRef]
- Tang, X. Evaluating two-layer models for velocity profiles in open-channels with submerged vegetation. J. Geosci. Environ. Prot. 2019, 7, 68–80. [Google Scholar] [CrossRef]
- Cheng, N.S. Representative roughness height of submerged vegetation. Water Resour. Res. 2011, 47, W08517. [Google Scholar] [CrossRef]
- Van Velzen, E.; Jesse, P.; Cornelissen, P.; Coops, H. Stromingsweerstand Vegetatie in Uiterwaarden; Handboek; Part 1 and 2 Technical Report; RIZA Reports 2003.028 and 2003.029; Rijksinstituut voor Integraal Zoetwaterbeheer en Afvalwaterbehandeling—RIZA: Arnhem, The Netherlands, 2003. [Google Scholar]
- López, F.; García, M. Open Channel Flow Through Simulated Vegetation: Turbulence Modeling and Sediment Transport; U.S. Army Corps of Engineers, Waterways Experiment Station; Wetland Research Technical Report WRP-CP-10; U.S. Army Corps of Engineers: Washington, DC, USA, 1997; p. 106. [Google Scholar]
- Katul, G.; Wiberg, P.; Albertson, J.; Hornberger, G. A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 2002, 38, 1250. [Google Scholar] [CrossRef]
- Abu-Aly, T.R.; Pasternack, G.B.; Wyrick, J.R.; Barker, R.; Massa, D.; Johnson, T. Effect of LiDAR-derived, spatially distributed vegetation roughness on two-dimensional hydraulics in a gravel-cobble river at flows of 0.2 to 20 times bankfull. Geomorphology 2014, 206, 468–482. [Google Scholar] [CrossRef]
- Phillips, J.V.; McDoniel, D.; Capesius, J.P.; Asquith, W. 1998b—Method to Estimate Effects of Flow-Induced Vegetation Changes on Channel Conveyances of Streams in Central Arizona; Water-Resources Investigations Report 98-4040; U.S. Geological Survey: Tucson, AZ, USA, 1998; p. 43.
- Phillips, J.V.; Tadayon, S. Selection of Manning’s Roughness Coefficient for Natural and Constructed Vegetated and Non-Vegetated Channels, and Vegetation Maintenance Plan Guidelines for Vegetated Channels in Central Arizona; Scientific Investigations Report 2006-5108; U.S. Geological Survey: Reston, VA, USA, 2007; p. 41.
- Carollo, F.G.; Ferro, V.; Termini, D. Flow resistance law in channel with flexible submerged vegetation. J. Hydraul. Eng. 2005, 131, 554–564. [Google Scholar] [CrossRef]
- Francalanci, S.; Paris, E.; Solari, L. On the vulnerability of woody riparian vegetation during flood events. Environ. Fluid Mech. 2020, 20, 635–661. [Google Scholar] [CrossRef]
- Armanini, A.; Righetti, M.; Grisenti, P. Direct measurement of vegetation resistance in prototype scale. J. Hydraul. Res. 2005, 42, 481–487. [Google Scholar] [CrossRef]
- Palmer, V.J. A method for designing vegetated waterways. J. Agric. Eng. 1945, 26, 516–520. [Google Scholar]
- Soil Conservation Service Handbook of Channel Design for Soil and Water Conservation; SCS-TP-61; United States Department of Agriculture: Washington, DC, USA, 1966.
- Ree, W.O.; Crow, F.R. Friction Factors for Vegetated Waterways of Small Slope; Pub. ARS-S-151; USDA Agricultural Research Service: Washington, DC, USA, 1977.
- Gwinn, W.R.; Ree, W.O. Maintenance effects on the hydraulic properties of a vegetation lined channel. Trans. of the ASAE 1980, 23, 636–642. [Google Scholar] [CrossRef]
- Temple, D.M.; Robinson, K.M.; Ahring, R.M.; Davis, A.G. Stability Design of Grass-Lined Open Channels; Agriculture Handbook Number 667; United States Department of Agriculture; United States Government Printing Office: Washington, DC, USA, 1987; p. 167.
- Kouwen, N.; Li, R.M.; Simons, D.B. Flow resistance in vegetated waterways. Trans. ASAE 1981, 24, 684–698. [Google Scholar] [CrossRef]
- Kouwen, N.; Unny, T.E. Flexible roughness in open channels. J. Hydraul. Eng. 1973, 99, 713–728. [Google Scholar]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Kouwen, N.; Fathi-Moghadam, M. Friction factors for coniferous trees along rivers. J. Hydraul. Eng. 2000, 126, 732–740. [Google Scholar] [CrossRef]
- Freeman, G.E.; Rahmeyer, W.J.; Copeland, R. Determination of Resistance Due to Shrubs and Woody Vegetation; ERDC/CHL TR-00-25; Engineer Research and Development Center, US Army Corps of Engineers: Washington, DC, USA, 2000. [Google Scholar]
- Västilä, K.; Järvelä, J.; Aberle, J. Characteristic reference areas for estimating flow resistance of natural foliated vegetation. J. Hydrol. 2013, 492, 49–60. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J. Estimation of drag forces caused by natural woody vegetation of different scales. J. Hydrodyn. 2014, 26, 608–623. [Google Scholar] [CrossRef]
- Fathi-Moghadam, M.; Kowen, N. Non-rigid, non-submerged, vegetation roughness in flood plains. J. Hydraul. Eng. 1997, 123, 51–57. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Koll, K.; Franca, M.J.; Schleiss, A.J.; Ferreira, R.M.L. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res. 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Caroppi, G.; Gualtieri, P.; Fontana, N.; Giugni, M. Vegetated channel flows: Turbulence anisotropy at flow–rigid canopy interface. Geosciences 2018, 8, 259. [Google Scholar] [CrossRef]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Rowiński, P.M.; Giugni, M. Turbulence at water-vegetation interface in open channel flow: Experiments with natural-like plants. Adv. Water Resour. 2019, 127, 180–191. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed roughness effects on the turbulence characteristics of flows through emergent rigid vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Anisotropy in the free stream region of turbulent flows through emergent rigid vegetation on rough beds. Water 2020, 12, 2464. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds Averaged Navier-Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, Art. 040802. [Google Scholar] [CrossRef]
- Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge coefficients for sluice gates set in weirs at different upstream wall inclinations. Water 2020, 12, 245. [Google Scholar] [CrossRef]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and numerical study of free-surface flows in a corrugated pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef]
- Alfonsi, G.; Ferraro, D.; Lauria, A.; Gaudio, R. Large-eddy simulation of turbulent natural-bed flow. Phis. Fluids 2019, 31, 085105. [Google Scholar] [CrossRef]
- Stoesser, T.; Neary, V.; Wilson, C.A.M.E. Modelling vegetated channel flows: Challenges and opportunities. In Proceedings of the WSEAS (The World Scientific and Engineering Academy and Society) Conference on Fluid Mechanics, Corfu, Greece, 20–22 August 2005. [Google Scholar]
- Cui, J.; Neary, V.S. Large eddy simulation (LES) of fully developed flow through vegetation. In Proceedings of the Fifth International Conference on Hydroinformatics, Cardiff, UK, 1–5 July 2002. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. Recent results from analysis of flow structures and energy modes induced by viscous wave around a surface-piercing cylinder. Math. Probl. Eng. 2017, 10, Art. 5875948. [Google Scholar] [CrossRef]
- Alfonsi, G.; Lauria, A.; Primavera, L. A study of vortical structures past the lower portion of the Ahmed car model. J. Flow Vis. Image Process. 2012, 19, 81–95. [Google Scholar] [CrossRef]
- Fischer-Antze, T.; Stoesser, T.; Bates, P.; Olsen, N.R.B. 3D numerical modelling of open-channel flow with submerged vegetation. J. Hydraul. Res. 2001, 39, 303–310. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T. Numerical analysis of turbulent open channel flow over a vegetation layer using a k−ε turbulence model. J. Hydrosci. Hydraul. Eng. 1994, 11, 57–67. [Google Scholar]
- Choi, S.U.; Kang, H. Reynolds stress modeling of vegetated open-channel flows. J. Hydraul. Res. 2004, 42, 3–11. [Google Scholar] [CrossRef]
- López, F.; García, M. Mean flow and turbulent structure of open channel flow through non-emergent vegetation. J. Hydraul. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- Kim, S.J.; Stoesser, T. Closure modeling and direct simulation of vegetation drag in flow through emergent vegetation. Water Resour. Res. 2011, 47, W10511. [Google Scholar] [CrossRef]
- Stoesser, T.; Wilson, C.A.M.E.; Bates, P.D.; Dittrich, A. Application of a 3D numerical model to a river with vegetated floodplains. J. Hydroinform. 2003, 5, 99–112. [Google Scholar] [CrossRef]
- Dudley, S.J.; Bonham, C.D.; Abt, S.R.; Fischenich, J.G. Comparison of methods for measuring woody riparian vegetation density. J. Arid Environ. 1998, 38, 77–86. [Google Scholar] [CrossRef]
- Hohenthal, J.; Alho, P.; Hyyppa, J.; Hyyppa, H. 2011—Laser scanning applications in fluvial studies. Prog. Phys. Geog. 2011, 35, 782–809. [Google Scholar] [CrossRef]
- Tomsett, C.; Leyland, J. Remote sensing of river corridors: A review of current trends and future directions. River Res. Appl. 2019, 35, 779–803. [Google Scholar] [CrossRef]
- Huylenbroeck, L.; Laslier, M.; Dufour, S.; Georges, B.; Lejeune, P.; Michez, A. Using remote sensing to characterize riparian vegetation: A review of available tools and perspectives for managers. J. Environ. Manag. 2019, 267. [Google Scholar] [CrossRef]
- Forzieri, G.; Castelli, F.; Preti, F. Advances in remote sensing of hydraulic roughness. Int. J. Remote Sens. 2012, 33, 630–654. [Google Scholar] [CrossRef]
- Van der Sande, C.J.; De Jong, S.M.; De Roo, A.P.J. A segmentation and classification approach of IKONOS-2 imagery for land cover mapping to assist flood risk and flood damage assessment. Int. J. Appl. Earth Obs. 2003, 4, 217–229. [Google Scholar] [CrossRef]
- Forzieri, G.; Degetto, M.; Righetti, M.; Castelli, F.; Preti, F. Satellite multispectral data for improved floodplain roughness modelling. J. Hydrol. 2011, 407, 41–57. [Google Scholar] [CrossRef]
- Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Multiple attribute decision-making for individual tree detection using high-resolution laser scanning. Forest Ecol. Manag. 2009, 258, 2501–2510. [Google Scholar] [CrossRef]
- Jalonen, J.; Järvelä, J.; Virtanen, J.P.; Vaaja, M.; Kurkela, M.; Hyyppa, H. Determining characteristic vegetation areas by terrestrial laser scanning for floodplain flow modeling. Water 2015, 7, 420–437. [Google Scholar] [CrossRef]
- Errico, A.; Lama, G.F.C.; Francalanci, S.; Chirico, G.B.; Solari, L.; Preti, F. Flow dynamics and turbulence patterns in a drainage channel colonized by common reed (Phragmites australis) under different scenarios of vegetation management. Ecol. Eng. 2019, 133, 39–52. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Veltri, M. Influenza della vegetazione sulle portate al colmo in un tratto di un piccolo bacino. In Proceedings of the Atti del Terzo Congresso Nazionale di Selvicoltura Per il Miglioramento e la Conservazione Dei Boschi Italiani, Taormina (Messina), Italy, 16–19 October 2008; 2009; pp. 475–481. (In Italian). [Google Scholar]
- Benifei, R.; Solari, L.; Vargas_Luna, A.; Geerling, G.; van Oorschot, M. Effects of vegetation on flooding: The study case of the Magra river. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Tsujimoto, T. Fluvial processes in streams with vegetation. J. Hydraul. Res. 1999, 37, 789–803. [Google Scholar] [CrossRef]
- Camporeale, C.; Perucca, E.; Ridolfi, L.; Gurnell, A.M. Modeling the interactions between river morphodynamics and riparian vegetation. Rev. Geophys. 2013, 51, 379–414. [Google Scholar] [CrossRef]
- Xu, Z.X.; Ye, C.; Zhang, Y.Y.; Wang, X.K.; Yan, X.F. 2D numerical analysis of the influence of near-bank vegetation patches on the bed morphological adjustment. Environ. Fluid Mech. 2020, 20, 707–738. [Google Scholar] [CrossRef]
- Shields, D.F., Jr.; Coulton, K.G.; Nepf, H. Representation of vegetation in two-dimensional hydrodynamic models. J. Hydraul. Eng. 2017, 143, 1–9. [Google Scholar] [CrossRef]
- Dombroski, D. A deterministic Spatially-Distributed Ecohydraulic Model for Improved Riverine System Management; Technical Rep. No. SRH-2014-26; Bureau of Reclamation: Denver, CO, USA, 2014. [Google Scholar]
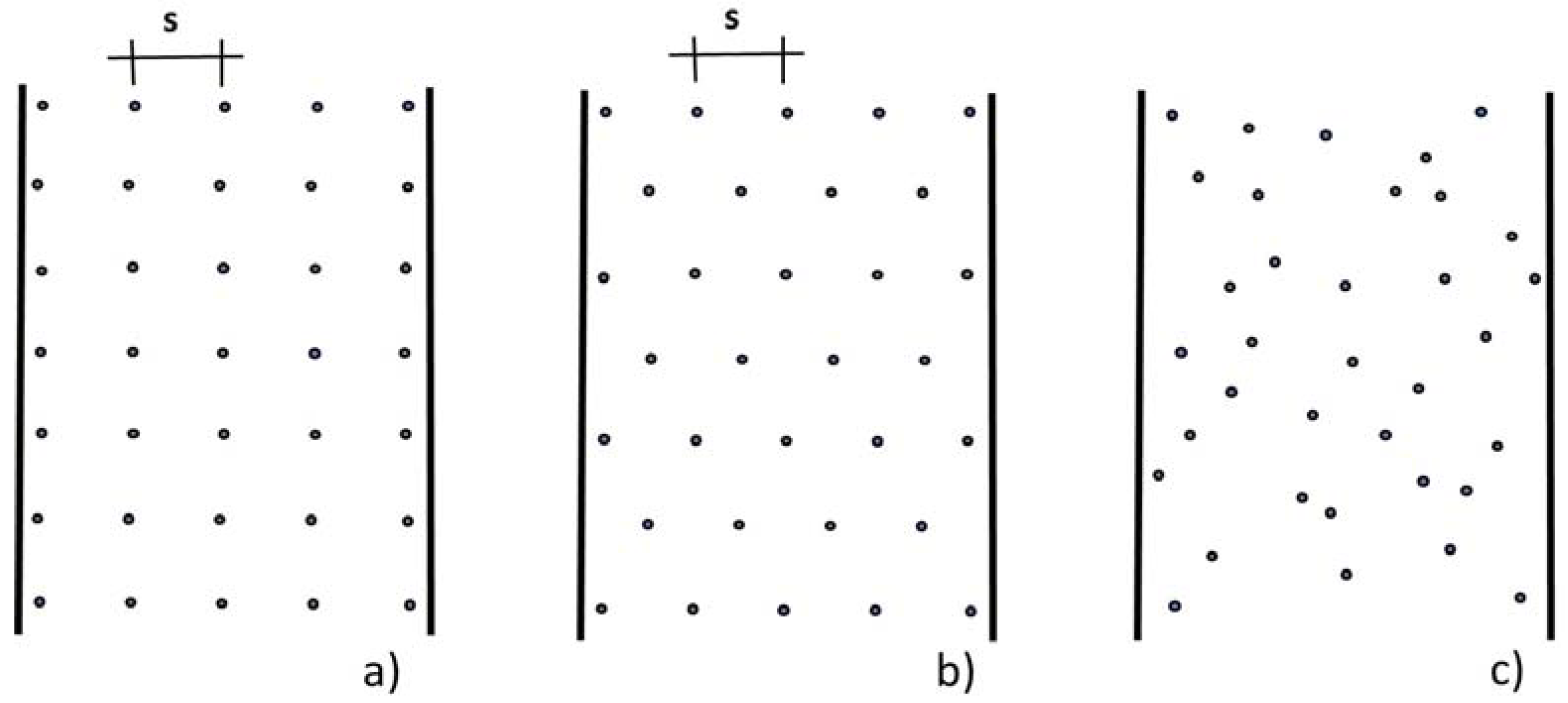

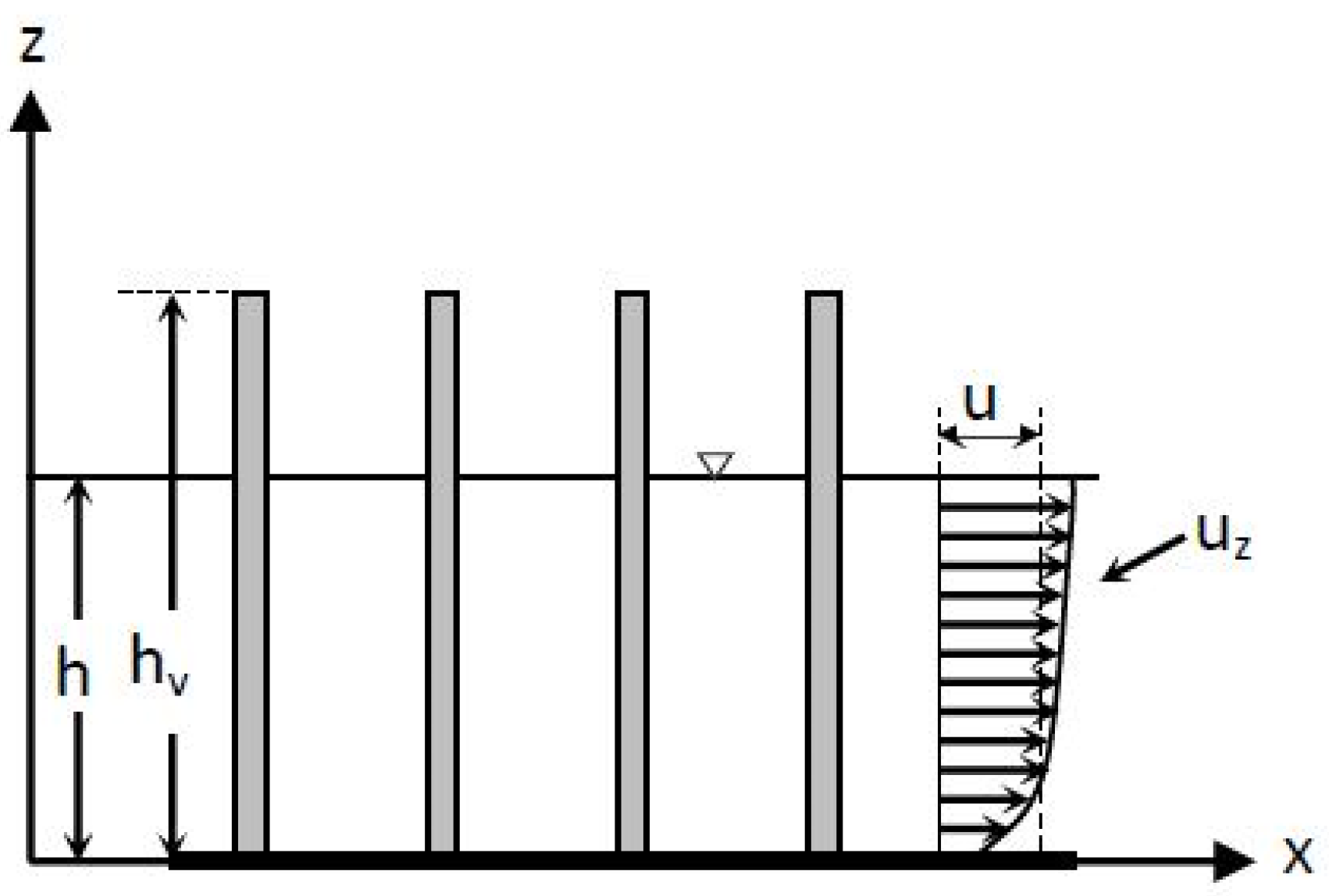
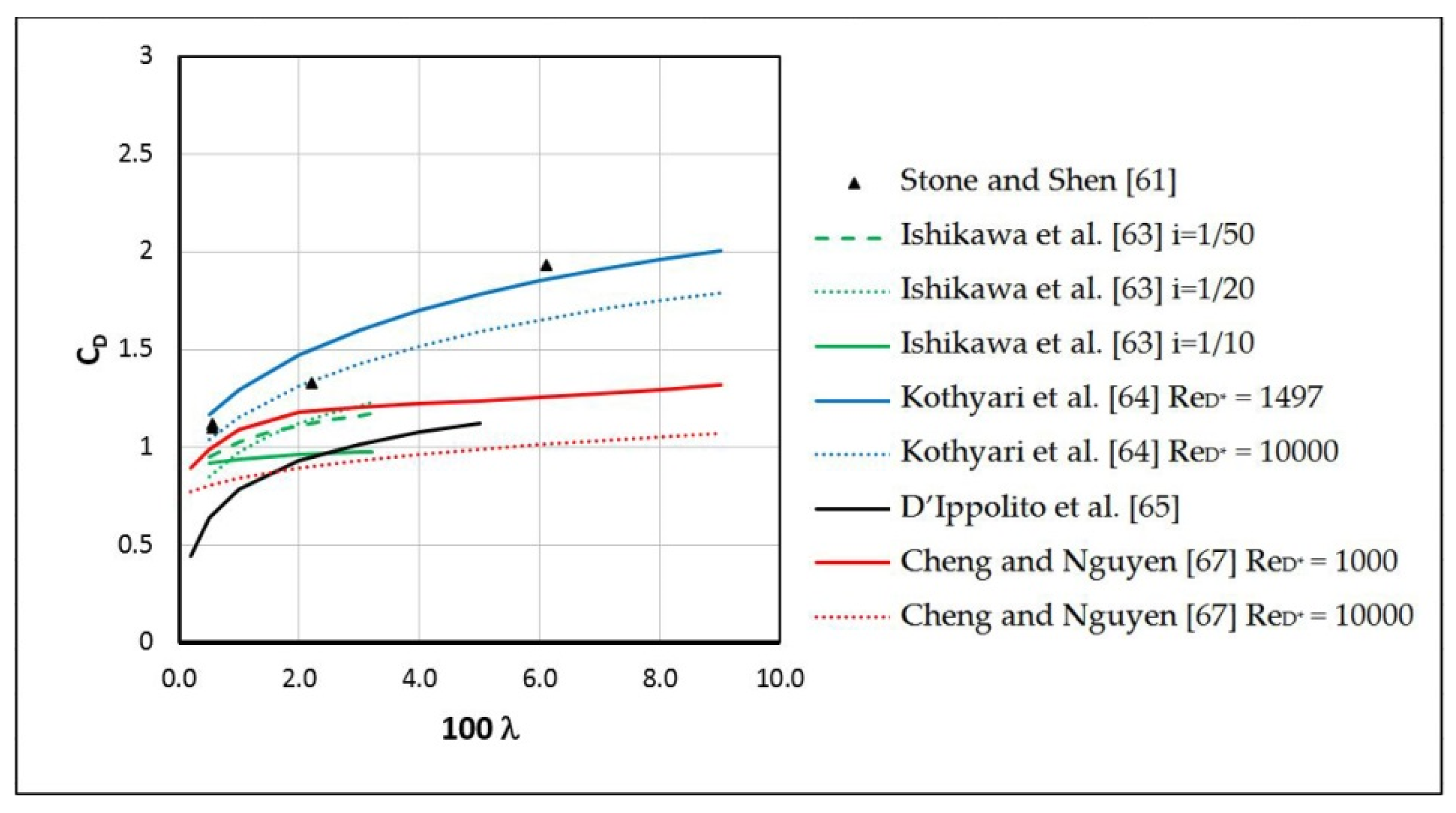
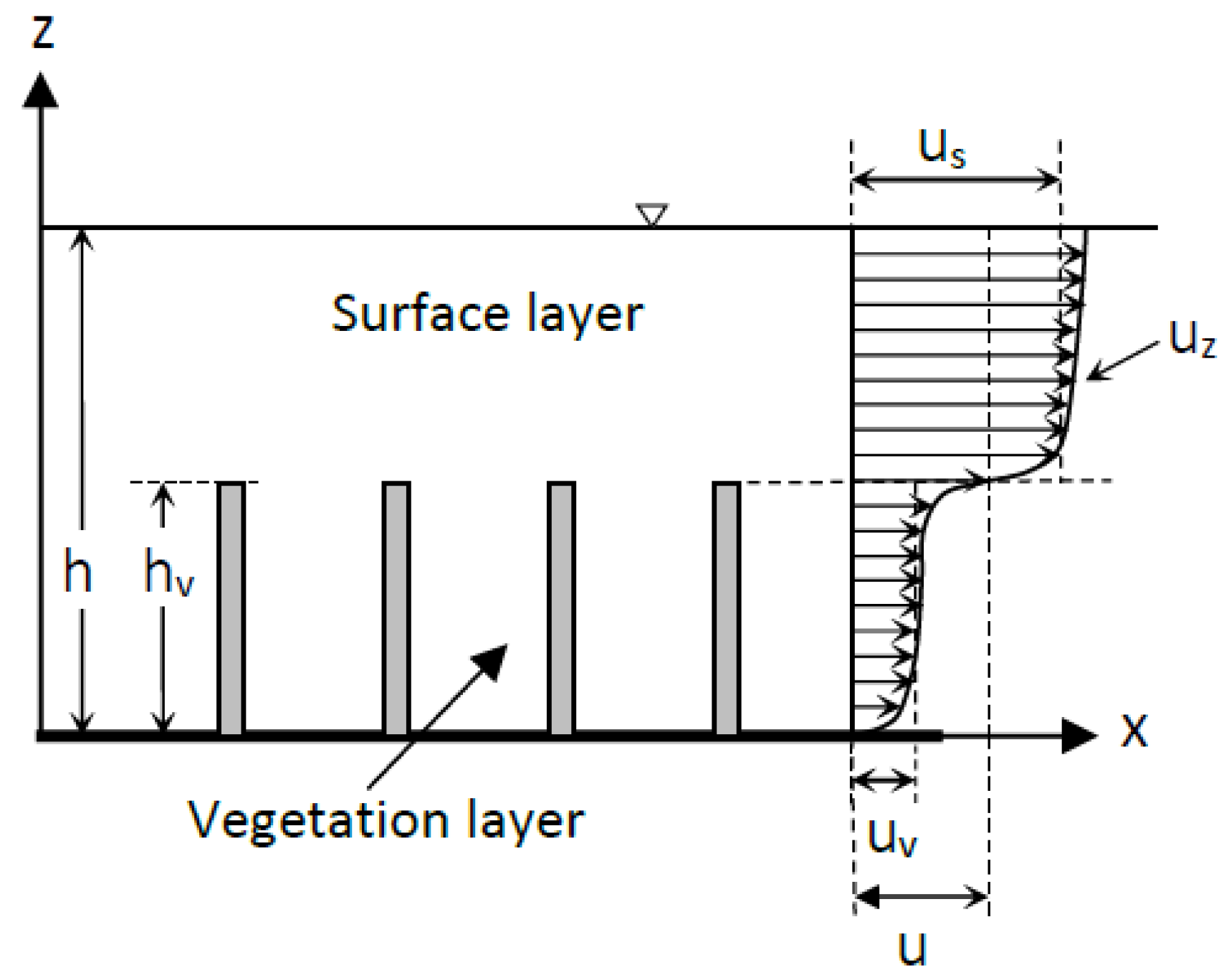
| Authors | Relationship |
|---|---|
| Ishikawa et al. [63] | |
| Tanino and Nepf [66] | |
| Kothyari et al. [64] | |
| Cheng and Nguyen [67] | |
| Cheng and Nguyen [67] | |
| Wang et al. [68] | |
| Sonnenwald et al. [69] | |
| D’Ippolito et al. [65] |
| Authors | Relationship |
|---|---|
| Baptist et al. [62] | |
| Huthoff et al. [75] | |
| Yang and Choi [76] | |
| Cheng [84] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ippolito, A.; Calomino, F.; Alfonsi, G.; Lauria, A. Flow Resistance in Open Channel Due to Vegetation at Reach Scale: A Review. Water 2021, 13, 116. https://doi.org/10.3390/w13020116
D’Ippolito A, Calomino F, Alfonsi G, Lauria A. Flow Resistance in Open Channel Due to Vegetation at Reach Scale: A Review. Water. 2021; 13(2):116. https://doi.org/10.3390/w13020116
Chicago/Turabian StyleD’Ippolito, Antonino, Francesco Calomino, Giancarlo Alfonsi, and Agostino Lauria. 2021. "Flow Resistance in Open Channel Due to Vegetation at Reach Scale: A Review" Water 13, no. 2: 116. https://doi.org/10.3390/w13020116
APA StyleD’Ippolito, A., Calomino, F., Alfonsi, G., & Lauria, A. (2021). Flow Resistance in Open Channel Due to Vegetation at Reach Scale: A Review. Water, 13(2), 116. https://doi.org/10.3390/w13020116






