1. Introduction
Riprap is one of the most common materials used to protect the stability of riverbeds and revetments, bridge abutments and pier foundations from scouring [
1]. The transport of riprap is similar to the bedload in the broad sense. In the condition of an underlying water surface, these methods used for riverbanks are no longer applicable [
2]. The stability evaluation of riprap adopts Monte Carlo simulation, inertia analysis, the Faroson blue point estimation method and others to calculate the riprap under the flow conditions [
3,
4]. Numerical simulation methods are usually used to simulate the changes in water flow, wind, waves and riverbed morphology caused by the implementation of stone dumping projects. The existing software is generally used for two-dimensional or three-dimensional simulation, and PFC software is commonly used [
5,
6], namely River2D [
7,
8], or the discrete element method is used to simulate the conditions and hydrodynamic methods to establish aggregation models, such as the DEM-SHP model [
9], DEM-CFD model [
10] and CFD-CSM model [
11]. Existing research focuses on the impact of stone dumping on the mass and the migration status of the stone. The complex process of riprap transport underwater can be approximated as the transport process of bedload in the river [
12], and the bedload transport model is often used to study the riprap movement. Therefore, the actual demand of river management and development has promoted the development of sediment discipline, and the development of the related disciplines has repaid the progress of river management and development of engineering practices. The important indicator of the development of particle flow is the improvement of the basic theoretical research level of river sediment. The study of particle movement in rivers originated from geomorphology and gradually evolved into a branch of hydraulics. Therefore, the traditional theory retains the traces of geomorphology to a certain extent. In addition, the traditional theory also draws heavily on the research results of fluid mechanics. However, according to the existing research results, it was found that the movement of sediment and riprap particles is a complex process that is cross-scale, highly random and coupled with multiple physical processes [
13]. Traditional research methods cannot accurately describe the motion characteristics of the complex process of riprap and sediment movement and its physical mechanism. Considering the above problems, new methods to study the movement of particles such as riprap are needed. The probability statistical method theory based on the particle velocity distribution function and its evolution equation can not only reflect the individuality of particle movement but also reflect the common characteristics of particle movement [
14]. Because of its cross-scale research advantages, it reflects the probability change process of particles appearing in velocity space and geometric space, as well as the extremely strong coupling ability of the motion characteristics of individual particles and the statistical characteristics of particle clusters. Recently, stochastic dynamics theory has been widely used in the field of gas molecular motion and particle flow [
15,
16].
The most basic stochastic transport process in science and engineering is the diffusion process. The classic model of the diffusion process is Brownian motion, which has been widely used in the scientific fields of physics, chemistry, biology, finance and others [
17,
18]. However, in recent decades, with the improvement of the level of research, more studies are concerned with systems with small scales and complicated conditions. These systems present features that deviate from Brownian motion and result from non-standard statistical physics. Therefore, they cannot be simulated well using the model with Brownian motion and standard statistical distributions [
19,
20]. All these non-Brownian diffusion processes are collectively referred to as “anomalous diffusion”. Due to the heterogeneity of the riverbed environment, the transport of riprap particles often deviates from conventional statistical physical results and exhibits anomalous transport. The application of random walk and random process theory is a novel and feasible research idea. The most important feature of the probability statistical theory of particle flow is the ability to reconstruct the missing links of microscopic motion characteristics and macroscopic statistical laws.
The riprap movement in the riverbed is similar to bedload sediment, which is an inherently stochastic process. Since Einstein proposed a statistical description of sediment transport, he modeled the sediment transport as a series of alternating step lengths and resting periods [
10,
21]. The probabilistic framework to characterize particle transport attracted substantial attention from scientists in the past two decades, especially the CTRW model [
19,
22,
23,
24]. The CTRW model has been successfully applied to predict the time-dependent kinetics of tracers in strongly inhomogeneous media and constant velocity experiments [
25,
26,
27,
28].
The movement of the riprap is controlled by the two aspects of necessity and chance [
29]. On one hand, for certain riprap particles, the movement is inevitably affected by the condition of the bottom flow rate, which is in accordance with the laws of mechanics. On the other hand, the particle size, the bottom flow rate, the position of the particles on the bed surface and the structural components of the riverbed are all random variables, and their changes conform to the laws of probability theory. In the operation of the riprap project, it is difficult to accurately capture and predict the difference between the transport behavior in different environments and the transformation of the transport process at different scales. Many parameters of the traditional model use empirical formulas or parameters that make them impossible to be directly applied in some specific engineering projects. The actual observations and theoretical calculations often have great deviations. Therefore, it is a practical and feasible direction to use statistics to study the transport of the riprap. The statistics of macroscopic data dismantle the deterministic nature of the transport properties of riprap in random behavior. The statistical results have made great progress under the rapid development of computer theory in recent years. In addition to the increase in computing speed, the statistical method has become one of the main research methods in different research directions through the big data analysis of macro data and the development of artificial intelligence. This study uses a combination of stochastic theory and engineering practice to determine the appropriate statistical distribution, establish a mechanical model for analyzing and simulating the anomalous transport of riprap in the river and quantify the relationship between the model parameters and the internal structure of the riverbed.
The random walking model is the most intuitive model to study the particle diffusion problem by using various statistical methods. It mainly analyzes the statistical law of the anomalous diffusion process and builds a random walking model by means of unconventional statistical methods. In the study of statistical methods for anomalous diffusion, the Lévy distribution is used the most and has been applied successfully to the analysis of anomalous diffusion phenomena in turbulent, aquifer, biological fluid, semiconductor and other media [
30]. Extended Gaussian distribution in porous media with a fractal structure demonstrates its advantages in the anomalous diffusion process. Mittag-Leffler distribution has also achieved breakthrough results in anomalous diffusion and signal processing and other fields. The theory of random walking was first proposed by Einstein [
29] when he studied molecular motion in fluids. Two fixed variables, such as fixed waiting time and a certain jump step, were proposed to study the Brownian motion behavior of equilibrium fluids. The random walking framework treats the particles as tracers, which will experience two states in the movement (i.e., rest and jump). The jump step is the distance of a single jump, and the waiting time is the elapsed time between two successive jumps. In the original theory, the behavior of random walking did not consider the distribution of jumps and waits but only fixed steps and time as considerations. On this basis, Montroll and Weiss [
31] established the continuous-time random walking method (CTRW). In a CTRW framework, a successful walk is decomposed into two parts: a random spatial jump interval and the waiting time between two successful jumps. The distributions of the two parts are dominated by their respective probability density distributions. Scher and Montroll [
32] first developed the CTRW model with a long-tailed distribution of waiting times to describe the motion of charged particles in amorphous semiconductors.
In this study, the long-tail waiting time and jump step distribution are used to simulate the anomalous transport behavior of the riprap movement in the river, and the field observation data further validated the effectiveness of the CTRW model in predicting the transport of riprap. We also discuss the spatial distribution of riprap particles with different hydraulic conditions and different particle sizes.
2. Materials and Methods
2.1. Random Walk Theory
The continuous-time random walking theory (CTRW) extends the assumption of a fixed step size and fixed waiting time to the jump step size and a waiting time dominated by probability density distribution on the basis of the random walking theory. In the continuous-time random walking theory, the particle jumping process is composed of the space jumping distance and the waiting time between two successful jumps. The two parameters are determined by the common joint probability density distribution. In actual research, it is found that the jumping step length and waiting time are often irrelevant. This assumption that the jump distance and the stay time are independent is adopted in this study. Then, the jump step distance and waiting time are determined by their own respective distribution densities. In the study,
are used to denote the probability density functions of the jump step and the waiting time, respectively. The generalized main equations of the CTRW process are obtained by the joint probability density function as follows [
30]:
where
is the probability density function for a tracer to just arrive at position
x at time
t, the initial distribution of particles is
and
represents the joint probability density function of the jump step and waiting time.
The probability density function
of the particle satisfies the following equation:
where
is the survival probability, indicating the probability that the particles will never move.
By substituting the generalized main Equation (1) into Equation (2), the probability density equation of continuous-time random walking is finally obtained:
In the CTRW framework, both space and time are defined as continuous variables, so Equation (3) can consider the equations satisfied in the phase space. Then, a Fourier-Laplace transformation can be applied to Equation (3):
Equation (4) in the Fourier-Laplace domain is called the Montroll–Weiss equation. In this equation, the probability density distribution properties of the jump step and waiting time can distinguish different transmission operations as the probability of the jump step. When the second-order moment of the distribution diverges and the first-order moment of the probability distribution of the waiting time converges, the transport operation is defined as super-diffusion transport. When the second-order moment of the probability distribution of the jump step converges and the first-order moment of the probability distribution of the waiting time diverges, the operation defines this as diffusion transport. Both are divergent with both the super-diffusion transport operation and this diffusion transport operation, both of which converge to the normal transport state.
2.2. Monte Carlo Modelling for the Riprap Movement
The Monte Carlo method, also known as the stochastic simulation method, is widely used in the context of the greatly improved computing power of today’s electronic computers [
33]. This method is based on statistical theory and uses repeated random sampling methods to obtain the numerical characteristics of statistics. When the number of repetitions is sufficient, the numerical solution obtained by the Monte Carlo method can infinitely converge to the real solution. Due to the complexity of the distribution used in this study, Equation (4) in the Fourier-Laplace domain has great difficulty in converting to the time domain. Here, we use the Monte Carlo method to obtain its numerical results. At the same time, this method has great advantages in tracking the trajectory of particles and analyzing the anomalous movement of particles.
The classic advection–diffusion equation (ADE) characterizes the law of fluid mass transport. By solving the ADE, the distribution of particles under the central limit theorem can be obtained. However, in actual observations, it has been found that the central limit theorem will be broken in many cases. For example, the heterogeneity of the aquifer and the non-uniformity of the riverbed structure will cause the equations that conform to the central limit theorem to fail to accurately describe the actual transport behavior. This type of transport that breaks the central limit theorem is called “anomalous transport”. The continuous-time random walking theory describes the “anomalous transport” behavior by defining jump steps and wait times for more of a “wide” probability density distribution. When the probability density distribution returns to satisfy the central limit theorem, the jump step distribution is normal distribution, the waiting time distribution is exponential, Equation (4) will return to the normal form of the advection–diffusion equation. In this study, in order to reflect the “anomalous transport” behavior of the riprap caused by the heterogeneity of the riverbed’s structure, the α stable distribution is used as the jump step distribution, and the Mittag-Leffler distribution is used as the waiting time distribution.
In this study, we divided the motion of the riprap into the direction of flow and perpendicular to the direction of flow and used independent and identically distributed random numbers to simulate the movement process of the whole riprap process.
The waiting time of the exercise process is determined by the following formula:
The displacement in the direction of the water flow is composed of the displacement caused by the collision of the particles and the displacement caused by carrying the water flow, which is determined by the following formula:
The displacement perpendicular to the direction of the water flow is only caused by the mutual collision of the particles, which is determined by the following formula:
where
is a random number that satisfies the Mittag-Leffler distribution and
and
are random numbers that satisfy the
stable distribution. Random number generation in the study was generated by the following formula.
Among them, the
stable distribution random number that meets the jump step is generated using Equation (8):
Random numbers satisfying the Mittag-Leffler distribution are generated using Equation (9):
where
are uniformly distributed random numbers and
is the scale factor generated by the random numbers.
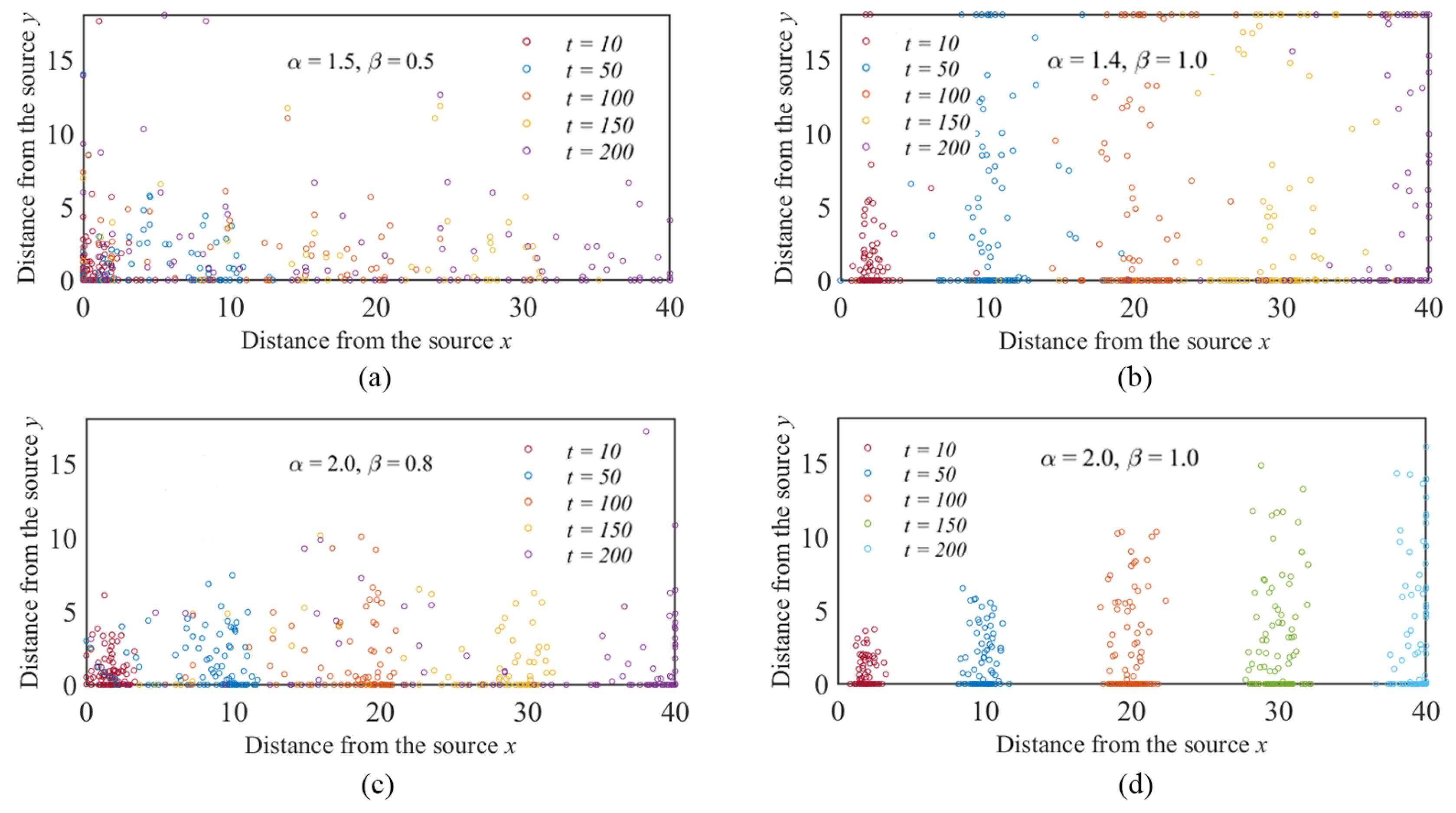
In the actual simulation, we used Equations (5)–(7) as the calculation of the movement displacement of the riprap along the flow direction and perpendicular to the flow direction. The random numbers of the waiting time and jumping step in the formula were determined by Equations (8) and (9), respectively. When the parameter was larger, the distribution of the jump step was more concentrated (otherwise, it was more dispersed), and when = 2.0, the distribution of the jump step returned to the normal distribution. When the parameter was larger, the waiting time distribution had the greater decay rate. When = 1.0, the waiting time distribution returned to the exponential distribution. A more dispersed jump step distribution means that the riprap particles have a greater probability of performing long-distance movement in a short time. While the waiting time distribution decay is slower, the probability of the riprap particles staying in the riverbed is greater. In the following research, we will analyze the transport behavior of the riprap in the riverbed based on this property. In the simulation, three parameters need to be determined: α is the parameter of α stable distribution which controls the strength of the super-diffusion, β is the parameter of the Mittag-Leffler distribution which controls the strength of subdiffusion, and v is the mean velocity of all the riprap particles. The boundary condition upstream is a Dirichlet condition, and the boundary condition downstream is natural.
2.3. Field Investigation of Riprap Projects
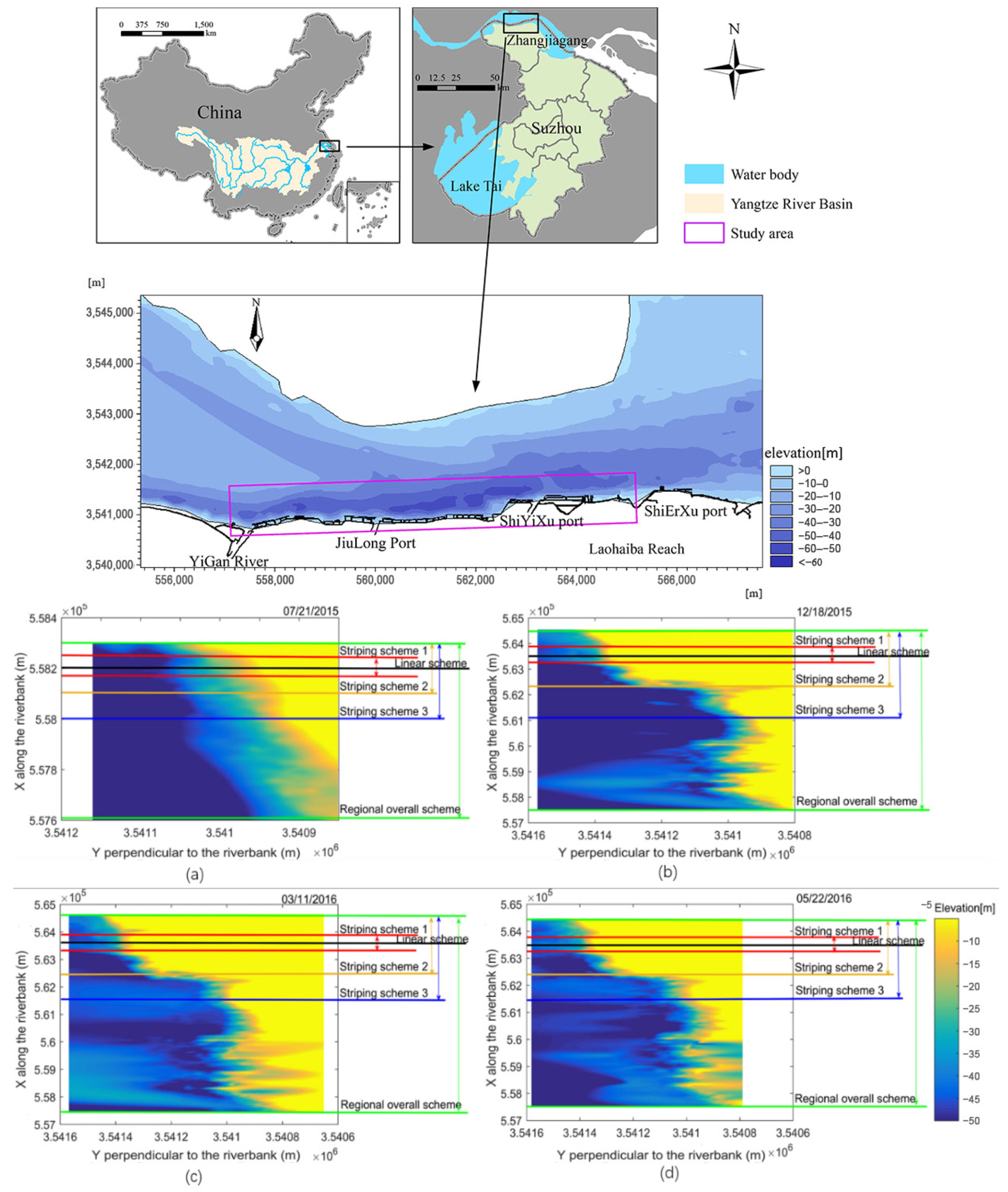
The old sea dam node comprehensive improvement project in Zhangjiagang, which is located in the Chengtong section of the lower Yangtze River, was selected as the study area. The channel is 2 km wide, and the water level during the simulation period was from −0.3 m to about 2.7 m (all based on the 1985 Chinese national elevation datum). The study area belongs to the tidal river section. Under the dual effects of runoff and tide, the flow velocity changes periodically (0.3–1.6 m/s). The river regime changes drastically, with siltation on the left bank and scouring on the right bank. The elevation of the riverbed presented is from −16 to about −5 m on the left bank and from −36 to about −50 m on the right bank. There are many thorough scour pits from −30 m to about −50 m, and the monthly variation of the scouring and silting thickness in individual locations is more than 10 m [
34].
Figure 1 shows the specific locations of the study area.
The stone dumping methods used in river improvement work are divided into two types: stone dumping on the outer slope of the embankment and stone dumping in the deep-water area out in front of the wharf. The anti-collapsing layer (particle size: 0.16~0.4 m) is first thrown along the slope foot and then thrown along the bank slope. There are large stones (particle size: 0.5 m~0.65 m), the designed riprap width is 40~120 m, and the total riprap volume reaches 2.442 million m
2 [
35].
For further verification of the applicability and spatial suitability of the continuous-time random walking model in the transport of the riprap, we used the biharmonic spline interpolation method to interpolate the data collected in the field test at intervals of 0.05 m and performed simulation analysis. The data acquisition used the R2SONIC 2024 multibeam bathymetry system, which uses multiple arrays and wide-angle transmission and reception and has the advantages of measurement accuracy and wide coverage. The horizontal accuracy was ±0.03 m, the sounding accuracy was ±0.05 m, and the range resolution was 0.0125 m. Here, we conducted on-site monitoring of the changes in riverbed elevation at different periods after the riprap projects. Six elevation datasets were obtained on 22 May 2015, 21 July 2015, 18 December 2015, 11 March 2016, 22 May 2016 and 4 July 2016. Among them, there was no riprap project after July 2015. Therefore, the change in riverbed elevation after July 2015 was mainly caused by the transport of the riprap in the river. In order to accurately predict the riprap movement and apply the data to the continuous-time random walking model, we first needed to understand the initial riverbed state before the simulation time and analyze the riverbed elevation data obtained by examining each time. We selected the riverbed elevation data captured for the second instance (21 July 2015) as the initial elevation state of the riverbed. The data measured on 22 May 2015 was not used as the initial state because the difference was too obvious compared with the subsequent data and the elevation distribution for 22 May 2015 was very uneven. This was caused relatively from the fact that the riprap project was still in progress during this period, which had a great impact on the river elevation. Using it as the initial data during the simulation would cause the simulation results to distort and not truly reflect the impact state of the riprap project after the implementation of the riprap project. In order to accurately characterize the degree of change of the riverbed at different times, several sets of data with uniform changes were selected for analysis, namely 20150721, 20151218, 20160311 and 20160522. Due to the difference in the amount of data collected at each time, the riverbed elevation of the uncollected part was subjected to a second interpolation calculation to keep the amount of data consistent. By analyzing the topographic characteristics of the study area and the construction conditions of the rubble project, it was found that the riverbed had a large elevation drop in the direction of the vertical river, and the riprap project was also implemented perpendicular to the riverbank. The change of two characteristics in the vertical riverbank direction was consistent, while the characteristics in each cross section were similar. Therefore, the problem of stone migration in the direction of the vertical riverbank could be generalized into a one-dimensional model for simulation. The simulation path selected by the linear scheme was the most representative feature location in the range, and the location was slightly different in different sessions. For details, refer to the location represented by the linear scheme in the riverbed topography distribution map of different simulation periods in
Figure 1.
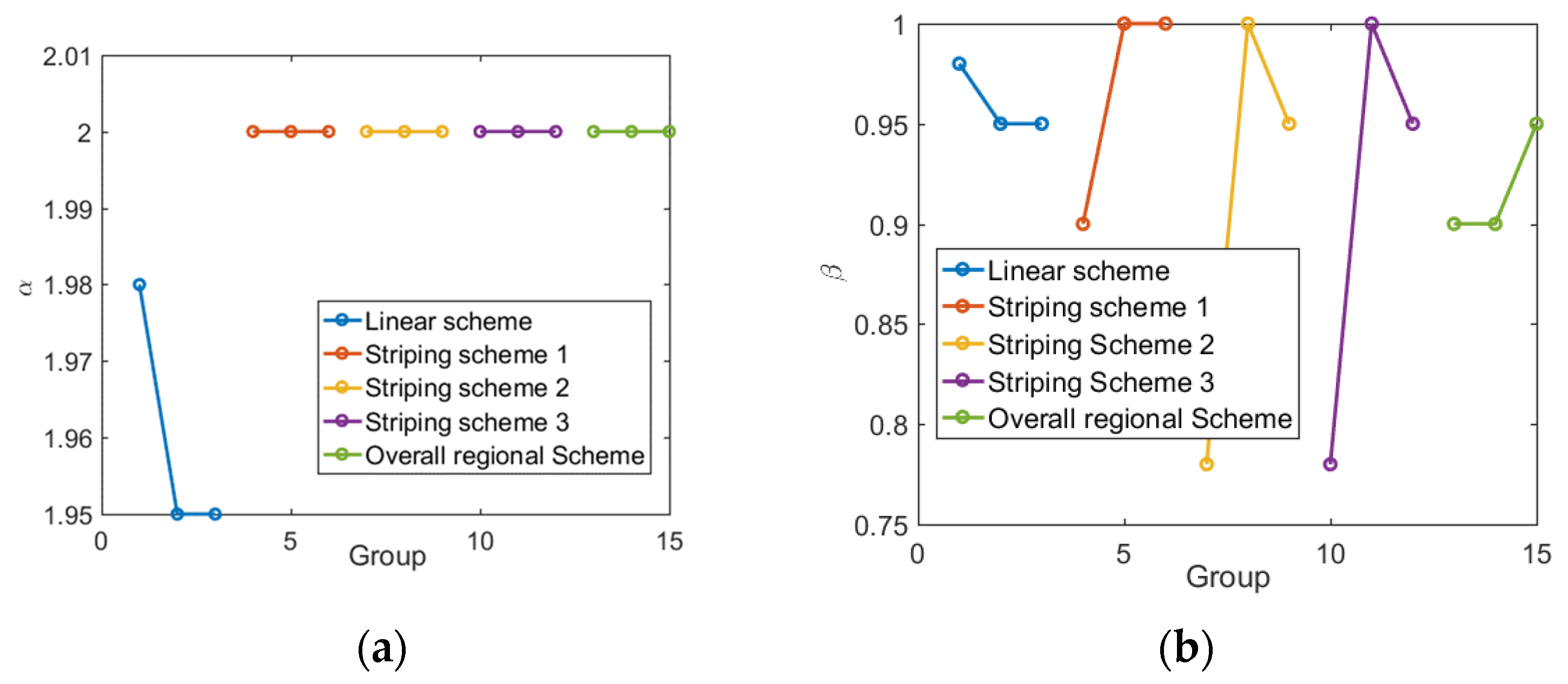
In order to verify the spatial suitability and spatial scale of continuous-time random walking in the simulation of the riprap movement, the region selection in the study shown in
Figure 1 adopted a linear scheme, strip scheme and regional overall scheme. In the linear scheme, the calculated path of the riverbed elevation was the path shown in the “linear scheme”. In each strip scheme, the calculation range was the area between the two straight lines indicated by the double arrow in
Figure 1 (different colors represent different stripping schemes), and the overall scheme was calculated in the entire space. The elevation of the calculation path of the stripping scheme, and the overall scheme was the mean value of the elevation along the stripping width direction (calculating the average height along the
X axis).
4. Discussion
Usually, after a period of implementation of the riprap project, there is no upstream supply of riprap particles, and the status of the riprap in the river is basically stable. At this time, the movement of the riprap is very similar to the transport of bedload in the river. This is due to the erosion of streamflow and the exchange with the riverbed. In order to analyze the transport situation of the riprap in this state, we mainly considered the following Markov birth–death system [
40]. The specific description of the system is as follows:
The unit window is taken in the system, and the number N of stone throwing movements in the window is counted. The change of the number N is affected by the following four assumptions:
The static particles in the riverbed enter the window, which will increase N, and the activation rate is c1;
The particles in the window will be redeposited as part of the riverbed, resulting in a decrease in N, and the deposition rate is c2;
The moving particles are washed out of the window, resulting in a decrease in N, and the window exit rate is c3;
The particles flushed into the window upstream will increase the amount of N, and the window entry rate is c4.
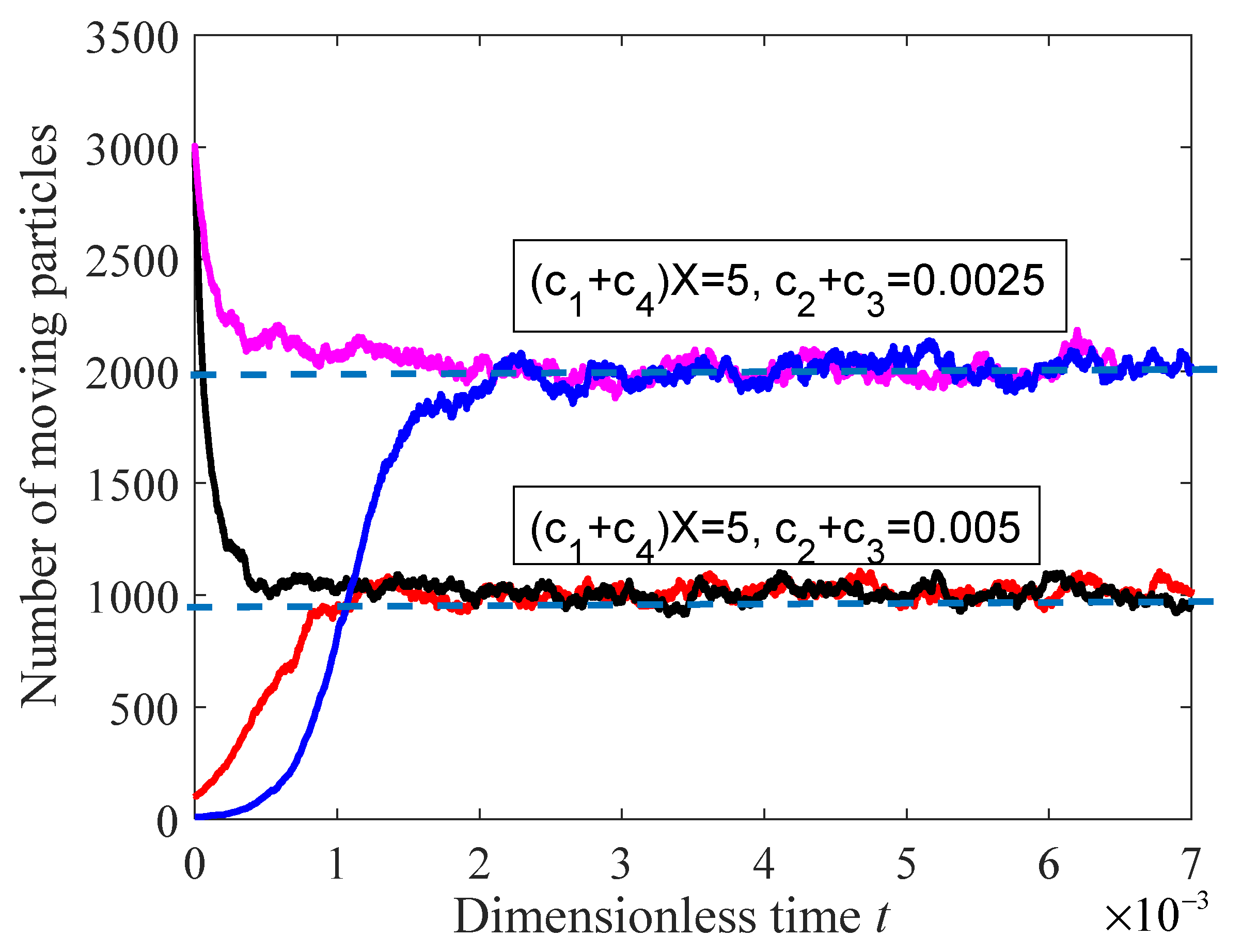
Figure 6 is a schematic diagram of the Markov birth–death system and the corresponding reaction chain.
N in the reaction chain represents the number of riprap particles in the window, and
X represents the number of particles in the riverbed and outside the window. In this system, the number of
X is unlimited (due to the amount of gravel contained in the riverbed itself being greater than the amount of gravel that was washed away under natural conditions). This system can be well described by Equation (10), but the steady state solution of Equation (10) is not unique, mainly because particles often occur in integers in the exchange, so continuous equations are solving discrete problems. There will be a certain conflict in the physical sense of time. In order to visualize the state of the Markov birth–death system, we used the Monte Carlo method for simulation. Intuitively, in order to obtain the distribution of waiting times related to the continuous-time random walking model, we defined the waiting time of the particle as the interval between two consecutive events where the particle moved out of the window as the waiting time:
Figure 7 is a graph showing the change trend of the number of particles in the window in two groups, and the number of initial particles in each group was quite different with the stabilized state. Through the simulation results, we found that in the Markov birth–death system, the moving particles of the riprap gradually stabilized after a long time, and the change in the number of particles was related to the initial number of moving particles. When the initial number of particles was smaller than the number of particles in the steady state, the overall number of moving particles increased. These results indicate that the probability that the riprap particles restarted in the riverbed was greater than the probability of the deposition of moving particles under these conditions. However, when the number of initial particles was greater than the steady state particles, the number of overall moving particles decreased, which indicates that the deposition probability of the moving particles in this state was greater than the restart probability of the particles.
The number of moving particles in the steady state was determined by the selected parameters c1, c2, c3 and c4, and the steady state value was (c1 + c4)X/(c2 + c3). When the deposition rate and the window exit rate increased, the number of particles moving in the window in the steady state decreased. When c2 + c3 tended toward infinity, this meant that almost all particles entering the window were deposited or moved out of the window, so there was no moving particle in the window in the steady state, which was consistent with the actual conjecture.
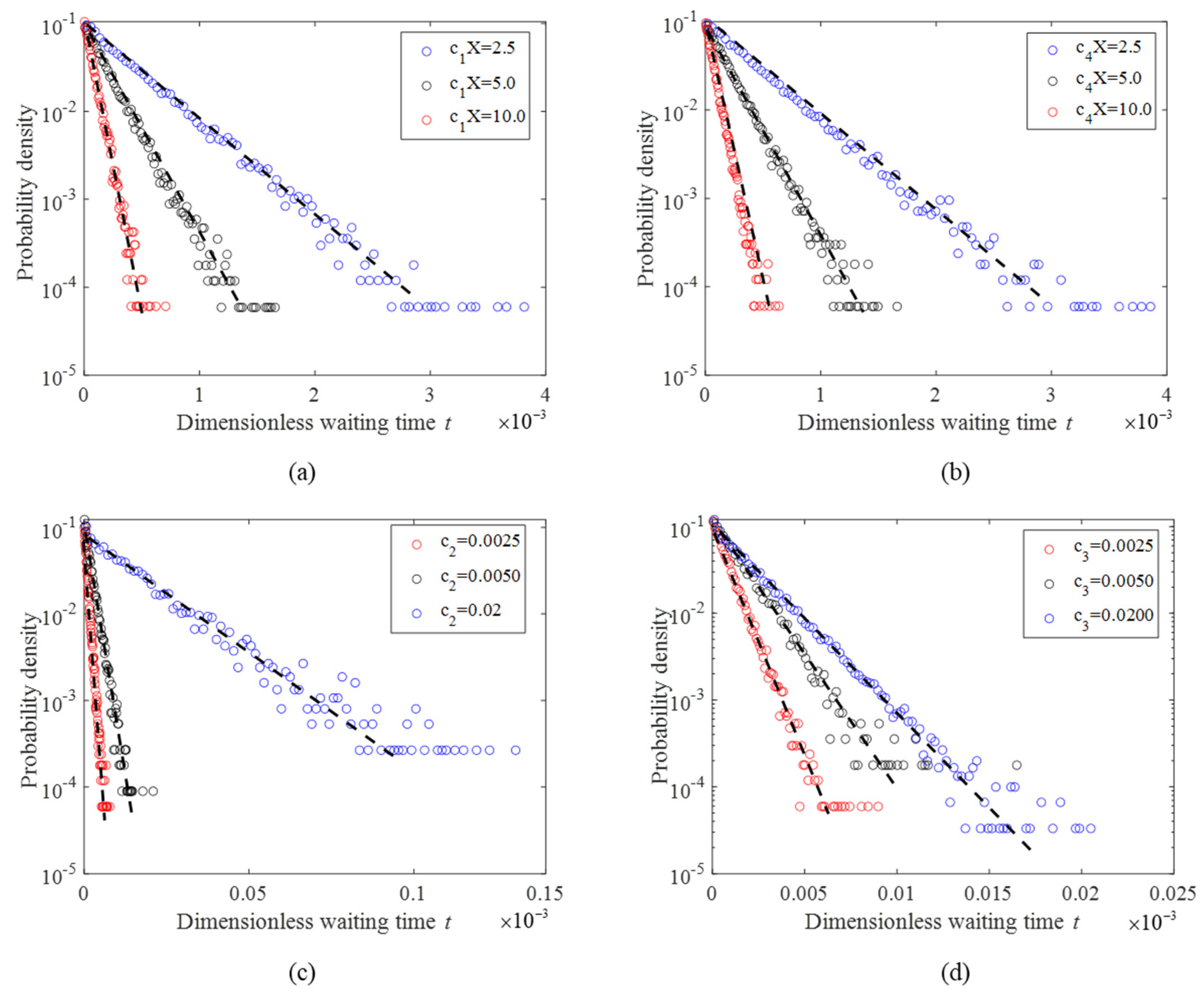
Figure 8 shows the distribution of the waiting time of the riprap particles under different parameter conditions. By comparing the decay behavior of the waiting time of each figure in
Figure 8, it can be found that after the riprap movement was stable, the distribution of the waiting time was an exponential distribution. The increase of parameters
c2 and
c3 made the distribution of waiting times decay more slowly, which means that the increase of the deposition rate and the windowing rate would lead to an increase in the probability of a long waiting time. Although it is not a power law decay, the relative probability particles stayed in the window. The distribution of waiting times exhibited more sensitivity to the deposition rate. In addition, the increase of parameters
c1 and
c4 would make the waiting time distribution decay faster, and its sensitivity to the waiting time distribution was basically the same. The above conclusions indicate that the transport of the riprap particles in the steady state behaved as a normal transport state rather than as a secondary diffusion transportation state after the implementation of the riprap project.