Micro-Clustering and Rank-Learning Profiling of a Small Water-Quality Multi-Index Dataset to Improve a Recycling Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Main Features
2.2. Case Study Summary
2.3. Data Manipulation Issues and New Approach Benefits
2.4. Methodological Design and Analysis Stages
- (1)
- Select a number of suitable characteristics that could provide a multi-lateral view of the water quality status of the tested samples.
- (2)
- Select a number of controlling factors that are relevant to screening the respective water quality properties.
- (3)
- Outline an adequately broad factorial landscape by pinpointing its operational end points.
- (4)
- Select an appropriate FFD/OA design that accommodates the group of the selected controlling factors from step 2 and decide on possible investigating factor non-linearity.
- (5)
- Execute the trial recipes according to the FFD/OA plan of step 4 and collect the data.
- (6)
- Apply cluster analysis to the multiresponse dataset.
- (7)
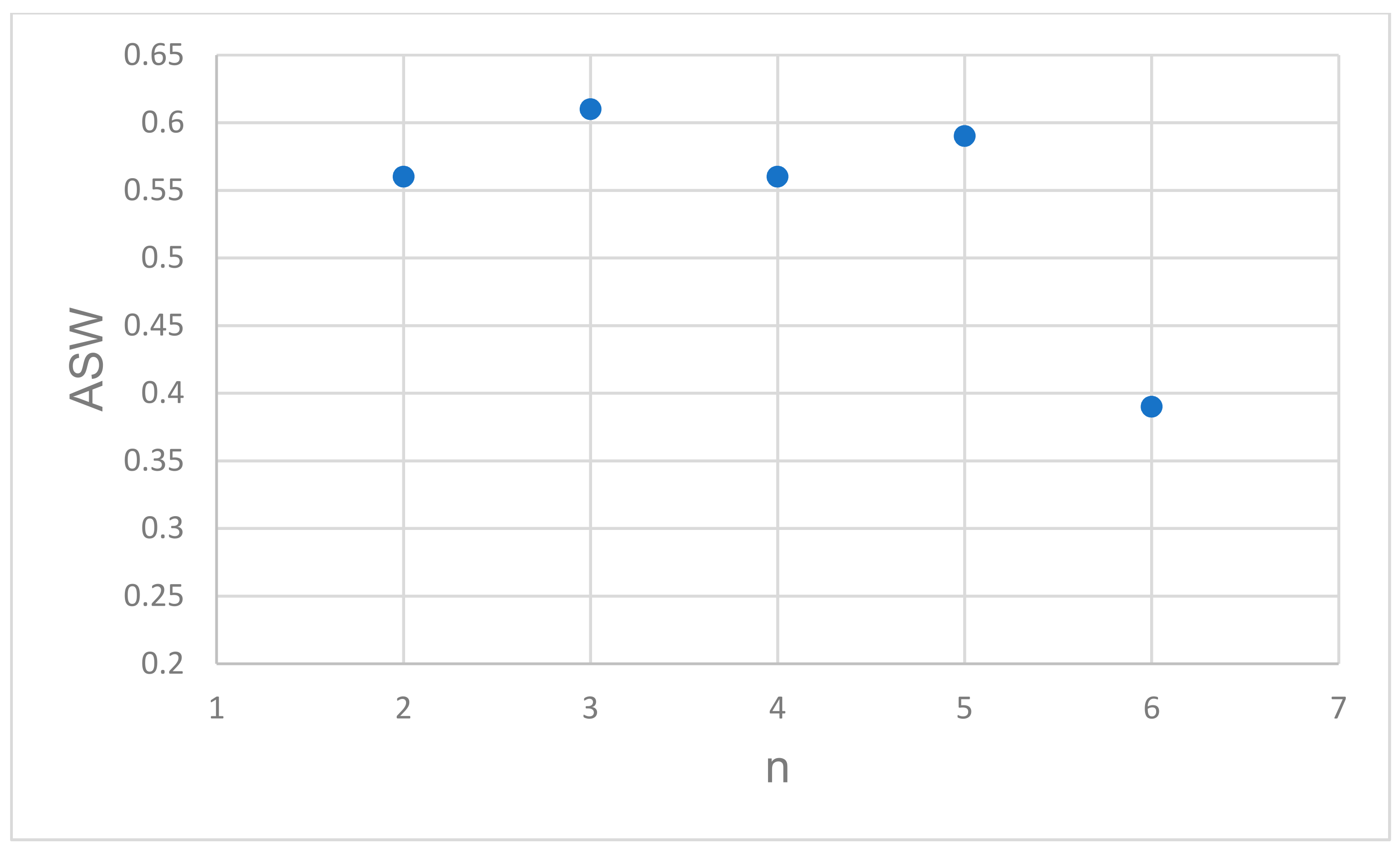
- Use the Silhouette method [57] to optimize the number of clusters by estimating the average silhouette width (ASW).
- (8)
- “De-nominalize” the cluster membership identification by “ordinalizing” the cluster label groups according to the direction of the desirable behavior of the examined physical characteristics.
- (9)
- Identify the strong effects
- (10)
- Confirm the results with additional data.
2.5. The Computational Aids
3. Results
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Finney, J. Water: A Very Short Introduction; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Ball, P. H2O: The Biography of Water; Orion Publishing Co.: London, UK, 2000. [Google Scholar]
- Ball, P. Water—An enduring mystery. Nature 2008, 452, 291–292. [Google Scholar] [CrossRef] [PubMed]
- Herring, J.G. Water: The Environmental, Technological, and Societal Complexity of a Simple Substance. In Encyclopedia of Water: Science, Technology, and Society; Patricia, A.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Pearce, F. When the Rivers Run Dry—Water: The Defining Crisis of the Twenty-First Century; Beacon Press: Boston, MA, USA, 2018. [Google Scholar]
- Newton, D.E. The Global Water Crisis: A Reference Handbook; ABC-CLIO: Santa Barbara, CA, USA, 2016. [Google Scholar]
- Dinar, A.; Tien, A.; Huynh, H. Water scarcity impacts on global food production. Glob. Food Secur. 2019, 23, 212–226. [Google Scholar] [CrossRef] [Green Version]
- WWAP (United Nations World Water Assessment Programme)/UN-Water. The United Nations World Water Development Report 2018: Nature-Based Solutions for Water; UNESCO: Paris, France, 2018. [Google Scholar]
- Vanham, D.; Bidoglio, G. A review on the indicator water footprint for the EU28. Ecol. Indic. 2013, 26, 61–75. [Google Scholar] [CrossRef]
- Goal 6: Ensure Access to Water and Sanitation for All, United Nations Sustainable Development. Available online: https://www.un.org/sustainabledevelopment/water-and-sanitation/ (accessed on 28 May 2019).
- Regional Information Center for Western Europe. Goal 6: Ensure Access to Water and Sanitation for All; United Nations: Bruxelles, Belgium; Available online: https://unric.org/en/sdg-6/ (accessed on 8 July 2021).
- SDG Compass. Ensure Availability and Sustainable Management of Water and Sanitation for All; United Nations: New York, NY, USA, 2015; Available online: https://sdgcompass.org/sdgs/sdg-6/ (accessed on 8 July 2021).
- WWAP (United Nations World Water Assessment Programme). The United Nations World Water Development Report 2017. Wastewater: The Untapped Resource; UNESCO: Paris, France, 2017. [Google Scholar]
- Burn, D.H.; McBean, E.A. Optimization modelling of water quality in an uncertain environment. Water Resour. Res. 1985, 21, 934–940. [Google Scholar] [CrossRef]
- Rehana, S.; Rajulapati, C.R.; Ghosh, S.; Karmakar, S.; Mujumdar, P. Uncertainty Quantification in Water Resource Systems Modeling: Case Studies from India. Water 2020, 12, 1793. [Google Scholar] [CrossRef]
- Hsien, C.; Low, J.S.C.; Chung, S.Y.; Tan, D.Z.L. Quality-based water and wastewater classification for waste-to-resource matching. Resour. Conserv. Recycl. 2019, 151, 104477. [Google Scholar] [CrossRef]
- Zito, R. Electrochemical Water Processing; Wiley-Scrivener: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tanaka, Y. Ion Exchange Membrane Electrodialysis: Fundamentals, Desalination, Separation; Nova Science: New York, NY, USA, 2013. [Google Scholar]
- U.S. Salinity Laboratory Staff. Diagnosis and Improvement of Saline and Alkali Soils. Handbook No. 60; USDA: Washington, DC, USA, 1954.
- Wilcox, L.V. Classification and Use of Irrigation Water; US Department of Agriculture: Washington, DC, USA, 1955.
- Ayer, R.S.; Westcot, D.W. Water Quality for Agriculture, FAO Irrigation and Drainage Paper No. 29; Food and Agriculture Organization of the United Nations: Rome, Italy, 1985; pp. 1–117. [Google Scholar]
- Abou-Shady, A. Recycling of polluted wastewater for agriculture purpose using electrodialysis: Perspective for large scale application. Chem. Eng. J. 2017, 323, 1–18. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters—Design, Innovation, and Discovery; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Taguchi, G.; Chowdhury, S.; Wu, Y. Quality Engineering Handbook; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ilzarbe, L.; Alvarez, M.J.; Viles, E.; Tanco, M. Practical applications of design of experiments in the field of engineering: A bibliographical review. Qual. Reliab. Eng. Int. 2008, 24, 417–428. [Google Scholar] [CrossRef]
- Tanco, M.; Viles, E.; Ilzarbe, L.; Alvarez, M.J. Implementation of Design of Experiments projects in industry. Qual. Reliab. Eng. Int. 2009, 25, 478–505. [Google Scholar] [CrossRef]
- Taguchi, G.; Chowdhury, S.; Taguchi, S. Robust Engineering: Learn. How to Boost Quality While Reducing Costs and Time to Market; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Lepeniotis, S.S.; Vigezzi, M.J. Lowering manufacturing cost of material by formulating it through statistical modeling and design. Chemom. Intell. Lab. Syst. 1995, 29, 133–139. [Google Scholar] [CrossRef]
- Madeni, S.; Koocheki, S. Application of Taguchi method in the optimization of wastewater treatment using spiral-wound reverse osmosis element. Chem. Eng. J. 2009, 119, 37–44. [Google Scholar] [CrossRef]
- Kaminari, N.M.S.; Schultz, D.R.; Ponte, M.J.J.S.; Ponte, H.A.; Marino, C.E.B.; Neto, A.C. Heavy metals recovery from industrial wastewater using Taguchi method. Chem. Eng. J. 2007, 126, 139–146. [Google Scholar] [CrossRef]
- Pardeshi, P.M.; Mungray, A.A.; Mungray, A.K. Mungray, Determination of optimum condition in forward osmosis using a combined Taguchi-neural approach. Chem. Eng. Res. Des. 2016, 109, 215–225. [Google Scholar] [CrossRef]
- Khan, R.; Inam, M.A.; Zam, S.Z.; Park, D.R.; Yeom, I.T. Assessment of Key Environmental Factors Influencing the Sedimentation and Aggregation Behavior of Zinc Oxide Nanoparticles in Aquatic Environment. Water 2018, 10, 660. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Liang, X.; Peng, Y.; Zhang, Y.; Yan, X.; Wu, J. Multi-Dimensional Interval Number Decision Model Based on Mahalanobis-Taguchi System with Grey Entropy Method and Its Application in Reservoir Operation Scheme Selection. Water 2020, 12, 685. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.P. Signal-to-noise ratios, performance criteria and transformation. Technometrics 1998, 30, 1–17. [Google Scholar] [CrossRef]
- Maghsoodloo, S.; Ozdemir, G.; Jordan, V.; Huang, C.-H. Strengths and limitations of Taguchi’s contributions to quality, manufacturing, and process engineering. J. Manuf. Syst. 2004, 23, 73–126. [Google Scholar] [CrossRef]
- Pignatiello, J.J.; Ramberg, J.S. Top ten triumphs and tragedies of Genichi Taguchi. Qual. Eng. 1992, 4, 211–225. [Google Scholar] [CrossRef]
- Stone, R.A.; Veevers, A. The Taguchi influence on designed experiments. J. Chemometr. 1994, 8, 103–110. [Google Scholar] [CrossRef]
- Hamada, M.; Balakrishnan, N. Analyzing unreplicated factorial experiments: A review with some new proposals. Stat. Sin. 1998, 8, 1–41. [Google Scholar]
- Daniel, C. Use of the half-normal plots in interpreting factorial two-level experiments. Technometrics 1959, 1, 311–341. [Google Scholar] [CrossRef]
- Lenth, R.V. Quick and easy analysis of unreplicated factorials. Technometrics 1989, 31, 469–473. [Google Scholar] [CrossRef]
- Box, G.E.P.; Meyer, R.D. An analysis for unreplicated fractional factorials. Technometrics 1986, 28, 11–18. [Google Scholar] [CrossRef]
- Carlson, R.; Nordahl, A.; Barth, T.; Myklebust, R. An approach to evaluating screening experiments when several responses are measured. Chemom. Intell. Lab. Syst. 1991, 12, 237–255. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Saeed, A.A.H.; Harun, N.Y.; Sufian, S.; Bilad, M.R.; Nufida, B.A.; Ismail, N.M.; Zakaria, Z.Y.; Jagaba, A.H.; Ghaleb, A.A.S.; Al-Dhawi, B.N.S. Modeling and Optimization of Biochar Based Adsorbent Derived from Kenaf Using Response Surface Methodology on Adsorption of Cd2+. Water 2021, 13, 999. [Google Scholar] [CrossRef]
- Besseris, G.J. Concurrent multiresponse multifactorial screening of an electrodialysis process of polluted wastewater using robust non-linear Taguchi profiling. Chemom. Intell. Lab. Syst. 2020, 200, 103997. [Google Scholar] [CrossRef]
- Fontdecaba, S.; Grima, P.; Tort-Martorell, X. Analyzing DOE with Statistical Software Packages: Controversies and proposals. Am. Stat. 2014, 68, 205–211. [Google Scholar] [CrossRef]
- R Core Team. R (Version 4.0.5): A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 25 July 2021).
- Lawson, J. Design and Analysis of Experiments with R; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Dilmi, S.; Ladjal, M. A novel approach for water quality classification based on the integration of deep learning and feature extraction techniques. Chemom. Intell. Lab. Syst. 2021, 214, 104329. [Google Scholar] [CrossRef]
- Yu, Y.; Song, X.; Zhang, Y.; Zheng, F. Assessment of Water Quality Using Chemometrics and Multivariate Statistics: A Case Study in Chaobai River Replenished by Reclaimed Water, North China. Water 2020, 12, 2551. [Google Scholar] [CrossRef]
- Díaz-Gonzalez, L.; Uscanga-Junco, O.A.; Rosales-Rivera, M. Development and comparison of machine learning models for water multidimensional classification. J. Hydrol. 2021, 598, 126234. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M. Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds. Water 2020, 12, 1584. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.Y.; An, K.-G. Multivariate Statistical Analysis of Water Quality and Trophic State in an Artificial Dam Reservoir. Water 2021, 13, 186. [Google Scholar] [CrossRef]
- Abdel-Fattah, M.K.; Abd-Elmabod, S.K.; Aldosari, A.A.; Elrys, A.S.; Mohamed, E.S. Multivariate Analysis for Assessing Irrigation Water Quality: A Case Study of the Bahr Mouise Canal, Eastern Nile Delta. Water 2020, 12, 2537. [Google Scholar] [CrossRef]
- Barclay, J.R.; Tripp, H.; Bellucci, C.J.; Warner, G.; Helton, A.M. Do waterbody classifications predict water quality? J. Environ. Manag. 2016, 183, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, S.P.; Uscanga-Junco, O.A.; Díaz-González, L. A statistically coherent robust multidimensional classification scheme for water. Sci. Total Environ. 2021, 750, 141704. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
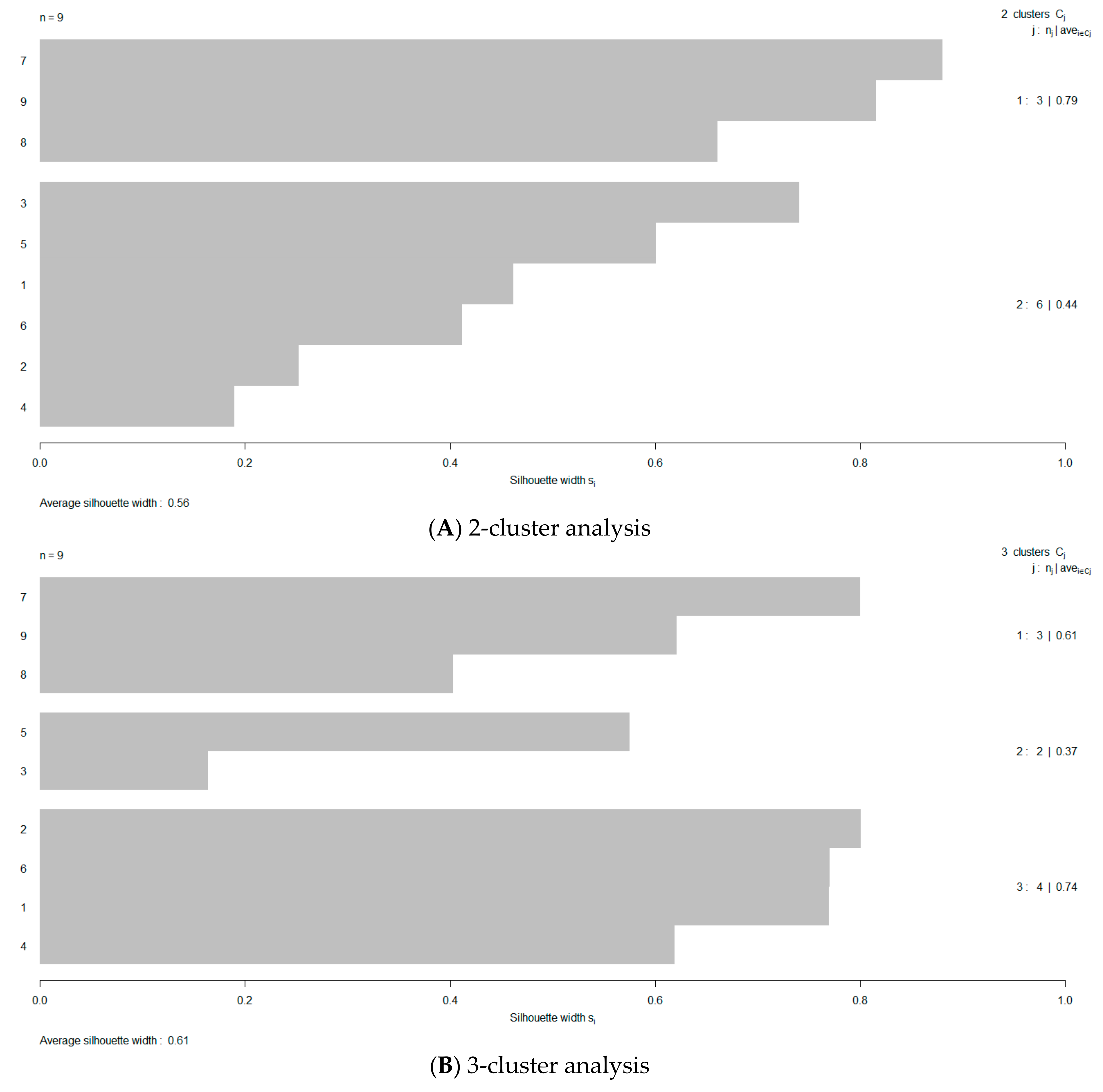

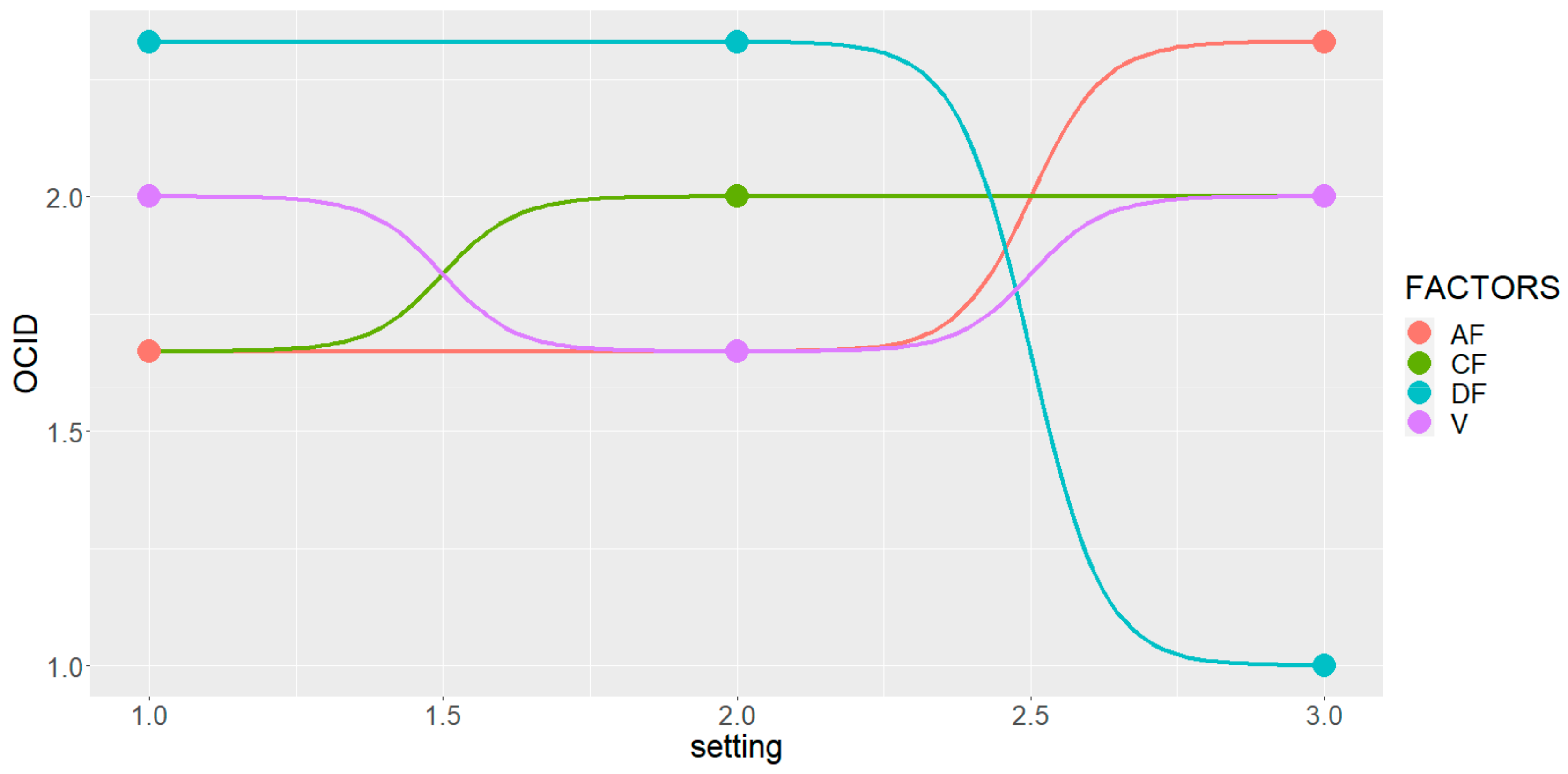
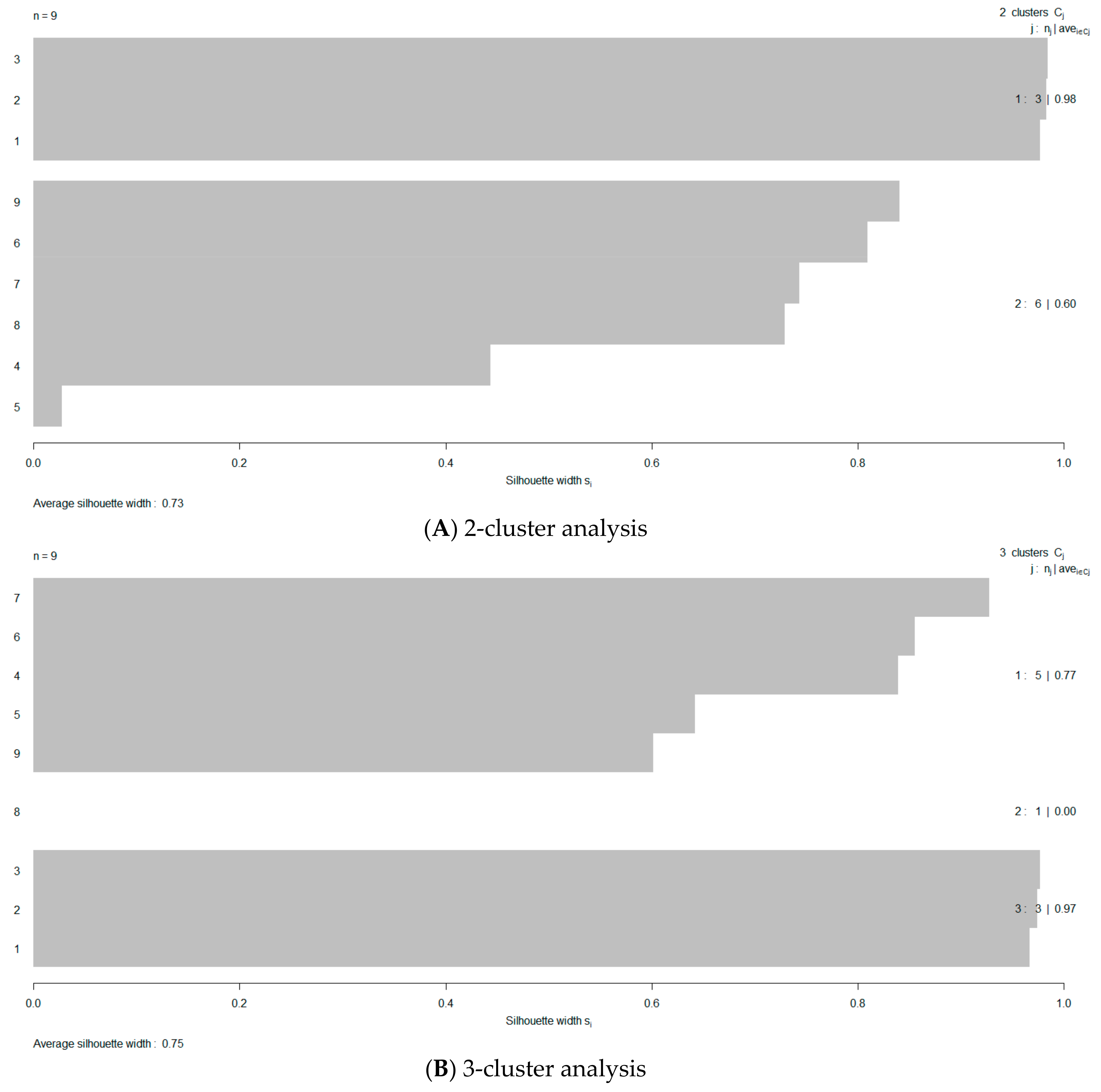


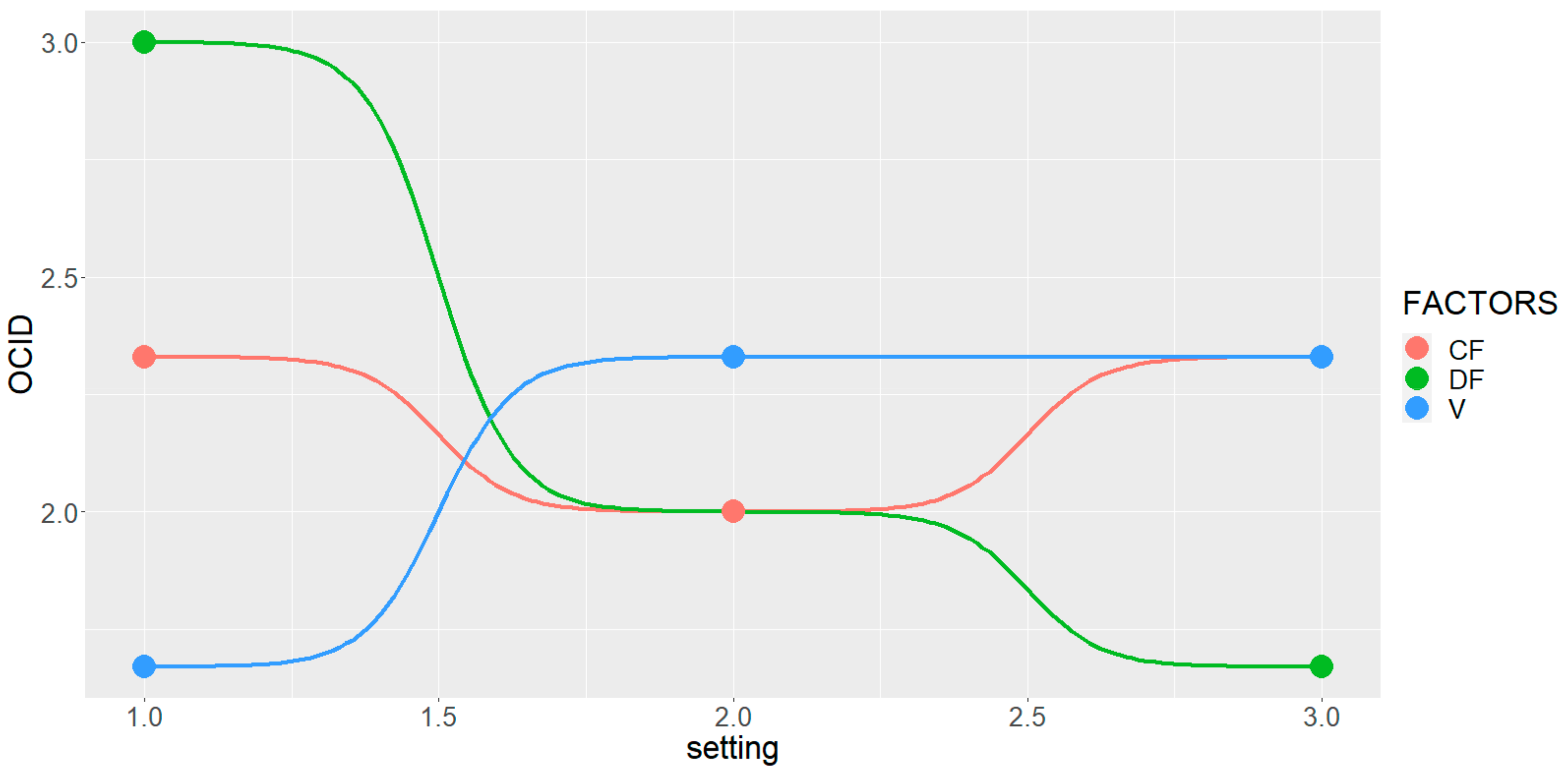
| Run # | Cluster ID | Ordinalized Cluster ID (OCID) |
|---|---|---|
| 1 | 3 | 2 |
| 2 | 3 | 2 |
| 3 | 2 | 3 |
| 4 | 3 | 2 |
| 5 | 2 | 3 |
| 6 | 3 | 2 |
| 7 | 1 | 1 |
| 8 | 1 | 1 |
| 9 | 1 | 1 |
| Variable | Cluster ID | Mean | SE Mean | Median |
|---|---|---|---|---|
| RS | 1 | 1.75 | 1.67 | 0.08 |
| 2 | 13.41 | 2.42 | 13.41 | |
| 3 | 5.73 | 0.81 | 5.75 | |
| SAR | 1 | 6.91 | 0.18 | 6.87 |
| 2 | 5.33 | 0.23 | 5.33 | |
| 3 | 5.83 | 0.15 | 5.86 | |
| SSP | 1 | 70.34 | 0.98 | 70.75 |
| 2 | 62.29 | 2.37 | 62.29 | |
| 3 | 64.45 | 1.18 | 64.66 |
| Run # | Cluster ID | Ordinalized Cluster ID (OCID) |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 3 | 3 |
| 3 | 3 | 3 |
| 4 | 1 | 2 |
| 5 | 1 | 2 |
| 6 | 1 | 2 |
| 7 | 1 | 2 |
| 8 | 2 | 1 |
| 9 | 1 | 2 |
| Variable | Cluster ID | Mean | SE Mean | Median |
|---|---|---|---|---|
| RS | 1 | 54.20 | 2.61 | 54.70 |
| 2 | 26.92 | - | 26.92 | |
| 3 | 80.04 | 0.88 | 80.26 | |
| SAR | 1 | 2.83 | 0.21 | 2.89 |
| 2 | 4.70 | - | 4.70 | |
| 3 | 1.36 | 0.084 | 1.42 | |
| SSP | 1 | 45.26 | 2.31 | 43.91 |
| 2 | 58.76 | - | 58.76 | |
| 3 | 31.01 | 1.89 | 32.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besseris, G. Micro-Clustering and Rank-Learning Profiling of a Small Water-Quality Multi-Index Dataset to Improve a Recycling Process. Water 2021, 13, 2469. https://doi.org/10.3390/w13182469
Besseris G. Micro-Clustering and Rank-Learning Profiling of a Small Water-Quality Multi-Index Dataset to Improve a Recycling Process. Water. 2021; 13(18):2469. https://doi.org/10.3390/w13182469
Chicago/Turabian StyleBesseris, George. 2021. "Micro-Clustering and Rank-Learning Profiling of a Small Water-Quality Multi-Index Dataset to Improve a Recycling Process" Water 13, no. 18: 2469. https://doi.org/10.3390/w13182469





