Mapping Interflow Potential and the Validation of Index-Overlay Weightings by Using Coupled Surface Water and Groundwater Flow Model
Abstract
1. Introduction
2. Materials and Methods
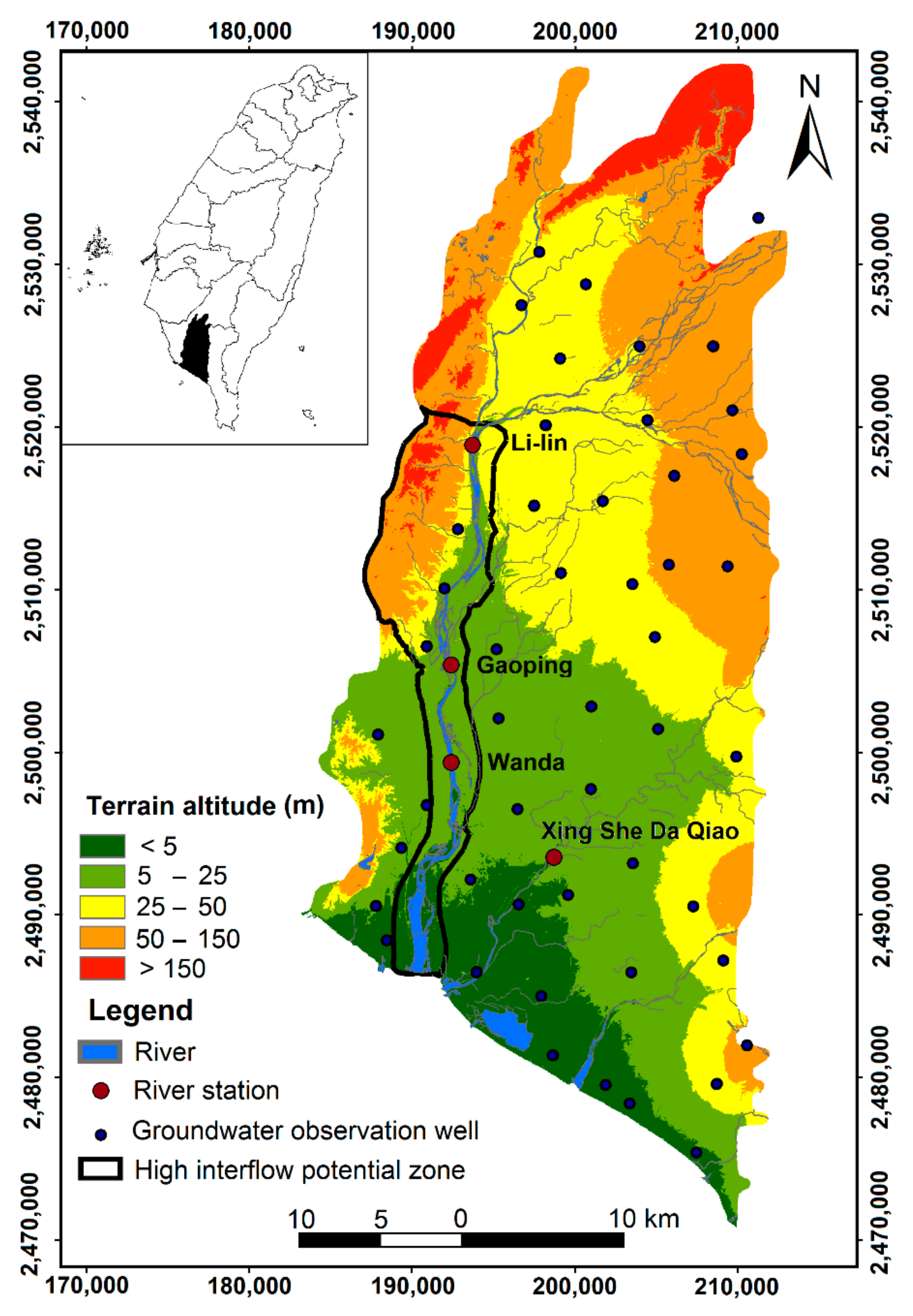
2.1. Study Area
2.2. Data Sources and Assumptions
3. Index-Overlay and Numerical Models
3.1. Index-Overlay Model
3.2. GSFLOW Numerical Model
4. Results and Discussion
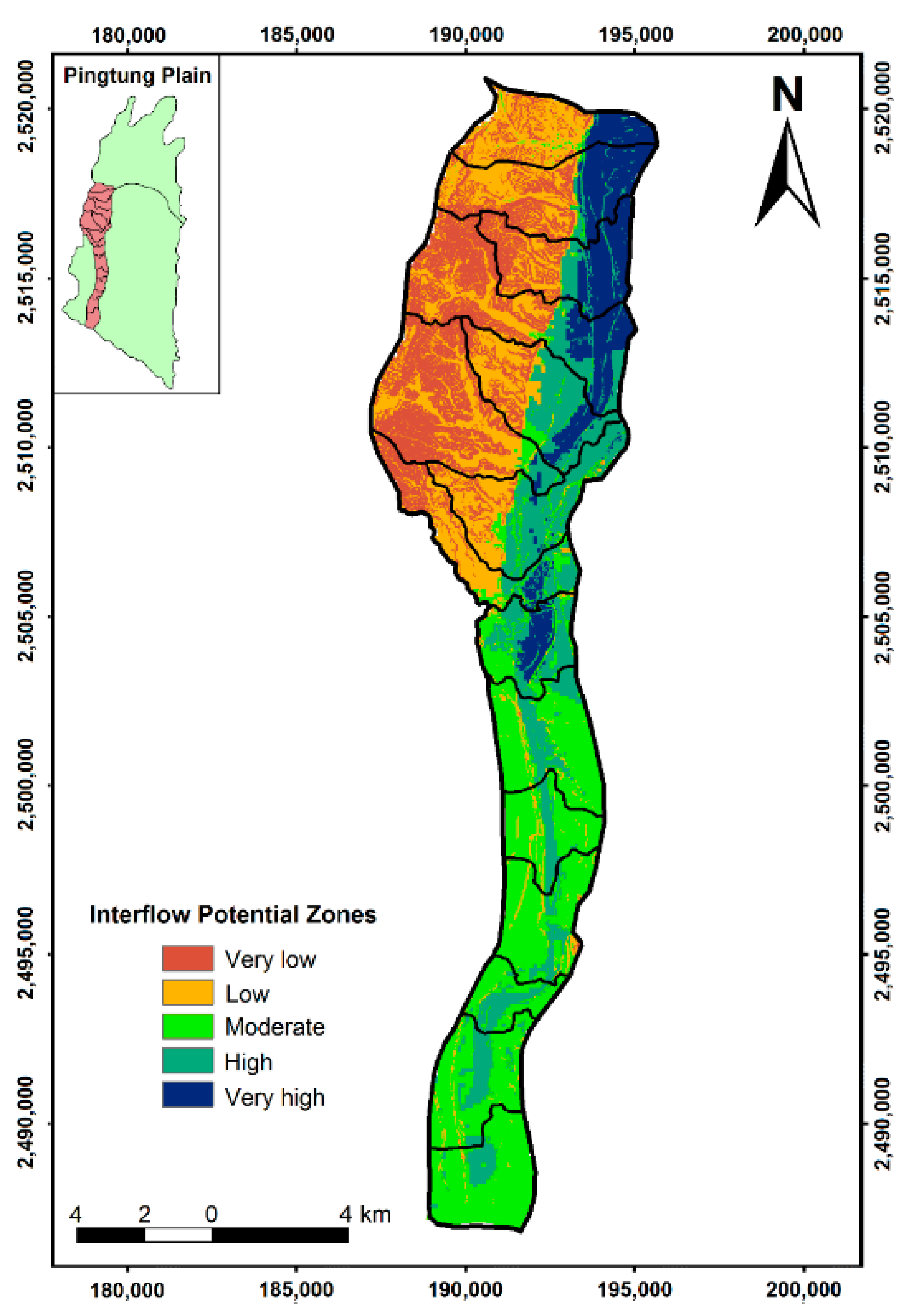
4.1. Interflow Potential Based on the Index-Overlay Model
4.2. Quantification of Interflow Potential Based on the GSFLOW Model
4.2.1. Model Calibration and Validation
4.2.2. Interflow Dynamics in the Sub-Model
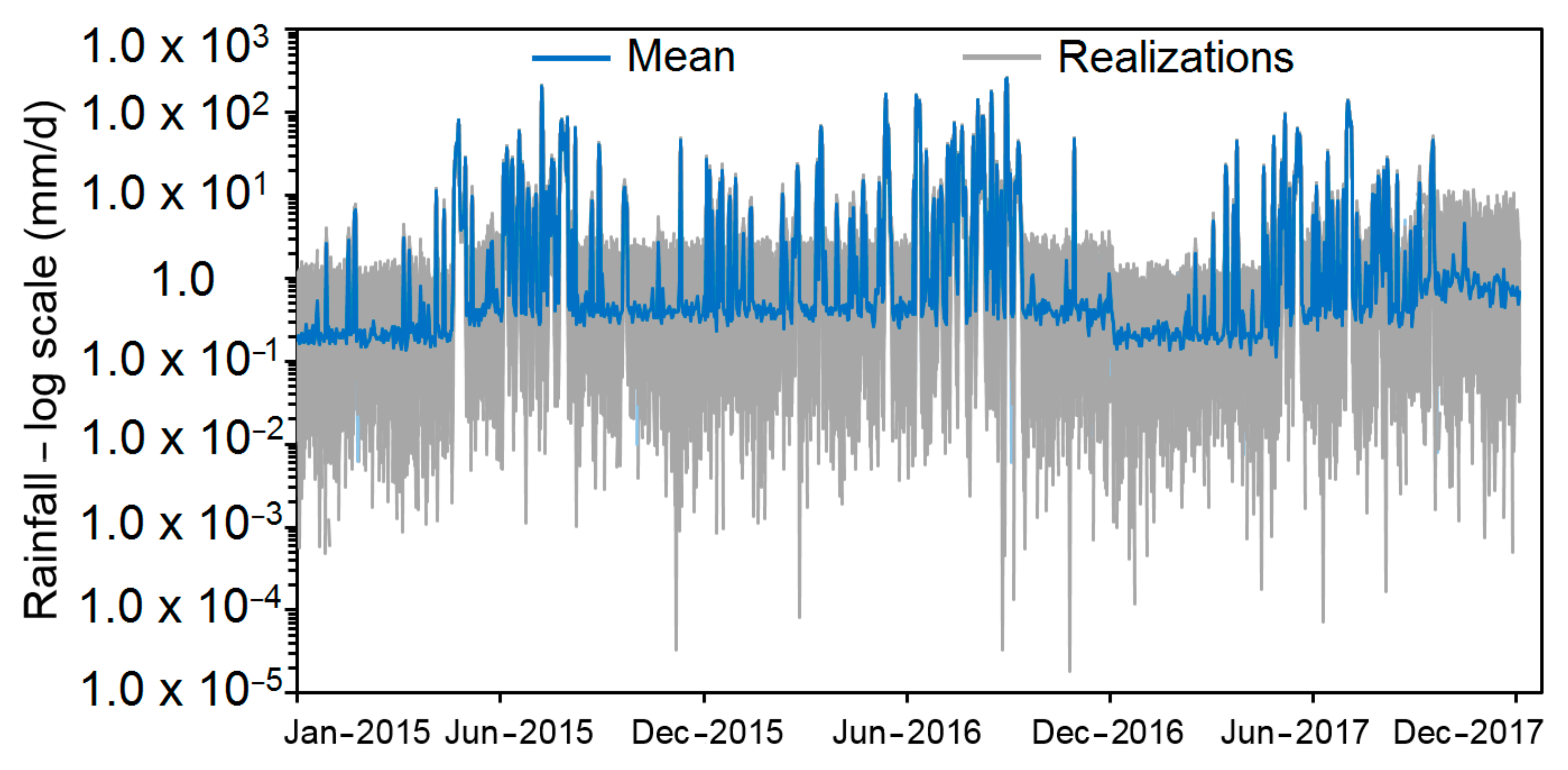
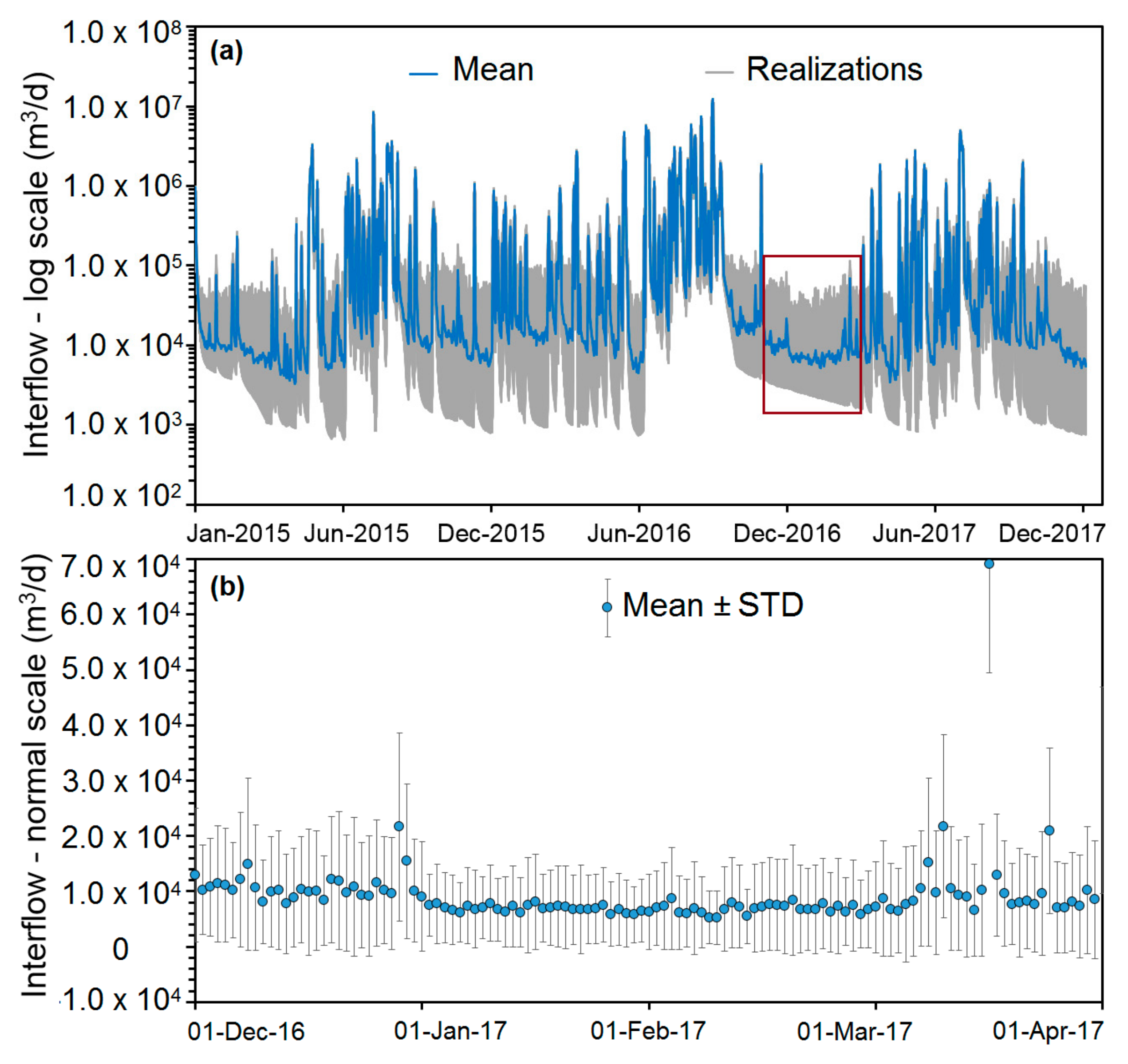
4.3. Interflow Uncertainty Induced by Precipitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [PubMed]
- Dragon, K.; Marciniak, M. Chemical composition of groundwater and surface water in the Arctic environment (Petuniabukta region, central Spitsbergen). J. Hydrol. 2010, 386, 160–172. [Google Scholar] [CrossRef]
- Barthel, R.; Banzhaf, S. Groundwater and Surface Water Interaction at the Regional-scale–A Review with Focus on Regional Integrated Models. Water Resour. Manag. 2016, 30, 1–32. [Google Scholar] [CrossRef]
- Vasconcelos, V.V. What maintains the waters flowing in our rivers? Appl. Water Sci. 2017, 7, 1579–1593. [Google Scholar] [CrossRef]
- Huntington, J.L.; Niswonger, R.G. Role of surface-water and groundwater interactions on projected summertime streamflow in snow dominated regions: An integrated modeling approach. Water Resour. Res. 2012, 48, 1–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Xu, C.Y.; Hong, Y.; Hardy, J.; Sun, Z. Examining the influence of river-lake interaction on the drought and water resources in the Poyang Lake basin. J. Hydrol. 2015, 522, 510–521. [Google Scholar] [CrossRef]
- Carroll, R.W.H.; Deems, J.S.; Niswonger, R.; Schumer, R.; Williams, K.H. The Importance of Interflow to Groundwater Recharge in a Snowmelt-Dominated Headwater Basin. Geophys. Res. Lett. 2019, 46, 5899–5908. [Google Scholar] [CrossRef]
- Demiroǧlu, M.; Dowd, J. The utility of vulnerability maps and GIS in groundwater management: A case study. Turkish J. Earth Sci. 2014, 23, 80–90. [Google Scholar] [CrossRef]
- Jang, W.S.; Engel, B.; Harbor, J.; Theller, L. Aquifer vulnerability assessment for sustainable groundwater management using DRASTIC. Water 2017, 9, 792. [Google Scholar] [CrossRef]
- Vu, T.D.; Ni, C.F.; Li, W.C.; Truong, M.H. Modified index-overlay method to assess spatial-temporal variations of groundwater vulnerability and groundwater contamination risk in areas with variable activities of agriculture developments. Water 2019, 11, 2492. [Google Scholar] [CrossRef]
- Vu, T.D.; Ni, C.F.; Li, W.C.; Truong, M.H.; Hsu, S.M. Predictions of groundwater vulnerability and sustainability by an integrated index-overlay method and physical-based numerical model. J. Hydrol. 2021, 596, 126082. [Google Scholar] [CrossRef]
- Díaz-Alcaide, S.; Martínez-Santos, P. Review: Advances in groundwater potential mapping. Hydrogeol. J. 2019, 27, 2307–2324. [Google Scholar] [CrossRef]
- Benjmel, K.; Amraoui, F.; Boutaleb, S.; Ouchchen, M.; Tahiri, A.; Touab, A. Mapping of Groundwater Potential Zones in Techniques, and Multicriteria Data Analysis ( Case of the Ighrem Region, Western Anti-Atlas, Morocco). Water 2020, 12, 471. [Google Scholar] [CrossRef]
- Tolche, A.D. Groundwater potential mapping using geospatial techniques: A case study of Dhungeta-Ramis sub-basin, Ethiopia. Geol. Ecol. Landscapes 2021, 5, 65–80. [Google Scholar] [CrossRef]
- Kaliraj, S.; Chandrasekar, N.; Magesh, N.S. Identification of potential groundwater recharge zones in Vaigai upper basin, Tamil Nadu, using GIS-based analytical hierarchical process (AHP) technique. Arab. J. Geosci. 2014, 7, 1385–1401. [Google Scholar] [CrossRef]
- Çelik, R. Evaluation of groundwater potential by GIS-based multicriteria decision making as a spatial prediction tool: Case study in the Tigris River Batman-Hasankeyf Sub-Basin, Turkey. Water 2019, 11, 2630. [Google Scholar] [CrossRef]
- Allafta, H.; Opp, C.; Patra, S. Identification of groundwater potential zones using remote sensing and GIS techniques: A case study of the shatt Al-Arab Basin. Remote Sens. 2021, 13, 112. [Google Scholar] [CrossRef]
- Ha, K.; Koh, D.C.; Yum, B.W.; Lee, K.K. Estimation of river stage effect on groundwater level, discharge, and bank storage and its field application. Geosci. J. 2008, 12, 191–204. [Google Scholar] [CrossRef]
- Saleh, F.; Ducharne, A.; Flipo, N.; Oudin, L.; Ledoux, E. Impact of river bed morphology on discharge and water levels simulated by a 1D Saint-Venant hydraulic model at regional scale. J. Hydrol. 2013, 476, 169–177. [Google Scholar] [CrossRef]
- Shaban, A.; Khawlie, M.; Abdallah, C. Use of remote sensing and GIS to determine recharge potential zones: The case of Occidental Lebanon. Hydrogeol. J. 2006, 14, 433–443. [Google Scholar] [CrossRef]
- Yeh, H.F.; Lee, C.H.; Hsu, K.C.; Chang, P.H. GIS for the assessment of the groundwater recharge potential zone. Environ. Geol. 2009, 58, 185–195. [Google Scholar] [CrossRef]
- Huang, C.C.; Yeh, H.F.; Lin, H.I.; Lee, S.T.; Hsu, K.C.; Lee, C.H. Groundwater recharge and exploitative potential zone mapping using GIS and GOD techniques. Environ. Earth Sci. 2013, 68, 267–280. [Google Scholar] [CrossRef]
- Bari, M.A.; Smettem, K.R.J. A conceptual model of daily water balance following partial clearing from forest to pasture. Hydrol. Earth Syst. Sci. 2006, 10, 321–337. [Google Scholar] [CrossRef]
- Watson, A.; Miller, J.; Fink, M.; Kralisch, S.; Fleischer, M.; De Clercq, W. Distributive rainfall-runoff modelling to understand runoff-to-baseflow proportioning and its impact on the determination of reserve requirements of the Verlorenvlei estuarine lake, west coast, South Africa. Hydrol. Earth Syst. Sci. 2019, 23, 2679–2697. [Google Scholar] [CrossRef]
- Meles Bitew, M.; Jackson, C.R.; Goodrich, D.C.; Younger, S.E.; Griffiths, N.A.; Vaché, K.B.; Rau, B. Dynamic domain kinematic modelling for predicting interflow over leaky impeding layers. Hydrol. Process. 2020, 34, 2895–2910. [Google Scholar] [CrossRef]
- Taylor, A.R.; Lamontagne, S.; Crosbie, R.S. Measurements of riverbed hydraulic conductivity in a semiarid lowland river system (Murray-Darling Basin, Australia). Soil Res. 2013, 51, 363–371. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Taylor, A.R.; Davis, A.C.; Lamontagne, S.; Munday, T. Evaluation of infiltration from losing-disconnected rivers using a geophysical characterisation of the riverbed and a simplified infiltration model. J. Hydrol. 2014, 508, 102–113. [Google Scholar] [CrossRef]
- Harvey, J.W.; Gooseff, M. River corridor science: Hydrologic exchange and ecological consequences from bedforms to basins. Water Resour. Res. 2015, 51, 6893–6922. [Google Scholar] [CrossRef]
- Cui, G.; Su, X.; Liu, Y.; Zheng, S. Effect of riverbed sediment flushing and clogging on river-water infiltration rate: A case study in the Second Songhua River, Northeast China. Hydrogeol. J. 2021, 29, 551–565. [Google Scholar] [CrossRef]
- Grodzka-Łukaszewska, M.; Nawalany, M.; Zijl, W. A Velocity-Oriented Approach for Modflow. Transp. Porous Media 2017, 119, 373–390. [Google Scholar] [CrossRef][Green Version]
- Diaz, M.; Sinicyn, G.; Grodzka-łukaszewska, M. Modelling of groundwater–surface water interaction applying the hyporheic flux model. Water 2020, 12, 3303. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating three hydrological distributed watershed models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef]
- Nasiri, S.; Ansari, H.; Ziaei, A.N. Simulation of water balance equation components using SWAT model in Samalqan Watershed (Iran). Arab. J. Geosci. 2020, 13, 421. [Google Scholar] [CrossRef]
- Taiwan Government Report (TGR). Hydrological Year Book of Taiwan; Ministry of Economic Affairs, Water Resources Agency: Taichung, Taiwan, 2011. (In Chinese)
- Taiwan, C.G.S. Hydrogeological Survey Report of Pingtung Plain, Taiwan; Central Geologic Survey, Ministry of Economic Affairs: Taichung, Taiwan, 2002; pp. 97–142.
- Taiwan Government Report (TGR). Review on the Regulation Planning of Kaoping River; Ministry of Economic Affair, Taiwan Water Resources Agency: Taichung, Taiwan, 2008. (In Chinese)
- Water Resources Agency. The Preliminary Investigation and Tests of Interflow Resources and Riverbank Water Intake Works Evaluation Near the Kaoping River; Southern Region Water Resources Office: Kaosiung, Taiwan, 2012.
- Tran, Q.D.; Ni, C.F.; Lee, I.H.; Truong, M.H.; Liu, C.J. Numerical modeling of surface water and groundwater interactions induced by complex fluvial landforms and human activities in the Pingtung plain groundwater basin, Taiwan. Appl. Sci. 2020, 10, 7152. [Google Scholar] [CrossRef]
- Chen, C.H.; Wang, C.H.; Hsu, Y.J.; Yu, S.B.; Kuo, L.C. Correlation between groundwater level and altitude variations in land subsidence area of the Choshuichi Alluvial Fan, Taiwan. Eng. Geol. 2010, 115, 122–131. [Google Scholar] [CrossRef]
- Chang, F.J.; Huang, C.W.; Cheng, S.T.; Chang, L.C. Conservation of groundwater from over-exploitation—Scientific analyses for groundwater resources management. Sci. Total Environ. 2017, 598, 828–838. [Google Scholar] [CrossRef] [PubMed]
- Obi Reddy, G.P.; Maji, A.K.; Gajbhiye, K.S. Drainage morphometry and its influence on landform characteristics in a basaltic terrain, Central India–A remote sensing and GIS approach. Int. J. Appl. Earth Obs. Geoinf. 2004, 6, 1–16. [Google Scholar] [CrossRef]
- Siddayao, G.P.; Valdez, S.E.; Fernandez, P.L. Analytic Hierarchy Process (AHP) in Spatial Modeling for Floodplain Risk Assessment. Int. J. Mach. Learn. Comput. 2014, 4, 450–457. [Google Scholar] [CrossRef]
- Nithya, C.N.; Srinivas, Y.; Magesh, N.S.; Kaliraj, S. Assessment of groundwater potential zones in Chittar basin, Southern India using GIS based AHP technique. Remote Sens. Appl. Soc. Environ. 2019, 15, 100248. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW Coupled Groundwater and Surface-Water FLOW Model. Based on The Integration of The Precipitation Runoff Modeling System (PRMS) and The Modular Groundwater Flow Model. (MODFLOW-2005). In U.S. Geological Survey Techniques and Methods 6-D1; U.S. Geological Survey: Reston, VA, USA, 2008; p. 240. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, The U.S. Geological Survey Modular Groundwater Model–The Groundwater Flow Process. In USGS Techniques and Methods 6-A16; USGS: Reston, VA, USA, 2005. [Google Scholar]
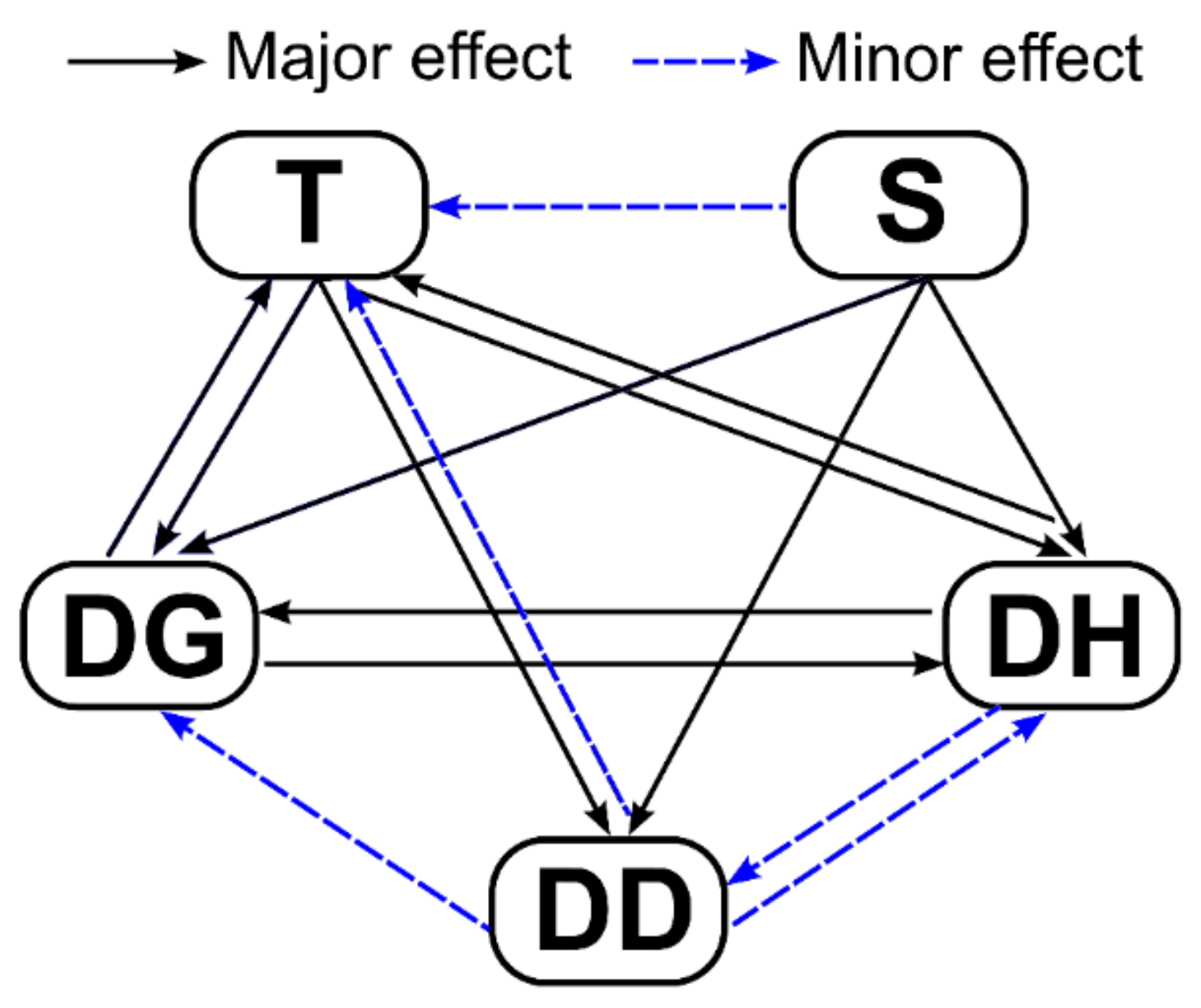
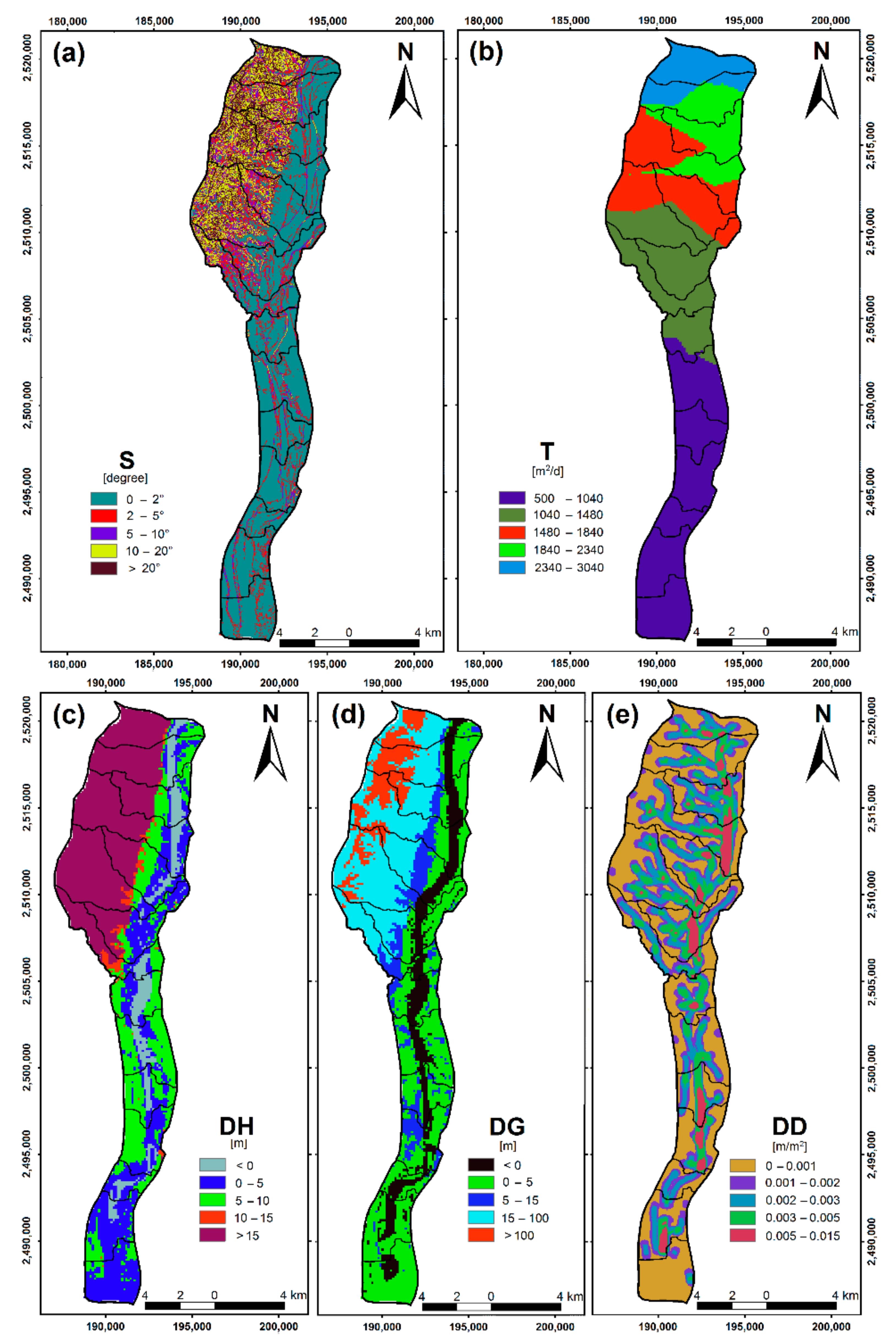

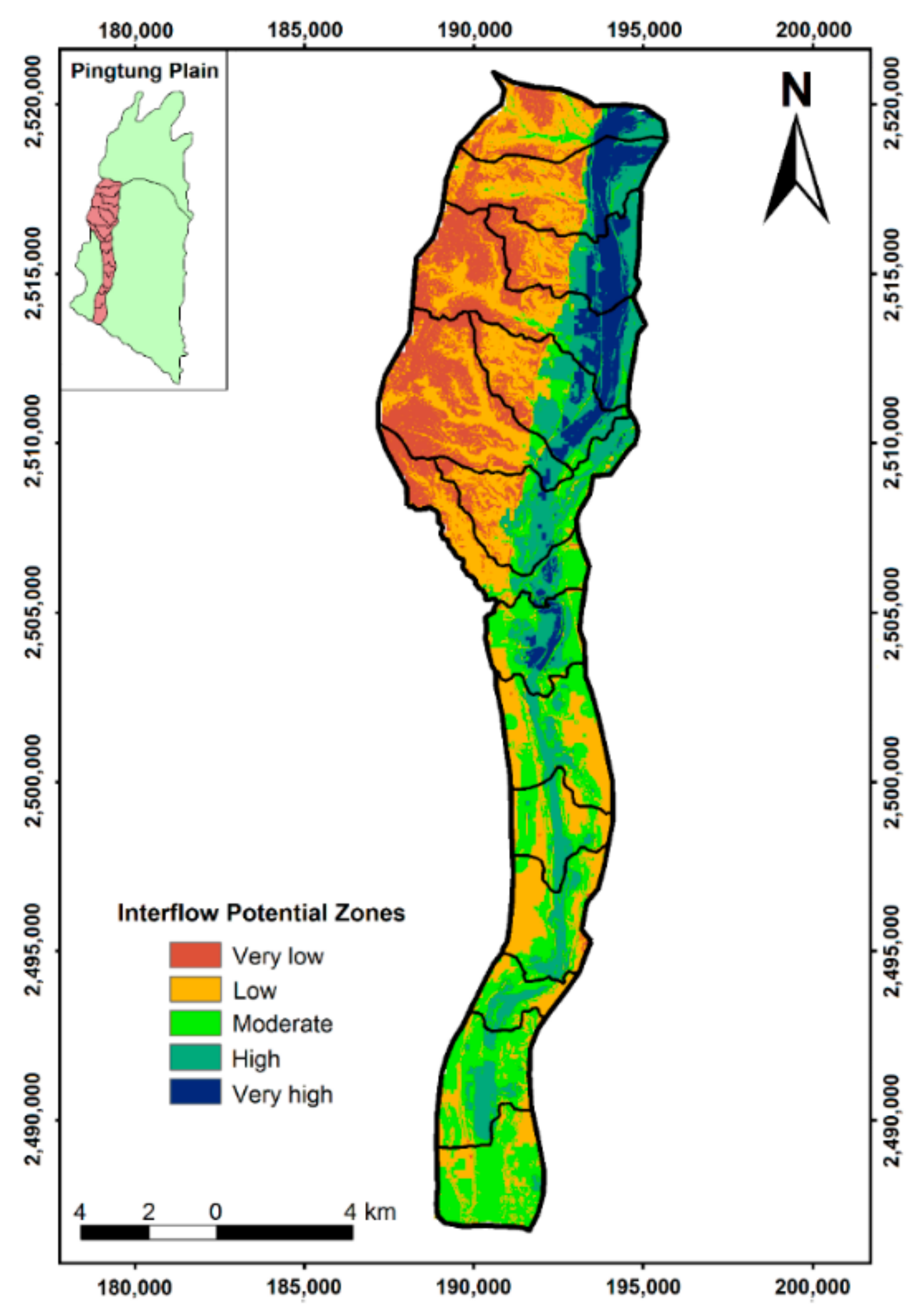
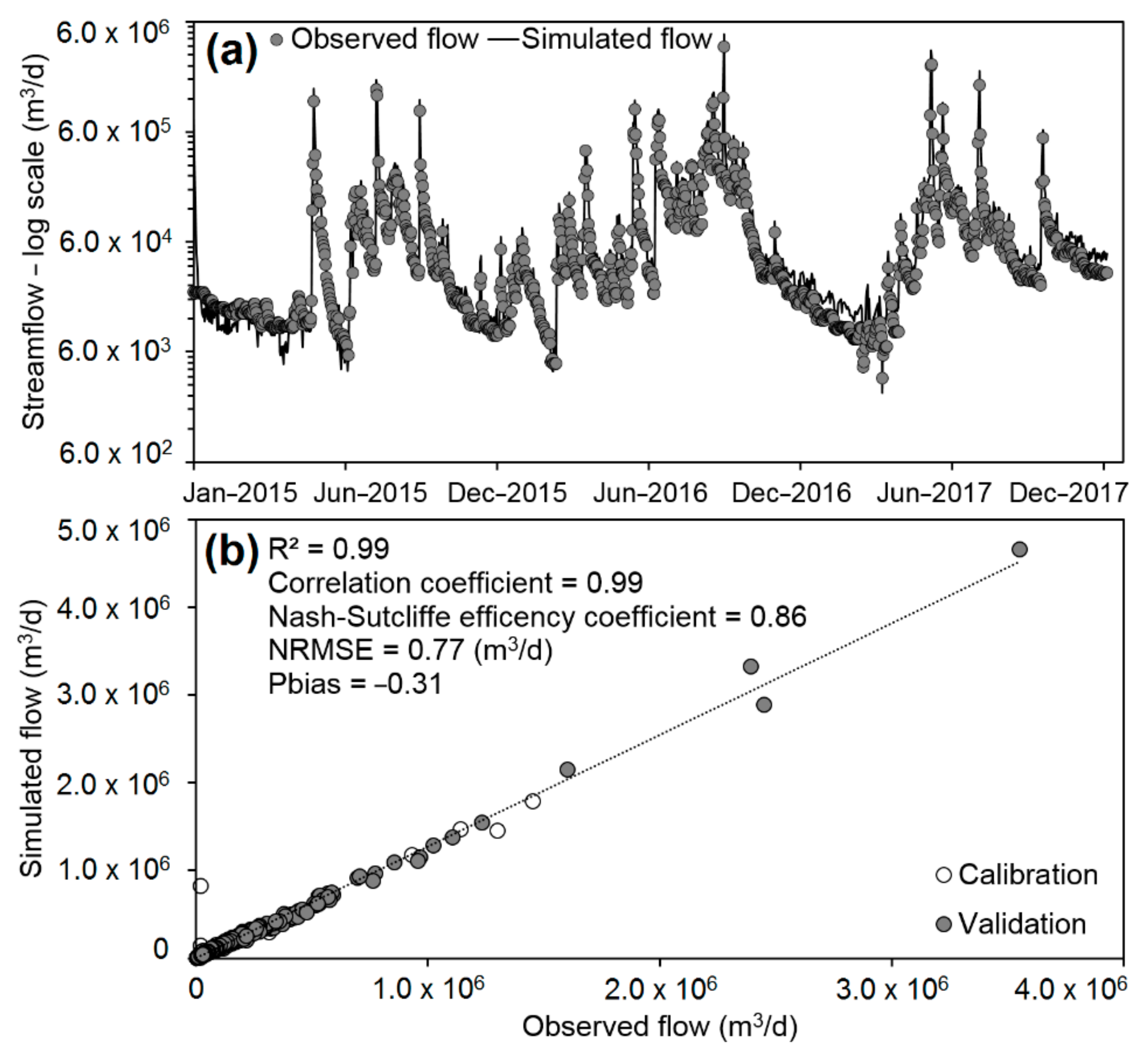
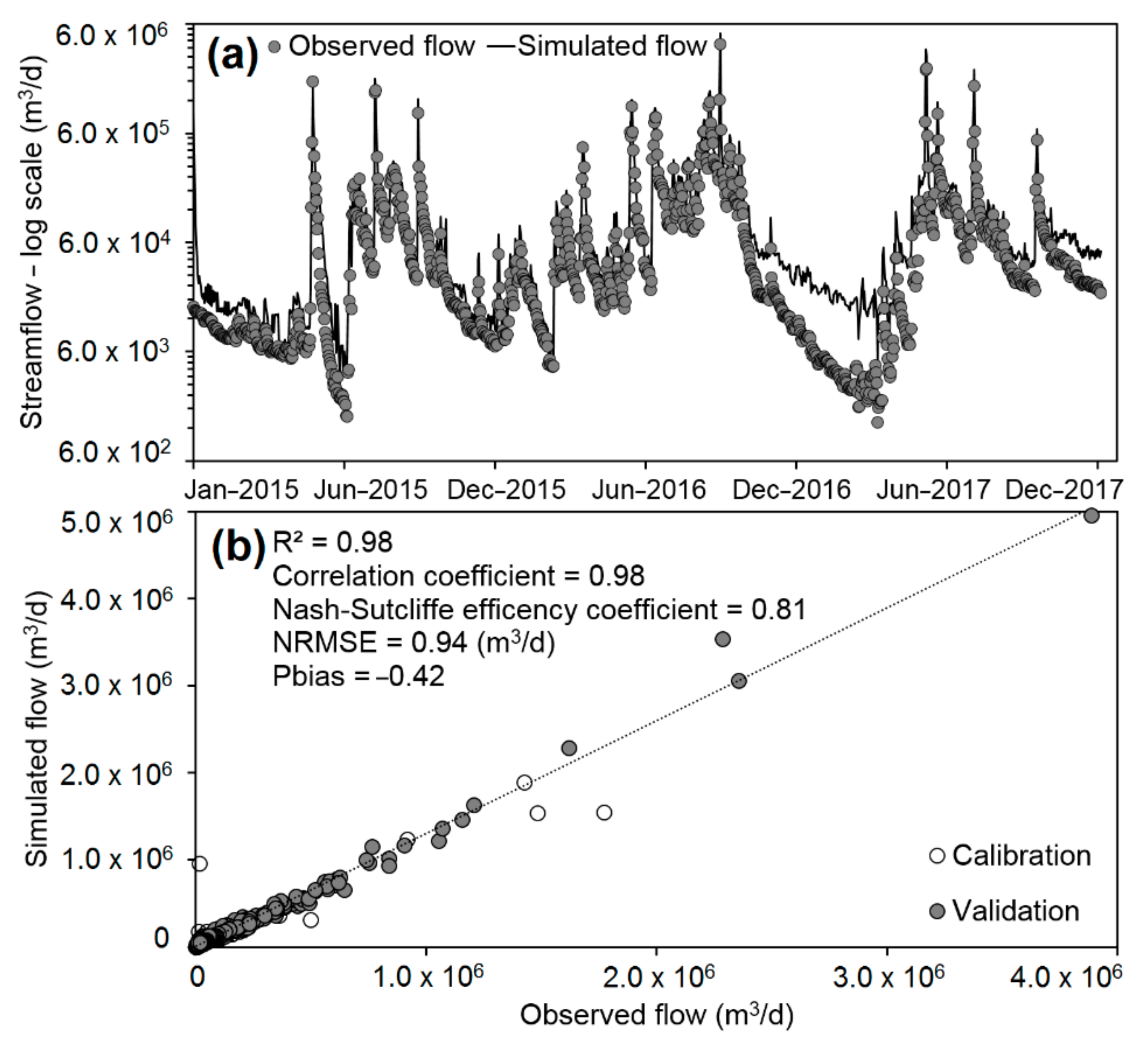
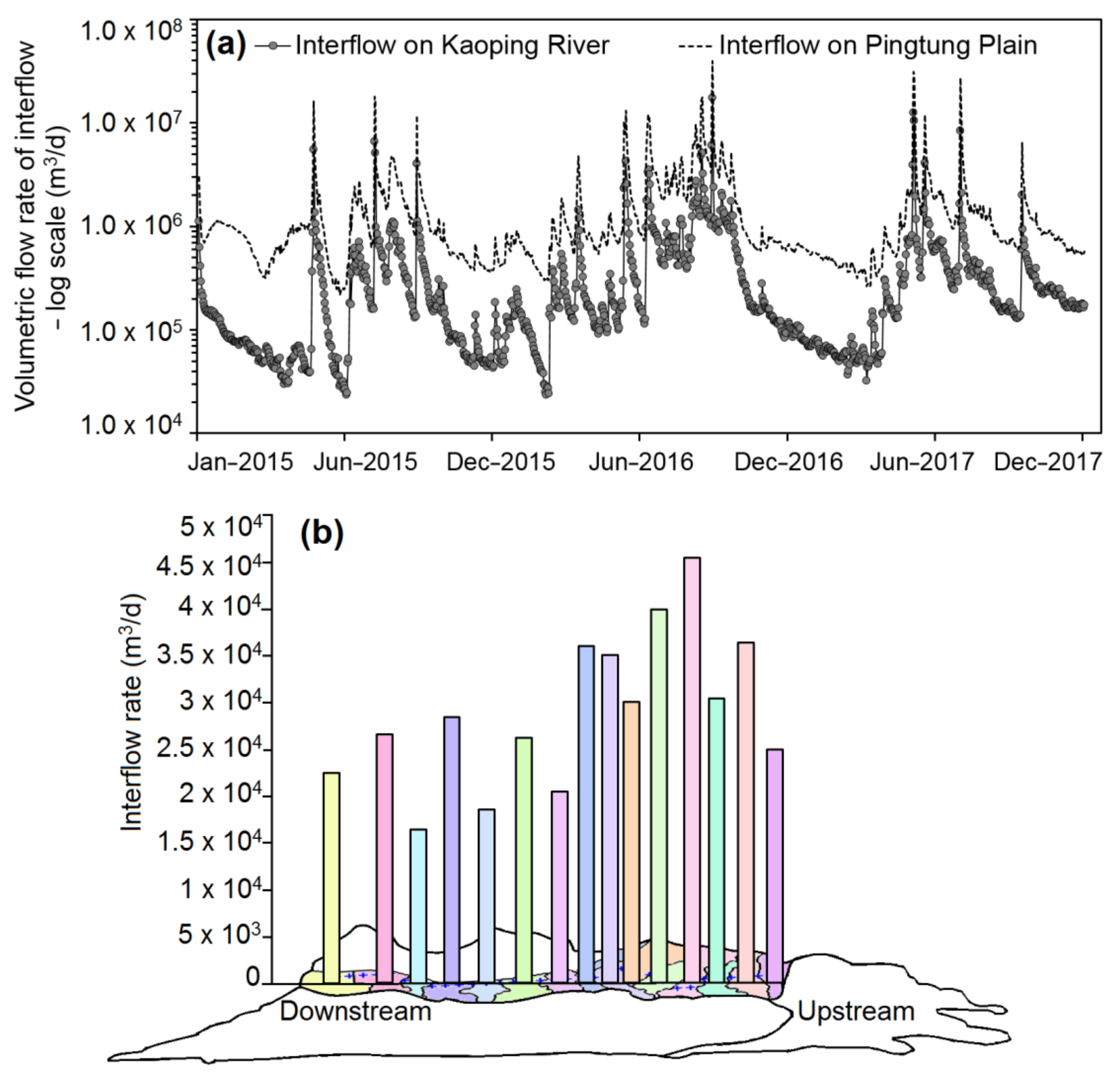

| Factor | S | T | DH | DG | DD | Scale Weight | Geometric Mean |
|---|---|---|---|---|---|---|---|
| S | 1.00 | 1.17 | 1.40 | 1.75 | 2.33 | 3.5 | 1.46 |
| T | 0.86 | 1.00 | 1.20 | 1.50 | 2.00 | 3.0 | 1.25 |
| DH | 0.71 | 0.83 | 1.00 | 1.25 | 1.67 | 2.5 | 1.04 |
| DG | 0.57 | 0.67 | 0.80 | 1.00 | 1.33 | 2.0 | 0.84 |
| DD | 0.43 | 0.50 | 0.60 | 0.75 | 1.00 | 1.5 | 0.63 |
| Factors | Descriptive Level | Domain of Effect | Assigned Weight (AW) | Geometric Mean (G) | Normalized Weight N = (AW/G) |
|---|---|---|---|---|---|
| Slope (S) | Very high | 0–2° | 9 | 1.46 | 6.16 |
| [degree] | High | 2–5° | 7 | 4.79 | |
| Moderate | 5–10° | 5 | 3.42 | ||
| Low | 10–20° | 3 | 2.05 | ||
| Very low | >20° | 1 | 0.68 | ||
| Transmissivity (T) | Very high | 2340–3040 | 7.5 | 1.25 | 5.99 |
| [m2/d] | High | 1840–2340 | 6 | 4.79 | |
| Moderate | 1480–1840 | 4 | 3.19 | ||
| Low | 1040–1480 | 2.5 | 2.00 | ||
| Very low | 500–1040 | 1 | 0.80 | ||
| River-GW level | Very high | <0 | 6.5 | 1.04 | 6.23 |
| difference (DH) | High | 0–5 | 6 | 5.75 | |
| [m] | Moderate | 5–10 | 5 | 4.79 | |
| Low | 10–15 | 1 | 0.96 | ||
| Very low | > 15 | 1 | 0.96 | ||
| Depth to | Very high | < 0 | 5 | 0.84 | 5.99 |
| groundwater (DG) | High | 0–5 | 4 | 4.79 | |
| [m] | Moderate | 5–15 | 3 | 3.59 | |
| Low | 15–100 | 2 | 2.39 | ||
| Very low | >100 | 1 | 1.20 | ||
| Drainage density (DD) | Very high | 0.005–0.015 | 4 | 0.63 | 6.39 |
| [m/m2] | High | 0.003–0.005 | 3 | 4.79 | |
| Moderate | 0.002–0.003 | 2 | 3.19 | ||
| Low | 0.001–0.002 | 1.5 | 2.39 | ||
| Very low | 0–0.001 | 1 | 1.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, C.-F.; Tran, Q.-D.; Lee, I.-H.; Truong, M.-H.; Hsu, S.M. Mapping Interflow Potential and the Validation of Index-Overlay Weightings by Using Coupled Surface Water and Groundwater Flow Model. Water 2021, 13, 2452. https://doi.org/10.3390/w13172452
Ni C-F, Tran Q-D, Lee I-H, Truong M-H, Hsu SM. Mapping Interflow Potential and the Validation of Index-Overlay Weightings by Using Coupled Surface Water and Groundwater Flow Model. Water. 2021; 13(17):2452. https://doi.org/10.3390/w13172452
Chicago/Turabian StyleNi, Chuen-Fa, Quoc-Dung Tran, I-Hsien Lee, Minh-Hoang Truong, and Shaohua Marko Hsu. 2021. "Mapping Interflow Potential and the Validation of Index-Overlay Weightings by Using Coupled Surface Water and Groundwater Flow Model" Water 13, no. 17: 2452. https://doi.org/10.3390/w13172452
APA StyleNi, C.-F., Tran, Q.-D., Lee, I.-H., Truong, M.-H., & Hsu, S. M. (2021). Mapping Interflow Potential and the Validation of Index-Overlay Weightings by Using Coupled Surface Water and Groundwater Flow Model. Water, 13(17), 2452. https://doi.org/10.3390/w13172452








