Effects of Decaying Hydraulic Conductivity on the Groundwater Flow Processes in a Managed Aquifer Recharge Area in an Alluvial Fan
Abstract
1. Introduction
2. Methodology
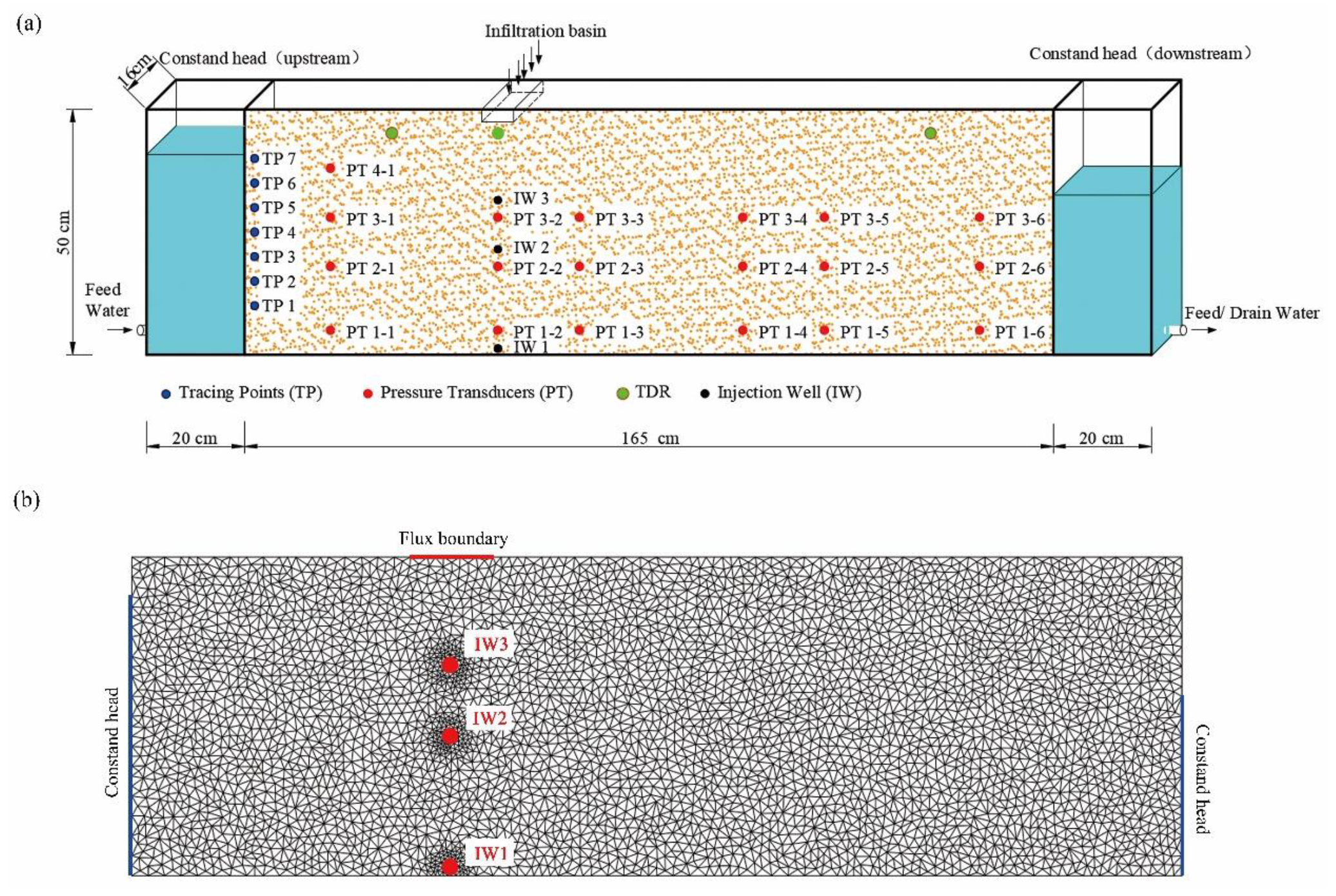
2.1. Laboratory Experiments
2.2. Numerical Simulation
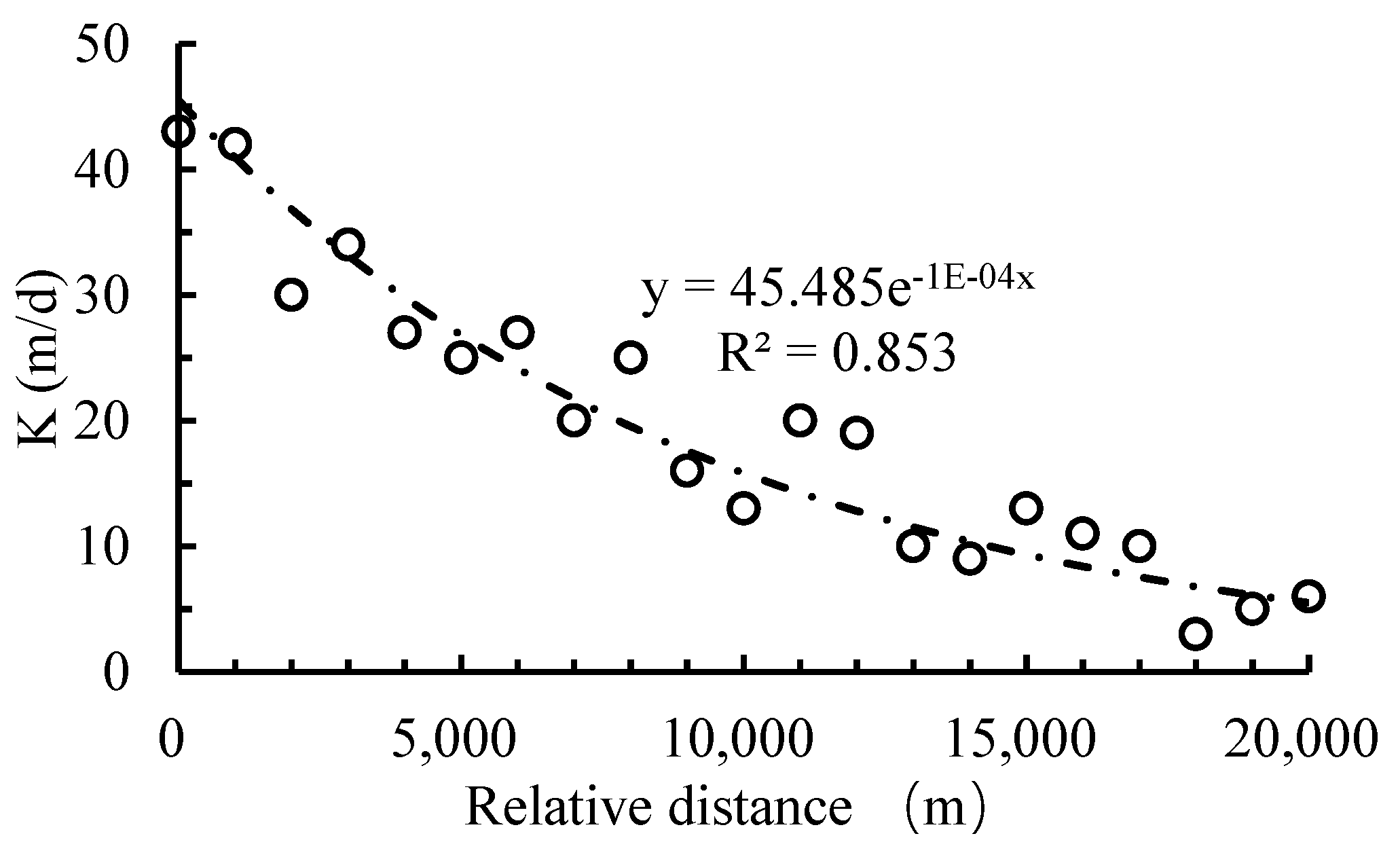
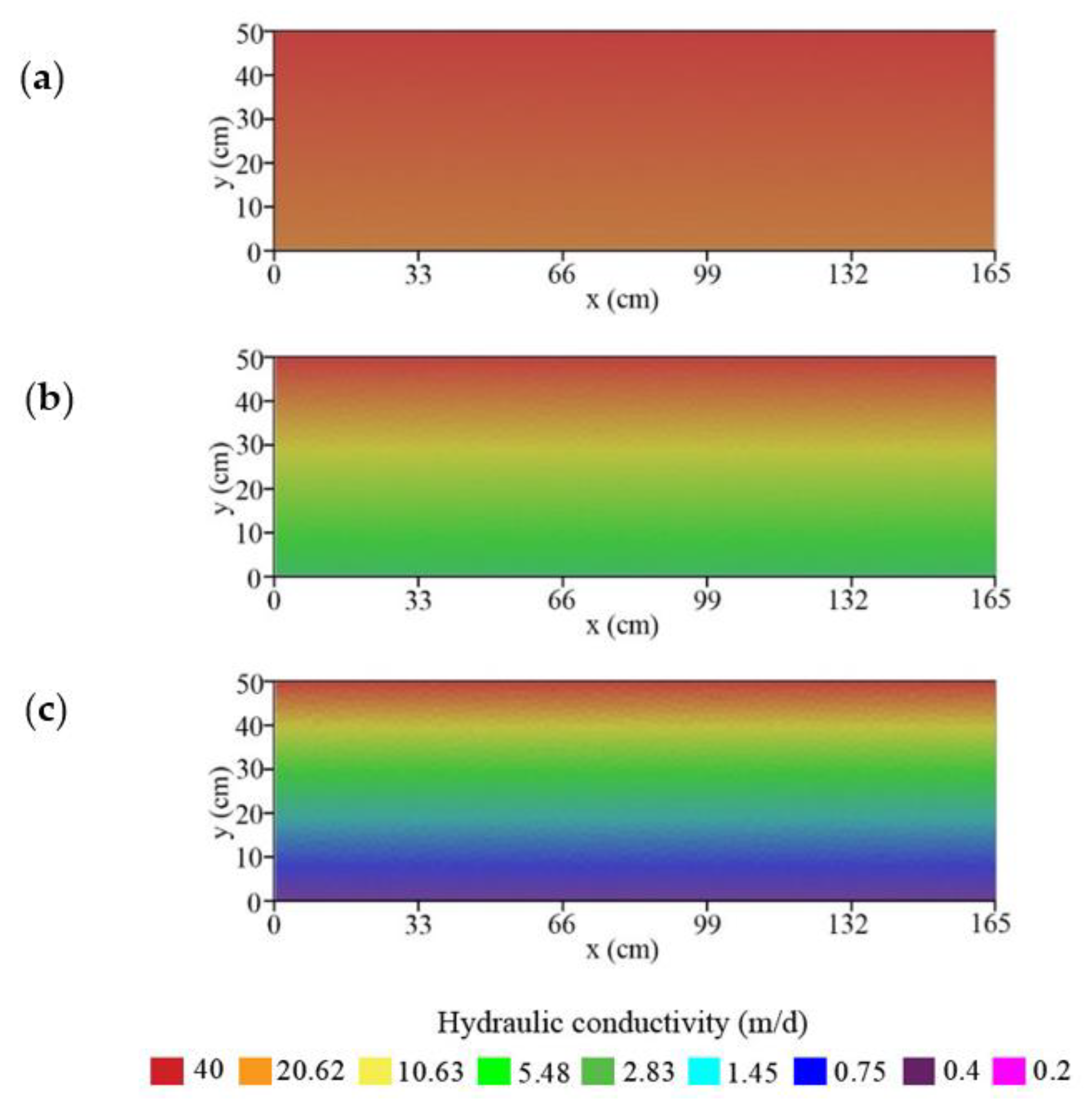
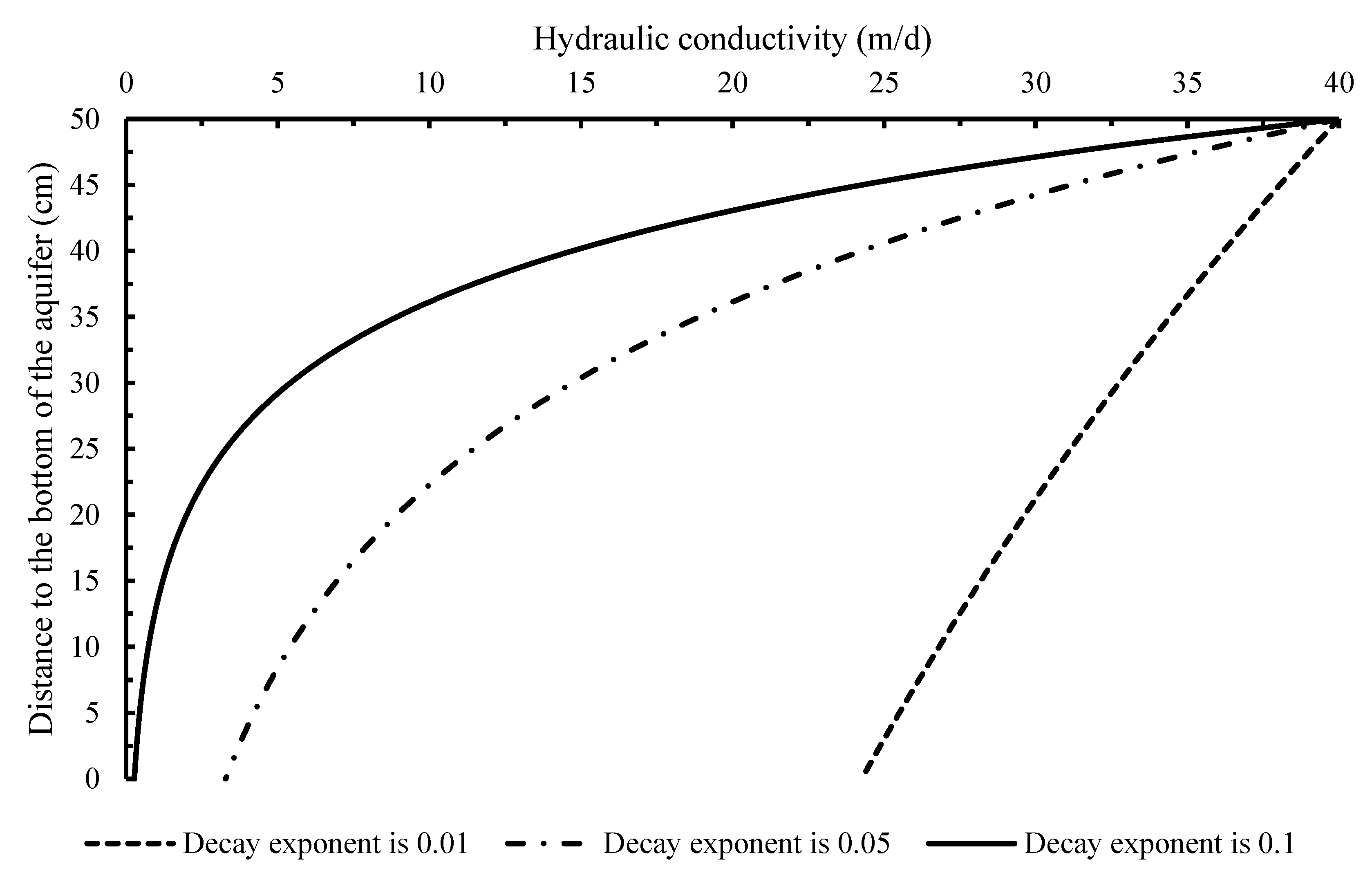
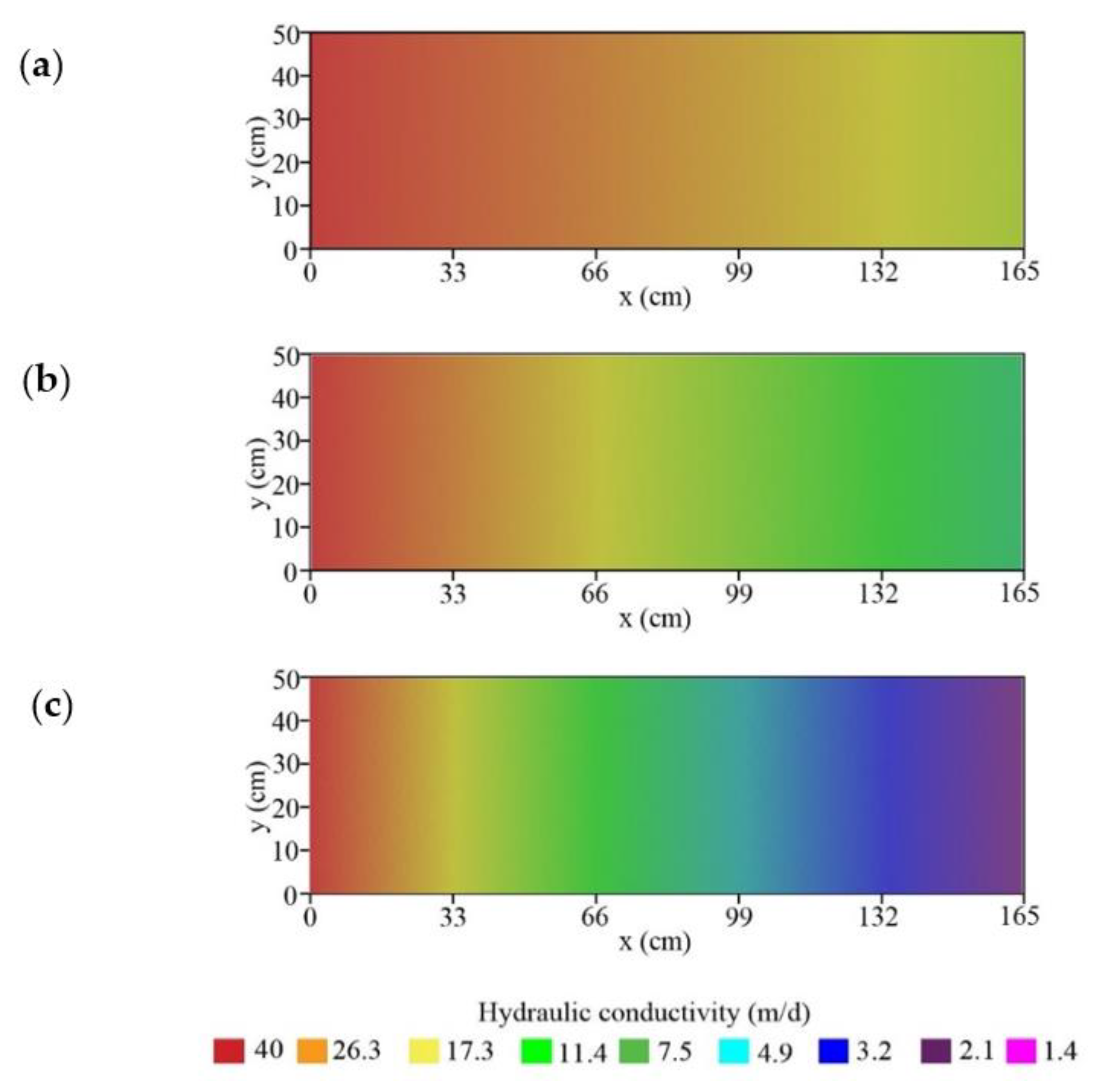
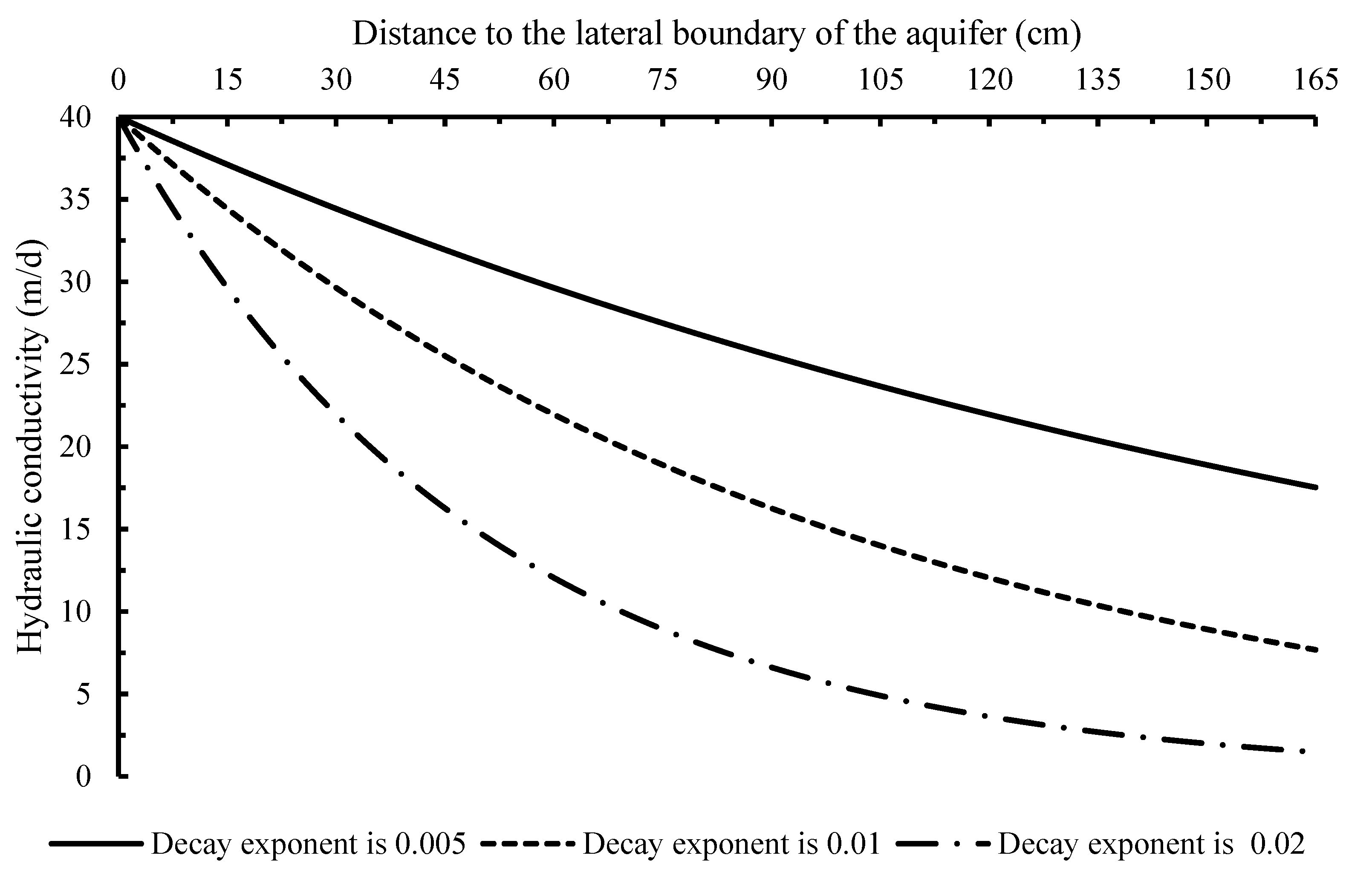
2.3. Scenario Definition
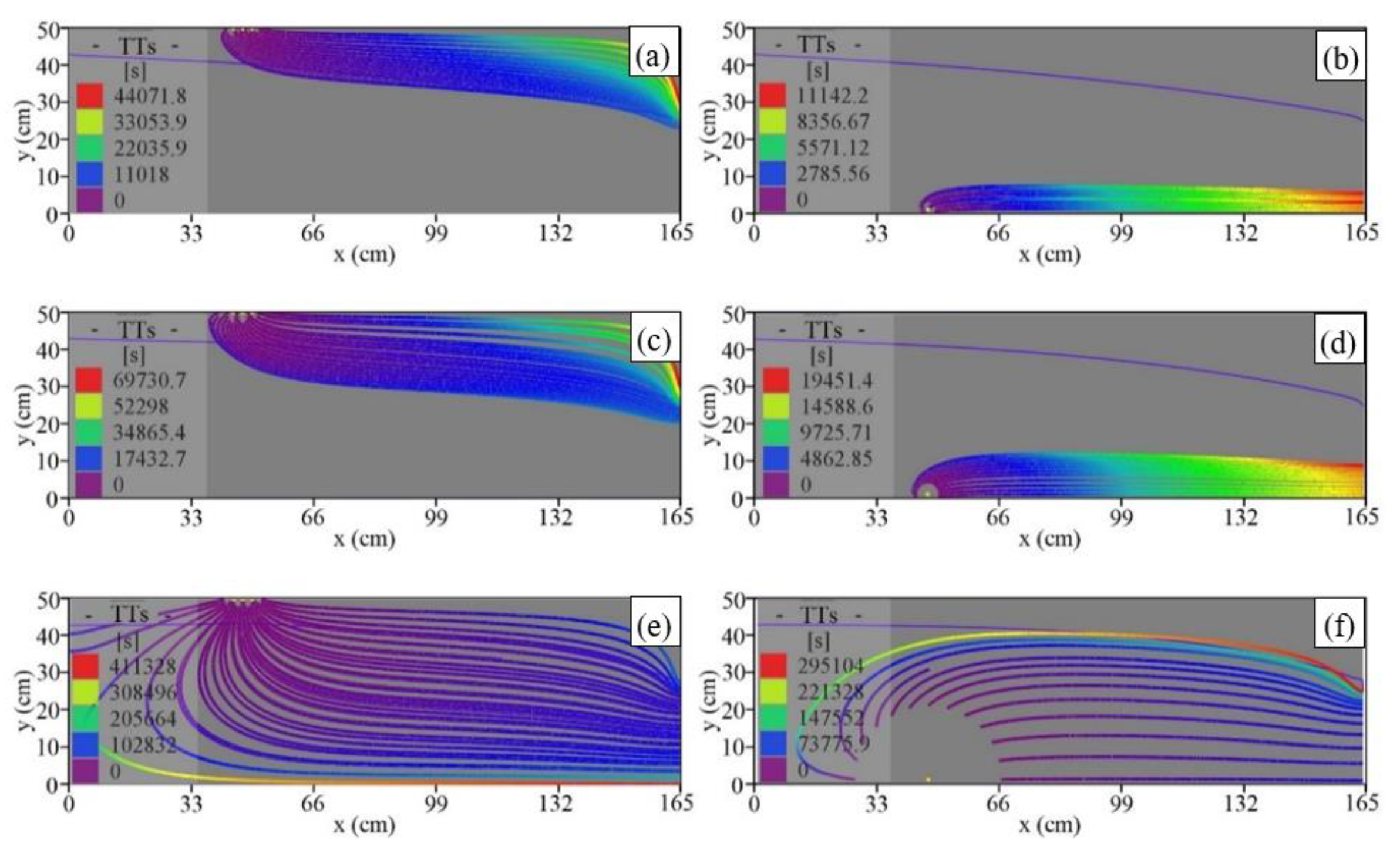
3. Results
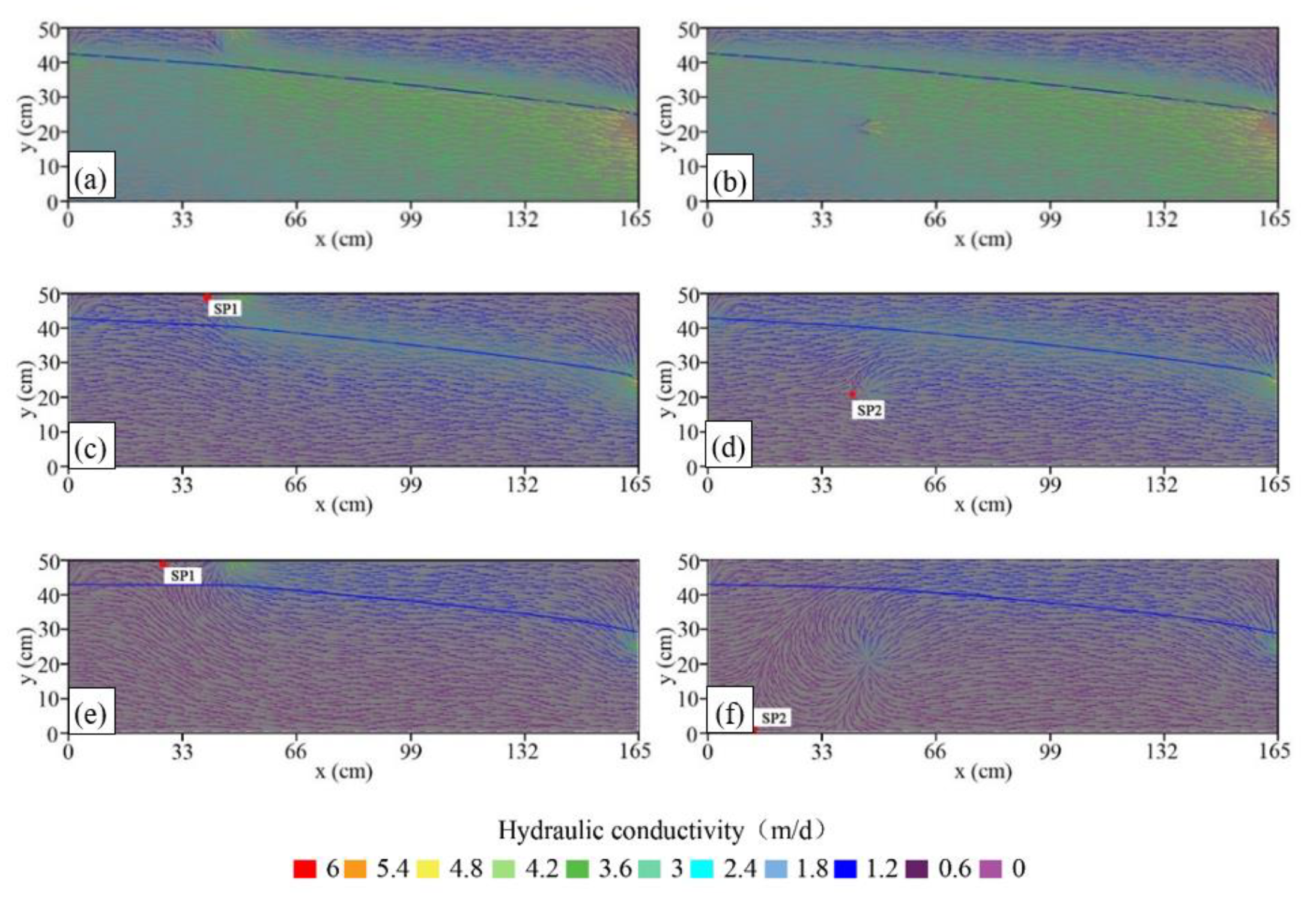
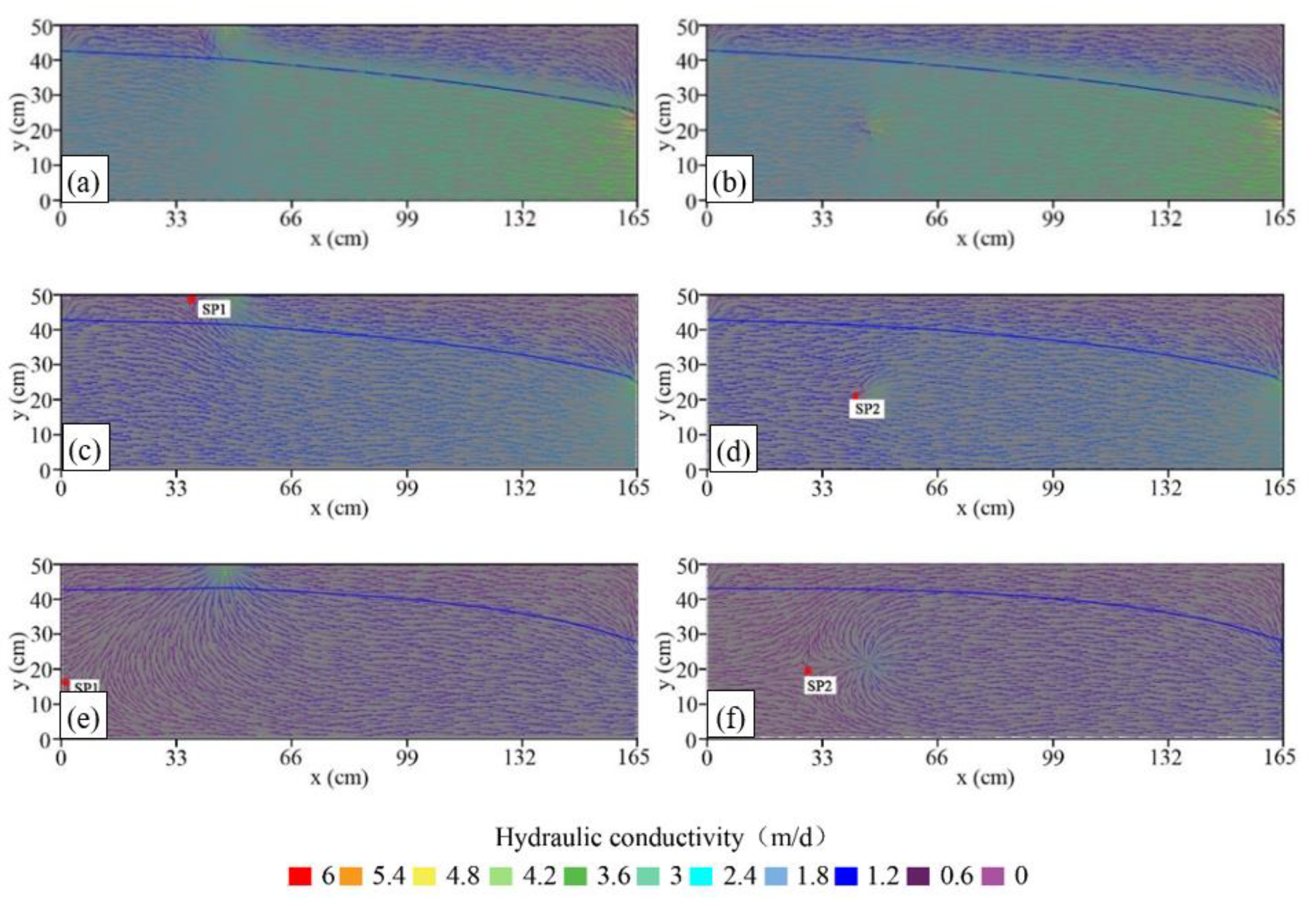
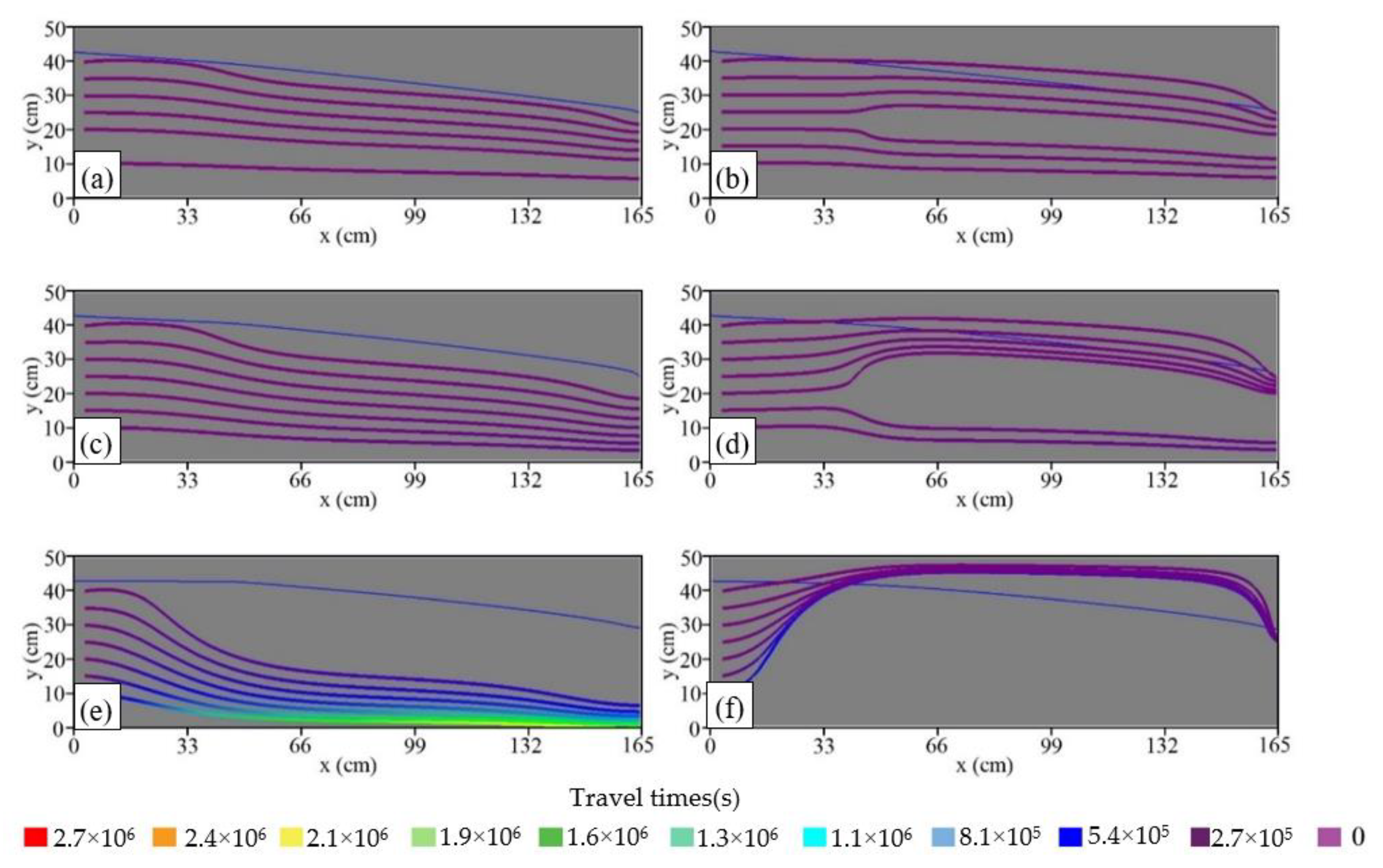
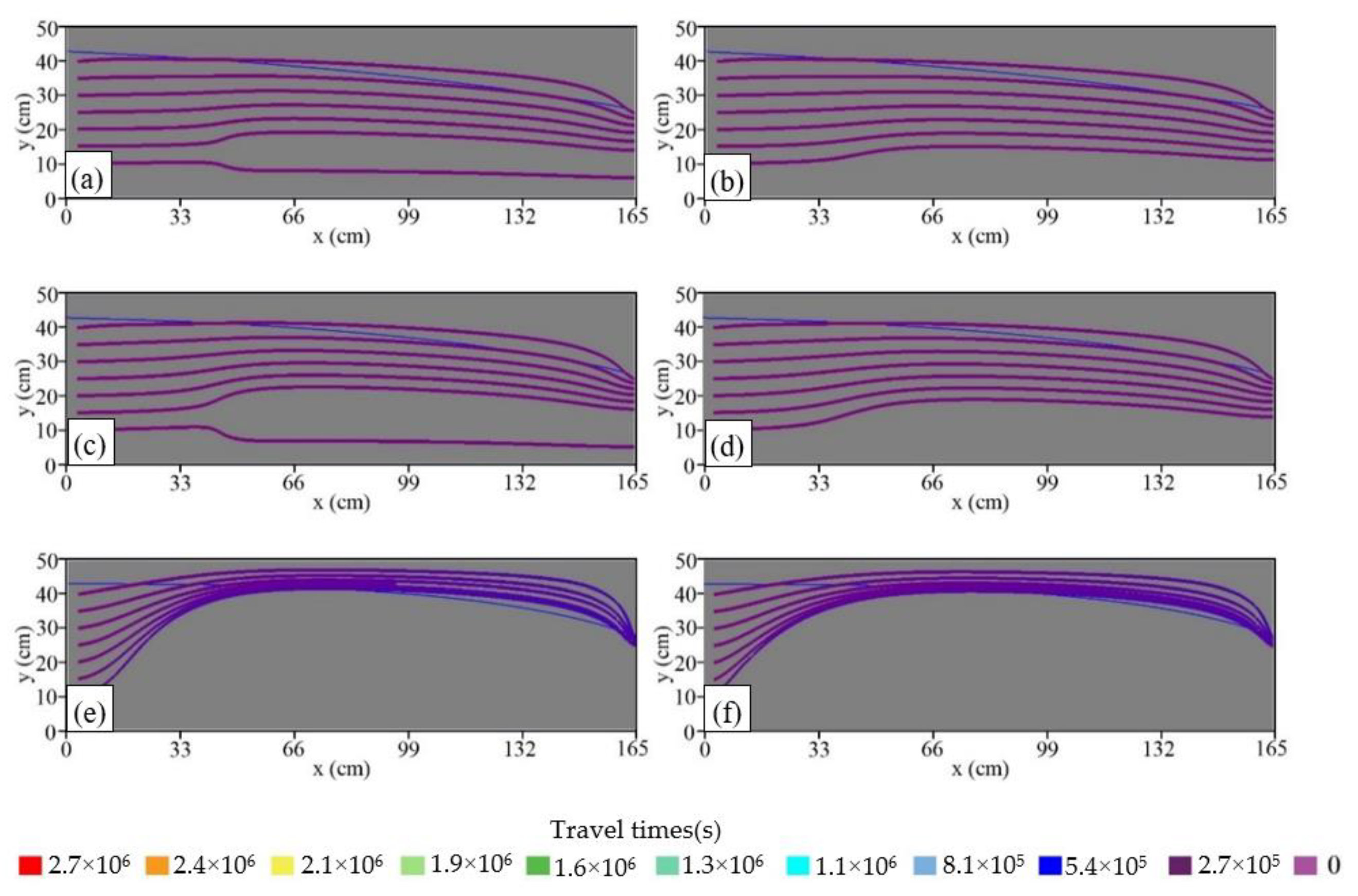
3.1. Groundwater Flow Patterns
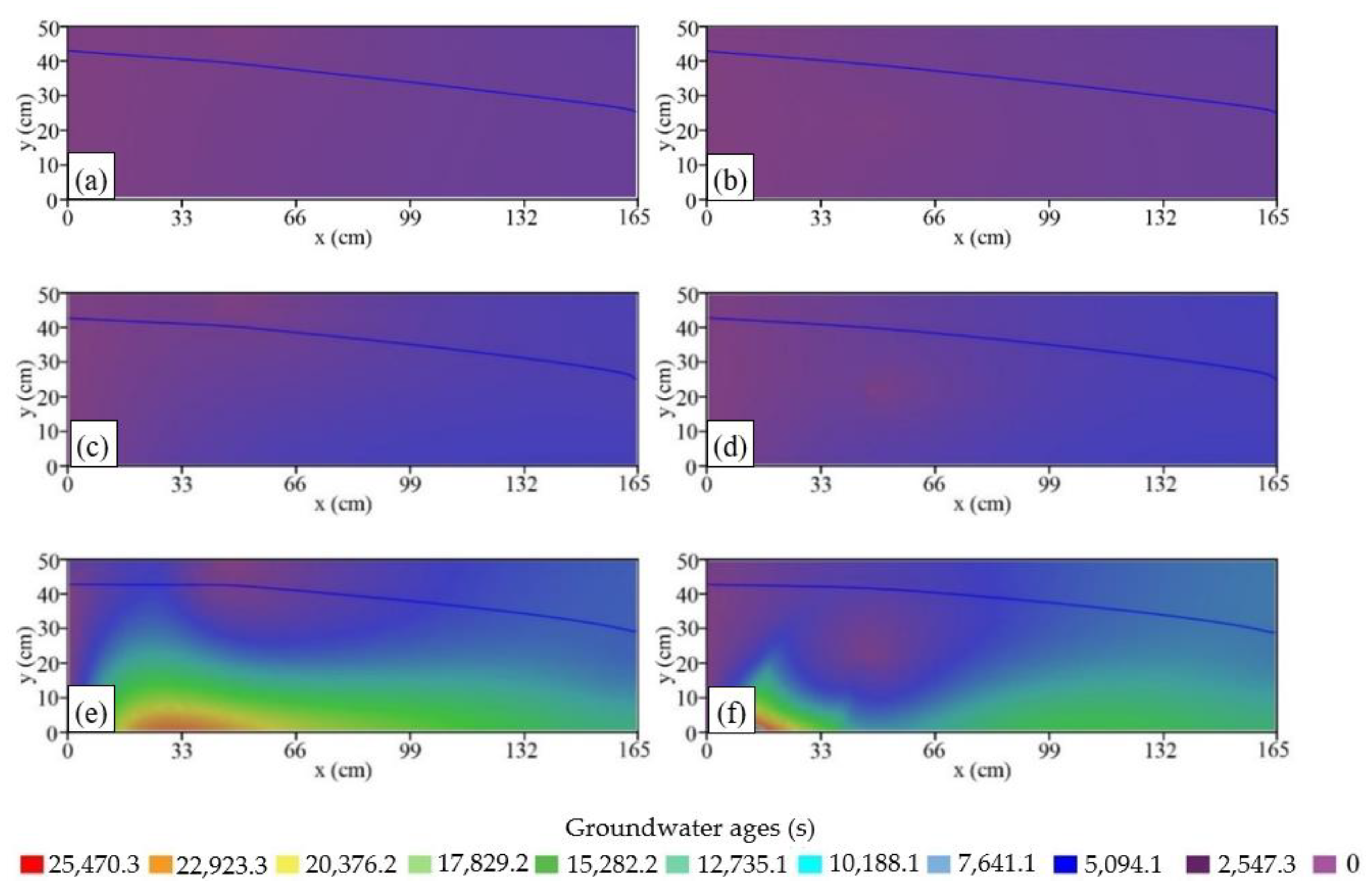
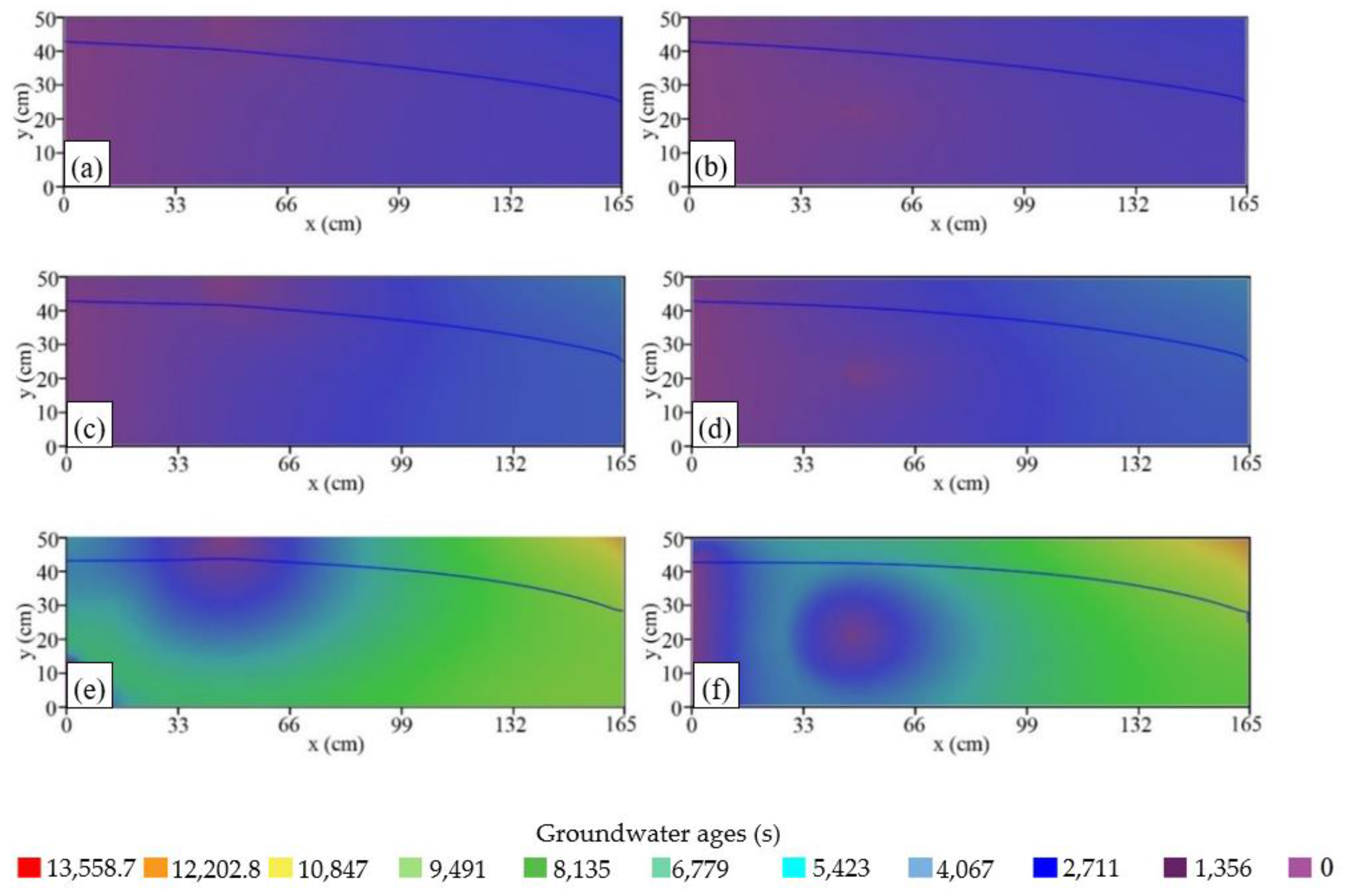
3.2. Groundwater Age
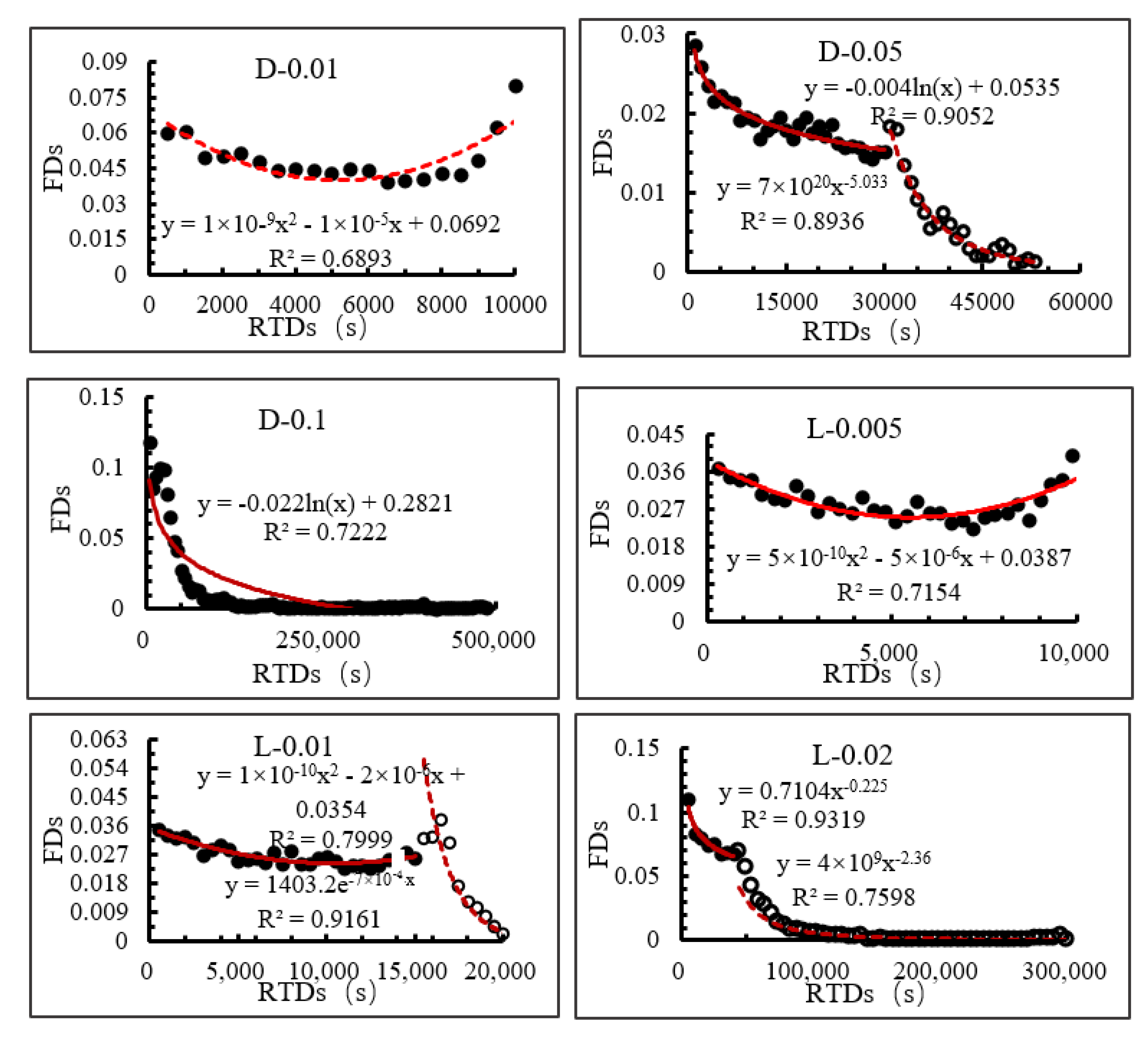
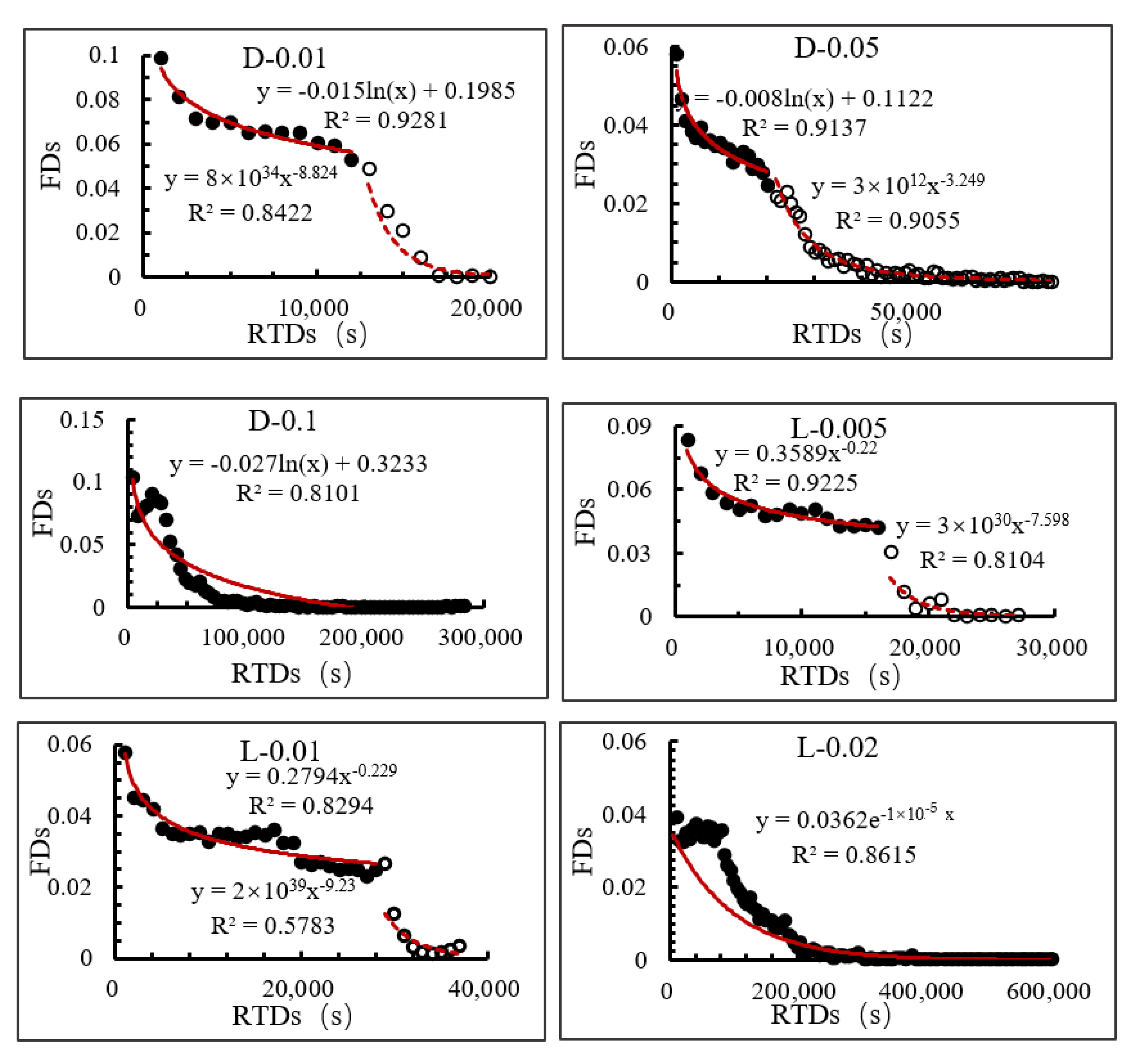
3.3. Residence Time Distributions
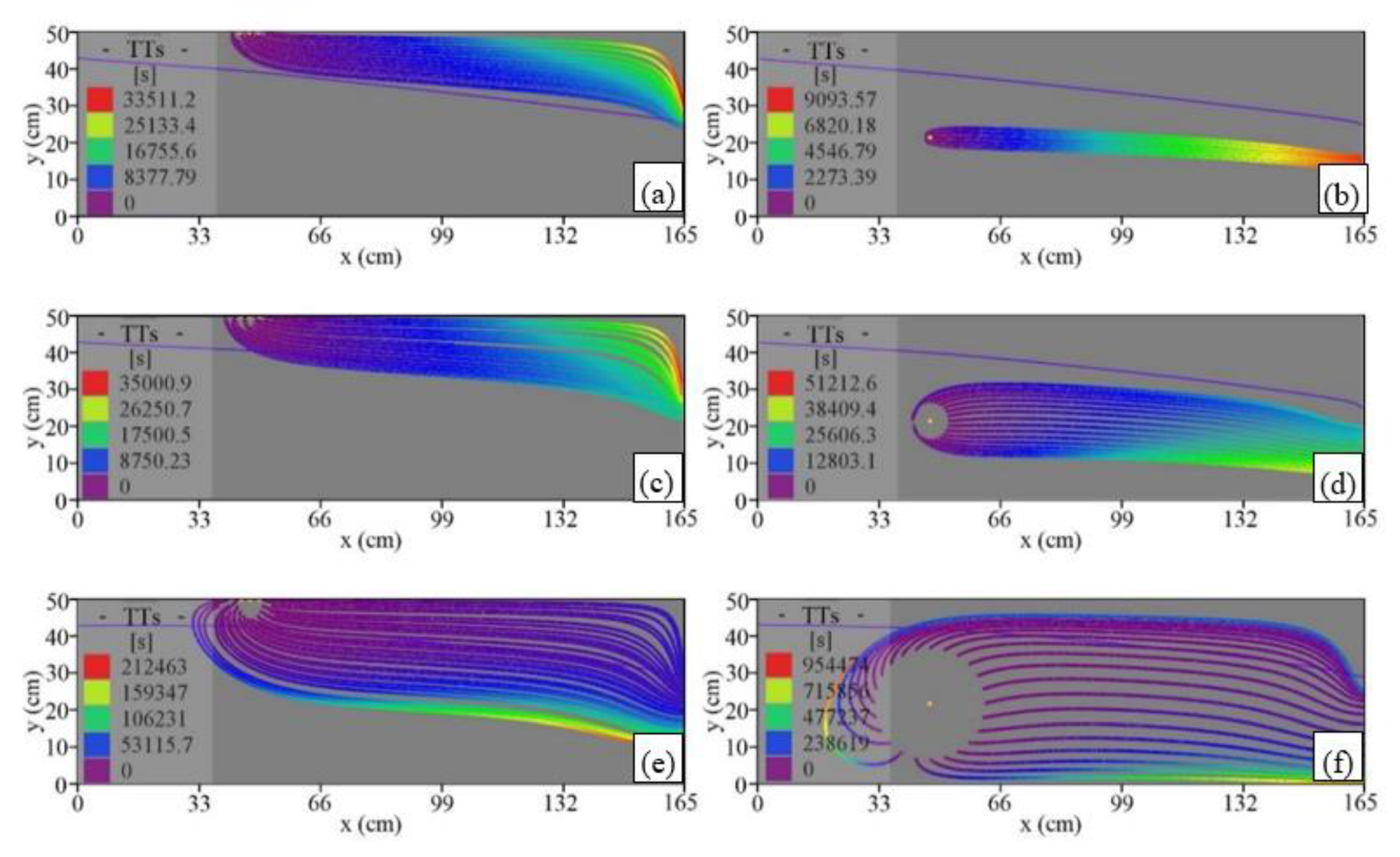
3.4. Ambient Groundwater Flow Paths
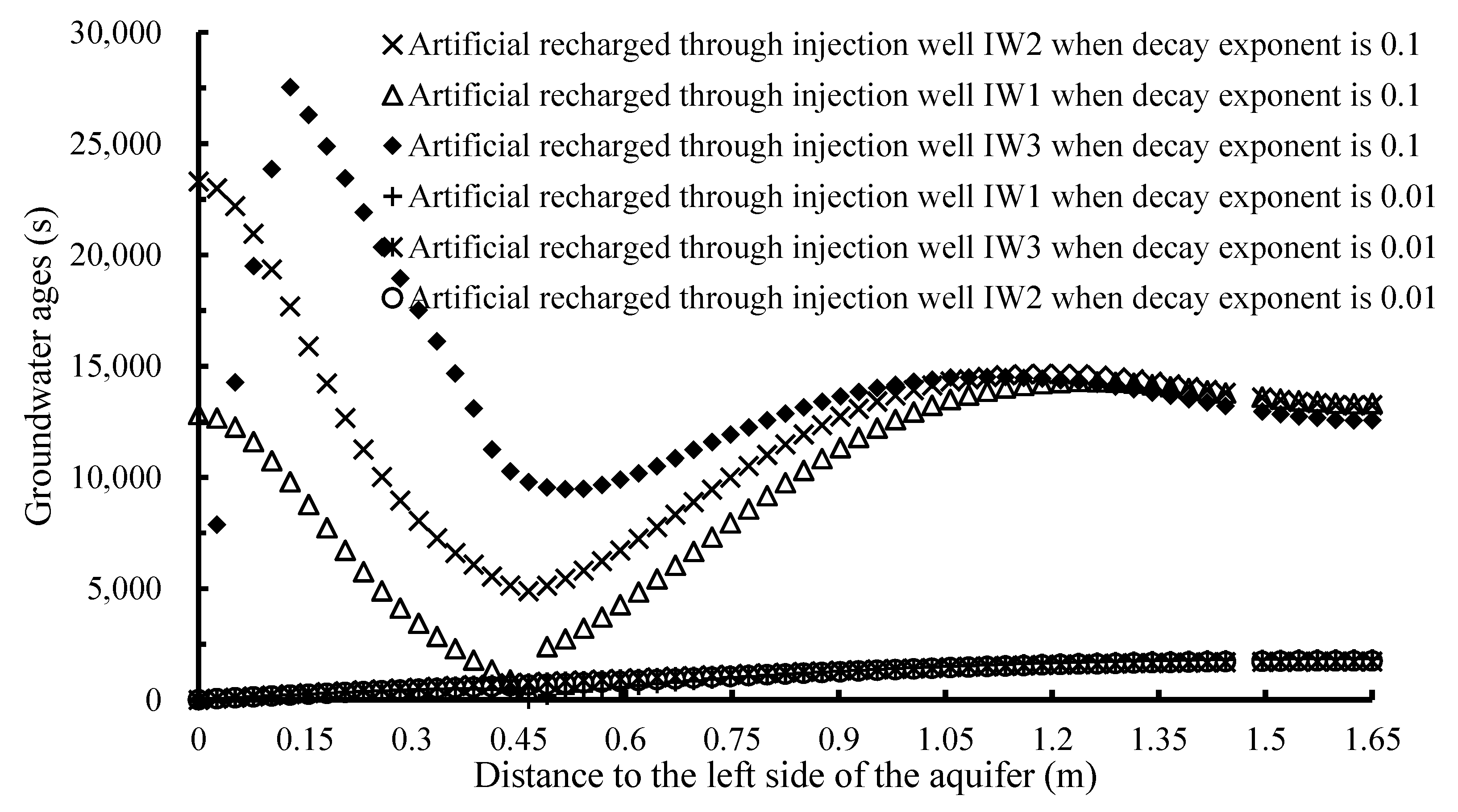
3.5. Artificially Recharged Water Lens
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, G.; Scanlon, B.R.; Han, D.; Zheng, C. Impacts of thickening unsaturated zone on groundwater recharge in the North China Plain. J. Hydrol. 2016, 537, 260–270. [Google Scholar] [CrossRef]
- Hsu, N.-S.; Chiang, C.-J.; Wang, C.-H.; Liu, C.-W.; Huang, C.-L.; Liu, H.-J. Estimation of pumpage and recharge in alluvial fan topography under multiple irrigation practices. J. Hydrol. 2013, 479, 35–50. [Google Scholar] [CrossRef]
- Kendy, E.; Gérard-Marchant, P.; Walter, M.T.; Zhang, Y.; Liu, C.; Steenhuis, T.S. A soil-water-balance approach to quantify groundwater recharge from irrigated cropland in the North China Plain. Hydrol. Process. 2003, 17, 2011–2031. [Google Scholar] [CrossRef]
- Tan, X.-C.; Wu, J.-W.; Cai, S.-Y.; Yang, J.-Z. Characteristics of Groundwater Recharge on the North China Plain. Ground Water 2013, 52, 798–807. [Google Scholar] [CrossRef]
- Wang, B.; Jin, M.; Nimmo, J.R.; Yang, L.; Wang, W. Estimating groundwater recharge in Hebei Plain, China under varying land use practices using tritium and bromide tracers. J. Hydrol. 2008, 356, 209–222. [Google Scholar] [CrossRef]
- Liu, Y.; Yamanaka, T.; Zhou, X.; Tian, F.; Ma, W. Combined use of tracer approach and numerical simulation to estimate groundwater recharge in an alluvial aquifer system: A case study of Nasunogahara area, central Japan. J. Hydrol. 2014, 519, 833–847. [Google Scholar] [CrossRef]
- Foster, S.; Garduno, H.; Evans, R.; Olson, D.; Tian, Y.; Zhang, W.; Han, Z. Quaternary Aquifer of the North China Plain?assessing and achieving groundwater resource sustainability. Hydrogeol. J. 2004, 12, 81–93. [Google Scholar] [CrossRef]
- Eastoe, C.J.; Hutchison, W.R.; Hibbs, B.J.; Hawley, J.; Hogan, J.F. Interaction of a river with an alluvial basin aquifer: Stable isotopes, salinity and water budgets. J. Hydrol. 2010, 395, 67–78. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Liu, Y.; Yamanaka, T. Tracing groundwater recharge sources in a mountain–plain transitional area using stable isotopes and hydrochemistry. J. Hydrol. 2012, 464–465, 116–126. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in california’s central valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Choi, B.-Y.; Yun, S.-T.; Mayer, B.; Chae, G.-T.; Kim, K.-H.; Kim, K.; Koh, Y.-K. Identification of groundwater recharge sources and processes in a heterogeneous alluvial aquifer: Results from multi-level monitoring of hydrochemistry and environmental isotopes in a riverside agricultural area in Korea. Hydrol. Process. 2009, 24, 317–330. [Google Scholar] [CrossRef]
- Du, X.Q.; Wang, Z.J.; Ye, X.Y. Potential clogging and fissolution effects during artificial recharge of groundwater using potable water. Water Resour. Manag. 2013, 27, 3573–3583. [Google Scholar] [CrossRef]
- Du, X.; Ye, X.; Zhang, X. Clogging of saturated porous media by silt-sized suspended solids under varying physical conditions during managed aquifer recharge. Hydrol. Process. 2018, 32, 2254–2262. [Google Scholar] [CrossRef]
- Wu, P.; Shu, L.; Yang, C.; Xu, Y.; Zhang, Y. Simulation of groundwater flow paths under managed abstraction and recharge in an analogous sand-tank phreatic aquifer. Hydrogeol. J. 2019, 27, 3025–3042. [Google Scholar] [CrossRef]
- Saito, K.; Oguchi, T. Slop of alluvial fans in humid regions of Japan, Taiwan and the Philippines. Geomorphology 2005, 70, 147–162. [Google Scholar] [CrossRef]
- Blair, T.C. Cause of dominance by sheet flood vs. debris flow processes on two adjoining alluvial fans, Death Valley, California. Sedimentology 1999, 46, 1015–1028. [Google Scholar] [CrossRef]
- Chen, X.; Song, J.; Wang, W. Spatial variability of specific yield and vertical hydraulic conductivity in a highly permeable alluvial aquifer. J. Hydrol. 2010, 388, 379–388. [Google Scholar] [CrossRef]
- Staley, D.M.; Wasklewicz, T.A.; Blaszczynski, J.S. Surficial patterns of debris flow deposition on alluvial fans in Death Valley, CA using airborne laser swath mapping data. Geomorphology 2006, 74, 152–163. [Google Scholar] [CrossRef]
- Ameli, A.A.; Mcdonnell, J.; Bishop, K. The exponential decline in saturated hydraulic conductivity with depth: A novel method for exploring its effect on water flow paths and transit time distribution. Hydrol. Process. 2016, 30, 2438–2450. [Google Scholar] [CrossRef]
- Price, W.G.; Potter, A.; Thomson, T.K.; Smith, G.E.P.; Hazen, A.; Beardsley, R.C. Discussion on dams on sand foundations. Trans. Am. Soc. Civ. Eng. 1911, 73, 190–208. [Google Scholar] [CrossRef]
- Jia, Y.F.; Guo, H.M.; Jiang, Y.X.; Wu, Y.; Zhou, Y.Z. Hydrogeochemical zonation and its implication for arsenic mobi-lization in deep groundwaters near alluvial fans in the Hetao Basin, Inner Mongolia. J. Hydrol. 2014, 518, 410–420. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Ling, X.-M.; Liu, M.-M.; Hu, R.; Yang, Z. Statistical distribution of hydraulic conductivity of rocks in deep-incised valleys, Southwest China. J. Hydrol. 2018, 566, 216–226. [Google Scholar] [CrossRef]
- Achtziger-Zupancic, P.; Loew, S.; Hiller, A. Factors controlling the permeability distribution in fault vein zones sur-rounding granitic intrusions (Ore Mountains/Germany). J. Geophys. Res. Solid Earth 2017, 122, 1876–1899. [Google Scholar]
- Cheng, C.; Song, J.; Chen, X.; Wang, D. Statistical distribution of streambed vertical hydraulic conductivity along the Platte River, Nebraska. Water Resour. Manag. 2010, 25, 265–285. [Google Scholar] [CrossRef]
- Hess, K.M.; Wolf, S.H.; Celia, M.A. Large-scale natural gradient tracer test in sand and gravel, Cape Cod, Massachusetts: 3. Hydraulic conductivity variability and calculated macrodispersivities. Water Resour. Res. 1992, 28, 2011–2027. [Google Scholar] [CrossRef]
- Rehfeldt, K.R.; Boggs, J.M.; Gelhar, L.W. Field study of dispersion in a heterogeneous aquifer: 3. Geostatistical analysis of hydraulic conductivity. Water Resour. Res. 1992, 28, 3309–3324. [Google Scholar] [CrossRef]
- Lu, C.; Qin, W.; Zhao, G.; Zhang, Y.; Wang, W. Better-fitted probability of hydraulic conductivity for a silty clay site and its effects on solute transport. Water 2017, 9, 466. [Google Scholar] [CrossRef]
- Faulkner, D.; Armitage, P. The effect of tectonic environment on permeability development around faults and in the brittle crust. Earth Planet. Sci. Lett. 2013, 375, 71–77. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Hydraulic conductivity of fractured upper crust: Insights from hydraulic tests in boreholes and fluid-rock interaction in crystalline basement rocks. Geofluids 2014, 15, 161–178. [Google Scholar] [CrossRef]
- Morrow, C.A.; Lockner, D.A. Permeability differences between surface-derived and deep drillhole core samples. Geophys. Res. Lett. 1994, 21, 2151–2154. [Google Scholar] [CrossRef]
- Ku, C.-Y.; Hsu, S.-M.; Chiou, L.-B.; Lin, G.-F. An empirical model for estimating hydraulic conductivity of highly disturbed clastic sedimentary rocks in Taiwan. Eng. Geol. 2009, 109, 213–223. [Google Scholar] [CrossRef]
- Saar, M.O.; Manga, M. Depth dependence of permeability in the Oregon Cascades inferred from hydrogeologic, thermal, seismic, and magmatic modeling constraints. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Jiang, X.W. Groundwater flow, transport, and residence times through topography-driven basins with exponentially decreasing permeability and porosity. Water Resour. Res. 2010, 46, W11538. [Google Scholar] [CrossRef]
- Jiang, X.-W.; Wan, L.; Wang, X.-S.; Ge, S.; Liu, J. Effect of exponential decay in hydraulic conductivity with depth on regional groundwater flow. Geophys. Res. Lett. 2009, 36, 36. [Google Scholar] [CrossRef]
- Jiang, X.-W.; Wang, X.-S.; Wan, L.; Ge, S. An analytical study on stagnation points in nested flow systems in basins with depth-decaying hydraulic conductivity. Water Resour. Res. 2011, 47, 47. [Google Scholar] [CrossRef]
- Rumynin, V.; Leskova, P.; Sindalovskiy, L.; Nikulenkov, A. Effect of depth-dependent hydraulic conductivity and anisotropy on transit time distributions. J. Hydrol. 2019, 579, 124161. [Google Scholar] [CrossRef]
- Nakaya, S.; Uesugi, K.; Motodate, Y.; Ohmiya, I.; Komiya, H.; Masuda, H.; Kusakabe, M. Spatial separation of groundwater flow paths from a multi-flow system by a simple mixing model using stable isotopes of oxygen and hydrogen as natural tracers. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Polizzotto, M.L.; Kocar, B.D.; Benner, S.G.; Sampson, M.; Fendorf, S. Near-surface wetland sediments as a source of arsenic release to ground water in Asia. Nat. Cell Biol. 2008, 454, 505–508. [Google Scholar] [CrossRef] [PubMed]
- Qin, D.J.; Zhao, Z.F.; Han, L.F. Determination of groundwater recharge regime and flow path in the Lower Heihe River basin in an arid area of Northwest China by using environmental tracers: Implications for vegetation degradation in the Ejina Oasis. Appl. Geochem. 2012, 27, 1133–1145. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Feng, X.; Chen, X.; Yao, K. Evolution of stream-aquifer hydrologic connectedness during pumping—Experiment. J. Hydrol. 2011, 402, 401–414. [Google Scholar] [CrossRef]
- Keeler, B.L.; Gourevitch, J.D.; Polasky, S.; Isbell, F.; Tessum, C.W.; Hill, J.D.; Marshall, J.D. The social costs of nitrogen. Sci. Adv. 2016, 2, e1600219. [Google Scholar] [CrossRef] [PubMed]
- Mi, L.; Xiao, H.; Zhang, J.; Yin, Z.; Shen, Y. Evolution of the groundwater system under the impacts of human activities in middle reaches of Heihe River Basin (Northwest China) from 1985 to 2013. Hydrogeol. J. 2016, 24, 971–986. [Google Scholar] [CrossRef]
- Xie, Y.; Batlle-Aguilar, J. Limits of heat as a tracer to quantify transient lateral river-aquifer exchanges. Water Resour. Res. 2017, 53, 7740–7755. [Google Scholar] [CrossRef]
- Atlabachew, A.; Shu, L.; Wu, P.; Zhang, Y.; Xu, Y. Numerical modeling of solute transport in a sand tank physical model under varying hydraulic gradient and hydrological stresses. Hydrogeol. J. 2018, 26, 2089–2113. [Google Scholar] [CrossRef]
- Xin, P.; Yuan, L.R.; Li, L.; Barry, D.A. Tidally driven multi-scale pore water flow in a creek-marsh system. Water Resour. Res. 2011, 47, 209–216. [Google Scholar] [CrossRef]
- Filippini, M.; Stumpp, C.; Nijenhuis, I.; Richnow, H.; Gargini, A. Evaluation of aquifer recharge and vulnerability in an alluvial lowland using environmental tracers. J. Hydrol. 2015, 529, 1657–1668. [Google Scholar] [CrossRef]
- Wang, W.K.; Li, J.T.; Wang, W.M.; Chen, X.H.; Cheng, D.H.; Jia, J. Estimating streambed parameters for a disconnected river. Hydrol. Process. 2014, 28, 3627–3641. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, Y.; Dong, S.; Becker, S.; Chen, Y. Attribution of decreasing annual and autumn inflows to the Three Gorges Reservoir, Yangtze River: Climate variability, water consumption or upstream reservoir operation? J. Hydrol. 2019, 579, 124180. [Google Scholar] [CrossRef]
- Cardenas, M.B. Potential contribution of topography-driven regional groundwater flow to fractal stream chemistry: Residence time distribution analysis of Tóth flow. Geophys. Res. Lett. 2007, 34, 05403. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Demonstrating fractal scaling of baseflow residence time distributions using a fully-coupled groundwater and land surface model. Geophys. Res. Lett. 2008, 35, 07402. [Google Scholar] [CrossRef]
- Lehmann, P.; Stauffer, F.; Hinz, C.; Dury, O.; Flühler, H. Effect of hysteresis on water flow in a sand column with a fluc-tuating capillary fringe. J. Contam. Hydrol. 1998, 33, 81–100. [Google Scholar] [CrossRef]
- Sawyer, A.H.; Cardenas, M.B.; Bomar, A.; Mackey, M. Impact of dam operations on hyporheic exchange in the riparian zone of a regulated river. Hydrol. Process. 2009, 23, 2129–2137. [Google Scholar] [CrossRef]
- Lu, C.; Chen, S.; Jiang, Y.; Shi, J.; Yao, C.; Su, X. Quantitative analysis of riverbank groundwater flow for the Qinhuai River, China, and its influence factors. Hydrol. Process. 2018, 32, 2734–2747. [Google Scholar] [CrossRef]
- Lu, S.; Wagner, R.; Schmidt, M.; Wiseman, L. Impact of Groundwater Seepage Flow on DO TMDL Development. Proc. Water Environ. Fed. 2009, 2009, 3246–3262. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Q.; Wang, W.; Yu, Z.; Chen, Y.D.; Lu, G.; Hao, Z.; Báron, A.; Zhao, C.; Chen, X.; et al. Review of advances in hydrologic science in china in the last decades: Impact study of climate change and human activities. J. Hydrol. Eng. 2013, 18, 1380–1384. [Google Scholar] [CrossRef]
- Jakóbczyk-Karpierz, S.; Sitek, S.; Jakobsen, R.; Kowalczyk, A. Geochemical and isotopic study to determine sources and processes affecting nitrate and sulphate in groundwater influenced by intensive human activity—carbonate aquifer Gliwice (southern Poland). Appl. Geochem. 2017, 76, 168–181. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Zhang, L.; Chang, B.; Wang, S. Effects of Decaying Hydraulic Conductivity on the Groundwater Flow Processes in a Managed Aquifer Recharge Area in an Alluvial Fan. Water 2021, 13, 1649. https://doi.org/10.3390/w13121649
Wu P, Zhang L, Chang B, Wang S. Effects of Decaying Hydraulic Conductivity on the Groundwater Flow Processes in a Managed Aquifer Recharge Area in an Alluvial Fan. Water. 2021; 13(12):1649. https://doi.org/10.3390/w13121649
Chicago/Turabian StyleWu, Peipeng, Lijuan Zhang, Bin Chang, and Shuhong Wang. 2021. "Effects of Decaying Hydraulic Conductivity on the Groundwater Flow Processes in a Managed Aquifer Recharge Area in an Alluvial Fan" Water 13, no. 12: 1649. https://doi.org/10.3390/w13121649
APA StyleWu, P., Zhang, L., Chang, B., & Wang, S. (2021). Effects of Decaying Hydraulic Conductivity on the Groundwater Flow Processes in a Managed Aquifer Recharge Area in an Alluvial Fan. Water, 13(12), 1649. https://doi.org/10.3390/w13121649




