Urban Pluvial Flood Management Part 1: Implementing an AHP-TOPSIS Multi-Criteria Decision Analysis Method for Stakeholder Integration in Urban Climate and Stormwater Adaptation
Abstract
:1. Introduction
2. Multi-Criteria Decision Analysis
Criticisms
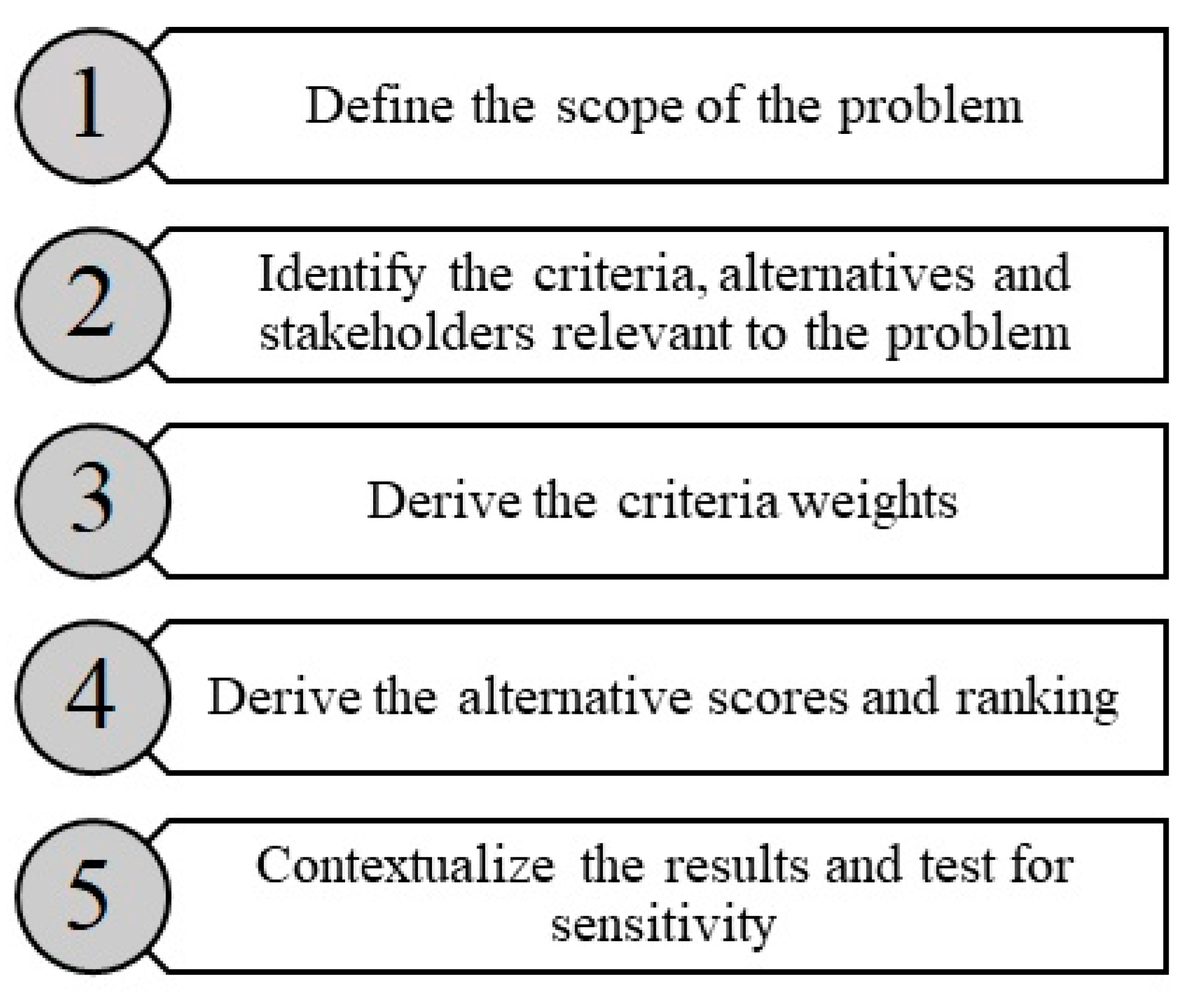
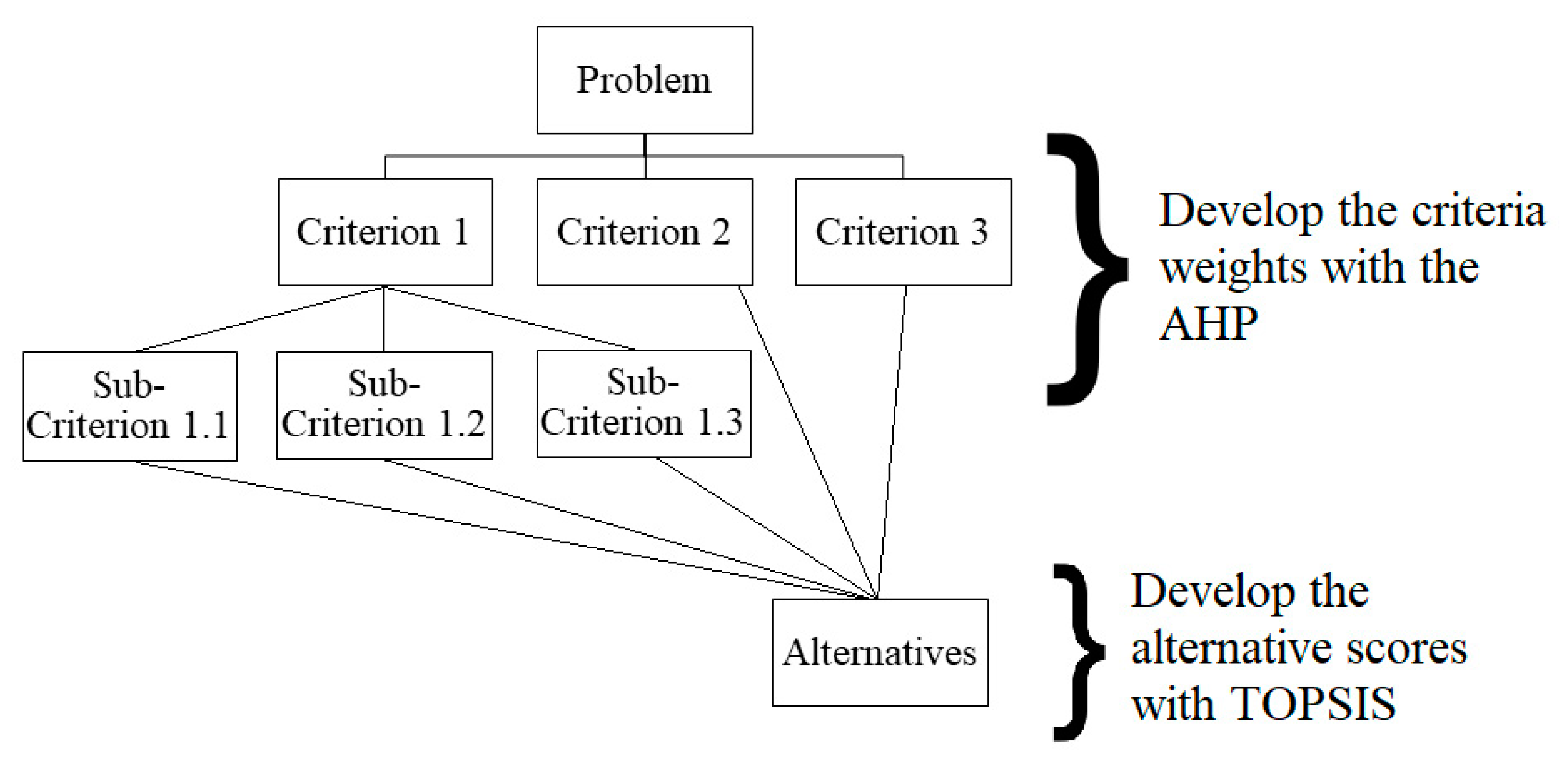
3. AHP-TOPSIS MCDA Methodology
3.1. Defining the Problem
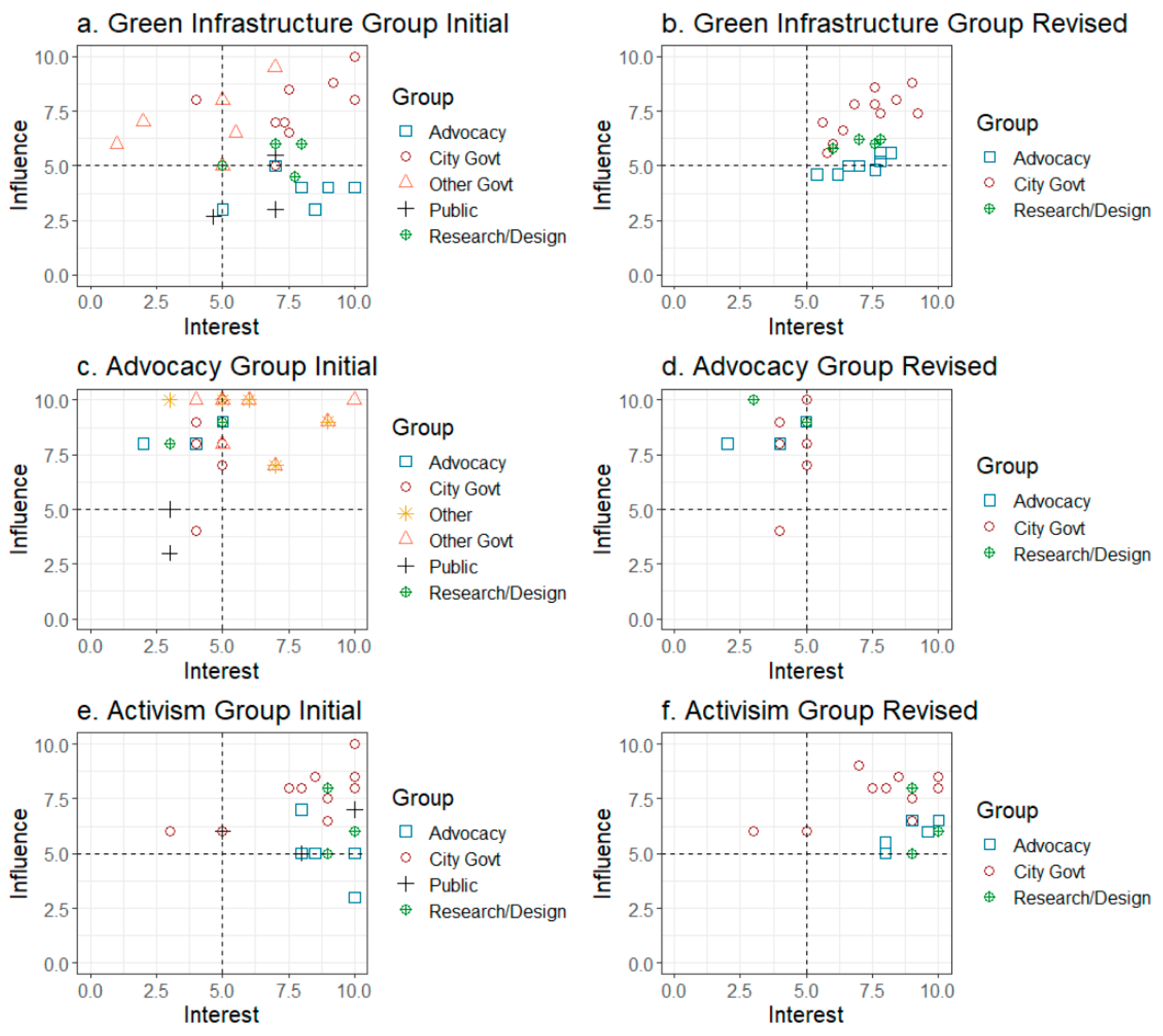
3.2. Alternative, Criteria, and Stakeholders
3.3. Criteria Weights and Alternative Scores
3.3.1. AHP
- (i)
- for and
- (ii)
- for and
- (i)
- and
- (ii)
3.3.2. Group Aggregation
- (i)
- for the set of decision-makers
- (i)
- (i)
- is the weight of the parent criterion in the decision hierarchy from the aggregated parent priority weight vector.
3.3.3. TOPSIS
- (i)
- Ai represents the alternative i and Cj represents the criteria j, for i = 1, …, m and j = 1, …, n
- (ii)
- fij represents the performance rating of Ai under Cj
- (iii)
- For k = 1, 2, …, r for the number of decision-makers
- (i)
- (i)
- is associated with positive criteria or benefits while is associated with negative criteria or costs
- (i)
- is associated with positive criteria or benefits while is associated with negative criteria or costs.
- (i)
- is the weight of criterion from the group priority weight vector
- wj is the weight of criterion from the group priority weight vector .
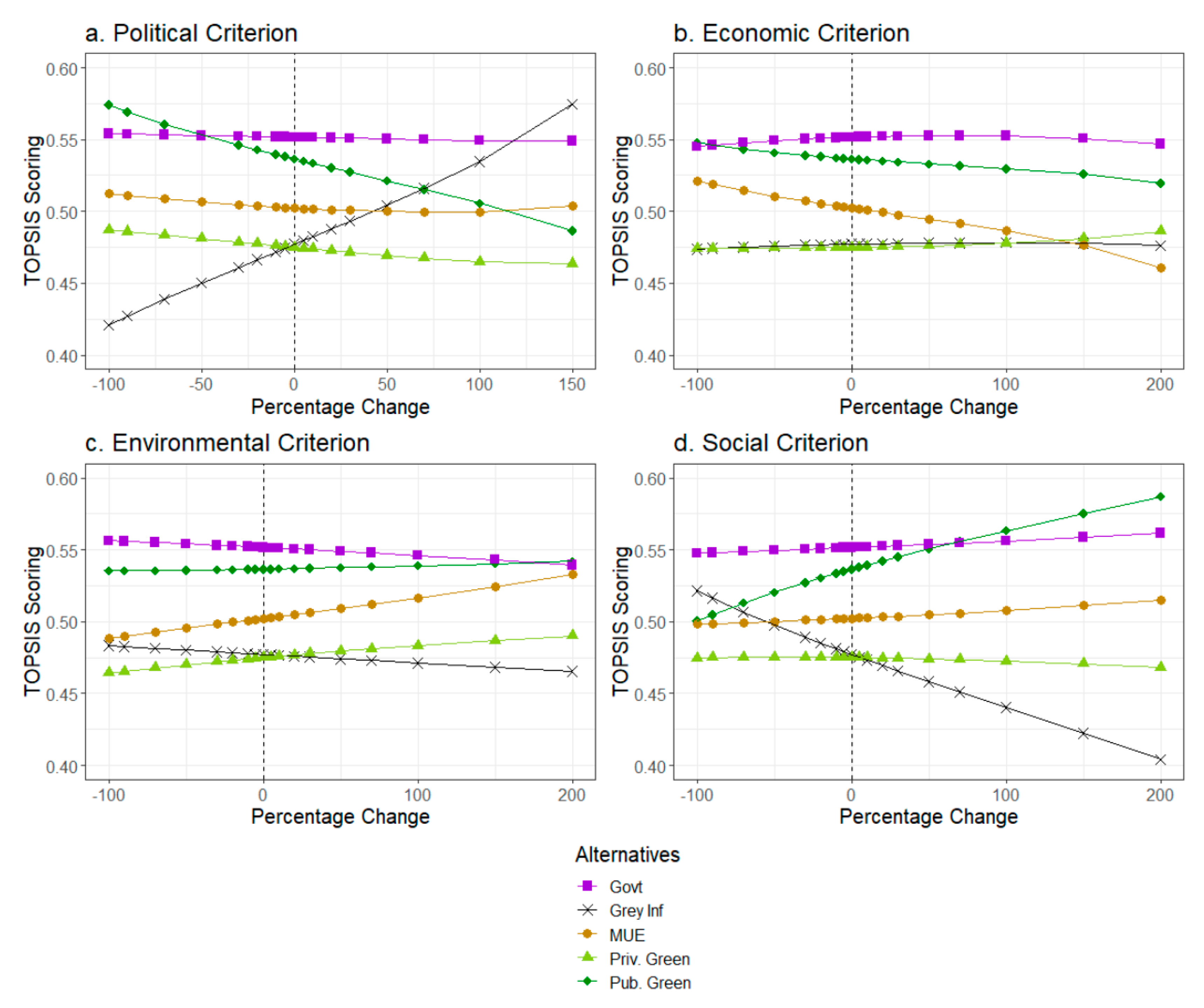
3.4. Sensitivity Analysis
- (i)
- , , , and are the new weights for criteria 1, 2, q, and n after the disturbance of
- (ii)
- and
4. New York City and MCDA Stormwater Results
4.1. Study Area
4.2. Defining the MCDA
4.3. Data Collection
4.4. Results
4.4.1. Criteria Weights
4.4.2. Alternative Scores
4.4.3. Sensitivity
4.4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Ethics Declaration
References
- Antrobus, D. Smart green cities: From modernization to resilience? Urban Pract. Res. 2011, 4, 207–214. [Google Scholar] [CrossRef]
- Qi, Y.; Chan, F.K.S.; Thorne, C.; O’Donnell, E.; Quagliolo, C.; Comino, E.; Pezzoli, A.; Li, L.; Griffiths, J.; Sang, Y.; et al. Addressing challenges of urban water management in Chinese sponge cities via nature-based solutions. Water 2020, 12, 2788. [Google Scholar] [CrossRef]
- Henstra, D.; Thistlethwaite, J.; Vanhooren, S. The governance of climate change adaptation: Stormwater management policy and practice. J. Environ. Plan. Manag. 2020, 63, 1077–1096. [Google Scholar] [CrossRef]
- Matthews, T.; Lo, A.Y.; Byrne, J.A. Reconceptualizing green infrastructure for climate change adaptation: Barriers to adoption and drivers for uptake by spatial planners. Landsc. Urban Plan. 2015, 138, 155–163. [Google Scholar] [CrossRef]
- Aylett, A. Institutionalizing the urban governance of climate change adaptation: Results of an international survey. Urban Clim. 2015, 14, 4–16. [Google Scholar] [CrossRef] [Green Version]
- Czako, V. Drowning the suburb: Settlement planning and climate change adaptation in a Hungarian metropolitan area. Urban Res. Pract. 2013, 6, 95–109. [Google Scholar] [CrossRef]
- Andre, K.; Simonsson, L.; Swartling, A.S.; Linner, B.-O. Method development for identifying and analyzing stakeholders in climate change adaptation processes. J. Environ. Policy Plan. 2012, 14, 243–261. [Google Scholar] [CrossRef]
- Gallo, E.M.; Bell, C.D.; Panos, C.L.; Smoith, S.M.; Hogue, T.S. Investigating tradeoffs of green to grey stormwater infrastructure using a planning-level decision support tool. Water 2020, 12, 5. [Google Scholar] [CrossRef]
- Torabi, E.; Dedekorkut-Howers, A.; Howes, M. A framework for using the concept of urban resilience in responding to climate-related disasters. Urban Res. Pract. 2021. [Google Scholar] [CrossRef]
- Axelsson, C.; Soriani, S.; Culligan, P.; Marcotullio, P. Urban policy adaptation toward managing increasing pluvial flooding events under climate change. J. Environ. Plan. Manag. 2020, 64, 1408–1427. [Google Scholar] [CrossRef]
- Pakfetrat, A.; Taghvaei, M.; Zarrabi, A. A comprehensive approach in green space site planning: An application of the three-stage multi-criteria decision support system. Urban Res. Pract. 2020, 13, 45–76. [Google Scholar] [CrossRef]
- Locatelli, L.; Guerrero, M.; Russo, B.; Martinez-Gomariz, E.; Sunyer, D.; Martinez, M. Socio-economic assessment of green infrastructure for climate change adaptation in the context of urban drainage planning. Sustainability 2020, 12, 3792. [Google Scholar] [CrossRef]
- Guarini, M.R.; Batisti, F.; Chiovitti, A. A methodology for the selection of multi-criteria decision analysis methods in real estate and land management processes. Sustainability 2018, 10, 507. [Google Scholar] [CrossRef] [Green Version]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- De Montis, A.; De Toro, P.; Droste-Franke, B.; Omann, I.; Stagl, S. Criteria for Quality Assessment of MCDA Methods. In Proceedings of the 3rd Biennial Conference of the European Society for Ecological Economics, Vienna, Austria, 3–6 May 2000. [Google Scholar]
- Guitouni, A.; Martel, J.M. Tentative guidelines to help choosing an appropriate MCDA method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Steele, K.; Carmel, Y.; Cross, J.; Wilcox, C. Uses and misuses of multicriteria decision analysis (MCDA) in environmental decision making. Risk Anal. 2009, 29, 26–33. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation; McGraw-Hill International: New York, NY, USA, 1980. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Fedrizzi, M.; Giove, S. Incomplete pairwise comparison and consistency optimization. Eur. J. Oper. Res. 2007, 183, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Fedrizzi, M.; Giove, S. Optimal sequencing in incomplete pairwise comparisons for large-dimensional problems. Int. J. Gen. Syst. 2013, 42, 366–375. [Google Scholar] [CrossRef]
- De Montis, A.; De Toro, P.; Droste-Franke, B.; Omann, I.; Stagl, S. Assessing the quality of different MCDA methods. In Alternatives for Environmental Valuation; Getzner, M., Spash, C.L., Stagl, S., Eds.; Routledge: London, UK, 2005; pp. 99–133. [Google Scholar]
- Saaty, T.L.; Ozdemir, M.S. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Young, K.D.; Younous, T.; Dymond, R.L.; Kibler, D.F.; Lee, D.H. Application of the Analytic Hierarchy Process for selecting and modeling stormwater best management practcies. J. Contemp. Water Res. Educ. 2010, 146, 50–63. [Google Scholar] [CrossRef]
- Sahin, O.; Siems, R.; van Staden, R.; Jenkins, G. Decision dilemma in adapting stormwater systems to climate change: A tale of three cities. In Water Conservation: Practices, Challenges and Future Implications; Imteaz, M.A., Ed.; Nova Science: Hauppauge, NY, USA, 2013. [Google Scholar]
- Siems, R.; Sahin, O. Adapting water systems to climate change: A multi actor-multiple criteria decision analysis in South-East Queensland, Australia. IWTJ 2014, 4, 135–141. [Google Scholar]
- Ebrahimian, A.; Ardeshir, A.; Rad, I.Z.; Ghodsypour, S.H. Urban stormwater construction method selection using a hybrid multi-criteria approach. Autom. Constr. 2015, 58, 118–128. [Google Scholar] [CrossRef]
- Alhumaid, M.; Ghumman, A.R.; Haider, H.; Al-Salamah, I.S.; Ghazaw, Y.M. Sustainability evaluation framework of urban stormwater drainage options for arid environments using hydraulic modeling and multicriteria decision-making. Water 2018, 10, 581. [Google Scholar] [CrossRef] [Green Version]
- Kordana, S.; Slys, D. Decision criteria for the development of stormwater management system in Poland. Resources 2020, 9, 20. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Gan, H.; Xiao, M.; Huang, B.; Zhu, D.Z.; Zhang, Z.; Wang, H.; Lin, Y.; Hou, Y.; Peng, S.; et al. Performance of permeable pavement systems on stormwater permeability and pollutant removal. Environ. Sci. Pollut. Res. 2021, 28, 28571–28584. [Google Scholar] [CrossRef]
- Jayasooriya, V.M.; Muthukumaran, S.; Ng, A.W.M.; Perera, B.J.C. Multi Criteria Decision Making in selecting stormwater management green infrastructure for industrial areas part 2: A case study with TOPSIS. Water Resour. Manag. 2018, 32, 4297–4312. [Google Scholar] [CrossRef]
- Hager, J.K. An Integrated Planning Framework for Urban Stormwater Management: A One Water Approach; University of British Columbia: Vancouver, BC, Canada, 2019. [Google Scholar]
- Luan, B.; Yin, R.; Xu, P.; Wang, X.; Yang, X.; Zhang, L.; Tang, X. Evaluationg green stormwater infrastructure strategies efficiencies in a rapidly urbanizing catchment using SWMM-based TOPSIS. J. Clean. Prod. 2019, 223, 680–691. [Google Scholar] [CrossRef]
- Zeng, J.; Lin, G.; Huang, G. Evaluation of the cost-effectiveness of green infrastructure in climate change scenarios using TOPSIS. Urban For. Urban Green. 2021, 64, 127287. [Google Scholar] [CrossRef]
- Gogate, N.G.; Kalbar, P.P.; Raval, P.M. Assessment of the stormwater management options in urban contexts using multiple attribute decision making. J. Clean. Prod. 2017, 142, 2046–2059. [Google Scholar] [CrossRef]
- Moghadas, M.; Asadzadeh, A.; Vafeidis, A.; Fekete, A.; Kotter, T. A multi-criteria approach for assessing urban flood resilience in Tehran, Iran. Int. J. Disaster Risk Reduct. 2019, 35, 101069. [Google Scholar] [CrossRef]
- Ekmekcioglu, O.; Koc, K.; Ozger, M. Stakeholder perceptions in flood risk assessment: A hybrid fuzzy AHP-TOPSIS approach for Istanbul, Turkey. Int. J. Disaster Risk Reduct. 2021, 60, 102327. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioglu, O.; Ozger, M. An integrated framework for the comprehensive evaluation of low impact development strategies. J. Environ. Manag. 2021, 294, 113023. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-M.; Luo, Y. On rank reversal in decision analysis. Math. Comput. Model. 2009, 49, 1221–1229. [Google Scholar] [CrossRef]
- Belton, V.; Gear, T. On a short-coming of Saaty’s method of analytic hierarchies. Omega 1983, 11, 228–230. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A comparative analysis of the rank reversal phenomenon in the EDAS and TOPSIS methods. Econ. Comput. Cybern. Stud. Res. 2018, 52, 121–134. [Google Scholar]
- Garcia-Cascales, M.S.; Lamata, M.T. On rank reversal and TOPSIS method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Fedrizzi, M.; Giove, S.; Predella, N. Rank reversal in the AHP with consistent judgement: A numerical study in single and group decision making. In Soft Computing Applications for Group Decision-making and Consensus Modelling; Collan, M., Kacprzyk, J., Eds.; Springer: Boston, MA, USA, 2018. [Google Scholar]
- Saaty, T.L.; Vargas, L.; Whitaker, R. Addressing with brevity criticism of the analytic hierarchy process. Int. J. Anal. Hierarchy Process 2009, 1, 2. [Google Scholar] [CrossRef]
- De FSM Russo, R.; Camanho, R. Criteria in AHP: A systematic review of literature. Procedia Comput. Sci. 2015, 55, 1123–1132. [Google Scholar] [CrossRef] [Green Version]
- Reed, M.S. Stakeholder participation for environmental management: A literature review. Biol. Conserv. 2008, 141, 2417–2431. [Google Scholar] [CrossRef]
- Reed, M.S.; Graves, A.; Dandy, N.; Posthumus, H.; Hubacek, K.; Morris, J.; Prell, C.; Quinn, C.H.; Stringer, L.C. Who’s in and why? A typology of stakeholder analysis methods for natural resources management. J. Environ. Manag. 2009, 90, 1933–1949. [Google Scholar] [CrossRef]
- Brugha, R.; Varvasovszky, Z. Stakeholder analysis: A review. Health Policy Plan. 2000, 15, 239–246. [Google Scholar] [CrossRef] [Green Version]
- Vogler, D.; Macey, S.; Sigouin, A. Stakeholder analysis in environmental and conservation planning. Lessons Conserv. 2017, 7, 5–16. [Google Scholar]
- Franek, J.; Kresta, A. Judgement scales and consistency measure in AHP. Procedia Econ. Financ. 2014, 12, 164–173. [Google Scholar] [CrossRef] [Green Version]
- Goepel, K.D. Comparison of judgement scales of the Analytical Hierarchy Process—A new approach. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 445–463. [Google Scholar] [CrossRef] [Green Version]
- ISAHP. Judgement Scales of the Analytical Hierarchy Process—The Balanced Scale; ISAHP: Hong Kong, China, 2018. [Google Scholar]
- Zhang, Z.; Liu, X.; Yang, S. A note on the 1–9 scale and index scale in AHP. In Cutting-Edge Research Topics on Multiple Criteria Decision Making; Shi, Y., Wang, S., Peng, Y., Li, J., Zeng, Y., Eds.; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 35. [Google Scholar]
- Saaty, T.L. Eigenvector and logarithmic least squares. Eur. J. Oper. Res. 1990, 48, 156–160. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Comparison of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Math. Model. 1984, 5, 309–324. [Google Scholar] [CrossRef] [Green Version]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgement matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar] [CrossRef]
- Barzilai, J. Notes on the Analytic Hierarchy Process. In Proceedings of the NSF Design and Manufacturing Research Conference, Tampa, FL, USA, 1–6 January 2001. [Google Scholar]
- Barzilai, J. Consistency measures for pairwise comparison matrices. J. Multi Criteria Decis. Analysis. 1998, 7, 123–132. [Google Scholar] [CrossRef]
- Barzilai, J. Deriving weights from pairwise comparison matrices. J. Oper. Res. Soc. 1997, 48, 1226–1232. [Google Scholar] [CrossRef]
- Barzilai, J.; Cook, W.D.; Golany, B. The Analytic Hierarchy Process: Structure of the Problem and Its Solutions. In Systems and Management Science by Extremal Methods; Phillips, F.Y., Rousseau, J.J., Eds.; Springer: Boston, MA, USA, 1992; pp. 361–371. [Google Scholar]
- Brunelli, M. Introduction to the Analytic Hierarchy Process; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef] [Green Version]
- Ishizaka, A. Development of an Intelligent Tutoring System for AHP (Analytic Hierarchy Process); University of Basel, Department of Business and Economics: Basel, Switzerland, 2004. [Google Scholar]
- Liu, Y.; Yang, L.; Jiang, W. Qualitative and quantitative analysis of the relationship between water pollution and economic growth: A case study in Nansi Lake catchment, China. Environ. Sci. Pollut. Res. 2020, 27, 4008–4020. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W. Managing aquifer recharge with multi-source water to realize sustainable management of groundwater resources in Jinan, China. Environ. Sci. Pollut. Res. 2021, 28, 10872–10888. [Google Scholar] [CrossRef]
- Chuansheng, X.; Dapeng, D.; Shengping, H.; Xin, X.; Yingjie, C. Safety evaluations of smart grid based on AHP-Entropy method. Syst. Eng. Procedia 2012, 4, 203–209. [Google Scholar] [CrossRef] [Green Version]
- Al-Aomar, R. A combined AHP-Entropy method for deriving subjective and objective criteria weights. Int. J. Ind. Eng. 2010, 17, 12–24. [Google Scholar]
- Aguaron, J.; Moreno-Jimenez, J.M. The geometric consistency index: Approximated thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]
- Wedley, W.C. Consistency prediction for incomplete AHP matrices. Math. Comput. Model. 1993, 17, 151–161. [Google Scholar] [CrossRef]
- Farnia, L.; Giove, S. Fuzzy Measures and Experts’ Opinion Elicitation. In Advances in Neural Networks: Computational and Theoretical Issues: Smart Innovation, Systems and Technologies; Bassis, S., Esposito, A., Morabito, F., Eds.; Springer: Cham, Switzerland, 2015; Volume 37. [Google Scholar]
- Carmo, D.K.; Marins, F.A.; Salomon, V.A.P.; Mello, C.H. On the aggregation of individual priorities in incomplete hierarchies. In Proceedings of the International Symposium on the Analytic Hierarchy Process; ISAHP: Kuala Lumpur, Malaysia, 2013. [Google Scholar]
- Aragon, T.J. Deriving Criteria Weights for Health Decision Making: A Brief Tutorial; School of Public Health: Berkeley, CA, USA, 2017; Available online: https://escholarship.org/uc/item/52755837 (accessed on 20 July 2020).
- Ivanco, M.; Hou, G.; Michaeli, J. Sensitivity analysis method to address user disparities in the analytic hierarchy process. Expert Syst. Appl. 2017, 90, 111–126. [Google Scholar] [CrossRef]
- Saardchom, N. Expert judgement based scoring model. J. Bus. Econ. 2012, 3, 164–175. [Google Scholar] [CrossRef]
- Ossadnik, W.; Schinke, S.; Kaspar, R.H. Group aggregation techniques for analytic hierarchy process and analytic network process: A comparative analysis. Group Decis. Negot. 2016, 25, 421–457. [Google Scholar] [CrossRef] [Green Version]
- Forman, E.; Peniwati, K. Aggregating individual judgements and priorities with the analytic hierarchy process. Eur. J. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Pauer, F.; Schmidt, K.; Babac, A.; Damm, K.; Frank, M.; von der Schulenburg, J.-M.G. Comparison of different approaches applied in Analytic Hierarchy Process- an example of information needs of patients with rare diseases. BMC Med. Inform. Decis. Mak. 2016, 16, 117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shih, H.-S.; Shyur, H.-J.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Li, W.-H. A study on aggregation of TOPSIS ideal solutions for group decision-making. Group Decis. Negot. 2012, 21, 461–473. [Google Scholar] [CrossRef]
- Erdogan, M.; Kaya, I. Prioritizing failures by using hybrid multi criteria decision making methodology with a real case application. Sustain. Cities Soc. 2019, 45, 117–130. [Google Scholar] [CrossRef]
- Vega, A.; Aguaron, J.; Garcia-Alcaraz, J.; Moreno-Jimenez, J.M. Notes on dependent attributes in TOPSIS. Procedia Comput. Sci. 2014, 31, 308–317. [Google Scholar] [CrossRef] [Green Version]
- Jiri, M. The robustness of TOPSIS results using sensitivity analysis based on weight tuning. In World Congress of Medical Physics and Biomedical Engineering; Lhotska, L., Sukupova, L., Lackovic, I., Ibbott, G., Eds.; Springer: Singapore, 2019. [Google Scholar]
- Li, P.; Qian, H.; Wu, J.; Chen, J. Sensitivity analysis of TOPSIS method in water quality assessment: I. Sensitivity to the parameter weights. Environ. Monit. Assess. 2013, 185, 2453–2461. [Google Scholar] [CrossRef] [PubMed]
- Song, J.Y.; Chung, E.-S. Robustness, uncertainty and sensitivity analyses of the TOPSIS method for quantitative climate change vulnerability: A case study of flood damage. Water Resour. Manag. 2016, 30, 4751–4771. [Google Scholar] [CrossRef]
- Gonzalez, J.E.; Ortiz, L.; Smith, B.K.; Devineni, N.; Colle, B.; Booth, J.F.; Ravindranath, A.; Rivera, L.; Horton, R.; Towey, K.; et al. New York City Panel on Climate Change 2019 Report Chapter 2: New Methods for Assessing Extreme Temperatures, Heavy Downpours, and Drought. Ann. N. Y. Acad. Sci. 2019, 1439, 30–70. [Google Scholar] [CrossRef] [Green Version]
- NYC Department of Environmental Protection. NYC Stormwater Management Program; NYC DEP: New York, NY, USA, 2019.
- NYC Department of Environmental Protection. Cloudburst Resiliency Planning Study: Executive Summary; NYC DEP: New York, NY, USA, 2017.
- Cappucci, M. Flooding rains keep hitting New York City. Another round is expected Monday night. The Washington Post, 12 July 2021. [Google Scholar]
- Mayne, R.; Green, D.; Guijt, I.; Walsh, M.; English, R.; Cairney, P. Using evidence to influence policy: Oxfam’s experience. Palgrave Commun. 2018, 4, 122. [Google Scholar] [CrossRef]
- Tabak, R.G.; Eyler, A.A.; Dodson, E.A.; Brownson, R.C. Accessing evidence to inform public health policy: A study to enhance advocacy. Public Health 2015, 129, 698–704. [Google Scholar] [CrossRef] [Green Version]
- Zoho ‘Survey’ Survey Software. 2021. Available online: https://www.zoho.com/ (accessed on 2 February 2021).
- Moore, T.L.; Gulliver, J.S.; Stack, L.; Simpson, M.H. Stormwater management and climate change: Vulnerability and capacity for adaptation in urban and suburban contexts. Clim. Chang. 2016, 138, 491–504. [Google Scholar] [CrossRef]
- Cloutier, G.; Joerin, F.; Dubois, C.; Labarthe, M.; Legay, C.; Viens, D. Planning adaptation based on local actors’ knowledge and participation: A climate governance experiment. Clim. Policy 2015, 15, 458–474. [Google Scholar] [CrossRef]
- Martinez-Juarez, P.; Chiabai, A.; Suarez, C.; Quiroga, S. Insights on urban and periurban adaptation strategies based on stakeholders’ perceptions on hard and soft responses to climate change. Sustainability 2019, 11, 647. [Google Scholar] [CrossRef] [Green Version]
- Garcia, R.A.; Aschenbrenner, M.; Durr, E.; Winder, G. Re-imagining cities as ecosystems: Environmental subject formation in Auckland and Mexico City. Urban Res. Pract. 2020. [Google Scholar] [CrossRef]
| Study | Year Published | Description and Context |
|---|---|---|
| AHP | ||
| Young et al. [24] | 2010 | The use of AHP in identifying stormwater management strategies in an American local municipality |
| Sahin et al. [25] | 2013 | The use of AHP in identifying stormwater management strategies across councils in an Australian state |
| Siems and Sahin [26] | 2014 | The use of AHP in identifying stormwater management strategies across councils in an Australian state. |
| Ebrahimian et al. [27] | 2015 | The use of fuzzy AHP and compromise programing in stormwater collection systems in an Iranian urban context |
| Alhumaid et al. [28] | 2018 | The use of AHP and PROMETHEE II in stormwater drainage system management in a Saudi Arabian urban context |
| Kordana and Slys [29] | 2020 | The use of AHP to evaluate stormwater management strategies in at a building in a Polish context |
| Yu et al. [30] | 2021 | The use of AHP in identifying optimal permeable pavement types for stormwater management. |
| TOPSIS | ||
| Jayasooriya et al. [31] | 2018 | The use of TOPSIS to identify green infrastructure for stormwater management in industrial sites an Australian urban area |
| Hager [32] | 2019 | The use of fuzzy TOPSIS to examine optimal stormwater management strategies in a Canadian context. |
| Luan et al. [33] | 2019 | The use of TOPSIS to evaluate green infrastructure for stormwater in a Chinese sponge city |
| Zeng et al. [34] | 2021 | The use of TOPSIS to identify green infrastructure solutions for stormwater management in a Chinese smart city |
| AHP-TOPSIS | ||
| Gogate et al. [35] | 2017 | The use of AHP-TOPSIS to identify stormwater management alternative performances in an Indian urban area |
| Moghadas et al. [36] | 2019 | The use of AHP-TOPSIS to evaluate flood risk in an Iranian urban area |
| Ekmekcioglu et al. [37] | 2021 | Fuzzy AHP-TOPSIS for flood risk mapping in a Turkish municipalities |
| Koc et al. [38] | 2021 | Fuzzy AHP-TOPSIS for stormwater management in a Turkish urban watershed. |
| Numeric Value | Description | Reciprocal Value |
|---|---|---|
| 1 | Equal Importance | 1 |
| 3 | Slight importance of one over another | 1/3 |
| 5 | Moderate importance of one over another | 1/5 |
| 7 | Very strong importance of one over another | 1/7 |
| 9 | Extreme importance of one over another | 1/9 |
| 2, 4, 6, 8 | Intermediate value | 1/2, 1/4, 1/6, 1/8 |
| Linguistic Value | Numerical Value |
|---|---|
| Very Low | 1 |
| Low | 3 |
| Moderate | 5 |
| High | 7 |
| Very High | 9 |
| Main Criteria | Full City | Advocacy | Research | Governance | |
|---|---|---|---|---|---|
| Political | 0.335 | 0.401 | 0.187 | 0.342 | |
| Economic | 0.301 | 0.280 | 0.201 | 0.351 | |
| Environmental | 0.182 | 0.133 | 0.335 | 0.170 | |
| Social | 0.181 | 0.187 | 0.277 | 0.138 | |
| Sub-Criteria (global weights) | |||||
| Political | Existing Legislative Framework | 0.084 | 0.095 | 0.060 | 0.083 |
| Project Feasibility | 0.102 | 0.165 | 0.035 | 0.088 | |
| Jurisdiction | 0.097 | 0.086 | 0.046 | 0.118 | |
| Implementation Time | 0.052 | 0.055 | 0.046 | 0.052 | |
| Economic | Public Costs | 0.109 | 0.100 | 0.055 | 0.142 |
| Private Costs | 0.054 | 0.054 | 0.028 | 0.064 | |
| Funding Availability | 0.104 | 0.088 | 0.088 | 0.115 | |
| Green Industry Growth | 0.035 | 0.038 | 0.030 | 0.030 | |
| Environmental | Stormwater Capacity | 0.062 | 0.029 | 0.101 | 0.081 |
| Stormwater Quality | 0.057 | 0.045 | 0.058 | 0.050 | |
| Ecosystem Support | 0.032 | 0.036 | 0.044 | 0.019 | |
| Energy Usage | 0.031 | 0.023 | 0.132 | 0.019 | |
| Social | Risk to Human Health and Safety | 0.071 | 0.079 | 0.065 | 0.053 |
| Civic Engagement | 0.029 | 0.033 | 0.049 | 0.019 | |
| Reducing Inequalities | 0.040 | 0.051 | 0.049 | 0.025 | |
| Synergies with other Adaptations | 0.042 | 0.024 | 0.113 | 0.040 | |
| Alternative Ranking | Full City | Advocacy | Research | Governance |
|---|---|---|---|---|
| 1 | Governmental Streamlining 0.552 | Governmental Streamlining 0.604 | Governmental Streamlining 0.615 | Public Green Infrastructure 0.557 |
| 2 | Public Green Infrastructure 0.537 | Public Green Infrastructure 0.523 | Maintaining Urban Environments 0.557 | Grey Infrastructure Overhauls 0.518 |
| 3 | Maintaining Urban Environments 0.502 | Maintaining Urban Environments 0.473 | Public Green Infrastructure 0.548 | Maintaining Urban Environments 0.5082 |
| 4 | Grey Infrastructure Overhauls 0.477 | Private Green Infrastructure 0.462 | Private Green Infrastructure 0.483 | Governmental Streamlining 0.5079 |
| 5 | Private Green Infrastructure 0.475 | Grey Infrastructure Overhauls 0.457 | Grey Infrastructure Overhauls 0.421 | Private Green Infrastructure 0.457 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Axelsson, C.; Giove, S.; Soriani, S. Urban Pluvial Flood Management Part 1: Implementing an AHP-TOPSIS Multi-Criteria Decision Analysis Method for Stakeholder Integration in Urban Climate and Stormwater Adaptation. Water 2021, 13, 2422. https://doi.org/10.3390/w13172422
Axelsson C, Giove S, Soriani S. Urban Pluvial Flood Management Part 1: Implementing an AHP-TOPSIS Multi-Criteria Decision Analysis Method for Stakeholder Integration in Urban Climate and Stormwater Adaptation. Water. 2021; 13(17):2422. https://doi.org/10.3390/w13172422
Chicago/Turabian StyleAxelsson, Charles, Silvio Giove, and Stefano Soriani. 2021. "Urban Pluvial Flood Management Part 1: Implementing an AHP-TOPSIS Multi-Criteria Decision Analysis Method for Stakeholder Integration in Urban Climate and Stormwater Adaptation" Water 13, no. 17: 2422. https://doi.org/10.3390/w13172422
APA StyleAxelsson, C., Giove, S., & Soriani, S. (2021). Urban Pluvial Flood Management Part 1: Implementing an AHP-TOPSIS Multi-Criteria Decision Analysis Method for Stakeholder Integration in Urban Climate and Stormwater Adaptation. Water, 13(17), 2422. https://doi.org/10.3390/w13172422






