Evaluation of Regional Climate Models (RCMs) Using Precipitation and Temperature-Based Climatic Indices: A Case Study of Florida, USA
Abstract
:1. Introduction
2. Materials and Methods
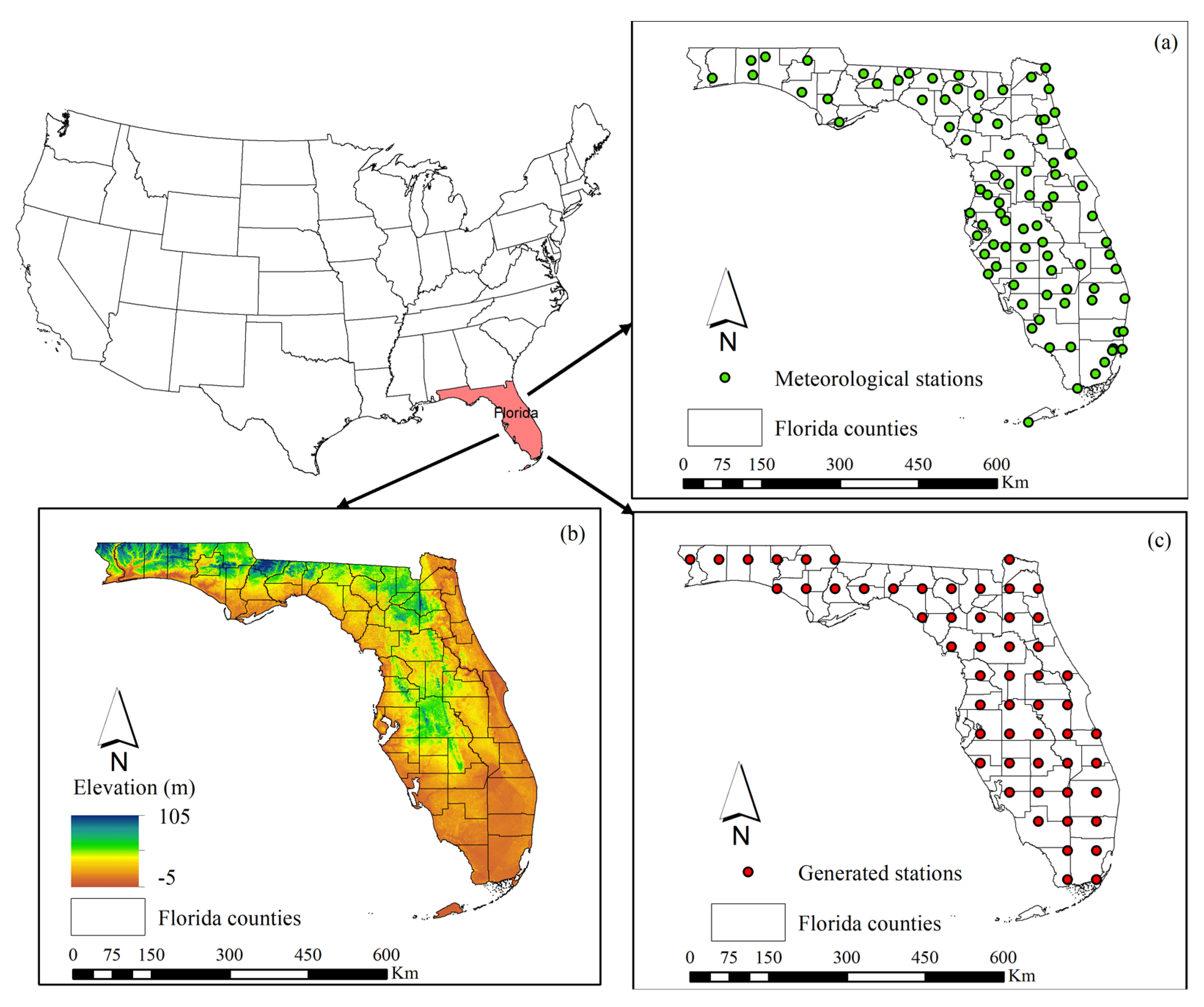
2.1. Study Region
2.2. Data Description
2.2.1. Regional and Global Climate Models (RCMs and GCMs)
2.2.2. Meteorological Observations
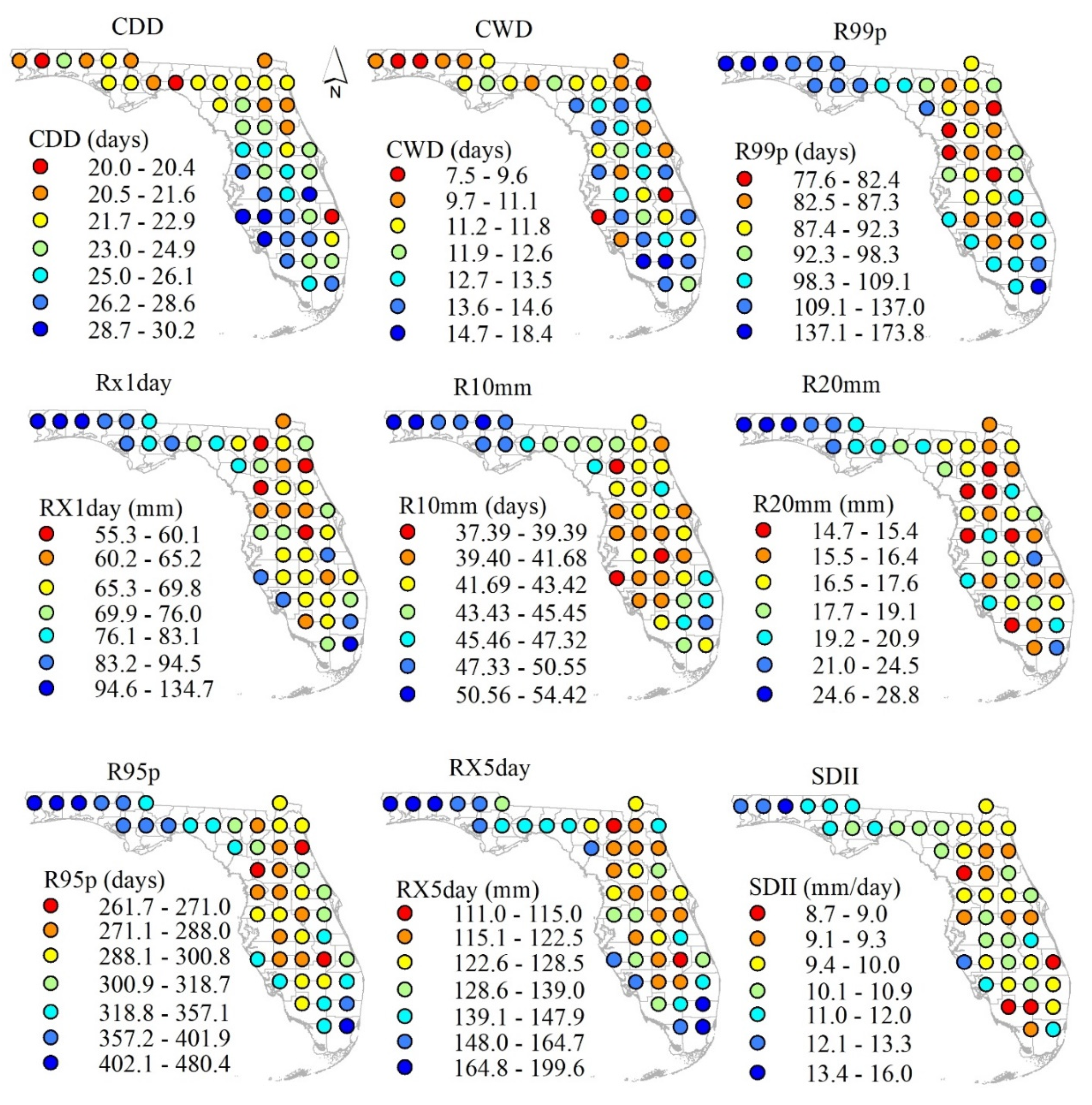
2.3. Climate Indices and Their Computation
2.4. Evaluation Metrics
3. Result and Discussion
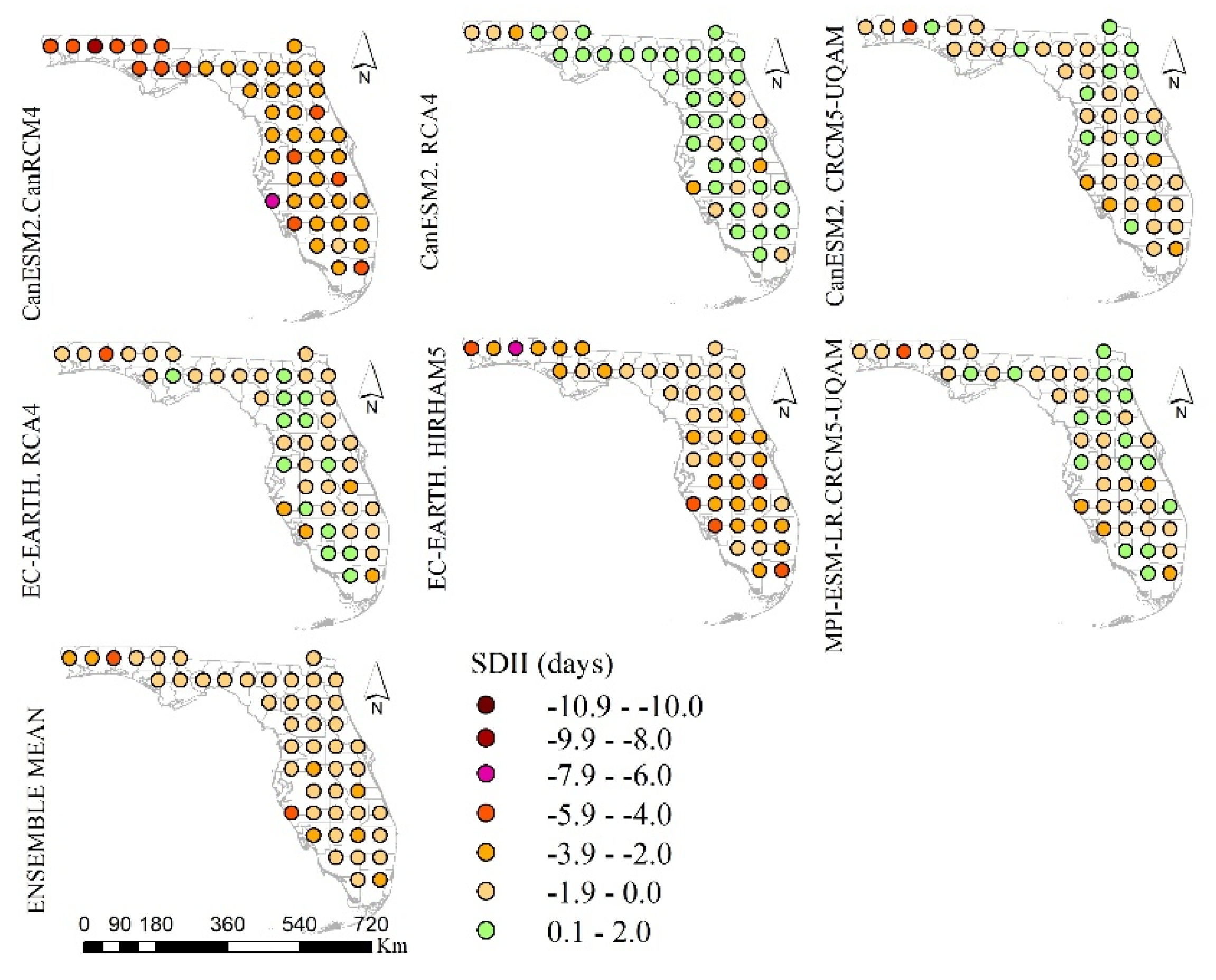
3.1. Absolute Biases between Model and Observed Climatology
3.1.1. Precipitation Based Climatic Indices
3.1.2. Temperature Based Climatic Indices
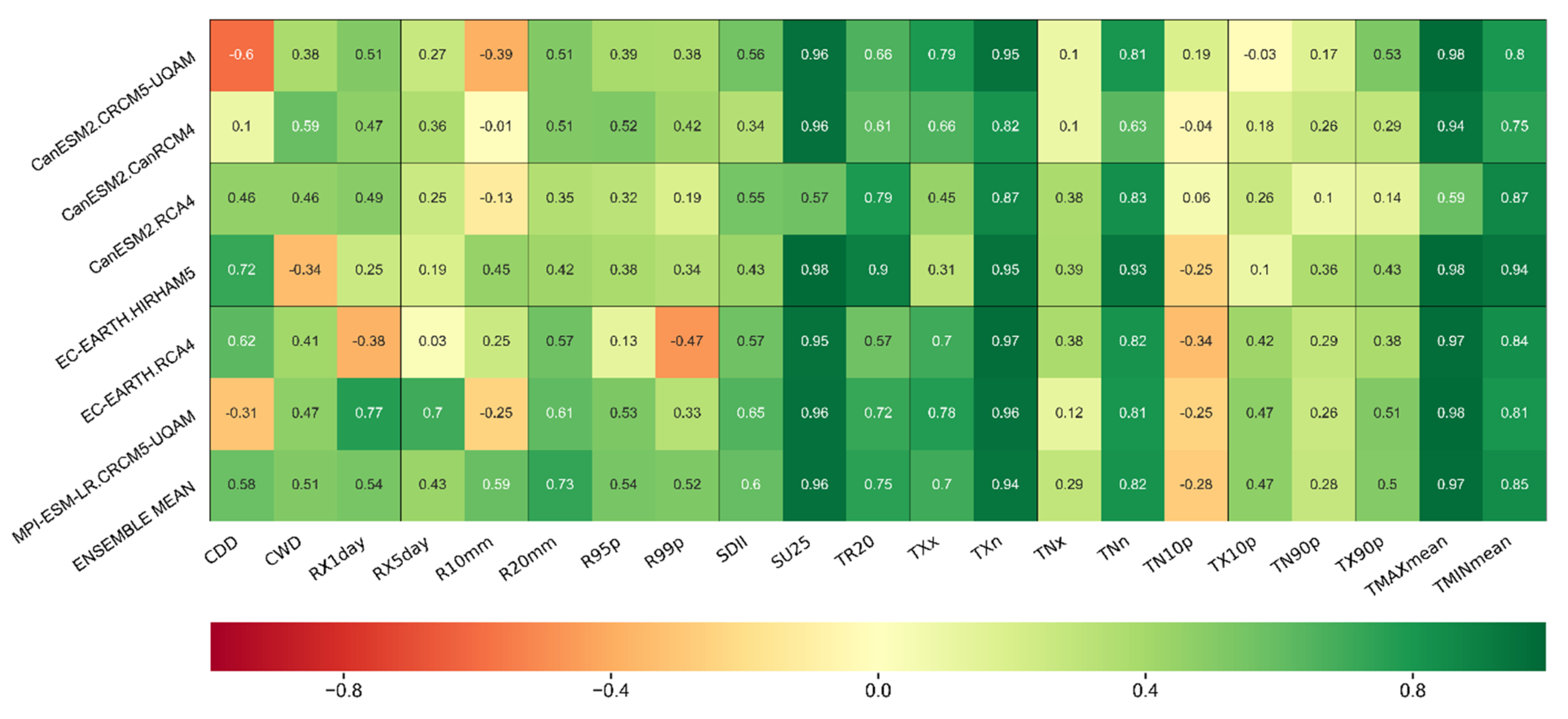
3.2. Evaluation of RCMs using Pattern Correlation
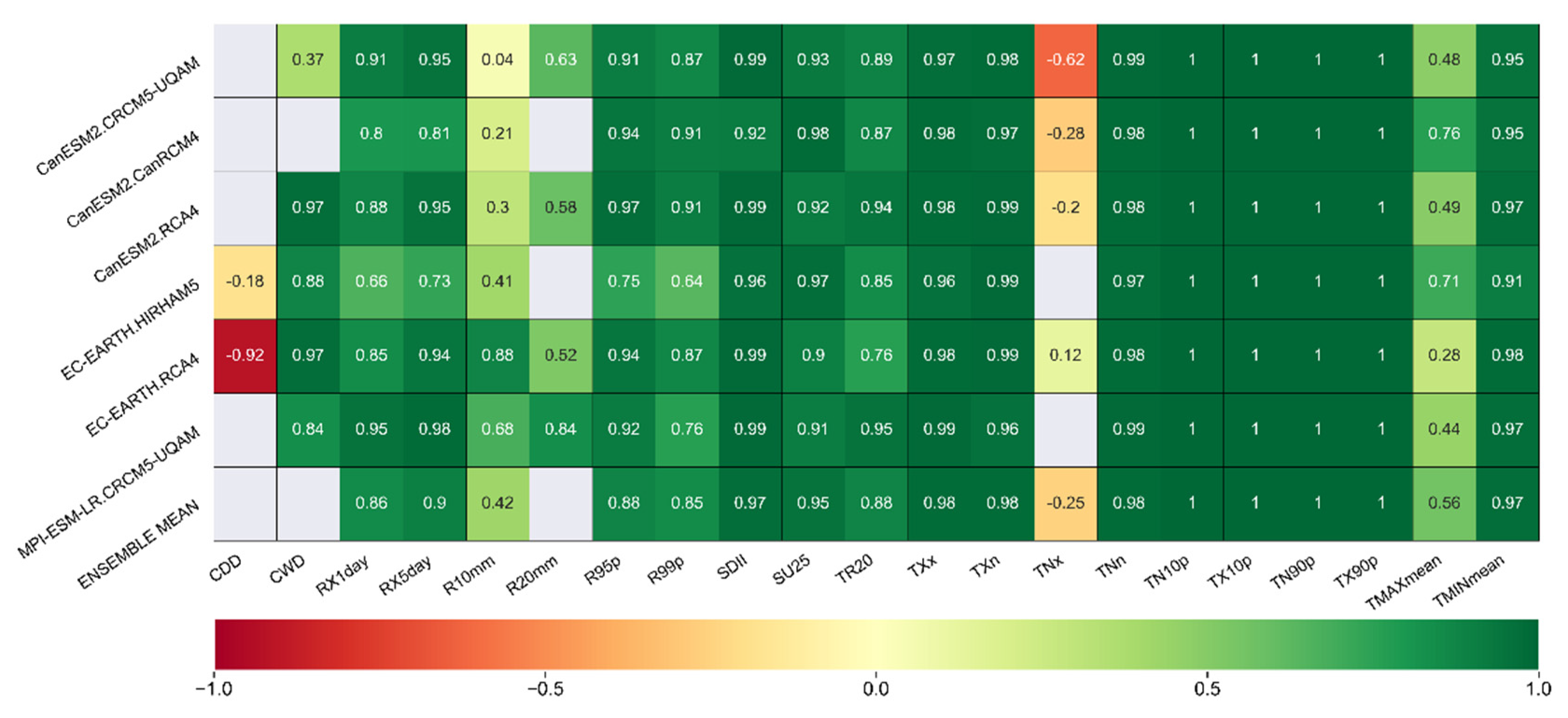
3.3. Evaluation of RCMs using Reduction of Variance (RV)
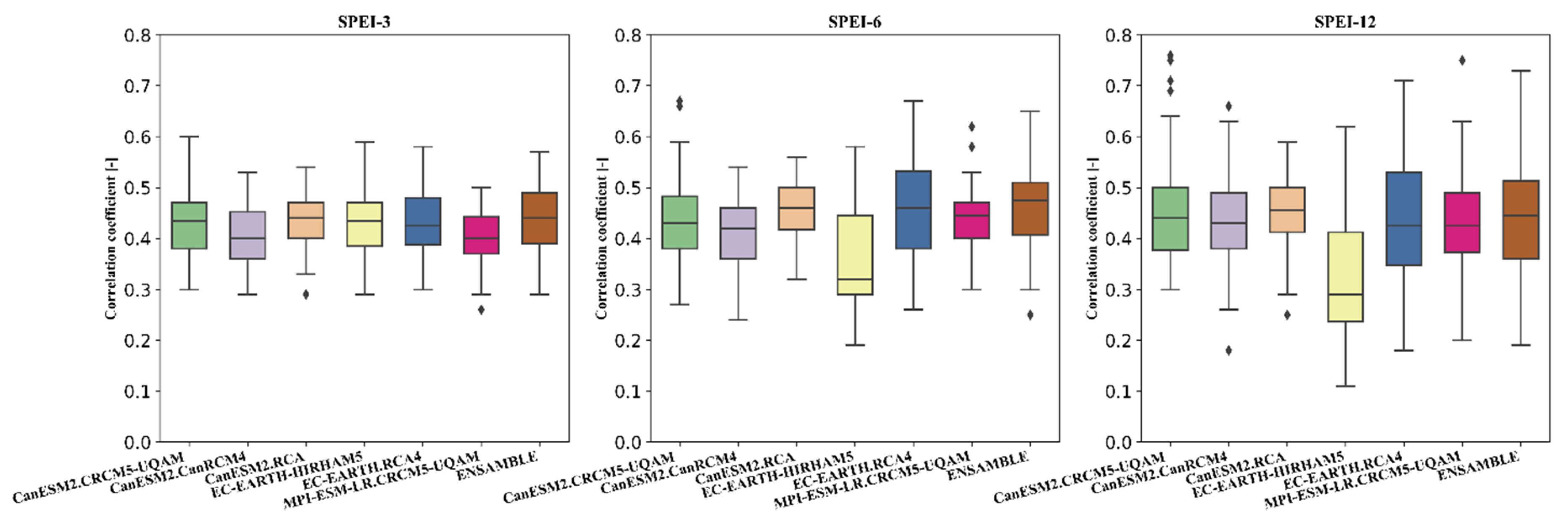
3.4. Evaluation of the Climate Model Based on SPEI
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, P.L. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.L.; Sloan, L.C.; Snyder, M.A. Regional changes in extreme climatic events: A future climate scenario. J. Clim. 2004, 17, 81–87. [Google Scholar] [CrossRef]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37. [Google Scholar] [CrossRef]
- Harley, C.D.; Hughes, A.R.; Hultgren, K.M.; Miner, B.G.; Sorte, C.J.; Thornber, C.S.; Rodriguez, L.F.; Tomanek, L.; Williams, S.L. The impacts of climate change in coastal marine systems. Ecol. Lett. 2006, 9, 228–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J.; et al. Climate change and forest disturbances: Climate change can affect forests by altering the frequency, intensity, duration, and timing of fire, drought, introduced species, insect and pathogen outbreaks, hurricanes, windstorms, ice storms, or landslides. BioScience 2001, 51, 723–734. [Google Scholar] [CrossRef] [Green Version]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816. [Google Scholar] [CrossRef]
- Beniston, M.; Stephenson, D.B.; Christensen, O.B.; Ferro, C.A.; Frei, C.; Goyette, S.; Halsnaes, K.; Holt, T.; Jylhä, K.; Koffi, B.; et al. Future extreme events in European climate: An exploration of regional climate model projections. Clim. Chang. 2007, 81, 71–95. [Google Scholar] [CrossRef] [Green Version]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.G.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting global climate models for regional climate change studies. Proc. Natl. Acad. Sci. USA 2009, 106, 8441–8446. [Google Scholar] [CrossRef] [Green Version]
- Duffy, P.B.; Arritt, R.W.; Coquard, J.; Gutowski, W.; Han, J.; Iorio, J.; Kim, J.; Leung, L.R.; Roads, J.; Zeledon, E. Simulations of present and future climates in the western United States with four nested regional climate models. J. Clim. 2006, 19, 873–895. [Google Scholar] [CrossRef] [Green Version]
- Wuebbles, D.; Meehl, G.; Hayhoe, K.; Karl, T.R.; Kunkel, K.; Santer, B.; Wehner, M.; Colle, B.; Fischer, E.M.; Fu, R.; et al. CMIP5 climate model analyses: Climate extremes in the United States. Bull. Am. Meteorol. Soc. 2014, 95, 571–583. [Google Scholar] [CrossRef] [Green Version]
- Maurer, E.P.; Brekke, L.; Pruitt, T.; Duffy, P.B. Fine-resolution climate projections enhance regional climate change impact studies. Eos Trans. Am. Geophys. Union 2007, 88, 504. [Google Scholar] [CrossRef]
- Prudhomme, C.; Wilby, R.L.; Crooks, S.; Kay, A.L.; Reynard, N.S. Scenario-neutral approach to climate change impact studies: Application to flood risk. J. Hydrol. 2010, 390, 198–209. [Google Scholar] [CrossRef] [Green Version]
- Rosenzweig, C.; Parry, M.L. Potential impact of climate change on world food supply. Nature 1994, 367, 133. [Google Scholar] [CrossRef]
- Mearns, L.O.; Arritt, R.; Biner, S.; Bukovsky, M.S.; McGinnis, S.; Sain, S. The North American regional climate change assessment program: Overview of phase I results. Bull. Am. Meteorol. Soc. 2012, 93, 1337–1362. [Google Scholar] [CrossRef]
- Christensen, J.H.; Carter, T.R.; Rummukainen, M.; Amanatidis, G. Evaluating the performance and utility of regional climate models: The PRUDENCE project. Clim. Chang. 2007, 81, 1–6. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Braconnot, P.; Harrison, S.P.; Kageyama, M.; Bartlein, P.J.; Masson-Delmotte, V.; Abe-Ouchi, A.; Otto-Bliesner, B.; Zhao, Y. Evaluation of climate models using palaeoclimatic data. Nat. Clim. Chang. 2012, 2, 417. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef] [Green Version]
- Haerter, J.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1073. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, F. RClimDex (1.0) User Manual; Climate Research Branch Environment Canada: Downsview, ON, Canada, 2004; Volume 22.
- Diaconescu, E.P.; Gachon, P.; Laprise, R.; Scinocca, J.F. Evaluation of precipitation indices over North America from various configurations of regional climate models. Atmosphere-Ocean 2016, 54, 418–439. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Lazarus, S.M. Florida climate: Past, present and future. AIP Conf. Proc. 2009, 1157, 32. [Google Scholar] [CrossRef]
- Hwang, S.; Graham, W.; Hernández, J.L.; Martinez, C.; Jones, J.W.; Adams, A. Quantitative spatiotemporal evaluation of dynamically downscaled MM5 precipitation predictions over the Tampa Bay region, Florida. J. Hydrometeorol. 2011, 12, 1447–1464. [Google Scholar] [CrossRef]
- Her, Y.G.; Boote, K.J.; Migliaccio, K.W.; Fraisse, C.; Letson, D.; Mbuya, O.; Anandhi, A.; Chi, H.; Ngatia, L.; Asseng, S. Climate change impacts and adaptation in Florida’s agriculture. In Florida’s Climate: Changes, Variations, & Impacts; Available online: http://fsu.digital.flvc.org/islandora/object/fsu%3A539159 (accessed on 21 December 2019).
- Wang, D.; Hagen, S.C.; Alizad, K. Climate change impact and uncertainty analysis of extreme rainfall events in the Apalachicola River basin, Florida. J. Hydrol. 2013, 480, 125–135. [Google Scholar] [CrossRef]
- Hwang, S.; Graham, W.D.; Adams, A.; Geurink, J. Assessment of the utility of dynamically downscaled regional reanalysis data to predict streamflow in west central Florida using an integrated hydrologic model. Reg. Environ. Chang. 2013, 13, 69–80. [Google Scholar] [CrossRef]
- Mukherjee, S.; Nateghi, R. Climate sensitivity of end-use electricity consumption in the built environment: An application to the state of Florida, United States. Energy 2017, 128, 688–700. [Google Scholar] [CrossRef]
- Stanton, E.A.; Ackerman, F. Florida and Climate Change: The Costs of Inaction. 2007. Available online: http://www.ase.tufts.edu/gdae/Pubs/rp/FloridaClimate.html (accessed on 27 February 2020).
- Hansen, J.W.; Hodges, A.W.; Jones, J.W. ENSO influences on agriculture in the southeastern United States. J. Clim. 1998, 11, 404–411. [Google Scholar] [CrossRef]
- Fraisse, C.W.; Breuer, N.E.; Zierden, D.; Ingram, K.T. From climate variability to climate change: Challenges and opportunities to extension. J. Ext. 2009, 47, 2FEA9. [Google Scholar]
- Heimlich, B.; Bloetscher, F. Effects of sea level rise and other climate change impacts on southeast Florida’s water resources. Fla. Water Resour. J. 2011, 63, 37–48. [Google Scholar]
- Obeysekera, J.; Irizarry, M.; Park, J.; Barnes, J.; Dessalegne, T. Climate change and its implications for water resources management in south Florida. Stoch. Environ. Res. Risk Assess. 2011, 25, 495–516. [Google Scholar] [CrossRef]
- Anyamba, A.; Small, J.L.; Britch, S.C.; Tucker, C.J.; Pak, E.W.; Reynolds, C.A.; Crutchfield, J.; Linthicum, K.J. Recent weather extremes and impacts on agricultural production and vector-borne disease outbreak patterns. PLoS ONE 2014, 9, e92538. [Google Scholar] [CrossRef]
- Bayissa, Y.A.; Moges, S.A.; Xuan, Y.; Van Andel, S.J.; Maskey, S.; Solomatine, D.P.; Griensven, A.V.; Tadesse, T. Spatio-temporal assessment of meteorological drought under the influence of varying record length: The case of Upper Blue Nile Basin, Ethiopia. Hydrol. Sci. J. 2015, 60, 1927–1942. [Google Scholar] [CrossRef]
- Mueller, T.G.; Pusuluri, N.B.; Mathias, K.K.; Cornelius, P.L.; Barnhisel, R.I.; Shearer, S.A. Map quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J. 2004, 68, 2042–2047. [Google Scholar] [CrossRef]
- Chen, F.W.; Liu, C.W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Shiferaw, A.; Tadesse, T.; Rowe, C.; Oglesby, R. Precipitation extremes in dynamically downscaled climate scenarios over the Greater Horn of Africa. Atmosphere 2018, 9, 112. [Google Scholar] [CrossRef] [Green Version]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Martynov, A.; Laprise, R.; Sushama, L.; Winger, K.; Šeparović, L.; Dugas, B. Reanalysis-driven climate simulation over CORDEX North America domain using the Canadian Regional Climate Model, version 5: Model performance evaluation. Clim. Dyn. 2013, 41, 2973–3005. [Google Scholar] [CrossRef] [Green Version]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of satellite-based rainfall estimates and application to monitor meteorological drought for the Upper Blue Nile Basin, Ethiopia. Remote. Sens. 2017, 9, 669. [Google Scholar] [CrossRef] [Green Version]
- Murphy, A.H. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather. Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Murphy, A.H.; Epstein, E.S. Skill scores and correlation coefficients in model verification. Mon. Weather. Rev. 1989, 117, 572–582. [Google Scholar] [CrossRef] [Green Version]
- Diaconescu, E.P.; Mailhot, A.; Brown, R.; Chaumont, D. Evaluation of CORDEX-Arctic daily precipitation and temperature-based climate indices over Canadian Arctic land areas. Clim. Dyn. 2018, 50, 2061–2085. [Google Scholar] [CrossRef] [Green Version]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Inter. J. Clim. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Bayissa, Y.; Maskey, S.; Tadesse, T.; van Andel, S.; Moges, S.; van Griensven, A.; Solomatine, D. Comparison of the performance of six drought índices in characterizing historical drought for the Upper Blue Nile Basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Stephens, G.L.; L Ecuyer, T.; Forbes, R.; Gettelmen, A.; Golaz, J.C.; Bodas-Salcedo, A.; Suzuki, K.; Gabriel, P.; Haynes, J. Dreary state of precipitation in global models. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]





| RCMs | GCMs (Boundary Condition) | Simulation Acronym | Description of the RCMs |
|---|---|---|---|
| CRCM5-UQAM | CanESM2 | CanESM2. CRCM5-UQAM | Canadian Regional Climate Model version 5 Université du Québec à Montréal |
| MPI-ESM-LR | MPI-ESM-LR. CRCM5-UQAM | ||
| CanRCM4 | CanESM2 | CanESM2. CanRCM4 | Canadian Regional Climate Model version 4 |
| RCA4 | CanESM2 | CanESM2. RCA4 | Rossby Center Regional Atmospheric Model |
| EC-EARTH | EC-EARTH. RCA4 | ||
| HIRHAM5 | EC-EARTH | EC-EARTH. HIRHAM5 | HIRHAM5, A Combination of High Resolution Limited Area Model (HIRLAM) and European Centre Hamburg Model (ECHAM)] |
| Indicator | Indicator Name | Definition | Units |
|---|---|---|---|
| CDD | Consecutive Dry Days | Largest Number of Consecutive Days where Precipitation <1 mm | Days |
| CWD | Consecutive Wet Days | Largest Number of Consecutive Days where Precipitation >1 mm | Days |
| RX1day | Maximum 1-Day Precipitation | Maximum 1-Day Precipitation Amount in a Given Period | mm |
| Rx5day | Maximum 5-Day Precipitation | Maximum Consecutive 5-Day Precipitation Amount in a Given Period | mm |
| R10mm | Heavy Precipitation Days | Total Number of Days when Precipitation ≥ 10 mm | Days |
| R20mm | Very Heavy Precipitation Days | Total Number of Days when Precipitation ≥ 20 mm | Days |
| R95p | Very Wet Days | Total Precipitation when Daily Rainfall >95th Percentile on Wet Days of the Reference Period from 1975 to 2005 | Days |
| R99p | Extremely Wet Days | Total Precipitation when Daily Rainfall >99th Percentile on Wet Days of the Reference Period from 1975 to 2005 | Days |
| SDII | Simple Daily Intensity Index | Annual Total Precipitation Divided by the Number of Wet Days (precipitation ≥ 1.0 mm) in the Year | mm/day |
| SU25 | Summer Days | Number of Days where TX (Daily Maximum) >25 °C | Days |
| TR20 | Tropical Nights | Number of Days where TN (Daily Minimum) >20 °C | Days |
| TXx | Max Tmax | Monthly Maximum Value of Daily Maximum Temperature | °C |
| TXn | Min Tmax | Monthly Minimum Value of Daily Maximum Temperature | °C |
| TNx | Max Tmin | Monthly Maximum Value of Daily Minimum Temperature | °C |
| TNn | Min Tmin | Monthly Minimum Value of Daily Minimum Temperature | °C |
| TN10p | Cool Nights | Percentage of Days when TN <10th Percentile | Days |
| TX10p | Cool Days | Percentage of Days when TX <10th Percentile | Days |
| TN90p | Warm Nights | Percentage of Days when TN >90th Percentile | Days |
| TX90p | Warm Days | Percentage of Days when TX >90th Percentile | Days |
| TMAXmean | Maximum Mean Temperature | Average Maximum Temperature | °C |
| TMINmean | Minimum Mean Temperature | Average Minimum Temperature | °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayissa, Y.; Melesse, A.; Bhat, M.; Tadesse, T.; Shiferaw, A. Evaluation of Regional Climate Models (RCMs) Using Precipitation and Temperature-Based Climatic Indices: A Case Study of Florida, USA. Water 2021, 13, 2411. https://doi.org/10.3390/w13172411
Bayissa Y, Melesse A, Bhat M, Tadesse T, Shiferaw A. Evaluation of Regional Climate Models (RCMs) Using Precipitation and Temperature-Based Climatic Indices: A Case Study of Florida, USA. Water. 2021; 13(17):2411. https://doi.org/10.3390/w13172411
Chicago/Turabian StyleBayissa, Yared, Assefa Melesse, Mahadev Bhat, Tsegaye Tadesse, and Andualem Shiferaw. 2021. "Evaluation of Regional Climate Models (RCMs) Using Precipitation and Temperature-Based Climatic Indices: A Case Study of Florida, USA" Water 13, no. 17: 2411. https://doi.org/10.3390/w13172411
APA StyleBayissa, Y., Melesse, A., Bhat, M., Tadesse, T., & Shiferaw, A. (2021). Evaluation of Regional Climate Models (RCMs) Using Precipitation and Temperature-Based Climatic Indices: A Case Study of Florida, USA. Water, 13(17), 2411. https://doi.org/10.3390/w13172411









