Uncertainty of Intensity-Duration-Frequency Curves Due to Adoption or Otherwise of the Temperature Climate Variable in Rainfall Disaggregation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.1.1. Metrological Data
2.1.2. Climate Data
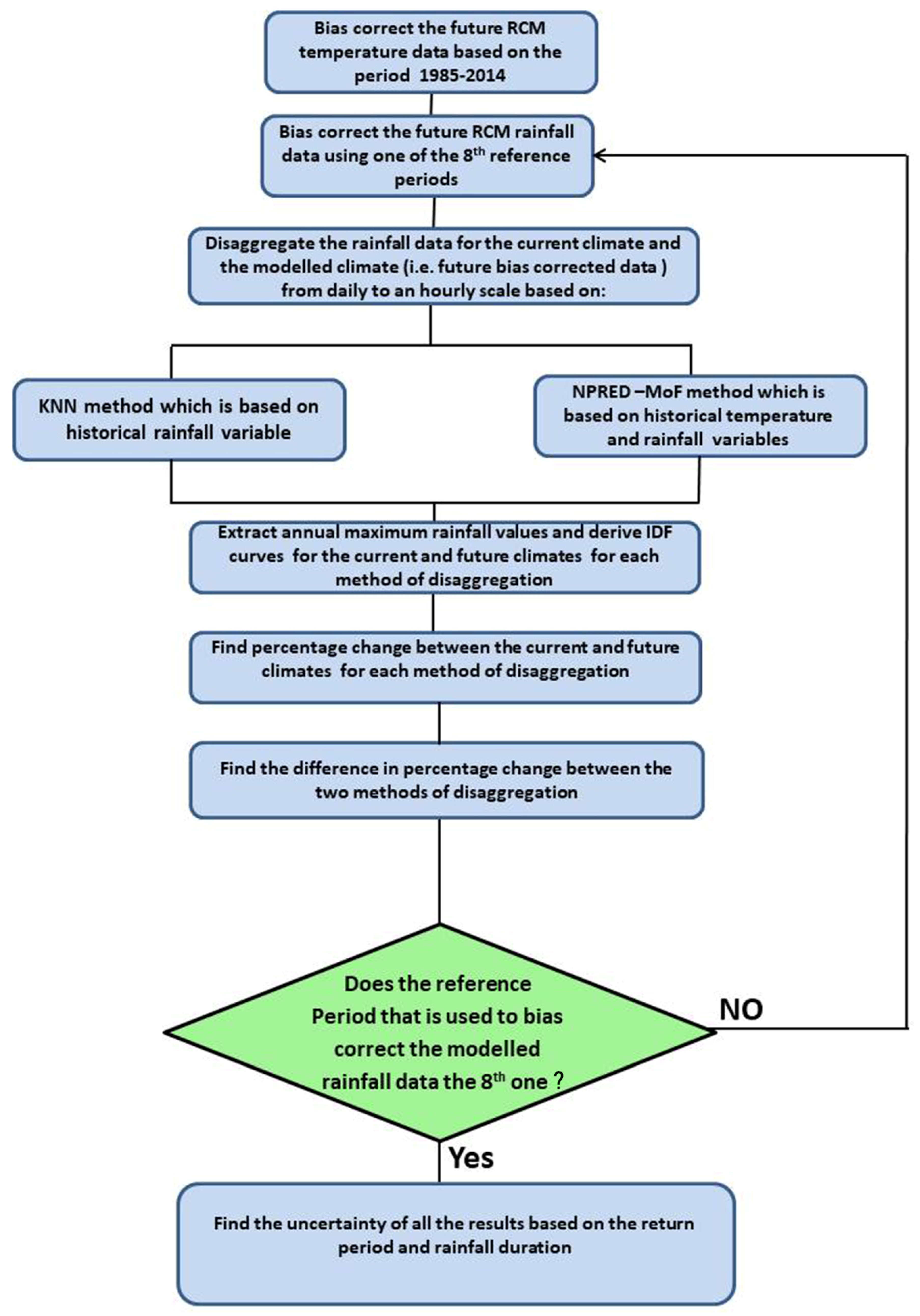
2.2. Methodology
2.2.1. Statistical Bias Correction Method
2.2.2. Disaggregation Methods
- By using the historical hourly rainfall data (i.e., the sum of 5 min radar data), find the fraction of 1 h, that is, the ratio between the maximum 1 h storm fraction on a particular day divided by the total amount of rainfall value for that day;
- By using the NPRED tool, fit a model between the predictor variables, which are daily temperature and daily rainfall (i.e., the sum of 5 min radar data), and the response, which is the 1 h fraction determined from step 1;
- To predict the future 1 h fraction, apply the model that resulted from step 2 to the predictors of the future climate data;
- To find the analogue for the future atmospheric state which was projected in step 3, apply the MoF framework with an optimal window size 15 [28] to search the historical data for such an analogue. Then, the rainfall temporal pattern can be resampled from one of these days (see Equation (2) in [33]).
2.2.3. Creation of IDF Curves
- Use a specific reference period to correct the bias of the future modeled rainfall data for the period 2069–2098.
- Disaggregate the future bias-corrected RCM from a daily to a 1 h timescale using the NPRED-MoF algorithm one time and the KNN method another time, and determine the areal average of the future hourly disaggregated rainfall data for the study area.
- Aggregate the disaggregated future hourly rainfall intensity to five durations (1, 3, 6, 12, and 24 h) depending on the concentration time. Due to the high uncertainty that may result from the methods that can be used to calculate the concentration time [61,62,63], it was noticed that the value of concentration time for the study area can vary depending on the method used for such a purpose. Thus, the value that fit to the purpose of the study was adopted (i.e., a concentration time of 1 h) [62]. Thus, the aggregation into five rainfall durations had to be done by applying a moving window equal to the concentration time (i.e., 1 h) to the full hourly disaggregated time series.
- Derive AM series of rainfall intensity for each duration then apply EV distribution for the derived series to find the rainfall depths for six different return periods (2, 5, 10, 25, 50, and 100 years).
3. Results and Discussion
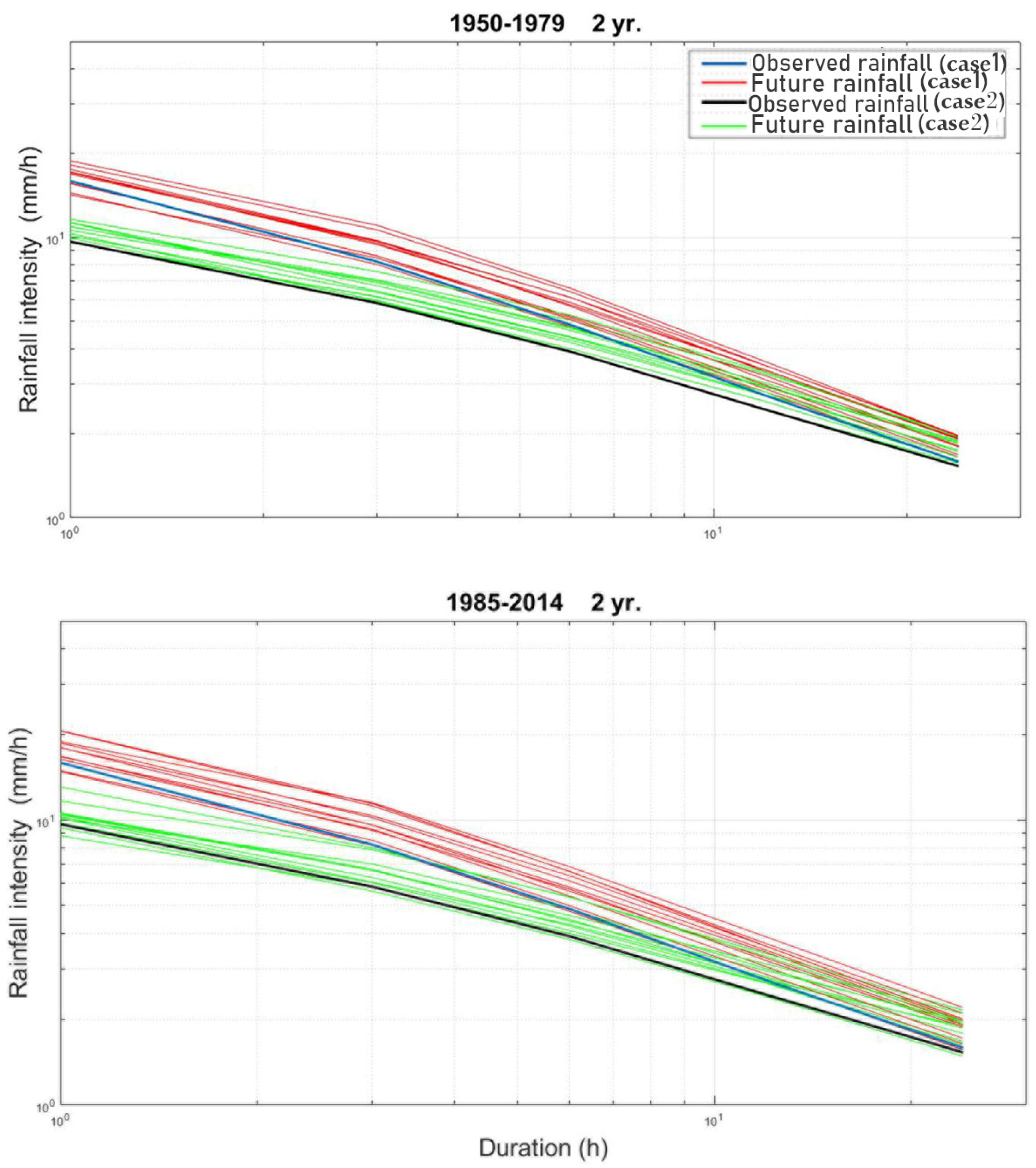
3.1. Rainfall Disaggregation
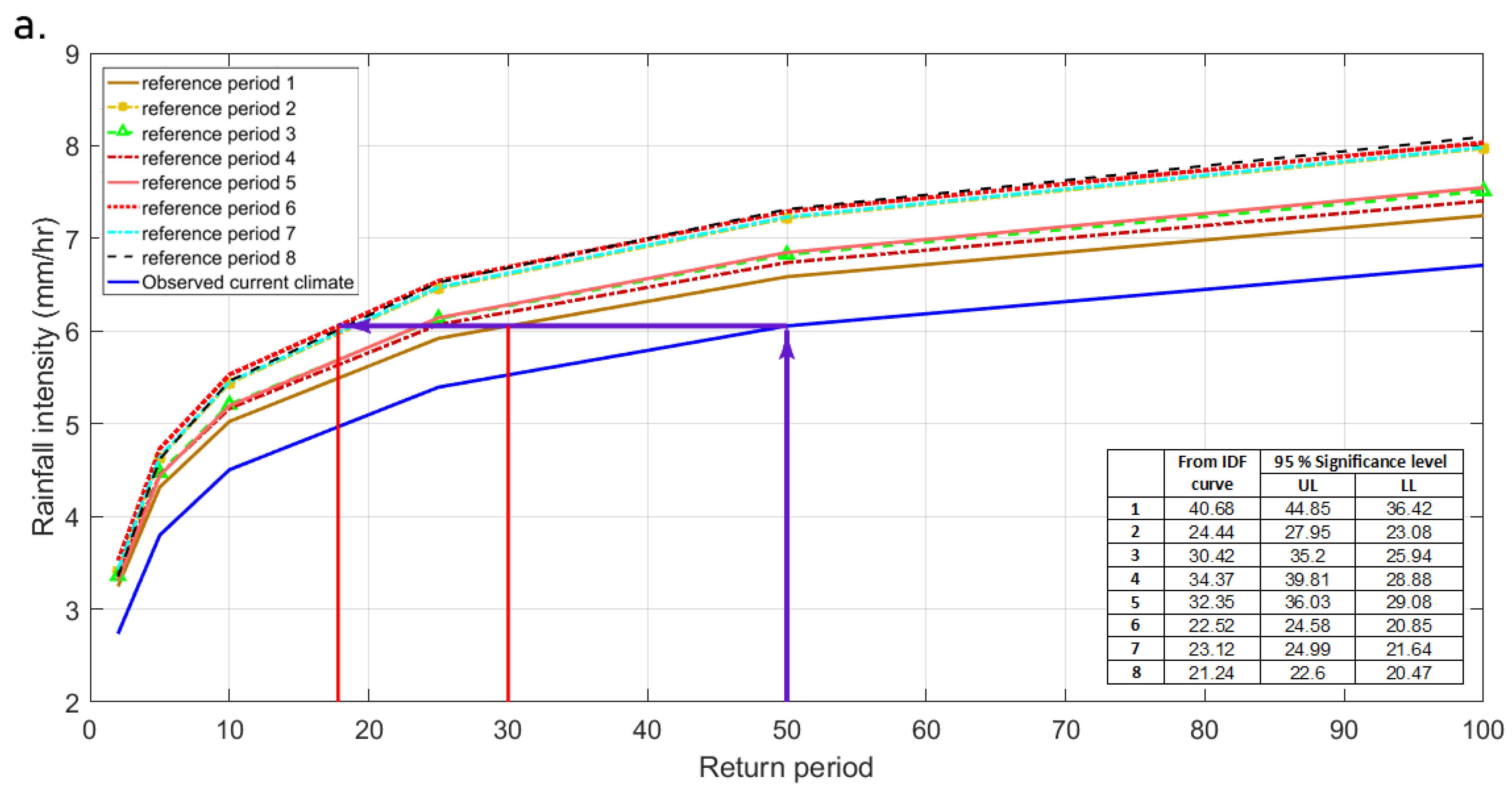
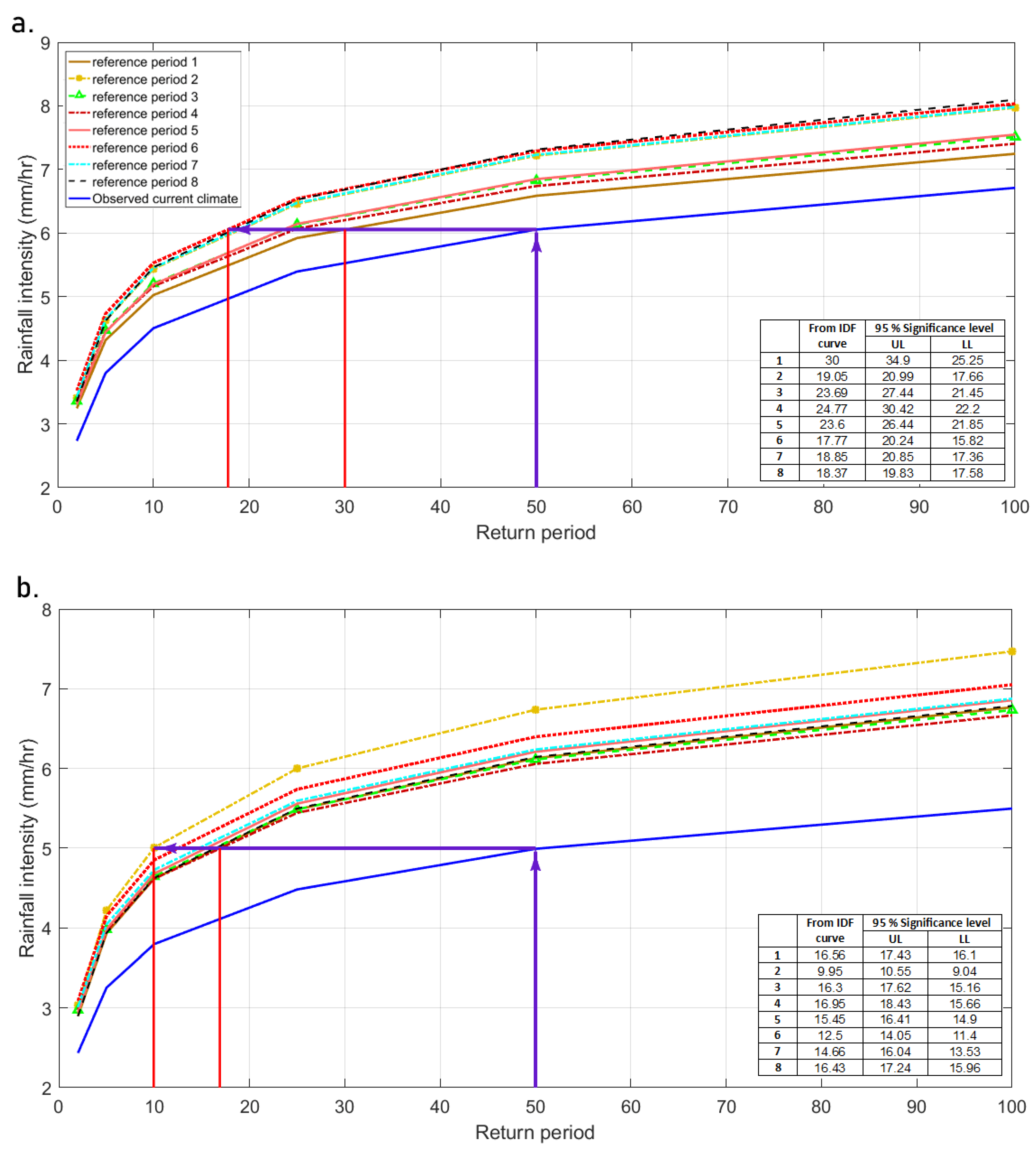
3.2. IDF Curves
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al Mamoon, A.; Joergensen, N.E.; Rahman, A.; Qasem, H. Design rainfall in Qatar: Sensitivity to climate change scenarios. Nat. Hazards 2016, 81, 1797–1810. [Google Scholar] [CrossRef]
- Aldosari, D.; Almedeij, J.; Alsumaiei, A.A. Update of intensity–duration–frequency curves for Kuwait due to extreme flash floods. Environ. Ecol. Stat. 2020, 27, 491–507. [Google Scholar] [CrossRef]
- Hosseinzadehtalaei, P.; Tabari, H.; Willems, P. Climate change impact on short-duration extreme precipitation and intensity–duration–frequency curves over Europe. J. Hydrol. 2020, 590, 125249. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Kinouchi, T.; Nguyen, H.Q. A framework for projecting future intensity-duration-frequency (IDF) curves based on CORDEX Southeast Asia multi-model simulations: An application for two cities in Southern Vietnam. J. Hydrol. 2021, 598, 126461. [Google Scholar] [CrossRef]
- Dahm, R.; Bhardwaj, A.; Weiland, F.S.; Corzo, G.; Bouwer, L.M. A temperature-scaling approach for projecting changes in short duration rainfall extremes from GCM data. Water 2019, 11, 313. [Google Scholar] [CrossRef] [Green Version]
- Mailhot, A.; Duchesne, S. Design Criteria of Urban Drainage Infrastructures under Climate Change. J. Water Resour. Plan. Manag. 2010, 136, 201–208. [Google Scholar] [CrossRef]
- Silva, D.F.; Simonovic, S.P.; Schardong, A.; Goldenfum, J.A. Introducing non-stationarity into the development of intensity-duration-frequency curves under a changing climate. Water 2021, 13, 1008. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Managing the risks of extreme events and disasters to advance climate change adaptation. In Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.K., Allen, S.K., et al., Eds.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Willems, P. Revision of urban drainage design rules after assessment of climate change impacts on precipitation extremes at Uccle, Belgium. J. Hydrol. 2013, 496, 166–177. [Google Scholar] [CrossRef]
- Watt, E.; Marsalek, J. Critical review of the evolution of the design storm event concept. Can. J. Civ. Eng. 2013, 40, 105–113. [Google Scholar] [CrossRef]
- Segond, M.-L.; Onof, C.; Wheater, H.S. Spatial-temporal disaggregation of daily rainfall from a generalized linear model. J. Hydrol. 2006, 331, 674–689. [Google Scholar] [CrossRef]
- Watt, W.E.; Waters, D.; McLean, R. Climate Variability and Urban Stormwater Infrastructure in Canada: Context and Case Studies; Toronto-Niagara Region Study Report and Working Paper Series, Report 2003-1; Meteorological Service of Canada: Waterloo, ON, Canada, 2003.
- Cowpertwait, P.S. Further developments of the Neyman–Scott clustered point process for modeling rainfall. Water Resour. Res. 1991, 27, 1431–1438. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, H.-H.; Lee, S.-O.; Kim, S. Regionalization of the modified Bartlett–Lewis rectangular pulse stochastic rainfall model across the Korean peninsula. J. Hydro-Environ. Res. 2016, 11, 123–137. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. Some models for precipitation based on stochastic point processes. Proc. R. Soc. London Ser. A 1987, 410, 269–288. [Google Scholar] [CrossRef]
- De Luca, D.L.; Petroselli, A. STORAGE (STOchastic RAinfall GEnerator): A user-friendly software for generating long and high-resolution rainfall time series. Hydrology 2021, 8, 76. [Google Scholar] [CrossRef]
- De Luca, D.L.; Petroselli, A.; Galasso, L. A transient stochastic rainfall generator for climate changes analysis at hydrological scales in Central Italy. Atmosphere 2020, 11, 1292. [Google Scholar] [CrossRef]
- Chandler, R.E.; Wheater, H.S. Analysis of precipitation variability using generalized linear models: A case study from the west of Ireland. Water Resour. Res. 2002, 38, 1192. [Google Scholar] [CrossRef] [Green Version]
- Cârsteanu, A.; Foufoula-Georgiou, E. Assessing dependence among weights in a multiplicative cascade model of temporal rainfall. J. Geophys. Res. 1996, 101, 26363–26370. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.C. A statistical analysis of mesoscale rainfall as a random cascade. J. Appl. Meteorol. 1993, 322, 251–267. [Google Scholar] [CrossRef]
- Muzy, J.F.; Baïle, R. Self-similar continuous cascades supported by random cantor sets: Application to rainfall data. Phys. Rev. E 2016, 93, 052305. [Google Scholar] [CrossRef] [Green Version]
- Rupp, D.E.; Keim, R.F.; Ossiander, M.; Brugnach, M.; Selker, J.S. Time scale and intensity dependency in multiplicative cascades for temporal rainfall disaggregation. Water Resour. Res. 2009, 45, W07409. [Google Scholar] [CrossRef] [Green Version]
- Burian, B.S.J.; Durrans, S.R.; Tomic, S.; Pimmel, R.L.; Wai, C.N. Rainfall disaggregation using Artificial Neural Networks. J. Hydrol. Eng. 2000, 5, 299–307. [Google Scholar] [CrossRef]
- Buishand, T.A.; Brandsma, T. Multisite simulation of daily precipitation and temperature in the Rhine basin by nearest-neighbor resampling. Water Resour. Res. 2001, 37, 2761–2776. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A nearest neighbor bootstrap for time series resampling. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Sharif, M.; Burn, D.H. Improved K-nearest neighbor weather generating model. J. Hydrol. Eng. 2007, 12, 42–51. [Google Scholar] [CrossRef] [Green Version]
- Yates, D.; Gangopadhyay, S.; Rajagopalan, B.; Strzepek, K. A technique for generating regional climate scenarios using a nearest-neighbor algorithm. Water Resour. Res. 2003, 39, SWC7-1–SWC7-14. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Qin, X.S. Multisite precipitation downscaling and disaggregation in a tropical urban area. J. Hydrol. 2014, 509, 55–65. [Google Scholar] [CrossRef]
- Sharma, A.; Srikanthan, S. Continuous rainfall simulation: A nonparametric alternative. In 30th Hydrology and Water Resources Symposium: Past, Present & Future; Conference Design: Tasmania, Australia, 2006; p. 86. [Google Scholar]
- Srikanthan, R.; McMahon, T.A. Stochastic Generation of Rainfall and Evaporation Data; Technical Report 84; Australian Water Resources Council, Department of Resources and Energy: Canberra, Australia, 1985. [Google Scholar]
- Westra, S.; Mehrotra, R.; Sharma, A.; Srikanthan, R. Continuous rainfall simulation: 1. A regionalized subdaily disaggregation approach. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Socolofsky, S.A.; Olivera, F. Hourly disaggregation of daily rainfall in Texas using measured hourly precipitation at other locations. J. Hydrol. Eng. 2008, 13, 476–487. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Meshgi, A.; Wang, X.; Zhang, J.; Tay, S.H.X.; Pijcke, G.; Manocha, N.; Ong, M.; Nguyen, M.T.; Babovic, V. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. Int. J. Clim. 2018, 38, e1119–e1138. [Google Scholar] [CrossRef]
- Pampaloni, M.; Sordo-Ward, A.; Bianucci, P.; Martin, I.G.; Caporali, E.; Garrote, L. A stochastic procedure for temporal disaggregation of daily rainfall data in SuDS design. Water 2021, 13, 403. [Google Scholar] [CrossRef]
- Pui, A.; Sharma, A.; Mehrotra, R.; Sivakumar, B.; Jeremiah, E. A comparison of alternatives for daily to sub-daily rainfall disaggregation. J. Hydrol. 2012, 470–471. [Google Scholar] [CrossRef] [Green Version]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Uncertainty of Intensity-Duration-Frequency (IDF) curves due to varied climate baseline periods. J. Hydrol. 2017, 547, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Westra, S.; Evans, J.P.; Mehrotra, R.; Sharma, A. A conditional disaggregation algorithm for generating fine time-scale rainfall data in a warmer climate. J. Hydrol. 2013, 479, 86–99. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Dai, Q.; Han, D.; Zhu, X.; Zhang, S. An uncertainty investigation of RCM downscaling ratios in nonstationary extreme rainfall IDF curves. Atmosphere 2018, 9, 151. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.S.; Elshorbagy, A. Quantification of the climate change-induced variations in Intensity-Duration-Frequency curves in the Canadian Prairies. J. Hydrol. 2015, 527, 990–1005. [Google Scholar] [CrossRef]
- Uraba, M.B.; Gunawardhana, L.N.; Al-Rawas, G.A.; Baawai, M.S. A downscaling-disaggregation approach for developing IDF curves in arid regions. Environ. Monit. Assess. 2019, 191, 245. [Google Scholar] [CrossRef] [PubMed]
- Butler, D.; Digman, C.J.; Makropoulos, C.; Davies, J.W. Urban Drainage, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wasko, C.; Sharma, A. Steeper temporal distribution of rain intensity at higher temperatures within Australian storms. Nat. Geosci. 2015, 8, 527–529. [Google Scholar] [CrossRef]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Sensitivity of peak flow to the change of rainfall temporal pattern due to climate change. J. Hydrol. 2018, 560, 546–559. [Google Scholar] [CrossRef] [Green Version]
- Keller, V.D.J.; Tanguy, M.; Prosdocimi, I.; Terry, J.A.; Hitt, O.; Cole, S.J.; Fry, M.; Morris, D.G.; Dixon, H. CEH-GEAR: 1 km resolution daily and monthly areal rainfall estimates for the UK for hydrological and other applications. Earth Syst. Sci. Data 2015, 7, 143–155. [Google Scholar] [CrossRef] [Green Version]
- Perry, M.; Hollis, D. The generation of monthly gridded datasets for a range of climatic variables over the UK. Int. J. Climatol. 2005, 25, 1041–1054. [Google Scholar] [CrossRef]
- Eden, P. Traditional weather observing in the UK: An historical overview. Weather 2009, 64, 239–245. [Google Scholar] [CrossRef]
- Met Office, U.K. Fact Sheet No. 15—Weather Radar. 2009. Available online: http://www.metoffice.gov.uk/learning/library/factsheets (accessed on 12 May 2014).
- Harrison, D.L.; Scovell, R.W.; Kitchen, M. High-resolution precipitation estimates for hydrological uses. Proc. Inst. Civ. Eng-Water Manag. 2009, 162, 125–135. [Google Scholar] [CrossRef]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Exploration of an adaptive merging scheme for optimal. J. Hydroinform. 2017, 19, 225–237. [Google Scholar] [CrossRef] [Green Version]
- Robinson, E.L.; Blyth, E.; Clark, D.B.; Comyn-Platt, E.; Finch, J.; Rudd, A.C. Climate Hydrology and Ecology Research Support System Meteorology Dataset for Great Britain (1961–2015) [CHESS-met]. NERC Environmental Information Data Centre. Available online: https://doi.org/10.5285/b745e7b1-626c-4ccc-ac27-56582e77b900 (accessed on 10 January 2017).
- Murphy, J.M.; Sexton, D.M.H.; Jenkins, G.J.; Booth, B.B.B.; Brown, C.C.; Clark, R.T.; Collins, M.; Harris, G.R.; Kendon, E.J.; Betts, R.A.; et al. UK Climate Projections Science Report: Climate Change Projections; Met Office Hadley Centre: Exeter, UK, 2009; p. 190. [Google Scholar]
- Newton, G.; Dadson, S.J.; Lafon, T.; Prudhomme, C. Scoping Study for Precipitation Downscaling and Bias-Correctio—Science Report/Project Note SC090016/PN3; CEH: Wallingford, UK, 2012; p. 41. Available online: http://nora.nerc.ac.uk/id/eprint/15043 (accessed on 19 August 2021).
- Prudhomme, C.; Dadson, S.; Morris, D.; Williamson, J.; Goodsell, G.; Crooks, S.; Watts, G. Future Flows Climate: An ensemble of 1-km climate change projections for hydrological application in Great Britain. Earth Syst. Sci. Data 2012, 4, 143–148. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Andreasson, J.; Graham, L.P.; Olsson, J.; Rosberg, J.; Wetterhall, F. Distribution-based scaling to improve usability of regional climate model projections for hydrological climate change impacts studies. Hydrol. Res. 2010, 41, 211–229. [Google Scholar] [CrossRef]
- Olsson, T.; Jakkila, J.; Veijalainen, N.; Backman, L.; Kaurola, J.; Vehvilainen, B. Impacts of climate change on temperature, precipitation and hydrology in Finland—Studies using bias corrected Regional Climate Model data. Hydrol. Earth Syst. Sci. 2015, 19, 3217–3238. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Mehrotra, R.; Li, J.W.; Jha, S. A programming tool for nonparametric system prediction using Partial Informational Correlation and Partial Weights. Environ. Model. Softw. 2016, 83, 271–275. [Google Scholar] [CrossRef]
- Mehrotra, R.; Westra, S.; Sharma, A.; Srikanthan, R. Continuous rainfall simulation: 2. A regionalized daily rainfall generation approach. Water Resour. Res. 2012, 48, 1536. [Google Scholar] [CrossRef] [Green Version]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models; Water Resources Research Report No. 077; Department of Civil and Environmental Engineering, University of Western Ontario London: London, ON, Canada, 2011; ISSN: 19133200; Available online: http://ir.lib.uwo.ca/wrrr/40 (accessed on 19 August 2021).
- Azizian, A. Uncertainty analysis of time of concentration equations based on first-order-analysis (FOA) method. Am. J. Eng. Appl. Sci. 2018, 11, 327–341. [Google Scholar] [CrossRef]
- Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the time of concentration: Shedding light on a paradox. Hydrol. Sci. 2018, 63, 721–740. [Google Scholar] [CrossRef] [Green Version]
- USDA, Natural Resources Conservation Service. National Engineering Handbook; Part 630; Chapter 15; Time of Concentration: Washington, DC, USA, 2010. [Google Scholar]


| Reference Period | Case 1 of Disaggregation | Case 2 of Disaggregation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 6 h | 12 h | 1 Day | 1 h | 3 h | 6 h | 12 h | 1 Day | |
| 1950–1979 | −14.71 | 6.96 | 11.05 | 11.58 | 12.58 | 14.60 | 19.60 | 21.61 | 21.64 | 15.67 |
| 1955–1984 | −9.09 | 14.78 | 19.22 | 20.73 | 21.38 | 22.12 | 28.81 | 31.89 | 31.85 | 24.51 |
| 1960–1989 | −8.06 | 11.95 | 15.70 | 15.59 | 17.26 | 18.99 | 23.56 | 22.68 | 22.36 | 19.39 |
| 1965–1994 | −8.71 | 10.52 | 14.57 | 14.69 | 16.34 | 19.20 | 22.06 | 21.43 | 21.57 | 19.07 |
| 1970–1999 | −7.20 | 10.39 | 14.80 | 15.31 | 17.34 | 15.39 | 19.93 | 22.46 | 23.26 | 20.13 |
| 1975–2004 | −0.27 | 17.46 | 21.01 | 22.81 | 22.75 | 22.99 | 26.54 | 28.13 | 27.77 | 27.02 |
| 1980–2009 | 0.65 | 16.54 | 20.53 | 21.06 | 22.19 | 22.43 | 23.36 | 21.93 | 24.55 | 25.77 |
| 1985–2014 | −1.46 | 18.35 | 21.40 | 21.26 | 23.29 | 24.67 | 22.03 | 18.18 | 21.85 | 26.27 |
| Wettest Ensemble Member | ||||||||||
| Reference Period | Case 1 of Disaggregation | Case 2 of Disaggregation | ||||||||
| 1 h | 3 h | 6 h | 12 h | 1 Day | 1 h | 3 h | 6 h | 12 h | 1 Day | |
| 1950–1979 | 31.93 | 18.25 | 10.65 | 5.81 | 3.14 | 19.69 | 12.08 | 8.65 | 5.42 | 3.11 |
| 1955–1984 | 35.18 | 20.12 | 12.04 | 6.40 | 3.50 | 21.81 | 12.96 | 9.85 | 6.07 | 3.43 |
| 1960–1989 | 37.98 | 18.33 | 11.12 | 5.96 | 3.32 | 21.68 | 12.97 | 8.85 | 5.54 | 3.24 |
| 1965–1994 | 36.10 | 17.44 | 10.67 | 5.90 | 3.30 | 21.74 | 13.11 | 8.78 | 5.51 | 3.23 |
| 1970–1999 | 36.21 | 20.69 | 11.75 | 6.51 | 3.59 | 22.56 | 14.56 | 10.03 | 5.95 | 3.58 |
| 1975–2004 | 42.11 | 20.74 | 12.33 | 6.61 | 3.63 | 23.53 | 14.14 | 9.81 | 5.96 | 3.63 |
| 1980–2009 | 46.58 | 22.99 | 13.67 | 7.53 | 4.22 | 23.22 | 13.56 | 9.16 | 6.46 | 4.20 |
| 1985–2014 | 39.36 | 21.98 | 12.91 | 7.01 | 3.87 | 25.46 | 14.16 | 9.05 | 5.49 | 3.85 |
| Driest Ensemble Member | ||||||||||
| Reference Period | Case 1 of Disaggregation | Case 2 of Disaggregation | ||||||||
| 1 h | 3 h | 6 h | 12 h | 1 Day | 1 h | 3 h | 6 h | 12 h | 1 Day | |
| 1950–1979 | 21.53 | 11.81 | 7.81 | 4.48 | 2.49 | 13.29 | 8.70 | 5.80 | 3.68 | 2.44 |
| 1955–1984 | 20.07 | 11.39 | 7.36 | 4.36 | 2.45 | 13.56 | 8.73 | 5.84 | 3.65 | 2.31 |
| 1960–1989 | 21.96 | 11.80 | 7.18 | 3.99 | 2.23 | 13.58 | 8.45 | 5.68 | 3.59 | 2.25 |
| 1965–1994 | 23.45 | 12.27 | 7.16 | 4.17 | 2.38 | 14.23 | 8.64 | 5.91 | 3.76 | 2.37 |
| 1970–1999 | 23.14 | 12.05 | 7.35 | 4.31 | 2.39 | 14.14 | 8.71 | 5.88 | 3.72 | 2.45 |
| 1975–2004 | 22.56 | 13.21 | 7.84 | 4.52 | 2.60 | 15.09 | 8.73 | 5.82 | 3.87 | 2.65 |
| 1980–2009 | 23.97 | 12.00 | 6.92 | 4.06 | 2.20 | 14.27 | 8.63 | 5.77 | 3.62 | 2.19 |
| 1985–2014 | 23.08 | 11.82 | 6.63 | 3.75 | 2.19 | 13.08 | 8.00 | 5.47 | 3.44 | 2.11 |
| Mean of Ensemble Members | ||||||||||
| Reference Period | Case 1 of Disaggregation | Case 2 of Disaggregation | ||||||||
| 1 h | 3 h | 6 h | 12 h | 1 Day | 1 h | 3 h | 6 h | 12 h | 1 Day | |
| 1950–1979 | 26.44 | 14.94 | 9.00 | 5.03 | 2.77 | 16.72 | 10.45 | 7.40 | 4.62 | 2.73 |
| 1955–1984 | 28.18 | 16.03 | 9.66 | 5.44 | 2.99 | 17.81 | 11.25 | 8.03 | 5.01 | 2.94 |
| 1960–1989 | 28.50 | 15.63 | 9.37 | 5.21 | 2.88 | 17.36 | 10.80 | 7.47 | 4.65 | 2.82 |
| 1965–1994 | 28.30 | 15.43 | 9.28 | 5.17 | 2.86 | 17.39 | 10.66 | 7.39 | 4.62 | 2.81 |
| 1970–1999 | 28.77 | 15.42 | 9.30 | 5.19 | 2.89 | 16.83 | 10.48 | 7.46 | 4.68 | 2.84 |
| 1975–2004 | 30.92 | 16.40 | 9.80 | 5.53 | 3.02 | 17.94 | 11.05 | 7.80 | 4.85 | 3.00 |
| 1980–2009 | 31.20 | 16.28 | 9.76 | 5.45 | 3.01 | 17.86 | 10.78 | 7.42 | 4.73 | 2.97 |
| 1985–2014 | 30.55 | 16.53 | 9.83 | 5.46 | 3.03 | 18.18 | 10.66 | 7.20 | 4.63 | 2.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fadhel, S.; Al Aukidy, M.; Saleh, M.S. Uncertainty of Intensity-Duration-Frequency Curves Due to Adoption or Otherwise of the Temperature Climate Variable in Rainfall Disaggregation. Water 2021, 13, 2337. https://doi.org/10.3390/w13172337
Fadhel S, Al Aukidy M, Saleh MS. Uncertainty of Intensity-Duration-Frequency Curves Due to Adoption or Otherwise of the Temperature Climate Variable in Rainfall Disaggregation. Water. 2021; 13(17):2337. https://doi.org/10.3390/w13172337
Chicago/Turabian StyleFadhel, Sherien, Mustafa Al Aukidy, and May Samir Saleh. 2021. "Uncertainty of Intensity-Duration-Frequency Curves Due to Adoption or Otherwise of the Temperature Climate Variable in Rainfall Disaggregation" Water 13, no. 17: 2337. https://doi.org/10.3390/w13172337
APA StyleFadhel, S., Al Aukidy, M., & Saleh, M. S. (2021). Uncertainty of Intensity-Duration-Frequency Curves Due to Adoption or Otherwise of the Temperature Climate Variable in Rainfall Disaggregation. Water, 13(17), 2337. https://doi.org/10.3390/w13172337







