Design and Simulation of Stormwater Control Measures Using Automated Modeling
Abstract
1. Introduction
- To develop a library of components for modeling RR and SCMs, compliant with the equation discovery tool ProBMoT (Process-Based Modeling Tool) [32];
- To apply the proposed automated model discovery approach to find the optimal RR model for an urban sub-catchment in the city of Ljubljana, Slovenia, which best fits the available pipe flow measurements;
- To find an optimal design of SCMs that would best fit the target catchment outflow.
2. Data and Methods
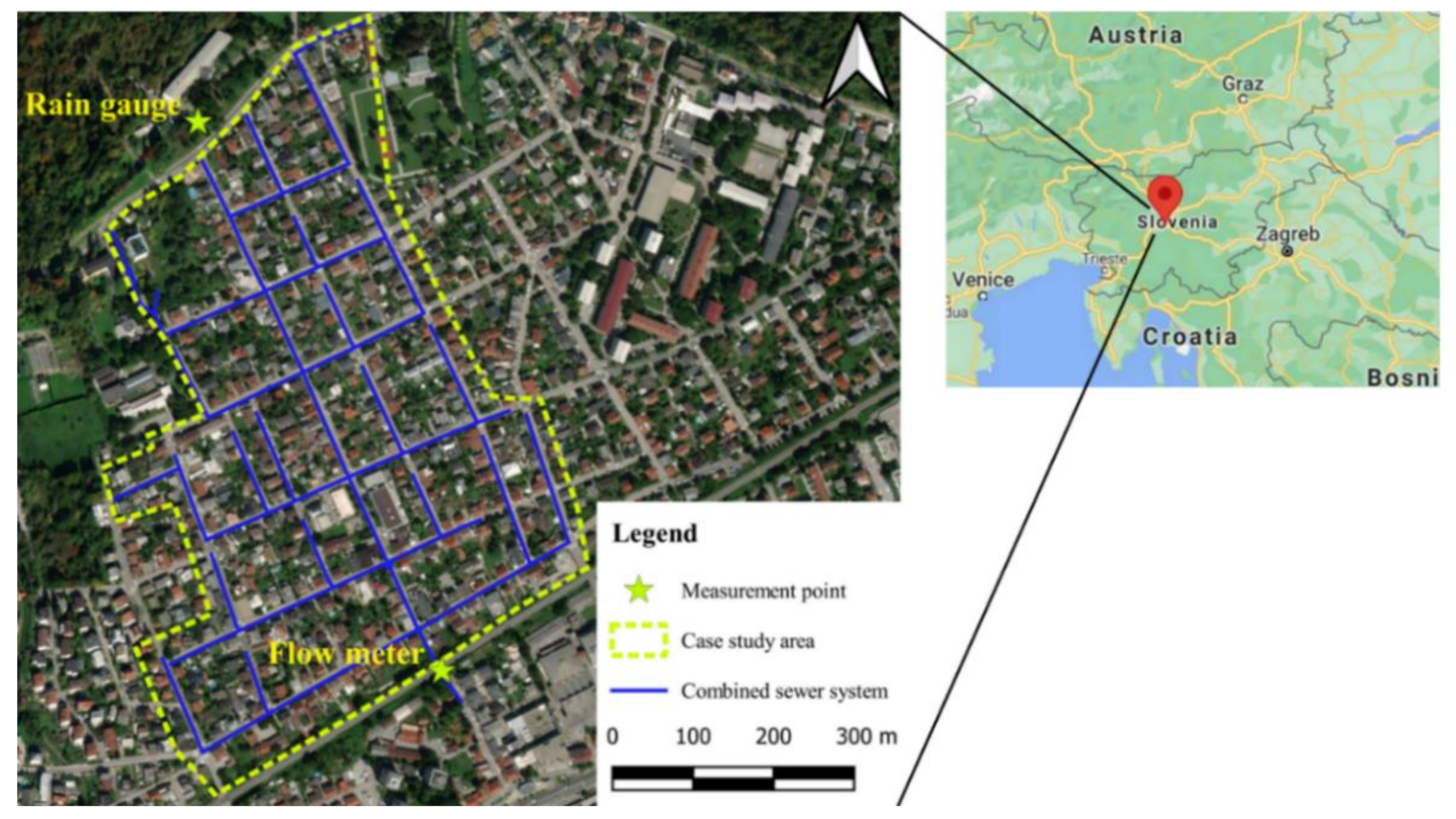
2.1. Case Study Area
2.2. Data
2.3. Rainfall-Runoff Model
2.3.1. SCS CN Method
2.3.2. Variable UK Runoff Equation
2.3.3. UK Water Industry Research Runoff Equation
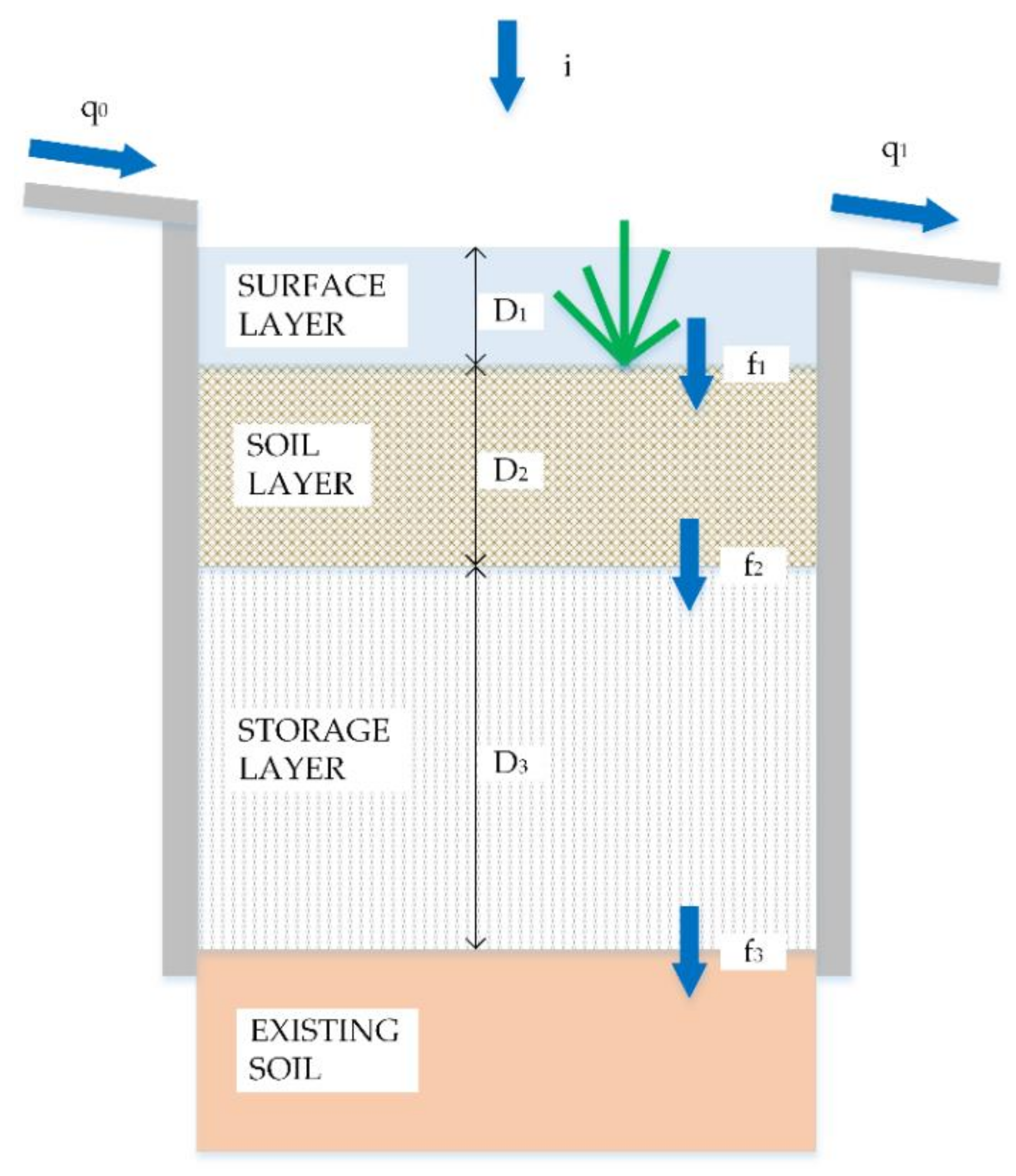
2.4. Stormwater Control Measures
2.4.1. Bio-Retention Cell
2.4.2. Rain Garden
2.4.3. Green Roof
2.4.4. Infiltration Trench
2.4.5. Detention Pond and Storage Tank
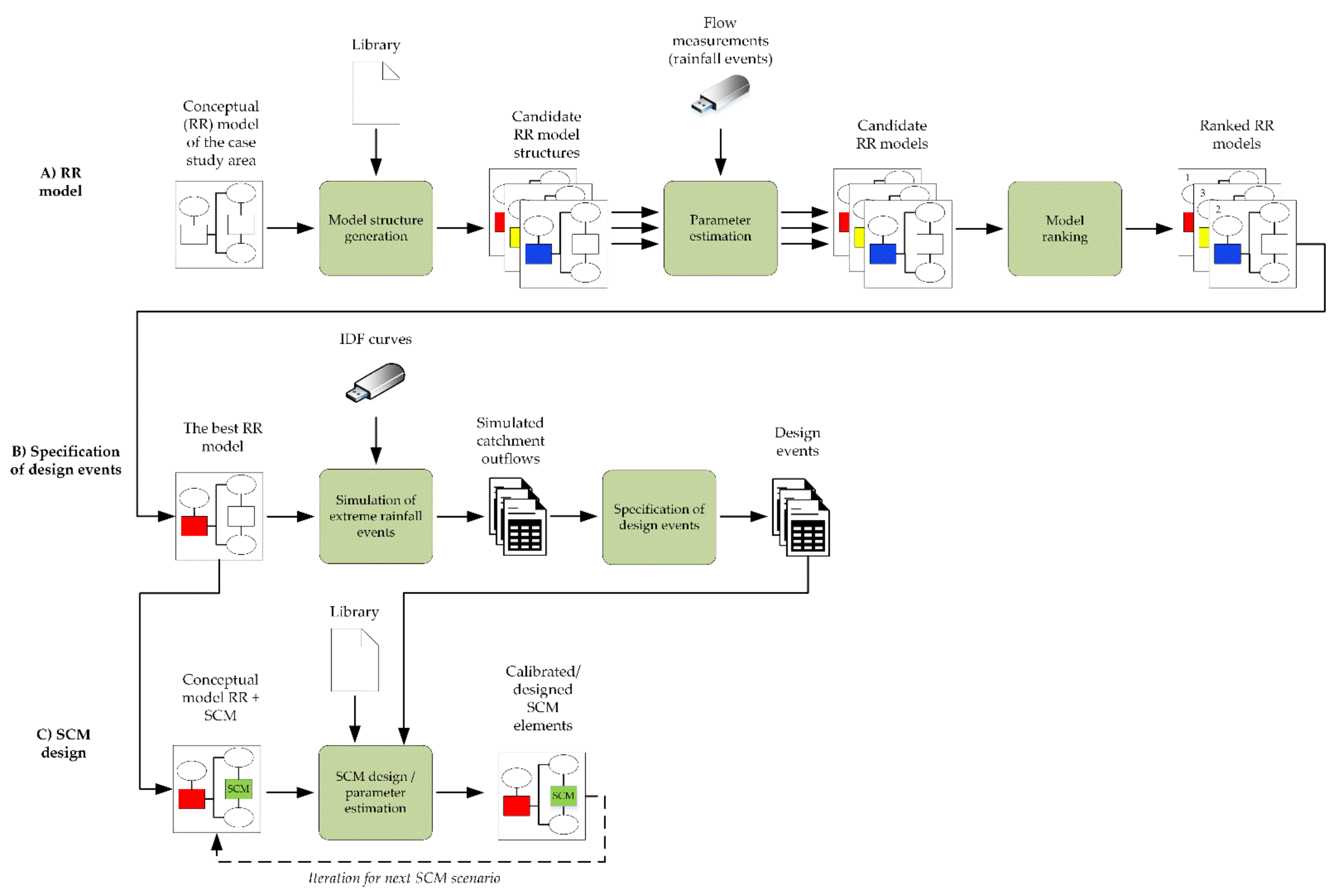
2.5. Equation Discovery and Process-Based Modeling
- (A.1)
- The RR models and SCM processes were encoded in a modeling library;
- (A.2)
- Conceptual models of the case study and SCM scenarios were elaborated;
- (A.3)
- ProBMoT was used to discover the optimal model structure and parameters among viable RR models, following the conceptual model of the case study and flow measurements;
- (B.1)
- The RR model with the best performance was used to simulate catchment outflow for rainfall events with a duration of 1 h and return periods of 5, 10, 25, and 50 years;
- (B.2)
- Three design events (i.e., data sets) that represent target catchment outflows were defined. The target outflow of precipitation (with a return period of 10, 25, or 50 years) was set to be the outflow typical for a 5-year return period;
- (C.1)
- ProBMoT was used to determine the optimal SCM parameters (i.e., SCM design), following the conceptual model for each SCM scenario and target catchment outflow (i.e., outflow reduction);
- (C.2)
- To determine the best SCM design, the conceptual models for SCMs were iteratively changed, based on the preliminary results of SCM design.
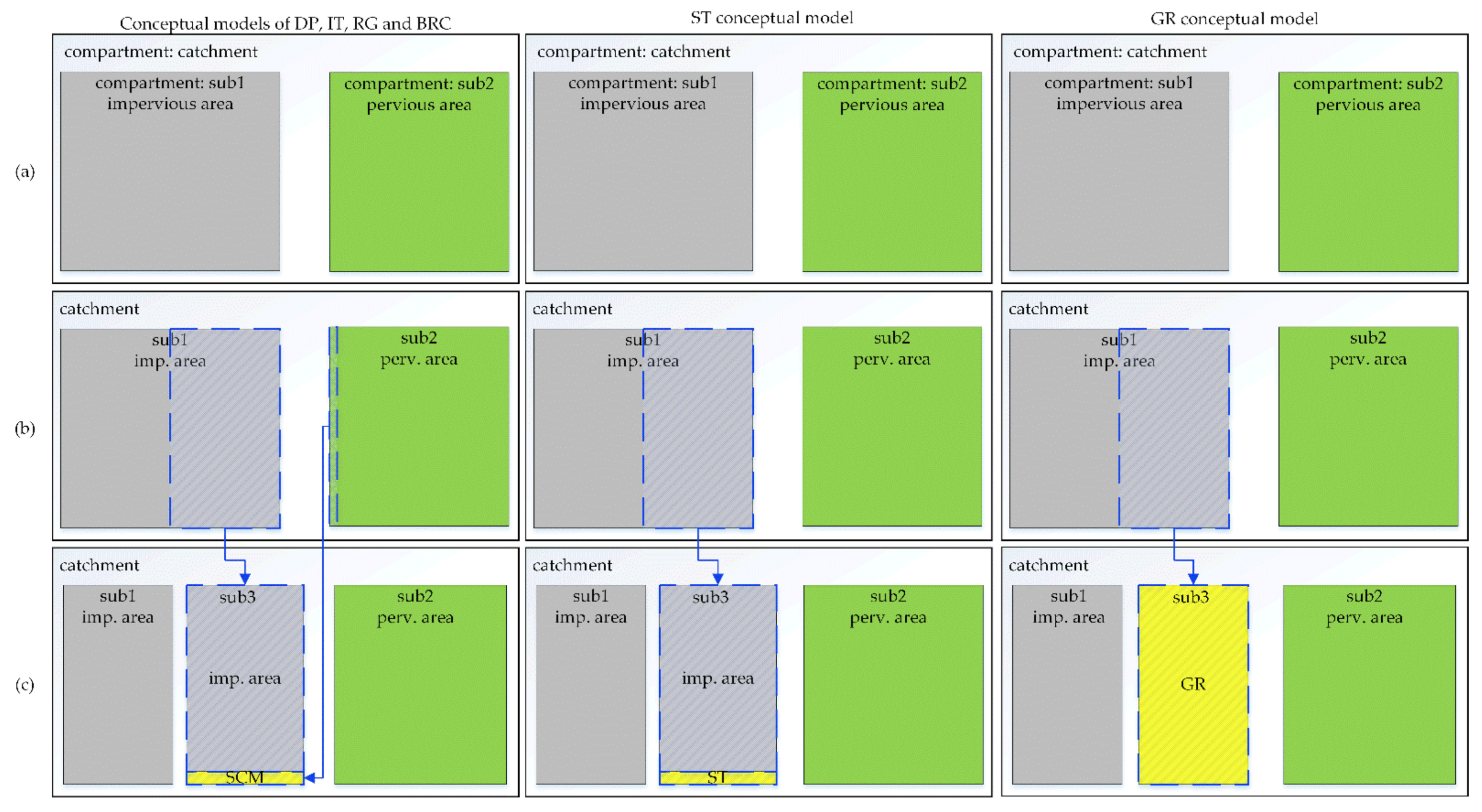
2.5.1. Library of Components for Modeling Rainfall-Runoff and Stormwater Control Measures
2.5.2. Conceptual Models of the Case Study Area and Stormwater Control Measures
3. Results
3.1. Rainfall-Runoff Models
3.2. Stormwater Control Measures
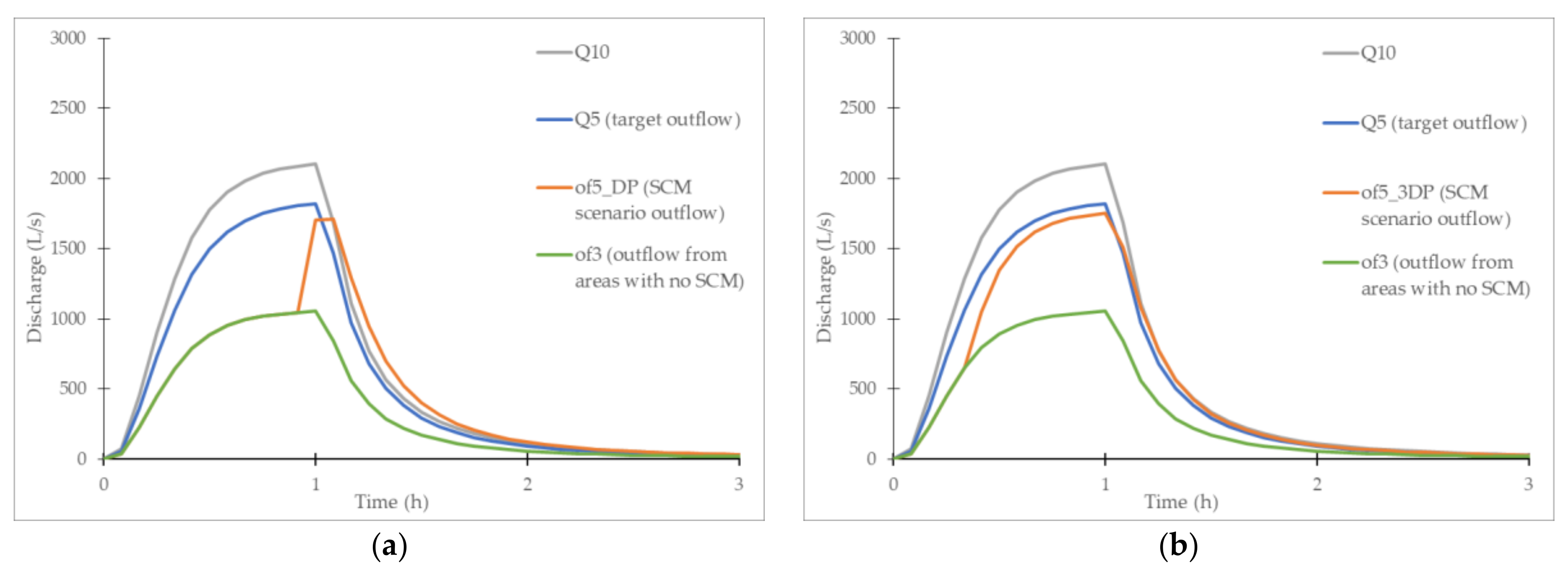
3.2.1. Detention Pond and Storage Tank
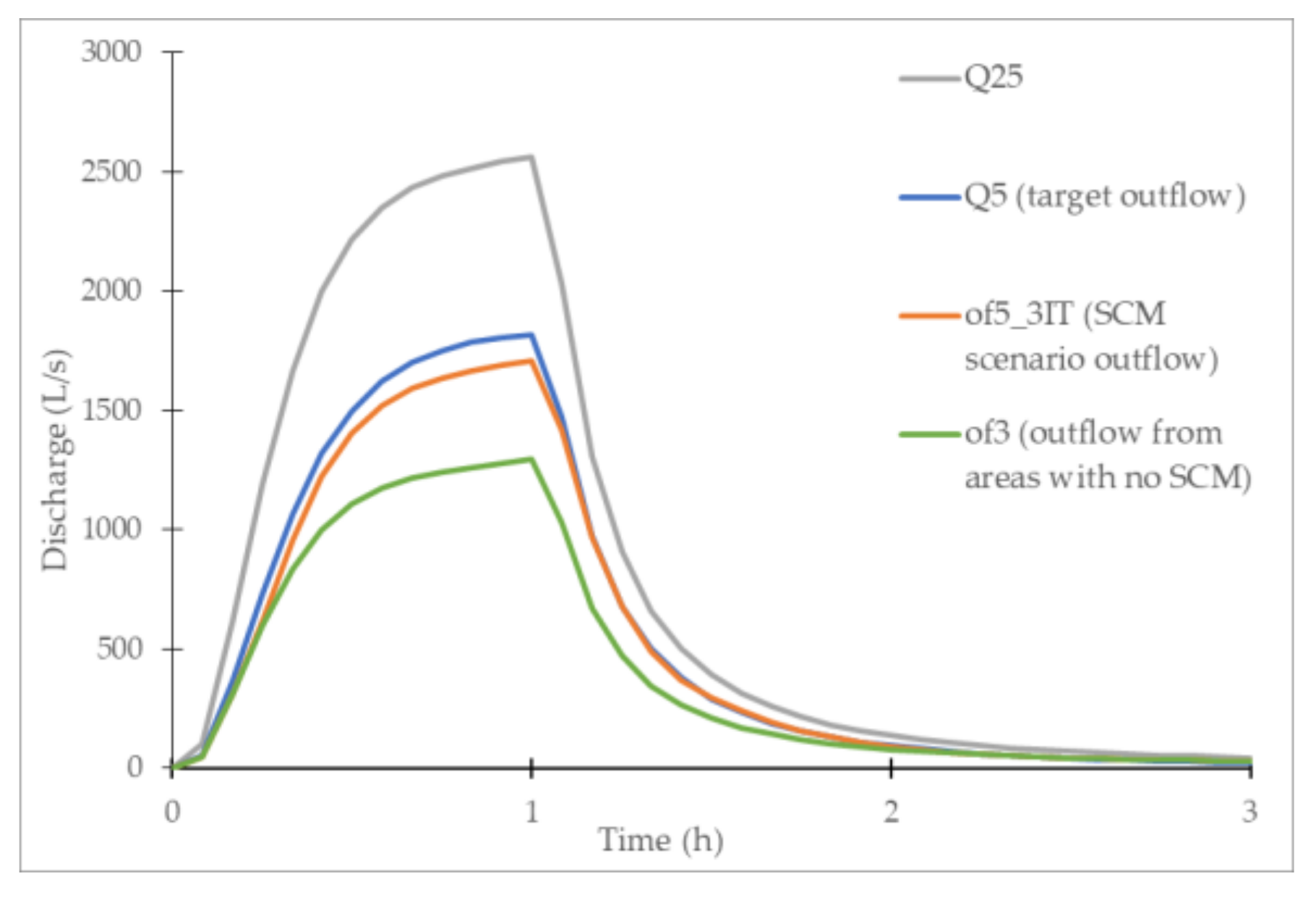
3.2.2. Infiltration Trench
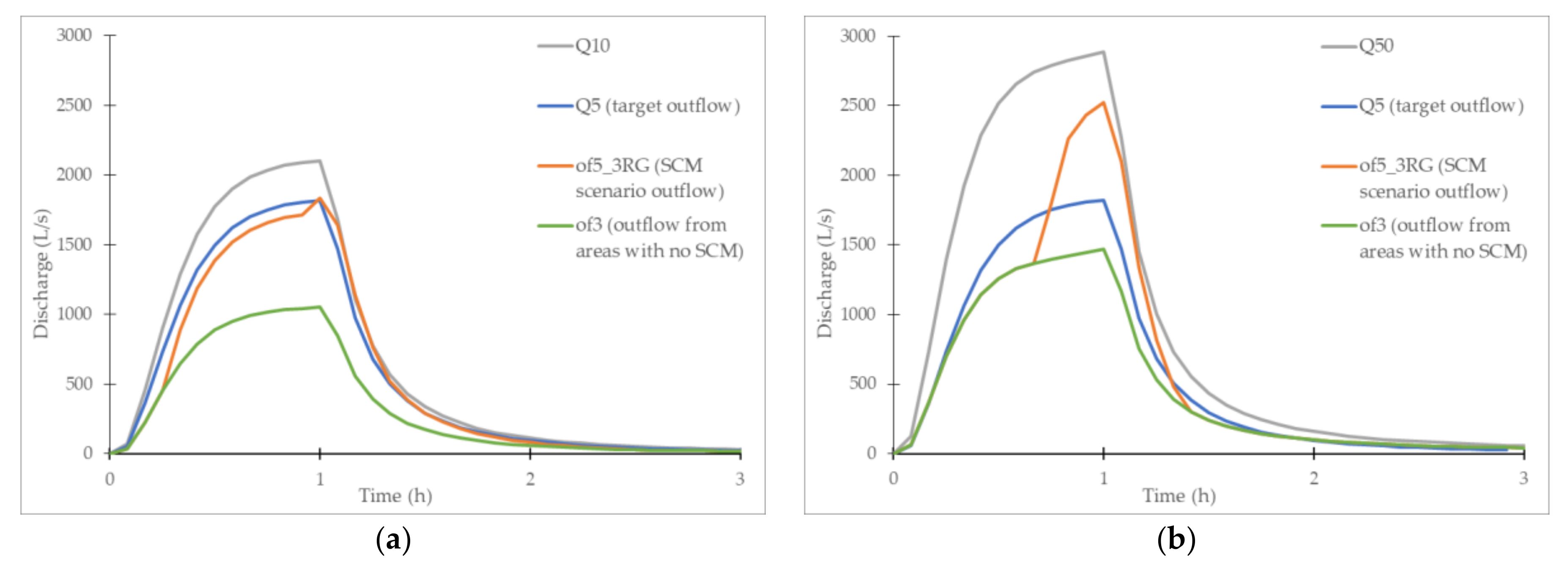
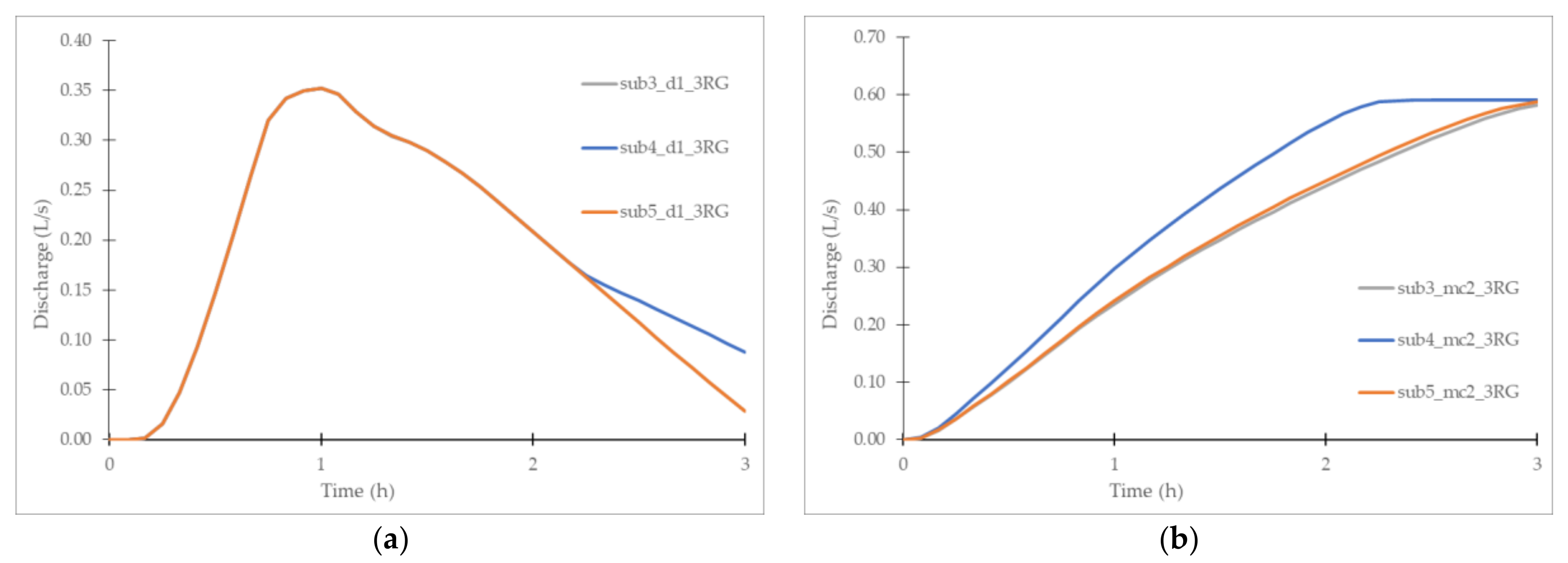
3.2.3. Rain Garden and Bio-Retention Cell
3.2.4. Green Roof
3.2.5. Stormwater Control Measures Performance
4. Discussion
4.1. Rainfall-Runoff Models
4.2. Stormwater Control Measures
5. Conclusions
- The proposed automated model discovery approach for finding the optimal RR models proved to be very efficient. Nine RR models were considered that generally had »very good« performance. The best performance was achieved by two models that used a combination of two different infiltration methods;
- The proposed automated model discovery approach enabled the design of six SCM scenarios and the assessment of their ability to achieve the target outflow;
- Detention ponds (DPs) and storage tanks (STs) provided comparable results. Namely, a near-perfect match between the target and simulated outflow was achieved for both measures (i.e., NSE value of 0.99). These are the two most space-efficient measures, with an average area of approx. 1000 m2);
- Infiltration trenches (ITs) achieved a good fit between the target and simulated outflow (i.e., NSE value of 0.99). When compared to ST and DP, these elements on average take 2.5 times more space, due to smaller maximum depth, smaller maximum voids fraction and limited infiltration rate of the existing soil;
- RGs and BRCs provided similar results, as they are both limited by the soil’s saturated hydraulic conductivity (i.e., parameter K2S). Therefore, both measures performed well only for the design event with the lowest intensity. Among the SCMs that are placed within existing pervious areas, these two SCM types take up the most space;
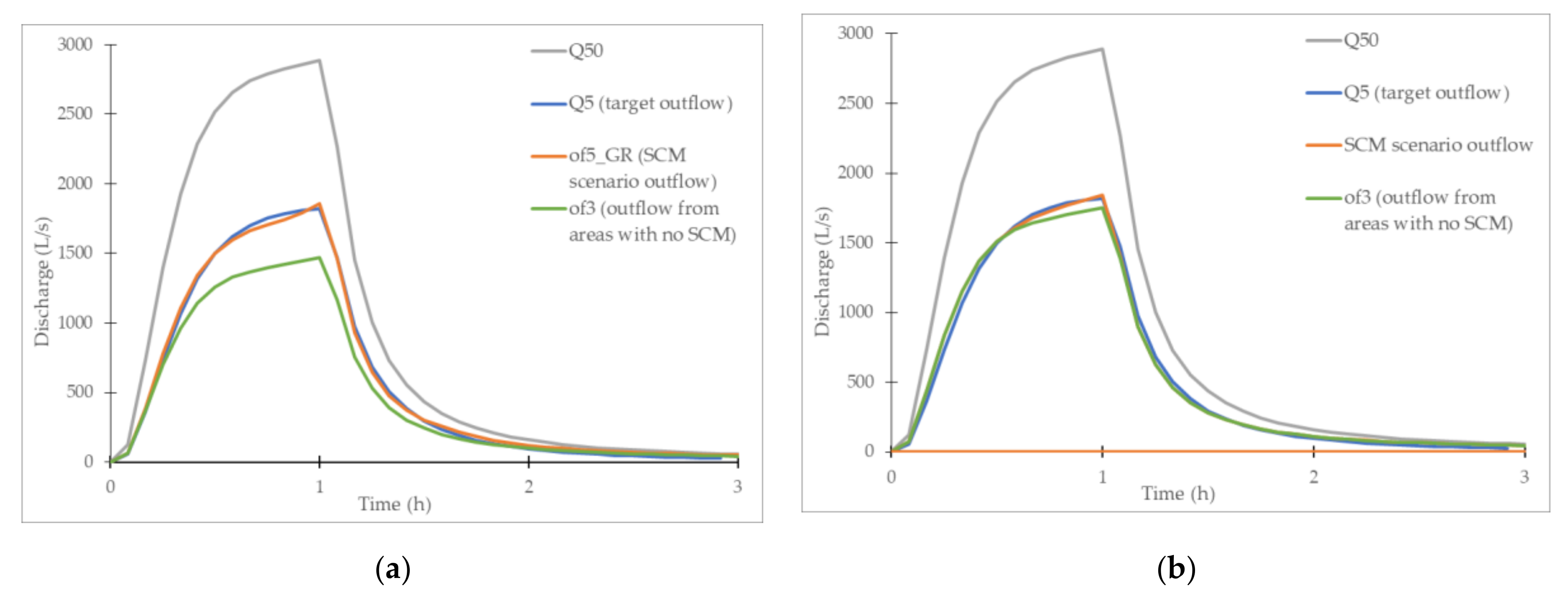
- The changes in the GR area have a direct influence on the size of the impervious area. Thus, the optimal GR area depends on the outflow from impervious and pervious areas. The outflow from impervious and pervious areas for the design event with a return period of 50 years almost matches the target outflow (i.e., Q5), if GRs replaced 40% of existing impervious areas.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | sub1 | sub2 | |
| SCS CN | SCS CN | UKWIR | SCS CN | VARUK | SCS CN | SCS CN | UKWIR | UKWIR | UKWIR | VARUK | UKWIR | SCS CN | VARUK | UKWIR | VARUK | VARUK | VARUK | |
| A | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 | 180,000 | 120,000 |
| S | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| W | 6092 | 3538 | 6083 | 5857 | 6000 | 5016 | 6000 | 3000 | 6033 | 6000 | 6141 | 6000 | 6112 | 3991 | 6103 | 5537 | 6164 | 6000 |
| ds | 0.0001 | 0.0060 | 0.0002 | 0.0005 | 0.0002 | 0.0048 | 0.0001 | 0.0060 | 0.0002 | 0.0026 | 0.0002 | 0.0014 | 0.0001 | 0.0005 | 0.0002 | 0.0018 | 0.0001 | 0.0017 |
| n | 0.08 | 0.67 | 0.08 | 0.15 | 0.08 | 0.75 | 0.08 | 0.25 | 0.08 | 0.15 | 0.08 | 0.15 | 0.08 | 0.26 | 0.08 | 0.15 | 0.08 | 0.18 |
| CN | 99 | 50 | null | 56 | null | 50 | 99 | null | null | null | null | null | 99 | null | null | null | null | null |
| PIMP | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 |
| IF | null | null | 0.90 | null | 0.85 | null | null | 0.75 | 0.83 | 0.78 | 0.81 | 0.90 | null | 0.75 | 0.88 | 0.83 | 0.83 | 0.76 |
| B | null | null | 0.72 | null | null | null | null | 0.77 | 0.69 | 0.50 | null | 0.74 | null | null | 0.50 | null | null | null |
| PIimp | null | null | 1.00 | null | null | null | null | 1.00 | 1.00 | 0.42 | null | 1.00 | null | null | 0.64 | null | null | null |
| PFimp | null | null | 11.16 | null | null | null | null | 11.70 | 13.02 | 10.00 | null | 12.62 | null | null | 12.20 | null | null | null |
| NAPI | null | null | 17.36 | null | 25.00 | null | null | 12.11 | 14.97 | 27.55 | 30.00 | 26.94 | null | 12.91 | 30.00 | 30.00 | 12.00 | 30.00 |
| PIp | null | null | 0.90 | null | null | null | null | 0.88 | 0.75 | 0.74 | null | 0.77 | null | null | 0.70 | null | null | null |
| Cr | null | null | 1.00 | null | null | null | null | 0.80 | 0.98 | 0.86 | null | 0.85 | null | null | 0.82 | null | null | null |
| SPR | null | null | 0.35 | null | null | null | null | 0.68 | 0.10 | 0.66 | null | 0.56 | null | null | 0.70 | null | null | null |
| PFp | null | null | 58.25 | null | 32.35 | null | null | 30.00 | 100.00 | 30.00 | 60.96 | 42.27 | null | 100.00 | 100.00 | 100.00 | 50.74 | 100.00 |
| 3ST | Results | ||||||
|---|---|---|---|---|---|---|---|
| A | D1 | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 250 | 0.50 | 0.97 | 0.94 | 0.96 |
| Sub4 | 364 | 4.70 | |||||
| Sub5 | 250 | 0.50 | |||||
| DE_Q5_P25 | Sub3 | 431 | 4.93 | 0.99 | 0.95 | 0.94 | |
| Sub4 | 499 | 3.99 | |||||
| Sub5 | 250 | 0.50 | |||||
| DE_Q5_P50 | Sub3 | 408 | 0.53 | 0.99 | 1.07 | 1.07 | |
| Sub4 | 462 | 5.00 | |||||
| Sub5 | 500 | 4.84 | |||||
| 3DP | Results | ||||||
|---|---|---|---|---|---|---|---|
| A | D1 | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 101 | 0.50 | 0.97 | 0.94 | 0.96 |
| Sub4 | 100 | 0.50 | |||||
| Sub5 | 500 | 5.00 | |||||
| DE_Q5_P25 | Sub3 | 497 | 4.89 | 0.99 | 0.95 | 0.94 | |
| Sub4 | 100 | 0.50 | |||||
| Sub5 | 500 | 5.00 | |||||
| DE_Q5_P50 | Sub3 | 471 | 4.90 | 0.99 | 1.07 | 1.07 | |
| Sub4 | 391 | 5.00 | |||||
| Sub5 | 100 | 2.16 | |||||
| 3IT | Results | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | D1 | D3 | VF1 | VF3 | K3S | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 983 | 0.26 | 3.50 | 1.00 | 0.39 | 2.6 × 10−5 | 0.98 | 0.92 | 0.95 |
| Sub4 | 100 | 0.00 | 0.90 | 1.00 | 0.20 | 2.6 × 10−5 | |||||
| Sub5 | 100 | 0.00 | 0.90 | 1.00 | 0.20 | 2.6 × 10−5 | |||||
| DE_Q5_P25 | Sub3 | 979 | 0.16 | 3.15 | 1.00 | 0.40 | 2.6 × 10−5 | 0.99 | 0.94 | 0.94 | |
| Sub4 | 100 | 0.00 | 0.90 | 1.00 | 0.20 | 2.6 × 10−5 | |||||
| Sub5 | 977 | 0.28 | 2.92 | 1.00 | 0.39 | 2.6 × 10−5 | |||||
| DE_Q5_P50 | Sub3 | 964 | 0.30 | 3.42 | 1.00 | 0.40 | 2.6 × 10−5 | 0.99 | 1.05 | 1.06 | |
| Sub4 | 951 | 0.29 | 3.50 | 1.00 | 0.39 | 2.6 × 10−5 | |||||
| Sub5 | 1000 | 0.00 | 1.01 | 1.00 | 0.21 | 2.6 × 10−5 | |||||
| 3RG | Results | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | D1 | D2 | D3 | VF1 | VF2 | VF3 | K2S | K3S | SH2 | HCO | IMC2 | FC | af_max | af_k | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 500 | 0.10 | 0.77 | null | 0.80 | 0.45 | null | 1.4 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.98 | 0.95 | 1.01 |
| Sub4 | 500 | 0.10 | 0.87 | null | 0.80 | 0.45 | null | 1.4 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 1.02 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P25 | Sub3 | 743 | 0.10 | 0.60 | null | 0.80 | 0.50 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.96 | 1.03 | 1.24 | |
| Sub4 | 2000 | 0.30 | 0.68 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 1.20 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P50 | Sub3 | 2000 | 0.30 | 1.03 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.87 | 1.08 | 1.38 | |
| Sub4 | 2000 | 0.30 | 0.82 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 1.01 | null | 0.80 | 0.60 | null | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| 3BRC | Results | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | D1 | D2 | D3 | VF1 | VF2 | VF3 | K2S | K3S | SH2 | HCO | IMC2 | FC | af_max | af_k | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 500 | 0.10 | 0.60 | 0.15 | 0.80 | 0.45 | 0.23 | 1.4 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.99 | 0.93 | 0.95 |
| Sub4 | 500 | 0.10 | 0.63 | 0.90 | 0.80 | 0.45 | 0.20 | 1.4 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 0.69 | 0.90 | 1.00 | 0.60 | 0.26 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P25 | Sub3 | 500 | 0.10 | 0.69 | 0.90 | 0.80 | 0.45 | 0.29 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.97 | 1.01 | 1.17 | |
| Sub4 | 2000 | 0.30 | 0.76 | 0.30 | 1.00 | 0.60 | 0.40 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 1.15 | 0.90 | 1.00 | 0.60 | 0.23 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P50 | Sub3 | 2000 | 0.12 | 0.66 | 0.27 | 0.80 | 0.60 | 0.37 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 0.91 | 1.10 | 1.37 | |
| Sub4 | 2000 | 0.30 | 0.88 | 0.65 | 1.00 | 0.60 | 0.36 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 2000 | 0.30 | 0.94 | 0.46 | 1.00 | 0.60 | 0.40 | 3.9 × 10−5 | 2.6 × 10−5 | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| 3GR | Results | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | width | slope | n1 | n3 | D1 | D2 | D3 | VF1 | VF2 | VF3 | K2S | K3S | SH2 | HCO | IMC2 | FC | af_max | af_k | NSE | TVR | PFR | |||
| Design event | DE_Q5_P10 | Sub3 | 24,000 | 2400 | 0.02 | 0.180 | 0.023 | 0.000 | 0.050 | 0.050 | 0.99 | 0.45 | 0.40 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 1.00 | 0.99 | 1.02 |
| Sub4 | 24,000 | 2400 | 0.02 | 0.174 | 0.020 | 0.000 | 0.050 | 0.019 | 0.99 | 0.45 | 0.40 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 24,000 | 2400 | 0.02 | 0.188 | 0.019 | 0.000 | 0.050 | 0.013 | 1.00 | 0.45 | 0.34 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P25 | Sub3 | 24,000 | 2400 | 0.02 | 0.206 | 0.020 | 0.066 | 0.142 | 0.041 | 0.87 | 0.60 | 0.21 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 1.00 | 1.00 | 1.02 | |
| Sub4 | 24,000 | 2400 | 0.02 | 0.400 | 0.010 | 0.000 | 0.050 | 0.010 | 1.00 | 0.45 | 0.20 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 24,000 | 2400 | 0.02 | 0.149 | 0.010 | 0.068 | 0.144 | 0.035 | 0.80 | 0.58 | 0.20 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| DE_Q5_P50 | Sub3 | 24,000 | 2400 | 0.02 | 0.242 | 0.015 | 0.003 | 0.141 | 0.036 | 1.00 | 0.54 | 0.20 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | 1.00 | 1.01 | 1.001 | |
| Sub4 | 24,000 | 2400 | 0.02 | 0.304 | 0.030 | 0.036 | 0.139 | 0.026 | 0.87 | 0.60 | 0.24 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
| Sub5 | 24,000 | 2400 | 0.02 | 0.102 | 0.030 | 0.073 | 0.137 | 0.011 | 0.88 | 0.60 | 0.30 | 3 × 10−6 | null | 0.05 | 39.3 | 0.08 | 0.15 | 1.0 | 0.001 | |||||
References
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Versini, P.A.; Kotelnikova, N.; Poulhes, A.; Tchiguirinskaia, I.; Schertzer, D.; Leurent, F. A distributed modelling approach to assess the use of Blue and Green Infrastructures to fulfil stormwater management requirements. Landsc. Urban Plan. 2018, 173, 60–63. [Google Scholar] [CrossRef]
- Ellis, J.B.; Viavattene, C. Sustainable urban drainage system modeling for managing urban surface water flood risk. CLEAN Soil Air Water 2014, 42, 153–159. [Google Scholar] [CrossRef]
- Joshi, P.; Leitão, J.P.; Maurer, M.; Bach, P.M. Not all SuDS are created equal: Impact of different approaches on combined sewer overflows. Water Res. 2021, 191, 116780. [Google Scholar] [CrossRef]
- Zanin, G.; Bortolini, L. Performance of Three Different Native Plant Mixtures for Extensive Green Roofs in a Humid Subtropical Climate Context. Water 2020, 12, 3484. [Google Scholar] [CrossRef]
- Chen, X.; Peltier, E.; Sturm, B.S.M.; Young, C.B. Nitrogen removal and nitrifying and denitrifying bacteria quantification in a stormwater bioretention system. Water Res. 2013, 47, 1691–1700. [Google Scholar] [CrossRef]
- Petit-Boix, A.; Sevigné-Itoiz, E.; Rojas-Gutierrez, L.A.; Barbassa, A.P.; Josa, A.; Rieradevall, J.; Gabarrell, X. Environmental and economic assessment of a pilot stormwater infiltration system for flood prevention in Brazil. Ecol. Eng. 2015, 84, 194–201. [Google Scholar] [CrossRef]
- Alam, T.; Mahmoud, A.; Jones, K.D.; Bezares-Cruz, J.C.; Guerrero, J. A Comparison of Three Types of Permeable Pavements for Urban Runoff Mitigation in the Semi-Arid South Texas, U.S.A. Water 2019, 11, 1992. [Google Scholar] [CrossRef]
- Cannavo, P.; Coulon, A.; Charpentier, S.; Béchet, B.; Vidal-Beaudet, L. Water balance prediction in stormwater infiltration basins using 2-D modeling: An application to evaluate the clogging process. Int. J. Sediment Res. 2018, 33, 371–384. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Li, Y. Simulation and optimization of rain gardens via DRAINMOD model and response surface methodology. Ecohydrol. Hydrobiol. 2020, 20, 413–423. [Google Scholar] [CrossRef]
- Li, G.; Xiong, J.; Zhu, J.; Liu, Y.; Dzakpasu, M. Design influence and evaluation model of bioretention in rainwater treatment: A review. Sci. Total Environ. 2021, 787, 147592. [Google Scholar] [CrossRef]
- Yazdi, A.; Hamzehpour, H.; Sahimi, M. Permeability, porosity, and percolation of two-dimensional disordered fracture networks. Phys. Rev. E 2011, 84, 046347. [Google Scholar] [CrossRef]
- Parteli, E.J.R.; da Silva, L.R.; Andrade, J.S., Jr. Self-organized percolation in multi-layered structures. J. Stat. Mech. 2010, 46, P03023. [Google Scholar] [CrossRef]
- NRCS. Urban Hydrology for Small Watersheds TR-55; USDA: Washington, DC, USA, 1986. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1; United States Environmental Protection Agency: Washington, DC, USA, 2015; 353p. [Google Scholar]
- Li, Y.; Huang, J.J.; Hu, M.; Yang, H.; Tanaka, K. Design of low impact development in the urban context considering hydrological performance and life-cycle cost. J. Flood Risk Manag. 2020, 13, e12625. [Google Scholar] [CrossRef]
- Kong, F.; Ban, Y.; Yin, H.; James, P.; Dronova, I. Modeling stormwater management at the city district level in response to changes in land use and low impact development. Environ. Model. Softw. 2017, 95, 132–142. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I. Hydrologic modeling of Low Impact Development systems at the urban catchment scale. J. Hydrol. 2015, 528, 361–368. [Google Scholar] [CrossRef]
- Chui, T.F.M.; Liu, X.; Zhan, W. Assessing cost-effectiveness of specific LID practice designs in response to large storm events. J. Hydrol. 2016, 533, 353–364. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm Water Management Model: Performance Review and Gap Analysis. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef]
- Hu, Y.; Scavia, D.; Kerkez, B. Are all data useful? Inferring causality to predict flows across sewer and drainage systems using directed information and boosted regression trees. Water Res. 2018, 145, 697–706. [Google Scholar] [CrossRef]
- Perin, R.; Trigatti, M.; Nicolini, M.; Campolo, M.; Goi, D. Automated calibration of the EPA-SWMM model for a small suburban catchment using PEST: A case study. Environ. Monit. Assess. 2020, 192, 374. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Özger, M. An integrated framework for the comprehensive evaluation of low impact development strategies. J. Environ. Manag. 2021, 294, 113023. [Google Scholar] [CrossRef]
- Shahed Behrouz, M.; Zhu, Z.; Matott, L.S.; Rabideau, A.J. A new tool for automatic calibration of the Storm Water Management Model (SWMM). J. Hydrol. 2020, 581, 124436. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, Z.; Chen, X.; Yu, G. An assessment of the hydrologic effectiveness of low impact development (LID) practices for managing runoff with different objectives. J. Environ. Manag. 2019, 231, 504–514. [Google Scholar] [CrossRef]
- Doherty, J.; Hunt, R.; Tonkin, M. Approaches to highly parameterized inversion: A guide to using PEST for model-parameter and predictive-uncertainty analysis. US Geol. Surv. Sci. Investig. Rep. 2011, 2010, 71. [Google Scholar]
- Džeroski, S.; Todorovski, L. Equation discovery for systems biology: Finding the structure and dynamics of biological networks from time course data. Curr. Opin. Biotechnol. 2008, 19, 360–368. [Google Scholar] [CrossRef] [PubMed]
- Atanasova, N.; Todorovski, L.; Džeroski, S.; Kompare, B. Constructing a library of domain knowledge for automated modelling of aquatic ecosystems. Ecol. Modell. 2006, 194, 14–36. [Google Scholar] [CrossRef]
- Škerjanec, M.; Atanasova, N.; Čerepnalkoski, D.; Džeroski, S.; Kompare, B. Development of a knowledge library for automated watershed modeling. Environ. Model. Softw. 2014, 54, 60–72. [Google Scholar] [CrossRef]
- Tanevski, J.; Todorovski, L.; Džeroski, S. Process-based design of dynamical biological systems. Sci. Rep. 2016, 6, 34107. [Google Scholar] [CrossRef]
- Simidjievski, N.; Todorovski, L.; Kocijan, J.; Džeroski, S. Equation Discovery for Nonlinear System Identification. IEEE Access 2020, 8, 29930–29943. [Google Scholar] [CrossRef]
- Džeroski, S.; Todorovski, L.; Čerepnalkoski, D.; Tanevski, J.; Simidjievski, N. Process-Based Modeling Tool (ProBMoT). Available online: http://probmot.ijs.si/ (accessed on 7 January 2019).
- Slovenian Environment Agency. Temperature and Condition of Soil. Available online: http://meteo.arso.gov.si/met/sl/agromet/recent/tsoil (accessed on 5 July 2018).
- Slovenian Forestry Institute. Slovenian Forestry Institute Database of the Slovenian Forestry Institute 2018–2019; Web application eEMIS® 2019; Slovenian Forestry Institute: Ljubljana, Slovenia, 2019. [Google Scholar]
- Onset Computer Corporation Davis® (0.01′′ or 0.2 mm) Rain Gauge Smart Sensor (S-RGC-M002, S-RGD-M002) Manual. Available online: https://www.onsetcomp.com/files/manual_pdfs/19878-A%20MAN-S-RGCD.pdf (accessed on 18 June 2020).
- Slovenian Environment Agency IDF Curves—Ljubljana. Available online: https://meteo.arso.gov.si/uploads/probase/www/climate/table/sl/by_variable/return-periods/Ljubljana%20Bezigrad.pdf (accessed on 5 July 2018).
- Raven-Eye Non-Contact Radar Flow Measuring System. Available online: http://www.trilobit.si/files/2_Tec-Spec%20RAVEN-EYE%20EN.pdf (accessed on 18 August 2020).
- Mannina, G.; Viviani, G. An urban drainage stormwater quality model: Model development and uncertainty quantification. J. Hydrol. 2010, 381, 248–265. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, L.; Shen, Z. A cellular automata (CA)-based method to improve the SWMM performance with scarce drainage data and its spatial scale effect. J. Hydrol. 2020, 581, 124402. [Google Scholar] [CrossRef]
- Butler, D.; Digman, C.J.; Makropoulos, C.; Davies, W.J. Urban Drainage, 4th ed.; Taylor & Francis e-Library: Boca Raton, FL, USA, 2018; ISBN 9788578110796. [Google Scholar]
- Packman, J.C. New hydrology model. In Proceedings of the WaPUG Conference, Glasgow, UK, 24 April 1990. [Google Scholar]
- Kellagher, R. A Guide to the Use of the UKWIR Runoff Equation; UK Water Industry Research: London, UK, 2014. [Google Scholar]
- Čerepnalkoski, D.; Taškova, K.; Todorovski, L.; Atanasova, N.; Džeroski, S. The influence of parameter fitting methods on model structure selection in automated modeling of aquatic ecosystems. Ecol. Modell. 2012, 245, 136–165. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.L.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Broekhuizen, I.; Leonhardt, G.; Marsalek, J.; Viklander, M. Event selection and two-stage approach for calibrating models of green urban drainage systems. Hydrol. Earth Syst. Sci. 2020, 24, 869–885. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
| Period ID | Rainfall Period —Start | Rainfall Period —End | Duration (h) | Season | Total Precipitation (mm) | Total Precipitation Time (h) | Average Precipitation Intensity (mm/5 min) | Total Measured Flow (m3) | Measured Peak Flow (L/s) |
|---|---|---|---|---|---|---|---|---|---|
| C1_1D | 01.12.2019 (23:00) | 02.12.2019 (19:00) | 20 | Autumn | 24.4 | 8.3 | 0.24 | 8948 | 278 |
| C2_1D | 15.05.2020 (05:00) | 16.05.2020 (03:00) | 22 | Spring | 29.6 | 7.3 | 0.34 | 7409 | 442 |
| C3_6D | 23.04.2019 (04:30) | 29.04.2019 (04:30) | 144 | Spring | 39.8 | 13.6 | 0.24 | 6562 | 308 |
| C4_7D | 11.11.2019 (12:30) | 18.11.2019 (11:30) | 167 | Autumn | 74.4 | 25.3 | 0.25 | 20,938 | 555 |
| V1_1D | 31.08.2020 (12:00) | 01.09.2020 (11:00) | 23 | Summer | 20.8 | 7.8 | 0.22 | 5417 | 238 |
| V2_2D | 21.12.2019 (08:00) | 23.12.2019 (02:00) | 42 | Winter | 56.4 | 14.3 | 0.33 | 17.045 | 429 |
| V3_5D | 28.09.2019 (12:00) | 03.10.2019 (01:00) | 109 | Autumn | 38.8 | 8.5 | 0.38 | 7.854 | 283 |
| V4_5D | 01.03.2020 (07:00) | 06.03.2020 (15:00) | 128 | Winter | 81 | 26.1 | 0.26 | 19,578 | 301 |
| Variables | |||
|---|---|---|---|
| SCS CN, VARUK, UKWIR Name | ProBMoT Name | Description | Unit |
| d | d | surface storage (ponded water) | m |
| i | i | rate of rainfall | m/s |
| f | f | infiltration rate | m/s |
| q | q | runoff flow rate per unit of surface area | m/s |
| * | cumulative infiltration at the beginning of a time step Δt | m | |
| * | cumulative infiltration at the end of a time step Δt | m | |
| F | * | cumulative infiltration | mm |
| P | p1, p2 | cumulative precipitation | mm |
| * | maximum storage capacity of soil | mm | |
| PR | * | percentage runoff for the model | |
| Constants | |||||
|---|---|---|---|---|---|
| SCS CN, VARUK, UKWIR Name | ProBMoT Name | Description | Unit | Range | |
| IMP. | PERV. | ||||
| A | A | surface area of the sub-catchment | m2 | 180,000 | 120,000 |
| W | W | sub-catchment width | m | 6000–18,000 | 3000–6000 |
| S | S | average slope of the sub-catchment | m/m | 0.002 | 0.002 |
| ds | depression storage depth | m | 0.00005–0.001 | 0.0005–0.006 | |
| n | n | the surface roughness coefficient | 0.01–0.08 | 0.15–0.80 | |
| Δt | time step | s | 300 | 300 | |
| CN | CN | tabulated coefficient that varies with the land use and soil type | 90–99 | 30–75 | |
| PIMP | percentage of imperviousness | 100 | 0 | ||
| IF | effective impermeability factor for a particular paved surface type | 0.5–1 | / | ||
| β | B | power coefficient for a paved surface | 0.5–0.8 | / | |
| PIimp | precipitation index for paved surfaces with a rapid decay coefficient | 0–1 | / | ||
| PFimp | soil store depth for a paved surface | mm | 10–15 | / | |
| NAPI | antecedent precipitation index for a particular pervious surface type | mm | / | 0–40 | |
| PIp | precipitation index for pervious surface with a decay coefficient | / | 0.7–0.9 | ||
| Cr | Cr | power coefficient for pervious surface | / | 0.8–1.0 | |
| SPR | SPR | standard percentage runoff | / | 0.1–0.7 | |
| PFp | soil storage depth for a particular pervious surface type | mm | / | 30–50 | |
| Variables | |||
|---|---|---|---|
| EPA-SWMM Name | ProBMoT Name | Description | Unit |
| d1 | depth of water stored on the surface | m | |
| d3 | depth of water in the storage layer | m | |
| mc2 | soil layer moisture content (volume of water/total volume of soil) | fraction | |
| i | i | precipitation rate falling directly on the surface layer | m/s |
| q0 | inflow to the surface layer from runoff captured from other areas | m/s | |
| q1 | surface layer runoff or overflow rate | m/s | |
| f1 | infiltration rate of surface water into the soil layer | m/s | |
| f2 | percolation rate of water through the soil layer into the storage layer | m/s | |
| f3 | exfiltration of water from the storage layer into native soil | m/s | |
| Constants | |||||
|---|---|---|---|---|---|
| EPA-SWMM Name | ProBMoT Name | Description | Unit | Range | |
| Minimum | Maximum | ||||
| A | A | surface area | m2 | 0 | ꚙ |
| W | W | surface width | m | 5000 | 10,000 |
| S | S | surface slope | m/m | 0.02 | 0.15 |
| n1 | surface roughness coeff. | s/m1/3 | 0.10 | 0.40 | |
| n3 | drainage mat roughness coeff. | s/m1/3 | 0.01 | 0.03 | |
| D1 | freeboard height for surface ponding | m | 0.00 | 5.0 | |
| D2 | thickness of the soil layer | m | 0.05 | 1.22 | |
| D3 | thickness of the storage layer | m | 0.01 | 3.66 | |
| VF1 | void fraction of any surface volume (i.e., the fraction of freeboard above the surface not filled with vegetation) | fraction | 0.80 | 1.00 | |
| VF2 | porosity of the soil layer (void volume/total volume) | fraction | 0.45 | 0.60 | |
| VF3 | void fraction of the storage layer (void volume/total volume) | fraction | 0.20 | 0.40 | |
| K2S | soil’s saturated hydraulic conductivity | m/s | 3 × 10−6 | 3.88 × 10−5 | |
| K3S | native soil’s saturated hydraulic conductivity | m/s | 1 × 10−5 | 8.20 × 10−5 | |
| SH2 | suction head at the infiltration wetting front formed in the soil | m | 0.05 | 0.10 | |
| HCO | HCO | percolation decay constant | / | 30.00 | 55.00 |
| IMC2 | soil’s initial moisture content or its wilting point | fraction | 0.05 | 0.20 | |
| FC | soil’s field capacity moisture content | fraction | 0.15 | 0.50 | |
| Model | Infiltration Method Sub 1 | Infiltration Method Sub 2 | C1_1D | C2_1D | C3_6D | C4_7D | V1_1D | V2_2D | V3_5D | V4_5D |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | SCS | SCS | 0.83 | 0.76 | 0.81 | 0.78 | 0.91 | 0.93 | 0.84 | 0.81 |
| M2 | UKWIR | SCS | 0.83 | 0.80 | 0.76 | 0.78 | 0.92 | 0.91 | 0.85 | 0.78 |
| M3 | VARUK | SCS | 0.82 | 0.81 | 0.78 | 0.78 | 0.93 | 0.93 | 0.85 | 0.81 |
| M4 | SCS | UKWIR | 0.84 | 0.77 | 0.81 | 0.77 | 0.91 | 0.92 | 0.84 | 0.83 |
| M5 | UKWIR | UKWIR | 0.89 | 0.76 | 0.71 | 0.80 | 0.89 | 0.88 | 0.77 | 0.79 |
| M6 | VARUK | UKWIR | 0.86 | 0.79 | 0.74 | 0.79 | 0.91 | 0.90 | 0.80 | 0.82 |
| M7 | SCS | VARUK | 0.87 | 0.75 | 0.76 | 0.78 | 0.90 | 0.90 | 0.80 | 0.81 |
| M8 | UKWIR | VARUK | 0.88 | 0.77 | 0.72 | 0.79 | 0.90 | 0.89 | 0.76 | 0.79 |
| M9 | VARUK | VARUK | 0.87 | 0.78 | 0.73 | 0.79 | 0.91 | 0.89 | 0.80 | 0.81 |
| Average: | 0.86 | 0.78 | 0.76 | 0.79 | 0.91 | 0.90 | 0.81 | 0.81 | ||
| Design Event | SCM Scenario | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3ST 1 | 3DP 2 | 3IT 3 | 3RG 4 | 3BRC 5 | 3GR 6 | |||||||
| TVR | PFR | TVR | PFR | TVR | PFR | TVR | PFR | TVR | PFR | TVR | PFR | |
| DE_Q5_P10 | 0.94 | 0.96 | 0.94 | 0.96 | 0.92 | 0.95 | 0.95 | 1.01 | 0.93 | 0.95 | 0.99 | 1.02 |
| DE_Q5_P25 | 0.95 | 0.94 | 0.95 | 0.94 | 0.94 | 0.94 | 1.03 | 1.24 | 1.01 | 1.17 | 1.00 | 1.02 |
| DE_Q5_P50 | 1.07 | 1.07 | 1.07 | 1.07 | 1.05 | 1.06 | 1.08 | 1.38 | 1.10 | 1.37 | 1.01 | 1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radinja, M.; Škerjanec, M.; Džeroski, S.; Todorovski, L.; Atanasova, N. Design and Simulation of Stormwater Control Measures Using Automated Modeling. Water 2021, 13, 2268. https://doi.org/10.3390/w13162268
Radinja M, Škerjanec M, Džeroski S, Todorovski L, Atanasova N. Design and Simulation of Stormwater Control Measures Using Automated Modeling. Water. 2021; 13(16):2268. https://doi.org/10.3390/w13162268
Chicago/Turabian StyleRadinja, Matej, Mateja Škerjanec, Sašo Džeroski, Ljupčo Todorovski, and Nataša Atanasova. 2021. "Design and Simulation of Stormwater Control Measures Using Automated Modeling" Water 13, no. 16: 2268. https://doi.org/10.3390/w13162268
APA StyleRadinja, M., Škerjanec, M., Džeroski, S., Todorovski, L., & Atanasova, N. (2021). Design and Simulation of Stormwater Control Measures Using Automated Modeling. Water, 13(16), 2268. https://doi.org/10.3390/w13162268







