Abstract
The quantitative prediction of hydrological components through hydrological models could serve as a basis for developing better land and water management policies. This study provides a comprehensive step by step modelling approach for a small agricultural watershed using the SWAT model. The watershed is situated in Petzenkirchen in the western part of Lower Austria and has total area of 66 hectares. At present, 87% of the catchment area is arable land, 5% is used as pasture, 6% is forested and 2% is paved. The calibration approach involves a sequential calibration of the model starting from surface runoff, and groundwater flow, followed by crop yields and then soil moisture, and finally total streamflow and sediment yields. Calibration and validation are carried out using the r-package SWATplusR. The impact of each calibration step on sediment yields and total streamflow is evaluated. The results of this approach are compared with those of the conventional model calibration approach, where all the parameters governing various hydrological processes are calibrated simultaneously. Results showed that the model was capable of successfully predicting surface runoff, groundwater flow, soil profile water content, total streamflow and sediment yields with Nash-Sutcliffe efficiency (NSE) of greater than 0.75. Crop yields were also well simulated with a percent bias (PBIAS) ranging from −17% to 14%. Surface runoff calibration had the highest impact on streamflow output, improving NSE from 0.39 to 0.77. The step-wise calibration approach performed better for streamflow prediction than the simultaneous calibration approach. The results of this study show that the step-wise calibration approach is more accurate, and provides a better representation of different hydrological components and processes than the simultaneous calibration approach.
1. Introduction
Hydrological models are becoming increasingly popular and necessary in hydrological studies because they serve as important time and cost-effective tools for simulating hydrological processes [1]. Models highlight the main drivers of hydrologic systems and therefore improve our understanding of the watersheds and contribute to the improvement and development in hydrologic management decisions. Moreover, models make it possible for users to manipulate system variables and provides a safe environment for testing different scenarios and management strategies which can play a major role in prevention of water-related natural disasters [2,3,4,5]. Since it is often not possible to acquire data at the required temporal and spatial scale, hydrological models provide a quick tool for estimating stream flow, sediment yield, nutrients and other parameters, thereby complementing field experiments and observations [6].
A variety of models have been successfully utilized in hydrological and soil erosion modelling. Among these models are the Water Erosion Prediction Project (WEPP) model [7], Agricultural Non-Point Source Pollution (AnnAGNPS) system [8] Areal Nonpoint Source Watershed Environment Response Simulation (ANSWERS) [9], Soil and Water Assessment Tool (SWAT) [10], MIKE-SHE [11] and Hydrological Simulation Program-Fortran (HSPF) [12]. These models are capable of representing appropriately spatial-temporal heterogeneity through a distributed or semi-distributed spatial discretization [13].
The Soil and Water Assessment Tool (SWAT) model [10] has been applied on a wide range of scales and watershed conditions to simulate streamflow and water yield across the world [14,15], and has proven to be an effective tool for assessing water resources and non-point source pollution problems [16,17,18]. The model has effectively been applied to simulate crop growth [19,20], river basin and hydrological modelling [21,22], sediment yields modelling [23,24], and soil water content assessment [17,25]. The SWAT model has been used extensively in hydrological modelling due to its computational efficiency and ability to predict long-term impacts [13].
The applicability of hydrologic models for the purpose of operational predictions depends on how well the model is calibrated [26]. Since hydrologic systems vary in time and space, calibration and validation processes are an integral part of hydrologic modelling. Model calibration attempts to adjust model parameters in such a way that the watershed response is closely and consistently approximated [2]. Model calibration and validation improves the model’s ability to correctly and reliably simulate hydrological processes. Various methods have been applied in model calibration and validation. Simultaneous and step by step calibration are the two most common ways of model calibration when there is more than one output and variable to be modelled [27].
Simultaneous flow calibration, which involves adjustment of multiple parameters concurrently, is by far the most commonly applied method. In this procedure, parameters influencing different flow components (groundwater flow, surface runoff, soil water movement and plant water uptake) are adjusted simultaneously in the ultimate stream flow output. Several studies have used simultaneous calibration for overall stream flow calibration [28,29,30]. The measure of fitness in the simultaneous calibration is therefore the model’s ability to correctly simulate the flow, and in that, an assumption is made that all the other hydrological processes are well estimated. On the other hand, in step-wise model calibration, parameter adjustment for hydrological components such as surface runoff, groundwater flow, crop yields and soil moisture are done separately in a sequential manner.
Amidst its widespread application, only a few studies have focused on step by step calibration of different hydrological components for the SWAT model. Santhi et al. [18] used an automated digital filter technique to separate groundwater flow from surface flow in their calibration process. Even though important in estimating surface runoff and nutrients cycling, crop yields are usually ignored in model calibrations [16,31]. Nair et al. [32] applied a four-stage approach in calibrating SWAT model. Their study found that including crop yields in the calibration process yielded better model performance. Sinnathamby et al. [19] also underlined the importance of plant growth parameter calibration in minimizing hydrological modelling errors. However, simulating crop yield remains a great challenge due to the limitations in the input data [33]. Rajib et al. [34] reported an improvement in streamflow prediction by the SWAT model when root zone soil moisture was used as a criterion for calibration.
Several parameter combinations from the optimized range can potentially produce behavioral solutions that are considered equally satisfactory in comparison with the observed data [35]. Data availability is a major limiting factor on the intensity and complexity of model calibration. Baseflow, soil moisture and crop yields data have therefore rarely been collectively used in a single calibration approach. Owing to the availability of robust and high-quality data, the objectives of this study are, therefore, to: (i) conduct a step-wise model calibration and validation procedure for SWAT model by considering runoff, groundwater flow, soil moisture, streamflow and sediment yield data, (ii) perform a simultaneous calibration and validation procedure for SWAT model by considering only the hydrology and sediment yield components, and (iii) compare the two calibration techniques.
2. Materials and Methods
2.1. Study Area
The study area is comprised of the Hydrological Open Air Laboratory (HOAL) catchment located in Petzenkirchen, Lower Austria (Figure 1). The basin has an area of 66 hectares. The elevation ranges from 257 m to 323 m above sea level with a mean slope of 8% [36]. Agricultural land is the primary land use in the area occupying 87% of the total watershed [37]. The average annual rainfall is 700 mm, and the mean annual temperature is 9 °C [38]. The remaining 13% of the catchment area is covered with pastures and paved surfaces. Winter wheat, winter barley, maize, and rapeseed are the primary crops cultivated in the catchment. The agricultural land is divided into 37 fields with different agricultural management practices. The field sizes range from less than a hectare to 12 hectares, with an average field size of 1.5 hectares. Crop rotation is associated with green manure to ensure natural fertilization of the soil. However, nitrogen fertilizers and natural fertilizers are also applied before sowing.
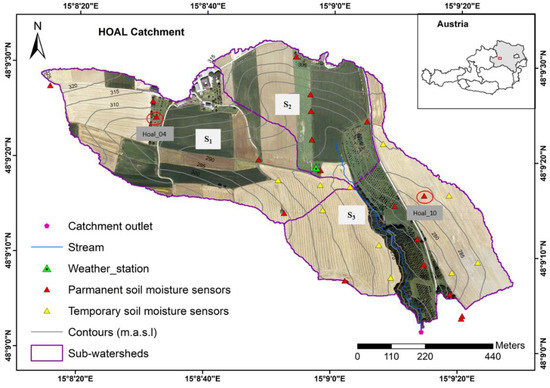
Figure 1.
The study area showing the map of Austria, elevation of the catchment, sub-watersheds (S1 (26 ha), S2 (15 ha), S3 (25 ha)), stream, weather station and the catchment outlet.
2.2. Soil and Water Assessment Tool (SWAT) Model Description
SWAT is a physically based, catchment scale, continuous model developed by the USDA Agricultural Research Service (ARS) to quantify the impact of land management practices on water, sediment, and agricultural chemical yields in large, complex watersheds with varying soils, land use, and management conditions over a long period of time that runs on a daily time step [10]. The major components of the model include hydrology, weather, soil erosion, plant growth, nutrients, pesticides, land management, and stream routing.
Spatial variability is integrated in the watershed by delineating the watershed into a number of sub watersheds based on the topography. Each sub-watershed is further discretized into hydrologic response units (HRUs) based on threshold percentages. HRUs are distinctive combination of categorized land uses, soil types and slope in a sub-watershed. Surface runoff, sediment yield, soil water content, nutrient cycles, crop growth and agricultural management practices are simulated for each HRU and then aggregated for the sub-basin. Channel routing is simulated using the variable storage or Muskingum method.
The hydrologic cycle in the SWAT model is based on the water balance equation;
where SWt is the final water content(mm), SW0 is the initial soil water content (mm), t is the time(days), Rday is the amount of precipitation per day(mm), Qsurf is the amount of surface runoff per day(mm), Ea is the amount of evapotranspiration per day (mm), Wseep in the amount of percolation and bypass flow exiting in the soil profile bottom layer (mm), and Qgw is the amount of baseflow per day (mm).
Erosion and sediment yield in SWAT are estimated at the HRU and sub-basin level using the Modified Universal Soil Loss Equation (MUSLE) [39] and surface runoff from daily rainfall is estimated using a modified Soil Conservation Service-Curve Number (SCS-CN) method. Using the SCS-CN method, the model allows the user to quantify the relative impact of management, soil, climate, and vegetation changes at the sub watershed level [40]. The MUSLE equation uses runoff as an indicator of the rainfall erosivity (R), as opposed to rainfall in the USLE equation, which makes it suitable for application at daily time scale [41]
Plant growth in SWAT is simulated using a simplified version of the generic crop growth model from EPIC [42]. Crop growth is based on the accumulation of heat units. Once the cumulative heat units required to reach crop maturity is surpassed, the crop growth stops. The daily biomass production is simulated by using static radiation use efficiency of the crop, LAI and absorbed photosynthetically active radiation [32].
2.3. Input Data
The basic data sets required to build the model input include: the digital elevation model (DEM), climate data, land use/cover and soils. The data for the HOAL catchment was obtained from the Federal Office of Water Management, Lower Austria.
A DEM of 1 m resolution was used for this study. The land use map was derived from the orthophoto maps, field surveys and farmer records. For each of the 37 fields, detailed information about date and type of land management, planted crops and crop yields as well as fertilizer applications were available for the period from 2008 to 2016. Approximately 200 kg/ha of nitrogen is applied per year. A soil map containing 27 soil units was used for soil classification (Figure 2). Soil physical and chemical properties of the catchment were determined from soil samples collected from a soil survey campaign of 300 cores, sampled on a 50 × 50 m grid in the catchment. The soil survey results contain information about saturated hydraulic conductivity [37], soil organic matter content (om), clay (cl), silt (si), and sand (sa) percentages at multiple depths. The soil properties from the soil samples were averaged for each respective soil unit in the soils map. Soil erodibility factor (K), was calculated using the erodibility equation by Williams [43]. Soil albedo was calculated using an equation proposed by Baumer [44]. Soil available water capacity was calculated as the difference between water held at field capacity and water present at wilting point [45].
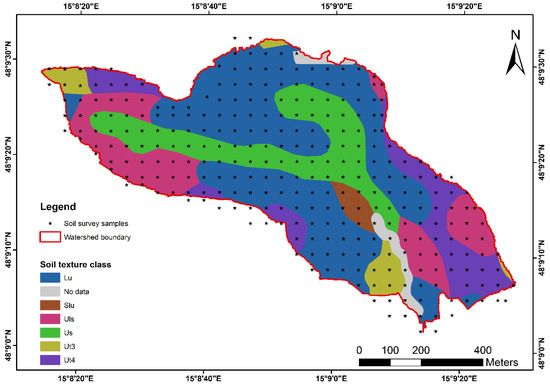
Figure 2.
Soil map showing soil texture classifications (Lu = silty loam, Slu = loamy silty sand, Uls = loamy sandy silt, Us = sandy silt, Ut3 = medium clayey silt, Ut4 = highly clayey silt [46]) and the 50 × 50 grids used for establishing soil properties.
The weather station is located in approximately the center of the catchment, and records data including: precipitation, air temperature, air humidity, wind speed and direction, and incoming and outgoing solar radiation. The meteorological measurements are taken at one-minute resolution. Discharge at the catchment outlet is monitored by an H-flume at 1-min resolution, while turbidity sensors installed at the catchment outlet are used for sediment monitoring. Discharge and turbidity data were available from 2012 to 2016. For purposes of comparison with SWAT simulated output, the model verification data including discharge and sediment was converted into daily averages. This was achieved by calculating the mean of all the recorded data points per day (1440 min).
Profile water content is monitored in the catchment by sensors installed at a number of sites in the watershed as shown in Figure 1. The sensors measure soil water content at four depths below ground surface (5 cm, 10 cm, 20 cm and 50 cm) using the time domain reflectometry (TDR) technique [47]. In this method, the dielectric permittivity of soil is measured and converted to the volumetric moisture content at different soil depths. The soil water content data was available from 2014 onwards and the measurements are taken at hourly intervals. The hourly values were converted to daily means and, thereafter, the mean daily profile water contents were calculated as weighted averages of the sensors up to a depth of 50 cm.
2.4. Model Setup
SWAT2012 rev 670 was used in this study to estimate all the components of water balance. Sub-basin and stream definition were undertaken with the automatic delineation tool incorporated in ArcSWAT. The tool uses DEM information to define basin boundaries and streamflow direction. Using a threshold drainage area of about 10 hectares a total of three sub-basins were delineated for the study area. These sub-basins were further subdivided into 212 HRUs by fixing a threshold value of 0% for land use, soil type and slope. Slopes were divided into two classes of 1% to 10%, and greater than 10%.
Agricultural management practices including crop rotations, planting and harvest dates, dates and implements used for tillage operations, and amounts and timing for fertilizer application were scheduled and used to build the management file for each field at HRU level. The primary crops grown in the HOAL catchment include corn, winter wheat, winter barley and rape seed. Corn is usually planted in mid-April and harvested in September, paving the way for winter wheat or winter barley in October or November, completing a yearly crop rotation schedule. Management operations were scheduled by dates as opposed to the default heat units.
The Hargreaves method [48] was used to simulate the potential evapotranspiration (PET). The model was run from 2008 until 2016. Model input data were available from 2008 to 2016 while observation data were available from 2012 to 2016. To account for initial conditions, the first four years were used as warm-up period. Daggupati et al. [49] recommends a warm-up period of between one to four years.
2.5. Model Evaluation
Successful application of hydrologic models is highly dependent on the sensitivity analysis and calibration of the model parameters [33,50]. The match between simulated and observed results were assessed via graphical and statistical techniques. The SWATplusR package [51], was applied for sensitivity analysis, calibration and validation of the model. The package provides tools for linking SWAT project with R, thereby enabling the execution of SWAT simulations and controlling changes in model parameters, simulation periods and time steps.
The goodness of fit between the simulated and measured data was evaluated by the coefficient of correlation (R2), the Nash-Sutcliffe efficiency (NSE) [52], percent bias (PBIAS) and root mean square error (RMSE). The equations representing these relationships are as shown below [53,54].
where Qm and Qs are the measured and simulated daily values, and are the average measured and simulated values.
Model performance was evaluated by a criteria suggested by [55] as shown in Table 1. The RMSE was evaluated by calculating the scatter index (SI) [56] (Equation (6)). SI less than one implies acceptable model results, while SI greater than one signifies unacceptable model results.

Table 1.
General performance ratings for Nash-Sutcliffe efficiency (NSE), coefficient of correlation (R²), percent bias (PBIAS) and root mean square error (RMSE), adopted from [55,57].
2.6. Sensitivity Analysis
Quantifying model sensitivity to parameter changes is an important step before conducting model calibration [40]. Sensitivity analysis identifies parameters which contribute the most to model output variance due to variability in the input, therefore enabling modelers to calibrate only the most influential parameters while reducing the number of parameters to be calibrated [58]. SWAT has a huge list of parameters from different processes ranging from runoff, groundwater, soil crop yields, nutrients and soil loss. Sensitivity analysis for all these parameters would be exhausting and time-consuming [59]. However, several researchers, have investigated and documented the most important parameters for SWAT model calibration [33,45]. These studies were used as basis for selecting parameters for sensitivity analysis.
For this study, 18 parameters governing streamflow, sediment yield, and soil moisture were chosen for sensitivity analysis. Crop yields parameter sensitivity analysis was conducted manually via the SWAT model. The Fourier amplitude sensitivity test (FAST) [60,61,62,63], a variance based global sensitivity analysis method was used for sensitivity analysis. FAST uses a periodic sampling procedure and a Fourier transformation to decompose the variance of a model output into partial variances contributed by model parameters [64]. Model sensitivity analysis was carried out with the R package FAST [65].
2.7. Model Calibration and Validation
During winter, temperatures drop to below 0 °C and therefore it is essential to consider the effect of snow on the hydrological cycle, even if the watershed is not strictly snow dominated [66]. After a successful model run with initial parameters, snow parameters; SFTMP (snowfall temperature), SMTMP (snow melt base temperature), SMFMX (melt factor on 21 June), and TIMP (snow pack temperature lag time) were first adjusted by running 500 simulations and the best parameter range fixed. This approach of fixing some parameters before starting model calibration is recommended by Hu et al. [67] because it makes simulations more reliable and physically meaningful. These parameters were not modified any further during the calibration process. This model is henceforth referred as the default simulation.
Relevant parameters selected after model sensitivity analysis were automatically adjusted within SWATplusR during the calibration and validation periods. The SWATplusR algorithm attempts to find the best combination of parameter values that give the best fit between the observed and simulated values. After every run, the results were evaluated using dotty plots and parameter ranges adjusted accordingly. Upon successful calibration, the same parameter range was used for model validation. The parameters adjustment was done until the best fit between the observed and simulated data was obtained. Two separate model calibration projects were set up. One project followed the step-wise calibration procedure while in the second, the simultaneous flow calibration method was applied. The Nash-Sutcliffe efficiency (NSE) [52] was used as the objective function for both calibration and validation.
In step-wise calibration method, different hydrological components were calibrated separately, whereby parameters governing surface runoff, groundwater flow, crop yields and soil water content were adjusted independently in a sequential manner. The step-wise calibration approach is illustrated in Figure 3. After successful calibration in each stage, the best parameter range was fixed and used for subsequent calibration steps. After that, these parameter ranges were applied for streamflow and sediment yields calibration. On the other hand, all flow-related hydrological components were calibrated concurrently in the simultaneous calibration approach. Soil moisture and crop yields were not calibrated in the simultaneous calibration method.
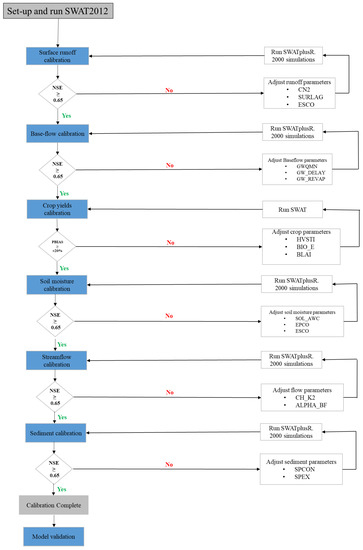
Figure 3.
Step-wise model calibration and validation flow procedure.
2.7.1. Step-Wise Model Calibration
Surface Runoff and Groundwater Flow Calibration
Groundwater flow analysis is a valuable approach in understanding groundwater movement to and from streams [68]. Groundwater flow calibration was achieved by iteratively adjusting groundwater parameters that govern the movement of water into and out of the aquifer systems. Since there are no measured data for groundwater flow in the catchment, the groundwater flow and runoff were extracted from the total flow. A recursive digital filter method based on the Lyne and Hollick [69] algorithm was used to remove the high-frequency quick flow signal to derive the low-frequency baseflow signal.
The baseflow is then computed as:
where qf(i) is the filtered quick flow for the ith sampling instant, q(i) is the original streamflow for the ith sampling instant, α is the filter parameter that enables the shape of the separation to be altered, and qb(i) is filtered baseflow response for the ith sampling instant.
The groundwater flow obtained from the recursive digital filter method includes both groundwater flow and sub-surface flow. Groundwater flow and sub-surface flow are simulated separately in the SWAT model. In order to calibrate the SWAT output against the separated groundwater flow, the groundwater and lateral flow columns were added up in the SWAT output.
Crop Yields Calibration
Three plant growth parameters namely, radiation use efficiency (BIO_E), maximum potential leaf area index (BLAI) and harvest index (HVSTI) were adjusted to calibrate crop yields for corn, winter wheat and rapeseed. These parameters were selected based on manual sensitivity analysis and previous published studies [19,67]. The selected plant growth parameters were adjusted manually to fit the observed harvest. Due to the robust crop rotation practiced in the catchment, a spatial method for crop yields calibration was adopted. Yields for each individual crop in each of the three sub-watersheds (S1, S2, and S3) as shown in Figure 1 were averaged for the period 2012 to 2016 and these data used for model calibration and validation. The long-term average for crop yields calibration was also used by Abbaspour et al. [33] at a continental scale, while Sinnathamby et al. [19] applied the spatial calibration/validation method. Parameters governing plant growth were optimized in S1 in the calibration procedure. On satisfactory performance, the adjusted parameters were further implemented in S2 and S3 without any further changes for crop yields validation.
Soil Moisture Calibration
Soil moisture measurements from two selected sensors were used for model calibration by comparing the measured data with the simulated profile water content at the specific HRUs where the sensors were placed. An assumption was made that the point measurements were representative of the average simulated values in the respective HRUs. Since SWAT simulates soil moisture content as plant available water (PAW) in millimeters, the simulated and observed soil water storage could not be compared directly. To overcome this discrepancy in data structure, water held at wilting point was calculated at each layer and added to the SWAT simulated soil moisture. Rajib et al. [34] applied a similar approach for the Upper Wabash and Cedar Creek watersheds by deducting water content held at wilting point from the soil moisture measurements.
The averaged soil water measurements, taken at a depth of 50 cm, were calibrated against simulated soil water storage at the third soil profile which ranges from 50–70 cm in depth. The comparisons between the measured and observed data were not, therefore, of the same exact depth.
Thereafter, streamflow and sediment yield calibration and validation followed. Streamflow and sediment calibration was done for three years from 2012 to 2014 on a daily time step, while validation was carried out from 2015 to 2016. Dedicated flow and sediment monitoring in the catchment were initiated in the year 2012, which explains the choice of calibration and validation periods.
2.8. Uncertainty Analysis
SUFI-2 program [70] was used for uncertainty analysis. The program predicts model uncertainty with the bandwidth between 2.5% and 97.5% levels of cumulative distribution output otherwise known as 95PPU band. The procedure is applied to parameter sets resulting from Latin hypercube sampling, which means any interactions between parameters are explicitly considered [70]. The model uncertainty is quantified by R-factor and P-factor. The P-factor is the percentage of measured data bracketed by the 95PPU while the R-factor is the average thickness of the 95PPU band divided by the standard deviation of the measured data. A P-factor greater than 0.7 and an R-factor of less than 1.5 are loosely suggested as measures of good model performance [45].
3. Results and Discussion
The investigated period for this study was between 2012 and 2016. The mean annual precipitation for the HOAL catchment during this period was 737 mm. The maximum annual precipitation was 915 mm (2013) while the minimum was 569 mm (2015). The mean flow for the stream was 3.6 L/s with the maximum recorded event of 115.5 L/s. The mean maximum daily temperature was 14 °C and the mean minimum daily temperature was 4 °C. Model sensitivity analysis, calibration and validation are presented in this section, as well as evaluations made through statistical coefficients and visual inspection of plots.
3.1. Sensitivity Analysis
Sensitivity analysis results showed SCS runoff curve number for moisture condition II (CN2), threshold depth for return flow of water in the shallow aquifer (GWQMN), available water capacity of soil layer (SOL_AWC) and peak rate adjustment factor (PRF) as the most sensitive parameters for surface runoff, groundwater flow, soil moisture and sediment yield respectively. Sensitivity analysis results are shown in Figure 4. A total of 12 parameters were selected for flow and soil moisture calibration, while three parameters (Table 2) were chosen for sediment calibration based on the sensitivity analysis results.
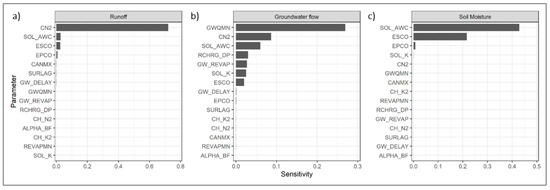
Figure 4.
Graphical representation of sensitivity ranking for runoff (a), groundwater flow (b) and soil moisture (c) parameters. Parameters definition can be found in Table 2.

Table 2.
Soil and Water Assessment Tool (SWAT) parameters modified during both simultaneous and step-wise calibration methods.
The parameters identified as the most influential during sensitivity analysis were also identified by other researchers as important parameters for SWAT model calibration in various studies across varying catchments [21,30,71,72,73].
The parameters used for model calibration and validation for both step-wise and simultaneous methods with the final adopted parameter ranges are shown in Table 2. Most of the parameter ranges were similar except that of GWQMN which showed a wider range for the simultaneous method (100–1500) mm compared to the step-wise method (100–800) mm. The CN2 parameter was also fine-tuned in the step-wise method. These parameters’ range differences are a result of runoff and groundwater flow calibration steps carried out during step-wise calibration. The SOL_AWC parameter also showed a clear trend in the step-wise method compared to simultaneous calibration. This is because the SOL_AWC parameter was adjusted based on soil moisture data for the step-wise calibration as opposed to streamflow in the simultaneous calibration approach.
3.2. Step-Wise Calibration and Validation
For model predictions to be valid and reliable, the model parameter values need to accurately reflect the hydrological systems they represent. However, not all model parameters can be measured directly. In this case, the parameter values can only be obtained through model calibration [2]. The parameters selected during sensitivity analysis were used for model calibration and validation.
The default model satisfactorily reproduced the hydrograph pattern of measured daily streamflow as shown in Figure 5. The R² value of 0.69 and PBIAS of 16.3% further suggest a good model performance. However, an NSE value of 0.39 indicates unsatisfactory model performance even though the results are within the acceptable range according to the criterion shown in Table 1. Furthermore, RMSE of 5.24 L/s translates to a scatter index (SI) of 1.29 pointing to unsatisfactory model performance. The mean simulated discharge during the calibration period was 4.71 L/s while the observed mean was 4.05 L/s; furthermore, the standard deviation for the simulated and observed discharge was 9.20 L/s and 6.74 L/s respectively.
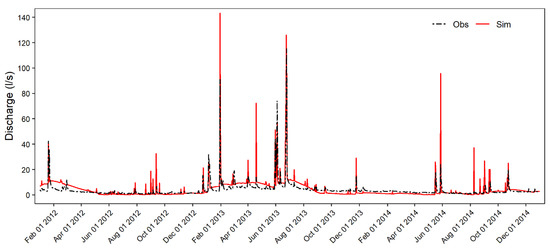
Figure 5.
Simulated and observed streamflow for the default model during the calibration period (2012–2014).
The default model performed better than the results obtained by Van Liew and Garbrecht [74] who reported the NSE value of −3.24. They attributed this poor model performance to model’s overestimation of peak flows and underestimation of groundwater flows. These results are similar to our findings as visual inspection of our default model points to overestimation of peak flows. The low flows, however, do not show a clear trend. Low flows are overestimated in wet year (2013) and underestimated in the dry year (2014). Fukunaga et al. [21] also reported an NSE value of −0.38 and PBIAS of −24%. The better performance can be attributed to the dedicated catchment monitoring initiated in 2012 which provided high quality and quantity of data for model set up.
The high peak flows could be due to the fact that the initial curve number values calculated by the model were too high. Strauch et al. [75] and Fukunaga et al. [21] also reported high CN2 values in their default SWAT models. This challenge was solved by decreasing the CN2 value during model calibration.
3.2.1. Surface Runoff and Groundwater Flow Calibration
To understand groundwater contribution into streamflow, analysis of the stream hydrograph which involves separating baseflow from quickflow is critical [68]. Groundwater flow and surface runoff components are constantly interacting within a watershed, which means changing one component will influence the others. Due to this interaction, it is common practice during model calibration to parameterize groundwater parameters and surface runoff parameters concurrently [45,71]. However, in our study, the parameters governing groundwater flow and surface runoff were adjusted separately to better understand the model’s simulation of flow components. This approach was also used by Santhi et al. [18]. Moriasi et al. [55] stressed the importance of calibrating all the hydrological constituents to be evaluated in watershed modeling. Hence, when the objective of the hydrological model is to be applied for predicting discharge, it would be sufficient to only calibrate the model for streamflow. However, if the model was to be used for evaluation of different land use scenarios and management strategies, for example, it becomes necessary to calibrate different flow components. Furthermore, Pinto et al. [76] reported that SWAT was unable to properly capture discharge during low flow periods in the simultaneous calibration approach in a baseflow dominated watershed. They attribute this to the type of objective function selected during calibration process as some functions, e.g., sum of square of the residuals, strongly influence peak discharges.
CN2 is the most influential parameter for surface runoff [73]. This parameter was, therefore, the basis for surface runoff calibration. The curve number estimates runoff based on the relationship between precipitation, hydrologic soil group and land uses [71]. The curve number is adjusted every day according to the prevailing moisture conditions in the watershed [74]. Maximum canopy storage (CANMX), surface runoff lag coefficient (SURLAG), plant uptake compensation factor (EPCO) and soil evaporation compensation factor (ESCO) were the other parameters adjusted for surface runoff calibration. Threshold water level in shallow aquifer for baseflow (GWQMN), groundwater revap coefficient (GW_REVAP), deep aquifer percolation fraction (RCHRG_DP), saturated hydraulic conductivity (SOL_K) parameters were adjusted for groundwater flow calibration. The parameter description and the final parameter ranges are shown in Table 2. The NSE and R² values (Table 3) denote a good model performance in predicting surface runoff. The PBIAS shows satisfactory results while an SI of 3 indicates an unsatisfactory RMSE value. The model performance in groundwater flow simulation was good as shown in Table 3 and Figure 6. The good fit between the observed and simulated surface runoff and groundwater flow is a good indicator that hydrologic processes in the HOAL catchment were modelled realistically.

Table 3.
Model performance for surface runoff and groundwater flow.
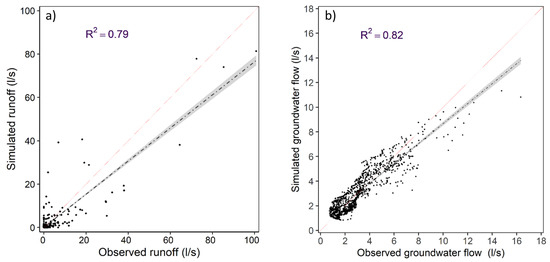
Figure 6.
Scatter plots showing (a) surface runoff calibration results, and (b) groundwater flow calibration results.
The simulated runoff showed very high uncertainty with a P-factor of 0.11 and R-factor of 0.49. On the other hand, good P-factor and R-factor values of 0.82 and 1.0 were achieved for groundwater flow.
3.2.2. Crop Yields Calibration
For efficient application of hydrological models in catchment assessment, it is essential that crop yields are appropriately simulated. This is due to the fact that integrating crop growth in hydrological models enables correct representation of biomass characteristics which are important in many hydrological processes [19].
Corn, winter wheat and rapeseed yields were underestimated by 17%, 24%, 57% respectively while winter barley yields were overestimated by 14% in S1. The model simulation for winter barley was considered satisfactory. For corn, winter wheat and rapeseed, a manual calibration procedure was adopted. The plant growth parameters considered for calibration were harvest index (HVSTI), radiation use efficiency (BIO_E) and maximum leaf area index (BLAI) as recommended by [19,53].
Model calibration significantly improved the simulation results for crop yields as shown in Table 4 and Figure 7. The harvest index (HVSTI) for corn was increased from the default 0.5 to 0.6, while that of winter wheat was increased from 0.4 to 0.45 and rapeseed from 0.23 to 0.4. Validation performed well in S2 but there was a bigger discrepancy between simulated and observed corn and rapeseed yields in S3. Whereas S1 and S2 have several fields under different management practices and cropping patterns, S3 is made up of one large field with similar agricultural practices. This could explain the difference in crop yields simulation. Overall, the long-term crop yields calibration and validation are satisfactory.

Table 4.
Crop yield calibration results for S1 and validation results for S2 and S3 for the period (2012–2016).
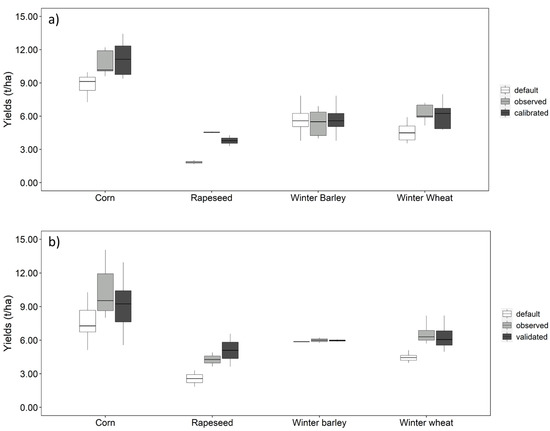
Figure 7.
Box plot for default, observed and simulated crop yields after (a) model calibration and (b) model validation.
Abbaspour et al. [33] also used the long-term crop yield averages for model calibration and reported good model performance. However, they highlighted the challenge of simulating crop yields due to limitations of obtaining input data at farm scale. It is worth noting that their study was a large-scale application covering an area of around 10.18 million square kilometers whereas our study was small-scale application. This challenge was also identified by Srinivasan et al. [77]. Their study suggested that more information on crop management practices could improve SWAT models performance for crop yields simulation. Sinnathamby et al. [19] reported an overestimation of corn yields for the default model contrary to the results of this study where initial corn yields were underestimated. This could be attributed to the geographical location and climatic conditions of the study areas as well as differences in management practices.
Even though the long-term average crop yields were well simulated, the annual variability especially for corn was not well captured. These findings are similar to Hu et al. [67], who reported poor model results in calibrating annual corn yields with NSE of −0.49. This study obtained a better NSE value of −0.07, although this value is unacceptable. Although we had detailed management practices data in our research, the inconsistencies in seasonal crop yield variability still persisted.
3.2.3. Soil Moisture Calibration
Soil moisture plays an important role in the energy and water balance in the hydrological cycle. The antecedent moisture conditions determine the potential for surface runoff and deep percolation to occur [17,78]. Ensuring accurate accounting of soil moisture in hydrologic models can, therefore, improve the model’s ability to simulate other hydrologic processes.
The calibrated parameter ranges for groundwater flow, surface runoff and crop yields calibration were used during soil moisture calibration without any further adjustment. Available water capacity (SOL_AWC) was the most sensitive parameter for soil moisture. The calibration procedure, therefore, involved adjusting this parameter. The mean measured soil profile water for the entire catchment was 183 mm for the top 50 cm, while the average simulated soil water content was 181 mm for approximately top 60 cm of the soil. The soils had high water content in winter periods and low water content during summer. Calibration was done on two locations hereby referred to as Hoal_04 and Hoal_10. Hoal_04 is located upstream with sensors positioned in pasture HRUs whereas Hoal_10 is located near the catchment outlet and the sensors are located in agricultural HRUs (Figure 1). In both locations, calibration results showed a good fit between the simulated and measured soil moisture content as shown in Figure 8. The NSE and R² values were both greater than 0.75 indicating a good model performance. Both sensors show a similar soil moisture trend, although Hoal_04 (Figure 8a) soil water profile values are slightly higher. This could be due to the aforementioned positioning of the Hoal_04 sensors in pasture grounds. Due to the small size of the study area, there are no big differences in soil properties across the whole catchment.
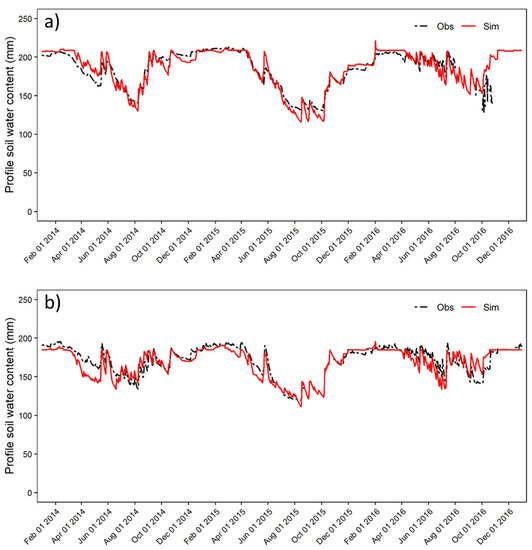
Figure 8.
Time series of simulated and observed profile soil water content during calibration period for (a) Hoal_04 sensor and (b) Hoal_10 sensor.
The soil moisture calibration in this study performed better than some previous published studies. Rajib et al. [34] calibrated the SWAT model for soil moisture for the top 60 cm for Cedar Creek watershed and reported R² value of 0.23 and PBIAS of −8.7. They attributed the bad model performance to limitations in model ET depletion mechanism which led to errors in model simulation during summer months. Even though the soil profile water content in our study was also underestimated during summer, the margin of error was much less than that reported by Rajib et al. [34]. The good performance of soil moisture calibration in this study can be attributed to high-quality soil data and extensive agricultural management practices data used during the model set-up.
Uncertainty analysis for the calibrated soil moisture obtained a P-factor of 1.0 in both calibration sites while R-factor value was 1.8 for Hoal_04 and 2.4 for Hoal_10. Whereas the P-factor falls within the acceptable range, the R-factor values were beyond the recommended threshold as shown in Table 1. Uniyal et al. [79] conducted uncertainty analysis for SWAT soil moisture calibration and obtained P-factor values ranging from 0.6 to 0.83 and an R-factor of between 0.5 to 1.3. Their study considered the top 30 cm of the soil profile as opposed to 50 cm in our study. Their study also implemented auto irrigation in the SWAT model while that was not the case in our study, as there is no irrigation in the HOAL catchment. Nevertheless, the results of model uncertainty analysis agree well in both studies, although our model performed worse. A reason for a poor model uncertainty results could be because soil moisture is simulated at the HRU level in SWAT compared to TDRs point measurements.
3.2.4. Streamflow Calibration
Streamflow was checked after every calibration step to evaluate the effect of each calibration step on total flow. The calibrated parameters for surface runoff, groundwater flow, crop yields and soil moisture were used for total stream flow calibration. Furthermore, after each calibration step, stream flow simulation was evaluated to ascertain the influence of calibration steps on the models’ streamflow simulation. The results of streamflow simulation in every step of calibration are shown in Table 5. The final streamflow calibration results showed a good fit between the simulated and observed flow, with NSE, R², PBIAS and RMSE of 0.83, 0.83, 6.5 and 2.8 L/s. The R-factor was found to be 0.56 while the P-factor was 0.74. 74% of the observed data was therefore bracketed by the 95PPU band and the average distance between the 2.5th and 97.5th percentiles was smaller than the standard deviation of the measured data implying a good simulation as suggested by [80]. These results are shown in Figure 9.

Table 5.
Effect of each calibration step on streamflow, soil moisture and sediment yield. OBS = Observed data, DM = Default model, ARC = After runoff calibration, AGC = After groundwater flow calibration, ACC = After crop yields calibration, ASC = After soil moisture calibration and ASEC = After sediment calibration.
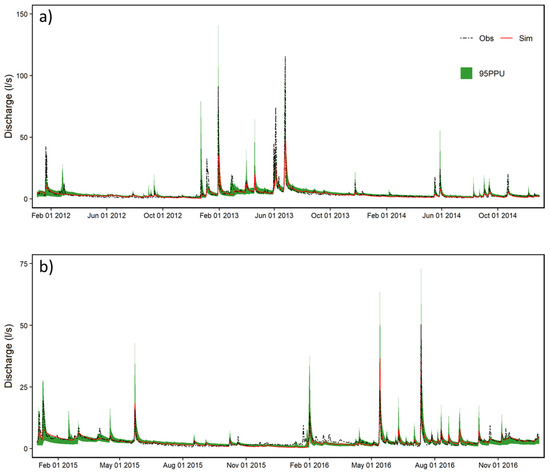
Figure 9.
Streamflow calibration (a) and validation (b) results for the step-wise calibration procedure with 95PPU uncertainty band.
Malagó et al. [13] applied a step-wise calibration approach using the SWAT model in the Danube river basin at multiple gauging stations and reported acceptable PBIAS value of ±25% in 70% of the gauging stations. However, they reported that some stations showed unsatisfactory PBIAS value. Furthermore, their study did not consider soil moisture calibration. Their model obtained better surface runoff results by increasing the CN2 value by 10% as opposed to our model, where decreasing the curve number by 1.2% produced better results. However, they state that because of no exact information about land use, a misrepresentation of agricultural practices in their study may be possible, which could explain the differences in the CN2 value. Based on the PBIAS value, our model performed better; however, our study area was much smaller and we used only one gauging station for model calibration whereas multiple gauging stations were used for calibration in the study by Malagó et al. [13].
3.2.5. Flow Validation
The model was validated for total streamflow at the outlet. The model performance was good for the validation period as shown in Figure 9 with NSE and R² greater than 0.65. The PBIAS was −4.4 while the RMSE was 1.38 L/s. However, the model performed poorly during validation compared to calibration. These findings are in agreement with Fukunaga et al. [21], who reported an NSE of 0.75 during calibration and which dropped to 0.67 during validation. This is expected because the parameters are optimized for the calibration period, therefore varying climatic and hydrological conditions and land management practices in the validation period may render the parameters obtained during calibration less optimal.
Furthermore, a P-factor and R-factor of 0.73 and 0.93 respectively shows a good model performance for streamflow during the validation period.
3.2.6. Sediment Yield Calibration and Validation
Since it is a small catchment, significant sediment yields are only observed during high-intensity rainfall. Sediment calibration was, therefore, highly dependent on the models’ capability to simulate these high flow events. The default model performed very well for sediment yield, with NSE of 0.82. Surface runoff had the highest impact on sediment yield, as shown in Table 5. This was expected because quick runoff is majorly responsible for detachment and transport of sediment in catchments. Sediment yields’ calibration included adjusting three parameters which included the exponent parameter for calculating sediment reentrained in channel sediment routing (PRF), linear parameter for calculating the maximum amount of sediment that can be reentrained during channel sediment routing (SPCON) and peak adjustment factor (SPEXP). Pinto et al. [76] also found SPCON and SPEXP parameters sensitive to sediment yields generation. Adjusting sediment yield parameters improved the model’s performance for sediment yield, obtaining a good NSE, R2 and PBIAS as shown in Table 5.
3.2.7. Effect of Calibration Steps on Hydrological Components
The results of streamflow simulation after each calibration step are shown in Table 5. The most significant improvement in streamflow results is observed after runoff calibration (ARC). The NSE value improved from 0.39 to 0.77, while R² value was 0.80 from the previous 0.69. A poorer PBIAS value was, however, obtained while the RMSE value improved by 2 L/s. Since the curve number (CN2) was the most sensitive parameter for streamflow, these results suggest that adjusting CN2 value is sufficient to obtain a good flow calibration for the HOAL catchment. These results are similar to Széles et al. [36] who applied the Hydrologiska Byråns Vattenbalansavdelning (HBV) model [81] in the HOAL catchment. They noted that the model was able to produce very good streamflow results after runoff calibration, whereby their model obtained a logarithmic NSE value of 0.81.
Groundwater flow calibration (AGC) did not significantly affect the total flow, the R², NSE and RMSE values were 0.80, 0.78 and 3.15 respectively. These values are similar to those obtained after runoff calibration (Table 5). However, the PBIAS value showed a significant improvement from −31.40 to −2.7. This is because the runoff calibrated model underestimated groundwater flow especially in 2014, which was corrected after groundwater flow calibration. These results, therefore, emphasize the need for groundwater flow calibration as a model could obtain good statistical values for streamflow while misrepresenting other hydrological processes. Good results achieved after surface runoff and groundwater flow parameters calibration indicate that these two steps are sufficient for streamflow calibration.
Crop yields (ACC) and soil moisture (ASC) parameter adjustment did not have any statistically significant change to streamflow output. This could be due to the fact that the initial model estimated fairly the soil moisture and crop yields and no major parameter alterations were required in the calibration. The NSE and R² values for the default model for soil moisture was 0.69 and 0.83 respectively as shown in Table 5. This shows good ability of the initial model to predict soil moisture.
Azimi et al. [82] assimilated satellite soil moisture data in their SWAT model for small watersheds in Italy and observed a slight improvement of NSE by around 0.1. Although they did not show results for soil moisture calibration, it can be concluded that assimilating soil moisture data in the streamflow calibration does not have a significant impact on streamflow simulation, especially when good quality soil data are used in modelling. Arias et al. [83] reported an underestimation of peak flows which they attributed to the models’ inability to simulate soil moisture conditions during high rainfall periods. High-quality soil data used during model set-up in our study can, therefore, be attributed to the good soil moisture simulation and, therefore, the negligible impact of soil moisture calibration on streamflow. Széles et al. [36] also did not report any significant improvement in streamflow prediction for the HOAL catchment after incorporating soil moisture data in their research; however, they reported an improved soil moisture prediction by the model. Rajib et al. [34] used in-situ soil moisture estimates for top 60 cm of soil profile in their multi-objective approach and reported an improvement of R² from 0.69 to 0.72 in streamflow calibration after soil moisture calibration.
Since streamflow is simulated on a daily time-step while crop yields are calibrated on seasonal basis, crop yields would not be expected to significantly alter the daily water budget. Nair et al. [32] also found only a slight improvement of the SWAT model’s ability to predict discharge upon calibration of plant growth parameters.
Step-wise model calibration had a negative impact on the NSE and PBIAS for sediment yield simulation, whereas the R² value improved slightly throughout the calibration steps. This shows that it is possible to have a well-calibrated model for streamflow which poorly represents the sediment yield in the catchment. Therefore, these results advocate for the step by step approach in model calibration.
3.3. Simultaneous Calibration and Validation
The simultaneous calibration procedure was performed with the same parameters used in the step-wise calibration method, with their default range. This calibration, therefore, produced different parameter ranges as shown in Table 2. This calibration method obtained good model results for streamflow with NSE, R², PBIAS and RMSE of 0.78, 0.79, −1.5, and 3.2 L/s respectively. The P and R factors were 0.97 and 0.9, respectively. The results suggest a good agreement between the simulated and observed data for the simultaneous calibration process.
SWAT simulations from previous studies have produced reasonable results using the simultaneous calibration approach for both annual and monthly scales [67,72,77,84,85] but some poor results for daily time-step [86]. Arias et al. [83] applied the SWAT model for Corbeira catchment in Spain on a daily time-scale and obtained an R², NSE and PBIAS of 0.80, 0.80 and −1.8, respectively, which points to a good model performance, even though they reported underestimation of peak flows during high flow periods. Their study area was also dominated by forest which occupied 65% of the total area, as opposed to the 87% agricultural area in our study. These results show that availability of high-quality data is key to god model performance. Pinto et al. [76] applied the shuffled complex evolution (SCE) method for SWAT model calibration for streamflow in the Lavrinha Creek watershed in Brazil and also reported very good model results. Contrary to Arias et al. [83], their model overestimated peak flows and underestimated low flows. Van Liew and Garbrecht [74] obtained an NSE value of between 0.40 and 0.60 for daily streamflow simulation. Rivas-Tabares et al. [87] also demonstrated that the SWAT model is capable of producing good results for streamflow in agriculture dominated watershed when high-quality soil data and crop management is used during model set-up. These results show that the SWAT model can be successfully applied in watersheds with different sizes, management practices and climatic conditions.
The NSE and R² were greater than 0.60 for the validation period, the PBIAS was −5.6 while RMSE was 1.680 L/s. A P-factor of 0.82 and R-factor of 1.50 was achieved for the validation. Abbaspour et al. [33] applied the SWAT model on a continental scale for Europe on a monthly time step and reported a P-factor ranging from 0.39 to 0.76 and R-factor ranging from 0.54 to 0.99.
3.4. Comparison between Step-Wise and Simultaneous Calibration and Validation Methods
3.4.1. Flow Calibration and Validation
Both calibration methods showed good results in streamflow simulation as shown in Table 6. The step-wise calibration method performed slightly better than the simultaneous calibration method. Therefore, it can be concluded that calibration of different hydrological components leads to a better model performance. The simultaneous calibration results showed an overestimation of soil profile water content during the calibration period as shown in Figure 10 while the groundwater flow was underestimated as shown in Figure 11. Based on these results, we can deduce that it is possible for the model to produce good streamflow results with incorrect representation of runoff, groundwater flow, crop yields and soil water content. One of the main achievements of the groundwater flow calibration step was rectifying the underestimated groundwater flow in late 2013 and early 2014 as discussed in Section 3.2.5. However, this issue persisted with the simultaneous calibration method. On the downside, the step-wise calibration method is time-consuming as also mentioned by Brighenti et al. [27], because of the number of simulations run in every calibration step, whereas in simultaneous calibration, only one calibration step is required.

Table 6.
Comparison between model performance for both simultaneous and step-wise calibration approaches for streamflow and sediment yield.
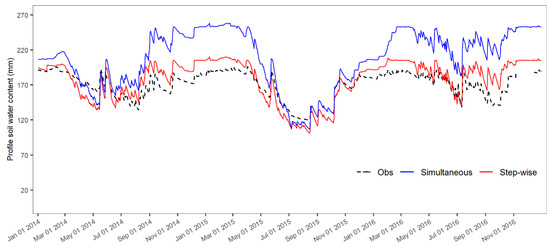
Figure 10.
Soil moisture output for both simultaneous and step-wise calibrated flow models during the calibration period.
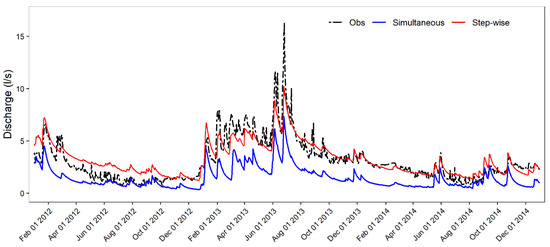
Figure 11.
Groundwater flow output for both simultaneous and step-wise calibrated flow models during the calibration period.
The statistical figures for the validation for both methods are shown in Table 6. Both validation techniques show a good performance; however, better results were obtained through the step-wise method. The validation results are, therefore, consistent with the results from model calibration, implying the step-wise method to be a more reliable option for model calibration. An R-factor of 1.51 for the simultaneous validation method compared to 0.93 for stepwise calibration also indicates poor model uncertainty results.
3.4.2. Sediment Yield Calibration and Validation
Sediment results were better for the step-wise method for the calibration period and simultaneous method for the validation period (Table 6). Since the default model was capable of predicting correctly sediment yield before calibration, it can be concluded that both methods do not show any significant difference. Alibuyog et al. [88] attained an R² of between 0.58 to 0.82 and NSE of −5.52 to 0.80 in simulating sediment yields in the Manupali River watershed. Therefore, this study obtained slightly better calibration results for sediment yields as shown in Table 6.
4. Conclusions
This study investigated the impact of incorporating runoff, groundwater flow, crop yields and soil moisture data during SWAT model calibration and validation, and compared the step-wise calibration method with the widely used simultaneous calibration method. The calibration process was carried out through SWATpluR package. The differences between the two methods are presented statistically and also graphically.
The results of this study show that both methods can be successfully used in SWAT model calibration for streamflow and sediment yields, but with some differences. In both calibration methods, R² and NSE values were greater than 0.75. In addition, the model was capable of correctly simulating crop yields, soil moisture, groundwater flow and surface runoff. Due to the comprehensive nature of the step-wise calibration method, there is better partitioning between surface runoff and groundwater flow components and also better soil moisture prediction accuracy. The step-wise calibration method performed slightly better for streamflow and sediment yields prediction. The simultaneous calibration method only relies on good correspondence between the observed and simulated streamflow and sediment yield, without necessarily checking surface runoff, groundwater flow or soil moisture. This implies that wrong parameter combinations could bring out a desirable output.
This study also demonstrated that data quality and quantity play a significant role in hydrological models performance. Since this research was undertaken on an extensively monitored catchment, high-resolution input data (DEM, soils, weather and land use data) were available, which led to good performance of the default model with initial parameters for streamflow, soil moisture, crop yields and sediment yield. The default model output for flow, soil moisture and sediment yield were acceptable. One-minute resolution weather data, high-quality DEM, detailed land and soil management practices and high-resolution calibration data contributed to the good initial model performance.
The step-wise calibration method can be time consuming compared to the simultaneous calibration method. If the main focus of the research is to study the hydrology of the catchment, simultaneous calibration would be recommended since it is fast and gives similar results to the stepwise method. For sub-surface water, land use and soil management scenarios, the step-wise method is recommended because it provides a better prediction of most hydrological components in catchments. Our study was conducted on a small experimental watershed with homogeneous weather, data availability and quality was, therefore, not a challenge. There were also no huge differences in soil physical and chemical properties and 87% of the catchment was used for agriculture. It would, therefore, be important to evaluate the impact of applying a similar calibration approach to large, heterogeneous watersheds.
Author Contributions
Supervision, A.K., P.S., Writing—original draft preparation, F.K.M., A.K.; Writing—review and editing, F.K.M., A.K., P.S., G.Z., R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was performed within the project “Soil Hydrology research platform underpinning innovation to manage water scarcity in European and Chinese cropping systems (SHui)”. Financial support was provided by the European Union, Grant Nr. 773903 and the Chinese Ministry of Science and Technology under CFM (China-EU Co-Funding Mechanism).
Acknowledgments
We would like to acknowledge the support of Austrian Agency for International Cooperation in Education and Research (OeAD-GmbH) through a scholarship award within the Austrian Partnership Program in Higher Education and Research for Development (APPEAR).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dakhlalla, A.O.; Parajuli, P.B. Assessing model parameters sensitivity and uncertainty of streamflow, sediment, and nutrient transport using SWAT. Inf. Process. Agric. 2019, 6, 61–72. [Google Scholar] [CrossRef]
- Sivakumar, B.; Berndtsson, R. Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; World Scientific Publishing: Davis, CA, USA, 2010; ISBN 9789814307970. [Google Scholar] [CrossRef]
- Fulton, E.A.; Boschetti, F.; Sporcic, M.; Jones, T.; Little, L.R.; Dambacher, J.M.; Gray, R.; Scott, R.; Gorton, R. A multi-model approach to engaging stakeholder and modellers in complex environmental problems. Environ. Sci. Policy 2015, 48, 44–56. [Google Scholar] [CrossRef]
- Busico, G.; Colombani, N.; Fronzi, D.; Pellegrini, M.; Tazioli, A.; Mastrocicco, M. Evaluating SWAT model performance, considering different soils data input, to quantify actual and future runoff susceptibility in a highly urbanized basin. J. Environ. Manag. 2020, 266, 110625. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Liu, Y.; Wang, T. How land use change contributes to reducing soil erosion in the Jialing River Basin, China. Agric. Water Manag. 2014, 133, 65–73. [Google Scholar] [CrossRef]
- Op de Hipt, F.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M.; Näschen, K. Modeling the effect of land use and climate change on water resources and soil erosion in a tropical West African catch-ment (Dano, Burkina Faso) using SHETRAN. Sci. Total Environ. 2019, 653, 431–445. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, D.C.; Ascough, J.C.; Nearing, M.A.; Laflen, J.M. The Water Erosion Prediction Project (WEPP) Model. Landsc. Eros. Evol. Model. 2001, 2001, 145–199. [Google Scholar] [CrossRef]
- Bingner, R.L.; Theurer, F.D.; Yuan, Y.; Taguas, E.V. AnnAGNPS Technical Process; Version 5.5; 2018. Available online: https://www.wcc.nrcs.usda.gov/ftpref/wntsc/H&H/AGNPS/downloads/AnnAGNPS_Technical_Documentation.pdf (accessed on 18 May 2021).
- Beasley, D.B.; Huggins, L.F.; Monke, E.J. ANSWERS: A model for watershed planning. Trans. Am. Soc. Agric. Eng. 1980, 23, 938–944. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Jaber, F.H.; Shukla, S. MIKE SHE: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1479–1489. [Google Scholar] [CrossRef]
- Duda, P.B.; Hummel, P.R.; Imhoff, J.C. BASINS/HSPF: Model use, Calibration, and Validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Malagó, A.; Bouraoui, F.; Vigiak, O.; Grizzetti, B.; Pastori, M. Modelling water and nutrient fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 603–604, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Tischbein, B.; Kusche, J.; Beg, M.K.; Bogardi, J.J. Impact of land-use change on the water resources of the Upper Kharun Catchment, Chhattisgarh, India. Reg. Environ. Chang. 2017, 17, 2373–2385. [Google Scholar] [CrossRef]
- Green, C.H.; van Griensven, A. Autocalibration in hydrologic modeling: Using SWAT2005 in small-scale watersheds. Environ. Model. Softw. 2008, 23, 422–434. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Mapfumo, E.; Chanasyk, D.S.; Willms, W.D. Simulating daily soil water under foothills fescue grazing with the soil and water assessment tool model (Alberta, Canada). Hydrol. Process. 2004, 18, 2787–2800. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT model on a large river basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Sinnathamby, S.; Douglas-Mankin, K.R.; Craige, C. Field-scale calibration of crop-yield parameters in the Soil and Water Assessment Tool (SWAT). Agric. Water Manag. 2017, 180, 61–69. [Google Scholar] [CrossRef]
- Luan, X.; Wu, P.; Sun, S.; Wang, Y.; Gao, X. Quantitative study of the crop production water footprint using the SWAT model. Ecol. Indic. 2018, 89, 1–10. [Google Scholar] [CrossRef]
- Fukunaga, D.C.; Cecílio, R.A.; Zanetti, S.S.; Oliveira, L.T.; Caiado, M.A.C. Application of the SWAT hydrologic model to a tropical watershed at Brazil. Catena 2015, 125, 206–213. [Google Scholar] [CrossRef]
- Shi, P.; Hou, Y.; Xie, Y.; Chen, C.; Chen, X.; Li, Q.; Qu, S.; Fang, X.; Srinivasan, R. Application of a SWAT Model for Hydrological Modeling in the Xixian Watershed, China. J. Hydrol. Eng. 2013, 18, 1522–1529. [Google Scholar] [CrossRef]
- Vigiak, O.; Malagó, A.; Bouraoui, F.; Vanmaercke, M.; Obreja, F.; Poesen, J.; Habersack, H.; Fehér, J.; Grošelj, S. Modelling sediment fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 599–600, 992–1012. [Google Scholar] [CrossRef] [PubMed]
- Yesuf, H.M.; Assen, M.; Alamirew, T.; Melesse, A.M. Modeling of sediment yield in Maybar gauged watershed using SWAT, northeast Ethiopia. Catena 2015, 127, 191–205. [Google Scholar] [CrossRef]
- Sun, C.; Ren, L. Assessing crop yield and crop water productivity and optimizing irrigation scheduling of winter wheat and summer maize in the Haihe plain using SWAT model. Hydrol. Process. 2014, 28, 2478–2498. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Brighenti, T.M.; Bonumá, N.B.; Grison, F.; de Mota, A.A.; Kobiyama, M.; Chaffe, P.L.B. Two calibration methods for modeling streamflow and suspended sediment with the swat model. Ecol. Eng. 2019, 127, 103–113. [Google Scholar] [CrossRef]
- Abbasi, Y.; Mannaerts, C.M.; Makau, W. Modeling pesticide and sediment transport in the Malewa River Basin (Kenya) using SWAT. Water 2019, 11, 87. [Google Scholar] [CrossRef]
- Briak, H.; Mrabet, R.; Moussadek, R.; Aboumaria, K. Use of a calibrated SWAT model to evaluate the effects of agricultural BMPs on sediments of the Kalaya river basin (North of Morocco). Int. Soil Water Conserv. Res. 2019, 7, 176–183. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Baumgart, P. Source Allocation of Suspended Sediment and Phosphorus Loads to Green Bay from the Lower Fox River Subbasin Using the Soil and Water Assessment Tool (SWAT)—Lower Green Bay and Lower Fox Tributary Modeling Report. [Oneida, Wisconsin]: Oneida Tribe of Indians of Wisconsin. 2005. Available online: https://books.google.at/books/about/Lower_Green_Bay_and_Lower_Fox_Tributary.html?id=CnuBzQEACAAJ (accessed on 18 May 2021).
- Nair, S.S.; King, K.W.; Witter, J.D.; Sohngen, B.L.; Fausey, N.R. Importance of crop yield in calibrating watershed water quality simulation tools. J. Am. Water Resour. Assoc. 2011, 47, 1285–1297. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Széles, B.; Parajka, J.; Hogan, P.; Silasari, R.; Pavlin, L.; Strauss, P.; Blöschl, G. The Added Value of Different Data Types for Calibrating and Testing a Hydrologic Model in a Small Catchment. Water Resour. Res. 2020, 56, e2019WR026153. [Google Scholar] [CrossRef] [PubMed]
- Picciafuoco, T.; Morbidelli, R.; Flammini, A.; Saltalippi, C.; Corradini, C.; Strauss, P.; Blöschl, G. On the estimation of spatially representative plot scale saturated hydraulic conductivity in an agricultural setting. J. Hydrol. 2019, 570, 106–117. [Google Scholar] [CrossRef]
- Strauss, P.; Leone, A.; Ripa, M.N.; Turpin, N.; Lescot, J.M.; Laplana, R. Using critical source areas for targeting cost-effective best management practices to mitigate phosphorus and sediment transfer at the watershed scale. Soil Use Manag. 2007, 23, 144–153. [Google Scholar] [CrossRef]
- Williams, J.R.; Berndt, H.D. Sediment Yield Prediction Based on Watershed Hydrology. Pap. Am. Soc. Agric. Eng. 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Baker, T.J.; Miller, S.N. Using the Soil and Water Assessment Tool (SWAT) to assess land use impact on water resources in an East African watershed. J. Hydrol. 2013, 486, 100–111. [Google Scholar] [CrossRef]
- Vigiak, O.; Malagó, A.; Bouraoui, F.; Vanmaercke, M.; Poesen, J. Adapting SWAT hillslope erosion model to predict sediment concentrations and yields in large Basins. Sci. Total Environ. 2015, 538, 855–875. [Google Scholar] [CrossRef]
- Williams, J.R.; Jones, C.A.; Kiniry, J.R.; Spanel, D.A. EPIC crop growth model. Trans. Am. Soc. Agric. Eng. 1989, 32, 497–511. [Google Scholar] [CrossRef]
- Williams, J.R. Chapter 25: The EPIC Model. In Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995; pp. 909–1000. ISBN 0022-1694. [Google Scholar]
- Baumer, O.W. Prediction of soil hydraulic parameters. In Hydrological Processes; SCS National Soil Survey Laboratory: Lincoln, NE, USA, 1990. [Google Scholar]
- Perez-Valdivia, C.; Cade-Menun, B.; McMartin, D.W. Hydrological modeling of the pipestone creek watershed using the Soil Water Assessment Tool (SWAT): Assessing impacts of wetland drainage on hydrology. J. Hydrol. Reg. Stud. 2017, 14, 109–129. [Google Scholar] [CrossRef]
- Bormann, H. Analysis of the suitability of the German soil texture classification for the regional scale application of physical based hydrological model. Adv. Geosci. 2007, 11, 7–13. [Google Scholar] [CrossRef][Green Version]
- Dwevedi, A.; Kumar, P.; Kumar, P.; Kumar, Y.; Sharma, Y.K.; Kayastha, A.M. Soil Sensors: Detailed Insight into Research Updates, Significance, and Future Prospects; Elsevier Inc.: Amsterdam, The Netherlands, 2017; ISBN 9780128042991. [Google Scholar]
- Hargreaves, H.G.; Allen, G.R. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Daggupati, P.; Pai, N.; Ale, S.; Douglas-Mankin, K.R.; Zeckoski, R.W.; Jeong, J.; Parajuli, P.B.; Saraswat, D.; Youssef, M.A. A recommended calibration and validation strategy for hydrologic and water quality models. Trans. ASABE 2015, 58, 1705–1719. [Google Scholar] [CrossRef]
- Mengistu, A.G.; van Rensburg, L.D.; Woyessa, Y.E. Techniques for calibration and validation of SWAT model in data scarce arid and semi-arid catchments in South Africa. J. Hydrol. Reg. Stud. 2019, 25, 100621. [Google Scholar] [CrossRef]
- Schürz, C. SWATplusR: Running SWAT2012 and SWAT+ Projects in R. R Package Version 0.2.7. 2019, Volume 4, pp. 1–3. Available online: https://github.com/chrisschuerz/SWATplusR (accessed on 17 May 2021).
- Nash, J.E.; Sutcliffe, J. V River Flow Forecasting Through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Faramarzi, M.; Yang, H.; Schulin, R.; Abbaspour, K.C. Modeling wheat yield and crop water productivity in Iran: Implications of agricultural water management for wheat production. Agric. Water Manag. 2010, 97, 1861–1875. [Google Scholar] [CrossRef]
- Wallace, C.W.; Flanagan, D.C.; Engel, B.A. Evaluating the effects ofwatershed size on SWAT calibration. Water 2018, 10, 898. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Zambresky, L. A Verification Study of the Global WAM Model 1989; ECMWF: Reading, UK, 1989. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Holvoet, K.; van Griensven, A.; Seuntjens, P.; Vanrolleghem, P.A. Sensitivity analysis for hydrology and pesticide supply towards the river in SWAT. Phys. Chem. Earth 2005, 30, 518–526. [Google Scholar] [CrossRef]
- Sohoulande Djebou, D.C. Assessment of sediment inflow to a reservoir using the SWAT model under undammed conditions: A case study for the Somerville reservoir, Texas, USA. Int. Soil Water Conserv. Res. 2018, 6, 222–229. [Google Scholar] [CrossRef]
- Schaibly, J.H.; Shuler, K.E. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. II Applications. J. Chem. Phys. 1973, 59, 3879–3888. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Cukier, R.I.; Schaibly, J.H.; Shuler, K.E. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. III. Analysis of the approximations. J. Chem. Phys. 1975, 63, 1140–1149. [Google Scholar] [CrossRef]
- Cukier, R.I.; Levine, H.B.; Shuler, K.E. Nonlinear sensitivity analysis of multiparameter model systems. J. Phys. Chem. 1977, 81, 2365–2366. [Google Scholar] [CrossRef]
- Xu, C.; Gertner, G. Understanding and comparisons of different sampling approaches for the Fourier Amplitudes Sensitivity Test (FAST). Bone 2008, 23, 1–7. [Google Scholar] [CrossRef]
- Reusser, D. Fast: Implementation of the Fourier Amplitude Sensitivity Test (FAST). Available online: https://rdrr.io/cran/fast/ (accessed on 25 November 2020).
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sáchez-Pérez, J.M. Assessing the capability of the SWAT model to simulate snow, snow melt and streamflow dynamics over an alpine watershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Hu, X.; McIsaac, G.F.; David, M.B.; Louwers, C.A.L. Modeling Riverine Nitrate Export from an East-Central Illinois Watershed Using SWAT. J. Environ. Qual. 2007, 36, 996–1005. [Google Scholar] [CrossRef] [PubMed]
- Brodie, R.S.; Hostetler, S. A review of techniques for analysing baseflow from stream hydrographs. In Proceedings of the NZHS-IAH-NZSSS 2005 Conference, Auckland, New Zealand, 28 November–2 December 2005. [Google Scholar]
- Lyne, V.; Hollick, M. Stochastic Time-Variable Rainfall-Runoff Modeling. Proc. Hydrol. Water Resour. Symp. 1979, 79, 89–92. [Google Scholar]
- Abbaspour, K.C. SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Eawag, Switzerland, 2014; p. 970. [Google Scholar]
- Anaba, L.A.; Banadda, N.; Kiggundu, N.; Wanyama, J.; Engel, B.; Moriasi, D. Application of SWAT to Assess the Effects of Land Use Change in the Murchison Bay Catchment in Uganda. Comput. Water Energy Environ. Eng. 2016, 6, 24–40. [Google Scholar] [CrossRef]
- Biru, Z.; Kumar, D. Calibration and validation of SWAT model using stream flow and sediment load for Mojo watershed, Ethiopia. Sustain. Water Resour. Manag. 2018, 4, 937–949. [Google Scholar] [CrossRef]
- Mulungu, D.M.M.; Munishi, S.E. Simiyu River catchment parameterization using SWAT model. Phys. Chem. Earth 2007, 32, 1032–1039. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Garbrecht, J. Hydrologic simulation of the Little Washita River experimental watershed using SWAT. J. Am. Water Resour. Assoc. 2003, 39, 413–426. [Google Scholar] [CrossRef]
- Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using precipitation data ensemble for uncertainty analysis in SWAT streamflow simulation. J. Hydrol. 2012, 414–415, 413–424. [Google Scholar] [CrossRef]
- Pinto, D.B.F.; Beskow, S.; De Mello, C.R.; Coelho, G. Application of the Soil and Water Assessment Tool (SWAT) for Sediment Transport Simulation at a Headwater Watershed in Minas Gerais State, Brazil. Trans. ASABE 2013, 56, 697–709. [Google Scholar]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the upper Mississippi River basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface- and root-zone ASCAT soil moisture products into rainfall-runoff modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Uniyal, B.; Dietrich, J.; Vasilakos, C.; Tzoraki, O. Evaluation of SWAT simulated soil moisture at catchment scale by field measurements and Landsat derived indices. Agric. Water Manag. 2017, 193, 55–70. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments. Smhi 1976, RHO 7, 134. [Google Scholar]
- Azimi, S.; Dariane, A.B.; Modanesi, S.; Bauer-Marschallinger, B.; Bindlish, R.; Wagner, W.; Massari, C. Assimilation of Sentinel 1 and SMAP—Based satellite soil moisture retrievals into SWAT hydrological model: The impact of satellite revisit time and product spatial resolution on flood simulations in small basins. J. Hydrol. 2020, 581, 124367. [Google Scholar] [CrossRef] [PubMed]
- Arias, R.; Rodríguez-Blanco, M.L.; Taboada-Castro, M.M.; Nunes, J.P.; Keizer, J.J.; Taboada-Castro, M.T. Water resources response to changes in temperature, rainfall and CO2 concentration: A first approach in NW Spain. Water 2014, 6, 3049–3067. [Google Scholar] [CrossRef]
- Shivhare, N.; Dikshit, P.K.S.; Dwivedi, S.B. A Comparison of SWAT Model Calibration Techniques for Hydrological Modeling in the Ganga River Watershed. Engineering 2018, 4, 643–652. [Google Scholar] [CrossRef]
- Rasoulzadeh, S.; Corresp, G.; Kharel, G.; Stoecker, A. Modeling the impacts of agricultural best management practices on runoff, sediment, and crop yield in an agriculture-pasture intensive watershed. PeerJ 2010, 7, e7093. [Google Scholar] [CrossRef] [PubMed]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watersheds using the SWAT model. Trans. Am. Soc. Agric. Eng. 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Rivas-Tabares, D.; Tarquis, A.M.; Willaarts, B.; De Miguel, Á. An accurate evaluation of water availability in sub-arid Mediterranean watersheds through SWAT: Cega-Eresma-Adaja. Agric. Water Manag. 2019, 212, 211–225. [Google Scholar] [CrossRef]
- Alibuyog, N.R.; Ella, V.B.; Reyes, M.R.; Srinivasan, R.; Heatwole, C.; Dillaha, T. Predicting the effects of land use change on runoff and sediment yield in manupali river subwatersheds using the swat model. Int. Agric. Eng. J. 2009, 18, 15. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).